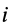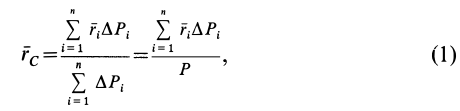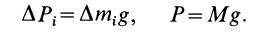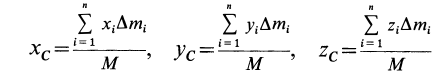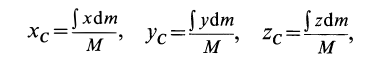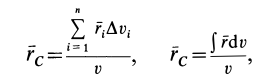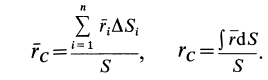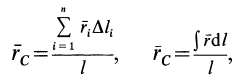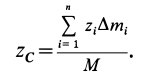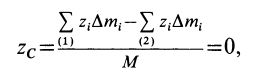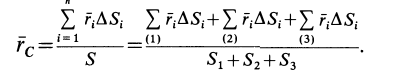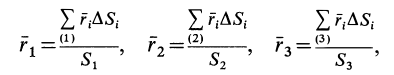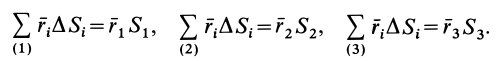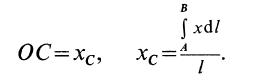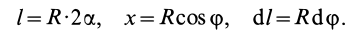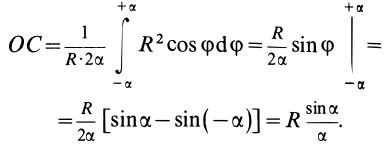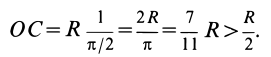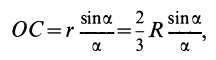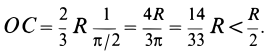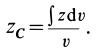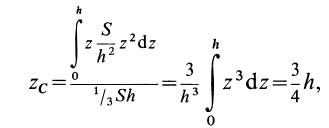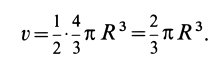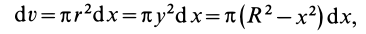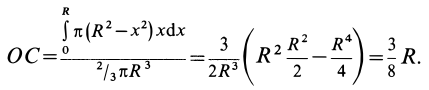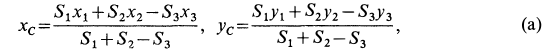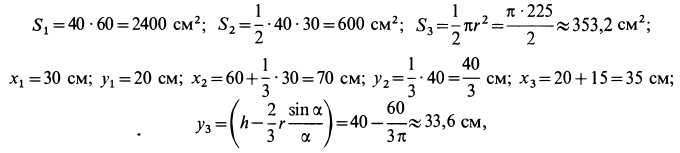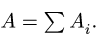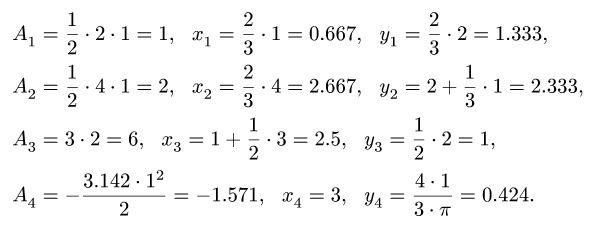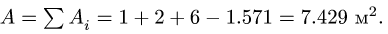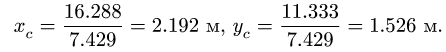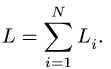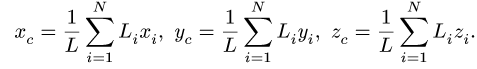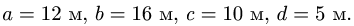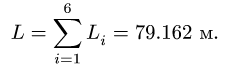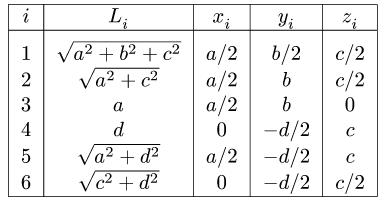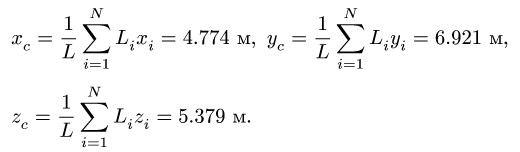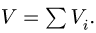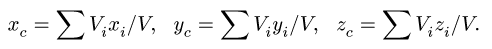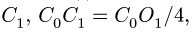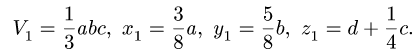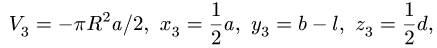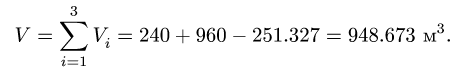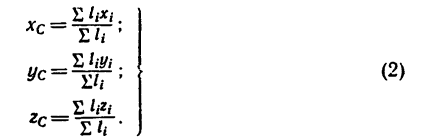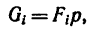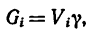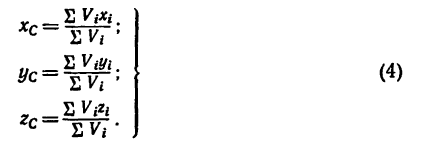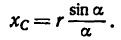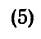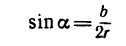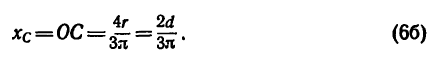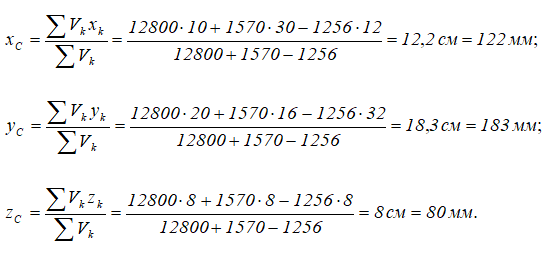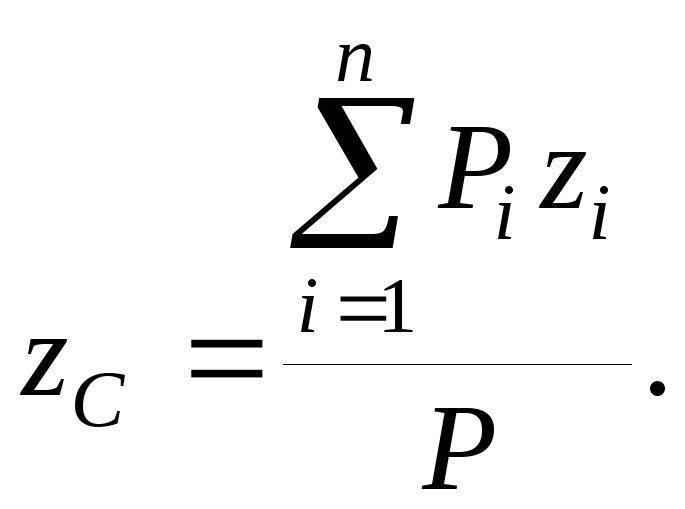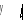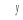Содержание:
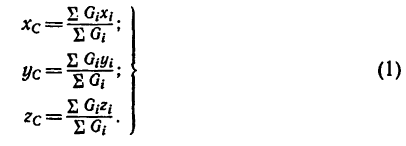
Центр тяжести:
При рассмотрении движения тел, особенно таких, как самолеты, ракеты, космические корабли, важное значение имеет понятие центра тяжести.
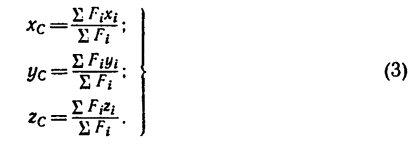
Определения и формулы для вычисления центров тяжести
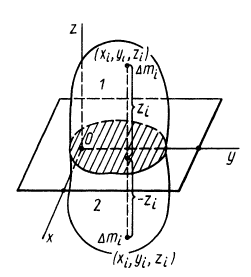
Для введения понятия центра тяжести разобьем мысленно рассматриваемое тело на достаточно большое число малых по сравнению с телом или элементарных его частей произвольной формы. Силу тяжести элементарной частицы тела с индексом
Радиус-вектор центра тяжести тела 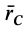
где 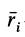

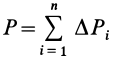

Рис. 88
Если в (1) перейти к пределу, увеличивая число элементарных частей 

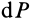
где 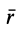
где 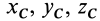
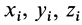
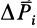
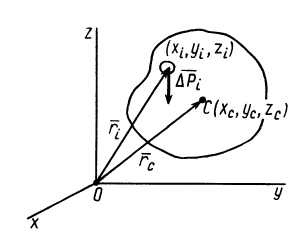
Используя понятие центра тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела и всего тела можно выразить через их массы 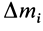
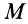

Подставляя эти значения сил тяжести в (1) и (1′) после сокращения на 
и соответственно
По формулам (2) и (2′) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор, которой вычисляется по формулам (2) или (2′). В проекциях на оси координат из (2) и (2′) получаем:
и
где 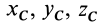
Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам
где 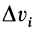


где 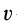


по которым определяют центр тяжести объема тела.
Если тело имеет форму поверхности, т. е. один из размеров мал по сравнению с двумя другими, как, например, у тонкого листа железа, то имеем
где 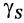
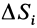
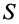
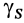
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам
где 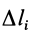
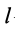
Методы определения центров тяжести (Центров масс)
Метод симметрии
При определении центров тяжести широко используется симметрия тел. Докажем, что для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии. Для доказательства выберем начало координат в плоскости симметрии тела и одну из осей координат, ось 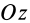
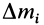
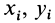
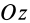
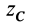
Разбивая сумму в числителе на две по симметричным частям тела, получаем, что
так как симметричные части тела 1 и 2 одинаковы.
Таким образом, центр масс расположен в плоскости симметрии и для его определения достаточно вычислить только две его координаты 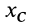
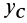
Аналогично доказывается, что для однородного тела, имеющего ось или центр симметрии, центр масс находится соответственно на оси симметрии или в центре симметрии.
Рис. 89
Метод разбиения на части (метод группировки)
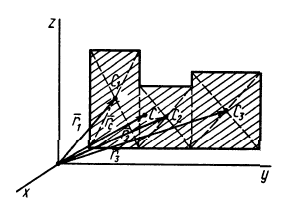
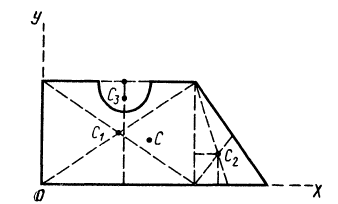
Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито. Покажем это на частном примере плоской фигуры, изображенной на рис. 90. Плоскую фигуру можно разбить на три части, центры тяжести которых 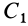
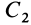
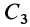
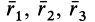
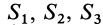
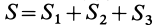
Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим
Радиусы-векторы центров тяжести частей тела выразятся в такой форме:
или
Используя эти формулы для радиуса-вектора всей фигуры, имеем
Полученная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.
Рис. 90
Метод отрицательных масс
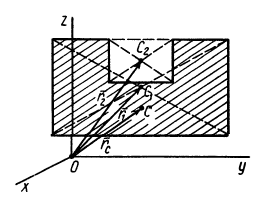
Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 91). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью 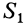
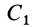
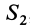
В отличие от обычного метода разбиения на части в формуле (4) массы и, следовательно, площади входят со знаком минус.
Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.
Рис. 91
Центры тяжести простейших тел
Для определения центров тяжести тел сложной формы методом разбиения на части или методом отрицательных масс необходимо уметь вычислять центры тяжести простейших тел, на которые разбивается тело сложной формы. Рассмотрим некоторые из тел, для определения центров тяжести которых известны простые способы их нахождения или вычисления по формулам.
Прямолинейный отрезок
Центр тяжести прямолинейного однородного отрезка располагается на его середине, а неоднородного— на самом отрезке и не может находиться вне отрезка.
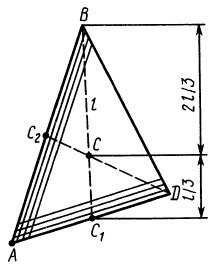
Площадь треугольника
Для определения центра тяжести площади треугольника разобьем его прямыми линиями, параллельными одной из его сторон 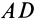

Затем разобьем треугольник на полоски прямыми линиями, параллельными другой стороне 
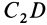

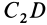
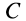

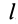
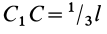
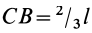
Рис. 92
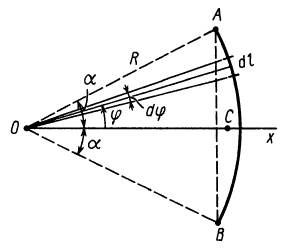
Дуга окружности
Дуга окружности 
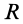
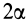
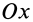

Рис. 93
В рассматриваемом случае
Подставляя эти значения в формулу для 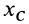
Таким образом,
Для полуокружности 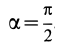
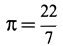
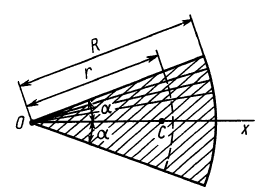
Площадь кругового сектора
Центр тяжести площади кругового сектора с радиусом 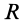
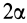
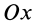
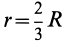
Рис. 94
Используя формулу для центра тяжести дуги окружности, получим
или
Для площади полукруга 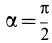
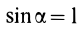
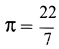
Объем пирамиды и конуса
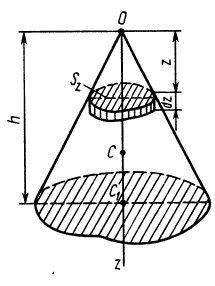
Определим положение центра тяжести объема конуса (рис. 95). Для простоты рассмотрим прямой конус, у которого высота является осью симметрии. Высотой конуса является отрезок, соединяющий его вершину 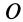
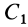
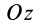
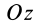
Разобьем конус плоскостями, перпендикулярными оси 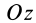
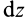
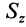
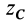
Отношения линейных размеров сечений к соответствующим размерам основания конуса пропорциональны их расстояниям до вершины конуса. Отношения площадей пропорциональны квадратам расстояний. Приняв 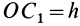
Учитывая, что
имеем
или
Таким образом, центр тяжести прямого конуса находится на расстоянии 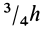
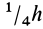
Рис. 95
Это справедливо для объема любого конуса и любой пирамиды, как прямых, так и наклонных, т. е. центр тяжести объема пирамиды или конуса находится на расстоянии 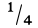
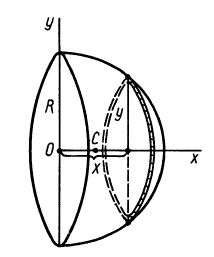
Объем полушара
Полушар имеет ось симметрии, которую примем за координатную ось 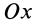
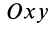
где 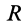
где 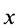
Объем элементарного диска
так как радиус диска 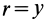
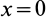
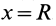
Таким образом, центр тяжести объема полушара находится от его центра на расстоянии
Это расстояние меньше половины радиуса полушара.
Рис. 96
Задача №1
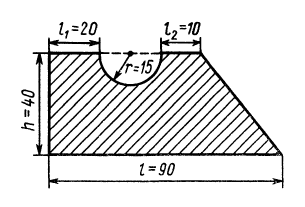
Определить координаты центра тяжести площади плоской фигуры, имеющей размеры, указанные на рис. 97.
Рис.97
Рис. 98
Решение. Присоединим к заданной фигуре дополнительно полукруг 3 и разобьем полученную фигуру на прямоугольник 1 и треугольник 2. Получили три фигуры, две из которых имеют положительные площади (прямоугольник 1 и треугольник 2) и одна — отрицательную (полукруг 3). В выбранной системе координат для координат центра тяжести заданной фигуры имеем
где 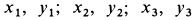
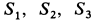
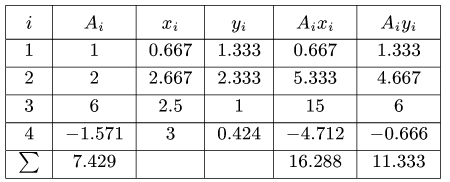
Вычислим площади и координаты центров тяжести отдельных фигур, учитывая рис. 98 Имеем:
так как 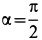
Подставляя полученные значения в (а), получим:
Центр тяжести плоской фигуры
постановка задачи. Найти площадь и координаты центра тяжести плоской фигуры.
План решения:
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
2. Выбираем систему координат. Вычисляем площади и координаты 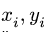
3. Находим общую площадь фигуры по формуле
4. Определяем координаты центра тяжести фигуры:
Задача №2
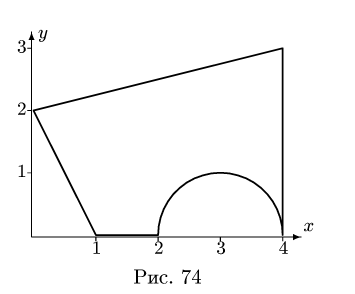
Найти площадь и координаты центра тяжести плоской фигуры. Криволинейный участок контура является половиной окружности с центром на оси Ох (рис. 74). Размеры на рисунке даны
Решение
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
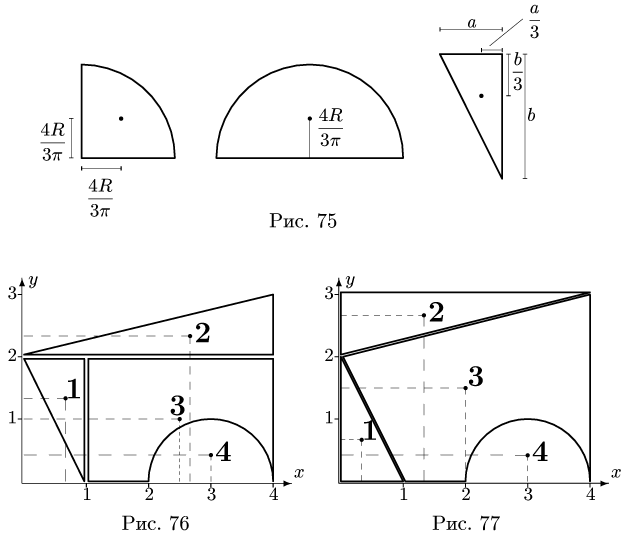
Центр тяжести прямоугольника находится в его геометрическом центре, положение центра тяжести других фигур, встречающихся в задачах, изображено на рис. 75
Представляем фигуру в виде двух треугольников 1,2, прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).
2. Вычисляем площадь (в 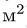
Площадь выреза берем со знаком минус.
3.Площадь фигуры
4. Находим координаты центра тяжести всей фигуры:
Вычисления удобно свести в таблицу:
Сначала заполняем столбцы 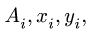
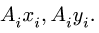
Замечание 1. Большинство задач на определение центра тяжести допускает несколько способов разбиения фигуры. Это можно использовать для проверки решения. Второй вариант разбиения фигуры в данном примере состоит из прямоугольника 3 с размерами 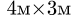
Замечание 2. Решение задачи в системе Maple V методом контурного интегрирования.
- Заказать решение задач по теоретической механике
Пространственная стержневая система
Постановка Задачи. Найти координаты центра тяжести пространственной фигуры, состоящей из N однородных стержней.
План решения:
1. Разбиваем фигуру на отдельные стержни.
2. Выбираем систему координат. Вычисляем длины и координаты 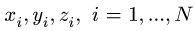
3. Находим суммарную длину стержней системы
4. Определяем координаты центра тяжести тела по формулам
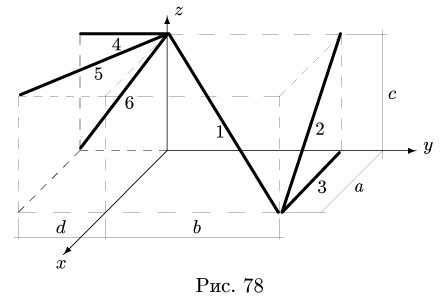
Задача №3
Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (рис. 78). Даны размеры:
Решение
1. Разбиваем фигуру на шесть стержней.
2. Выбираем систему координат (рис. 78). Вычисляем длины и координаты 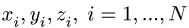
3. Находим суммарную длину стержней системы:
Промежуточные результаты удобно занести в таблицу:
4. Определяем координаты центра тяжести тела по формулам
Постановка задачи. Найти координаты центра тяжести однородного объемного тела.
План решения:
1. Разбиваем тело на простые части, положение центров тяжести которых известно.
2. Выбираем систему координат. Вычисляем объемы 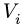
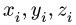
3. Находим общий объем тела по формуле
4. Определяем координаты центра тяжести тела:
Задача №4
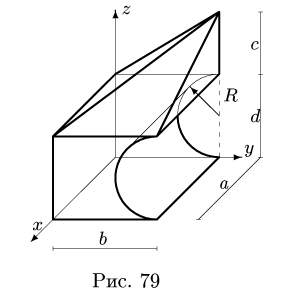
Найти координаты центра тяжести однородного объемного тела (рис.79);
Решение
1. Разбиваем тело на пирамиду 1, параллелепипед 2 и половину цилиндра 3 (рис. 80).
2. Выбираем систему координат. Вычисляем объемы 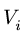
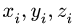
Центр тяжести параллелепипеда 2 совпадает с его геометрическим центром:
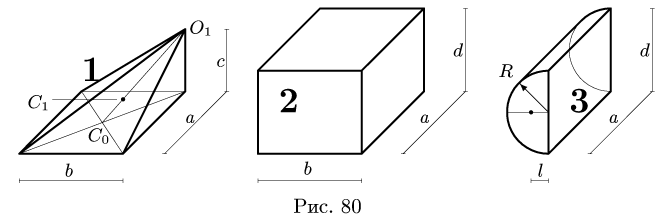
Объем половины цилиндра 3 берем со знаком минус:
где 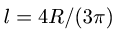
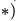
3. Находим общий объем тела:
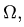
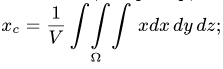
4. Определяем координаты центра тяжести тела:
Центр тяжести
Центр тяжести — точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
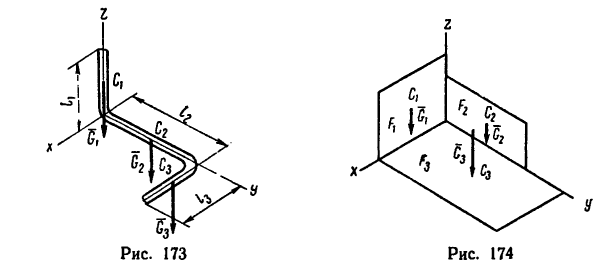
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес 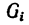
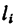
где d — постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо 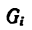
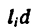
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174),
то вес каждой плоскости (поверхности) можно представить так:
где 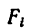
После подстановки этого значения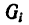
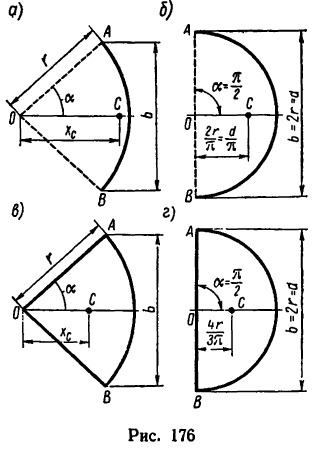
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
где 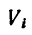
После подстановки значений 
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
Если известен радиус дуги г и центральный угол 2а, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 176, а) относительно центра дуги О определится формулой
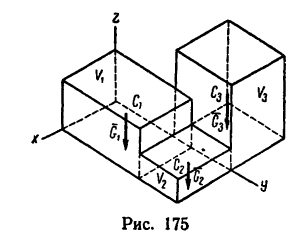
Если же задана хорда 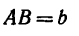
и тогда
В частном случае для полуокружности обе формулы примут вид (рис. 176, б)
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы
Если же задана хорда сектора, то
В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
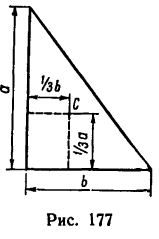
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
При решении задач на определение положения центра тяжести любого однородного тела, й составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
- выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
- разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
- определить или длины, или площади, или объемы составных частей;
- выбрать расположение осей координат;
- определить координаты центров тяжести составных частей;
- найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
- по найденным координатам указать на рисунке положение центра тяжести тела.
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Условия равновесия системы сил
- Плоская система сил
- Трение
- Пространственная система сил
ВИДЕО УРОК
Центр тяжести.
Центр тяжести имеется у каждого тела.
ПРИМЕР:
Возьмём длинную линейку и
подвесим её на нити, обвязав петлёй так, чтобы петлю можно было перемещать по
линейке. Меняя положение петли, добьёмся, чтобы линейка пришла в равновесие,
то есть, чтобы ни одна ни другая её часть не перевешивала. В этом случае говорят,
что линейка подвешена в центре тяжести. Равновесие линейки можно
добиться также, положив её на какую-нибудь опору, например карандаш или палец.
Если тело подвесить в центре тяжести, то оно будет находиться в равновесии.
Что такое центр тяжести и как его можно отыскать ?
Тяжестью, или весом, обладает не только тело в целом, но и каждая его
часть. Очевидно, что общий вес тела является суммой весов всех составляющих его
частиц. Вес каждой частицы тела приложен непосредственно к самой частице, вес
же всего тела приложен к точке, которая называется центром
тяжести тела.
Как же найти положение центра тяжести в различных телах ?
ОПЫТ:
Возьмём кусок картона, какой угодно формы, и
повесим его на гвоздь вместе с отвесом.
На кусок картона, находящийся в
подвешенном состоянии, действуют две силы: сила тяжести, приложенная в центре
тяжести картона, и сила, которая удерживает картон на гвозде. Так как картон
находится в покое, действующие на него силы взаимно уравновешиваются, то есть
они равны по величине и направлены по вертикали в противоположные стороны.
Отсюда можно сделать
заключение, что точки приложения сил – центр тяжести и точка подвеса – лежат на
одной вертикальной прямой, отмечаемой отвесом.
Проведём на куске картона вертикальную линию по
отвесу. Затем подвесим картон за другую точку и снова проведём по отвесу
вертикальную линию. Сколько бы мы ни проводили таким способом линий, на каждой
из них будет находиться центр тяжести, поэтому они все пересекутся в одной
точке – центре тяжести.
Как это проверить ?
Возьмём карандаш, и остриё его поместим под
найденный нами центр тяжести – картон окажется в равновесии.
Можно подвесить кусок
картона на нити, укрепив её вцентре тяжести, – картон тоже будет находиться в
равновесии.
Во время опыта мы несколько раз меняли положение куска картона, но центр
тяжести его оставался в одной и той же точке.
Следовательно, при любом положении тела центр тяжести его
находится в одной и той же точке.
Центр тяжести шара, например, лежит в его
геометрическом центре,
У параллелепипеда он находится в точке
пересечения диагоналей,
У цилиндра – на середине линии, соединяющей
центры его оснований.
Иногда центр тяжести может находиться и вне
тела, например, в кольце он лежит на пересечении диаметров. Это можно проверить
на опыте, подвесив кольцо за точку пересечения нитей, расположенных по
диаметрам кольца.
Кольцо будет находиться в равновесии.
Центр масс.
Изучая движение тел под действием различных сил, мы не обращали внимания на
то, что тела имеют размеры. Определяя ускорение тел, мы считали их
материальными точками.
Такое упрощение верно, если тело движется поступательно. Выясним, к какой
точке тела должна быть приложена сила для того, чтобы его ускоренное движение
было действительно поступательным.
ОПЫТ:
Возьмём широкую линейку. Прикрепим к её концу в
точке А нить и
потянем за эту нить с некоторой силой
в направлении,
перпендикулярном оси линейки.
Линейка при этом повернётся.
При таком повороте разные точки линейки проходят различные пути и движутся с
различными скоростями, то есть их движения неодинаковы и линйка движется не
поступательно.
Изменим теперь направление силы: будем тянуть
линейку вдоль её длинной стороны вправо.
Теперь линейка движется так,
что скорости и перемещения всех её точек одинаковы. Линейка совершает
поступательное движение.
Если сила
не уравновешена другими
силами, тело движется с ускорением. Нетрудно убедиться в том, что если нить
прикреплена к точке А, то существует только одна прямая, вдоль
которой должна быть направлена сила
чтобы она вызвала ускоренное
поступательное движение линейки. При действии силы вдоль любой другой прямой
линейка будет поворачиваться.
Можно изменить направление силы на
противоположное, прикрепив нить к точке В.
Движение линейки опять будет
поступательным. Значит, важно лишь положение прямой, вдоль которой действует
сила (линия действия силы).
Прикрепим теперь нить в какой-нибудь другой
точке линейки, например в точке С.
Будем опять менять направления
натяжения нити (на рисунке некоторые направления показаны
прямыми, исходящими из точки С). Снова убедимся в том, что линейка совершает
поступательное движение только в том случае, если сила направлена вдоль
некоторой определённой прямой. На рисунке это направление силы показано красной
линией. При всех других направлениях силы, приложенной к точке С,
линейка будет непременно поворачиваться.
Прикрепляя нить к другим точкам линейки, можно
убедиться в том, что в каждой точке есть одно направление силы, при котором
линейка движется поступательно, без поворотов. На рисунке
показано, как должны быть
направлены силы, при движении в разных точках линейки, чтобы она двигалась
поступательно. Опыт показывает, что прямые линии, вдоль которых действуют эти
силы, сходятся в одной точке О.
Подобные опыты с разными телами приводят нас к важному выводу о том, что
для каждого тела существует такая точка, в которой пересекаются направления
действия сил, сообщающих телу ускоренное поступательное движение. Эта точка
получила название центр масс. Всякая же сила, которая действует вдоль прямой
линии, не проходящей через центр масс, вызывает поворот тела.
Центром масс тела называют точку пересечения прямых,
вдоль которых должны быть направлены силы, чтобы тело двигалось поступательно.
В опыте с линейкой легко убедиться в том, что центр масс совпадает с точкой
пересечения диагоналей. Но это только в том случае, если линейка однородна (изготовлена
из одного материала), имеет правильную форму и одинаковую толщину. Если бы,
например, она была изготовлена наполовину из дерева, а наполовину из стали,
центр масс находился бы где-то в стальной половине, то есть ближе к той части,
которая имеет большую массу.
Положение центра масс определяется, как показывает опыт, тем, как
распределена масса по его объёму.
Центр масс может
оказаться и вне тела. Ясно, например, что поступательное движение однородного
обруча
Возможно только в том случае, если приложенные к нему силы направлены по
радиусам. Линии действия таких сил сходятся, конечно, в геометрическом центре
обруча. Там и находится его центр масс.
Если различные части обруча изготовлены из разных материалов, то центр масс
может и не совпадать с геометрическим центром обруча. Тогда его нужно искать
опытным путём. Существуют способы вычисления координат центра масс, но они
трудны, а иногда вычисление и невозможно.
Но зачем нужно знать положение центра масс ? дело в том, что если тело
движется поступательно под действием одной силы или нескольких сил, то это
значит, что эта сила или равнодействующая всех сил проходит через центр масс
тела.
Центр масс тела в этом случае движется так, как будто в
нём сосредоточена вся масса тела и к нему приложены все силы, действующие на
тело. Поэтому, когда мы видим, что тело движется с ускорением поступательно, то
это значит, что равнодействующая сил, приложенных к телу, проходит через его
центр масс, как будто в центре масс сосредоточена вся масса тела, а ускорение тела
– это ускорение центра масс.
Частным случаем
поступательного движения является движение тела под действием силы тяжести,
если, конечно, оно не было приведено во вращение до начала падения. Но сила
тяжести действует на все точки тела. И если под действием всех этих сил тело
движется поступательно, то это значит, что их равнодействующая при любом
положении тела проходит через его центр масс. Поэтому центр
масс часто называют центром тяжести тела.
В цилиндрический стакан
наливают воду. При каком положении уровня воды в стакане центр тяжести стакана
с водой занимает наинизшее положение ?
РЕШЕНИЕ:
Предположим, что центр тяжести стакана
расположен так, как показано на рисунке.
Это значит, что верхняя часть
стакана весит столько же, сколько нижняя. Начнём добавлять воду в стакан.
Сначала уровень воды в стакане мал – то есть мы увеличиваем вес нижней части
стакана. Если нижняя часть становится <<влиятельнее>>,
следовательно, центр тяжести системы смещается вниз. Он будет расположен где-то
между центром тяжести воды и центром тяжести пустого стакана. Возможное место
расположения центра тяжести системы показано рыжей линией.
Затем нальём воды ровно по уровень центра
тяжести пустого стакана.
Центр тяжести системы
расположен где-то между центром тяжести воды и центром тяжести пустого стакана,
потому что пока мы утяжелили только нижнюю часть стакана. И утяжелили её до
предела: если наливать воду дальше, то вес этой воды
уже будет увеличивать вес верхней половины стакана.
Снова прибавим воды. Теперь утяжеляется уже
верхняя часть, следовательно, центр тяжести смещается выше.
Наконец, видно, что
дальнейшее прибавление количества воды будет <<сдвигать>>центр
тяжести всё выше и выше.
Но по-прежнему центр тяжести
системы расположен между центром тяжести воды и стакана.
Центр тяжести стакана с водой занимает одно из
возможных наинизших положений, пока уровень воды не сравняется с центром
тяжести пустого стакана.
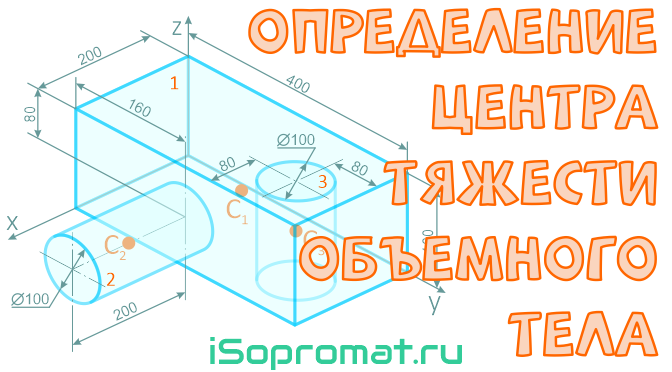
Пример решения задачи по определению координат положения центра тяжести объемного тела сложной формы по заданным размерам.
Задача
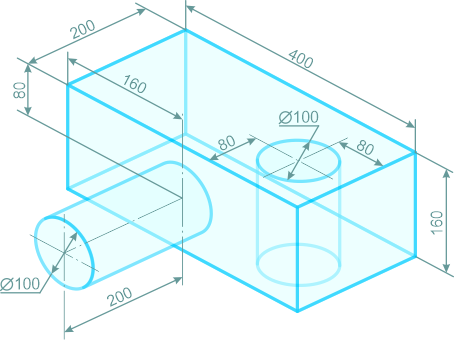
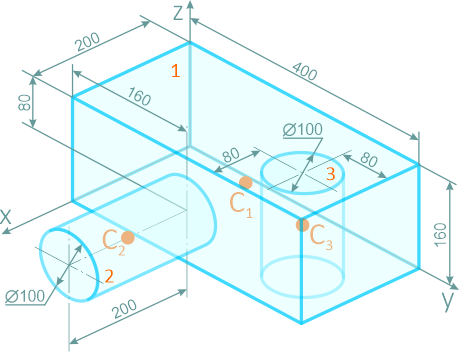
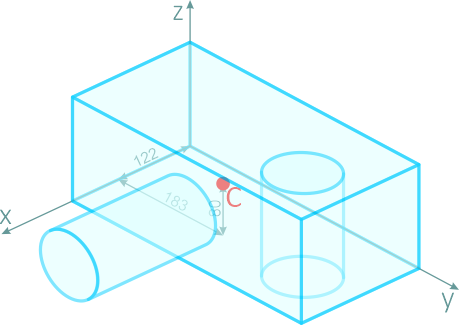
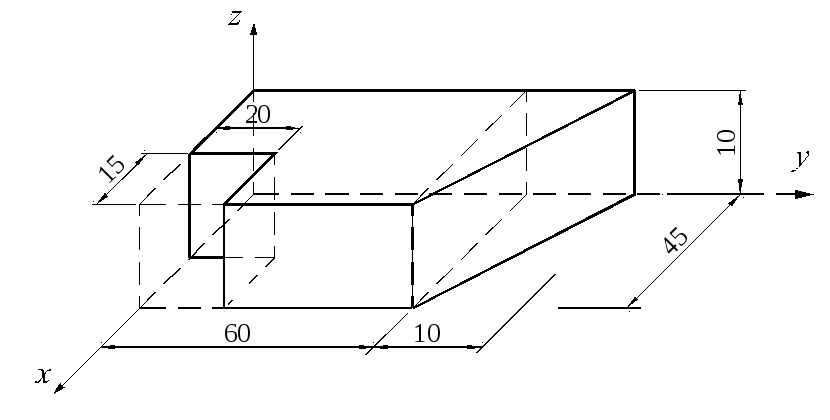
Определить положение центра тяжести тела, форма и размеры которого показаны на рисунке 2.7 (размеры указаны в мм)
Рисунок 2.7
Другие примеры решений >
Помощь с решением задач >
Решение
Тело состоит из прямоугольного параллелепипеда 1 с центром тяжести C1, цилиндра 2 (C2) и цилиндра 3 (C3), объем которого считаем отрицательным.
Найдем объемы составных частей и координаты xk , yk , zk их центров тяжести (в см):
V1= 12800 см3; C1 (10; 20; 8);
V2= 1570 см3; C2 (30; 16; 8);
V3= -1256 см3; C3 (12; 32; 8).
Определим координаты центра тяжести тела:
Таким образом, центр тяжести данного тела находится в точке C с координатами (122;183;80).
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Центром
тяжести твердого тела называется центр
параллельных сил тяжести
частиц данного тела.
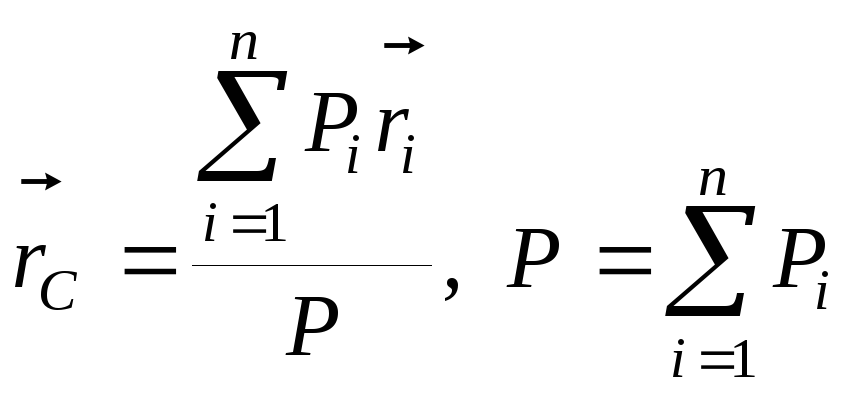
или
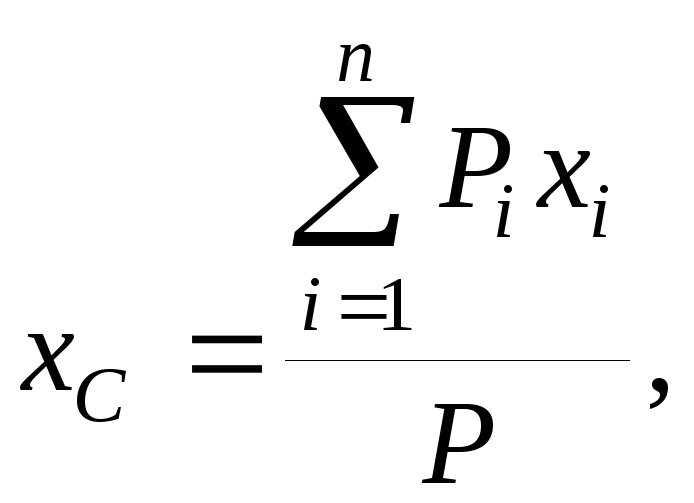
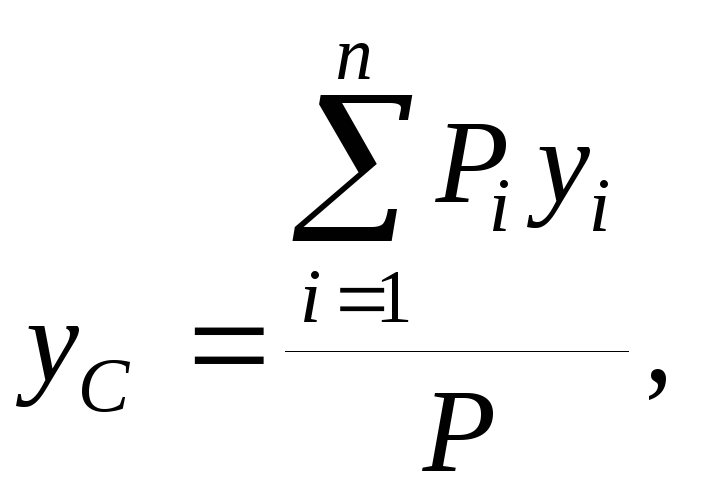
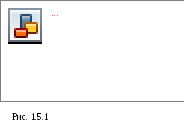
определения положения центра тяжести
однородных тел используют метод
симметрии, метод разбиения на тела
простой формы с известным положением
центров тяжести, а также метод отрицательных
масс (линий, площадей, объемов).
Пример
1.5.1. Определить координаты центра
тяжести плоской фермы (рис. 1.5.1),
составленной из однородных стержней с
одинаковым погонным весом.
Решение:
1.
Применим метод разбиения, то есть
представим ферму как совокупность семи
стержней.
2.
Найдем координаты центра тяжести фермы
по формулам:
;
,
где
,
,
– длина и координаты центра тяжести
стержня с номером .
Длины
и координаты центров тяжести стержней:
Тогда
,
Пример
1.5.2. Торцевая стена ангара (рис. 1.5.2)
имеет форму полукруга 1 радиуса
с прямоугольным дверным проемом 2
высотой
и шириной
Определить координаты центра тяжести
стены.
Решение:
1.
Применим методы симметрии и отрицательных
площадей, рассматривая полукруг 1
и прямоугольный вырез 2.
2.
Найдем координаты центра тяжести стены.
Поскольку
ось Оy является
осью симметрии, то координата
Координату
центра тяжести пластины определим по
формуле
где
,
,
,
– площади и координаты центров тяжести
фигур 1 и 2.
Площади
и координаты центров тяжести фигур:
Тогда
Задачи
1.5.1 – 1.5.4. Определить координаты
центров тяжести плоских ферм (рис.
1.5.3 – 1.5.6), составленных
из однородных стержней с одинаковым
погонным весом.
Ответы
к задачам 1.5.1 – 1.5.4:
|
Номер |
1.5.1 |
1.5.2 |
1.5.3 |
1.5.4 |
|
|
1,52 |
3,88 |
3,0 |
1,59 |
|
|
0,69 |
1,96 |
1,73 |
0,17 |
|
|
|
|
Рис. 1.5.3 |
Рис. 1.5.4 |
|
|
|
|
Рис. 1.5.5 |
Рис. 1.5.6 |
|
|
|
|
Рис. 1.5.7 |
Рис. 1.5.8 |
Задачи
1.5.5 – 1.5.7. Определить координаты
центров тяжести однородных составных
линий (рис. 1.5.7 – 1.5.9).
Ответы
к задачам 1.5.5 – 1.5.7:
|
Номер |
1.5.5 |
1.5.6 |
1.5.7 |
|
|
|
14 |
19 |
–4,76 |
|
|
|
9 |
14,16 |
3,31 |
|
|
|
|
|
Рис. 1.5.9 |
Рис. 1.5.10 |
|
|
|
|
Рис. 1.5.11 |
Рис. 1.5.12 |
Задача 1.5.8. Изогнутая
под прямым углом однородная проволока
подвешена на нити (рис. 1.5.10). Найти
соотношение между длинами участков AD
и AE, при котором участок
AE находится в
горизонтальном положении. АВ = 0,3 l1.
Ответ:
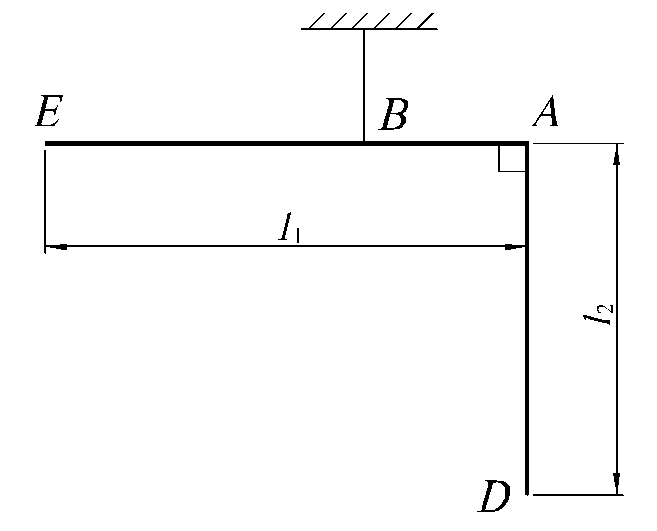
Задача
1.5.9. Определить координаты центра
тяжести однородной проволоки (рис.
1.5.11), если a = 3 м,
b = 2 м,
c = 1,5 м.
Ответ:
xC = 1,69
м, yC = 1,38
м, zC = 1,33
м.
Задача
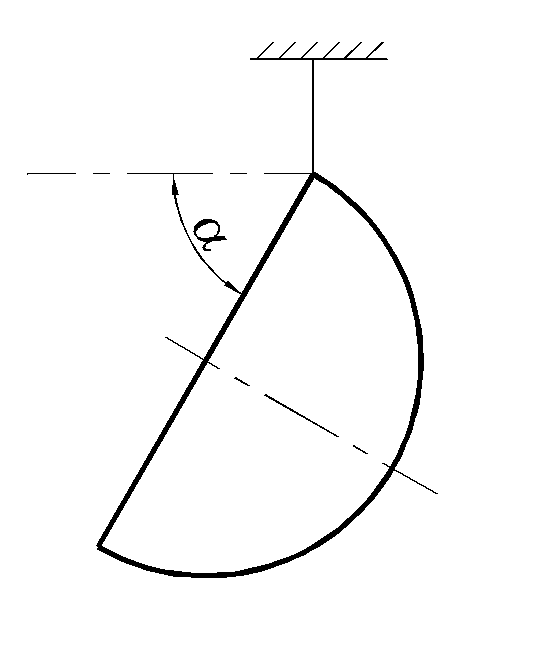
1.5.10. Однородный замкнутый контур,
ограничивающий полукруг, подвешен на
нити (рис. 1.5.12). Определить угол α
между горизонталью и диаметром
полуокружности.
Ответ:
α = 68,74º.
Задачи
1.5.11 – 1.5.14. Определить координаты
центров тяжести однородных плоских
фигур (рис. 1.5.13 – 1.5.16).
Ответы
к задачам 1.5.11 – 1.5.14:
|
Номер |
1.5.11 |
1.5.12 |
1.5.13 |
1.5.14 |
|
|
0 |
37,07 |
32,38 |
2,31 |
|
|
11,88 |
0 |
24,83 |
1,56 |
|
|
|
|
Рис. 1.5.13 |
Рис. 1.5.14 |
|
|
|
|
Рис. 1.5.15 |
Рис. 1.5.16 |
|
|
|
|
Рис. 1.5.17 |
Рис. 1.5.18 |
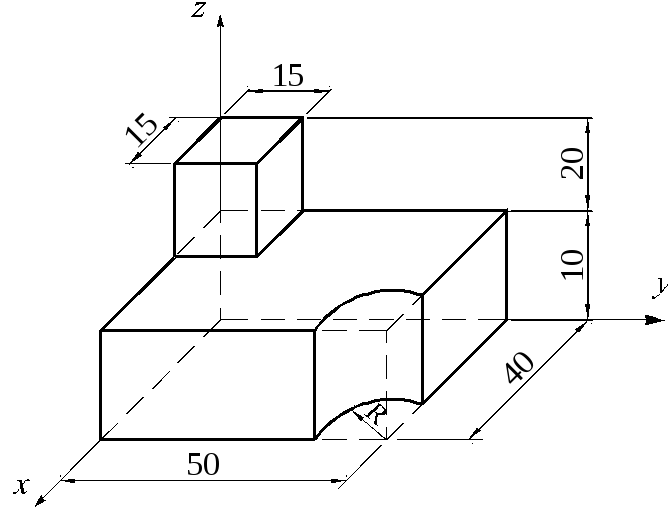
Задача 1.5.15. Подставка
для цапфы подшипника представляет собой
деталь, состоящую из опоры в виде
параллелепипеда и шпонки в форме куба
(рис. 1.5.17). Определить координаты центра
тяжести подставки. Размеры указаны в
миллиметрах.
Ответ:
Задача
1.5.16. Цапфа подшипника скольжения
представляет собой деталь, состоящую
из параллелепипеда и цилиндрической
опоры (рис. 1.5.18). Определить координаты
центра тяжести цапфы. Размеры
указаны в миллиметрах.
Ответ:
,
,
Задача
1.5.17. Однородное тело, сечение которого
изображено на рисунке 1.5.19,
состоит из полушара, цилиндрической
части и кругового конуса. Определить
координаты центра тяжести тела. Размеры
указаны в миллиметрах.
Ответ:
,
,
Задача
1.5.18. Ствол танковой пушки имеет
форму усеченного конуса длины
(рис. 1.5.20). Наружный диаметр ствола в
месте крепления к казенной части пушки
наружный диаметр в сечении, соответствующем
дульному срезу канала ствола,
Калибр пушки d =100 мм.
Определить координату
центра тяжести ствола.
Ответ:
Задача
1.5.19. Определить координаты центра
тяжести однородного тела, состоящего
из двух прямоугольных параллелепипедов
(рис. 1.5.21). В нижнем параллелепипеде
сделан вырез в форме четверти цилиндра
с радиусом основания R = 10 см.
Размеры на рисунке указаны в см.
Ответ:
xC = 17,1
см, yC = 20,99
см, zC = 7,84
см.
Задача
1.5.20. Определить координаты центра
тяжести однородного тела (рис. 1.5.22),
состоящего из треугольной призмы и
параллелепипеда с вырезом. Размеры на
рисунке указаны в см.
|
|
|
|
Рис. 1.5.19 |
Рис. 1.5.20 |
|
|
|
|
Рис. 1.5.21 |
Рис. 1.5.22 |
Ответ:
xC = 20,14
см, yC = 35,14
см, zC = 5
см.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение центра тяжести произвольного тела путем последовательного сложения сил, действующих на отдельные его части,— трудная задача; она облегчается только для тел сравнительно простой формы.
Пусть тело состоит только из двух грузов массы
и
, соединенных стрежнем (рис. 125). Если масса стержня мала по сравнению с массами
и
, то ею можно пренебречь. На каждую из масс действуют силы тяжести, равные соответственно
и
; обе они направлены вертикально вниз, т. е. параллельно друг другу. Как мы знаем, равнодействующая двух параллельных сил приложена в точке
, которая определяется из условия
или
.

Рис. 125. Определение центра тяжести тела, состоящего из двух грузов
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Если это тело подвесить в точке
, оно останется в равновесии.
Так как две равные массы имеют общий центр тяжести в точке, делящей пополам расстояние между этими массами, то сразу ясно, что, например, центр тяжести однородного стержня лежит в середине стержня (рис. 126).
Поскольку любой диаметр однородного круглого диска делит его на две совершенно одинаковые симметричные части (рис. 127), то центр тяжести должен лежать на каждом диаметре диска, т. е. в точке пересечения диаметров — в геометрическом центре диска
. Рассуждая сходным образом, можно найти, что центр тяжести однородного шара лежит в его геометрическом центре, центр тяжести однородного прямоугольного параллелепипеда лежит на пересечении его диагоналей и т. д. Центр тяжести обруча или кольца лежит в его центре. Последний пример показывает, что центр тяжести тела может лежать вне тела.

Рис. 126. Центр тяжести однородного стержня лежит в его середине
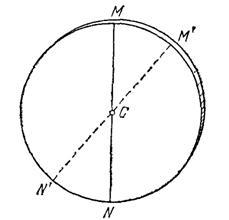
Рис. 127. Центр однородного диска лежит в его геометрическом центре
Если тело имеет неправильную форму или если оно неоднородно (например, в нем есть пустоты), то расчет положения центра тяжести часто затруднителен и это положение удобнее найти посредством опыта. Пусть, например, требуется найти центр тяжести куска фанеры. Подвесим его на нити (рис. 128). Очевидно, в положении равновесия центр тяжести тела
должен лежать на продолжении нити, иначе сила тяжести будет иметь момент относительно точки подвеса, который начал бы вращать тело. Поэтому, проведя на нашем куске фанеры прямую, представляющую продолжение нити, можем утверждать, что центр тяжести лежит на этой прямой.
Действительно, подвешивая тело в разных точках и проводя вертикальные прямые, мы убедимся, что все они пересекутся в одной точке. Эта точка и есть центр тяжести тела (так как он должен лежать одновременно на всех таких прямых). Подобным образом можно определить положение центра тяжести не только плоской фигуры, но и более сложного тела. Положение центра тяжести самолета определяют, вкатывая его колесами на платформы весов. Равнодействующая сил веса, приходящихся на каждое колесо, будет направлена по вертикали, и найти линию, по которой она действует, можно по закону сложения параллельных сил.

Рис. 128. Точка
пересечения вертикальных линий, проведенных через точки подвеса
и
есть центр тяжести тела
При изменении масс отдельных частей тела или при изменении формы тела положение центра тяжести меняется. Так, центр тяжести самолета перемещается при расходовании горючего из баков, при загрузке багажа и т. п. Для наглядного опыта, иллюстрирующего перемещение центра тяжести при изменении формы тела, удобно взять два одинаковых бруска, соединенных шарниром (рис. 129). В том случае, когда бруски образуют продолжение один другого, центр тяжести лежит на оси брусков. Если бруски согнуть в шарнире, то центр тяжести оказывается вне брусков, на биссектрисе угла, который они образуют. Если на один из брусков надеть дополнительный груз, то центр тяжести переместится в сторону этого груза.

Рис. 129. а) Центр тяжести соединенных шарниром брусков, расположенных на одной прямой, лежит на оси брусков, б) Центр тяжести согнутой системы брусков лежит вне брусков
81.1.
Где находится центр тяжести двух одинаковых тонких стержней, имеющих длину 12 см и скрепленных в виде буквы Т?
81.2.
Докажите, что центр тяжести однородной треугольной пластины лежит на пересечении медиан.
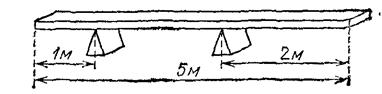
Рис. 130. К упражнению 81.3
81.3.
Однородная доска массы 60 кг лежит на двух опорах, как показано на рис. 130. Определите силы, действующие на опоры.