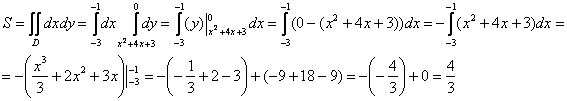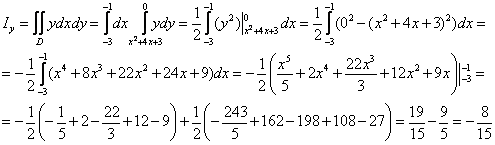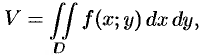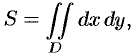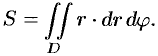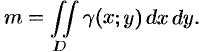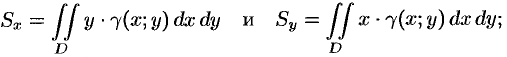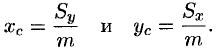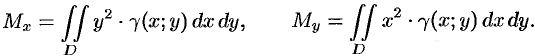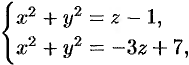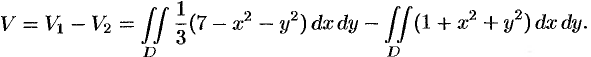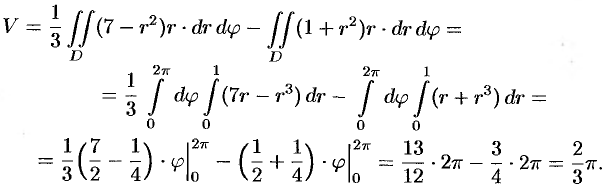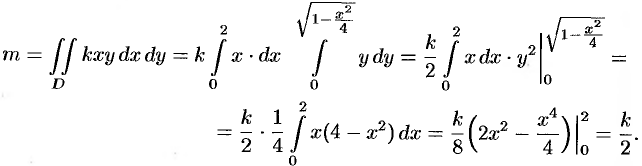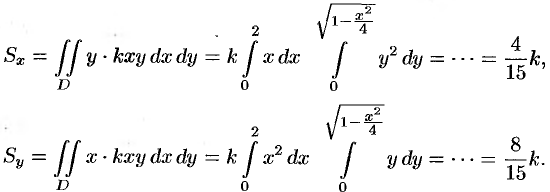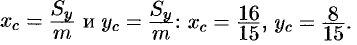Как найти центр тяжести фигуры ограниченной - Avtoru.top

(схема 42)

1. Вычисление объема тела

Пусть функция f(x;y) ≥ 0.
Рассмотрим тело, ограниченное
поверхностью z = f(x;y), плоскостью z=0 и цилиндрической поверхностью, образующие которой
параллельны оси 0z, а направляющей
служит граница области D. Как было показано
выше, согласно формуле (6.3) объем данного тела равен

(6.18)

Пример 6.9. Вычислить объём тела, ограниченного параболоидом z= x²+y²+1,
плоскостью x+y
–3=0 и координатными плоскостями.

Решение. Основанием тела служит треугольник ОАВ. Область D в данном
случае определяется неравенствами:

. Заметим, что тело, заданное по условию, аналогично телу,
изображенному на рисунке 6.6 (пример 6.5). Следовательно, используя формулу
(6.18), получим:

2.
Вычисление площади плоской фигуры

Если положить в формуле (6.18) f(x,y)=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой h=1. Объем такого цилиндра,

как
известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:

(6.19)

или, в полярных
координатах,

(6.20)

Пример
6.10. Вычислить площадь фигуры,
ограниченной прямой y=2x+1 и параболой y=x²+1.

Решение. Решая совместно систему

, находим точки пересечения этих линий: A(0;1)
и B(2;5).

Применяя формулу (6.19), будем иметь:

Пример 6.11. Вычислить площадь фигуры ограниченной лемнискатой

(рис. 6.9).

Решение. Переходим к полярной системе координат, полагая x=r cosφ и y=r sinφ; тогда получаем

. В силу симметрии кривой относительно координатных осей
можно вычислить сначала ту часть, которая расположена первой четверти. В этом случае угол φ будет изменяться от 0 до, а радиус r от 0 до . По формуле (6.20) получим:

3.
Вычисление массы плоской фигуры (пластины)

Масса плоской пластинки D с
переменной плотностью γ=γ(x,y) находится
по формуле

. (6.21)

4.
Определение статических моментов и координат центра тяжести плоской фигуры

Статические моменты фигуры D относительно осей 0x и 0y могут быть вычислены по формулам

; (6.22)

а
координаты центра масс фигуры – по формулам

. (6.23)

Статические моменты широко используются в
сопротивлении материалов и других технических науках.

5.
Определение моментов инерции плоской
фигуры

Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на
квадрат расстояния d точки до оси, т.е. . Моменты инерции плоской фигуры относительно 0x и 0y могут быть
вычислены по формулам:

(6.24)

Момент
инерции фигуры относительно начала координат – по формуле

. (6.25)

Пример
6.12. Найти массу, статические
моменты и координаты центра тяжести фигуры, лежащей в первой четверти,
ограниченной эллипсом и координатными осями.
Поверхностная плотность в каждой точке фигуры пропорциональна произведению
координат точки.

Решение. По
формуле (6.21) находим массу пластины. По условию, γ=γ(x,y)=k∙xy, где k –
коэффициент пропорциональности.Тогда

Находим
статические моменты пластинки по формулам (6.22):

Находим
координаты центра тяжести пластинки, используя формулы (6.23):

6. Поверхностный интеграл I рода

Обобщением двойного интеграла является поверхностный интеграл. Пусть в трехмерном пространстве Оxyz в точках некоторой поверхности площади S определена непрерывная функция u = f (x;y;z). Разобьем поверхность на конечное число n частей S_i, площади которых равны ∆S_i, а диаметры – d_i, . Выберем в каждой части S_i произвольную точку M_i(x_i;y_i;z_i)
и составим сумму произведений вида

. (6.26)

Она
называется интегральной суммой для функции f(x;y;z) по поверхности S. Если при интегральная
сумма (6.26) имеет предел, который не зависит ни от способа разбиения поверхности S, ни от выбора точек M_i(x_i;y_i;z_i), то он называется поверхностным интегралом I рода от
функции f(x;y;z) по поверхности S и обозначается . Следовательно,

. (6.27)

Теорема 6.3
(о существовании поверхностного интеграла). Если поверхность S гладкая (в каждой ее точке существует касательная
плоскость, которая непрерывно меняется с перемещением точки по поверхности), а
функция f(x;y;z) непрерывна на этой поверхности, то поверхностный
интеграл существует

Формула (6.28)

выражает интеграл по поверхности
S
через двойной интеграл по проекции S на плоскость x0y. Отметим, что если поверхность S задана
уравнением вида y=y(x;z) или x=x(y;z), то аналогично получим:

и (6.29)

, (6.30)

где
D₁ и D₂ –
проекции поверхности S на
координатные плоскости xОz и yОz
соответственно.

Пример 6.13. Вычислить , где S – часть цилиндрической поверхности , отсеченной плоскостями z = 0 и z = 3.

Решение. Из уравнения заданной
цилиндрической поверхности выразим и учтём, что
при x = 0 в плоскости xОy: . Так как частные производные равны , то согласно формуле (6.30),
имеем

Приведем некоторые примеры применения
поверхностного интеграла I рода.

6.1. Площадь
поверхности

Если поверхность S задана уравнением z = f(x;y), a ее проекция на
плоскость x0y есть область D, в которой z = f(x;y), z_x(x;y) и z_y(x;y) –
непрерывные функции, то ее площадь S
вычисляется по формуле:

. (6.31)

Пример 6.14. Вычислить площадь части плоскости x+y+z=4,
вырезаемой цилиндром x²+y² =4 (рис. 6.10).

Решение. Применим формулу (6.31). Область интегрирования D есть круг
радиуса r=2. Находим частные производные и заданной
функции z=4 – x – y:

. Тогда .

Чтобы вычислить этот интеграл, введём полярные
координаты. Область D определяется: . Следовательно,

Кроме того, поверхностный интеграл применяют для
вычисления массы, координат центра масс, моментов инерции материальных
поверхностей с известной поверхностной плотностью распределения массы γ=γ(x;y;z). Все эти величины
определяются одним и тем же способом:

– данную область разбивают на конечное число мелких частей;

– делают для каждой такой части предположения, упрощающие задачу;

– находят приближенное значение искомой величины;

– переходят к пределу при неограниченном измельчении разбиения
области.

Проиллюстрируем описанный способ на примере
определения массы материальной поверхности.

6.2. Масса
поверхности

Пусть плотность распределения массы материальной
поверхности есть γ=γ(x;y;z). Для нахождения
массы поверхности:

1. Разбиваем поверхность S на n частей S_i, , площадь которых обозначим ∆S_i.

2. Выберем произвольную точку M_i(x_i;y_i;z_i) в каждой области S_i. Предполагаем, что
в переделах области S_i
плотность постоянна и равна её

значению в
точке M_i.

3. Масса m_i области S_iмало отличается от
массы γ(x_i;y_i;z_i)∙∆S_i однородной области с постоянной полностью γ= γ(x_i;y_i;z_i).

4. Суммируя m_i
по всей области, получаем:.

5. За точное значение массы материальной поверхности S
принимается предел, к которому стремится полученное приближенное значение при
стремлении к нулю диаметров областей S_i, то есть

. (6.32)

6.3. Моменты
и центр тяжести поверхности. Статические
моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по
соответствующим формулам:

Пример 6.15.
Вычислить координаты центра тяжести
однородной поверхности параболоида z=x²+y², ограниченной плоскостью z=1.

Решение. Вершина заданного параболоида совпадает с началом
координат. Так как поверхность однородная (постоянная плотность массы), то,
основываясь на ее симметрии, можно сделать вывод, что центр тяжести расположен
на оси 0z. Тогда x_c=0, y_c=0
и по формуле (6.36) аппликата. Пересечем параболоид поверхностью z=1,
спроектируем линию пересечения на плоскость x0y – получим окружность x²+y²=1 в
качестве области D. Вычислим элемент поверхности параболоида z=x²+y² по
формуле (6.31), учитывая, что:

Аналогично, переходя к полярным координатам на
плоскости x0y, получим:

Таким образом,, то есть центр тяжести заданного параболоида, ограниченного плоскостью z=1, находится в точке (0;0;1) и совпадает с точкой
пересечения поверхности с плоскостью

Источник

1.6. Центр тяжести плоской фигуры

Это популярное физическое приложение двойного интеграла.

О центре тяжести плоской фигуры я рассказывал ещё в курсе аналитической геометрии, и сейчас мы на пальцах

повторим, что это такое. Вырежьте из тонкого куска картона произвольную фигуру, какую захотИте. …Есть? Поднимите указательный

палец строго вверх J. Теперь положите картонку на палец и добейтесь того, чтобы она не сваливалась. Эта точка картонной

фигуры – и есть её центр тяжести.

В студенческой практике для решения, как правило, предлагается простейший случай – плоская ограниченная однородная фигура,

то есть фигура постоянной физической плотности – стеклянная, деревянная, оловянная ~~чугунные игрушки, тяжёлое детство~~ и т.д.

Далее по умолчанию речь пойдёт только о таких фигурах.

Первое правило и простейший пример: если у плоской фигуры есть центр симметрии, то он является

центром тяжести данной фигуры. Например, центр круглой или квадратной однородной пластины. Логично и по-житейски

понятно – масса такой фигуры «справедливо распределена во все стороны» относительно центра.

Однако в суровых реалиях вам вряд ли подкинут такую халяву, и поэтому на помощь придётся привлечь серьёзный математический

аппарат:

Координаты центра тяжести плоской однородной ограниченной фигуры рассчитываются по

следующим формулам:

, их также можно

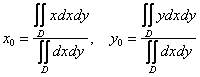
записать так:

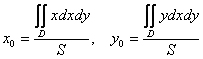
, где – площадь фигуры (области

И наиболее компактная запись:
, где

Интеграл будем

условно называть «иксовым» интегралом, а интеграл – «игрековым» интегралом.

Примечание-справка: для плоской ограниченной неоднородной фигуры, плотность которой задана функцией , формулы более

сложные:
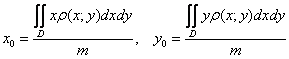
, где – масса фигуры;
в случае однородной плотности фигуры эти формулы упрощаются до вышеприведённых формул.

На формулах, собственно, вся новизна и заканчивается, остальное – это ваше умение решать двойные интегралы, кстати, сейчас предоставляется прекрасная возможность

потренироваться и усовершенствовать свою технику. А совершенству, как известно, нет предела: …или есть?

Пример 29

Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями .

Решение: линии здесь элементарны: задаёт ось абсцисс, а уравнение – банальную параболу. Я выполню сразу весь чертёж с

готовой точкой центра тяжести фигуры:

Правило второе: если у фигуры существует ось симметрии, то центр тяжести данной фигуры

обязательно лежит на этой оси.

В нашем случае фигура симметрична относительно прямой (проведена пунктиром), то есть фактически мы уже знаем

«иксовую» координату точки «эм».

Также обратите внимание, что по вертикали центр тяжести смещён ближе к оси абсцисс, поскольку там фигура более массивна.

Полезная рекомендация: ещё до вычислений постарайтесь определить примерное расположение центра тяжести «на глазок» – это

поможет проверить полученные значения на предмет явных ошибок.

…Да, возможно, ещё не все до конца поняли, что такое центр тяжести: пожалуйста, поднимите вверх указательный палец и

мысленно поставьте на него заштрихованную «подошву» точкой . Теоретически фигура не должна упасть.

Координаты центра тяжести фигуры найдём по формулам , где .
Порядок обхода области (фигуры) здесь очевиден:

Внимание! Определяемся с наиболее выгодным порядком обхода один раз – и используем его для всех двойных интегралов! А их тут будет три штуки:

1) Сначала вычислим площадь фигуры. Ввиду относительной простоты интеграла решение можно оформить «одной строкой», главное,

не запутаться в вычислениях:

Смотрим на чертёж и прикидываем по клеточкам площадь. Получилось около дела.

2) Иксовая координата центра тяжести уже найдена «графическим методом», поэтому можно

сослаться на симметрию и перейти к следующему пункту. Но делать так-таки не советую – велика вероятность, что вас заставят

решать по формуле.
В этой связи координату лучше рассчитать формально. Вычислим «иксовый» интеграл:

Таким образом: 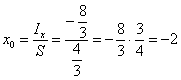, что и требовалось получить.
3) Найдём ординату центра тяжести. Вычислим «игрековый» интеграл, внутри

используем правило умножения

многочленов:

В результате: 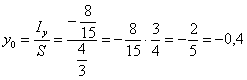, что

очень и очень похоже на правду. На заключительном этапе отмечаем на чертеже точку и записываем
Ответ:
Заметьте, что по условию не требовалось ничего чертить, но в большинстве задач мы волей-неволей вынуждены изобразить фигуру.

Зато есть безусловный плюс – визуальная и довольно эффективная проверка результата.

Следующие два примера для самостоятельного решения.

Попроще:

Пример 30

Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями

И посложнее:

Пример 31

Найти центр тяжести однородной плоской фигуры, ограниченной линиями . Фигуру и её центр тяжести изобразить на чертеже.

И это как раз тот случай, когда вроде бы выполнены предпосылки для перехода к полярной

системе координат, но в результате получаются настолько харкордные интегралы, что уж лучше решать в декартовых

координатах.

Примерные образцы решений в конце книги.

Но, разумеется, есть задачи, где решение в полярных координатах оправдано. Желающие могут в качестве тренировки найти

центр тяжести фигуры из Примера 23, тем более, там уже найдена площадь. Верный ответ . С подробным решением этого, а также более сложных

примеров можно ознакомиться в соответствующей статье

сайта.

Ну а сейчас пришло время немного отдохнуть и повысить ставки:

2. Тройные инетгралы

1.5. Как вычислить двойной интеграл в полярных координатах?

| Оглавление |

Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Приложения двойного интеграла

Приведем некоторые примеры применения двойного интеграла.

Объем тела

Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле

где 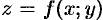— уравнение поверхности, ограничивающей тело сверху.

Площадь плоской фигуры

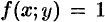
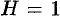
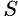
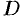
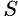
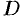
Если положить в формуле (53.4) , то цилиндрическое тело «превратится» в прямой цилиндр с высотой . Объем такого цилиндра, как известно, численно равен площади основания . Получаем формулу для вычисления площади области :

или, в полярных координатах,

Масса плоской фигуры

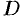
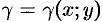
Как уже показано (п. 53.2), масса плоской пластинки с переменной плотностью находится по формуле

Статические моменты и координаты центра тяжести плоской фигуры

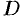
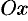
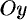
Статические моменты фигуры относительно осей и (см. п. 41.6) могут быть вычислены по формулам

а координаты центра масс фигуры — по формулам

Моменты инерции плоской фигуры

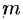
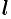
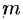
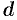
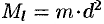
Моментом инерции материальной точки массы относительно оси называется произведение массы на квадрат расстояния точки до оси, т. е. . Моменты инерции плоской фигуры относительно осей и могут быть вычислены по формулам:

Момент инерции фигуры относительно начала координат — по формуле .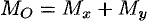

Замечание. Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).

Пример №53.3.

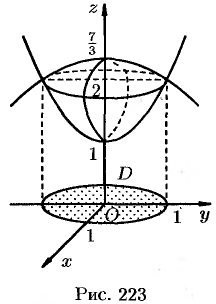
Найти объем тела, ограниченного поверхностями 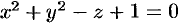и .

Решение:

Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему

находим уравнение линии их пересечения: .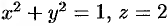

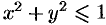
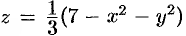
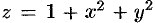
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг ) и ограниченных сверху соответственно поверхностями и . Используя формулу (53.4), имеем

Переходя к полярным координатам, находим:

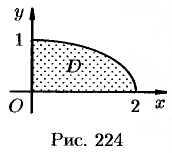
Пример №53.4.

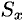
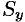
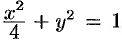
Найти массу, статические моменты и и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом и координатными осями (см. рис. 224). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.

Решение:

По формуле (53.6) находим массу пластинки. По условию, 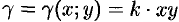, где — коэффициент пропорциональности.

Находим статические моменты пластинки:

Находим координаты центра тяжести пластинки, используя формулы

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Источник

Статические моменты и координаты центра тяжести

Вычисление статических моментов и координат центра тяжести кривой

а) Пусть материальная точка массы отстоит от оси ell на расстоянии . Статическим моментом этой точки относительно оси ell называют число . Статическим моментом системы материальных точек A_1,A_2,ldots,A_n , расположенных по одну сторону от оси ell , массы которых равны m_1,m_2,ldots,m_n , а расстояния от оси ell равны d_1,d_2,ldots,d_n называют число

$S_{ell}= sumlimits_{k=1}^{n}m_kd_k,.$

Если же эти точки расположены по разные стороны от оси, то для точек, находящихся по одну сторону оси, расстояния берутся положительными, а для точек по другую сторону от оси — отрицательными.

Поэтому если точки A_1,A_2,ldots,A_n расположены на координатной плоскости,

A_k=A_k(x_k;y_k) , то $S_x=sumlimits_{k=1}^{n}m_ky_k,,~~ S_y=sumlimits_{k=1}^{n}m_kx_k,,$

где S_x — статический момент относительно оси и S_y — относительно оси .

б) Рассмотрим теперь случай, когда масса равномерно распределена по некоторой кривой Gamma или по некоторой области lambda . Будем считать, что плотность распределения равна единице. Тогда масса дуги численно равна ее длине, а масса области — ее площади.

Начнем со случая кривой линии Gamma , задаваемой уравнением y=f(x),~a leqslant x leqslant b , причем предположим, что функция f(x) непрерывна и неотрицательна.

Как обычно, разобьем отрезок [a;b] на части точками a=x_0<x_1< ldots<x_n=b и обозначим через m_k и M_k наименьшее и наибольшее значения функции f(x) на отрезке $[x_k;x_{k+1}]$ , Этому разбиению соответствует разбиение дуги Gamma на части $gamma_0,ldots, gamma_{n-1}$ (рис. 60). Из физических соображений ясно, что статический момент S_k части gamma_k относительно оси абсцисс заключен между m_kell_k и , где ell_k —длина этой части, ell_k=ell(gamma_k) (напомним, что мы положили линейную плотность дуги равной единице). Таким образом,

Разбиение отрезка на части точками

m_kcdotell_k leqslant S_k leqslant M_kcdotell_k . Поэтому $sumlimits_{k=0}^{n-1} m_kell_k leqslant S_x leqslant sumlimits_{k=0}^{n-1}M_kell_k$ , то есть

$sumlimits_{k=0}^{n-1}m_k intlimits_{x_k}^{x_{k+1}} sqrt{1+(y')^2},dx leqslant S_x leqslant sumlimits_{k=0}^{n-1}M_k intlimits_{x_k}^{x_{k+1}} sqrt{1+(y')^2},dx,.$

Так как на отрезке $[x_k;x_{k+1}]$ выполняется неравенство

$m_kcdot sqrt{1+(y')^2} leqslant ycdot sqrt{1+(y')^2} leqslant M_kcdot sqrt{1+(y')^2},,$

то в тех же границах, что и S_x , заключен интеграл $intlimits_{a}^{b} ysqrt{1+(y')^2},dx$ . Значит,

$S_x= intlimits_{a}^{b}ysqrt{1+(y')^2},dx,.$

(1)

Этот интеграл обозначают также следующим образом: $intlimits_{Gamma}y,dell$ или $intlimits_{0}^{ell}y,dell$ .

Физики обычно заменяют проведенное рассуждение более коротким. Они берут «бесконечно малый участок дуги» dell . Его статический момент равен y,dell . А статический момент всей дуги равен сумме элементарных статических моментов, т. е. $intlimits_{a}^{b} y,dell$ . Преимуществом этого вывода является его наглядность. Однако в нем не определено, что такое «бесконечно малый участок дуги», или как еще говорят, «элемент дуги». При уточнении этого понятия мы вновь приходим к более длинному выводу, изложенному ранее. В дальнейшем для краткости изложения мы будем использовать принятый в физике метод рассуждений. С его помощью сразу выводим, что

$S_y=intlimits_{a}^{b}xsqrt{1+(y')^2},dx= intlimits_{0}^{ell}x,dell,.$

(2)

Как формула (1), так и формула (2) верны и в случае, когда кривая Gamma пересекает оси координат.

в) Введем понятие центра тяжести.

Определение. Центром тяжести тела называется такая точка , что если в ней сосредоточить всю его массу, то статический момент этой точки относительно любой оси будет равен статическому моменту всего тела относительно той же оси.

Обозначим через и eta расстояния центра тяжести кривой от осей ординат и абсцисс.

Тогда, пользуясь определением центра тяжести кривой, получим:

$S_x= ellcdoteta= intlimits_{0}^{ell}y,dell,;qquad S_y=ellcdotxi= intlimits_{0}^{ell}x,dell,.$

Разрешая полученные равенства относительно и eta , найдем координаты центра тяжести плоской кривой Gamma:

$xi=frac{1}{ell} intlimits_{0}^{ell} x,dell,;qquad eta=frac{1}{ell} intlimits_{0}^{ell}y,dell,.$

Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.

Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.

Пример 1. Найти статический момент полуокружности относительно диаметра.

Решение. Выберем систему координат так, чтобы центр окружности совпал с началом координат, а диаметр, относительно которого мы ищем статический момент, совпал с осью . Тогда статический момент полуокружности относительно диаметра выразится формулой

$S_x=intlimits_{0}^{ell} y,dell$ , где $dell=sqrt{1+(y')^2},dx$ — дифференциал дуги кривой y=f(x) .

В выбранной системе координат уравнение полуокружности запишется так: $y=sqrt{R^2-x^2}$ . Тогда

$y'=-frac{x}{sqrt{R^2-x^2}},~~1+(y')^2= frac{R^2}{R^2-x^2}$ и потому $dell=frac{R,dx}{sqrt{R^2-x^2}}$ .

Следовательно,

$S_x=intlimits_{-R}^{R}! sqrt{R^2-x^2}cdot frac{R,dx}{sqrt{R^2-x^2}}= 2R intlimits_{0}^{R}dx= 2R^2.$

Пример 2. Найдем центр тяжести четверти окружности x^2+y^2=4 , расположенной в первом квадранте.

Решение. Данная кривая расположена симметрично относительна биссектрисы первого координатного угла, следовательно, центр тяжести этой кривой лежит на биссектрисе, а потому xi=eta . Достаточно найти только $xi=frac{1}{ell} intlimits_{0}^{ell} x,dell$ .

Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:

$begin{cases}x=2cos{t},,\ y=2sin{t},,end{cases} 0 leqslant t leqslant frac{pi}{2},.$

Отсюда находим, что $x'_t=-2sin{t},~ y'_t=2cos{t}$ и

$dell= sqrt{(x'_t)^2+(y'_t)^2},dt= sqrt{4sin^2t+4cos^2t},dt= 2,dt,.$

Поскольку длина ell четверти данной окружности равна $frac{1}{4}cdot 2picdot2=pi$ , то

$xi=frac{1}{pi} intlimits_{0}^{2pi} 2cos{t}cdot2,dt= left.{frac{4}{pi} sin{t}}right|_{0}^{pi/2}= frac{4}{pi},.$

Вычисление статических моментов и координат центров тяжести плоских фигур

Найдем статический момент прямоугольника со сторонами и ell относительно стороны . Разобьем этот прямоугольник на элементарные прямоугольники, имеющие стороны и (рис. 61). Масса элементарного прямоугольника равна его площади k,dy (напомним, что по предположению плотность распределения массы равна единице). Поэтому элементарный статический момент равен ky,dy , а статический момент всего прямоугольника равен

Разбиение прямоугольника на элементарные прямоугольники

$intlimits_{0}^{ell} ky,dy= left.{frac{k}{2},y^2}right|_{0}^{ell}= frac{kell^2}{2},.$

(1)

Теперь уже легко найти статический момент криволинейной трапеции, ограниченной сверху кривой y=f(x) , где f(x) — непрерывная и неотрицательная функция на отрезке [a;b] , снизу осью абсцисс, а с боков прямыми x=a,~ x=b .

Разобьем криволинейную трапецию на элементарные прямоугольники, основание каждого из которых равно и высота . Статический момент такого прямоугольника относительно оси абсцисс по формуле (1) равен $frac{y^2}{2},dx$ , а потому статический момент всей криволинейной трапеции равен $frac{1}{2}intlimits_{a}^{b} y^2,dx$ . В случае, когда не выполняется предположение о неотрицательности функции y=f(x) , эту формулу надо заменить такой:

$S_x=frac{1}{2} intlimits_{a}^{b} y|y|,dx$

(части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в S_x ).

Поскольку по предположению плотность равна единице, то масса криволинейной трапеции равна ее площади, т. е. интегралу $intlimits_{a}^{b} |y|,dx$ , а потому ордината центра тяжести этой трапеции выражается формулой

$eta=frac{intlimits_{a}^{b} y|y|,dx}{2 intlimits_{a}^{b} |y|,dx},.$

Нетрудно найти и статический момент криволинейной трапеции относительно оси ординат. Для этого достаточно заметить, что расстояние элементарного прямоугольника от этой оси равно . Поэтому его статический момент равен x|y|,dx , а статический момент всей трапеции выражается формулой

$S_y=intlimits_{a}^{b} x|y|,dx$ . Следовательно, абсцисса центра тяжести выражается так: $xi=frac{intlimits_{a}^{b} x|y|,dx}{intlimits_{a}^{b} |y|,dx}$ .

Пример 3. Найти статический момент (относительно оси ) фигуры, ограниченной осью абсцисс и одной аркой циклоиды:

$begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}),end{cases} 0leqslant tleqslant2pi,.$

Решение. Так как параметр одной арки циклоиды изменяется от до 2pi , то

$begin{aligned}S_x&= frac{1}{2} intlimits_{0}^{2pi} a^2(1-cos{t})^2a(1-cos{t}),dt= frac{a^3}{2} intlimits_{0}^{2pi} (1-cos{t})^3,dt=\ &= left.{frac{a^3}{2}! left[t-3sin{t}+ frac{3}{2}! left(t+frac{1}{2} sin2tright)- left(sin{t}-frac{1}{3} sin^3tright)right] }right|_{0}^{2pi}=\ & =frac{a^3}{2}! left(2pi+frac{3}{2}cdot 2piright) = frac{5}{2},pi a^3.end{aligned}$

Пример 4. Найти центр тяжести фигуры, ограниченной осью и одной полуволной синусоиды y=sin{x} .

Решение. Так как фигура под полуволной синусоиды расположена симметрично относительно прямой $x=frac{pi}{2}$ , то центр тяжести лежит на этой прямой и, следовательно, $xi=frac{pi}{2}$ . Ордината eta центра тяжести находится по формуле $eta=frac{1}{2S} intlimits_{0}^{pi} y^2,dx$ .

Так как $S=intlimits_{0}^{pi} sin{x},dx= Bigl.{-cos{x}}Bigr|_{0}^{pi}=2$ , то $eta=frac{1}{4} intlimits_{0}^{pi}sin^2x,dx = frac{pi}{8}$ .

Итак, центр тяжести данной фигуры находится в точке $left(frac{pi}{2}; frac{pi}{8}right)$ .

Пример 5. Найти центр тяжести фигуры, ограниченной осью абсцисс и одной аркой циклоиды $begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}).end{cases}$ .

Решение. Данная фигура расположена симметрично относительно прямой x=pi a , следовательно, центр тяжести ее находится на этой прямой, и потому xi=pi a . Найдем eta по формуле $eta=frac{1}{2S} intlimits_{a}^{b} y^2,dx$ .

Площадь данной фигуры была вычислена раньше, она равна 3pi a^2 . Следовательно,

$eta=frac{1}{6pi a^2} intlimits_{0}^{2pi} a^3(1-cos{t})^3,dt= frac{5}{6},a,.$

Центр тяжести данной фигуры находится в точке $left(pi a; frac{5}{6},aright)$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Вычисление центра тяжести плоской ограниченной фигуры с помощью двойного интеграла

Махсуд Тулкин угли Усмонов maqsudu32@gmail .com Ташкентский университет информационных технологий

Каршинский филиал

Аннотация: Данная статья посвящена наиболее распространённому на практике приложению двойного интеграла — вычислению центра тяжести плоской ограниченной фигуры. Если у плоской фигуры есть центр симметрии, то он является центром тяжести данной фигуры. Например, центр круглой однородной пластины.

Ключевые слова: центр тяжести плоской ограниченной фигуры, двойной интеграл.

Calculating the center of gravity of a planar bounded figure

using a double integral

Mahsud Tulgin oglu Usmonov maqsudu32@gmail .com Tashkent University of Information Technologies

Karshi branch

Abstract: This article is devoted to the most common application of the double integral in practice — the calculation of the center of gravity of a plane bounded figure. If a plane figure has a center of symmetry, then it is the center of gravity of this figure. For example, the center of a round uniform plate.

Keywords: center of gravity of a plane bounded figure, double integral.

Координаты 7l° ‘ -У|:’ центра тяжести № плоской однородной ограниченной фигуры ^рассчитываются по следующим формулам:

|| xdxdy |ydxdy

х = JL_ у = JL_

|| dxdy || dxdy

D D , или:

|J xdxdy JJ’ ydxdy

У о =

3 , где ^ — площадь области £ (фигуры); или совсем

коротко:

= i yi} = i S = \dxdy, к = Ц xdxdy, /v = ¡¡ydxdy

, где

Интеграл ^ будем условно называть «иксовым» интегралом, а интеграл ^ — «игрековым» интегралом.

Примечание-справка: для плоской ограниченной неоднородной фигуры, плотность которой задана функцией Р&у) , формулы более сложные:

Ц хр(х, у)ЛхЛу \ур(х-,у) <1х<1у

т т , где в — масса фигуры; в

случае однородной плотности Р~СОП81 0ни упрощаются до вышеприведённых формул.

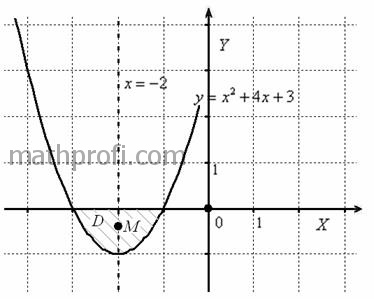
Пример 1

Найти координаты центра тяжести однородной плоской фигуры,

ограниченной линиями

Решение: линии здесь элементарны: ^ = 0 задаёт ось абсцисс, а уравнение

у = д- +4д-+3 _ параб0Лу5 которая легко и быстро строится с помощью геометрических преобразований графиков:

единицы влево и на 1 единицу вниз.

Я выполню сразу весь чертёж с готовой точкой

центра тяжести

фигуры:

Правило второе: если у фигуры существует ось симметрии, то центр тяжести данной фигуры обязательно лежит на этой оси.

, то есть

x=-2

В нашем случае фигура симметрична относительно прямой

фактически мы уже знаем х координату ~ точки т.

Полезная рекомендация: ещё до вычислений постарайтесь определить примерное расположение центра тяжести «на глазок» — это поможет проверить

полученные значения ‘ *Уо на предмет явных ошибок.

Да, возможно, ещё не все до конца поняли, что такое центр тяжести: пожалуйста, поднимите вверх указательный палец и мысленно поставьте на него заштрихованную «подошву» точкой №. Теоретически фигура не должна упасть.

Координаты центра тяжести фигуры найдём по формулам

s = || dxdv, /,. = || xdxdy, ly = Qydxdy

_ h J у S’ Уо ~S

где

Порядок обхода области В (фигуры) здесь очевиден:

1) Сначала вычислим площадь фигуры. Ввиду относительной простоты интеграла решение можно оформить компактно, главное, не запутаться в вычислениях:

Смотрим на чертёж и прикидываем по клеточкам площадь. Получилось около дела.

2) Иксовая координата х° ~ центра тяжести уже найдена «графическим методом», поэтому можно сослаться на симметрию и перейти к следующему пункту. Однако так делать всё-таки не советую — велика вероятность, что решение забракуют с формулировкой «используйте формулу».

В этой связи координату лучше рассчитать формально. Вычислим x интеграл:

Таким образом:

, что и требовалось получить. 3) Найдём ординату ^ центра тяжести. Вычислим у интеграл:

А вот тут без калькулятора пришлось бы тяжко. На всякий случай закомментирую, что в результате умножения многочленов

О +4*+3) =0 +4* + 3)(;г +4х+3) получается 9 членов, причём некоторые из них подобны. Подобные слагаемые я привёл устно (как это обычно принято делать в похожих случаях) и сразу записал итоговую сумму х* + 3х1 + 22х2 + 24х+ 9 _ В результате:

, что очень и очень похоже на правду.

Ч-Ч)

На заключительном этапе отмечаем на чертеже точку 4 Л По условию не требовалось ничего чертить, но в большинстве задач мы волей-неволей вынуждены изобразить фигуру. Зато есть безусловный плюс -визуальная и довольно эффективная проверка результата.

Пример 4

Найти центр тяжести однородной плоской фигуры, ограниченной линиями

х +у = 4, х-у-2 = 0 (х-у -2> 0) ^ фИГуру и её центр тяжести изобразить на чертеже.

Решение:

Прямая = 0 рассекает круг на 2 части, и дополнительная оговорка

х-у- 2> О линейные неравенства) указывает на то, что речь идёт именно о маленьком заштрихованном кусочке.

ч % ч Y

% ч ч ч

ч ч ч ч 1

Оч ч 1 / X

1-х* л V

у= х- ч ч

Фигура симметрична относительно прямой у = ~х (изображена пунктиром), поэтому центр тяжести должен лежать на данной линии. И, очевидно, что его координаты равны по модулю. Отличный ориентир, практически исключающий ошибочный ответ!

Порядок обхода фигуры:

1) Вычислим площадь фигуры

2 х-2 2 2

dx = (x-2-{

-2

-2 -(-ч/ГГ

))äx—

0 0 0 Первый интеграл рациональнее взять подведением под знак дифференциала^

А во втором интеграле проведём стандартную замену:

х — 2 зт I

14 — х2 = д/4- (2 зтО2 = л/4-4зт2г = ,/4(1-зт йх = (2зт = 2соз£й&

‘ t) = 2л/соз21 = 2cosi

Вычислим новые пределы интегрирования:

j/2

zß

+ 12 cosí — 2zostdt = — (О2 — (-2)2) + 4 Jcos2 = — (0 — 4) + 4 ■ — J (1 + eos 2í)afí:

= -2 + 2

t + — sin 21

iß _

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Весьма достоверно, едем дальше: 2) Найдём Ч

2 иг—а 2

Ix = JJ xdxdy= J JTÚÍ* J dy = J * ■ (7) л 0 0

¡r-2

-JT-Í2

-üfa

= 2 + j4-x2)dx =

2 2

¡{x2-2x)dx+x-j4-0 o

í2dx—

/ 3

X 2

— — X

1.3 /

Ц(4-х2)~Ч(4-х2) =

= ^—4-(0-0)J-4

_ 3 _

1 2 2 3

4 1 4 8 4

= —-(0-8) = —+-=-3 3 3 3 3

1,17

£ Л—2 3(л- 2)

3) Исходя из проведённого ранее анализа, осталось убедиться, что Уо й

L =

2 х-2 i 2

\ydxdy = dx J ydy = — J (у2

х-2

dx = -¡((x-2y-(:

x2)2)dx—

= U(x-2)2dO

If, > , 11

2)-^¡(4-x’)dx

2 3

4x- —

Отлично:

i(o+s)-I. —= ¿— = -¿

6 2 3 3 3 3

Изобразим точку 4 на чертеже. В соответствии с

формулировкой условия запишем её как окончательный ответ:

Иногда бывает целесообразен переход к полярным координатам в двойных интегралах. Это зависит от фигуры.

XJ + 0 …1у……

г = 2sin (р 1

0 1

h 1

Давайте найдём центр тяжести данной фигуры. Схема та же:

. Значение -у’:1 ~ ^ просматривается прямо из чертежа, а х координата должна быть смещена чуть ближе к оси ординат, поскольку там располагается более массивная часть полукруга.

В интегралах используем стандартные формулы перехода:

2 Ssinji 1 2

2j„ _ 1 Г/„3

4 = Qxdxdy= jj г cos g>-rdrdg>= J cos <pdg> jr2dr =

2 i ill ti-

ll: О 3

<pd<p =

* 8 -J(8sins iP-03)- C0scpdcp= — jsin3 (pdisvo. qfy

8 1 4 .

—(sin Ф)

3 4

2 2 -(1-0) = -3 3

= i = I = 1.2=±w042

S £T 3 jt Ъл

2 asinjf 1 2

2 j„ _ 1 Г / „3

= |Jydxdy = JJV sin <p-rdrdq>= J sin q>dq> Jr2dr = — J

tO|^sin <pdg>—

* 8 : [ (8sin5 q>-03) ■ sin q>dq> = — [ sin+ q>d(p-

: J 3 J

8 1(3 . ^ sin 4x —— x — sin 2x +-

3 4 L 2 8 ,

3 7T 2 ~2

-0 + 0-(0-0 + 0) =

0 S Л

2 , что и требовалось получить.

Готово.

Использованная литература

1. Киселёв, Андрей Петрович // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969-1978.

2. Андронов И. К., А. П. Киселев., «Математика в школе», 1941, № 2

3. Маргулис А. Я., Андрей Петрович Киселев, «Математика в школе», 1948,

№ 4

References

1. Kiselev, Andrey Petrovich // Great Soviet Encyclopedia: [in 30 volumes] / Ch. ed. A.M. Prokhorov. — 3rd ed. — M.: Soviet Encyclopedia, 1969-1978.

2. Andronov IK, AP Kiselev., «Mathematics at school», 1941, no. 2

3. Margulis A. Ya., Andrey Petrovich Kiselev, «Mathematics at school», 1948,

no. 4

Источник

1.6. Центр тяжести плоской фигуры

Приложения двойного интеграла

Объем тела

Площадь плоской фигуры

Масса плоской фигуры

Статические моменты и координаты центра тяжести плоской фигуры

Моменты инерции плоской фигуры

Пример №53.3.

Пример №53.4.

Статические моменты и координаты центра тяжести

Вычисление статических моментов и координат центра тяжести кривой

Вычисление статических моментов и координат центров тяжести плоских фигур

Не пропустите также: