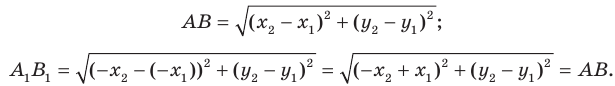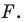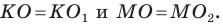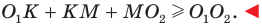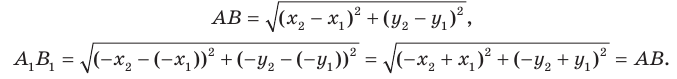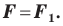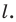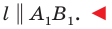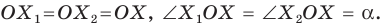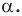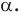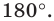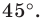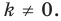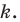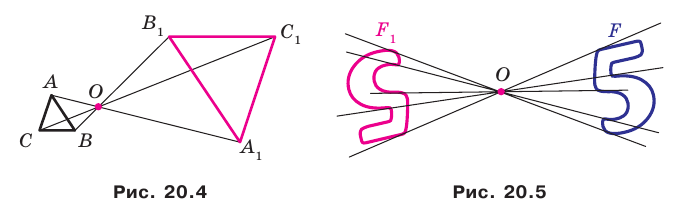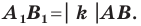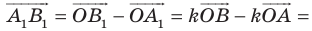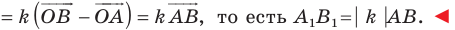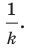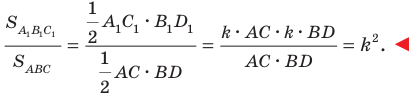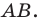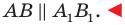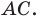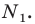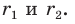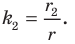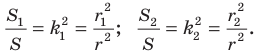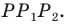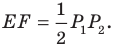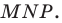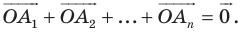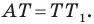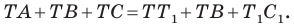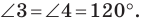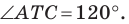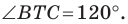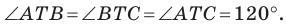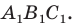План урока:
Отображение плоскости на себя
Понятие движение в геометрии
Свойства движения
Параллельный перенос
Поворот
Использование движения в задачах
Отображение плоскости на себя
Пусть есть некоторое правило, которое устанавливает для каждой точки плоскости какую-нибудь точку этой же плоскости. Подобное правило именуют отображением плоскости на себя.
Лучше всего пояснить это понятие на конкретных примерах. Так, уже изученная нами ранее осевая симметрия может считаться отображением плоскости на себя. Проведем на плоскости прямую m, которая сыграет роль оси симметрии. Далее отметим несколько произвольно выбранных точек А, В, С, D:
Для каждой из отмеченных точек несложно определить точку, симметричную ей относительно оси симметрии. Чтобы сделать это, надо опустить из точек перпендикуляры АА’, ВВ’, СС’на прямую m, а потом на продолжении этих перпендикуляров отложить отрезки А’A’’, B’B’’, C’C’’ так, чтобы выполнялись равенства:
Тогда точки А и А’’, В и В’’, С и С’’ будут симметричны относительно m. Можно сказать, что точки А, В и С отобразились соответственно в точки А’’, В’’, С’’:
Обратите внимание на точку D, которая непосредственно лежит на m. Для нее не получится выполнить такое же построение, как для А, В и C, однако считается, что она симметрична сама себе. Поэтому можно сказать, что точка D преобразуется в точку D’’, которая совпадает с самой D. То есть точка отобразилась сама на себя.
Таким образом, любую точку можно отобразить симметрично относительно произвольной прямой m, и такое отображение как раз является примером отображения плоскости на себя.
В качестве ещё одного примера можно привести центральную симметрию. Отметим на плоскости произвольную точку О, которая будет центром симметрии, а также некоторые точки А, В, С. Отобразим их симметрично относительно О. Для этого надо просто построить прямые АО, ВО и СО, а потом от О отложить на этих прямых отрезки А’О, В’O, C’O:
Можно сказать, что А, В и С отобразились в точки А’, В’ и C’. Если бы мы захотели отобразить с помощью центральной симметрии саму точку О, то она отобразилась бы сама в себя. Таким образом, центральная симметрия также представляет собой отображение плоскости на себя, так как с помощью описанного алгоритма можно найти отображение любой точки на плоскости.
Важно понимать, что бывают отображения плоскости, которые вовсе не являются симметриями. Например, снова возьмем точку О ещё три точки А, В, С. Снова построим прямые АО, ВО и СО, но теперь уже от самих точек А, В и С отложим отрезки, равные АО, ВО и СО, и обозначим их как АА’, ВВ’ и CС’:
В результате наших действий мы снова каждой точке А, В, С поставили в соответствие точку А’, В’, С’. То есть имеет место отображение плоскости. Такое преобразование называется гомотетией (точнее говоря, это частный случай гомотетии), и оно симметрией не является.
Все три описанных примера отображений плоскости на себя объединяет то, что они содержат описание правила (алгоритма), по которому произвольной точке А может быть поставлена в соответствие какая-то произвольная точка А’. При этом точку А’ называют отображением, или образом точки А. В свою очередь А можно назвать прообразом точки А’. Ещё раз отметим, что допускается ситуация, когда точки А и А’ совпадают. Попробуйте сами придумать ещё несколько алгоритмов, которые представляют собой отображения плоскости.
Понятие движения в геометрии
Среди всех отображений плоскости в особую группу объединяют те преобразования, при которых не изменяется расстояние между отображаемыми точками. Эти отображения именуются движениями. Также используются термины перемещение и изометрия.
Центральная и осевая симметрия– это как раз примеры движений. Докажем это для осевой симметрии. Рассмотрим две точки А и В, расположенные так, как это показано на рисунке, а также ось симметрии m. Отобразим А и В относительно mпо правилам осевой симметрии:
Здесь Н и К – это точки прямой m, на которые упали перпендикуляры, опущенные из А и В. Проведем отрезки НВ и НВ’. Теперь исследуем ∆KBH и ∆KB’H. Они оба являются прямоугольными, у них один катет общий (HK), а вторые катеты равны по свойству осевой симметрии. Из этого вытекает равенство ∆KBH и ∆KB’H, а это значит, что
Далее рассмотрим ∆АВН и ∆А’B’H. Только что мы выяснили, что у них есть одинаковые углы ∠BHA и ∠B’HA’. Прилегающие к ним стороны также одинаковы:
Надо отметить, что приведенное доказательство не является полным, так как рассматривает один случай расположения точек А и В. Возможны ещё как минимум 6 случаев расположения А и В:
В рамках полного доказательства следовало бы полностью рассмотреть каждый из этих случаев и для каждого из них доказать равенство
но мы не будем тратить на это время, можете попробовать самостоятельно сделать это.
Далее проанализируем центральную симметрию, она также представляет собой движения. Отобразим точки А и В в образы А’и В’ относительного произвольного центра симметрии О:
Сравним ∆АОВ и А’OB’. У них одинаковы∠АОВ и ∠А’ОВ’, так как они – вертикальные. По свойству центральной симметрии можно записать, что
Надо понимать, что не всякое отображение плоскости представляет собой движение. Например, рассмотренная нами гомотетия изменяет расстояния между точками, а потому она не относится к движениям.
Свойства движения
При движении, как и при любом отображении, можно отображать не только отдельные точки, но и их множества, то есть геометрические фигуры. Сформулируем важную теорему:
Действительно, пусть есть отрезок MN, все точки которого мы отобразили с помощью движения. Произвольную точку отрезка MN обозначим как Р. После отображения мы получим точки M’, N’ и Р’. Соединим М’ и N’ и получим отрезок M’N’.Докажем, что Р’ принадлежать отрезку M’N’.
Р лежит на NP, поэтому справедливо равенство:
Заметим, что это равенство как раз может выполняться только в случае, если Р’ принадлежит M’N’. Действительно, если Р’ не лежит на M’N’, то существует ∆M’N’P’, для которого, в силу неравенства треугольника, можно записать
Итак, мы показали, что всякая точка Р исходного отрезка MN обязательно будет отображаться на отрезок M’N’. Однако этого мало. Вдруг на M’N’ есть такая точка Р’, что ее прообраз не лежит на исходном отрезке MN?Для того, чтобы опровергнуть такую возможность, надо рассуждать в «обратную сторону». Для Р’, лежащей на M’N’, выполняется равенство
Такое равенство означает, что Р лежит на MN. В итоге мы смогли показать, что отрезок MN отображается именно в отрезок M’N’.
Доказанное нами свойство позволяет доказать следующий факт:
В результате отрезки АВ, АС, и ВС отобразятся в равные им отрезки А’B’, А’С’ и B’C’. Но тогда ∆АВС и ∆А’В’С’ будут равны, ведь у них одинаковы все 3 стороны, ч. т. д.
Из этого факта легко показать, что при движении остаются неизменными не только расстояния, но и углы. Пусть есть некоторый ∠А. Отметим на его сторонах точки В и C, в результате получим ∆АВС (если только ∠А не является развернутым). При движении ∆АВС отобразится в равный ему ∆А’В’С’. Из равенства треугольников вытекает и равенство углов:
ч. т. д.
Аналогичными рассуждениями можно продемонстрировать, что вообще любая фигура, изученная нами в курсе геометрии (прямая, луч, многоугольник, окружность) будет отображаться в равную ей фигуру.
Более того, если между двумя фигурами есть некоторая взаимосвязь, то она сохраняется после движения. Например, при движении две параллельные прямые отображаются в две другие параллельные прямые, и расстояние между ними не меняется. Если движению подвергают окружность и прямую, являющуюся касательной к ней, то в результате получают новую окружность и прямую, причем прямая останется касательной к окружности.
Параллельный перенос
Мы уже изучили два вида движения – осевую и центральную симметрию. Однако есть ещё несколько видов движений. Один из них именуется параллельным переносом. Для выполнения параллельного переноса необходимо предварительно задать некоторый вектор а. При параллельном переносе точки М она отображается в точку M’ так, что вектор MM’ оказывается равным а. Переносить можно сразу множество точек.
Докажем, что параллельный перенос действительно представляет собой движение. Для этого надо всего лишь продемонстрировать, что при нем расстояние между двумя произвольными точками не меняется. Пусть в результате параллельного переноса на вектор а некоторые точки M и N отобразились в M’ и N’ соответственно:
Рассмотрим получившийся четырехугольник NMM’N’. Две его стороны, MM’ и NN’, параллельны и имеют одинаковую длину, так являются равными векторами. Это значит, что NMM’N’ – это параллелограмм (согласно одному из признаков параллелограмма). Но тогда и две другие стороны NMM’N’, то есть MN и M’N’, также одинаковы, ч. т. д.
Примечание. Возможен частный случай, когда отрезок MN параллелен вектору а. В этом частном случае построить параллелограмм не удастся, но вы можете убедиться самостоятельно, что и в этом случае расстояние между M и N не изменяется.
Параллельный перенос может быть использован при решении ряда задач, в том числе и связанных с построением.
Задание. Даны две непересекающиеся окружности с различными радиусами. Постройте общие внешние касательные к этим окружностям.
Решение. Предположим, что нам удалось построить обе внешние касательные. Обозначим точки касания как К, Р, M и N:
Теперь осуществим параллельный перенос касательных. Касательную КР перенесем на вектор КО1, а MN – на вектор MО1. В результате точки K и M отобразятся в О1, а точки Р и N – в точки Р’ и N’:
Так как при движении углы сохраняются, то прямые О1Р’ и О2N’ останутся перпендикулярными радиусам О2Р и О2N. Значит, если построить окружность с радиусом О2Р’ (а его величина равна R – r), то для нее эти прямые останутся касательными. Отсюда легко понять алгоритм построения внешних касательных. Сначала надо построить отрезок длиной R– r (на рисунке показан зеленым цветом):
Далее из О2 проводим окружность с радиусом R– r:
Теперь из точки О1 проводим касательные к новой окружности. Построение таких касательных – отдельная геометрическая задача, изучаемая ещё в 8 классе. В результате мы сможем найти точки касания Р’ и N’:
Далее надо найти осуществить параллельный перенос касательных. Для этого продолжаем радиусы О2Р’ и О2N’, пока они не пересекутся с большей окружностью в точках Р и N соответственно. Чтобы найти точки касания меньшей окружности, надо просто провести перпендикуляры к касательным:
Поворот
Ещё одно движение, используемое в планиметрии – это поворот. Для того, чтобы его совершить, необходимо указать центр поворота и выбрать угол поворота, а также задать направление вращение. На следующем рисунке показан поворот точки М относительно О на угол 45° по часовой стрелке:
В общем случае поворот относительно точки О на некоторый угол α– это такое отображение, при котором произвольная точка М преобразуется в М’, и при этом выполняется два равенства:
Поворачивать можно не только точки, но и целые фигуры. Например, ниже продемонстрирован поворот треугольника:
Докажем, что поворот действительно является движением, то есть при его применении расстояния не искажаются. Пусть точки M и N поворачиваются на угол α относительно точки О:
Тогда по определению поворота можно записать:
ч. т. д.
Использование движения в задачах
Мы уже рассмотрели одну задачу на построение, в которой применялся параллельный перенос прямой. Однако чаще в задачах используется поворот, а также различные виды симметрии.
Задание. Точки А и В лежат по одну сторону от прямой m. Как, используя только циркуль и линейку, отметить на m такую точку C, что сумма длин отрезков АС и ВС будет минимально возможной?
Решение. Отобразим А симметрично относительно прямой m и получим точку А’. После этого соединим А’ с В. Отрезок пересечет m в точке, которая как раз и будет искомой точкой С:
Действительно, по свойству движения отрезки АС и А’С одинаковы, поэтому сумма длин АС и ВС будет совпадать с суммой А’С и ВС, то есть будет равна длине А’В. Если бы выбрали вместо С какую-нибудь другую точку К, не лежащую на А’В, то сумма длин А’K и ВК оказалась бы больше, чем длина А’В вследствие неравенства треугольника, записанного для ∆А’KB.
Задание. Петя и Ваня играют в игру. Они по очереди кладут одинаковые круглые фишки на прямоугольный стол. До тех пор, пока это возможно сделать. Если игрок не может сделать ход, то он проигрывает. Какова оптимальная стратегия в этой игре и кто, используя ее, выиграет игру?
Решение. Заметим, что прямоугольный стол обладает центральной симметрией относительно своего центра (центр прямоугольника можно определить как точку, в которой пересекаются его диагонали). Пусть первый игрок положит первую фишку ровно в центр стола:
Далее на любой второго игрока первый игрок может положить свою фишку симметрично относительно центра стола (число в центре круга – номер хода):
Получается, что на ход второго игрока первый всегда сможет ответить. То есть первый игрок никак не может проиграть, используя эту тактику. Так как игра когда-нибудь окончится (ведь свободная площадь на столе рано или поздно закончится), и она не может завершиться вничью, то именно первый игрок и выиграет.
Задание. Для произвольного ∆АВС отмечены точки А1, В1 и С1 так, что ∆А1ВС, ∆АВ1С и ∆АВС1 являются равносторонними, причем никакие из этих четырех треугольников не имеют общей площади (в таких случаях говорят, что треугольники построены внешним образом). Докажите, что отрезки АА1, ВВ1 и СС1 имеют одинаковую длину.
Решение. Напомним, что в равносторонних треугольниках все углы составляют по 60°. Выберем любую из вершин ∆АВС (например, С) и повернем отрезок АА1 на 60° против часовой стрелки. Тогда точка А1 отобразится в В, а точка А – в точку В1.
В итоге отрезок АА1 отобразился в отрезок ВВ1. Это значит, что они одинаковы. Аналогичным образом, осуществляя поворот вокруг вершины А, можно показать, что отрезок ВВ1 переходит в отрезок СС1, и потому они также одинаковы. Таким образом, все три отрезка имеют одну и ту же длину.
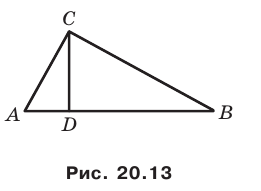
Задание. В ∆АВС проведена медиана СМ. На стороне АС внешним образом построен квадрат АСDE, а на стороне ВС – квадрат ВСKF (также внешним образом). Докажите, что СМ вдвое короче KD, и СМ перпендикулярен KD.
Решение. Повернем ∆АВС на 90° против часовой стрелки вокруг точки С вместе с медианой СМ. Тогда точка А перейдет в точку D, а М и B отобразятся в некоторые точки M’ и B’ соответственно:
Заметим, что ∠ВСК – прямой, так как это угол квадрата. ∠ВСВ’ также прямой, ведь поворот мы осуществили как раз на 90°. Тогда ∠В’СКокажется развернутым:
Это значит, что точки В’, С и К лежат на одной прямой. Отрезки ВС и СК одинаковы как стороны квадрата, а отрезок В’С имеет ту же длину, что и ВС (так как он получен поворотом ВС, а при повороте расстояния не искажаются). Тогда можно записать, что
то есть отрезки СК и В’C также одинаковы. Это означает, что С – середина В’К.
М – это середина АВ (по определению медианы), поэтому и при повороте М’ останется серединой В’D. Получается, что отрезок СМ’ соединяет середины сторон В’К и В’D в ∆В’KD, то есть отрезок СМ’ является средней линией. Отсюда сразу вытекает два факта:
1) М’C вдвое короче КD;
2) М’C параллелен KD.
Ясно, что отрезки МС и М’C одинаковы по определению движения, поэтому МС также будет в 2 раза короче KD:
МC = М’C = KD/2
Отрезки МС и М’C перпендикулярны, ведь поворот мы выполнили на 90°. Но тогда МС также будет перпендикулярен и КD, ведь KD и М’C параллельны, ч. т. д.
Сегодня мы познакомились с понятием отображения плоскости на себя и его частным случаем – движением. При движении сохраняются все расстояния между точками, все углы, формы фигур и все соотношения между геометрическими объектами. Это свойство движения позволяет находить краткие решения весьма сложных геометрических задач.
Лучший ответ
-
1
0ovod (75)
7 (86376)81875
13 лет
Взять пару соответствующих точек (т.е. одна на первой фигуре, а вторая образ этой точки на второй фигуре при повороте), соединить их отрезком и провести перпендикуляр к этому отрезку через его середину.
Сделать то же самое с другой парой соответствующих точек, выбранных так, чтобы соединяющий их отрезок не был параллелен первому отрезку.
Точка пересечения этих двух перпендикуляров и будет искомым центром поворота.
Ответы
-
0
0StrangeManiac (33)
5 (4049)249
13 лет
На глазок
Параллельным переносом фигуры называется перенос всех точек пространства на одно расстояние в одном направлении.
Параллельный перенос определяет вектор, по которому совершается перенос.
Чтобы совершить параллельный перенос, нужно знать направление и расстояние, что означает задать вектор.
Рис. (1). Параллельный перенос треугольника (ABC) на вектор (a).
Чтобы при параллельном переносе построить изображение многоугольника, достаточно построить изображения вершин этого многоугольника.
Первоначальная фигура и фигура, полученная после параллельного переноса, равны.
Параллельный перенос используется для конструирования графиков функций.
На рисунке изображена парабола и два результата параллельного переноса.
Рис. (2). Параллельный перенос параболы.
Параллельный перенос можно встретить в реальной жизни.
Если одна фигура получена из другой фигуры поворотом всех её точек относительно центра (O) на один и тот же угол в одном и том же направлении, то такое преобразование фигуры называется поворотом.
Чтобы поворот имел место, должен быть задан центр (O) и угол поворота
α
.
Против часовой стрелки — положительный угол поворота, наоборот — отрицательный угол поворота (так же как углы поворота в единичной окружности).
Треугольник (ABC) повёрнут в положительном направлении (приблизительно на α (= 45) градусов).
Рис. (4). Поворот треугольника (ABC) на угол
α
.
Если угол поворота равен (180) или (-180) градусам, то фигура отображается как центрально симметричная данной, и этот поворот называется случаем центральной симметрии.
Рис. (5). Поворот треугольника (ABC) на угол
180°
.
Источники:
Рис. 3. Окна. nadia_if / Shutterstock.com
Содержание:
Геометрические преобразования:
В этой лекции вы узнаете, что такое преобразование фигуры. Ознакомитесь с такими видами преобразований, как параллельный перенос, центральная симметрия, осевая симметрия, поворот, гомотетия, подобие.
Вы научитесь применять свойства преобразований при решении задач и доказательстве теорем.
Движение (перемещение) фигуры. Параллельный перенос
Пример:
На рисунке 17.1 изображены отрезок
Мы указали правило, с помощью которого каждой точке 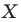
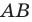
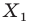
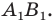
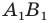
Пример:
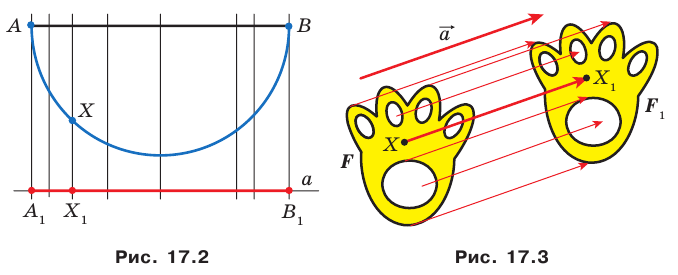
На рисунке 17.2 изображены полуокружность 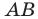
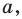
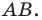
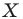
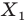
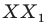
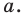
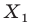
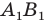
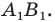
Пример:
Пусть даны некоторая фигура 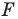
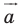
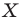
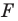
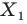
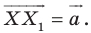
Обобщим приведенные примеры.
Пусть задана некоторая фигура 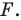
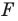
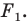
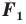
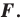
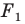
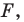
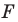
Так, в примере 1 отрезок 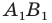
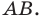
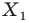
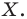
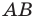
Обратим внимание на то, что в примере 3 фигура 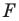
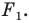
Какими же свойствами должно обладать преобразование, чтобы образ и прообраз были равными фигурами? Оказывается, что достаточно лишь одного свойства: преобразование должно сохранять расстояние между точками, то есть если 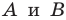
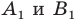
Что такое преобразование фигур
Определение. Преобразование фигуры 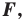
Если каждой точке 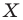
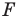
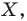
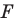
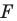
Мы давно используем понятие «равенство фигур», хотя не давали ему строгого определения.
На то, что движение связано с равенством фигур, указывают следующие свойства движения.
Если преобразование является движением, то:
- образом прямой является прямая,
- образом отрезка является отрезок, равный данному;
- образом угла является угол, равный данному,
- образом треугольника является треугольник, равный данному.
Доказательство этих свойств выходит за рамки рассматриваемого курса геометрии.
Свойства движения подсказывают следующее определение.
Определение. Две фигуры называют равными, если существует движение, при котором одна из данных фигур является образом другой.
Запись 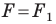
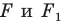
Если существует движение, при котором фигура 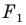
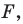
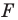
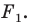
Замечание. Ранее равными фигурами мы называли такие фигуры, которые совпадали при наложении. Термин «наложение» интуитивно понятен, и в нашем представлении он связывается с наложением реальных тел. Но геометрические фигуры нельзя наложить в буквальном смысле этого слова. Теперь наложение фигуры 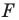
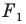
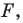
Термин «движение» также ассоциируется с определенным физическим действием: изменением положения тела без деформации.
Именно с этим связано появление этого термина в математике. Однако в геометрии предметом исследования является не процесс, происходящий во времени, а лишь свойства фигуры и ее образа.
То, что изображенные на рисунке 17.3 фигуры 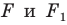
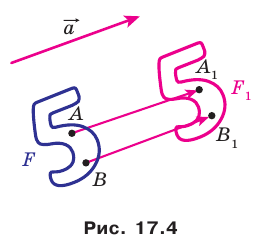
Теорема 17.1 (свойство параллельного переноса). Параллельный перенос является движением.
Доказательство: Пусть 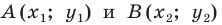
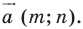
Имеем: 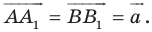
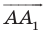
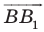
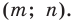
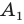
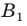
Найдем расстояние между точками
Найдем расстояние между точками
Следовательно, мы показали, что 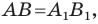
Следствие. Если фигура 
Это свойство используется при создании рисунков на тканях, обоях, покрытиях для пола и т. п. (рис. 17.5).
Если фигура 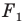
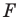
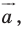
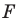
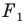
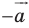
Параллельные переносы на векторы 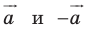
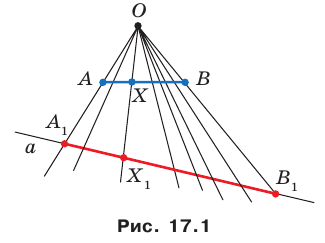
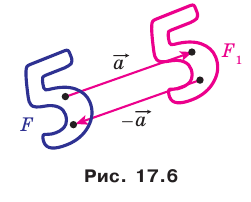
Пример №1
Каждой точке 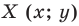
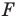
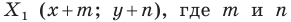
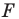
Решение:
Рассмотрим вектор 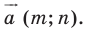
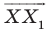
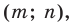
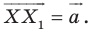
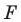
Пример №2
Точка 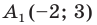
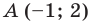
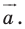
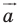
Решение:
Из условия следует, что 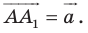
Пусть 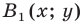
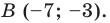
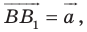
Ответ:
Пример №3
Даны угол 
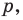
Решение:
Рассмотрим вектор 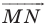

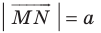
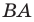
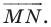
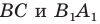
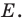
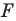
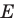
Приведенные рассуждения подсказывают следующий алгоритм построения:
- найти образ луча
при параллельном переносе на вектор
- отметить точку пересечения луча
с построенным образом;
- через найденную точку провести прямую
параллельную прямой
Прямая
будет искомой.
Осевая симметрия
Определение. Точки 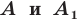
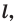
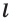
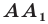
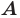
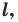
Например, точки 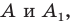
Рассмотрим фигуру 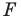
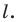
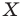
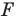
В результате такого преобразования фигуры 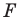
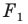
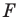
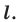
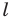
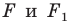
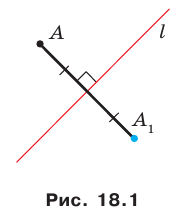
Теорема 18.1 (свойство осевой симметрии). Осевая симметрия является движением.
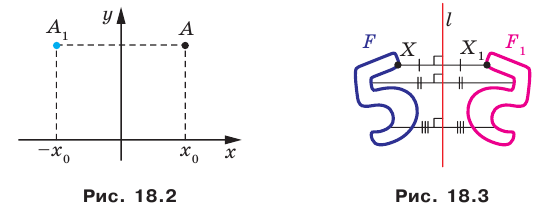
Доказательство: Выберем систему координат так, чтобы ось симметрии совпала с осью ординат. Пусть 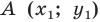
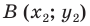
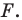
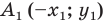
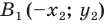
Мы получили, что 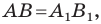
Следствие. Если фигуры 
Определение. Фигуру называют симметричной относительно прямой 
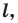
Прямую 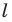
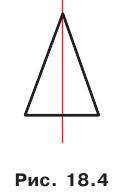
Приведем примеры фигур, имеющих ось симметрии. На рисунке 18.4 изображен равнобедренный треугольник. Прямая, содержащая его высоту, проведенную к основанию, является осью симметрии треугольника.
Любой угол имеет ось симметрии — это пря-Рис. 18.5 мая, содержащая его биссектрису (рис. 18.5).
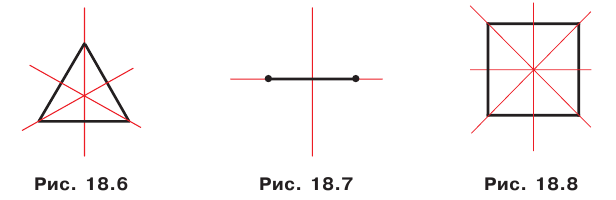
Равносторонний треугольник имеет три оси симметрии (рис. 18.6). Две оси симметрии имеет отрезок: это его серединный перпендикуляр и прямая, содержащая этот отрезок (рис. 18.7).
Квадрат имеет четыре оси симметрии (рис. 18.8).
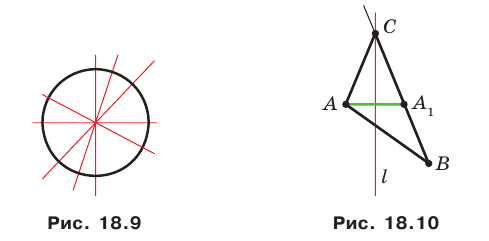
Существуют фигуры, имеющие бесконечно много осей симметрии, например окружность. Любая прямая, проходящая через центр окружности, является ее осью симметрии (рис. 18.9).
Бесконечно много осей симметрии имеет и прямая: сама прямая и любая прямая, ей перпендикулярная, являются ее осями симметрии.
Пример №4
Начертили неравнобедренный треугольник 
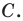
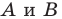
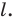
Решение:
Поскольку прямая 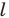
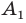
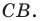
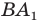
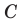
Эти соображения подсказывают, как построить искомый треугольник: строим точку 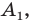
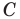
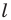
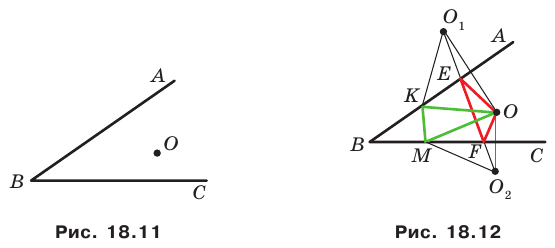
Пример №5
Точка 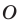
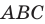
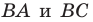
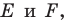
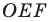
Решение:
Пусть точки 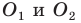
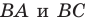
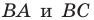
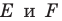
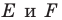
Заметим, что отрезки 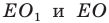
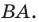
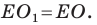
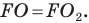
Покажем, что построенный треугольник имеет наименьший периметр из возможных.
Рассмотрим треугольник 
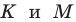
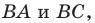
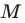
Понятно, что
Тогда периметр треугольника 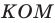
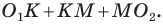
Центральная симметрия. Поворот
Определение. Точки 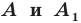
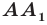
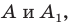
Рассмотрим фигуру 
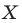
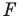
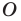
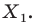
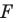
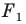
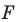
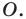
Теорема 19.1 (свойство центральной симметрии). Центральная симметрия является движением.
Доказательство: Выберем систему координат так, чтобы центр симметрии совпал с началом координат. Пусть 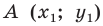
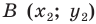
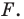
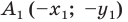
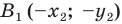
Мы получили, что 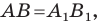
Следствие. Если фигуры 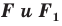
Определение. Фигуру называют симметричной относительно точки 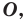
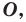
Точку 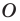
Приведем примеры фигур, имеющих центр симметрии.
Центром симметрии отрезка является его середина (рис. 19.4).
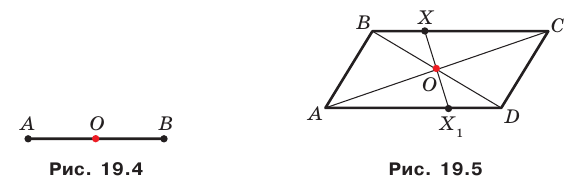
Точка пересечения диагоналей параллелограмма является его центром симметрии (рис. 19.5).
Существуют фигуры, имеющие бесконечно много центров симметрии. Например, каждая точка прямой является ее центром симметрии.
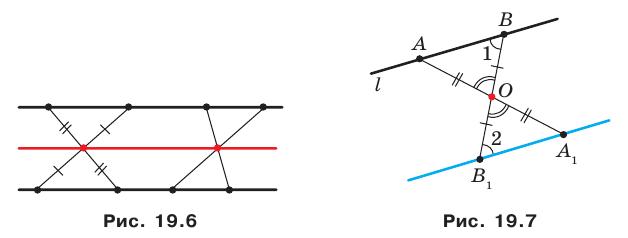
Также бесконечно много центров симметрии имеет фигура, состоящая из двух параллельных прямых. Любая точка прямой, равноудаленной от двух данных, является центром симметрии рассматриваемой фигуры (рис. 19.6).
Пример №6
Докажите, что образом данной прямой 
Решение:
Поскольку центральная симметрия — это движение, то образом прямой 
Выберем на прямой 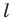
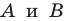
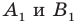
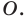
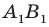
Поскольку 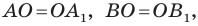
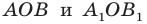
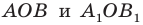
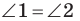
Пример №7
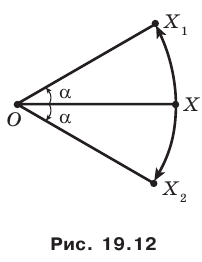
Точка 
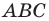
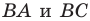
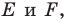
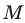
Решение:
Пусть прямая 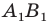
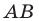
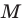
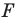
Найдем прообраз точки 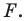
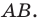
Обозначим эту точку буквой 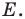
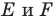
Изучая окружающий мир, мы часто видим примеры проявления симметрии в природе (рис. 19.10). Объекты, имеющие ось или центр симметрии, легко воспринимаются и радуют взгляд. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота».
Идея симметрии широко используется в изобразительном искусстве, архитектуре и технике (рис. 19.11).
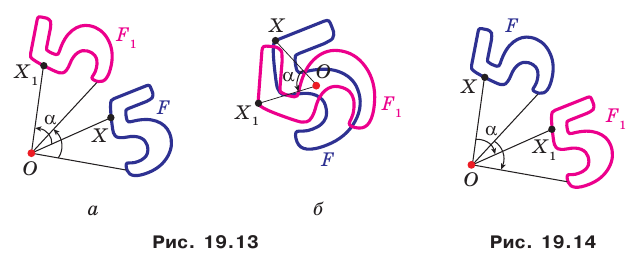
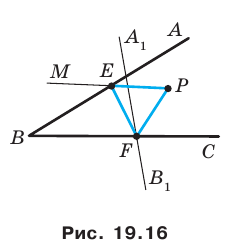
На рисунке 19.12 изображены точки 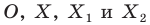
Говорят, что точка 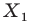
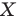
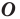
Так же говорят, что точка 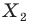
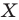
Точку 
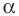
Рассмотрим фигуру 
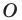
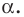
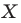
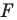
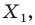
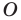
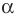
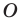
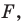
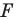
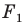
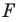
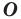
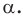
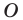
Аналогично определяют преобразование поворота фигуры 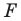
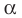
Заметим, что центральная симметрия является поворотом вокруг центра симметрии на угол
Теорема 19.2 (свойство поворота). Поворот является движением.
Докажите эту теорему самостоятельно.
Следствие. Если фигура 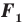
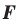
Пример №8
Даны прямая 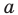
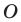
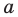
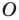
Решение:
Поскольку поворот — это движение, то образом прямой 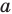
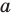
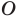
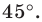
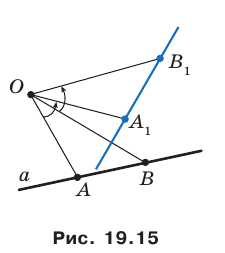
Пример №9
Точка 
Решение:
Пусть прямая 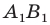
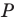
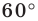
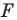
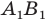
Пусть точка 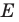
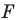
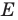
Эти соображения подсказывают, как построить искомый треугольник.
Строим прямую 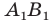
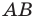
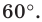
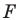
Строим угол 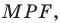
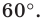
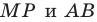
Имеем: 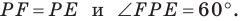
Подобие фигур
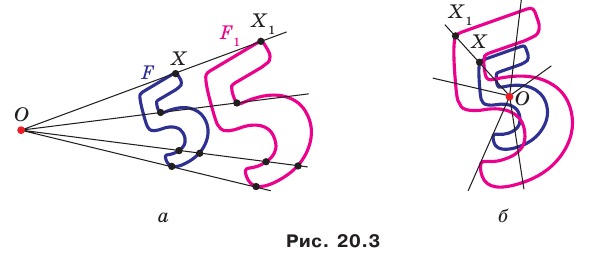
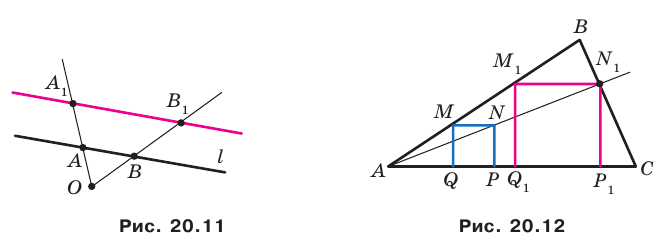
На рисунке 20.1 изображены точки 
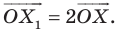
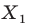
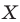
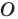
На рисунке 20.2 изображены точки 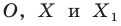
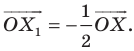
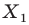
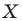
Вообще, если точки 
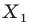
Точку 
Рассмотрим фигуру 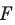
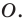
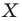
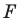
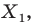
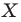
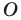
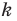
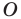
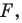
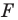
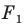
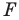
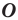
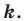
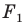
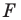
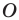
Например, на рисунке 20.4 треугольник 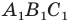
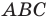
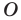
можно сказать, что треугольник 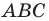
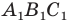
Отметим, что при 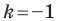
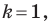
Очевидно, что при 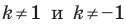
Теорема 20.1. При гомотетии фигуры 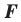
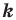
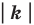
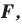
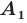
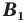
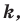
Доказательство: Пусть точка 
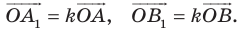
Следствие. Если треугольник 
Для доказательства этого утверждения достаточно воспользоваться теоремой 20.1 и третьим признаком подобия треугольников.
Гомотетия обладает целым рядом других свойств.
При гомотетии:
Эти свойства вы можете доказать на занятиях математического кружка.
Перечисленные свойства гомотетии указывают на то, что это преобразование может изменить размеры фигуры, но не меняет ее форму, то есть при гомотетии образ и прообраз являются подобными фигурами. Заметим, что в курсе геометрии 8 класса, говоря о подобии фигур, мы давали определение только подобных треугольников. Сейчас определим понятие подобия для произвольных фигур.
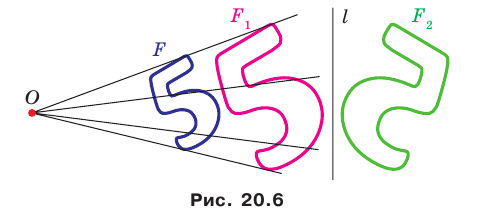
На рисунке 20.6 фигура 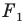
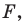
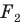
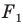
Говорят, что фигура 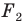
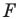
Поскольку 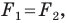
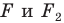
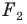
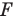
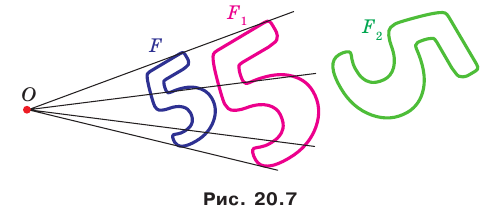
На рисунке 20.7 фигура 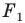
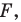
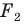
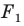
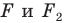
Из сказанного следует, что целесообразно принять такое определение.
Определение. Две фигуры называют подобными, если одну из них можно получить из другой в результате композиции двух преобразований: гомотетии и движения.
Это определение иллюстрирует схема, изображенная на рисунке 20.8.
Запись 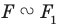
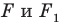
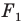
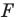
Из приведенного определения следует, что при преобразовании подобия фигуры 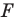
Так как тождественное преобразование является движением, то из схемы, изображенной на рисунке 20.8, следует, что гомотетия — частный случай преобразования подобия.
Пусть 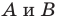
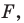
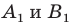
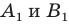
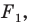
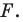
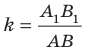
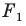
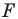
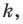
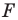
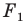
Заметим, что преобразование подобия с коэффициентом 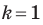
С преобразованием подобия мы часто встречаемся в повседневной жизни (рис. 20.9). Например, в результате изменения масштаба карты получаем карту, подобную данной. Фотография — это преобразование негатива в подобное изображение на фотобумаге. Перенося в свою тетрадь рисунок, сделанный учителем на доске, вы также выполняете преобразование подобия. 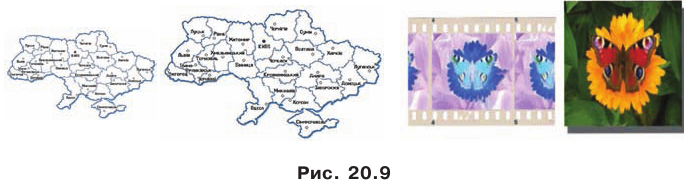
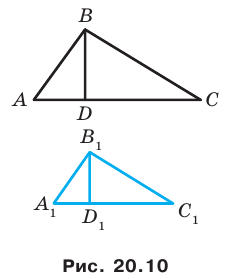
Доказательство этой теоремы выходит за рамки рассматриваемого курса геометрии. Мы докажем ее для частного случая, рассмотрев подобные треугольники.
Доказательство: Пусть треугольник 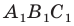
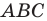
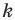
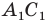
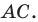
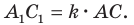
Поскольку при преобразовании подобия сохраняются углы, то отрезок 
Тогда 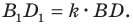
Пример №10
Докажите, что образом прямой 
Решение:
Из свойств гомотетии следует, что образом прямой 
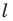
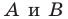
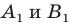
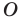
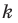
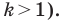
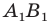
При доказательстве теоремы 20.1 мы показали, что 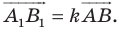
Пример №11
В остроугольный треугольник 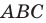
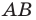
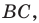
Решение:
Из произвольной точки 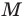
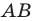
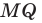
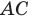
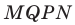
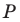
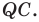
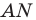
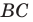
Рассмотрим гомотетию с центром 
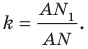
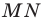
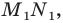
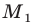
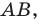
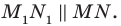
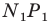
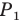
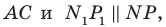
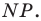
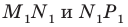
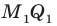
Пример №12
Отрезок 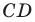
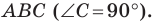
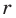
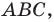
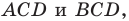
Решение:
Поскольку угол 
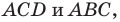
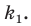
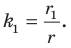
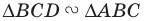
Обозначим площади треугольников 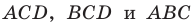
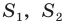
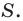
Отсюда 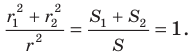
Ответ:
Применение преобразований фигур при решении задач
Преобразование фигур — эффективный метод решения целого ряда геометрических задач. Проиллюстрируем это на примерах.
Пример №13
На сторонах 
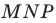
Решение:
Пусть 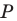
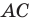
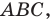
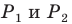
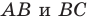
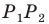
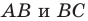
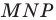
Заметим, что отрезок 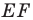
Тогда
Поскольку 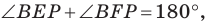
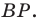
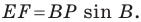
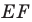
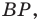
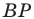
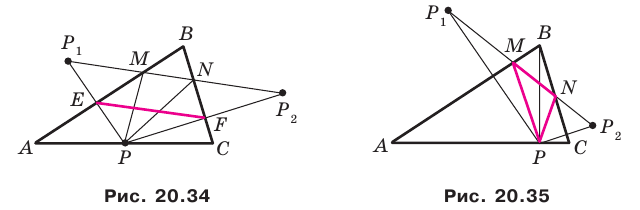
На рисунке 20.35 отрезок 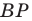
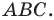
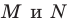
Из построения следует, что периметр любого другого треугольника, вершины которого лежат на сторонах треугольника 
Можно показать (сделайте это самостоятельно), что точки 
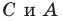
Следовательно, вершины искомого треугольника — это основания высот данного треугольника 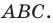
Пример №14
Точка 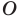
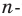
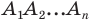
Решение:
Пусть 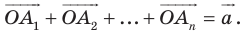
Пример №15
Внутри треугольника 
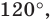
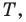
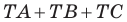
Решение:
Пусть 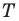
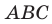
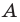
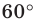
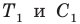
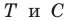
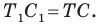
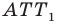
Имеем:
Понятно, что сумма 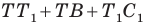
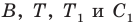
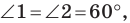
Так как угол 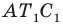
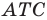
Итак, точки 
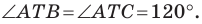
Таким образом, сумма 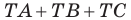
Найти точку 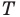
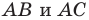
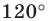
Понятно, что если один из углов треугольника 
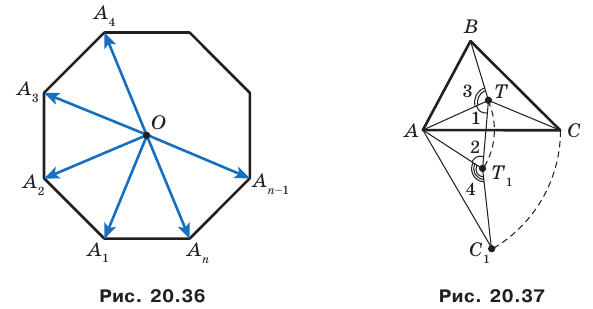
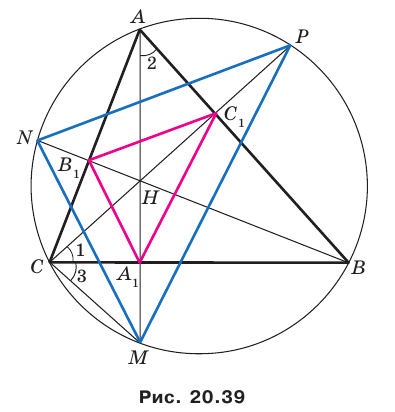
Пример №16
Отрезки 
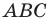
Решение:
Пусть прямые 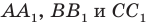
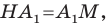
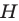
Имеем:
Углы 2 и 3 равны как вписанные, опирающиеся на дугу 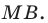
Тогда в треугольнике 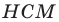
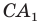
Аналогично можно доказать, что
Теперь понятно, что треугольник 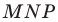
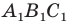
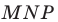
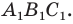
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Возникновение геометрии
- Призма в геометрии
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
А чем строить не важно?
Проводим прямую через начальные точки двух отрезков $%AA’$%, из точки $%B$% проводим прямую параллельную полученной, из точки $%A’$% циркулем проводим дугу с радиусом $%A’B’$% до пересечения с прямой из точки $%B$%, получаем точку $%B’_1$%. Строим к прямой $%B’B’_1$% перпендикуляр через точку $%A’$%. Он по идее пройдёт через середину отрезка $%B’B’_1$%. Так же из середины отрезка $%AA’$% строим перпендикуляр. Точка пересечения перпендикуляров будет центром поворота, что можно легко проверить тем же циркулем.






















































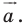
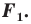
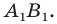
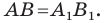
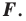
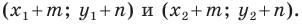
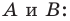
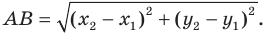

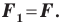

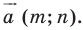

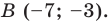
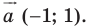
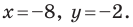
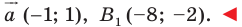
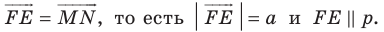
 при параллельном переносе на вектор
при параллельном переносе на вектор 
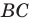 с построенным образом;
с построенным образом;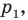 параллельную прямой
параллельную прямой 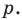 Прямая
Прямая 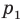 будет искомой.
будет искомой.