Как найти центр окружности за 5 ходов

В Euclidea нет встроенных решений. Проверяется не построение, а его результат.

Вероятно, ваше решение не принимается, поскольку оно приблизительное, то есть не является точным. Есть несколько способов это проверить:

Перечитайте условие задачи. Его можно посмотреть, нажав на карточку в левом верхнем углу экрана. Если вы забыли какое-нибудь определение, нажмите на знак вопроса, расположенный под условием.

Убедитесь, что искомый объект действительно построен. К примеру, вы могли забыть поставить точку на одном из концов отрезка.

Выберите инструмент «Перемещение» («Рука») и попробуйте подвигать разные точки. Решение должно удовлетворять условию задачи для любой конфигурации точек и фигур из условия.

Проверьте красные точки. Они не закреплены и их можно перемещать. В общем случае их не нужно избегать: некоторые оптимальные решения невозможны без красных точек. Однако стоит помнить, что, например, средняя точка или точка касания никогда не могут быть красными.

Войдите в режим Исследования (оранжевая кнопка) и посмотрите, как ответ зависит от конфигурации точек. Сравните это со своим решением.

Попробуйте доказать, что ваше построение удовлетворяет условию задачи. Визуального совпадения с правильным ответом недостаточно.

Если ничего не помогает, напишите нам, пожалуйста: support@euclidea.xyz.

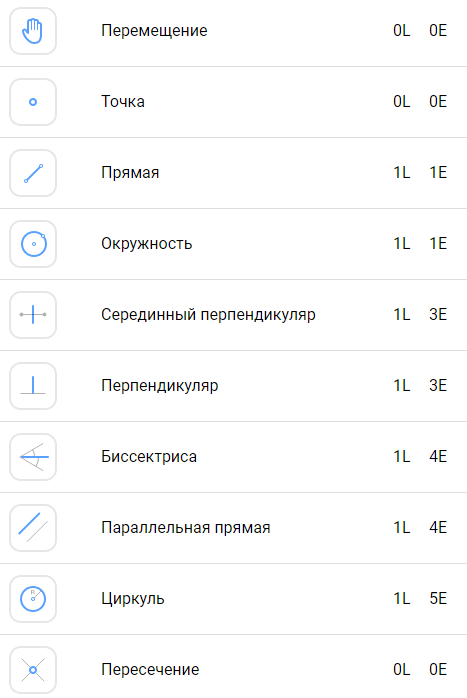
Каждое решение оценивается в двух типах ходов: L (линии) и E (элементарные евклидовы построения). При этом построение точек не учитывается.

L подсчитывает действия инструментов: построение прямой, перпендикуляра, и так далее. E — количество ходов, как если бы построение делалось только с помощью настоящих циркуля и линейки. Каждый продвинутый инструмент имеет свою условную Е цену (см. таблицу).

Целью является решение задачи за наименьшее количество ходов. L и E цели могут достигаться независимо. Многие задачи имеют универсальное решение, удовлетворяющее обеим целям. Но некоторые задачи придётся решить дважды: одно решение, чтобы достигнуть L цели, второе — для E цели.

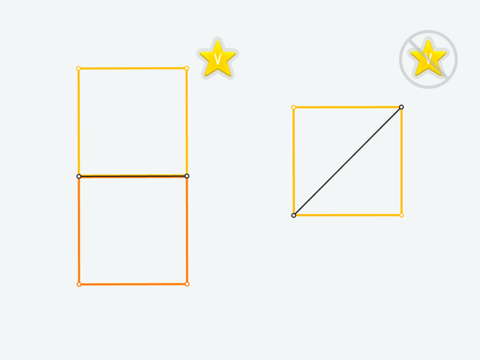
Если условию задачи удовлетворяет несколько фигур, вы можете получить скрытую V-звезду, построив их все на одном экране. Например, по заданной стороне можно построить два квадрата (V-звезда доступна), а если изначально дана диагональ, то квадрат определяется единственным образом (V-звезды нет). Обычно дополнительные решения получаются простым отражением или подразумевают некую симметрию.

Полезные подсказки:

Внимательно читайте формулировку задачи. Например, если в ней упоминается диагональ, рассмотрите варианты использования разных диагоналей.

Проверьте точки пересечения, на которых основано ваше построение. Например, окружность может пересекать прямую или другую окружность в двух точках. Если одна из этих точек используется при построении следующих фигур, попробуйте использовать для этого и вторую.

У некоторых задач может быть 3 или даже 4 ответа. Если вторая фигура принимается (подсвечена оранжевым), но V-звезда не дается, значит нужно продолжить поиск других ответов и достроить их.

В игре есть подсказки про V-звёзды. Они показывают количество ответов в текущем уровне. Откройте меню в правом верхнем углу игрового экрана (три горизонтальные линии), нажмите на «Лампочку» и выберите подсказку «V-звезда».

Нажмите на кнопку для вызова меню в правом верхнем углу игрового экрана, затем на стрелку вправо.

Чтобы переключить язык в игре:

Нажмите на шестерёнку на главном экране.
В открывшемся диалоге выберите второй пункт.
Выберите нужный язык в списке и нажмите на нижнюю кнопку, чтобы его применить.

Вы можете переносить свой игровой прогресс (полученные звёзды и сохраненные решения задач) между устройствами, используя учетную запись Euclidea. Авторизуйтесь, чтобы не потерять свои результаты.

Euclidea — это игра, соревнование. Наша цель — пробудить у людей желание изучать геометрию.

Euclidea не хочет лишать своих пользователей удовольствия самостоятельно найти решение. Поэтому мы не предоставляем готовых ответов к задачам, а только даём подсказки.

Если вы хотите продолжить игру без совершения встроенной покупки, необходимо собрать все звёзды в первых двух разделах. Пожалуйста, проверьте, что у вас всего 74 звезды. (См. Как найти скрытые V-звёзды?)

Примечание. После покупки звёзды перестают учитываться, и задачи открываются одна за другой по мере их решения. Можно также пропустить любую задачу.

Есть несколько способов играть в Euclidea бесплатно.

На мобильном устройстве (телефоне или планшете) с iOS либо Android:

Решать каждую задачу на максимальный балл. Вы можете пройти всю игру, если получаете все звёзды (L, E и V). Это трудно, но возможно.
Если у вас нет возможности приобрести встроенную покупку, снимающую это ограничение, но вы любите геометрию, то можно попросить промокод в нашей группе ВКонтакте. Там также помогут с решением задач, если они не поддаются.

Играйте в браузерную версию Euclidea. В ней не надо собирать все звёзды, чтобы пройти дальше. Новые задачи открываются по мере решения предыдущих.

Android: Чтобы выйти из приложения Euclidea, используйте системную кнопку «назад». Если виртуальные кнопки скрыты, проведите пальцем вверх от нижнего края экрана для вызова панели навигации.

Точки не учитываются. Любой другой инструмент, порождающий прямую или окружность, стоит 1L. E-цена индивидуальна:

Подсказка. E-цена выбранного инструмента отображается в левом верхнем углу кнопки в виде маленьких точек.

Циркуль Евклида «схлопывался», отрываясь от чертежа. В Euclidea ему соответствует инструмент «Окружность». Циркуль, сохраняющий расстояние, тоже есть, он появляется в разделе Дзета.

Покупки восстанавливаются автоматически, если вы используете тот же Google аккаунт или Apple ID. Т.е. после прохождения паков Альфа и Бета, пак Гамма должен разблокироваться автоматически. Если вы используете другой аккаунт, то покупка не восстановится.

iOS: Чтобы восстановить покупки выберите «Настройки» -> «Покупки» -> «Восстановить покупки».

Euclidea: Типичные ошибки и заблуждения

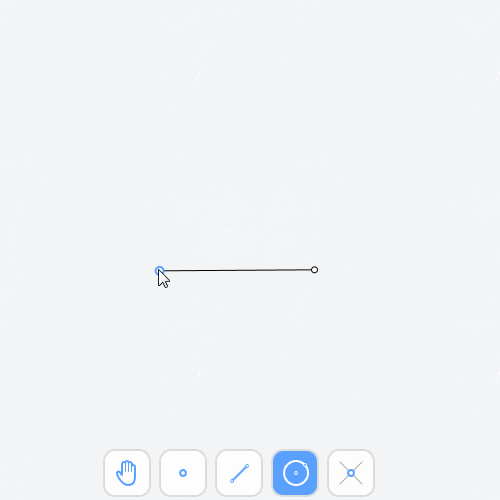
Распространённой ошибкой в обучающем уровне «Равносторонний треугольник» является построение окружностей на глаз.

Выберите инструмент «Перемещение» («Рука») и убедитесь, что ваше построение не содержит красные точки. Красным помечаются точки, которые не являются фиксированными и могут быть перемещены.

Чтобы пройти этот уровень, при построении окружности следует провести пальцем от центра до второй точки так, чтобы она «прилипла».

Точное построение

Приближенное построение

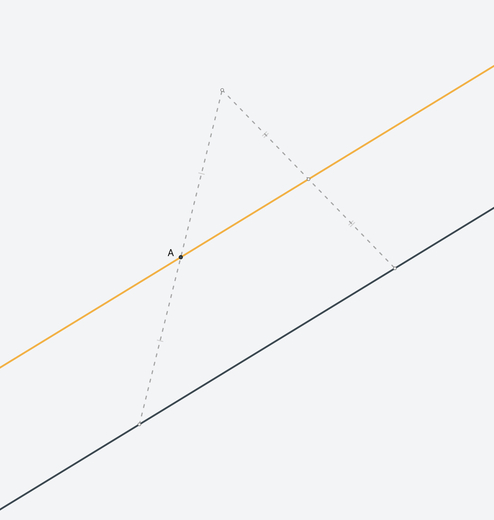
Пунктирная линия является только декорацией инструмента «Серединный перпендикуляр», и для построений её нельзя использовать.

Неправильное построение

Красная точка не закреплена, её можно перемещать.

Напомним, что ромб — это четырёхугольник, у которого все стороны равны.

Общей ошибкой в уровне «Ромб, вписанный в прямоугольник» является предположение, что угол ромба равен 60 градусам.

Чтобы проверить правильность своего построения, выберите инструмент «Перемещение» («Рука») и подвигайте левую верхнюю вершину прямоугольника. Правильное построение должно быть устойчивым к подобным трансформациям, и ромб должен оставаться ромбом.

Для решения этой задачи вспомните, что диагональ ромба — серединный перпендикуляр к другой диагонали.

Пример неправильного построения

В задаче «Квадрат, вписанный в окружность» данная точка, лежащая на окружности, должна быть одной из вершин квадрата.

Пример неправильного построения

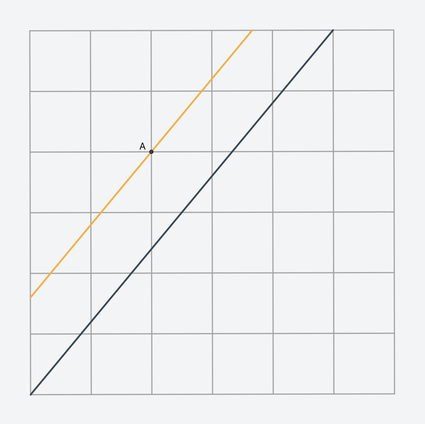
Чтобы проверить правильность своего построения в уровне 2.5 «Разрезание прямоугольника»:

Включите режим Исследования с помощью оранжевой кнопки в правом нижнем углу экрана (в нем отображаются искомые объекты).
Повторите свои построения.
Выберите инструмент «Перемещение» («Рука») и подвигайте левую верхнюю вершину прямоугольника.

Правильное построение должно совпадать с ответом (оранжевая прямая) при любой конфигурации точек и фигур.

Ключ к решению этой задачи легко найти, заметив закономерность движения оранжевой прямой (ответа) при перемещении заданной точки в режиме Исследования.

Пример неправильного построения

Euclidea: Подсказки и хитрости

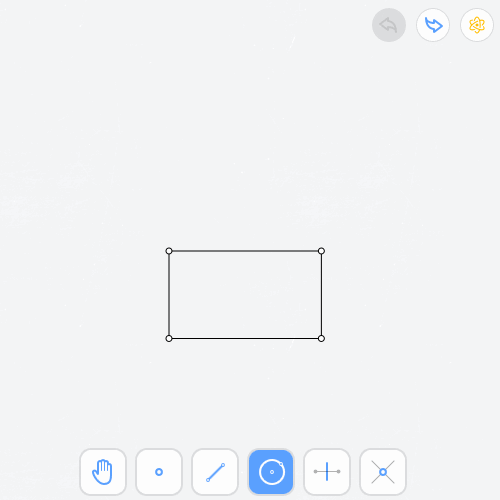
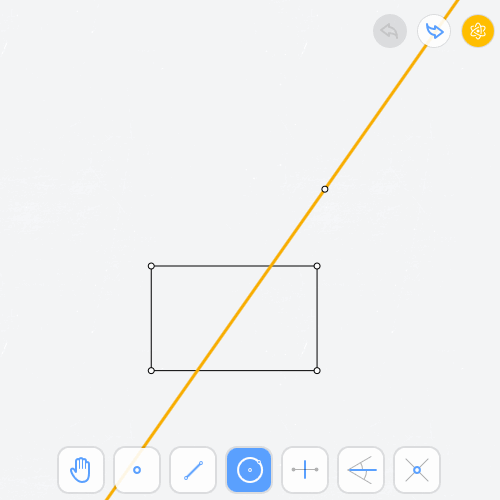
Чтобы получить 3 звезды в задаче 1.6 «Центр окружности», нужно её решить два раза — одно решение за 2L (две линии) для L-звезды, а другое за 5E (пять элементарных построений — окружностей или прямых) для E-звезды.

L и E цели являются независимыми, хотя у некоторых задач существуют универсальные решения, за которые можно получить сразу три звезды.

Чтобы найти решение 5E для задачи 1.6 «Центр окружности», попробуйте построить 2 серединных перпендикуляра с помощью окружностей и прямых. Затем останется понять, как сэкономить одну окружность. Последовательность инструментов — OOO// (3 окружности и 2 прямые).

Задача 1.7 «Квадрат, вписанный в окружность» может быть решена с помощью следующей последовательности инструментов: OO///// (2 окружности и 5 прямых). Попробуйте проанализировать, как именно надо построить эти линии.

Первая окружность — единственно возможная.
Вторая окружность позволяет получить нижнюю вершину искомого квадрата.
Последние 4 прямые — стороны квадрата.

Остаётся понять, как построить третью прямую, чтобы получить ещё полезные точки. Экспериментировать удобно в режиме Исследования (оранжевая иконка), в котором отображаются искомые объекты.

Прием, используемый для оптимизации решения задачи 2.2, аналогичен примененному в уровне 1.6 («Центр окружности»). Две биссектрисы строятся с помощью окружностей и прямых, но некоторые окружности используются повторно, сокращая количество ходов. В частности, все 4 окружности оказываются одного радиуса.

Чтобы решить задачу 2.6 «Опустить перпендикуляр» за 3Е, постройте точку, симметричную данной относительно прямой (2 окружности). Затем соедините точки.

Для решения задачи 2.7 «Восстановить перпендикуляр» за 3E можно заметить, что вписанный угол, опирающийся на диаметр, является прямым. Последовательность инструментов: O// (окружность и 2 прямые).

Чтобы решить задачу 2.7 «Восстановить перпендикуляр» за один ход, вам понадобится всего один единственный инструмент. Обратите внимание, что 180 / 2 = 90.

Задача 2.8 «Касательная к окружности в точке» может быть решена с помощью следующей последовательности инструментов: OO/ (2 окружности и прямая). Примечательно, что для этого решения не нужен центр окружности.

Чтобы решить задачу 4.1 «Удвоенный отрезок», пользуясь только циркулем, необходимо построить 3 окружности. Первые 2 окружности — единственно возможные. Остаётся понять, как построить третью окружность, чтобы получить в пересечении искомую точку.

Последовательность инструментов для решения: OOА (2 окружности и биссектриса). Последний шаг даст вам ключ к первым двум. Обратите внимание, что не всякая точка подходит в качестве центра первой окружности. В частности, она не лежит на заданном луче.

Задача о трисекции угла в общем случае неразрешима. Поэтому нужно воспользоваться одним из равенств:

54 / 3 = 18
90 — 54 = 36 = 2 * 18

Euclidea: Предложения и пожелания

Сейчас Euclidea доступна на следующих языках:

английский
русский
французский
немецкий
итальянский
испанский
португальский (Бразилия)
греческий
японский
корейский
упрощенный китайский
голландский
украинский
польский
словацкий

Если вы хотите помочь с переводом на другие языки, пожалуйста, напишите нам на support@euclidea.xyz.

Мы рассматривали возможность добавить отдельный режим для свободного рисования, однако пришли к выводу, что в игре это будет выглядеть неуместно. Поэтому мы решили сделать отдельное приложение, основанное на Euclidea, где можно было бы выполнять произвольные построения, сохранять их, изменять стили линий и т.д.

iOS: Встречайте Euclidea: Sketches.

Мы не планируем добавлять в игру инструмент, стирающий линии.

Пифагория: Общие вопросы

Чтобы пропустить уровень в Пифагории и Пифагории 60°, несколько раз нажмите на кнопку Вперед (стрелка вправо), пока она не заполнится цветом. Можно посмотреть видео в нашем Instagram. С каждым разом количество нажатий для пропуска будет увеличиваться, так что не злоупотребляйте.

Пифагория: Подсказки

Чтобы пройти уровень 1.13, попробуйте построить вспомогательную прямую, которая проходила бы через середину данного отрезка.

Например, это может быть вертикальная линия — серединный перпендикуляр отрезка (для его построения тоже потребуются дополнительные линии, как в задаче 1.12).

Задача со звёздочкой: решить 1.13 с помощью всего одной дополнительной прямой.

Есть несколько способов решить задачу 2.19.

Например, можно подобрать такой треугольник с вершинами в узлах сетки, чтобы одна его сторона лежала на заданной прямой, данная точка была серединой второй стороны, и можно было легко найти середину третьей. Средняя линия такого треугольника будет ответом к задаче.

Пифагория: Распространенные ошибки

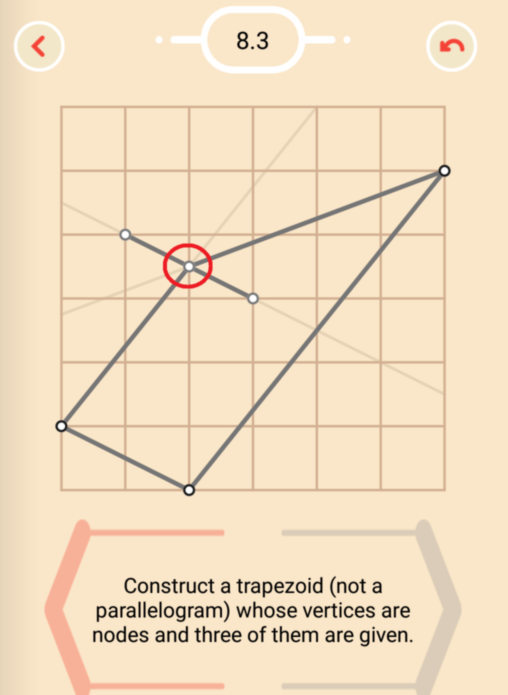
Вершины искомой трапеции в задаче 8.3 должны находиться в узлах сетки, то есть в точках пересечения линий сетки. Чтобы посмотреть определения в глоссарии, нажмите кнопку «i» на игровом экране.

XSection: Общие вопросы

XSection на Android мы выпустили позднее iOS версии и реализовали в нем несколько новых идей. Дизайн приложения был полностью обновлен, а задачи распределены по-новому.

Обновление XSection для iOS пока не планируется.

XSection: Типичные заблуждения

В задаче 9.5 нет ошибки. В диагональном сечении куба прямоугольник, а не квадрат, и его диагонали не перпендикулярны. Это заблуждение очень популярно у наших пользователей, поэтому мы специально выложили визуализацию таких сечений куба.

Исследовательская работа «Как найти центр окружности»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №1 с. Александров – Гай

Исследовательская работа по математике:

Подготовил: Амиров Марат, ученик 6 «а»

класса МБОУ СОШ №1 с. Александров – Гай

Руководитель: Кушкумбаева С.М., учитель математики МБОУ СОШ №1 с. Александров — Гай

С. Александров – Гай

Глава 1 «Способы нахождения окружности» …………………………………..4

Глава 2 «Практическая часть»…………………………………………………..6

Список литературы и источников………………………………………………12

Окружность — совокупность точек, находящихся на равном расстоянии от одной точки, называемой центром. Однако в тех случаях, когда вам дана одна только окружность, нахождение ее центра может быть непростой задачей. Поэтому цель моей исследовательской работы: изучить способы определения центра окружности. Исходя из цели были поставлены задачи:

— найти самый простой способ определения центра окружности;

— сравнить несколько способов определения центра окружности;

— практические способы определения центра окружности.

Актуальность ислледовательской работы заключается в том, что в повседневной жизни людей часто приходится находить центр окружности, но не каждый знает как это правильно сделать. Поэтому изучение данной темы поможет найти правильное решение проблемы и определить оптимальный вариант для человека любой професии.

При написании исследовательской работы были использованны электронные источники и литература. Электронные источники помогли найти теоретический материал по теме, а учебники по математике были использованны для подбора задач и практической части работы.

Глава 1. Способы нахождения центра окружности.

1.Самый простой способ нахождения центра окружности — согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной окружности. Затем лист можно согнуть в другом направлении, получив тем самым второй диаметр. Точка их пересечения и будет центром окружности.

2. Для того чтобы найти центр окружности, надо сначала вписать ее в квадрат. То есть все стороны четырехугольника должны касаться круга. Для этого проведите с помощью линейки четыре ровные линии. Теперь соедините по диагонали два противоположных угла. Следите за тем, чтобы линия разбивала угол квадрата на две равные части. Соедините прямыми все 4 угла квадрата. Точка пересечения данных прямых и будет центром окружности.

3. Для любого треугольника центр описанной окружности находится в точке пересечения срединных перпендикуляров. Если этот треугольник — прямоугольный, то центр описанной окружности всегда совпадает с серединой гипотенузы. Следовательно, если вписать в окружность прямоугольный треугольник, то его гипотенуза будет диаметром этой окружности.
В качестве трафарета для этого способа подойдет любой прямой угол — школьный или строительный угольник, или просто лист бумаги. Поместите вершину прямого угла в любую точку окружности и сделайте отметки там, где стороны угла пересекают границу круга. Это конечные точки диаметра.
Тем же способом найдите второй диаметр. В точке их пересечения

4.На круглую деталь накладываем лист бумаги так, что бы один его угол находился на окружности или крае круга. И отмечаем точки, где лист соприкасается другими краями с кругом. Отмечаем эти точки .

Проводим прямую линию между отмеченными точками. Расстояние между ними является диаметром этого круга. Обрезаем лишнюю бумагу и проводим на детали прямую линию — диаметр.

Достаточно переместить наш треугольник в другое положение и нарисовать еще один диаметр круга, как тут же в точке пересечения диаметров мы и получим искомый центр окружности…

5. Диаметр и радиус окружности.

Диаметр окружности — это отрезок прямой, соединяющий пару наиболее удаленных друг от друга точек окружности, проходящий через центр окружности. Слово «диаметр» произошло от греческого слова «diametros» — поперечный. Обычно диаметр обозначается латинской буквой D или значком Ø.

Диаметр можно найти по формуле: D = 2R, где диаметр равен удвоенному радиусу окружности.
Радиус — расстояние от центра до любой точки окружности. Обозначается латинской R.
Если известен радиус окружности, допустим, он равен 8 см, то значит D = 2 * 8 = 16 см.

Радиус окружности определяется по формуле : R = D :2

Глава 2 «Практическая часть»

Прямой угол детали закруглен дугой радиуса R

Для решения задачи с центром в вершине прямого угла проводят окружность радиуса R , которая пересекает стороны прямого угла в точках А и В.

С центрами в точках А и В строят еще две окружности радиуса R ; С – их точка пересечения. Дуга окружности радиуса R с центром в точке С и будет искомым закруглением.

Быстрый способ, как найти центр окружности

В данном обзоре автор поделится с нами довольно простым способом, как быстро найти центр окружности.

Для этого нам потребуется всего два предмета: угольник и карандаш. Первым делом необходимо провести прямую линию в любом месте окружности.

Советуем также прочитать: как изготовить своими руками антенну для усиления 4G сигнала на даче или в частном доме.

После того, как начертили линию, измеряем длину, и делим это расстояние ровно пополам.

В данном случае длина линии составляет 210 мм. Разделив ее пополам, получаем 105 мм — ставим в этом месте отметку.

С помощью угольника проводим вторую линию, которая должна быть перпендикулярна первой (то есть проходить под углом 90 градусов).

Основные этапы работ

На следующем этапе проделываем те же операции с другой стороны окружности (только не параллельно, а немного в стороне).

Чертим линию, измеряем ее длину (в данном случае — 218 мм), делим пополам (109 мм) и откладываем в этом месте точку. После этого проводим перпендикулярную линию, как и в предыдущем случае.

Пересечение двух линий, которые мы чертили под углом 90 градусов, и будет являться центром круга.

Подробно об этом способе можно посмотреть на видео ниже. Статья подготовлена на основе видео с YouTube канала « ПОГРАНЕЦ 13 ».

источники:

http://infourok.ru/issledovatelskaya-rabota-kak-nayti-centr-okruzhnosti-552229.html

http://sdelairukami.ru/bystryj-sposob-kak-najti-czentr-okruzhnosti/

Источник

Для определения центра данной окружности с помощью одного циркуля, когда начерчена только сама окружность, можно использовать метод построения обратных точек (рис. 1).

Из произвольно взятой на окружности точки А проводим дугу произвольным радиусом d, пересекающую данную окружность в точках В и С. Из этих точек как центров описываем дуги (В, d) и (С, d), пересекающиеся, кроме точки А, еще в точке D. Тогда неизвестный центр О есть точка, обратная точке D относительно окружности с центром А. Из точки D описываем дугу радиусом DА, пересекающую дугу (А, d) в точках Е и F. В заключительном построении проведем две дуги (Е, d) и (F, d), пересекающиеся в искомой точке О.

Второй метод построения центра начерченной окружности изображен на рис. 2.

Источник

Загрузить PDF

Найдя центр круга или окружности, вы сможете решать различные геометрические задачи, например, на вычисление длины окружности или площади круга. Найти центр круга можно разными способами. Вы можете провести пересекающиеся отрезки; вы можете начертить пересекающиеся окружности; вы можете воспользоваться линейками.

1
Начертите окружность. Сделайте это при помощи циркуля. Радиус (диаметр) круга может быть любым. Если окружность вам дана, новую окружность чертить не нужно.
- Циркуль – это инструмент, предназначенный для черчения окружностей и их измерения. Циркуль можно купить в канцелярском магазине или в магазине для школьников.^[1]
2
Проведите хорду. Хорда – это отрезок, соединяющий любые две точки, лежащие на окружности, и не проходящий через центр окружности.^[2] Обозначьте эту хорду как АВ.
- Проводите прямые и отрезки при помощи карандаша, чтобы иметь возможность стереть их после нахождения центра окружности. Не давите на карандаш, чтобы вам было легче стереть нарисованные линии.
3

Проведите вторую хорду. Она должна быть параллельна и равна первой хорде АВ. Обозначьте эту хорду как CD.^[3]
4

Соедините точки А и С. Эта третья хорда АС должна проходить через центр окружности, но для его нахождения вам понадобится провести четвертую хорду.
5

Соедините точки B и D. Это четвертая хорда BD, которая должна пересекаться с третьей хордой AC.
6

Найдите центр окружности. Если вы правильно провели все отрезки (хорды), то центр окружности – это точка пересечения хорд AC и BD.^[4] Отметьте центр окружности ручкой или карандашом. Если вам нужно отметить только центр окружности, сотрите четыре хорды, которые вы провели ранее.

Реклама

1

Между двумя точками окружности проведите хорду. Воспользуйтесь линейкой, чтобы соединить две точки на окружности. Точки можно выбрать произвольно. Обозначьте точки как А и В.
2
При помощи циркуля начертите две пересекающиеся окружности. Окружности должны быть одного радиуса. Центром первой окружности сделайте точку А, а второй окружности – точку В. Чертите окружности так, чтобы они пересекались наподобие диаграммы Венна.
- Чертите окружности карандашом, а не ручкой, чтобы иметь возможность стереть их.
3

Проведите вертикальную прямую через точки пересечения начерченных окружностей. Окружности будут пересекаться в двух точках, которые расположены одна над другой. Проведите прямую при помощи линейки; убедитесь, что обе точки лежат на этой прямой. Точки, в которых эта прямая пересекает исходную окружность, обозначьте как С и D. Отрезок СD является диаметром исходной окружности.
4

Сотрите две начерченные вами окружности. Это необходимо для того, чтобы очистить пространство для последующих действий. Теперь на вашем листе останется исходная окружность и два перпендикулярных друг другу отрезка. Не стирайте центры стертых окружностей (эти центры расположены в точках А и В). Далее вы начертите две новые окружности.
5

Начертите две новые окружности. Для этого воспользуйтесь циркулем. Центром первой окружности будет точка С, а второй окружности – точка D. Эти окружности также должны пересекаться наподобие диаграммы Венна. Помните, что точки С и D – это точки пересечения вертикальной прямой с исходной окружностью.
6

Проведите прямую через две точки, в которых пересекаются начерченные вами окружности. Эта прямая будет расположена горизонтально. Полученный отрезок представляет собой второй диаметр исходной окружности и должен быть перпендикулярен первому диаметру.
7

Найдите центр окружности. Точка пересечения двух диаметров является центром исходной окружности. Отметьте эту точку. Если нужно, сотрите начерченные вами окружности и диаметры.

Реклама

1

К данной окружности проведите две касательные. Касательные можно провести к двум произвольным точкам окружности. Но вы облегчите себе работу, если проведете касательные под прямым или острым углом друг к другу.^[5]
2

Теперь проведите еще две касательные, которые будут параллельны касательным, которые вы провели в предыдущем шаге. Таким образом, проведенные четыре касательные образуют подобие параллелограмма или прямоугольника.
3

Проведите диагонали параллелограмма. Точка пересечения этих диагоналей является центром окружности.
4

Проверьте правильность нахождения центра окружности при помощи циркуля. Центр окружности расположен строго в точке пересечения диагоналей, только если вы не допустили ошибку при проведении параллельных касательных или диагоналей. Сотрите параллелограмм и его диагонали.

Реклама

Советы

Вместо чистого листа или листа в линейку работайте на листе в клетку. Так вам будет проще проводить перпендикулярные прямые.
Центр окружности можно вычислить математически через дополнение до полного квадрата.^[6] Это работает в том случае, если вам дано уравнение окружности, а не сама окружность.

Предупреждения

Поверочная линейка немного отличается от обычной линейки. В отличие от обычной линейки на поверочной линейке нет шкалы. Вы можете превратить поверочную линейку в обычную, если нанесете на нее измерительную шкалу.
Чтобы найти «истинный» центр окружности, используйте циркуль и поверочную линейку.

Что вам понадобится

Карандаш
Бумага
Линейка
Циркуль

Об этой статье

Эту страницу просматривали 232 087 раз.

Была ли эта статья полезной?

Источник

Download Article

Finding the center of a circle can help you perform basic geometric tasks like finding the circumference or area. There are several ways to find the center point! You can draw crossed lines, you can draw overlapping circles, or you can use a straightedge and ruler.

Things You Should Know

Measure out and draw a set of crossed lines inside of a circle to pinpoint the center.
Sketch two separate sets of overlapping circles to identify the exact center point.
Draw a square snugly around the circle. Sketch an «X» between all 4 corners of the square to find the circle’s center.

1
Draw a circle. Use a compass, or trace any circular object. The size of the circle does not matter. If you’re finding the center of an existing circle, then you don’t need to draw a new circle.
- A geometry compass is a tool specifically designed to draw and measure circles. Buy one in a school or office supply store!^[1]
2
Sketch a chord between two points. A chord is a straight line segment that links any two points along the edge of a curve.^[2] Name the chord AB.
- Consider using a pencil to sketch your lines. This way, you can erase the marks once you’ve found the center. Draw with a light touch so that it’ll be easier to erase.
Advertisement
3

Draw a second chord. This line should be parallel and equal in length to the first chord that you drew. Name this new chord CD.^[3]
4

Make another line between A and C. This third chord (AC) should stretch through the center of the circle – but you will need to draw one more line to find the exact center point.
5

Join B and D. Draw one final chord (BD) across the circle between Point B and Point D. This new line should cross over the third chord (AC) that you drew.
6

Find the center. If you have drawn straight and accurate lines, then the center of the circle lies at the intersection of the crossed lines AC and BD.^[4] Mark the center point with a pen or pencil. If you only want the center point marked, then erase the four chords that you drew.

1

Draw a chord between two points. Use a ruler or straightedge to draw a straight line inside the circle, from one edge to another. The points that you use don’t matter. Label the two points A and B.
2
Use a compass to draw two overlapping circles. The circles should be the exact same size. Make A the center of one circle, and B the center of the other. Space the two circles so that they overlap like a Venn diagram.
- Draw these circles in pencil, not pen. The process will be simpler if you are able to erase these circles later on.
3

Draw a vertical line through the two points at which the circles intersect. There will be a point at the top and a point at the bottom of the «Venn diagram» space created between the overlap of the circles. Use a ruler to make sure that the line protrudes straight through these points. Finally, label the two points (C and D) at which this new line crosses the rim of the original circle. This line marks the diameter of the original circle.
4

Erase the two overlapping circles. This should clear up your work space for the next step of the process. Now, you should have a circle with two perpendicular lines running through it. Do not erase the center points (A and B) of these circles! You will be drawing two new circles.
5

Sketch two new circles. Use your compass to draw two equal circles: one with the point C at its center, and one with the point D. These circles, too, should overlap like a Venn diagram. Remember: C and D are the points at which the vertical line intersects the main circle.
6

Draw a line through the points at which these new circles intersect. This straight, horizontal line should cut through the overlap space of the two new circles. This line is the second diameter of your original circle, and it should be exactly perpendicular to the first diameter line.
7

Find the center. The intersection point of the two straight diameter lines is the exact center of the circle! Mark this center point for reference. If you want to clean up the page, feel free to erase the diameter lines and the non-original circles.

1

Draw two straight, intersecting tangent lines onto the circle. The lines can be completely random. However, the process will be easier if you make them roughly square or rectangular.^[5]
2

Translate both of the lines to the other side of the circle. You will end up with four tangent lines forming a parallelogram or a rough rectangle.
3

Draw the diagonals of the parallelogram. The point where these diagonal lines intersect is the circle’s center.
4

Check the accuracy of the center with a compass. The center should be on target as long as you didn’t slip while translating the lines or when drawing the diagonals. Feel free to erase the parallelogram and diagonal lines.

Practice Problems and Answers

Add New Question

Question

How do you find the center of a circle if you’re only given the equation?

David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.

Academic Tutor

Expert Answer
Question

How do you find the center of the circle if you’re only given the endpoints of the diameter?

David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.

Academic Tutor

Expert Answer
Question

In the first method, what do I do if the chords are of different lengths?

It’s not easy to construct parallel chords of equal length. In practice, it would be a process of trial and error until you get the chords you need. But the real goal here is to find the center of a circle, and here’s a way to do it without worrying about equal and parallel chords: (1) draw any two or more chords; (2) perpendicularly bisect each chord (using either a compass or a ruler and right triangle; (3) the perpendicular bisectors will intersect at the circle’s center.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

You can also find the center of a circle by mathematically «completing the square.»^[6] This is useful if you are given a circle equation, but you aren’t working with a physical circle.
Try using graph paper instead of blank or ruled paper. It might help to have the perpendicular lines and boxes for guidance.
If you have right angled square, place the corner anywhere along the circumference. Draw the 2 lines that intersect the circumference. Draw a line between those 2 points. Repeat on any other point on the circle. Where the lines intersect is the centrepoint.

A straightedge is not the same as a ruler. A straightedge can be any straight and even surface, but a ruler shows measurements. You can turn a straightedge into a functional ruler by marking it with inch or centimeter increments.
In order to find the true center of a circle, you must use a geometric compass and a straightedge.

Things You’ll Need

Pencil
Paper
Straightedge
Geometric compass
Grid paper

References

About This Article

Article SummaryX

To find the center of a circle, start by drawing a straight line between 2 points on the circle. Don’t worry about trying to draw the straight line so it’s in the center — anywhere on the circle will do. Then, draw a second straight line that’s parallel to the first line on the opposite side of the circle. Next, draw a diagonal line from the first end of the first line to the opposite end of the second line. Repeat with the other two ends so that you’ve drawn an “X.” The point where the lines intersect is the center of the circle! If you want to learn how to draw overlapping circles to find the center, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 757,122 times.

Reader Success Stories

«I had a circular piece of wood that was a circular tabletop that I wanted to use for something else. I needed to…» more

Did this article help you?

Источник

: October 15 2017, 11:33

Category:

Общество
Cancel

Как найти центр окружности без измерительных инструментов?

Действительно как? Вот у вас есть круг. И есть необходимость или желание узнать, где у него центр.
Самое простое — это вписать в круг квадрат или прямоугольник.
Затем провести диагонали соединяющие противоположные углы. Место пересечения этих линий и будет центром окружности, а каждая из этих линий будет являться её диаметром. Место пересечения диаметров окружности всегда будет является её центром.

Из этого так же следует, что гипотенуза вписанного в окружность прямоугольного треугольника так же всегда является ее диаметром. И здесь, чтобы найти центр окружности, достаточно найти ее середину. Ну, а середина находится легко: из вершины треугольника (прямого угла) к основанию (гипотенузе) проводится перпендикулярная линия. В прямоугольном треугольнике она делит основание ровно пополам. А так как гипотенуза — это диаметр окружности, то поделённая пополам, дает два радиуса и соответственно центр окружности.

Но центр можно найти не только с помощью прямоугольного треугольника. Можно вписать в окружность равносторонний или равнобедренный треугольник. С первым вообще все просто, как и с прямоугольником. У него все стороны равны и не составит труда вписать его в окружность. Здесь достаточно провести две медианы (они же высоты) из любых углов. Место их пересечения и будет центр окружности. Если их продолжить до линии окружности, то получим два пересекающихся диаметра.

Для нахождения центра круга при помощи равнобедренного треугольника необходимо произвести следующие действия. Вписать в окружность два любых равнобедренных треугольника. Форма треугольников и длина их бедер не имеют значения. После из вершин этих треугольников необходимо провести к основанию треугольника медиану/высоту. И продолжить ее до соприкосновения с окружностью. Место пересечения этих медиан/высот и будет центром круга. А они, как уже вы догадались, будут являться его диаметрами.

Как нетрудно увидеть, если чуть-чуть подумать, то можно вообще не чертить никаких фигур. Надо просто отложить внутри окружности две любых линии (хорды), не параллельных друг другу. Провести перпендикулярные линии через середины этих хорд к противоположной точке на окружности. И снова пересечение этих двух будет являться центром.

Так же центр окружности можно найти с помощью вписанной в круг трапеции. Используя трапеции несложно начертить прямоугольник или прямоугольный треугольник. А уже имея их — найти центр.

Но как начертить трапецию, треугольник или даже квадрат, не имея линейки с разметкой и транспортира? Как получить прямой угол? Ведь не все люди обладают точным глазомером и твердостью руки.
Для этого достаточно иметь под рукой веревку, полоску бумаги, да просто прямую палку. С помощью любого из этих подручных средств можно отложить на окружности линию (хорду). Далее, имея постоянную длинную отрезка, соединяя любые четыре точки на окружности, можно легко получить квадрат или равносторонний треугольник, соединив три точки. Ну а для верности, чтобы получить прямой угол можно применить лист бумаги, коробок спичек, симкарту, стол — любые предметы которые имеют прямой угол.
Осталось добавить, что выше перечисленные способы справедливы и в том случае, если окружность вписана в квадрат или равнобедренный треугольник, или проведены касательные к окружности.

Источник