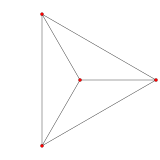
Центр — грань — правильный тетраэдр
Cтраница 1
Центры граней правильного тетраэдра служат вершинами нового тетраэдра.
[1]
Центры граней правильного тетраэдра служат вершинами нового правильного тетраэдра.
[2]
Центры граней правильного тетраэдра служат вершинами нового тетраэдра.
[3]
Определить расстояние от центра грани правильного тетраэдра до другой его грани, зная радиус вписанного шара.
[4]
При этом каждая из четырех граней может быть выбрана в качестве ее основания. Перпендикуляр, опущенный из любой вершины тетраэдра на противолежащую грань, проходит через ее центр. Центры граней правильного тетраэдра являются вершинами вписанного в него правильного тетраэдра.
[5]
Страницы:
1
Центры тяжести многоугольников и многогранников
Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.
Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.
В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.
Двумерный случай: многоугольники
На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:
- Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
- Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
- Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.
Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.
Центр масс системы точек
Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:
где — массы точек, — их радиус-векторы (задающие их положение относительно начала координат), и — искомый радиус-вектор центра масс.
В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:
Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке , в которой сумма моментов всех сил равна нулю. В данном случае это превращается в условие того, чтобы сумма радиус-векторов всех точек относительно точки , домноженных на массы соответствующих точек, равнялась нулю:
и, выражая отсюда , мы и получаем требуемую формулу.
Центр масс каркаса
Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.
Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.
Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:
где — точка-середина -ой стороны многоугольника, — длина -ой стороны, — периметр, т.е. сумма длин сторон.
Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).
Центр масс сплошной фигуры
Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.
Случай треугольника
Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:
Случай треугольника: доказательство
Приведём здесь элементарное доказательство, не использующее теорию интегралов.
Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian «Finding Centroids the Easy Way».
Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.
Разобьём данный треугольник на четыре, соединив середины сторон, как показано на рисунке:
Четыре получившихся треугольника подобны треугольнику с коэффициентом .
Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого лежит в точке пересечения его диагоналей (поскольку это фигура, симметричная относительно обеих диагоналей, а, значит, её центр масс обязан лежать на каждой из двух диагоналей). Точка находится посередине общей стороны треугольников №1 и №2, а также лежит на медиане треугольника :
Пусть теперь вектор — вектор, проведённый из вершины к центру масс треугольника №1, и пусть вектор — вектор, проведённый из к точке (которая, напомним, является серединой стороны, на которой она лежит):
Наша цель — показать, что вектора и коллинеарны.
Обозначим через и точки, являющиеся центрами масс треугольников №3 и №4. Тогда, очевидно, центром масс совокупности этих двух треугольников будет точка , являющаяся серединой отрезка . Более того, вектор от точки к точке совпадает с вектором .
Искомый центр масс треугольника лежит посередине отрезка, соединяющего точки и (поскольку мы разбили треугольник на две части равных площадей: №1-№2 и №3-№4):
Таким образом, вектор от вершины к центроиду равен . С другой стороны, т.к. треугольник №1 подобен треугольнику с коэффициентом , то этот же вектор равен . Отсюда получаем уравнение:
Таким образом, мы доказали, что вектора и коллинеарны, что и означает, что искомый центроид лежит на медиане, исходящей из вершины .
Более того, попутно мы доказали, что центроид делит каждую медиану в отношении , считая от вершины.
Случай многоугольника
Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.
Окончательная формула получается следующей:
где — центроид -го треугольника в триангуляции заданного многоугольника, — площадь -го треугольника триангуляции, — площадь всего многоугольника.
Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники , где .
Случай многоугольника: альтернативный способ
С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка , а затем суммируются знаковые площади треугольников, образованных этой точкой и точками многоугольника: . Аналогичный приём можно применить и для поиска центра масс: только теперь мы будем суммировать центры масс треугольников , взятых с коэффициентами, пропорциональными их площадям, т.е. итоговая формула для центра масс такова:
где — произвольная точка, — точки многоугольника, — центроид треугольника , — знаковая площадь этого треугольника, — знаковая площадь всего многоугольника (т.е. ).
Трёхмерный случай: многогранники
Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:
- Центр масс системы точек — вершин многогранника.
- Центр масс каркаса — рёбер многогранника.
- Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
- Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.
Центр масс системы точек
Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:
который в случае равных масс превращается в среднее арифметическое координат всех точек.
Центр масс каркаса многогранника
Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.
Центр масс поверхности многогранника
Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.
Центр масс сплошного многогранника
Случай тетраэдра
Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.
Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).
Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.
Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:
(это можно вывести из того факта, что центроид делит медианы в отношении )
Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.
Случай произвольного многогранника
Перейдём теперь к общему случаю — случаю произвольного многогранника.
Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.
Пирамида
Пирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.
По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Верно и обратное.
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр
Верно и обратное.
Виды пирамид
Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Пирамида. Правильная пирамида
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Данный видеоурок поможет пользователям получить представление о теме Пирамида. Правильная пирамида. На этом занятии мы познакомимся с понятием пирамиды, дадим ей определение. Рассмотрим, что такое правильная пирамида и какими свойствами она обладает. Затем докажем теорему о боковой поверхности правильной пирамиды.
http://interneturok.ru/lesson/geometry/10-klass/mnogogranniki/piramida-pravilnaya-piramida
Избранные теоремы геометрии тетраэдра
Выпускная квалификационная
работа
Избранные теоремы геометрии
тетраэдра
Специальность / направление
подготовки Математика
Специализация / профиль Математика
— информатика
Содержание
Введение
Глава I.
Виды тетраэдров и теоремы о тетраэдрах
1.1 Теоремы о тетраэдрах
§1. Теорема Менелая
§2. Теорема Чевы
§3. Свойства медиан и бимедиан
тетраэдра
1.2 Различные виды тетраэдров.
§1. Пифагоровы тетраэдры
§2. Ортоцентрические тетраэдры
§3. Каркасные тетраэдры
§4. Равногранные тетраэдры
§5. Инцентрические тетраэдры
§6. Соразмерные тетраэдры
§7. Правильные тетраэдры
Глава II.
Тетраэдр в курсе математики средней
школы
§1. Сравнительная характеристика
изложения темы «тетраэдр» в школьных
учебниках
§2. Тестирование уровня развития
пространственного мышления у учеников
средней школы
Введение
Интерес к изучению
тетраэдра возник у человечества с
древних времен и не угасает до сих пор.
Это связано не только с его красотой,
но и с большой практической ценностью.
Тетраэдр является
одним из основных фигур стереометрии,
однако его изучение в курсе средней
школы недостаточно подробно. В некоторых
учебниках авторы избегают самой
терминологии, предпочитая называть
фигуру «треугольной пирамидой» (и
рассматривают её именно в таком ключе),
а об изучении различных видов тетраэдров
зачастую и говорить не приходится.
Роль задач о тетраэдрах
в математическом развитии школьников
трудно переоценить. Они стимулируют
накопление конкретных геометрических
представлений, способствуют развитию
пространственного мышления, что особенно
важно в процессе изучения стереометрии.
Изучению тетраэдра как школе,
так и в вузах посвящено лишь небольшое
количество занятий, поэтому целью
дипломной работы является изучение
различных видов тетраэдров, а также
теорем, связанных с геометрией тетраэдра.
В соответствии с целью сформулированы
следующие задачи:
Собрать сведения о тетраэдре
из различных источников и привести их
в систему; разобрать доказательства
теорем, связанных с тетраэдром;
Проанализировать
методику изложения материала в различных
школьных учебниках;
Разработать курс занятий о
тетраэдре для средней школы.
В первой главе моей
дипломной работы речь пойдёт о различных
видах тетраэдра и некоторых теоремах,
касающихся этой фигуры. Вторая глава
посвящена анализу учебного материала
для средней школы по заданной теме и
разработке курса занятий.
Глава I.
Виды тетраэдров и теоремы о тетраэдрах
1.1 Теоремы
о тетраэдрах
§1. Теорема Менелая
Теорема Менелая для треугольника.
Пусть точки А>1>>
>и С>1>
лежат на сторонах ВC
и АC
треугольника АВС,
точка В>1>>
>на продолжении стороны
АС этого
треугольника. Для того чтобы точки А>1>,
В>1>,
С>1>
лежали на одной прямой необходимо и
достаточно, чтобы выполнялось равенство
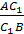
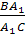
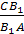
Доказательство.
Сначала докажем необходимость.
Пусть точки А>1>,В>1>,С>1>
лежат на прямой l
и AA>0>=h>1>,
CC>0>=h>3>>
>- перпендикуляры, опущенные
соответственно из точек А,
В, С на прямую l.
Из подобия треугольников АА>0>С>1>>
>и ВВ>0>С>1>>
>получаем
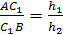
Аналогично, рассматривая другие пары
подобных треугольников, получаем
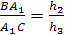
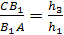
Перемножая полученные пропорции,
приходим к требуемому равенству.
Теперь докажем достаточность.
Пусть точки А>1>,
В>1>, С>1>,
лежащие на прямых ВС, АС, АВ таковы, что
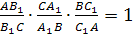
Докажем, что точки А>1>,
В>1>,
С>1>
лежат на одной прямой.
Проведем прямую А>1>В>1>>
>и докажем, что точка С>1>
ей принадлежит. Предположим, что это не
так. Сначала заметим, прямая А>1>В>1>>
>не параллельна прямой
АВ. Пусть Т
— точка пересечения А>1>В>1>>
>и АВ,
тогда
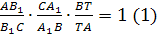
Из условия и равенства (1) следует, что
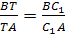
Так как точки Т
и С>1>>
>лежат вне отрезка АВ,
их совпадение вытекает из следующей
леммы.
Лемма 1.
Пусть А и В две различные точки,
тогда для любого k>0, k≠1 на прямой АВ
существуют две точки U и V такие, что
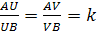
причем одна из этих точек принадлежит
отрезку АВ, а другая лежит вне отрезка.
Доказательство.
Введем на прямой АВ
координаты, приняв точку А
за начало координат. Пусть для
определенности k>1,
тогда координата искомой точки U,
лежащей внутри отрезка АВ,
удовлетворяет уравнению
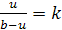
откуда
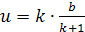
Точка V
находится вне отрезка AB,
из уравнения
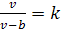
откуда
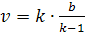
Случай 0<k<1
отличается от рассмотренного лишь тем,
что точку V
следует искать левее точки А.
Теорема Менелая допускает
интересное стереометрическое обобщение.
Теорема Менелая для тетраэдра.
Если плоскость μ
пересекает ребра АВ, ВС, CD
и DA тетраэдра
АВСD в точках
А>1>,
В>1>,
С>1>,
D>1>, то
(2).
Обратно, если для четырех точек
А>1>,
В>1>,
С>1>,
D>1>,
лежащих соответственно
на ребрах АВ, ВС, СD, DA
тетраэдра, выполнено равенство (2), то
эти четыре точки лежат в одной плоскости.
Доказательство.
Пусть h>1>,
h>2>,
h>3, >h>4>>
>- расстояния от точек
А, В, С, D соответственно до
плоскости μ,
тогда
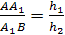
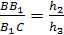
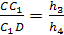
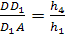
Осталось перемножить полученные
отношения.
Для доказательства обратной
теоремы построим плоскость А>1>,
В>1>, С>1>.
Пусть эта плоскость пересекает ребро
DA в точке Т.
По доказанному
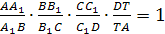
а по условию
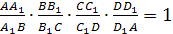
поэтому (и по лемме) точки Т
и D>1>>
>совпадают.>
>Утверждение доказано.
§2. Теорема Чевы
Теорема Чевы для треугольника.
Пусть точки А>1>,
В>1>,С>1>>
>лежат соответственно на
сторонах ВС, АС
и ВА треугольника
АВС (см. рис).
Для того чтобы отрезки АА>1>,
ВВ>1>,
СС>1>
пересекались в одной точке, необходимо
и достаточно, чтобы выполнялось
соотношение:
(3) (отрезки АА>1>,
ВВ>1>,
СС>1>>
>иногда называют чевианами).
Доказательство.
Необходимость. Пусть отрезки
АА>1>,
ВВ>1>,
СС>1>>
>пересекаются в точке М
внутри треугольника АВС.
Обозначим через S>1>,
S>2>,
S>3>>
>площади треугольников
АМС, СМВ, АМВ,
а через h>1>,
h>2> —
расстояния от точек А
и В до прямой
МС. Тогда
аналогично
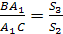
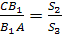
Перемножив полученные пропорции,
убеждаемся в справедливости теоремы.
Достаточность. Пусть точки А>1>,
В>1>,
С>1>>
>лежат на сторонах ВС,
СА, АС треугольника, и
выполнено соотношение (3), М
— точка пересечения отрезков АА>1>и
ВВ>1>,
а отрезок СМ
пересекает сторону АВ
в точке Q.
Тогда, по уже доказанному
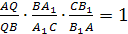
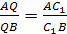
Из леммы снова следует совпадение точек
Q=C>1>.
Достаточность доказана.
Перейдем теперь к пространственному
обобщению теоремы Чевы.
Теорема Чевы для тетраэдра.
Пусть М
— точка внутри тетраэдра АВСD,
а А>1>,
В>1>,
С>1>
и D>1> —
точки пересечения плоскостей СМD,
AMD, АМВ и СМВ
с ребрами АВ, ВC,
СD и DA
соответственно. Тогда
(4). Обратно: если для точек
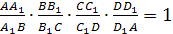
то плоскости АВС,
ВСD>1>
и DAB>1>>
>проходят через одну точку.
Доказательство.
Необходимость легко получить,
если заметить, что точки А>1>,
В>1>,>
>С>1>,
D>1>
лежат в одной плоскости (эта плоскость
проходит через прямые А>1>С>1>
и В>1>D>1>,
пересекающиеся в точке М),
и применить теорему Менелая. Обратная
теорема доказывается так же, так и
обратная теореме Менелая в пространстве:
нужно провести плоскость через точки
А>1>,
В>1>,
С>1> и
доказать с помощью леммы, что эта
плоскость пересечет ребро DA
в точке D>1>.
§3. Свойства медиан и бимедиан
тетраэдра
Медианой тетраэдра называется
отрезок, соединяющий вершину тетраэдра
с центром тяжести противоположной грани
(точкой пересечения медиан).
Теорема (Применение теоремы
Менелая).
Медианы тетраэдра пересекаются
в одной точке. Эта точка делит каждую
медиану в отношении 3:1, считая от вершины.
Доказательство.
Проведем две медианы: DD>1>
и CC>1>
тетраэдра ABCD.
Эти медианы пересекутся в точке F.
CL
– медиана грани ABC,
DL
– медиана грани ABD,
а D>1>,
C>1>
– центры тяжести грани ABC
и ABD.
По теореме Менелая:
и
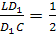
Запишем теорему для треугольника DLD>1>:
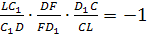
=>
Доказательство производится аналогично
для любой другой пары медиан.
Теорема (Применение теоремы
Чевы).
Для начала дадим определения
некоторых элементов тетраэдра. Отрезок,
соединяющий середины скрещивающихся
ребер тетраэдра называется бимедианой.
Бивысотами (по аналогии) называют общие
перпендикуляры скрещивающихся ребер.
Теорема.
Бимедианы тетраэдра пересекаются
в той же самой точке, что и медианы
тетраэдра.
Доказательство.
В треугольнике LDC
отрезки DC
и LF
пересекутся в точке K.
По теореме Чевы для этого треугольника:
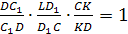
т.е.
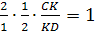
CK=KD,
LK
– бимедиана.
Замечание 1.
FL=FK.
Теорема Менелая для треугольника DLK:
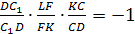
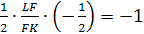
отсюда LF=FK.
Замечание 2.
Точка F
является центром тяжести тетраэдра.
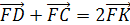
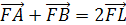
значит
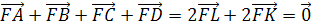
1.2 Различные
виды тетраэдров
§1. Пифагоровы
тетраэдры
Треугольник называется пифагоровым,
если у него один угол прямой, а отношение
любых сторон рационально (т.е применяя
подобие, можно из него получить
прямоугольный треугольник с целыми
длинами сторон).
По аналогии с этим, тетраэдр
называют пифагоровым, если его плоские
углы при одной из вершин прямые, а
отношение любых двух ребер рационально
(из него с помощью подобия можно получить
тетраэдр с прямыми плоскими углами при
одной из вершин и целыми длинами ребер).
Попробуем вывести «Уравнение
пифагоровых тетраэдров», т.е. такое
уравнение с тремя неизвестными ξ, η, ζ,
что любой пифагоров тетраэдр дает
рациональное решение этого уравнения,
и наоборот, любое рациональное решение
уравнения дает пифагоров тетраэдр.
Сначала дадим способ описания
всех пифагоровых треугольников.
На рисунке треугольник ОАВ
— прямоугольный, длины его катетов
обозначены через а
и b, а дина
гипотенузы — через р.
Число
(1) условимся называть параметром
прямоугольного треугольника ОАВ
(или точнее, параметром «относительно
катета а«).
Используя соотношение р2=а2+b2,
имеем:
Из этих уравнений непосредственно
получим формулы, выражающие отношения
сторон прямоугольного треугольника
через его параметр:
и
(2).
Из формул (1) и (2) непосредственно
вытекает следующее утверждение: для
того, чтобы прямоугольный треугольник
был пифагоровым, необходимо и достаточно,
чтобы число ξ было рациональным. В самом
деле, если треугольник пифагоров, то из
(1) следует, что ξ рационально. Обратно,
если ξ рационально, то согласно (2)
отношения сторон рациональны, то есть
треугольник пифагоров.
Пусть теперь ОАВС
— тетраэдр, у которого плоские углы при
вершине О
прямые. Длины ребер, исходящих из вершины
О, обозначим через a,b,с,
а длины оставшихся ребер через р,
q, r.
Рассмотрим параметры трех
прямоугольных треугольников ОАВ,
ОВС, ОСА:
(3)
Тогда по
формулам (2) можно выразить отношения
сторон этих прямоугольных треугольников
через их параметры:
(4),
(5).
Из (4) непосредственно
вытекает, что параметры ξ,
η, ζ, удовлетворяют
соотношению
(6). Это и есть общее уравнение пифагоровых
тетраэдров.
Из формул (3) — (5) непосредственно
вытекает следующее утверждение: для
того чтобы тетраэдр ОАВС
с прямыми плоскими углами при вершине
О был пифагоровым, необходимо и достаточно,
чтобы параметры ξ, η, ζ
(удовлетворяющие уравнению (6)) были
рациональными.
Продолжая аналогию пифагорова
треугольника с пифагоровым тетраэдром,
попробуем сформулировать и доказать
пространственное обобщение теоремы
Пифагора для прямоугольных тетраэдров,
которая, очевидно, будет верна и для
пифагоровых тетраэдров. В этом нам
поможет следующая лемма.
Лемма 1.
Если площадь многоугольника
равна S, то
площадь его проекции на плоскость π
равна
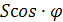
где φ — угол
между плоскостью π и плоскостью
многоугольника.
Доказательство.
Утверждение леммы очевидно для
треугольника, одна сторона которого
параллельна линии пересечения плоскости
π с плоскостью многоугольника. В самом
деле, длина этой стороны при проекции
не изменяется, а длина высоты, опущенной
на нее при проекции, изменяется в cosφ
раз.
Докажем теперь, что любой
многогранник можно разделить на
треугольники указанного вида.
Проведем для этого через все
вершины многоугольника прямые,
параллельные линии пересечения
плоскостей, многоугольник разрежется
при этом на треугольники и трапеции.
Остается разрезать каждую трапецию по
любой из ее диагоналей.
Теорема 1 (пространственная
теорема Пифагора).
В прямоугольном тетраэдре АВСD,
с плоскими углами при вершине D,
сумма квадратов площадей трех его
прямоугольных граней равна квадрату
площади грани АВС.
Доказательство.
Пусть α — угол между плоскостями
АВС и DВС,
D’ — проекция точки D
на плоскость АВС.
Тогда S>ΔDBC>=СоsαS>ΔАBC>>
>и S>ΔD’BC>=cоsαS>ΔDBC>>
>(по лемме 1), поэтому cоsα
=
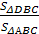
>S>Δ>>D>>‘>>BC>>
>=
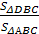
Аналогичные равенства можно
получить и для треугольников D’АВ
и D’АС. Складывая
их и учитывая, что сумма площадей
треугольников D’ВС,
D’АС и D’АВ
равна площади треугольника АВС,
получаем требуемое.
Задача.
Пусть все плоские углы при вершине
D
прямые; a,b,c
– длины ребер, выходящих из вершины D
на плоскость ABC.
Тогда
Доказательство.
По теореме Пифагора для
прямоугольного тетраэдра
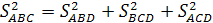
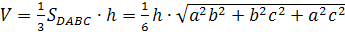
С другой
стороны
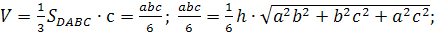
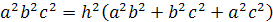
1=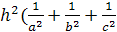
=>
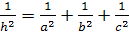
§2. Ортоцентрические
тетраэдры
В отличие от треугольника, высоты
которого всегда пересекаются в одной
точке — ортоцентре, не всякий тетраэдр
обладает аналогичным свойством. Тетраэдр,
высоты которого пересекаются в одной
точке, называется ортоцентрическим. мы
начнем изучение ортоцентрических
тетраэдров с необходимых и достаточных
условий ортоцентричности, каждое из
которых можно принять за определение
ортоцентрического тетраэдра.
(1) Высоты тетраэдра пересекаются
в одной точке.
(2) Основания высот тетраэдра
являются ортоцентрами граней.
(3) Каждые два противоположных
ребра тетраэдра перпендикулярны.
(4) Суммы квадратов противоположных
ребер тетраэдра равны.
(5) Отрезки, соединяющие середины
противоположных ребер тетраэдра, равны.
(6) Произведения косинусов
противоположных двугранных углов равны.
(7) Сумма квадратов площадей
граней вчетверо меньше суммы квадратов
произведений противоположных ребер.
Докажем некоторые из них.
Доказательство (3).
Пусть каждые два противоположных
ребра тетраэдра перпендикулярны.
Следовательно, высоты тетраэдра
попарно пересекаются. Если несколько
прямых попарно пересекаются, то они
лежат в одной плоскости или проходят
через одну точку. В одной плоскости
высоты тетраэдра лежать не могут, так
как иначе в одной плоскости лежали бы
и его вершины, поэтому они пересекаются
в одной точке.
Вообще говоря, для того чтобы
высоты тетраэдра пересекались в одной
точке, необходимо и достаточно потребовать
перпендикулярность только двух пар
противоположных ребер. Доказательство
этого предложения напрямую следует из
следующей задачи.
Задача 1.
Дан произвольный тетраэдр ABCD.
Докажите, что
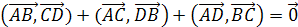
Решение.
Пусть а=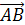
b=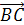
с=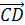
Тогда
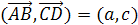
и
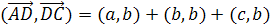
складывая эти равенства, получаем
требуемое.
Далее докажем свойство (4).
Пусть а=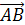
b=
и с=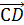
Равенство
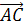
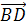
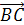
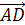
что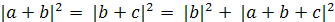
т.е. (а,с)=0.
Применяя данный алгоритм к другим парам
противоположных ребер, очевидно, получим
искомое утверждение.
Приведем оказательство свойства
(6).
Для доказательства используем
следующие теоремы:
Теорема
синусов. «Произведение длин двух
противоположных ребер тетраэдра,
деленное на произведение синусов
двугранных углов при этих ребрах, одно
и то же для всех трех пар противоположных
ребер тетраэдра».
Теорема
Бертшнейдера. «Если a
и b
– длины двух скрещивающихся ребер
тетраэдра, а
— двугранные углы при этих ребрах, то
величина
не зависит от выбора пары скрещивающихся
ребер.
Воспользовавшись теоремой
синусов для тетраэдра и теоремой
Бертшнейдера, получаем, что произведения
косинусов противоположных двугранных
углов равны тогда и только тогда, когда
равны суммы квадратов противоположных
ребер, из чего и следует справедливость
свойства (6) ортоцентрического тетраэдра.
В заключение пункта об
ортоцентрическом тетраэдре решим
несколько задач на эту тему.
Задача 2.
Докажите, что в ортоцентрическом
тетраэдре выполняется соотношение
ОН2=4R2-3d2,
где О — центр
описанной сферы, H
— точка пересечения высот, R
— радиус описанной сферы, d
— расстояние между серединами
противоположных ребер.
Решение.
Пусть К
и L — середины
ребер АВ и СD
соответственно. Точка Н
лежитт в плоскости, проходящей через
СD перепендикулярно
АВ, а точка О
— в плоскости, проходящей черех К
перпендикулярно АВ.
Эти плоскости симметричны
относительно центра масс тетраэдра —
середины отрезка KL.
Рассматривая такие плоскости для всех
ребер, получаем, что точки Н
и О симметричны
относительно М,
а значит КLМО
— параллелограмм. Квадраты его сторон
равны
и
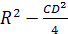
поэтому
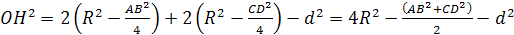
Рассматривая сечение, проходящее через
точку М
параллельно АВ
и СD, получаем
что АВ2+CD2=4d2.
Здесь можно добавить, что прямую,
на которой лежат точки О,
М и Н,
называют прямой Эйлера ортоцентрического
тетраэдра.
Замечание.
Наряду с прямой Эйлера можно
отметить существование сфер Эйлера для
ортоцентрического тераэдра, о которых
и пойдет речь в следующих задачах.
Задача 3.
Доказать, что для ортоцентрического
тетраэдра окружности 9 точек каждой
грани принадлежат одной сфере (сфере
24 точек). Для решения этой задачи
необходимо доказать условие следующей
задачи.
Задача 4.
Доказать, что середины сторон
треугольника, основания высот и середины
отрезков высот от вершин до точки их
пересечения лежат на одной окружности
— окружности 9 точек (Эйлер).
Доказательство.
Пусть АВС
— данный треугольник, Н
— точка пересечения его высот, А>1>,
В>1>,
С>1> —
середины отрезков АН, ВН,
СН; АА>2>
— высоты, А>3>
— середина ВС.
Будем считать для удобства, что АВС
— остроугольный треугольник. Поскольку


и ΔВ>1>А>2>С>1>=ΔВ>1>НС>1>,
то


—

т.е. точки А>1>,
В>1>,
А>2>,
С>1>>
>лежат на одной окружности.
Также легко увидеть, что


—

т.е. точки А>1>,
В>1>,
А>3>,
С>1>>
>тоже лежат на одной (а
значит на той же) окружности. Отсюда
следует, что все 9 точек, о которых
говорится в условии, лежат на одной
окружности. Случай тупоугольного
треугольника АВС
рассматривается аналогично.
Заметим, что окружность 9 точек
гомотетична описанной окружности с
центром в Н и коэффициентом
(именно так расположены треугольники
АВС и А>1>В>1>С>1>).
С другой стороны, окружность 9 точек
гомотетична описанной окружности с
центром в точке пересечения медиан
треугольника АВС
и коэффициентом
(именно так расположены треугольники
АВС и треугольник с вершинами в серединах
его сторон).
Теперь, после определения
окружности 9 точек, можно перейти к
доказательству условия задачи 3.
Доказательство.
Сечение ортоцентрического
тетраэдра любой плоскостью, параллельной
противоположным ребрам и проходящей
на равном расстоянии от этих ребер, есть
прямоугольник, диагонали которого равны
расстоянию между серединами противоположных
ребер тетраэдра ( все эти расстояния
равны между собой, см. необходимое и
достаточное условие ортоцентричности
(5). Отсюда следует, что середины всех
ребер ортоцентрического тетраэдра
лежат на поверхности сферы, центр которой
совпадает с центром тяжести данного
тетраэдра, а диаметр равен расстоянию
между серединами противоположных ребер
тетраэдра. Значит, все четыре окружности
9 точек лежат на поверхности этой сферы.
Задача 5.
Доказать, что для ортоцентрического
тетраэдра центры тяжести и точки
пересечения высот граней, а также точки
, делящие отрезки каждой высоты тетраэдра
от вершины до точки пересечения высот
в отношении 2:1, лежат на одной сфере (
сфере 12 точек).
Доказательство.
Пусть точки О, М
и Н — соответственно
центр описанного шара, ценетр тяжести
и ортоцентр ортоцентрического тетраэдра;
М — середина
отрезка ОН
(см. задачу 2). Центры тяжести граней
тетраэдра служат вершинами тетраэдра,
гомотетичного, с центром гомотетиии в
точке М и
коэффициентом
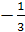
при этой гомотетии точка О
перейдет в точку О>1>,
расположенную на отрезке МН
так, что
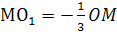
О>1>
будет центром сферы проходящей через
центры тяжестей граней.
С другой стороны, точки, делящие
отрезки высот тетраэдра от вершин до
ортоцентра в отношении 2:1, служат
вершинами тетраэдра, гомотетичного
данному с центром гомотетии в Н
и коэффициентом
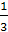
При этой гомотетии точка О,
как легко видеть, перейдет в ту же точку
О>1>.
Таким образом, восемь из двенадцати
точек лежат на поверхности сферы с
центром в О>1>
и радиусом, втрое меньшим, чем радиус
сферы, описанной около тетраэдра.
Докажем, что точки пересечения
высот каждой грани лежат на поверхности
той же сферы.
Пусть О`, Н`
и М` — центр
описанной окружности, точка пересечения
высот и центр тяжести какой-либо грани.
О` и Н`
являются проекциями точек О
и Н на плоскость
этой грани, а отрезок М`
делит отрезок О`Н`
в отношении 1:2, считая от О`(известный
планиметрический факт). Теперь легко
убедиться (см. рис), что проекция О>1>
на плоскость этой грани — точка О`>1>
совпадает с серединой отрезка М`Н`,
т.е. О>1>>
>равноудалена от М`
и Н`, что и
требовалось.
§3. Каркасные
тетраэдры
Каркасным называется тетраэдр,
для которого существует сфера, касающаяся
всех шести ребер тетраэдра. Не всякий
тетраэдр каркасный. Например, легко
понять, что нельзя построить сферу,
касающуюся всех ребер равногранного
тетраэдра, если его описанный параллелепипед
«длинный».
Перечислим свойства каркасного
тетраэдра.
(1) Существует сфера, касающаяся
всех ребер тетраэдра.
(2) Суммы длин скрещивающихся
ребер равны.
(3) Суммы двугранных углов при
противоположных ребрах равны.
(4) Окружности, вписанные в грани,
попарно касаются.
(5) Все четырехугольники,
получающиеся на развертке тетраэдра,
— описанные.
(6) Перпендикуляры, восстановленные
к граням из центров вписанных в них
окружностей, пересекаются в одной точке.
Докажем несколько свойств
каркасного тераэдра.
Доказательство (2).
Пусть О
— центр сферы, касающейся четырех ребер
во внутренних точках. заметим теперь,
что если из точки Х
провести касательные ХР
и ХQ к сфере с
центром О, то
точки Р и Q
симметричны относительно плоскости,
проходящей прямую ХО
и середину отрезка PQ,
а значит плоскости РОХ
и QОХ образуют
с плоскостью ХРQ
равные углы.
Проведем 4 плоскости, проходящие
через точку О и рассматриваемые ребра
тетраэдра. Они разбивают каждый из
рассматриваемых двугранных углов на
два двугранных угла. Выше было показано,
что полученные двугранные углы,
прилегающие к одной грани тетраэдра,
равны. Как в одну, так и в другую
рассматриваемую сумму двугранных углов
входит по одному полученному углу для
каждой грани тетраэдра. Проводя
аналогичные рассуждения для других пар
скрещивающихся ребер, получим
справедливость свойства (2).
Вспомним некоторые свойства
описанного четырехугольника:
Плоский
четырехугольник будет описанным тогда
и только тогда, когда суммы его
противоположных сторон равны;
Если
описанный четырехугольник разбить
диагональю на два треугольника, то
вписанные в треугольники окружности
касаются
Учитывая эти свойства, легко
доказать остальные свойства каркасного
тетраэдра. Свойство (3) тетраэдра напрямую
следует из свойства (b), а свойство (4) из
свойства (a)
и свойства (1) тетраэдра. Свойство (5) из
свойства (3). Действительно, ведь окружности
вписанные в грани тетраэдра, являются
пересечениями его граней со сферой,
касающейся ребер, откуда очевидно, что
перпендикуляры, восстановленные в
центрах вписанных в грани окружностей
неминуемо пересекутся в центре этой
сферы.
Задача 1.
Сфера касается ребер АВ,
ВС, СD и DA
тетраэдра АВСD
в точках L, M, N, K,
являющихся вершинами квадрата. Докажите,
что если эта сфера касается ребра АС,
то она касается и ребра BD.
Решение.
По условия КLMN
— квадрат. Проведем через точки К,
L, M, N плоскости, касающиеся
сферы. Т.к все эти плоскости одинаково
наклонены к плоскости КLMN,
то они пересекаются в одной точке S,
расположенной на прямой ОО>1>,
где — центр сферы, а О>1>>
>- центр квадрата. Эти
плоскости пересекают поверхность
квадрата KLMN
по квадрату TUVW,
серединами сторон которого являются
точки К, L, M, N.
В четырехгранном угле STUVW с вершиной S
все плоские углы равны, а точки К,
L, M, N лежат на биссектрисах
его плоских углов, причем SK=SL=SM=SN.
Следовательно,
SA=SC и SD=SB,
а значит АК=АL=CM=CN
и ВL=BM=DN=DK. По
условию АС
тоже касается шара, поэтому АC=АК+CN=2АК.
А так как SK —
биссектриса угла DSA,
то DK:КА=DS:SA=DВ:АС.
Из равенства АС=2АК
следует теперь, что DВ=2DK.
Пусть Р —
середина отрезка DВ,
тогда Р лежит
на прямой SO.
Треугольники DOK
и DOP равны,
т.к. DK=DP и


Поэтому ОР=ОК=R,
где R — радиус
сферы, а значит, DB
тоже касается сферы.
§4. Равногранные
тетраэдры
Равногранным называется тетраэдр,
все грани которого равны. Чтобы представить
себе равногранный тетраэдр, возьмем
произвольный остроугольный треугольник
из бумаги, и будем сгибать его по средним
линиям. Тогда три вершины сойдутся в
одну точку, а половинки сторон сомкнутся,
образуя боковые ребра тетраэдра.
(0) Грани конгруэнтны.
(1) Скрещивающиеся ребра попарно
равны.
(2) Трехгранные углы равны.
(3) Противолежащие двугранные
углы равны.
(4) Два плоских угла, опирающихся
на одно ребро, равны.
(5) Сумма плоских углов при каждой
вершине равна 180°.
(6) Развертка тетраэдра — треугольник
или параллелограмм.
(7) Описанный параллелепипед
прямоугольный.
(8) Тетраэдр имеет три оси симметрии.
(9) Общие перпендикуляры
скрещивающихся ребер попарно
перпендикулярны.
(10) Средние линии попарно
перпендикулярны.
(11) Периметры граней равны.
(12) Площади граней равны.
(13) Высоты тетраэдра равны.
(14) Отрезки, соединяющие вершины
с центрами тяжести противоположных
граней, равны.
(15) Радиусы описанных около граней
окружностей равны.
(16) Центр тяжести тетраэдра
совпадает с центром описанной сферы.
(17) Центр тяжести совпадает с
центром вписанной сферы.
(18) Центр описанной сферы совпадает
с центром вписанной.
(19) Вписанная сфера касается
граней в центрах описанных около этих
граней окружностей.
(20) Сумма внешних единичных
нормалей (единичных векторов,
перпендикулярных к граням), равна
нулю.
(21) Сумма всех двугранных углов
равна нулю.
Практически все свойства
равногранного тетраэдра следуют из его
определения, поэтому докажем
только некоторые из них.
Доказательство (16).
Т.к. тетраэдр ABCD
равногранный, то по свойству (1) AB=CD.
Пусть точка К
отрезка АВ, а
точка L середина
отрезка DC,
отсюда отрезок KL
бимедиана тетраэдра ABCD,
откуда по свойствам медиан тетраэдра
следует, что точка О
— середина отрезка KL,
является центром тяжести тетраэдра
ABCD.
К тому же медианы тетраэдра
пересекаются в центре тяжести, точке
О, и делятся
этой точкой в отношении 3:1, считая от
вершины. Далее, учитывая вышесказанное
и свойство (14) равногранного тетраэдра,
получаем следующее равенство отрезков
АО=ВО=СО=DО, из
которого и следует, что точка О
является центром описанной сферы (по
определению описанной около многогранника
сферы).
Обратно. Пусть К
и L — середины
ребер АВ и СD
соответственно, точка О
— центр описанной сферы тетраэдра, т.е.
середина отрезка KL.
Т.к. О — центр
описанной сферы тетраэдра, то треугольники
AOB и COD
— равнобедренные с равными боковыми
сторонами и равными медианами OK
и OL. Поэтому
ΔAOB=ΔCOD.
А значит AB=CD.
Аналогично доказывается равенство
других пар противоположных ребер, из
чего по свойству (1) равногранного
тетраэдра и будет следовать искомое.
Доказательство (17).
Рассмотрим биссектор двугранного
угла при ребре AB,
он разделит отрезок DC в отношении
площадей граней ABD
и ABC.
Т.к. тетраэдр ABCD
равногранный, то по свойству (12)
S>ΔABD>=S>ΔABD>=>DL=LС,
откуда следует, что биссектор ABL
содержит бимедиану KL.
Применяя аналогичные рассуждения для
остальных двугранных углов, и принимая
во внимание тот факт, что биссекторы
тетраэдра пересекаются в одной точке,
которая является центром вписанной
сферы, получаем, что эта точка неминуемо
будет центром тяжести данного равногранного
тетраэдра.
Обратно. Из того, что центр тяжести
и центр вписанной сферы совпадают имеем
следующее: DL=LC=>SABD=SADC.
Доказывая подобным образом равновеликость
всех граней и, применяя свойство (12)
равногранного тетраэдра, получаем
искомое.
Теперь докажем свойство (20). Для
этого сначала нужно доказать одно из
свойств произвольного тетраэдра.
тетраэдр теорема
школьный учебник
Лемма 1.
Если длины векторов перпендикулярных
к граням тетраэдра численно равны
площадям соответствующих граней, то
сумма этих векторов равна нулю.
Доказательство.
Пусть Х
— точка внутр и многогранника, h>i
>(i=1,2,3,4)
— расстояние от нее до плоскости i-ой
грани.
Разрежем многогранник на пирамиды
с вершиной Х,
основаниями которых служат его грани.
Объем тетраэдра V
равен сумме объемов этих пирамид, т.е.
3 V=∑h>i>S>i>,
где S>i>>
>площадь i-ой
грани. Пусть далее, n>i>>
>- единичный вектор внешней
нормали к i-ой грани, M>i >-
произвольная точка этой грани. Тогда
h>i >=(ХM>i>,
S>i>n>i>),
поэтому 3V=∑h>i>S>i>=∑(ХM>i>,
S>i>n>i>)=(ХО,
S>i>n>i>)+(ОM>i>,
S>i>n>i>)=(ХО,
∑S>i>n>i>)+3V,
где О — некоторая
фиксированная точка тетраэдра,
следовательно, ∑S>i>n>i>=0.
Далее очевидно, что свойство
(20) равногранного тетраэдра является
частным случаем вышеуказанной леммы,
где S>1>=>
>S>2>=>
>S>3>=>
>S>4>=>n>1>=n>2>=n>3>=n>4>,
и так как площади граней не равны нулю,
получаем верное равенство n>1>+n>2>+n>3>+n>4>=0.
В заключение рассказа о равногранном
тетраэдре приведем несколько задач на
эту тему.
Задача 1.
Прямая, проходящая через центр
масс тетраэдра и центр описанной около
него сферы, пересекает ребра AB
и CD. Докажите,
что AC=BD и AD=BC.
Решение.
Центр масс тетраэдра лежит на
прямой, соединяющей середины ребер АВ
и СD.
Следовательно, на этой прямой
лежит центр описанной сферы тетраэдра,
а значит, указанная прямая перпендикулярна
ребрам АВ и
СD. Пусть С`
и D` — проекции
точек C и D
на плоскость, проходящую через прямую
АВ параллельно
СD. Т.к. AC`BD`
— параллелограмм (по построению), то
АС=ВD и АD=ВС.
Задача 2.
Пусть h
— высота равногранного тетраэдра, h>1>>
>и h>2>>
>- отрезки, на которые одна
из высот грани делится точкой пересечения
высот этой грани. Доказать, что h2=4h>1>h>2>;
доказать также, что основание высоты
тетраэдра и точка пересечения высот
грани, на которую эта высота опущена,
симметричны относительно центра
окружности, описанной около этой грани.
Доказательство.
Пусть АВСD
— данный тетраэдр, DH
— его высота, DA>1>,
DВ>1>,
DС>1>>
>- высоты граней, опущенные
из вершины D
на стороны ВС, СА и АВ.
Разрежем поверхность тетраэдра
вдоль ребер DA, DB, DC,
и сделаем развертку. Очевидно, что Н
есть точка пересечения высот треугольника
D>1>D>2>D>3>.
Пусть F — точка
пересечения высот треугольника ABC,
АК — высота этого треугольника,
АF=h>1>,
FК=h>2>.
Тогда D>1>Н=2h>1>,
D>1>A>1>=h>1>-h>2>.
Значит, поскольку h
— высота нашего тетраэдра, h2=DН2=DA2
— НA>1>2=
(h>1+>
h>2>)2
— (h>1>—
h>2>)2=4h>1>h>2.>>
>Пусть теперь М
— центр тяжести треугольника ABC
(он же центр тяжести треугольника
D>1>D>2>D>3>),
О — центр
описанной около него окружности.
Известно, что F, М
и О лежат на
одной прямой (прямая Эйлера), причем М
— между F и О,
FM=2МО,
С другой стороны, треугольник D>1>D>2>D>3>>
>гомотетичен треугольнику
АВС с центром
в М и коэффициентом
(-2), значит МН=2FM.
Из этого следует, что ОН=FO.
Задача 3.
Доказать, что в равногранном
тетраэдре основания высот, середины
высот и точки пересечения высот граней
лежат на поверхности одной сферы (сферы
12 точек).
Доказательство.
Решая задачу 2, мы доказали, что
центр описанной около тетраэдра сферы
проецируется на каждую грань в середину
отрезка, концами которого является
основание высоты, опущенной на эту
грань, и точка пересечения высот этой
грани. А поскольку расстояние от центра
описанной около тетраэдра сферы до
грани равно
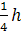
где h — высота
тетраэдра, центр описанной сферы удален
от данных точек на расстояние
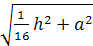
где а — расстояние
между точкой пересечения высот и центром
описанной около грани окружности.
§5. Инцентрические
тетраэдры
Отрезки, соединяющие центры
тяжести граней тетраэдра с противоположными
вершинами (медианы тетраэдра), всегда
пересекаются в одной точке, эта точка
— центр тяжести тетраэдра. Если в этом
условии заменить центры тяжести граней
на ортоцентры граней, то оно превратится
в новое определение ортоцентрического
тетраэдра. Если же заменить их на центры
вписанных в грани окружностей, называемых
иногда инцентрами, мы получим определение
нового класса тетраэдров — инцентрических.
Признаки класса инцентрических
тетраэдров тоже довольно интересны.
Отрезки,
соединяющие вершины тетраэдра с центрами
окружностей, вписанных в противоположные
грани, пересекаются в одной точке.
Биссектрисы
углов двух граней, проведенному к общему
ребру этих граней, имеют общее основание.
Произведения
длин противоположных ребер равны.
Треугольник,
образованный вторыми точками пересечения
трех ребер, выходящих из одной вершины,
с любой сферой, проходящей через три
конца этих ребер, является равносторонним.
Доказательство (2).
По свойству (1), если DF,
BE, CF, AM — биссектрисы
соответственных углов в треугольниках
АВС и FBD,
то отрезки КС
и LD будут иметь
общую точку I
(см. рис). Если же прямые DK
и СL не
пересекаются в точке F,
то, очевидно, КС
и DL не
пересекаются, чего быть не может (по
определению инцентрического тетраэдра).
Доказательство (3).
Учитывая свойство (2) и свойство
биссектрисы, получаем соотношения:
;
.
§6.
Соразмерные
тетраэдры
Соразмерными называются тетраэдры,
у которых
Бивысоты
равны.
Проекция
тетраэдра на плоскость, перпендикулярную
любой бимедиане, есть ромб.
Грани
описанного параллелепипеда равновелики.
4а2а>1>2—
(b2+b>1>2-c2-c>1>2)2=4b2b>1>2—
(c2+c>1>2-a2-a>1>2)2=4c2c>1>2—
(a2+a>1>2-b2-b>1>2)2,
где а
и а>1>,
b
и b>1>,
с
и с>1>
— длины противоположных ребер.
Для доказательства эквивалентности
определений (1) — (4) достаточно заметить,
что бивысоты тетраэдра равны высотам
параллелограмма, являющегося его
проекцией, упоминавшейся в свойстве
(2), и высотам описанного параллелепипеда,
и что квадрат площади параллелепипеда,
содержащей, скажем, ребро с,
равен
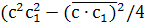
а скалярное произведение
выражается через ребра тетраэдра по
формуле (4).
Добавим сюда ещё два условия
соразмерности:
Для
каждой пары противоположных ребер
тетраэдра плоскости, проведенные через
одно из них и середину второго,
перпендикулярны.
В
описанный параллелепипед соразмерного
тетраэдра можно вписать сферу.
§7. Правильные тетраэдры
Если ребра тетраэдра равны между
собой, то равны между собой будут и
трехгранные, и двугранные, и плоские
углы. В таком случае тетраэдр называется
правильным. Заметим
также, что такой тетраэдр является и
ортоцентрическим, и каркасным, и
равногранным, и инцентрическим, и
соразмерным.
Замечание 1.
Если тетраэдр является равногранным
и принадлежит к одному из следующих
видов тетраэдров: ортоцентрический,
каркасный, инцентрический, соразмерный,
то он будет и правильным.
Замечание 2.
Тетраэдр является правильным,
если он принадлежит к двум любым видам
тетраэдров из перечисленных:
ортоцентрический, каркасный, инцентрический,
соразмерный, равногранный.
Свойства правильного тетраэдра:
Каждая его вершина является
вершиной трех треугольников. А значит,
сумма плоских углов при каждой вершине
будет равна 180º
В правильный тетраэдр можно
вписать октаэдр, притом четыре (из
восьми) грани октаэдра будут совмещены
с четырьмя гранями тетраэдра, все шесть
вершин октаэдра будут совмещены с
центрами шести рёбер тетраэдра.
Правильный тетраэдр состоит из
одного вписанного октаэдра (в центре)
и четырёх тетраэдров (по вершинам),
причем ребра этих тетраэдров и октаэдра
вдвое меньше ребер правильного тетраэдра
Правильный тетраэдр можно
вписать в куб двумя способами, притом
четыре вершины тетраэдра будут совмещены
с четырьмя вершинами куба.
Правильный тетраэдр можно
вписать в икосаэдр, притом, четыре
вершины тетраэдра будут совмещены с
четырьмя вершинами икосаэдра.
Задача 1.
Доказать, что скрещивающиеся
ребра правильного тетраэдра взаимно
перпендикулярны.
Решение:
Пусть DH – высота
правильного тетраэдра, точка H – центр
правильного ΔABC.
Тогда проекцией отрезка AD на плоскость
основания ABC будет отрезок BH.
Т.к. BHAC,
то по теореме о трех
перпендикулярах наклонная BD
AC.
Задача 2.
Дан правильный тетраэдр МАВС
с ребром 1. найдите расстояние между
прямыми AL и
МО, где
L-середина
ребра МС,
О-центр грани
АВС.
Решение:
1. Расстояние между двумя
скрещивающимися прямыми — это длина
перпендикуляра, опущенного из одной
прямой, к плоскости, параллельной этой
прямой и содержащей вторую прямую.
2. Строим проекцию AK
отрезка AL на
плоскость ABC.
Плоскость AKL
перпендикулярна плоскости ABC,
параллельна прямой MO
и содержит прямую AL.
Значит, искомая длина — это длина
перпендикуляра ON,
опущенного из точки O
к AK.
3. Найдем S>Δ>>KHA>
двумя способами.
S>Δ>=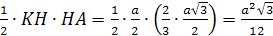
С другой стороны: S>Δ>>KHA>=
поэтому ρ
.
Найдём ON:
ρ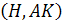
.
Задача 3.
Каждое ребро треугольной
пирамиды PABC равно
1; BD –
высота треугольника ABC .
Равносторонний треугольник BDE лежит
в плоскости, образующей угол ϕ с
ребром AC ,
причём точки P и E лежат
по одну сторону от плоскости ABC .
Найдите расстояние между точками P и E .
Решение. Поскольку
все рёбра пирамиды PABC равны,
это правильный тетраэдр. Пусть M
– центр
основания ABC , N
–
ортогональная проекция вершины E равностороннего
треугольника BDE на
плоскость ABC ,
K
–
середина BD ,
F
– основание
перпендикуляра, опущенного из точки E на
высоту PM тетраэдра
PABC .
Так как
EK 
то по теореме о трёх перпендикулярах
NK 
поэтому EKN –
линейный угол двугранного угла,
образованного плоскостями ABC и BDE ,
а т.к. NK
|| AC ,
то 
= ϕ .
Далее имеем:
BD
=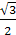
MD
= 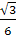
KD
= 
BD
= 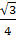
PM
= 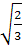
KM
= KD
— MD
= 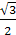
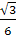
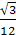
EK
= BD· 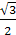

EN
= EK
sin
ϕ
= 
ϕ,
NK = EK cos
ϕ
= 
ϕ,
MN2 =
NK2 +
KM2 = 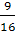
+ 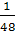
PE2 =
EF2 +
PF2 =
MN2 + (PM
— MF)2 =
MN2 + (PM
— EN)2 =
= 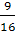
+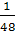
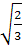

ϕ)2 = 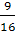
+ 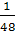
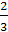
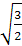
ϕ
+ 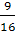
== 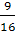
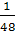

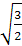
ϕ
= 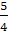
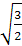
ϕ
= 
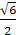
ϕ.
Следовательно,
PE =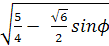
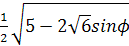
Задача 4.
Найди углы между скрещивающимися
высотами соседних граней тетраэдра.
Решение.
Случай №1.
Пусть BK
и DF – высоты
граней ABC и
BCD.

FD = α.
Обозначим длину ребра тетраэдра как a.
Проведем FL || BK,
тогда α
=
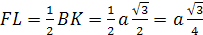
KL=LC.
Запишем теорему косинусов для
ΔDLF:
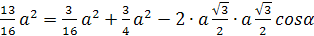
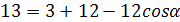
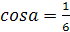
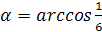
Случай
№2 (высота расположена иначе).
BK
и CN
– высоты граней ABC
и BCD. Проведем
FP || CN и FL
|| BK.
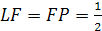
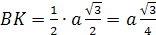
Найдем LP.
DO – высота правильного
тетраэдра, DO
=
, Q
– проекция P
на плоскость ABC,
.
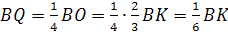
;
.
Запишем теорему косинусов для
ΔLFP:
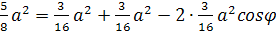
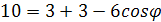
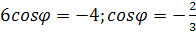
Так как угол между прямыми по
определению острый
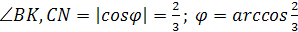
Глава II. Тетраэдр в курсе
математики средней школы
§1. Сравнительная характеристика
изложения темы «тетраэдр» в школьных
учебниках
В школьном курсе
геометрии на изучение основ темы
«Тетраэдр» отводится достаточно много
времени. Методических проблем проведения
этой темы практически не возникает, так
как учащиеся знают, что такое пирамида
(в т.ч. и треугольная), как из пропедевтических
курсов прежних лет обучения математики,
так из жизненного опыта. Правильный
тетраэдр ассоциируется с его плоским
аналогом — правильным треугольником, а
равенство сторон с равенством ребер
или граней.
Однако проблемы в
изучении темы для учащихся существуют,
и разные учебники пытаются решить их
разными способами (порядком изложения
теоретического материала, уровнем
сложности задач и т.п.). Дадим краткую
характеристику распространенных
учебников геометрии в аспекте изучения
тетраэдра.
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Атанасяна Л. С. и др.
В базовом
учебнике «Геометрия» для 10-11 классов
средней школы Атанасяна
Л. С. и др.
информацию о тетраэдре можно найти в 7
параграфах (12, 14, 28, 29, 32, 33, 69).
Авторы учебника
определяют тетраэдр как поверхность,
составленную из четырёх треугольников.
Из теоретической базы учебника для 10
класса можно почерпнуть знания о гранях,
рёбрах и вершинах тетраэдра, о построении
сечений тетраэдра плоскостью, вычислении
площади полной поверхности тетраэдра,
в т.ч. и усечённого (глава III, §
2 «Пирамида»).
Далее рассматриваются
правильные многогранники и элементы
симметрии правильных многогранников.
Формула нахождения объёма пирамиды
приводится в заключительной главе
учебника (глава VII «Объемы тел»).
Теоретический
материал учебника изложен компактно и
стилистически единообразно. Некоторый
теоретический материал расположен в
практической части учебника (доказательства
некоторых теорем производится в задачах).
Практический материал учебника разделён
на два уровня сложности (есть т.н. «задачи
повышенной трудности», отмеченные
специальным символом «*»). Кроме того,
в конце учебника есть задачник с задачами
высокой сложности, некоторые из которых
касаются тетраэдра. Рассмотрим некоторые
задачи учебника.
Решение задач.
Задача 1 (№300).
В правильной треугольной пирамиде DABC
точки E, F
и P
— середины сторон BC,
AB
и AD.
Определите вид сечения и найдите его
площадь, если сторона основания пирамиды
равна a,
боковое ребро равно b.
Решение.
Строим сечение
плоскостью, проходящей через точки E,
F, P. Проведём
среднюю линию треугольника ABC,
EF ||
AC,
EF ||
AC, а
AC
лежит в пл.
DCA,
значит EF
|| пл.
DCA. Плоскость
сечения пересечёт грань DCA
по прямой
PK.
Т.к. плоскость сечения
проходит через прямую EF
параллельную
плоскости DCA
и пересекает
плоскость DCA,
то линия
пересечения PK
параллельна
прямой EF.
Построим в грани BDA
отрезок
FP, а
в грани BDC
— отрезок
EK.
Четырёхугольник
EFOK и
есть искомое сечение. EF
|| AC,
PK || EF
|| AC,
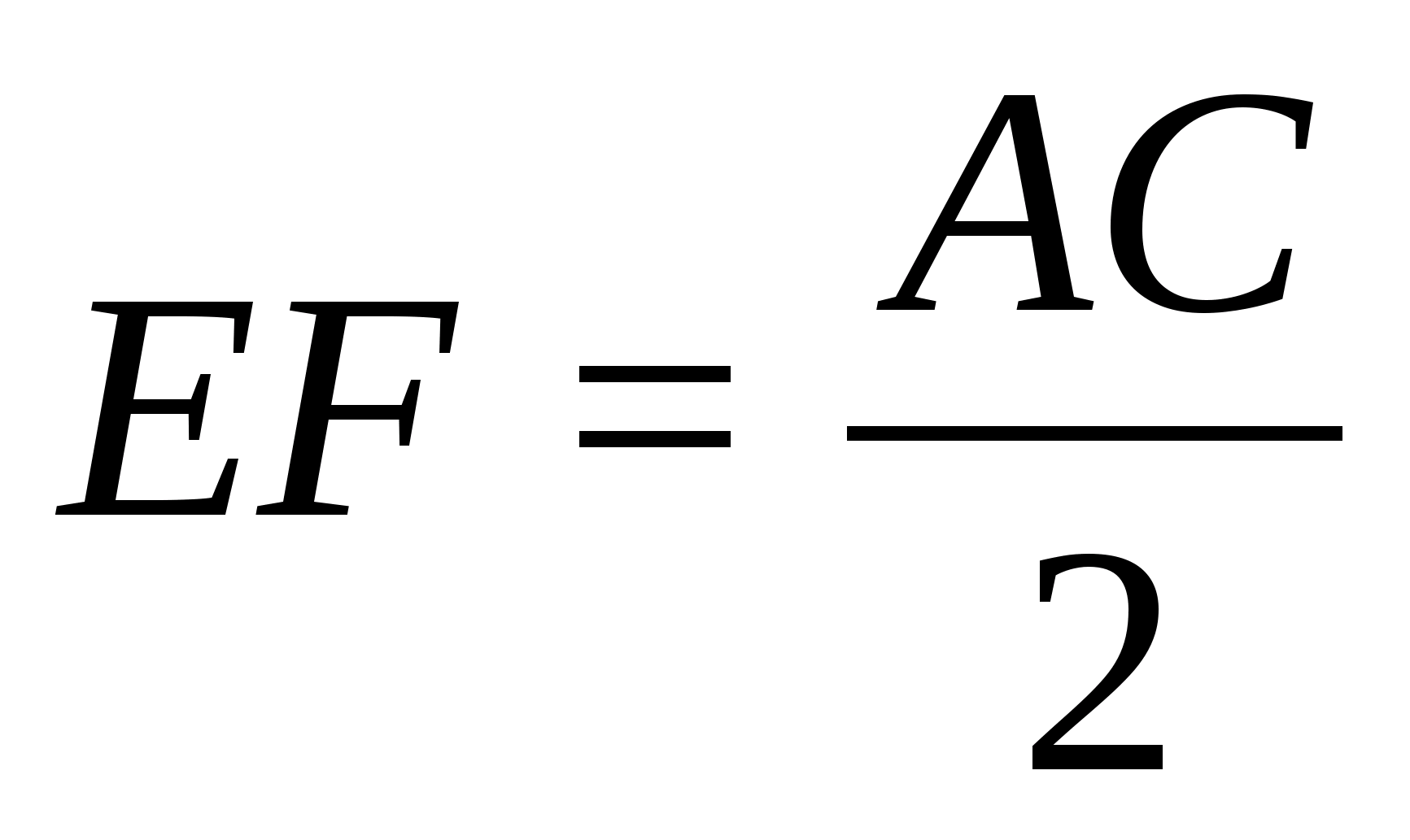
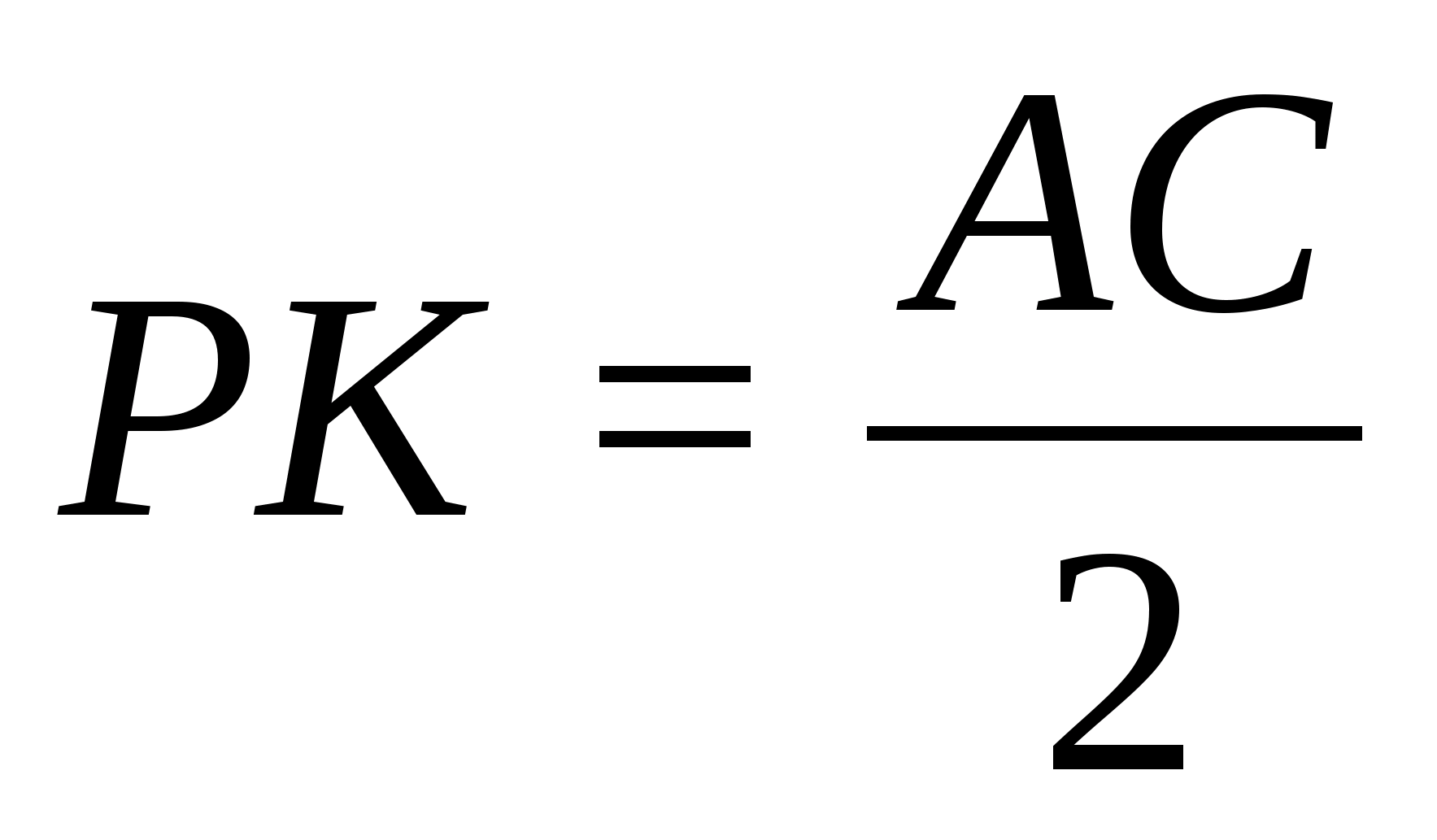
значит
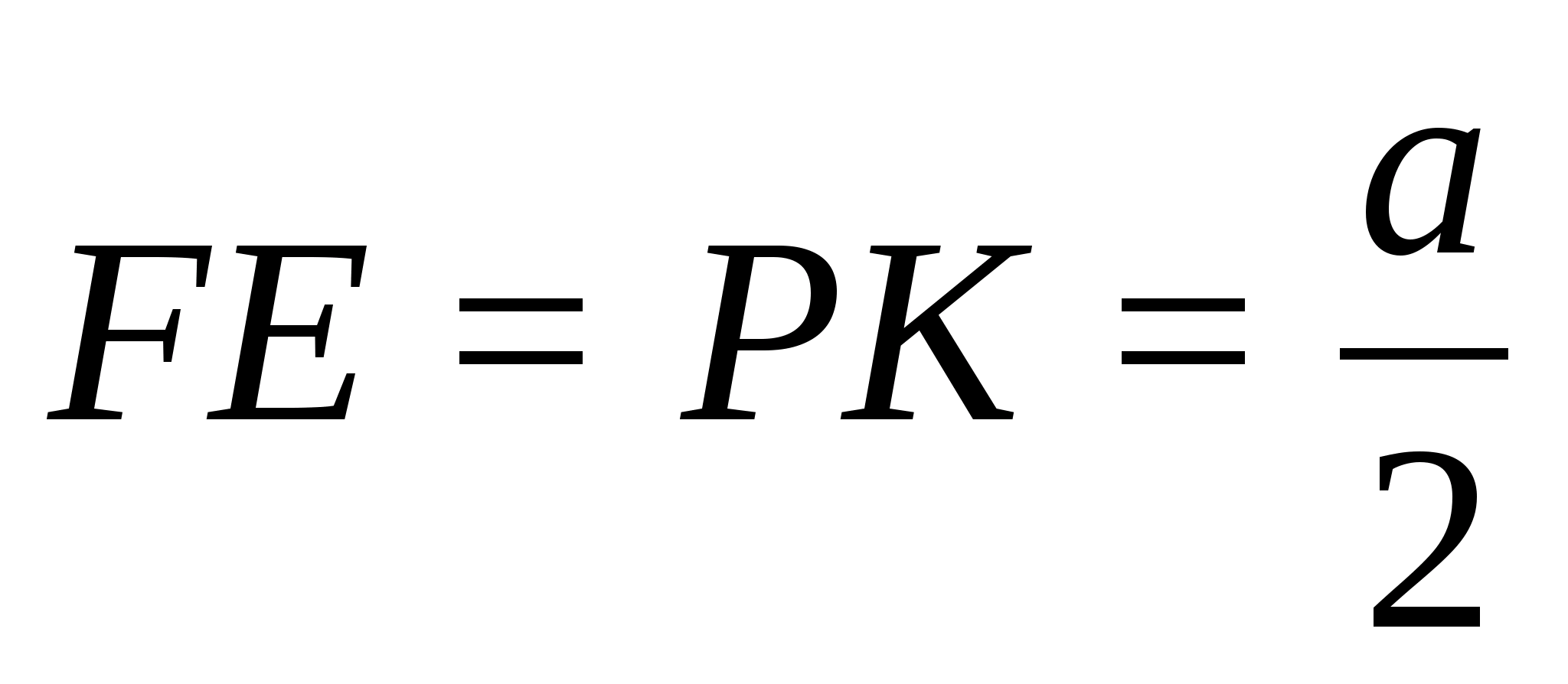
Т.к. PK
|| EF
и PK = EF,
то EFPK
— параллелограмм.
Таким образом, EK
|| EP, EP — средняя
линия треугольника BCD,
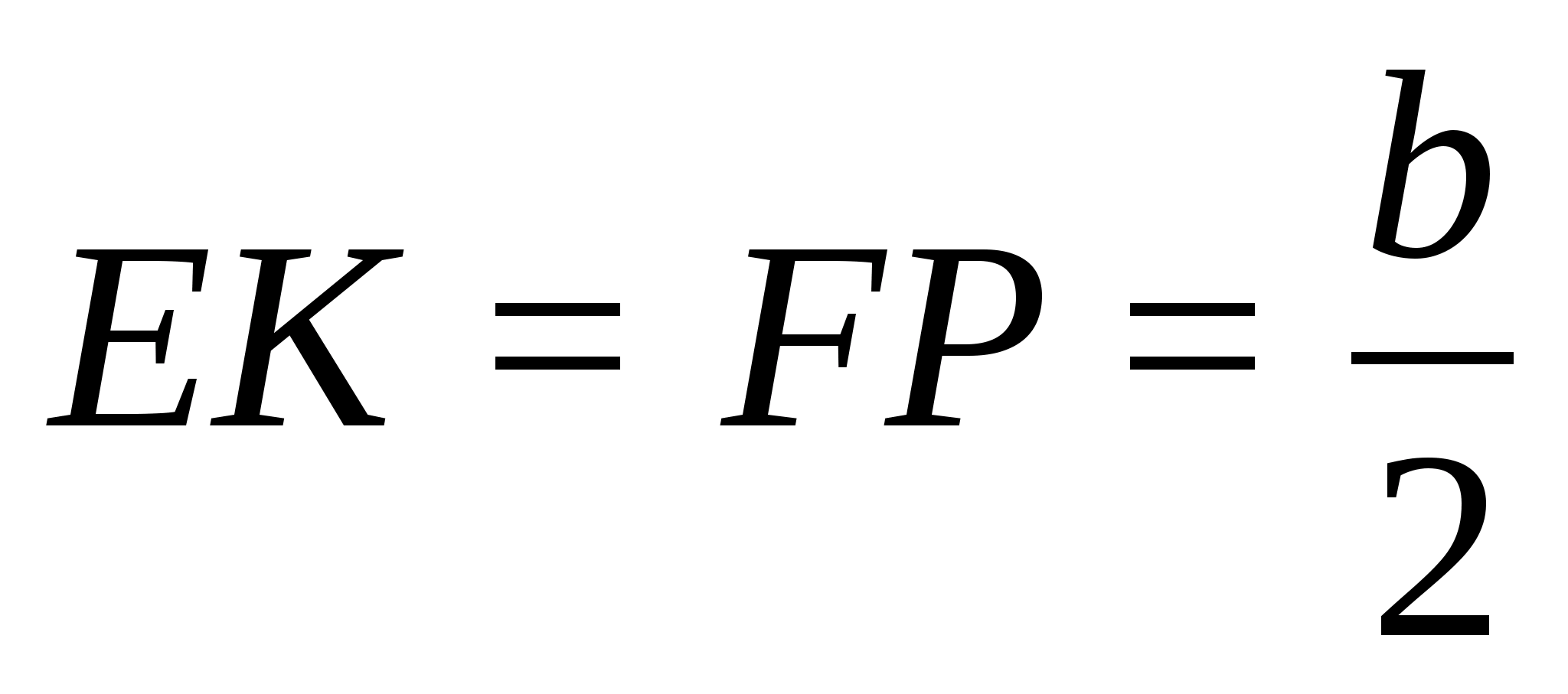
Угол между
скрещивающимися прямыми DB
и CA
равен 90°.
Докажем это. Построим высоту пирамиды
DO.
Точка O
— центр правильного треугольника ABC.
Продолжим отрезок BO
до пересечения со стороной AC
в точке M.
В правильном треугольнике ABC:
BM — высота,
медиана и биссектриса, следовательно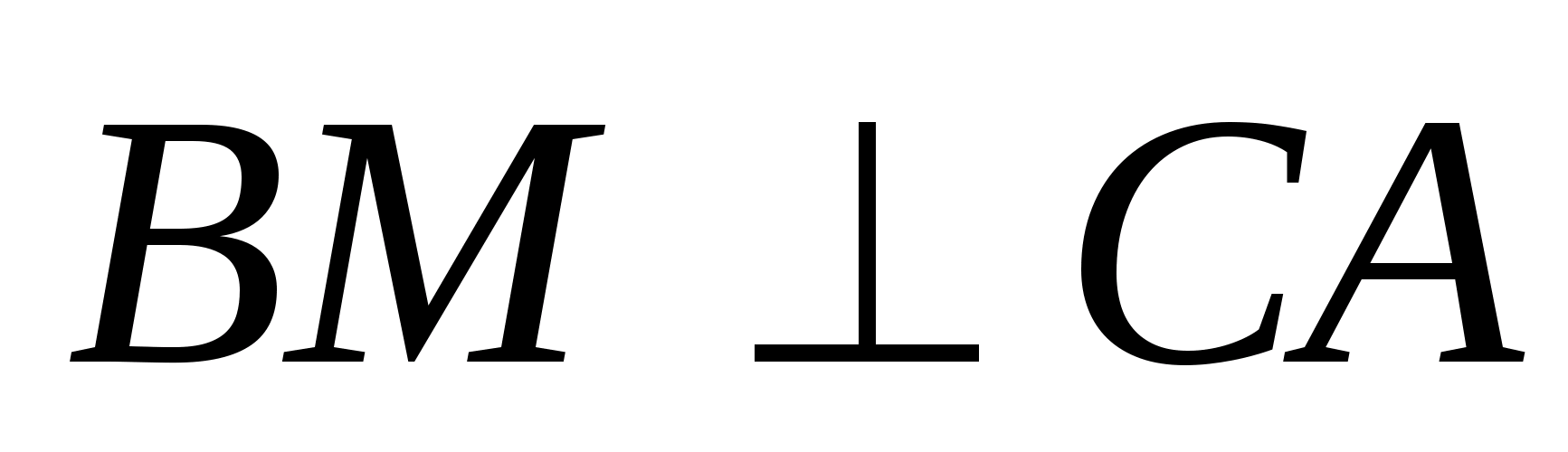
Имеем, что
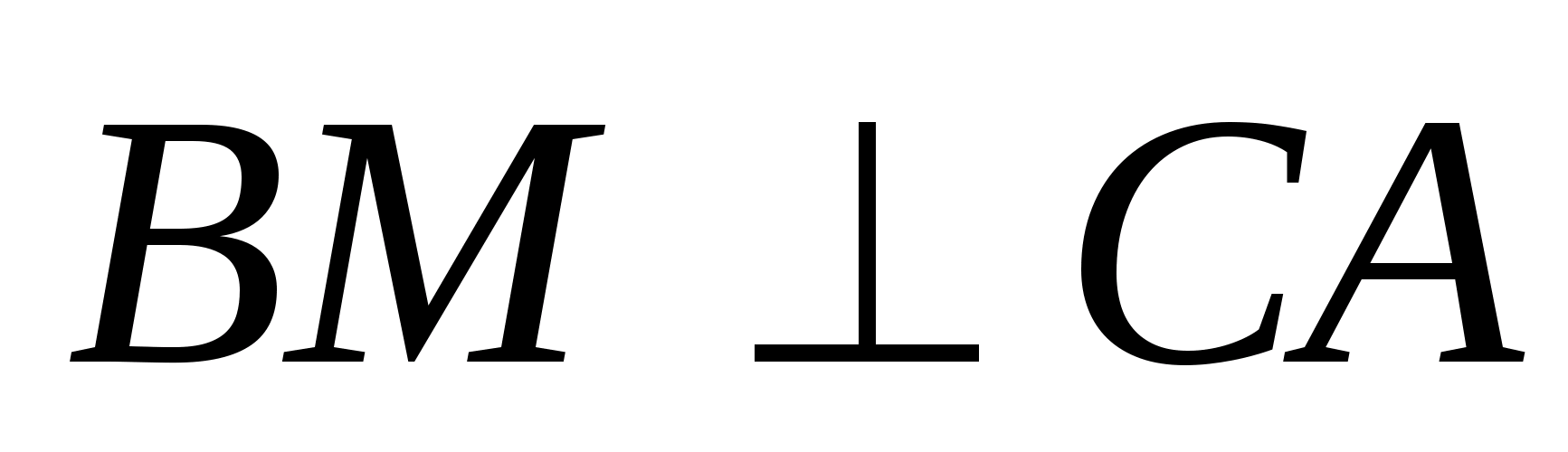
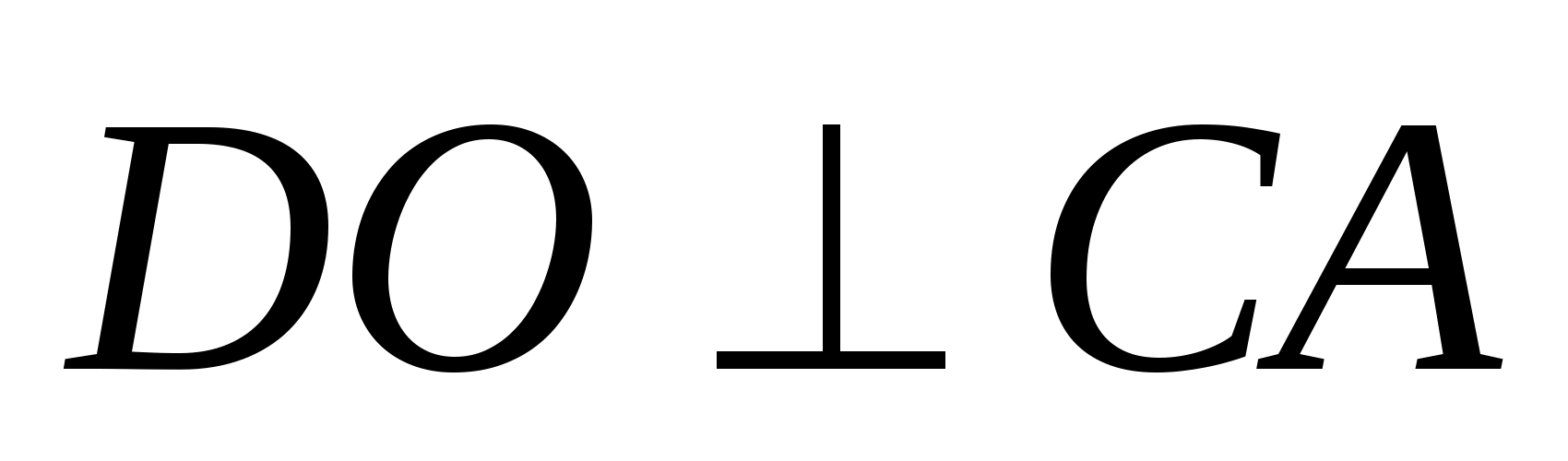
тогда по признаку перпендикулярности
прямой и плоскости
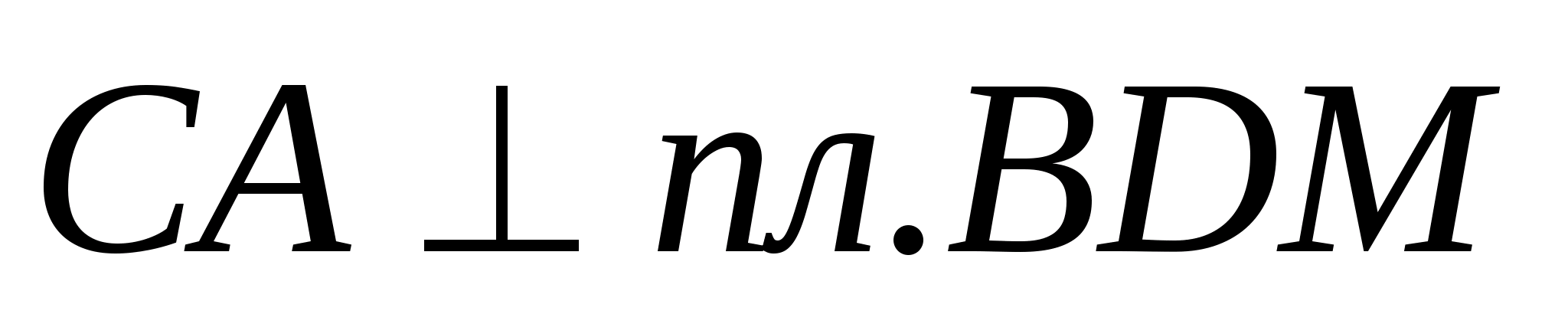
тогда
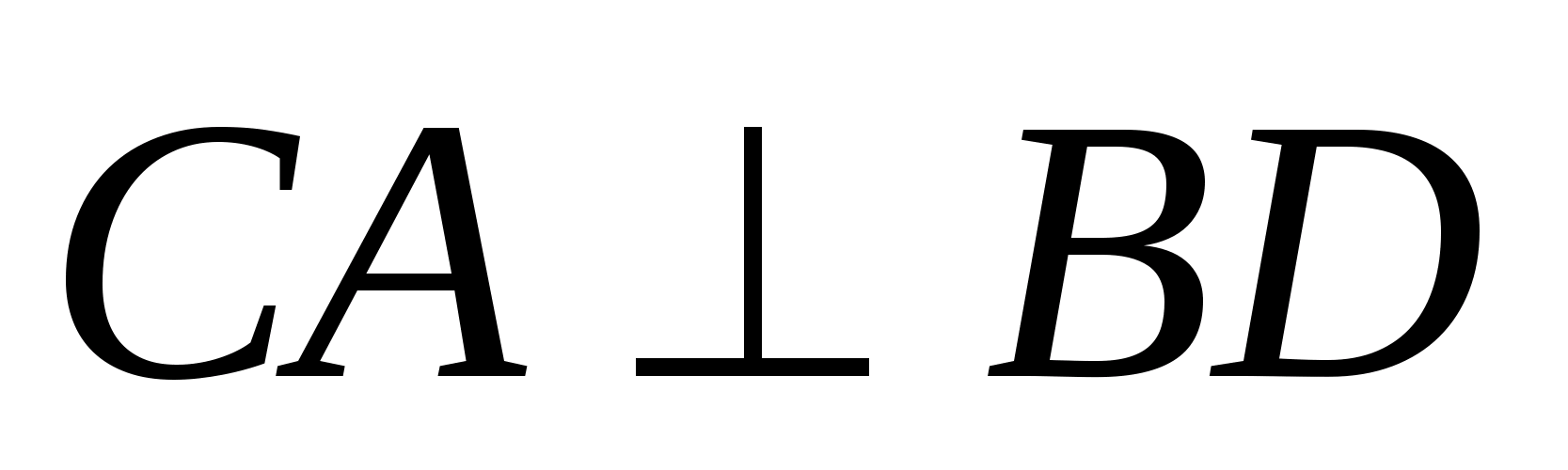
Т.к.
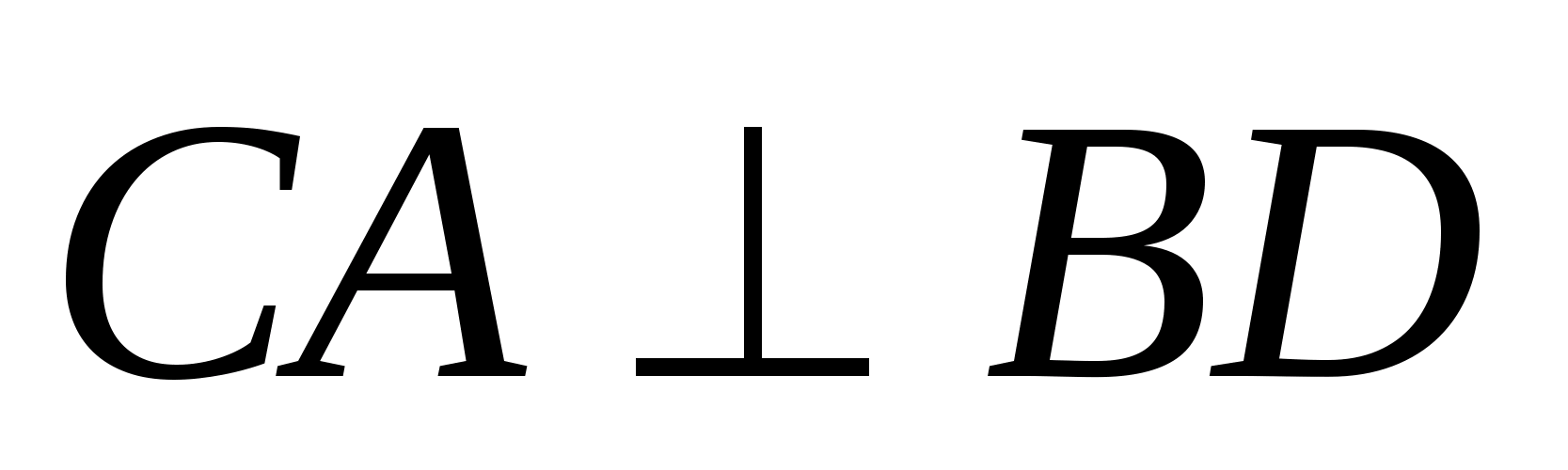
PK ||
CA
и EK
|| BD,
то
и EFPK
— прямоугольник.
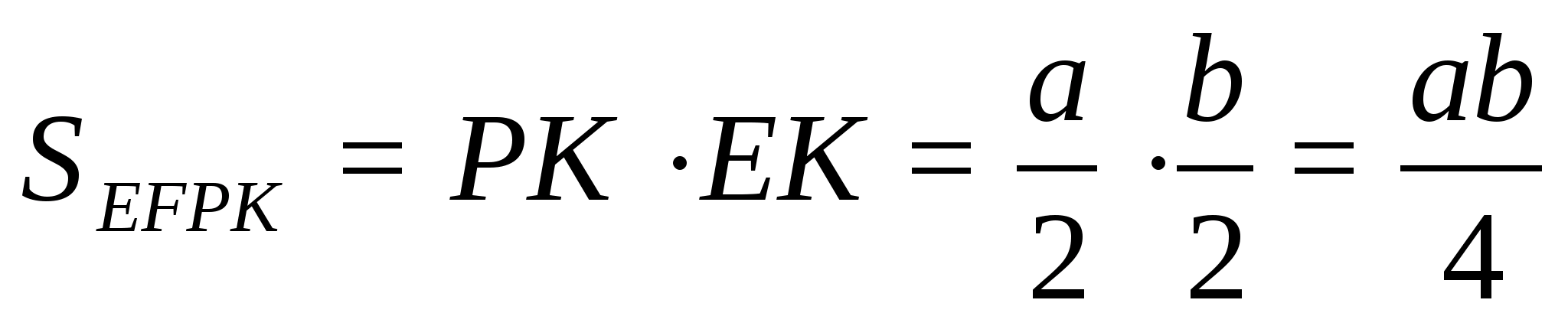
Задача 2 (№692).
Основанием пирамиды
является прямоугольный треугольник с
катетами a
и b.
Каждое её боковое ребро наклонено к
плоскости основания под углом φ.
Найдите объём пирамиды
Решение:
ABCD — пирамида,
угол ABC —
прямоугольный,
AC = b, BC = a, углы
DAO, DBO, DCO равны
. Найдем
V>DABC0>.
1) ∆DAO=∆ADC=∆DBO
по катету
и острому углу, значит
AO=OC=OB=R окружности,
описанной около
∆ABC. Т.к.
∆ABC — прямоугольный,
то
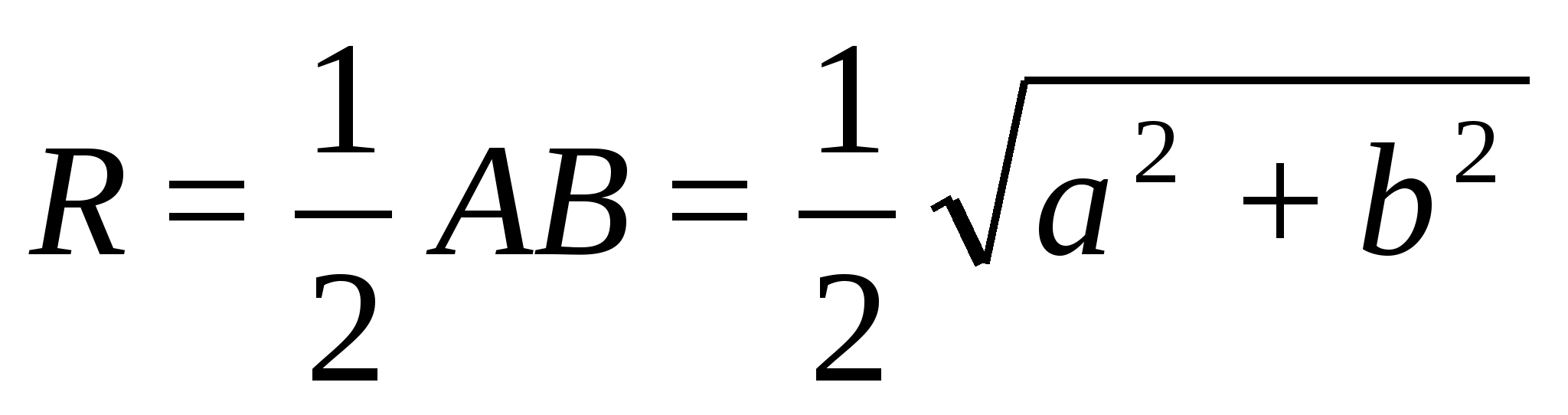
2) Из ∆DOC:
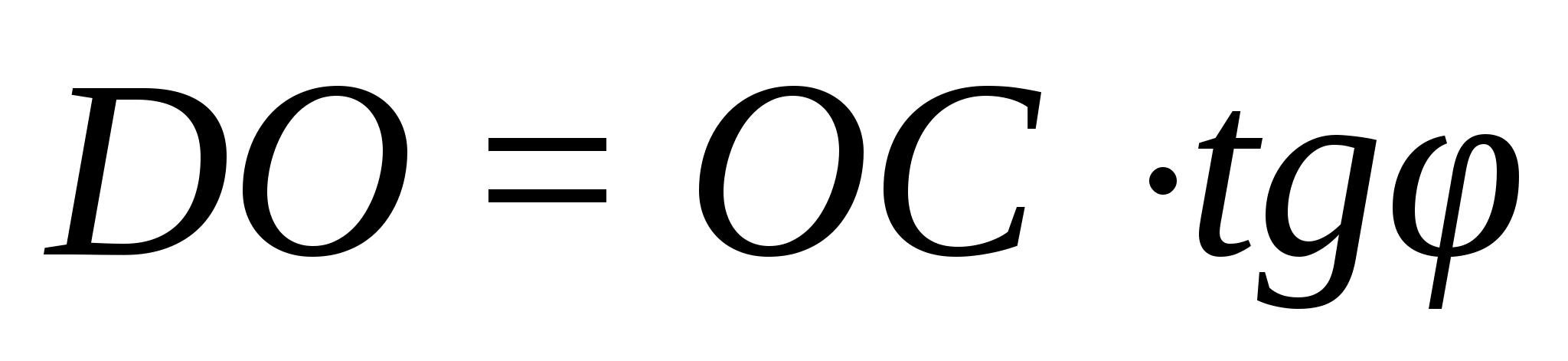
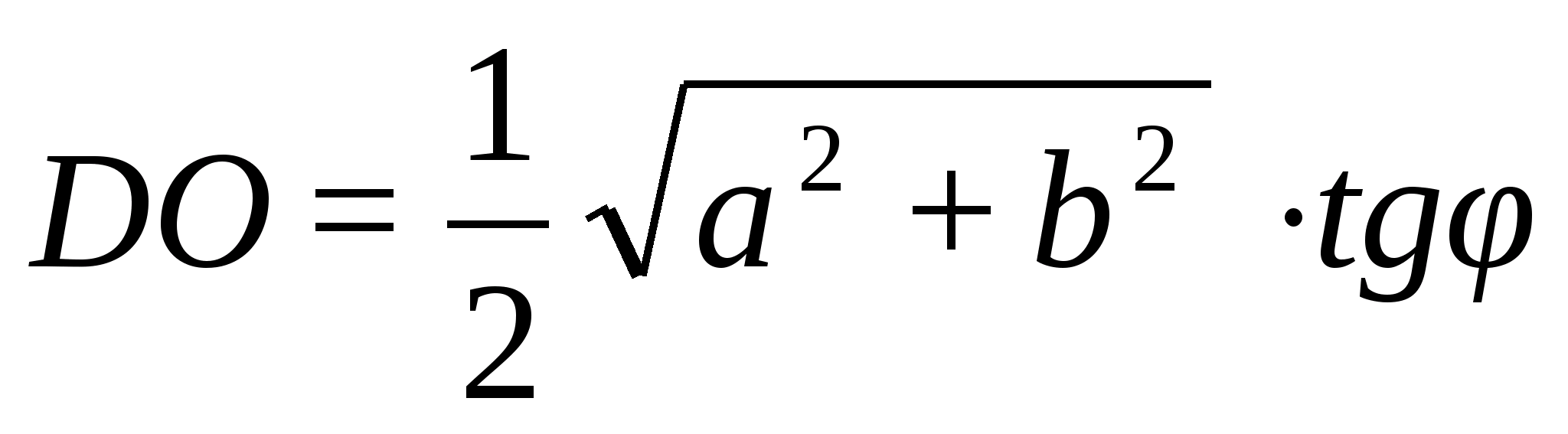
3)
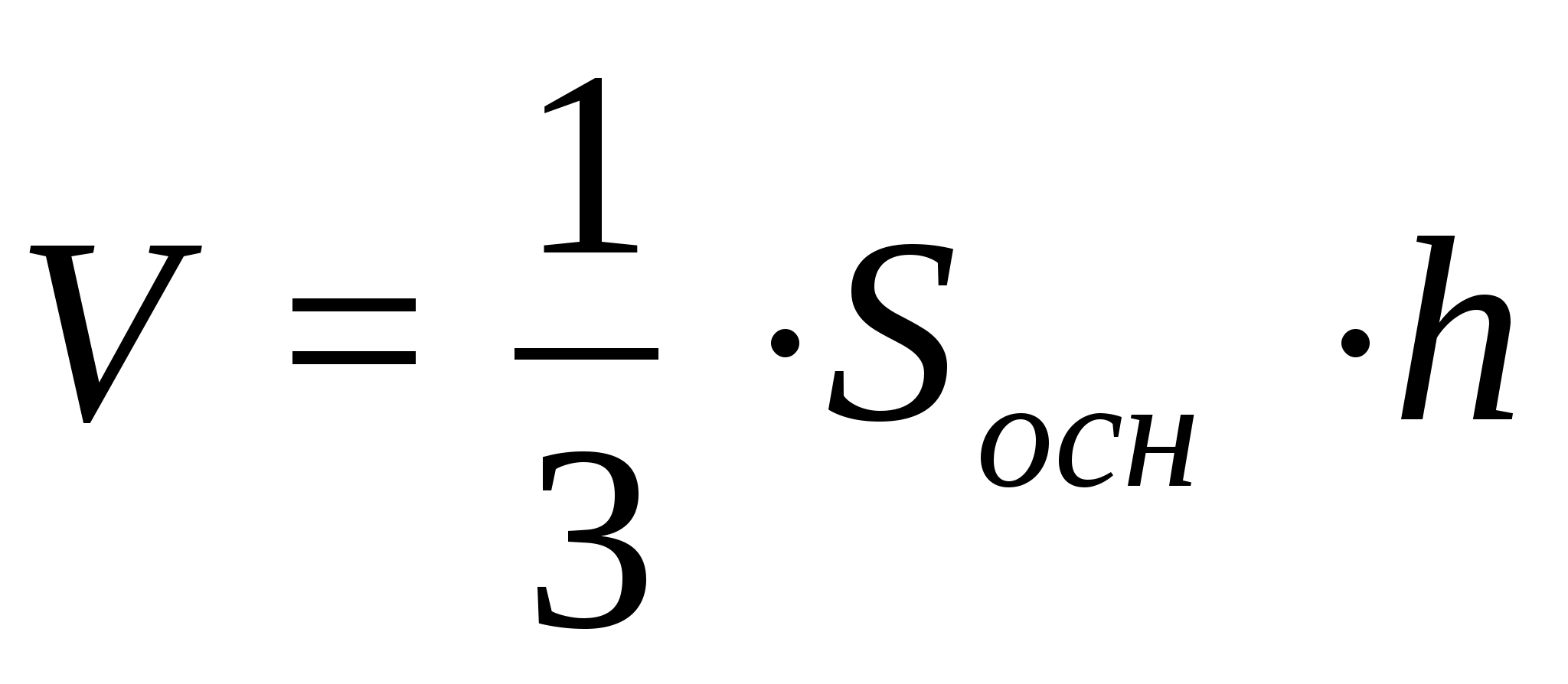
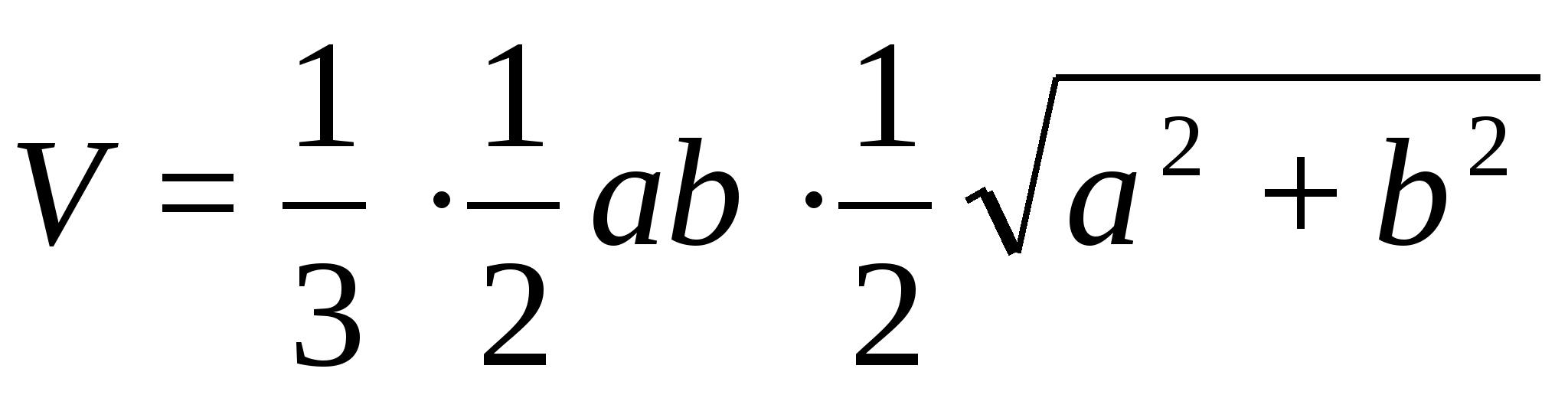
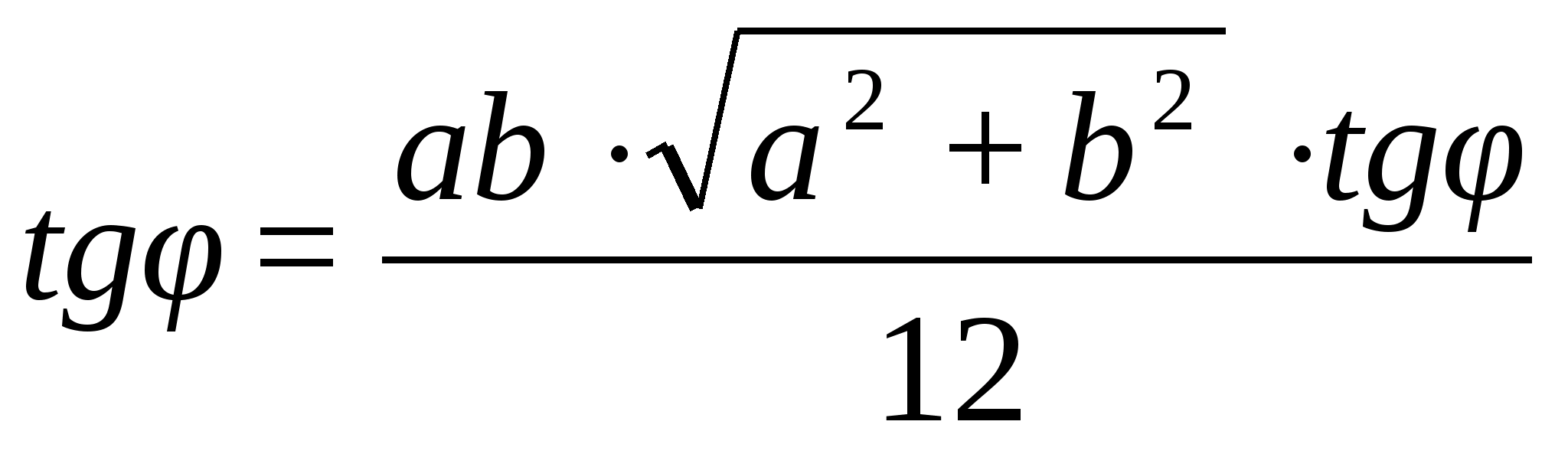
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 7-11 классов
Погорелова А.В.
В другом базовом
учебнике А.В. Погорелова и др.
теоретический
материал в той или иной степени касающийся
темы «Тетраэдр» содержится в пунктах
176-180, 186, 192, 199, 200.
В пункте 180 “Правильные
многогранники” содержится определение
понятия «правильный тетраэдр» (“Тетраэдр
представляет собой треугольную пирамиду,
у которой все рёбра равны”), доказательство
некоторых свойств и теорем о пирамиде
проиллюстрировано чертежами тетраэдра.
Однако в данном учебном пособии акцент
на изучении фигуры не ставится, и в этом
смысле его информативность (касательно
тетраэдра) можно оценить как низкую.
Практический же материал учебника
содержит удовлетворительное количество
заданий, касающихся пирамиды, в основании
которой расположен треугольник (что по
сути и есть тетраэдр). Приведём примеры
решения некоторых задач.
Решение задач.
Задача 1 (№ 41 из пункта
«Многогранники»).
Основание пирамиды
— равнобедренный треугольник, у которого
основание равно 12 см, а боковая сторона
— 10 см. Боковые грани образуют с основанием
равные двугранные углы, содержащие по
45°. Найдите высоту пирамиды.
Решение:
Проведем перпендикуляр
SO к плоскости
основания и перпендикуляры
SK, SM и
SN к сторонам
ΔABС. Тогда
по теореме о трех перпендикулярах
OK
ОМ
и ON
Тогда,

=

=

= 45° — как
линейные углы данных двугранных углов.
А следовательно, прямоугольные
треугольники SKO,
SMO и
SNO равны
по катету и острому углу.
Так что
OK=OM=ON, то
есть точка
О является
центром окружности, вписанной
в
ΔАВС.
Выразим площадь
прямоугольника
АВС:
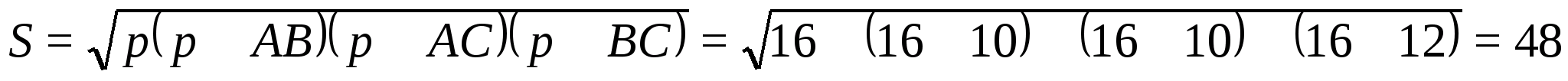
С другой стороны,
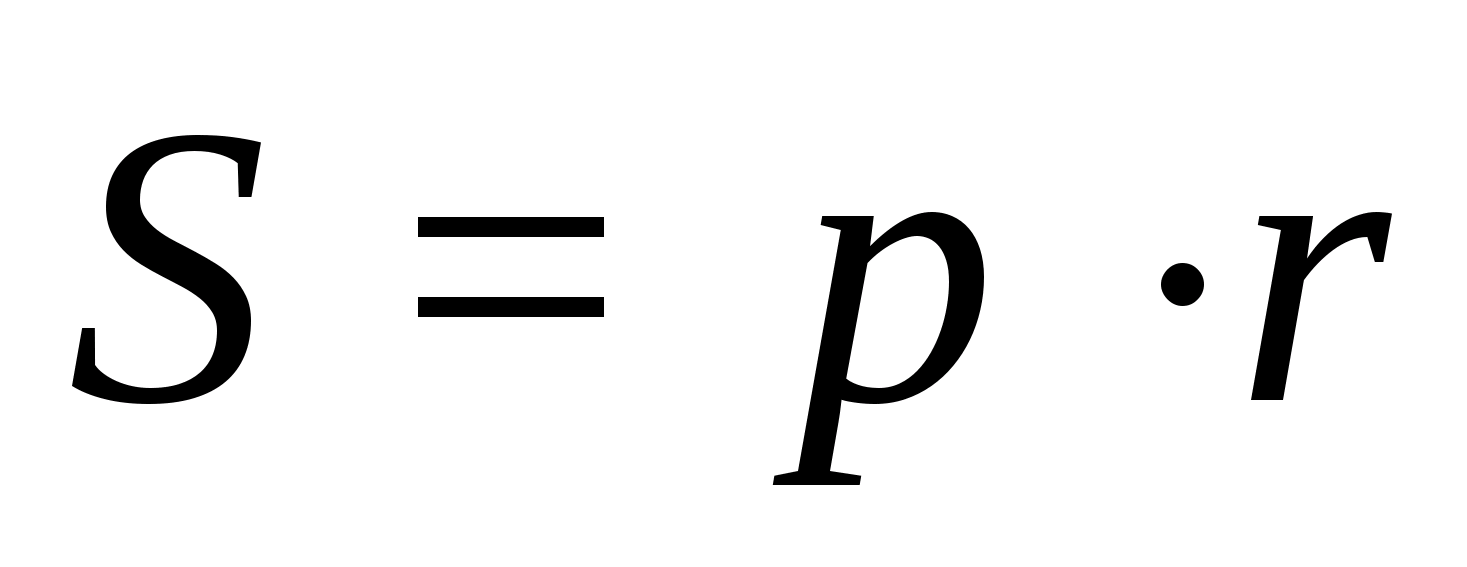
Так что
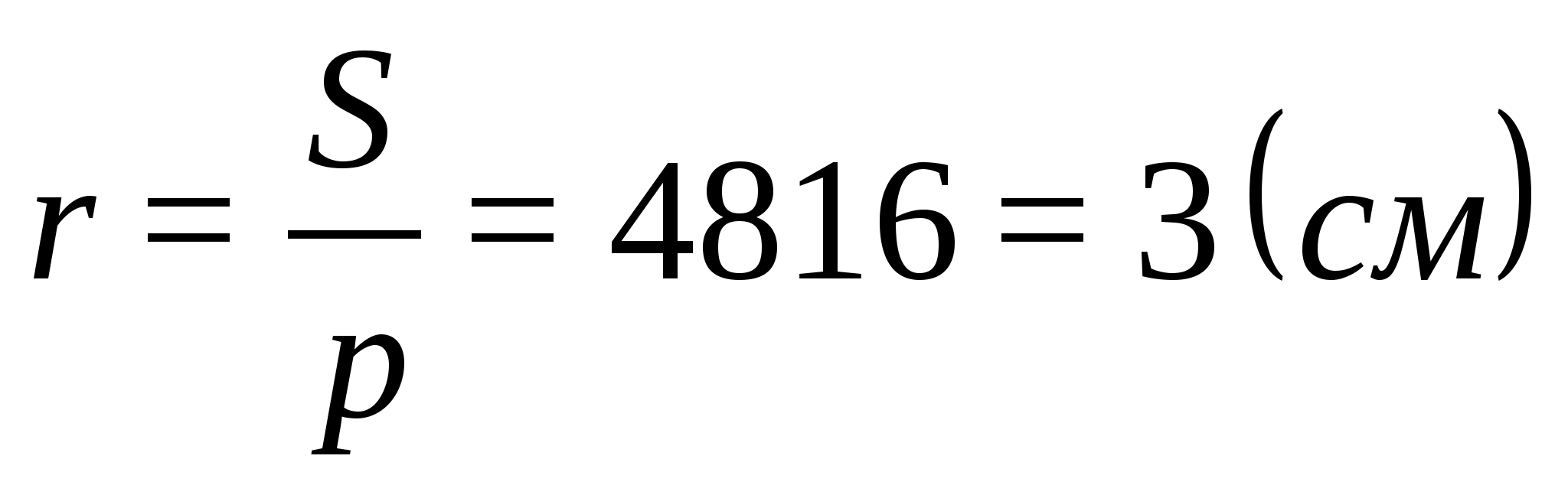
ОК=r=3 см. Так
как в прямоугольном треугольнике
SOK острый
угол равен
45°,
то
ΔSOK является
равнобедренным и
SO=OK=3(см).
Задача 2 (№ 43 из
пункта «Объёмы многогранников»).
Найдите объем
пирамиды, имеющий основанием треугольник,
два угла которого
a и β; радиус
описанного круга
R. Боковые
ребра пирамиды наклонены к плоскости
ее основания под углом
γ.
Решение.
Так как все боковые
ребра пирамиды наклонены к плоскости
основания под одним и тем же углом, то
высота пирамиды
O>1>O
проходит
через центр описанной около основания
окружности. Так что
Далее, в прямоугольном
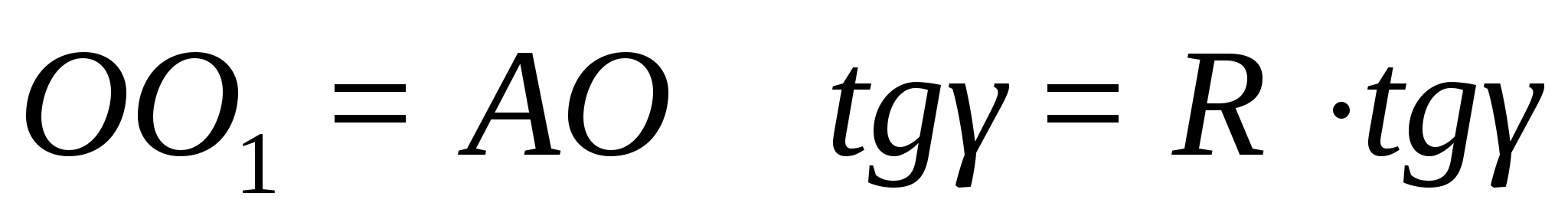
В ΔАВС
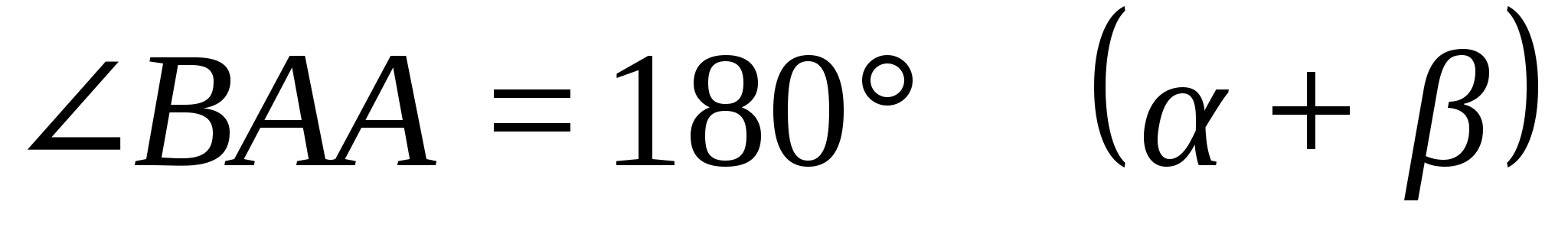
Тогда
согласно теореме синусов
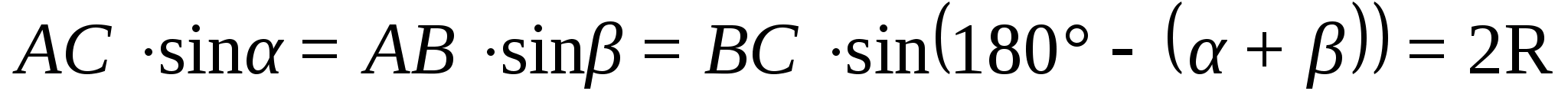
Так что
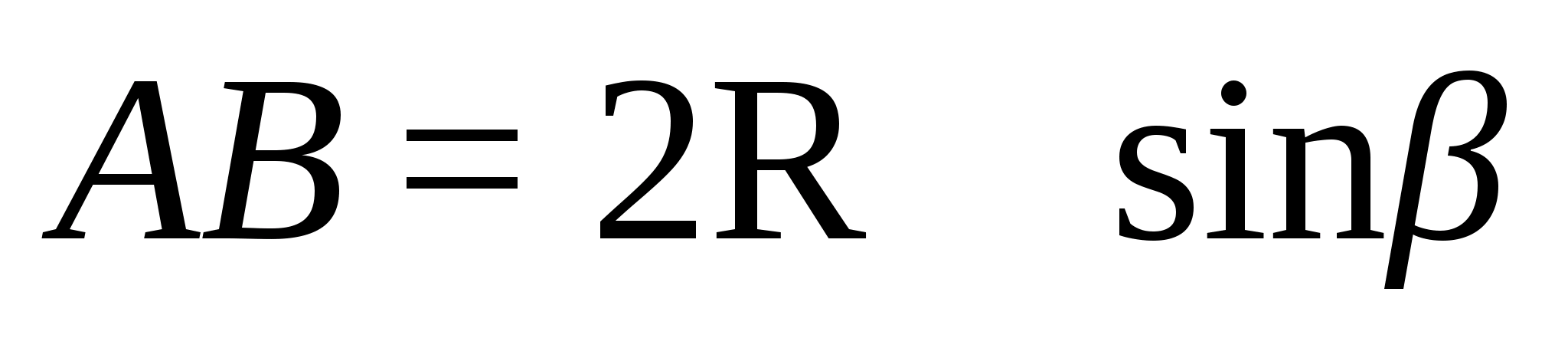
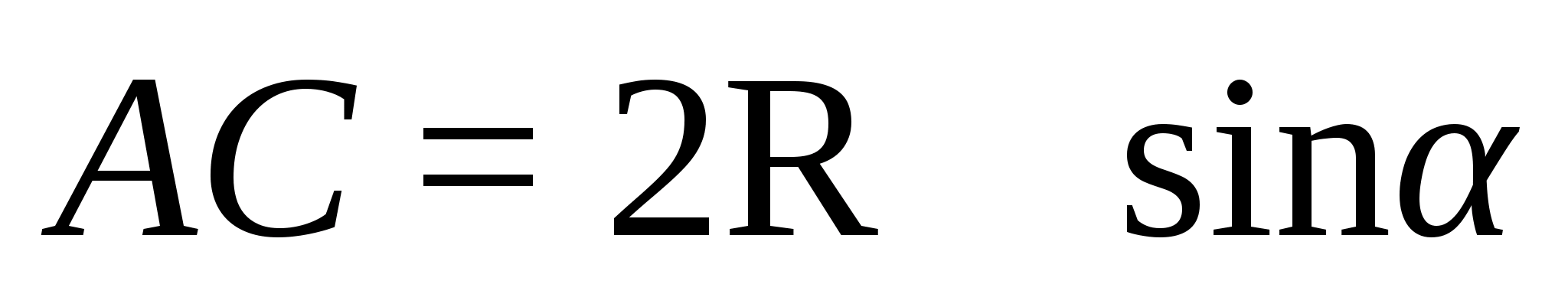
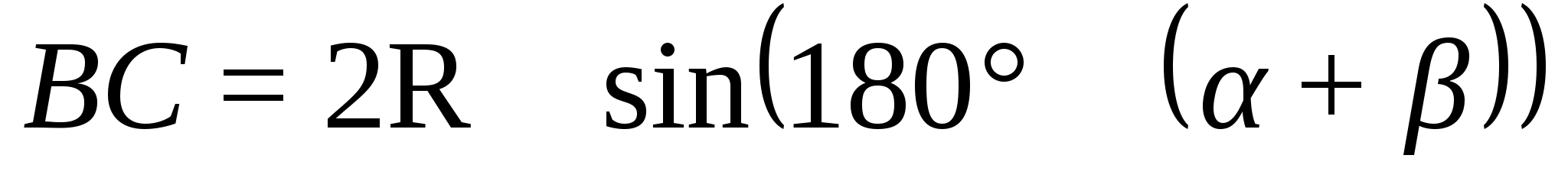
=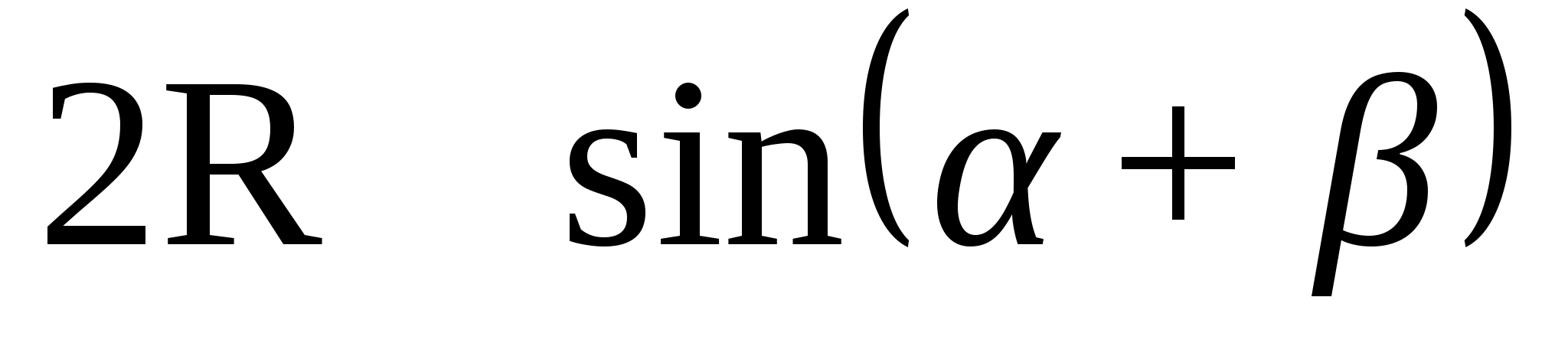
Площадь треугольника
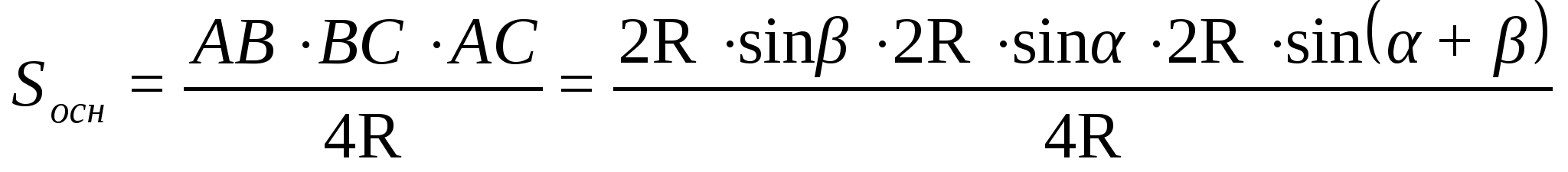
Тогда
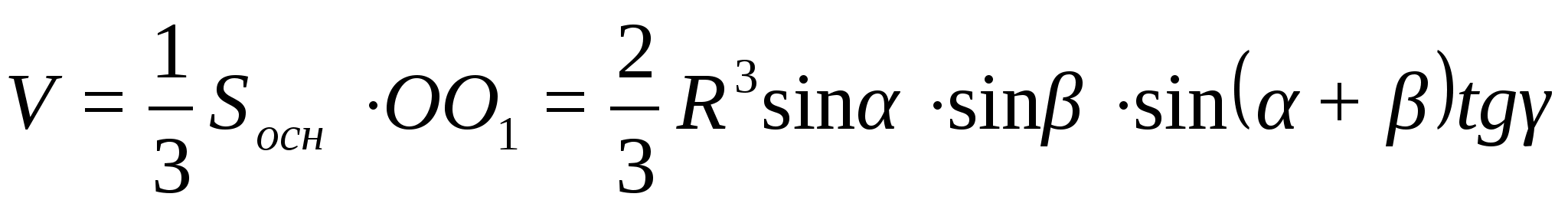
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Александрова А.Д.
Рассмотрим учебное пособие
Александрова А.Д. и др. «Геометрия:
учебник для учащихся 11 кл. с углубленным
изучением математики». Отдельных
параграфов, посвящённых тетраэдру в
этом учебнике нет, однако тема присутствует
в виде фрагментов других параграфов.
Впервые тетраэдр упоминается в
§21.3. В материале параграфа рассматривается
теорема о триангуляции многогранника,
в качестве примера выполняют триангуляцию
выпуклой пирамиды. Само понятие
«многогранник» в учебнике трактуется
двумя способами, второе определение
понятия напрямую связано с тетраэдром:
«Многогранник – это фигура, являющаяся
объединением конечного числа тетраэдров…».
Познания, касающиеся правильной пирамиды
и некоторых аспектов симметрии тетраэдра
можно обнаружить в §23.
В §26.2 описано применение теоремы
Эйлера («о правильных сетях») для
правильных многогранников (в т.ч. для
тетраэдра), а в §26.4 рассматриваются виды
симметрий, характерные для этих фигур.
Формулу для нахождения объёма
пирамиды авторы вводят в задаче №30.1(2),
а площадь боковой поверхности пирамиды
вводится в материале параграфа «Площадь
поверхности конуса и цилиндра» (§32.5).
Также, в учебнике можно найти
информацию о средней линии тетраэдра,
центре масс (§35.5) и классе равногранных
тетраэдров. Движения I
и II
рода демонстрируются в ходе решения
задач о тетраэдрах.
Отличительная особенность
учебника — высокая научность, которую
авторам удалось совместить с доступным
языком и чёткой структурой изложения.
Приведём примеры решения некоторых
задач.
Решение задач.
Задача 1.
В данную правильную
треугольную усечённую пирамиду с боковым
ребром a можно поместить сферу, касающуюся
всех граней, и сферу, касающуюся всех
рёбер. Найдите стороны оснований
пирамиды.
Решение.
Изобразим на чертеже
«полную» пирамиду. Данная пирамида
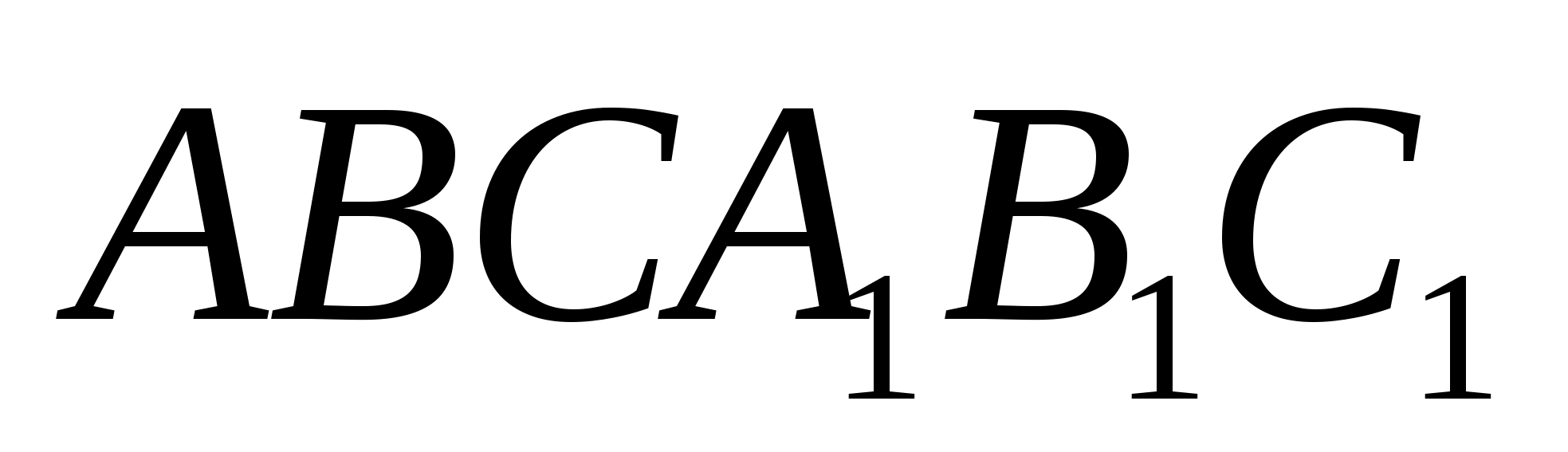
— высота «полной» пирамиды,
— ее часть до верхнего основания
усеченной. Задача сводится к
планиметрической, при этом не надо
рисовать ни одной из данных сфер. Т.к. в
усеченную пирамиду можно вписать сферу,
касающуюся всех ребер, то в её боковую
грань можно вписать окружность. Обозначим
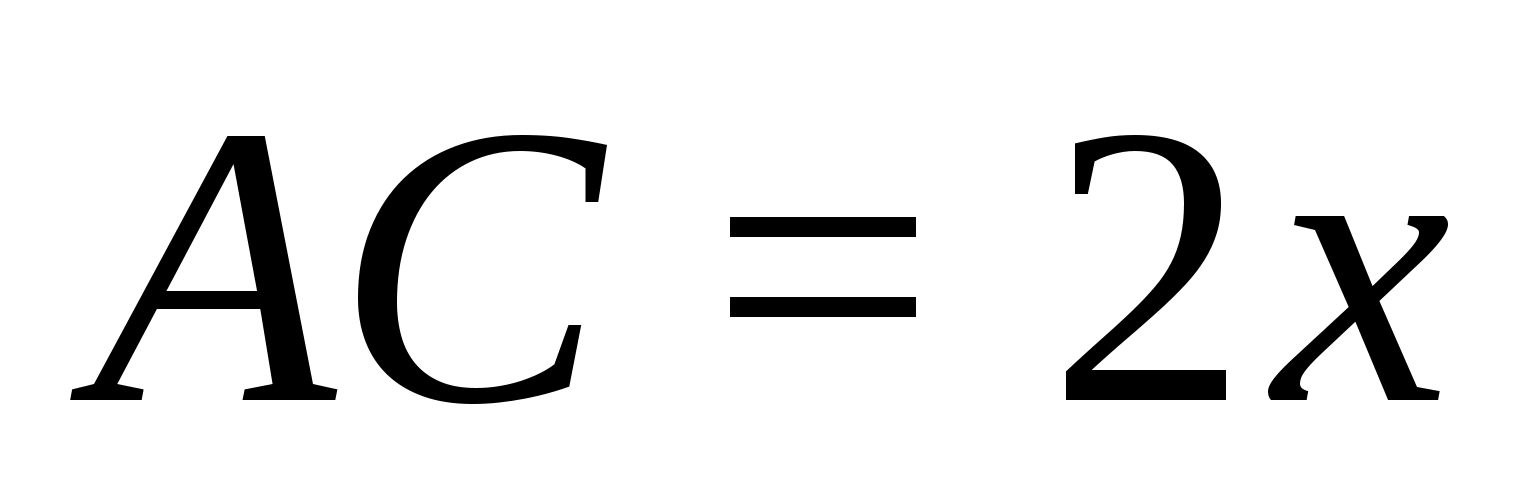
(для удобства деления пополам) и для
описанного четырехугольника
получим, что
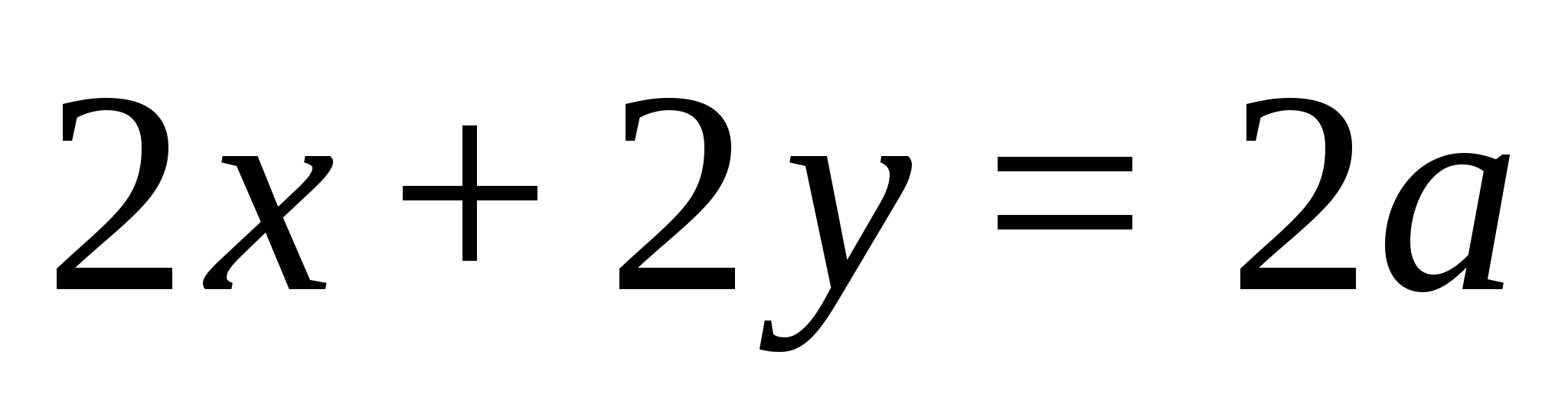
откуда
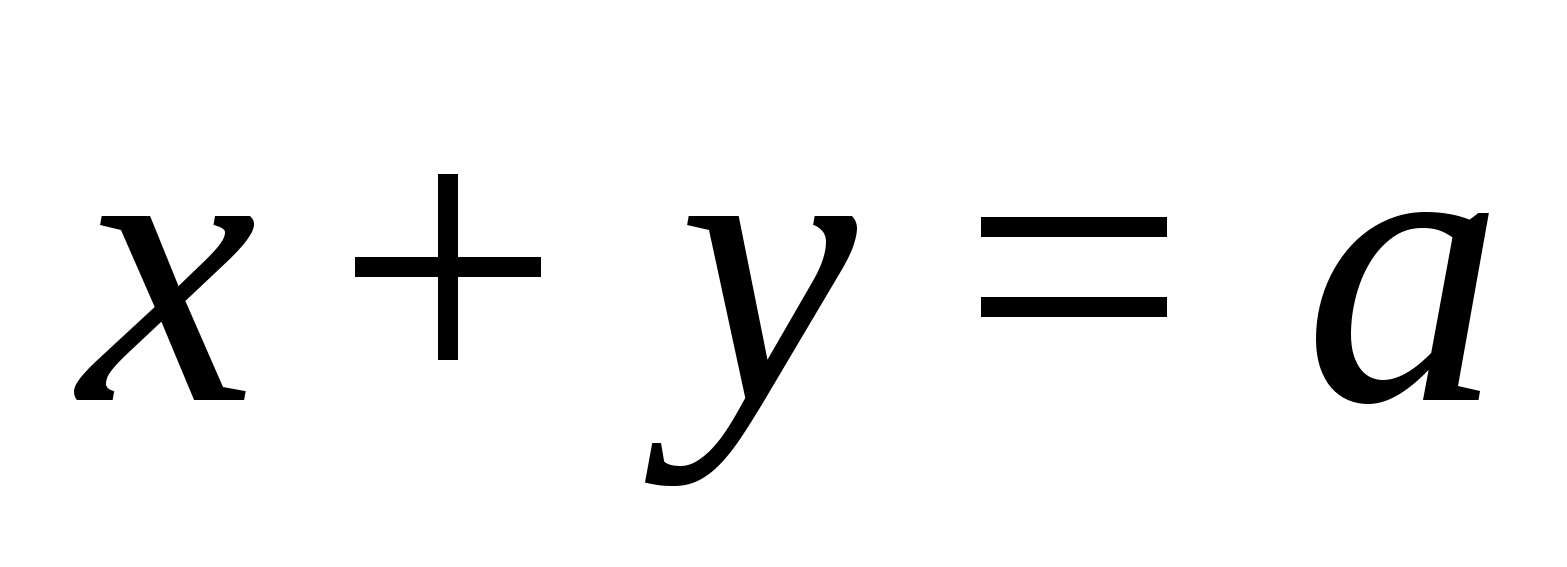
Из существования
вписанного шара следует, что существует
полуокружность, расположенная в трапеции
(
— апофема «полной» пирамиды) так, что
ее центр лежит в середине
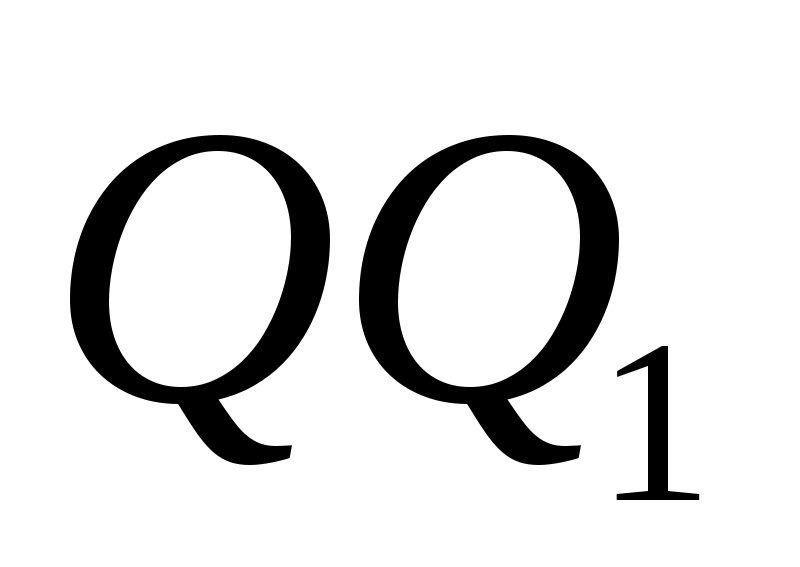
а сама она касается остальных трёх
сторон трапеции.
— центр шара,
и
— точки касания. Тогда
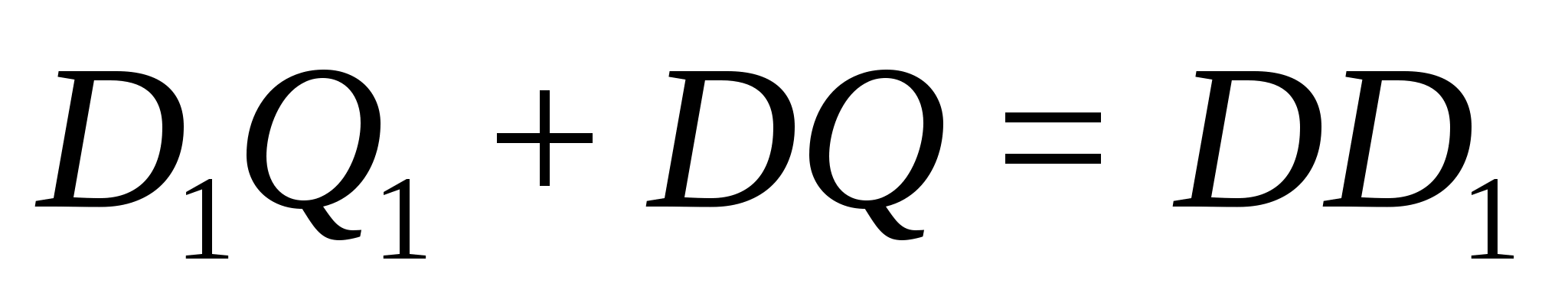
Выразим эти величину через
и
Из
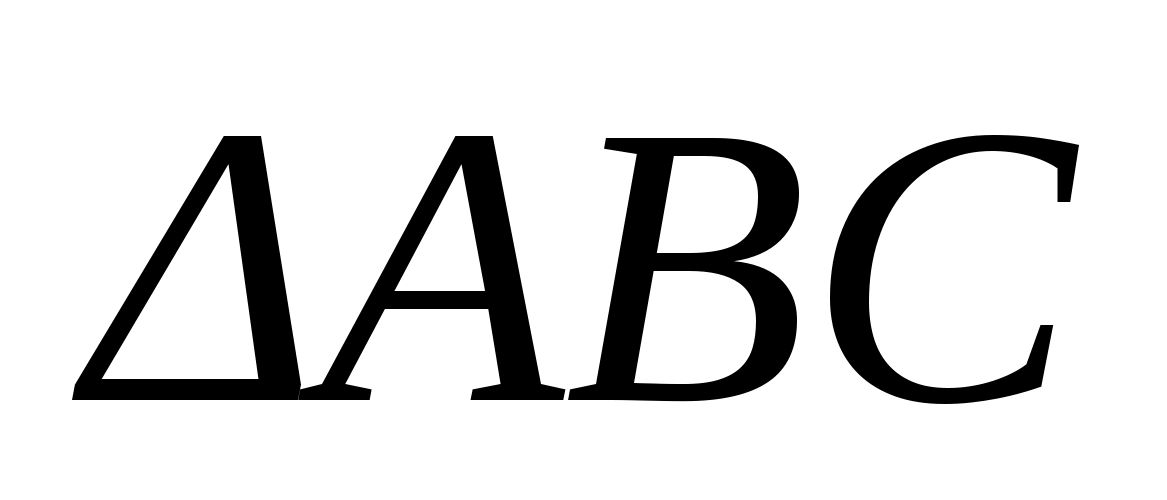
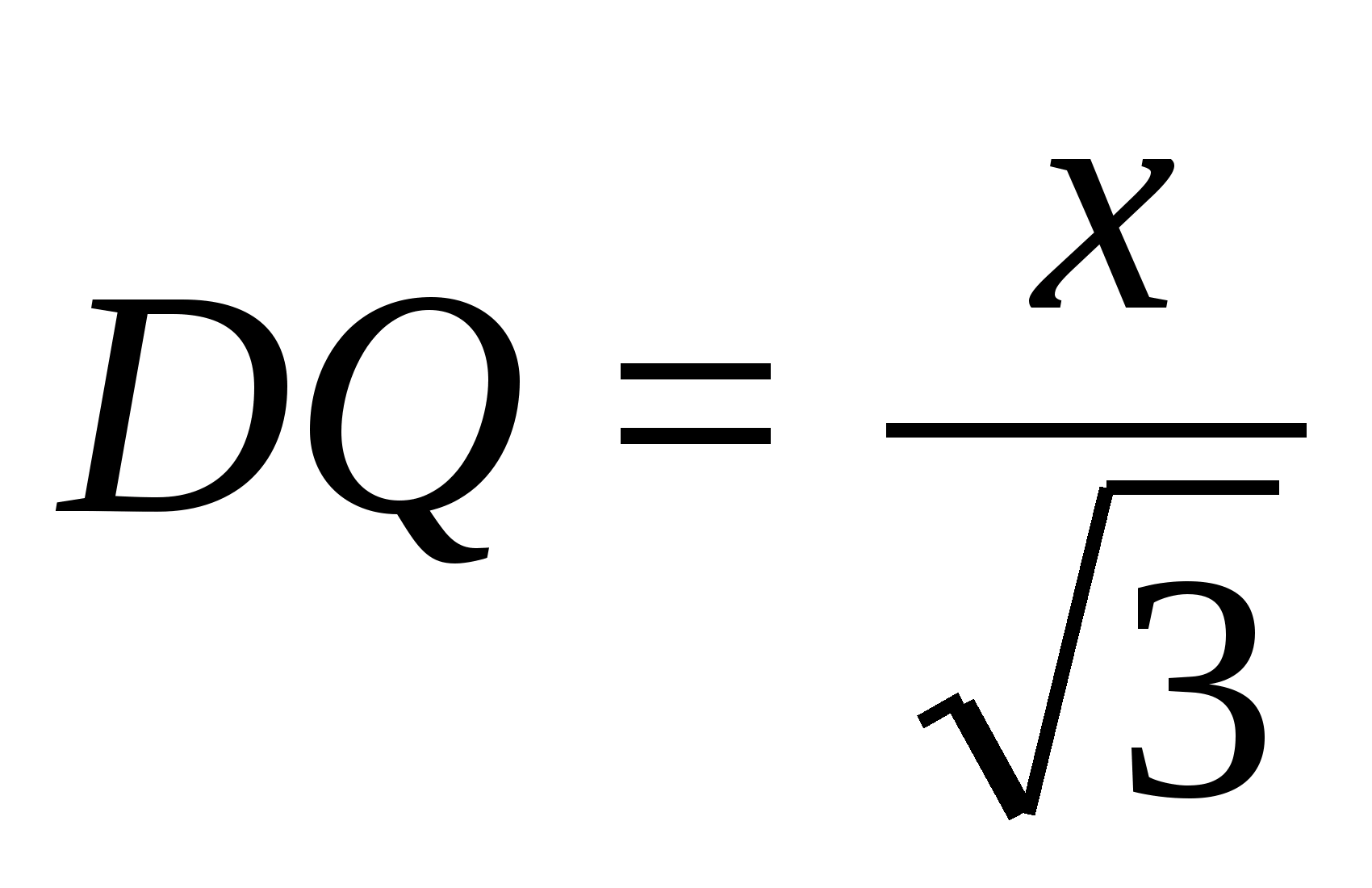
Из

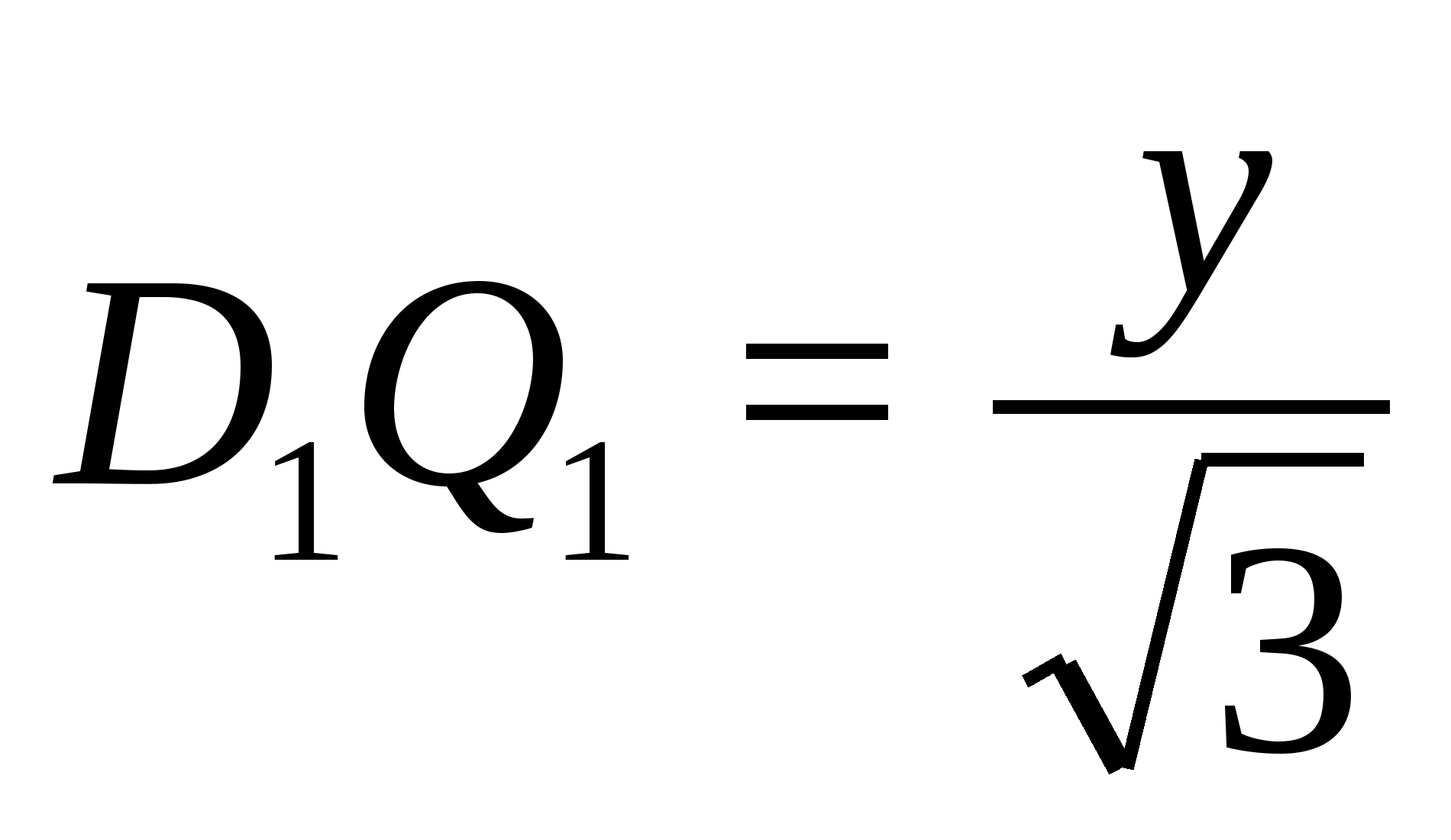
Из трапеции
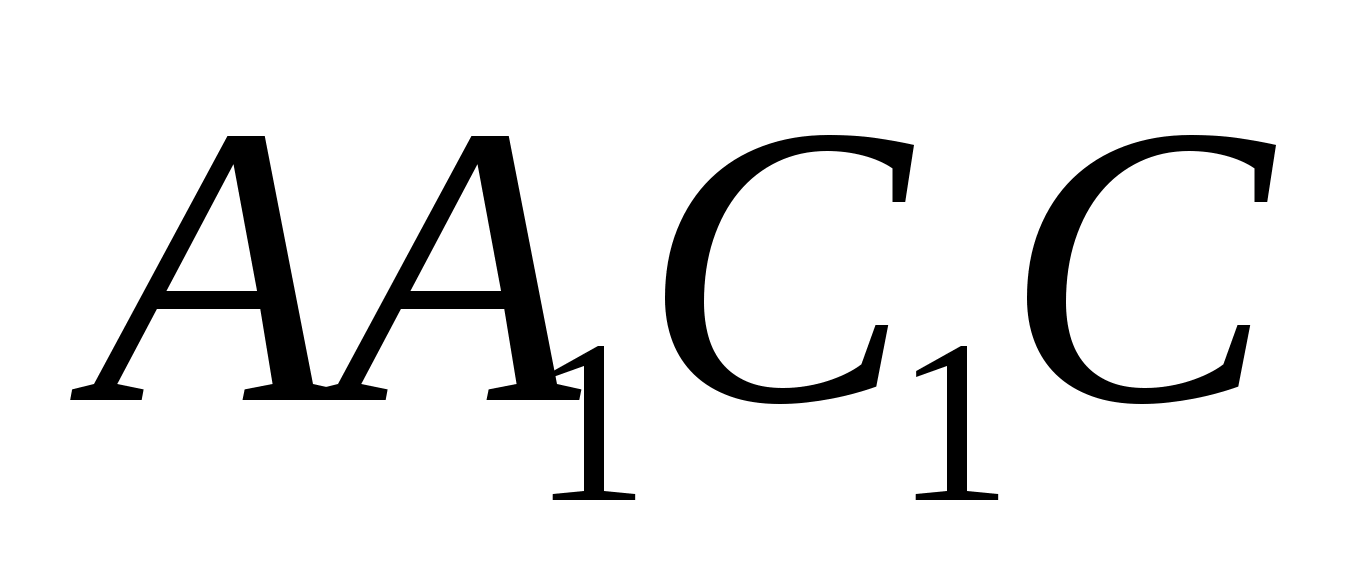
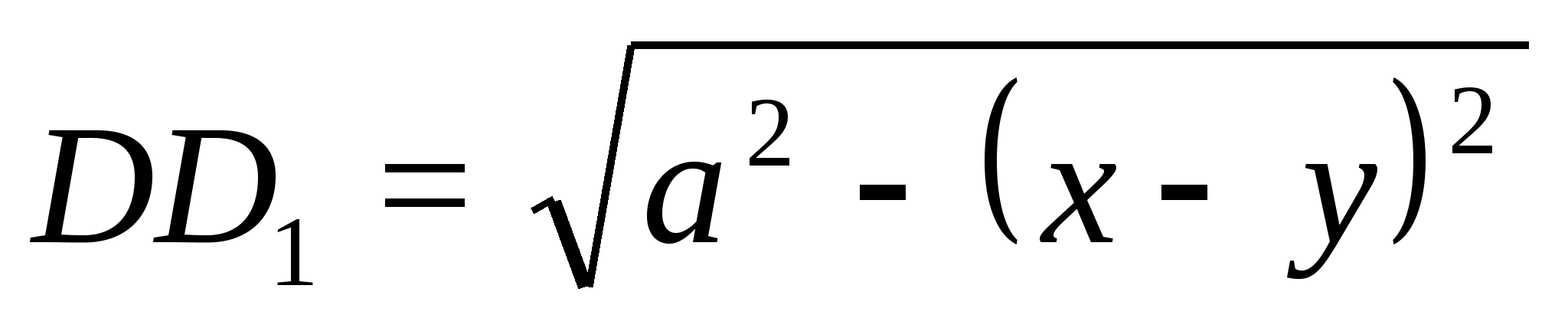
Получаем уравнение:
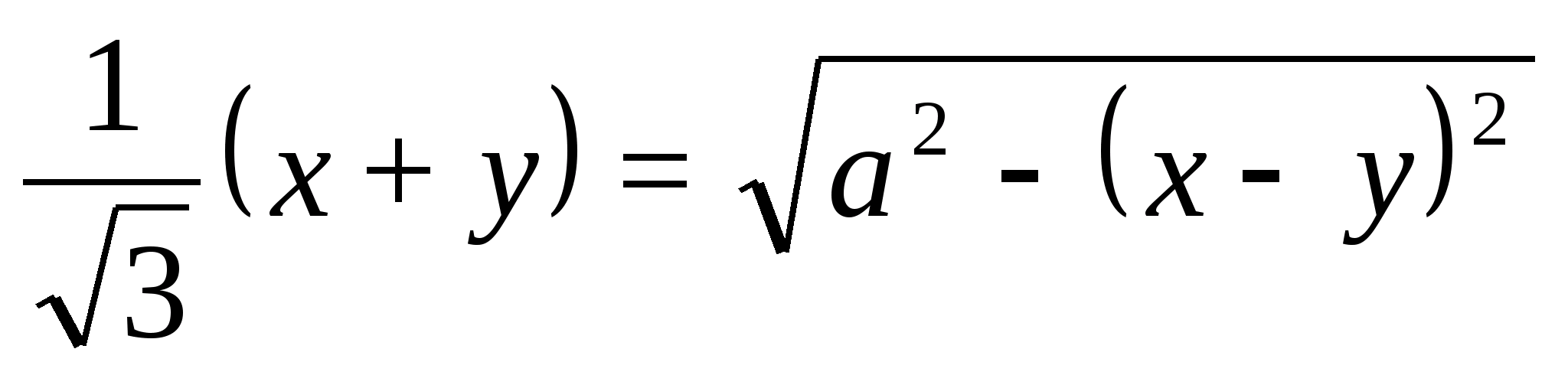
Решив систему
уравнений (1) и (2), получим, что стороны
оснований равны
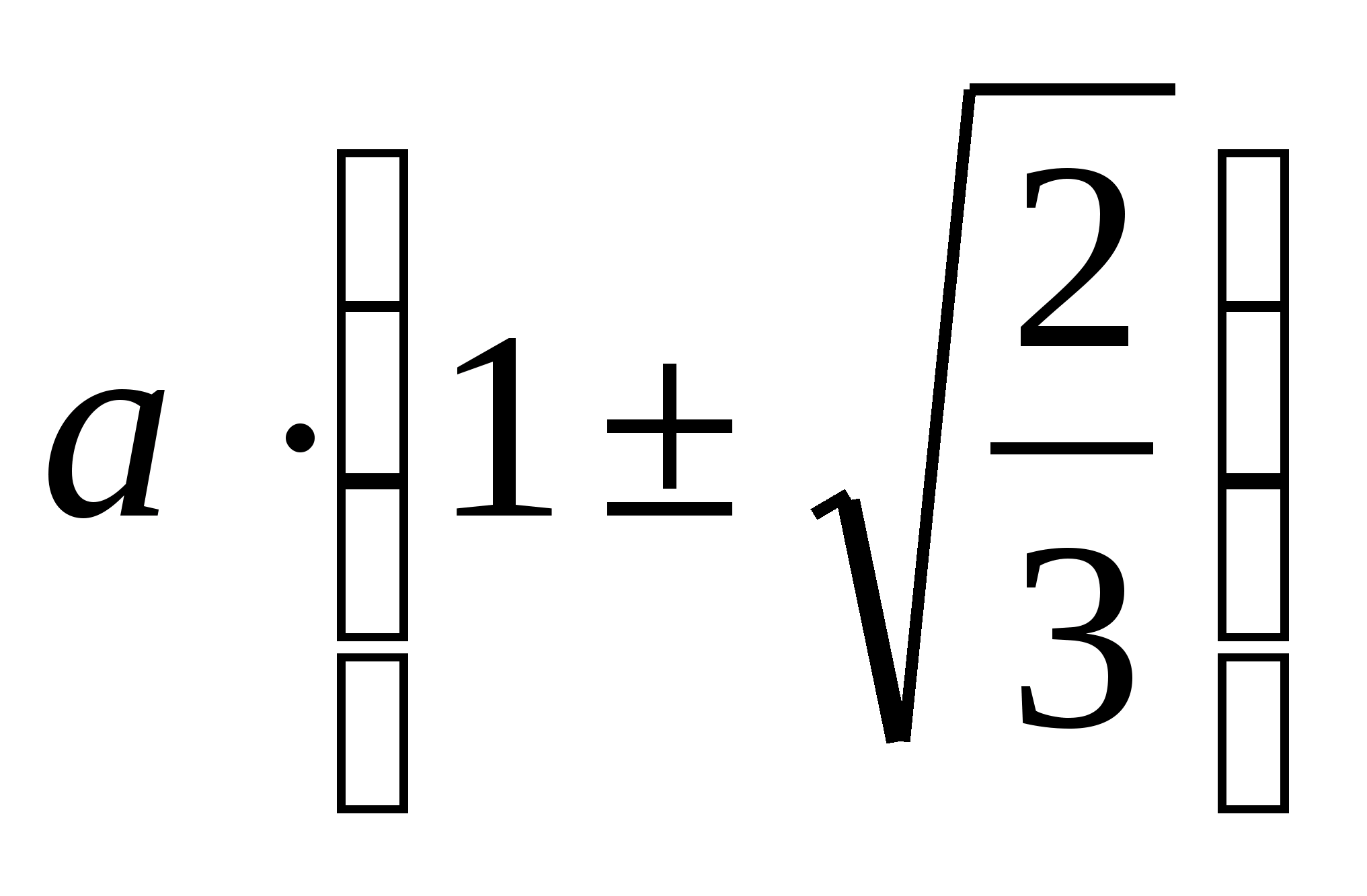
Задача 2.
Внутри правильного
тетраэдра с ребром a
расположены четыре равные сферы так,
что каждая сфера касается трех других
сфер и трех граней тетраэдра. Найти
радиус этих сфер.
Решение.
— данный тетраэдр,
— его высота,
— центры сфер,
— точка пересечения прямой
с плоскостью
Заметим, что центры равных сфер
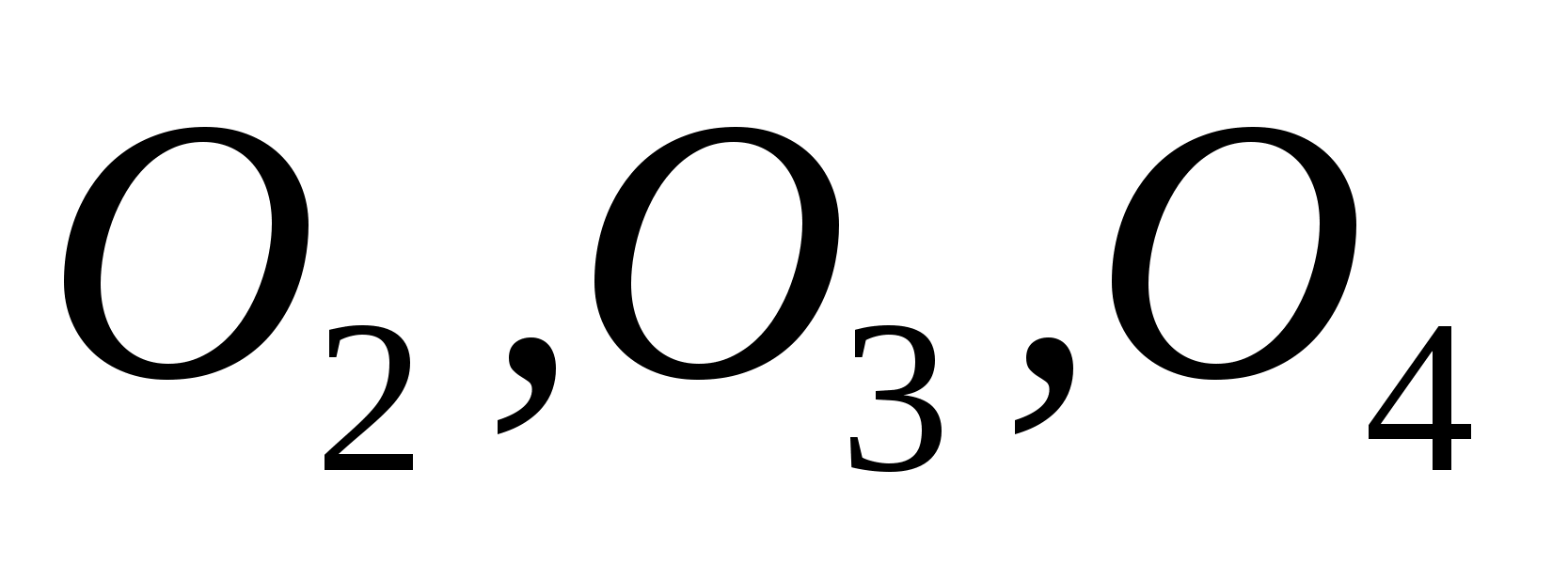
касающихся плоскости
удалены от нее на равные расстояния,
каждое из которых равно радиусу шара
(обозначием его как x).
Значит плоскости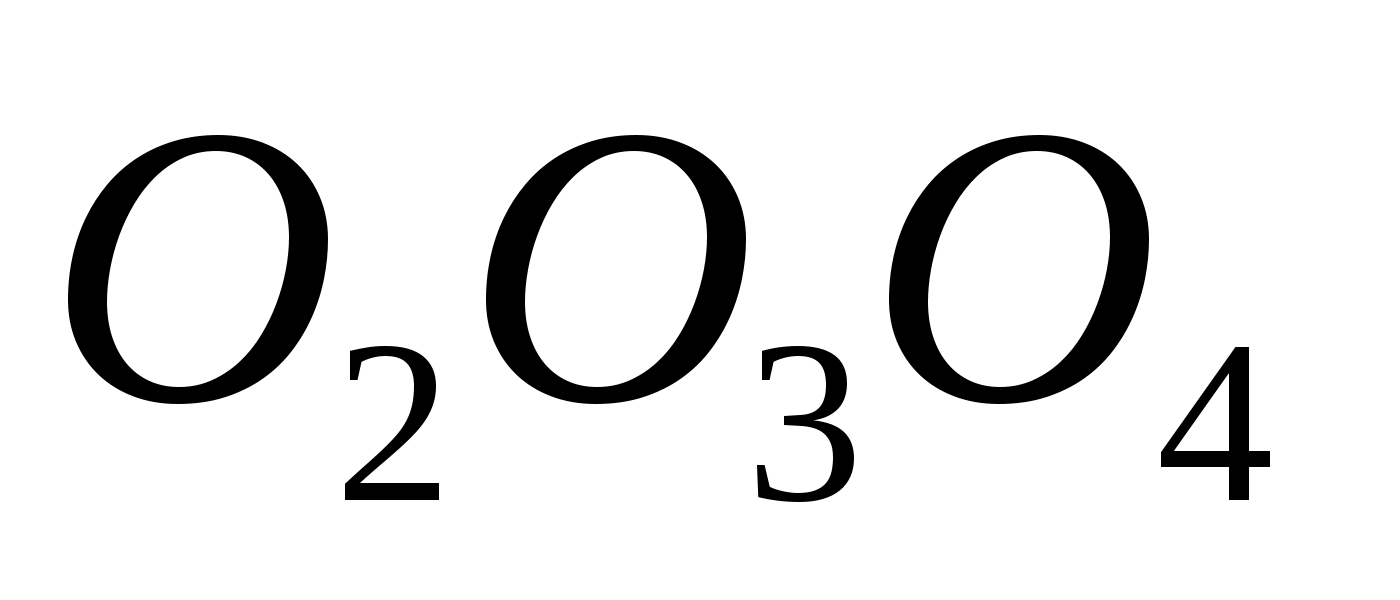
параллельны, а потому
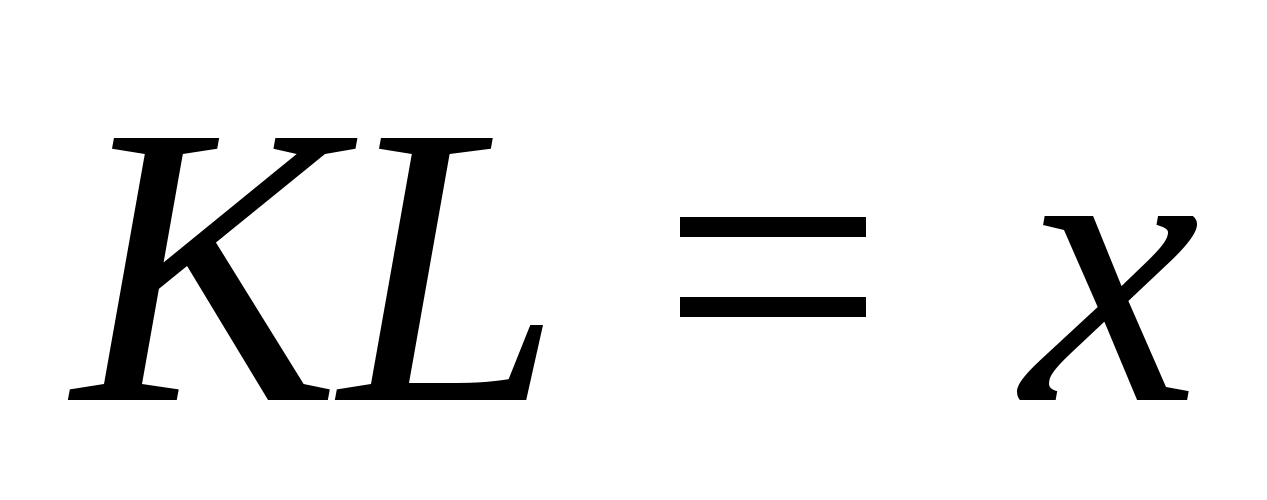
Далее, каждая пара
шаров касается между собой, а потому
расстояние между центрами равно сумме
их радиусов, то есть 2x.
Имеем:
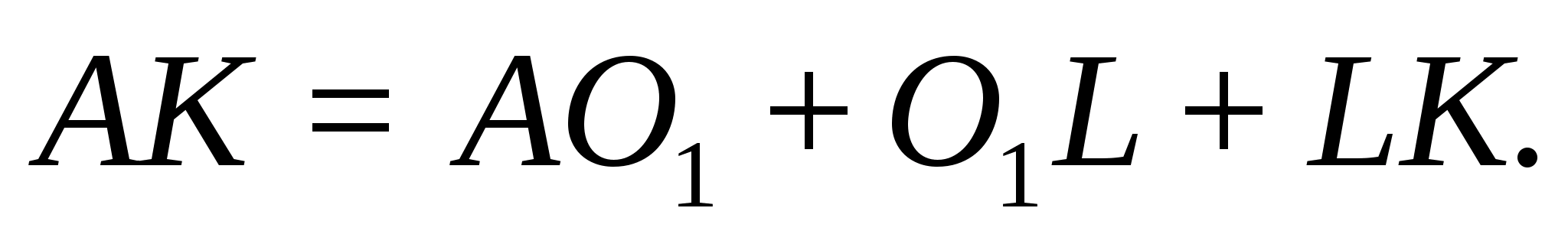
Но
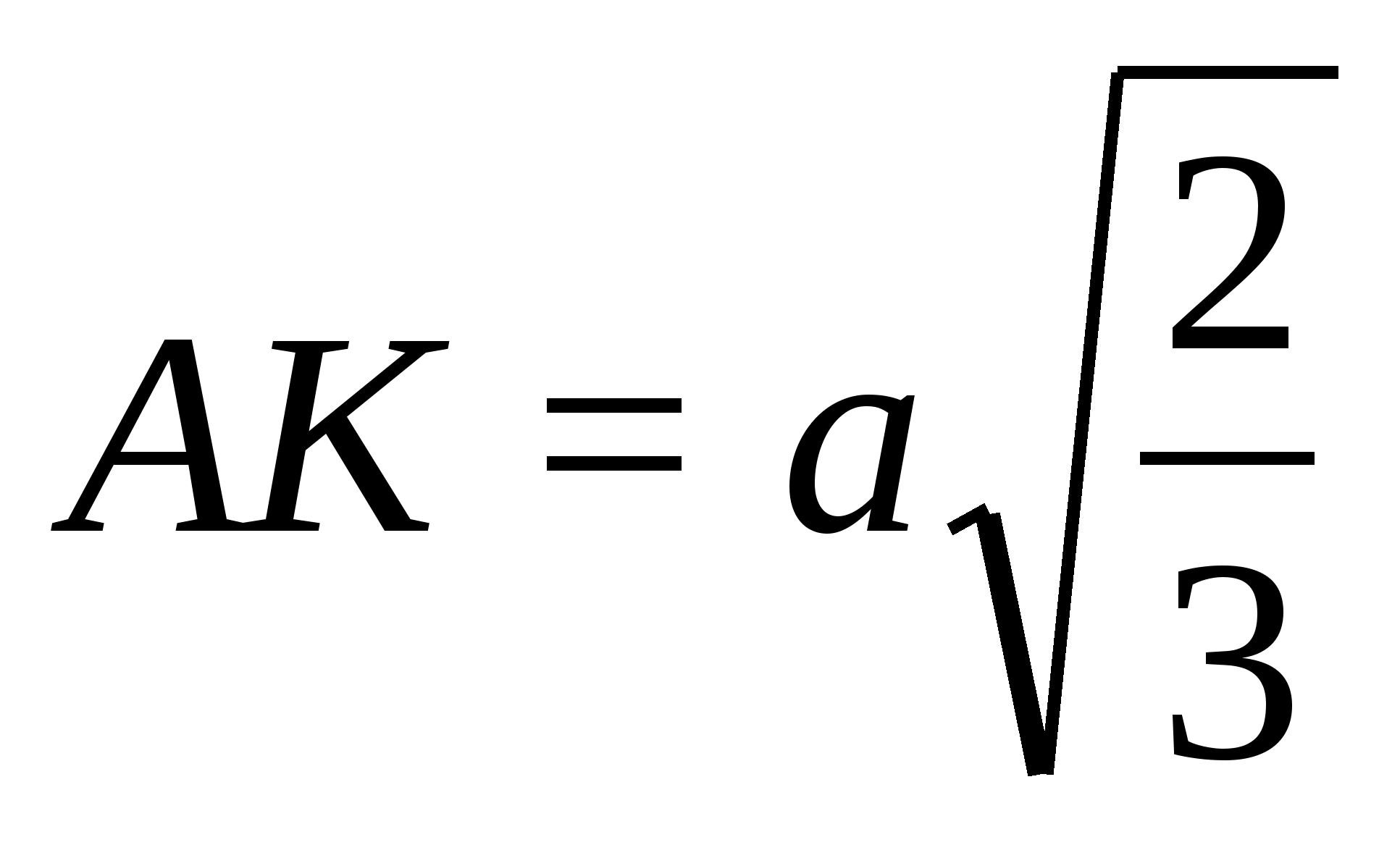
высота правильного тетраэдра с ребром
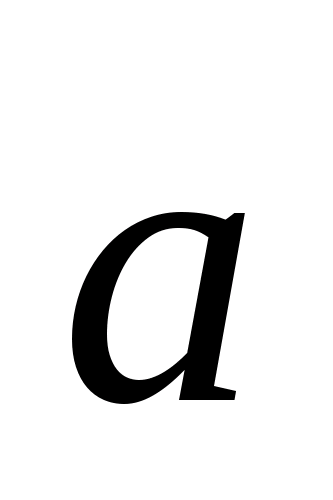
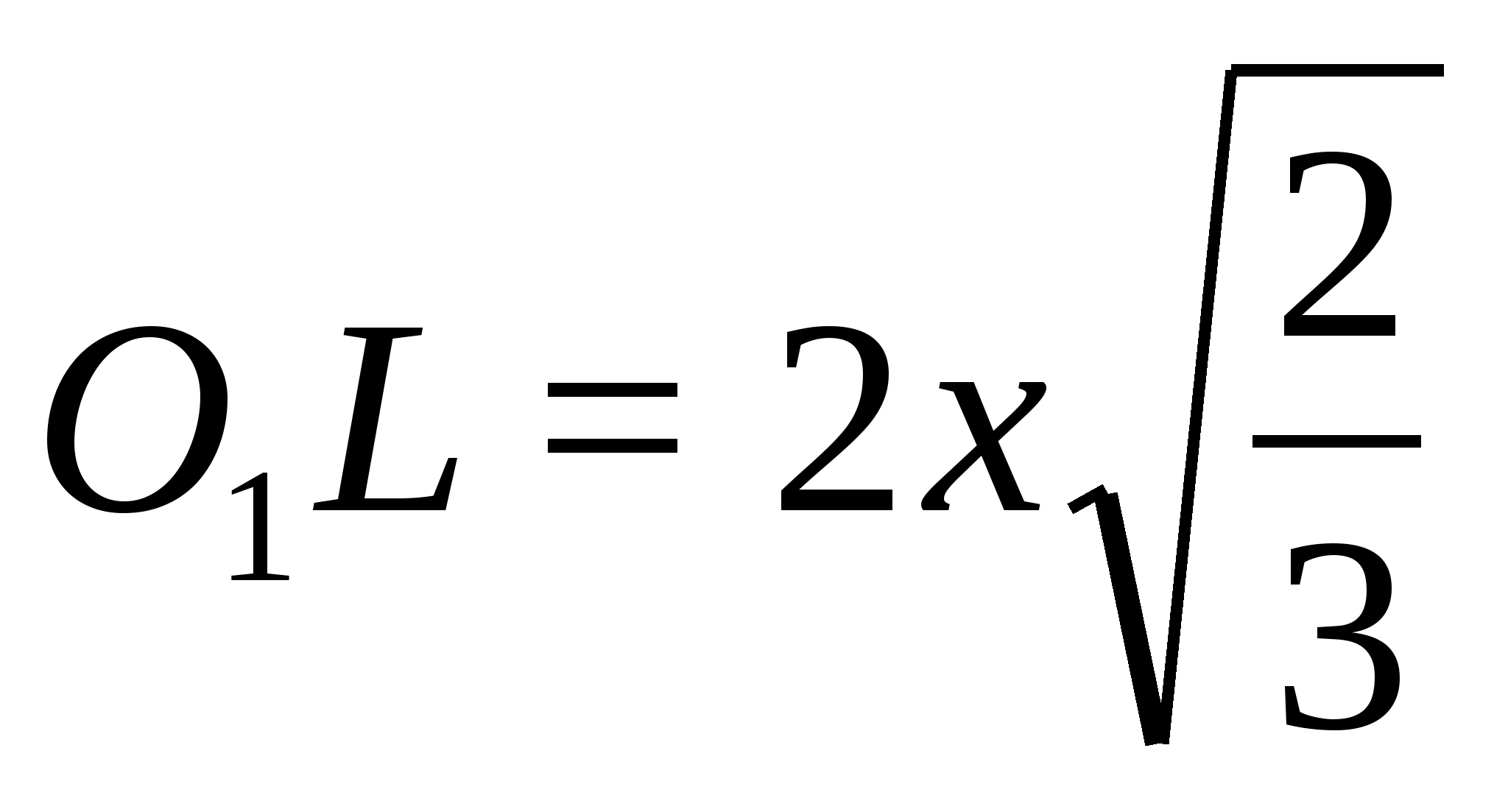
высота правильного тетраэдра с ребром
2x;
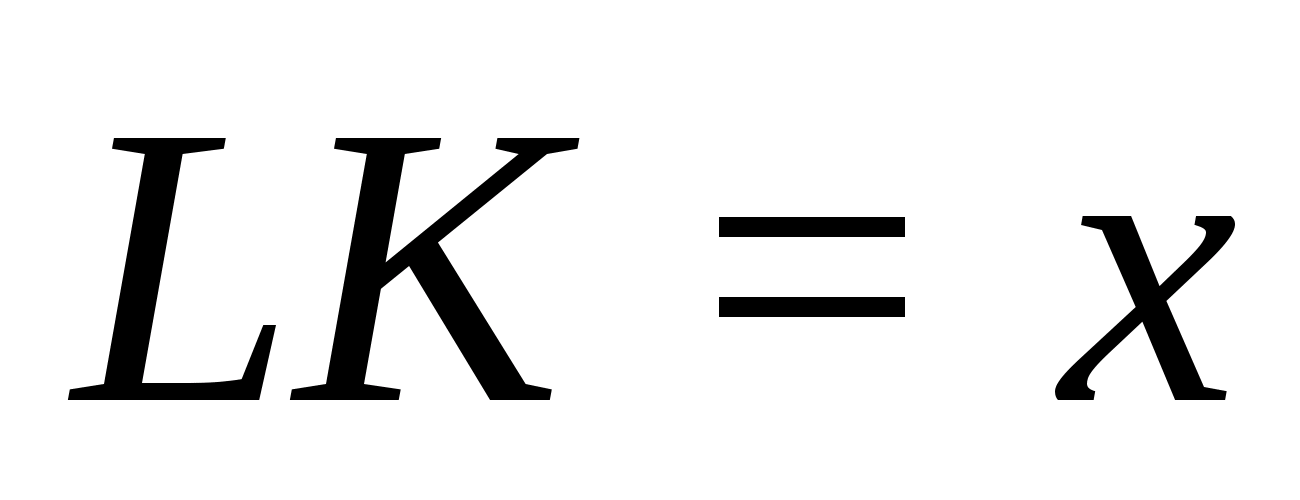
Осталось выразить
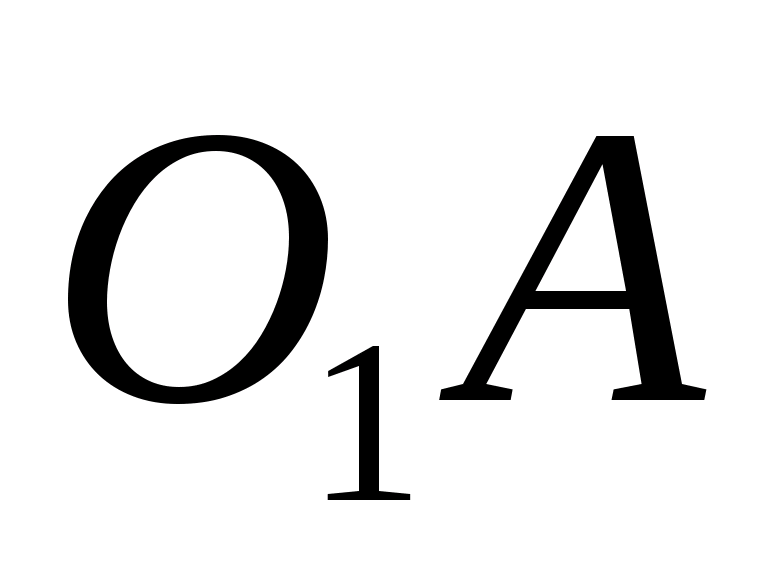
Заметим, что точка
находится внутри трехгранного угла и
удалена от его граней на расстояние
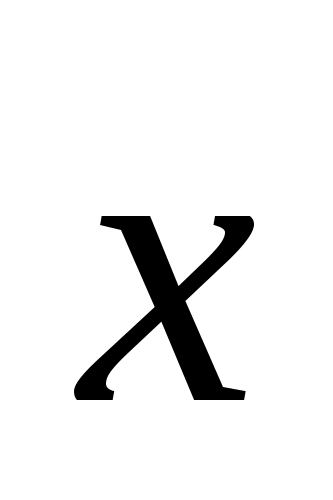
а плоские углы трехгранного угла равны

Не сложно получить то, что
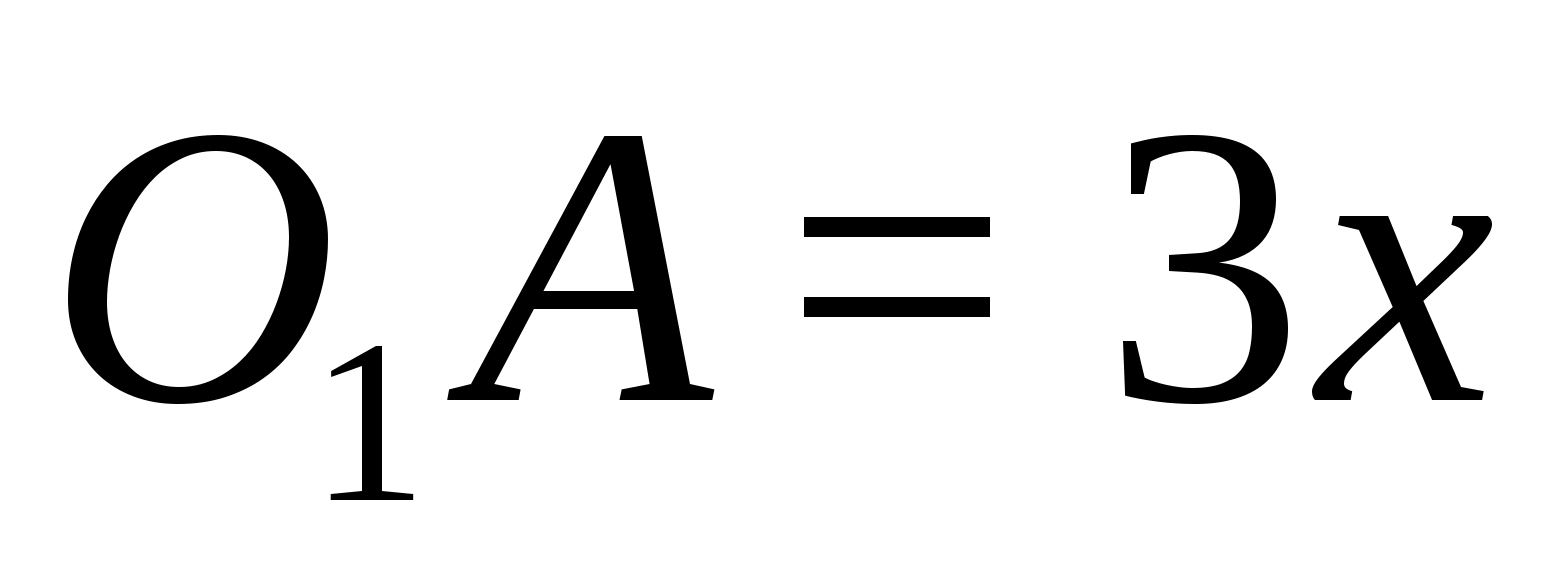
Приходим к уравнению:
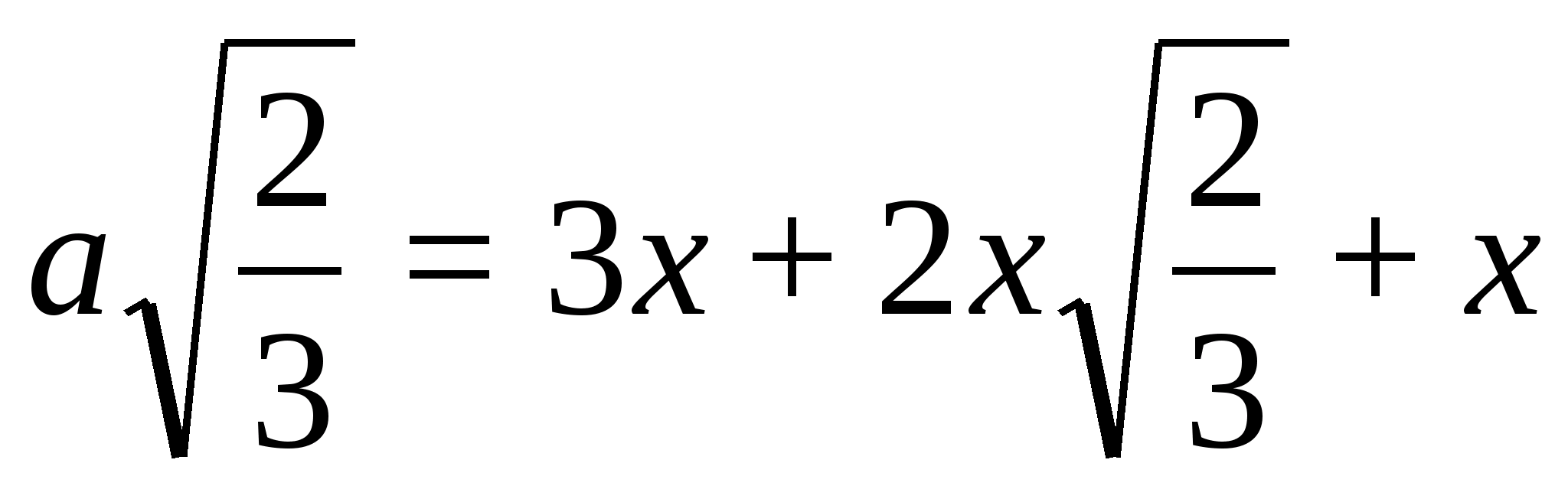
откуда после упрощений получаем
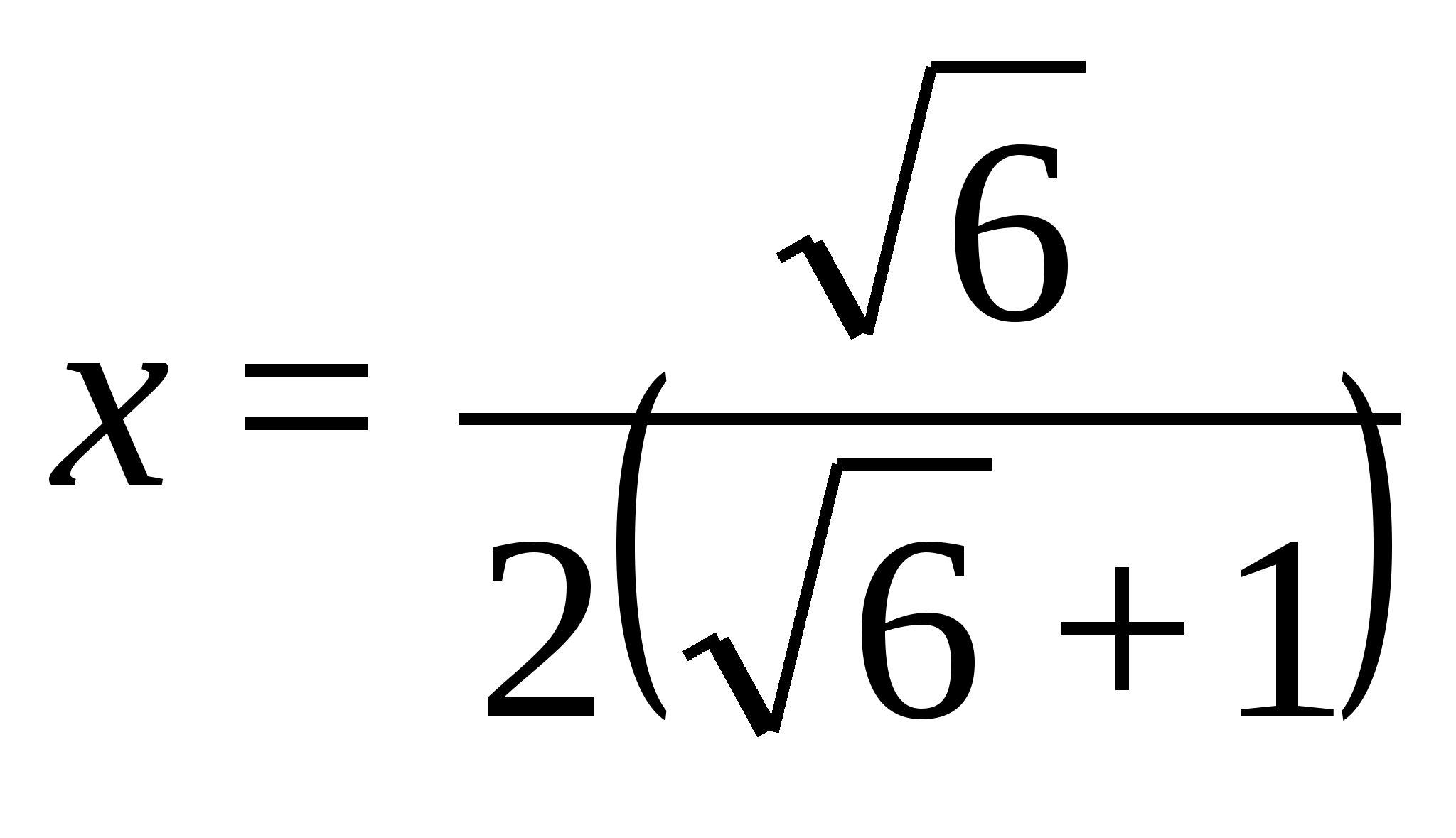
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Смирновой И.М.
Изложению темы «Тетраэдр» в
учебнике для 10-11 классов гуманитарного
профиля Смирновой И.М. посвящены
следующие занятия: 18,
19, 21, 22, 28-30, 35.
После изучения
теоремы о том, что «Всякий
выпуклый многогранник может быть
составлен из пирамид с общей вершиной,
основания которых образуют поверхность
многогранника» рассматривается теорема
Эйлера для некоторых таких многогранников,
в частности, выполнение условий теоремы
рассмотрено и для треугольной пирамиды,
которая, в сущности, и есть тетраэдр.
Учебник интересен
тем, что в нём рассматривается топология
и топологически правильные
многогранники(тетраэдр,
октаэдр, икосаэдр, куб, додекаэдр),
чье существование обосновывается при
помощи той же теоремы Эйлера.
Помимо этого в
учебнике приведено определение понятия
«правильная пирамида»; рассматриваются
теоремы о существовании вписанной и
описанной сфер тетраэдра, некоторые
свойства симметрии, касающиеся тетраэдра.
На заключительном занятии (35) приводится
формула нахождения объёма треугольной
пирамиды.
Для данного учебного
пособия характерен большой объем
иллюстративного и исторического
материала, а также небольшой объём
практического материала, обусловленный
направленностью учебника. Рассмотрим
также учебник Смирновой И.М. и др. для
10-11 классов естественно-научного профиля.
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Смирновой И.М. и др.
От предыдущего учебного пособия
данное отличается компоновкой тем и
уровнем сложности предлагаемых к решению
задач. Отличительной особенностью
изложения материала является деление
его на «семестры», которых в учебнике
четыре. Тетраэдр упоминается в самом
первом параграфе («Введение в стереометрию»)
, понятие «пирамида» определяется в §3.
Как и в предыдущем учебнике
практический материал дополнен заданиями
с развёрткой стереометрических фигур.
В материале §26 можно найти теорему о
сфере, вписанной в тетраэдр. Остальной
теоретический материал, касающийся
тетраэдра, фактически совпадает с
материалами учебника, охарактеризованного
выше.
Решение задач.
Задача 1.
Найдите кратчайший
путь по поверхности правильного тетраэдра
ABCD
соединяющий
точки E
и F,
расположенные на высотах боковых граней
в 7 см от соответствующих вершин тетраэдра.
Ребро тетраэдра равно 20 см.
Решение.
Рассмотрим развертку
трех граней тетраэдра. Кратчайшим путем
будет отрезок, соединяющий точки E
и F.
Его длина равна
20 см.
Задача 2.
В основании пирамиды
лежит прямоугольный треугольник, один
из катетов которого равен 3 см, а прилежащий
к нему острый угол равен 30 градусам. Все
боковые ребра пирамиды наклонены к
плоскости основания под углом в 60
градусов. Найдите объем пирамиды.
Решение.
Площадь треугольника
ABC равна
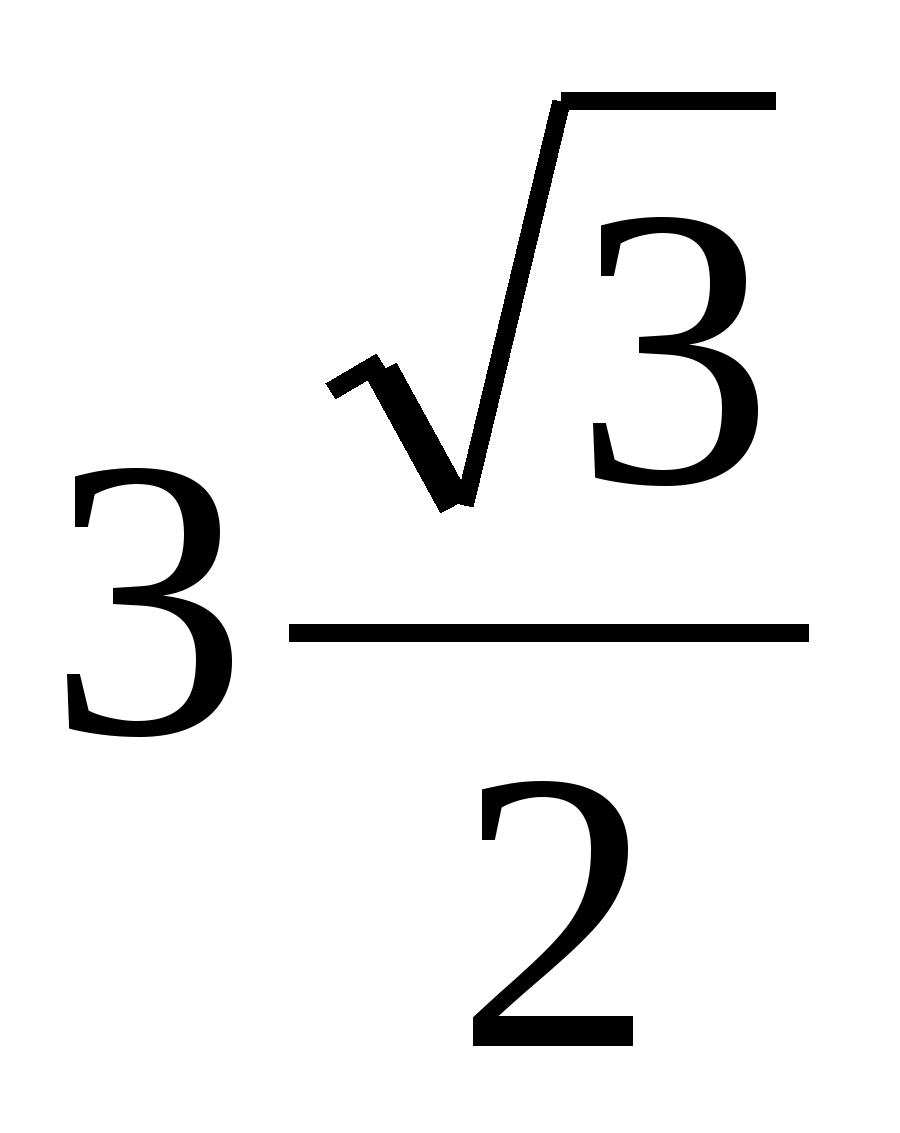
Основанием высоты
служит середина
Треугольник SAC — равносторонний.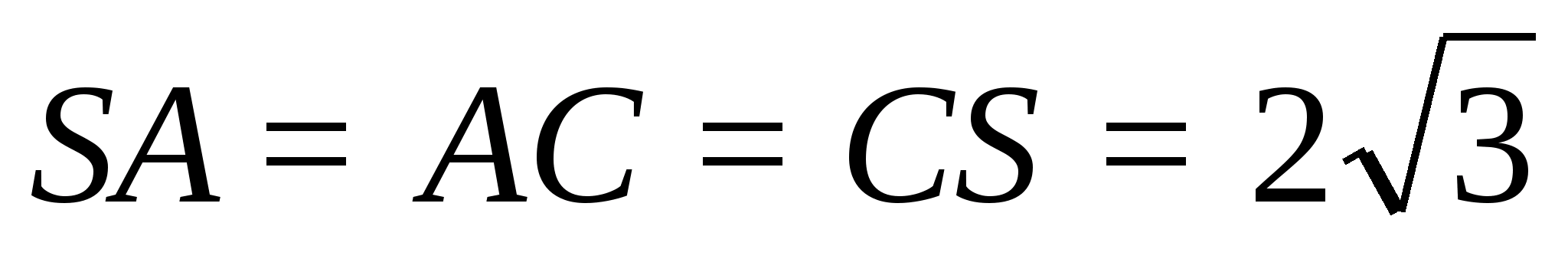
Отсюда
и, следовательно,
объем пирамиды равен
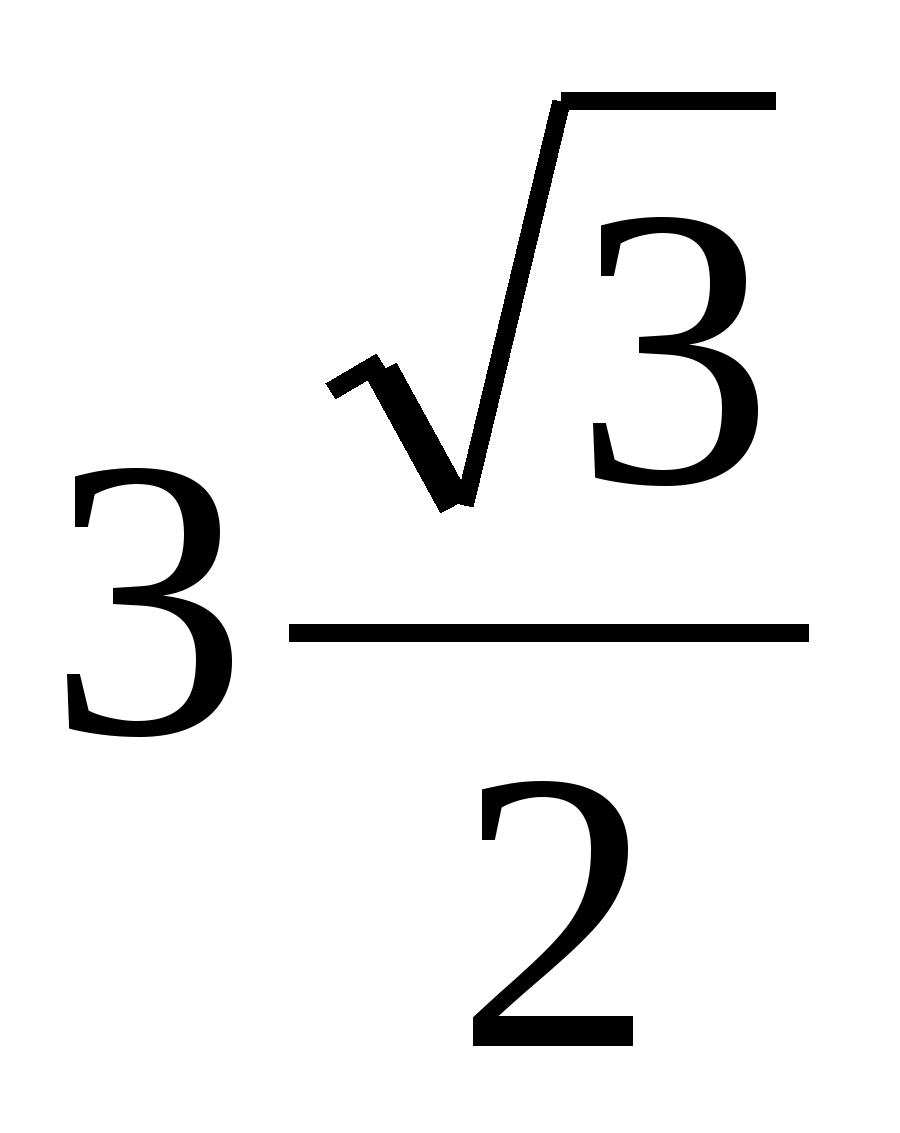
Вывод.
Отличительной
особенностью учебника Атанасяна Л.С. и
др. является то, что изучение тетраэдра
начинается достаточно рано, материал
разбросан по всему курсу и представлен
в различных уровнях сложности. В учебнике
Погорелова А.В. материал расположен
компактно, понятие «тетраэдр» как и
понятия других пространственных фигур,
вводится достаточно поздно (в конце 10
класса), практический материал,
представленный в учебнике, небольшого
объема. В учебнике Смирновой И.М. и др.
теоретический материал, как и практический
имеет небольшой объем, практический
задания низкого уровня сложности,
учебник отличается большим объём
материала из истории математики. В
учебнике Александрова А.Д. и др. уровень
сложности материала выше, сам материал
разнообразнее, множество практических
заданий содержит некоторую часть теории,
имеются экстремальные задачи и задачи
в виде вопросов, что выгодно выделяет
его на фоне остальных.
§2. Тестирование уровня развития
пространственного мышления у учеников
средней школы
Интеллект — это способность к
обучению или пониманию, которая присуща
всем людям. Одни люди обладают ею в
большей степени, другие — в меньшей,
однако у каждого человека в течение
жизни эта способность сохраняется
практически без изменений. Именно
благодаря интеллекту мы способны
правильно действовать и учиться на
своих ошибках.
В психологии интеллект определяется,
как способность воспринимать знания и
использовать их в других, принципиально
новых ситуациях. В условиях тестирования
можно определить, насколько успешно
адаптируется человек к необычным
ситуациям. Определение уровня общего
интеллектуального развития посредством
теста – довольно трудная и ёмкая по
времени работа, поэтому в тексте данной
работы будет использоваться часть
методики тестирования интеллекта,
отвечающая на вопрос об уровне развития
пространственного мышления. Пространственное
мышление – это
специфический вид мыслительной
деятельности, которая имеет место в
решении задач, требующих ориентации в
практическом и теоретическом пространстве
(как видимом, так и воображённом). В
своих наиболее развитых формах это
мышление образцами, в которых фиксируются
пространственные свойства и отношения.
Оперируя исходными образами, созданными
на различной наглядной основе, мышление
обеспечивает их видоизменение,
трансформацию и создание новых образов,
отличных от исходных.
Используемый тест («Мини-тест
уровня развития пространственного
мышления» из «Первого теста на коэффициент
развития интеллекта» Ф. Картера, К.
Рассела) универсален для всех возрастных
групп и занимает малый объём времени
(30 минут). Текст теста и его ключи можно
найти в «Приложении №1» к диплому.
| Regular tetrahedron | |
|---|---|
 (Click here for rotating model) |
|
| Type | Platonic solid |
| Elements | F = 4, E = 6 V = 4 (χ = 2) |
| Faces by sides | 4{3} |
| Conway notation | T |
| Schläfli symbols | {3,3} |
| h{4,3}, s{2,4}, sr{2,2} | |
| Face configuration | V3.3.3 |
| Wythoff symbol | 3 | 2 3 | 2 2 2 |
| Coxeter diagram | |
| Symmetry | Td, A3, [3,3], (*332) |
| Rotation group | T, [3,3]+, (332) |
| References | U01, C15, W1 |
| Properties | regular, convexdeltahedron |
| Dihedral angle | 70.528779° = arccos(1⁄3) |
 3.3.3 (Vertex figure) |
 Self-dual (dual polyhedron) |
 Net |
3D model of regular tetrahedron.
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra.[1]
The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex.
The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a «triangular pyramid».
Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets.[1]
For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere (the insphere) tangent to the tetrahedron’s faces.[2]
Regular tetrahedron[edit]
A regular tetrahedron is a tetrahedron in which all four faces are equilateral triangles. It is one of the five regular Platonic solids, which have been known since antiquity.
In a regular tetrahedron, all faces are the same size and shape (congruent) and all edges are the same length.
Five tetrahedra are laid flat on a plane, with the highest 3-dimensional points marked as 1, 2, 3, 4, and 5. These points are then attached to each other and a thin volume of empty space is left, where the five edge angles do not quite meet.
Regular tetrahedra alone do not tessellate (fill space), but if alternated with regular octahedra in the ratio of two tetrahedra to one octahedron, they form the alternated cubic honeycomb, which is a tessellation. Some tetrahedra that are not regular, including the Schläfli orthoscheme and the Hill tetrahedron, can tessellate.
The regular tetrahedron is self-dual, which means that its dual is another regular tetrahedron. The compound figure comprising two such dual tetrahedra form a stellated octahedron or stella octangula.
Coordinates for a regular tetrahedron[edit]
The following Cartesian coordinates define the four vertices of a tetrahedron with edge length 2, centered at the origin, and two level edges:
Expressed symmetrically as 4 points on the unit sphere, centroid at the origin, with lower face parallel to the 




with the edge length of 
Still another set of coordinates are based on an alternated cube or demicube with edge length 2. This form has Coxeter diagram and Schläfli symbol h{4,3}. The tetrahedron in this case has edge length 2√2. Inverting these coordinates generates the dual tetrahedron, and the pair together form the stellated octahedron, whose vertices are those of the original cube.
- Tetrahedron: (1,1,1), (1,−1,−1), (−1,1,−1), (−1,−1,1)
- Dual tetrahedron: (−1,−1,−1), (−1,1,1), (1,−1,1), (1,1,−1)
Regular tetrahedron ABCD and its circumscribed sphere
Angles and distances[edit]
For a regular tetrahedron of edge length a:
| Face area | 
|
| Surface area[3] | 
|
| Height of pyramid[4] | 
|
| Centroid to vertex distance | 
|
| Edge to opposite edge distance | 
|
| Volume[3] | 
|
| Face-vertex-edge angle |  (approx. 54.7356°) |
| Face-edge-face angle, i.e., «dihedral angle»[3] |  (approx. 70.5288°) |
| Vertex-Center-Vertex angle,[5] the angle between lines from the tetrahedron center to any two vertices. It is also the angle between Plateau borders at a vertex. In chemistry it is called the tetrahedral bond angle. This angle (in radians) is also the length of the circular arc on the unit sphere resulting from centrally projecting one edge of the tetrahedron to the sphere. |  (approx. 109.4712°) |
| Solid angle at a vertex subtended by a face |  (approx. 0.55129 steradians) (approx. 1809.8 square degrees) |
| Radius of circumsphere[3] | 
|
| Radius of insphere that is tangent to faces[3] | 
|
| Radius of midsphere that is tangent to edges[3] | 
|
| Radius of exspheres | 
|
| Distance to exsphere center from the opposite vertex | 
|
With respect to the base plane the slope of a face (2√2) is twice that of an edge (√2), corresponding to the fact that the horizontal distance covered from the base to the apex along an edge is twice that along the median of a face. In other words, if C is the centroid of the base, the distance from C to a vertex of the base is twice that from C to the midpoint of an edge of the base. This follows from the fact that the medians of a triangle intersect at its centroid, and this point divides each of them in two segments, one of which is twice as long as the other (see proof).
For a regular tetrahedron with side length a, radius R of its circumscribing sphere, and distances di from an arbitrary point in 3-space to its four vertices, we have[6]
Isometries of the regular tetrahedron[edit]
The proper rotations, (order-3 rotation on a vertex and face, and order-2 on two edges) and reflection plane (through two faces and one edge) in the symmetry group of the regular tetrahedron
The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron (see above, and also animation, showing one of the two tetrahedra in the cube). The symmetries of a regular tetrahedron correspond to half of those of a cube: those that map the tetrahedra to themselves, and not to each other.
The tetrahedron is the only Platonic solid that is not mapped to itself by point inversion.
The regular tetrahedron has 24 isometries, forming the symmetry group Td, [3,3], (*332), isomorphic to the symmetric group, S4. They can be categorized as follows:
- T, [3,3]+, (332) is isomorphic to alternating group, A4 (the identity and 11 proper rotations) with the following conjugacy classes (in parentheses are given the permutations of the vertices, or correspondingly, the faces, and the unit quaternion representation):
- identity (identity; 1)
- rotation about an axis through a vertex, perpendicular to the opposite plane, by an angle of ±120°: 4 axes, 2 per axis, together 8 ((1 2 3), etc.; 1 ± i ± j ± k/2)
- rotation by an angle of 180° such that an edge maps to the opposite edge: 3 ((1 2)(3 4), etc.; i, j, k)
- reflections in a plane perpendicular to an edge: 6
- reflections in a plane combined with 90° rotation about an axis perpendicular to the plane: 3 axes, 2 per axis, together 6; equivalently, they are 90° rotations combined with inversion (x is mapped to −x): the rotations correspond to those of the cube about face-to-face axes
Orthogonal projections of the regular tetrahedron[edit]
The regular tetrahedron has two special orthogonal projections, one centered on a vertex or equivalently on a face, and one centered on an edge. The first corresponds to the A2 Coxeter plane.
| Centered by | Face/vertex | Edge |
|---|---|---|
| Image | 
|

|
| Projective symmetry |
[3] | [4] |
Cross section of regular tetrahedron[edit]
A central cross section of a regular tetrahedron is a square.
The two skew perpendicular opposite edges of a regular tetrahedron define a set of parallel planes. When one of these planes intersects the tetrahedron the resulting cross section is a rectangle.[7] When the intersecting plane is near one of the edges the rectangle is long and skinny. When halfway between the two edges the intersection is a square. The aspect ratio of the rectangle reverses as you pass this halfway point. For the midpoint square intersection the resulting boundary line traverses every face of the tetrahedron similarly. If the tetrahedron is bisected on this plane, both halves become wedges.
A tetragonal disphenoid viewed orthogonally to the two green edges.
This property also applies for tetragonal disphenoids when applied to the two special edge pairs.
Spherical tiling[edit]
The tetrahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
|

|
| Orthographic projection | Stereographic projection |
|---|
Helical stacking[edit]
Regular tetrahedra can be stacked face-to-face in a chiral aperiodic chain called the Boerdijk–Coxeter helix.
In four dimensions, all the convex regular 4-polytopes with tetrahedral cells (the 5-cell, 16-cell and 600-cell) can be constructed as tilings of the 3-sphere by these chains, which become periodic in the three-dimensional space of the 4-polytope’s boundary surface.
Irregular tetrahedra[edit]
Tetrahedra which do not have four equilateral faces are categorized and named by the symmetries they do possess.
If all three pairs of opposite edges of a tetrahedron are perpendicular, then it is called an orthocentric tetrahedron. When only one pair of opposite edges are perpendicular, it is called a semi-orthocentric tetrahedron.
An isodynamic tetrahedron is one in which the cevians that join the vertices to the incenters of the opposite faces are concurrent.
An isogonic tetrahedron has concurrent cevians that join the vertices to the points of contact of the opposite faces with the inscribed sphere of the tetrahedron.
Trirectangular tetrahedron[edit]
Kepler’s drawing of a regular tetrahedron inscribed in a cube, and one of the four trirectangular tetrahedra that surround it, filling the cube.
In a trirectangular tetrahedron the three face angles at one vertex are right angles, as at the corner of a cube.
Kepler discovered the relationship between the cube, regular tetrahedron and trirectangular tetrahedron.[8]
Disphenoid[edit]
A space-filling tetrahedral disphenoid inside a cube. Two edges have dihedral angles of 90°, and four edges have dihedral angles of 60°.
A disphenoid is a tetrahedron with four congruent triangles as faces; the triangles necessarily have all angles acute. The regular tetrahedron is a special case of a disphenoid. Other names for the same shape include bisphenoid, isosceles tetrahedron and equifacial tetrahedron.
Orthoschemes[edit]
A cube dissected into six characteristic orthoschemes.
A 3-orthoscheme is a tetrahedron where all four faces are right triangles.[a] An orthoscheme is an irregular simplex that is the convex hull of a tree in which all edges are mutually perpendicular. In a 3-dimensional orthoscheme, the tree consists of three perpendicular edges connecting all four vertices in a linear path that makes two right-angled turns. The 3-orthoscheme is a tetrahedron having two right angles at each of two vertices, so another name for it is birectangular tetrahedron. It is also called a quadrirectangular tetrahedron because it contains four right angles.[9]
Coxeter also calls quadrirectangular tetrahedra characteristic tetrahedra, because of their integral relationship to the regular polytopes and their symmetry groups.[10] For example, the special case of a 3-orthoscheme with equal-length perpendicular edges is characteristic of the cube, which means that the cube can be subdivided into instances of this orthoscheme. If its three perpendicular edges are of unit length, its remaining edges are two of length √2 and one of length √3, so all its edges are edges or diagonals of the cube. The cube can be dissected into six such 3-orthoschemes
four different ways, with all six surrounding the same √3 cube diagonal. The cube can also be dissected into 48 smaller instances of this same characteristic 3-orthoscheme (just one way, by all of its symmetry planes at once).[b] The characteristic tetrahedron of the cube is an example of a Heronian tetrahedron.
Every regular polytope, including the regular tetrahedron, has its characteristic orthoscheme.[c] There is a 3-orthoscheme which is the characteristic tetrahedron of the regular tetrahedron. The regular tetrahedron is subdivided into 24 instances of its characteristic tetrahedron
by its planes of symmetry.[d]
| Characteristics of the regular tetrahedron[13] | |||||
|---|---|---|---|---|---|
| edge | arc | dihedral | |||
| 𝒍 | 
|
109°28′16″ | 
|
70°31′44″ | 
|
| 𝟀 | 
|
70°31′44″ | 
|
60° | 
|
| 𝝓 | 
|
54°44′8″ | 
|
60° | 
|
| 𝟁 | 
|
54°44′8″ | 
|
60° | 
|

|

|
||||

|

|
||||

|

|
||||

|
35°15′52″ | 
|
If the regular tetrahedron has edge length 𝒍 = 2, its characteristic tetrahedron’s six edges have lengths 

















Space-filling tetrahedra[edit]
A space-filling tetrahedron packs with directly congruent or enantiomorphous (mirror image) copies of itself to tile space.[14] The cube can be dissected into six 3-orthoschemes, three left-handed and three right-handed (one of each at each cube face), and cubes can fill space, so the characteristic 3-orthoscheme of the cube is a space-filling tetrahedron in this sense.[e] A disphenoid can be a space-filling tetrahedron in the directly congruent sense, as in the disphenoid tetrahedral honeycomb. Regular tetrahedra, however, cannot fill space by themselves.[f]
Fundamental domains[edit]
For Euclidean 3-space, there are 3 simple and related Goursat tetrahedra. They can be seen as points on and within a cube.
An irregular tetrahedron which is the fundamental domain[15] of a symmetry group is an example of a Goursat tetrahedron. The Goursat tetrahedra generate all the regular polyhedra (and many other uniform polyhedra) by mirror reflections, a process referred to as Wythoff’s kaleidoscopic construction.
For polyhedra, Wythoff’s construction arranges three mirrors at angles to each other, as in a kaleidoscope. Unlike a cylindrical kaleidoscope, Wythoff’s mirrors are located at three faces of a Goursat tetrahedron such that all three mirrors intersect at a single point.[g]
Among the Goursat tetrahedra which generate 3-dimensional honeycombs we can recognize an orthoscheme (the characteristic tetrahedron of the cube), a double orthoscheme (the characteristic tetrahedron of the cube face-bonded to its mirror image), and the space-filling disphenoid illustrated above.[10] The disphenoid is the double orthoscheme face-bonded to its mirror image (a quadruple orthoscheme). Thus all three of these Goursat tetrahedra, and all the polyhedra they generate by reflections, can be dissected into characteristic tetrahedra of the cube.
Isometries of irregular tetrahedra[edit]
The isometries of an irregular (unmarked) tetrahedron depend on the geometry of the tetrahedron, with 7 cases possible. In each case a 3-dimensional point group is formed. Two other isometries (C3, [3]+), and (S4, [2+,4+]) can exist if the face or edge marking are included. Tetrahedral diagrams are included for each type below, with edges colored by isometric equivalence, and are gray colored for unique edges.
| Tetrahedron name | Edge equivalence diagram |
Description | |
|---|---|---|---|
| Symmetry | |||
| Schön. | Cox. | Orb. | Ord. |
| Regular tetrahedron | 
|
Four equilateral triangles It forms the symmetry group Td, isomorphic to the symmetric group, S4. A regular tetrahedron has Coxeter diagram |
|
| Td T |
[3,3] [3,3]+ |
*332 332 |
24 12 |
| Triangular pyramid | 
|
An equilateral triangle base and three equal isosceles triangle sides It gives 6 isometries, corresponding to the 6 isometries of the base. As permutations of the vertices, these 6 isometries are the identity 1, (123), (132), (12), (13) and (23), forming the symmetry group C3v, isomorphic to the symmetric group, S3. A triangular pyramid has Schläfli symbol {3}∨( ). |
|
| C3v C3 |
[3] [3]+ |
*33 33 |
6 3 |
| Mirrored sphenoid |
Two equal scalene triangles with a common base edge This has two pairs of equal edges (1,3), (1,4) and (2,3), (2,4) and otherwise no edges equal. The only two isometries are 1 and the reflection (34), giving the group Cs, also isomorphic to the cyclic group, Z2. |
||
| Cs =C1h =C1v |
[ ] | * | 2 |
| Irregular tetrahedron (No symmetry) |
Four unequal triangles Its only isometry is the identity, and the symmetry group is the trivial group. An irregular tetrahedron has Schläfli symbol ( )∨( )∨( )∨( ). |
||
| C1 | [ ]+ | 1 | 1 |
| Disphenoids (Four equal triangles) | |||
| Tetragonal disphenoid | 
|
Four equal isosceles triangles It has 8 isometries. If edges (1,2) and (3,4) are of different length to the other 4 then the 8 isometries are the identity 1, reflections (12) and (34), and 180° rotations (12)(34), (13)(24), (14)(23) and improper 90° rotations (1234) and (1432) forming the symmetry group D2d. A tetragonal disphenoid has Coxeter diagram |
|
| D2d S4 |
[2+,4] [2+,4+] |
2*2 2× |
8 4 |
| Rhombic disphenoid |
Four equal scalene triangles It has 4 isometries. The isometries are 1 and the 180° rotations (12)(34), (13)(24), (14)(23). This is the Klein four-group V4 or Z22, present as the point group D2. A rhombic disphenoid has Coxeter diagram |
||
| D2 | [2,2]+ | 222 | 4 |
| Generalized disphenoids (2 pairs of equal triangles) | |||
| Digonal disphenoid |  
|
Two pairs of equal isosceles triangles This gives two opposite edges (1,2) and (3,4) that are perpendicular but different lengths, and then the 4 isometries are 1, reflections (12) and (34) and the 180° rotation (12)(34). The symmetry group is C2v, isomorphic to the Klein four-group V4. A digonal disphenoid has Schläfli symbol { }∨{ }. |
|
| C2v C2 |
[2] [2]+ |
*22 22 |
4 2 |
| Phyllic disphenoid |
Two pairs of equal scalene or isosceles triangles This has two pairs of equal edges (1,3), (2,4) and (1,4), (2,3) but otherwise no edges equal. The only two isometries are 1 and the rotation (12)(34), giving the group C2 isomorphic to the cyclic group, Z2. |
||
| C2 | [2]+ | 22 | 2 |
General properties[edit]
Volume[edit]
The volume of a tetrahedron is given by the pyramid volume formula:
where A0 is the area of the base and h is the height from the base to the apex. This applies for each of the four choices of the base, so the distances from the apices to the opposite faces are inversely proportional to the areas of these faces.
For a tetrahedron with vertices
a = (a1, a2, a3),
b = (b1, b2, b3),
c = (c1, c2, c3), and
d = (d1, d2, d3), the volume is 1/6|det(a − d, b − d, c − d)|, or any other combination of pairs of vertices that form a simply connected graph. This can be rewritten using a dot product and a cross product, yielding
If the origin of the coordinate system is chosen to coincide with vertex d, then d = 0, so
where a, b, and c represent three edges that meet at one vertex, and a · (b × c) is a scalar triple product. Comparing this formula with that used to compute the volume of a parallelepiped, we conclude that the volume of a tetrahedron is equal to 1/6 of the volume of any parallelepiped that shares three converging edges with it.
The absolute value of the scalar triple product can be represented as the following absolute values of determinants:
or
where
are expressed as row or column vectors.
Hence
where
which gives
where α, β, γ are the plane angles occurring in vertex d. The angle α, is the angle between the two edges connecting the vertex d to the vertices b and c. The angle β, does so for the vertices a and c, while γ, is defined by the position of the vertices a and b.
If we do not require that d = 0 then
Given the distances between the vertices of a tetrahedron the volume can be computed using the Cayley–Menger determinant:
where the subscripts i, j ∈ {1, 2, 3, 4} represent the vertices {a, b, c, d} and dij is the pairwise distance between them – i.e., the length of the edge connecting the two vertices. A negative value of the determinant means that a tetrahedron cannot be constructed with the given distances. This formula, sometimes called Tartaglia’s formula, is essentially due to the painter Piero della Francesca in the 15th century, as a three dimensional analogue of the 1st century Heron’s formula for the area of a triangle.[16]
Let a, b, c be three edges that meet at a point, and x, y, z the opposite edges. Let V be the volume of the tetrahedron; then[17]
where
The above formula uses six lengths of edges, and the following formula uses three lengths of edges and three angles.
Heron-type formula for the volume of a tetrahedron[edit]
Six edge-lengths of Tetrahedron
If U, V, W, u, v, w are lengths of edges of the tetrahedron (first three form a triangle; with u opposite U, v opposite V, w opposite W), then[18]
where
Volume divider[edit]
Any plane containing a bimedian (connector of opposite edges’ midpoints) of a tetrahedron bisects the volume of the tetrahedron.[19]
Non-Euclidean volume[edit]
For tetrahedra in hyperbolic space or in three-dimensional elliptic geometry, the dihedral angles of the tetrahedron determine its shape and hence its volume. In these cases, the volume is given by the Murakami–Yano formula.[20] However, in Euclidean space, scaling a tetrahedron changes its volume but not its dihedral angles, so no such formula can exist.
Distance between the edges[edit]
Any two opposite edges of a tetrahedron lie on two skew lines, and the distance between the edges is defined as the distance between the two skew lines. Let d be the distance between the skew lines formed by opposite edges a and b − c as calculated here. Then another volume formula is given by
Properties analogous to those of a triangle[edit]
The tetrahedron has many properties analogous to those of a triangle, including an insphere, circumsphere, medial tetrahedron, and exspheres. It has respective centers such as incenter, circumcenter, excenters, Spieker center and points such as a centroid. However, there is generally no orthocenter in the sense of intersecting altitudes.[21]
Gaspard Monge found a center that exists in every tetrahedron, now known as the Monge point: the point where the six midplanes of a tetrahedron intersect. A midplane is defined as a plane that is orthogonal to an edge joining any two vertices that also contains the centroid of an opposite edge formed by joining the other two vertices. If the tetrahedron’s altitudes do intersect, then the Monge point and the orthocenter coincide to give the class of orthocentric tetrahedron.
An orthogonal line dropped from the Monge point to any face meets that face at the midpoint of the line segment between that face’s orthocenter and the foot of the altitude dropped from the opposite vertex.
A line segment joining a vertex of a tetrahedron with the centroid of the opposite face is called a median and a line segment joining the midpoints of two opposite edges is called a bimedian of the tetrahedron. Hence there are four medians and three bimedians in a tetrahedron. These seven line segments are all concurrent at a point called the centroid of the tetrahedron.[22] In addition the four medians are divided in a 3:1 ratio by the centroid (see Commandino’s theorem). The centroid of a tetrahedron is the midpoint between its Monge point and circumcenter. These points define the Euler line of the tetrahedron that is analogous to the Euler line of a triangle.
The nine-point circle of the general triangle has an analogue in the circumsphere of a tetrahedron’s medial tetrahedron. It is the twelve-point sphere and besides the centroids of the four faces of the reference tetrahedron, it passes through four substitute Euler points, one third of the way from the Monge point toward each of the four vertices. Finally it passes through the four base points of orthogonal lines dropped from each Euler point to the face not containing the vertex that generated the Euler point.[23]
The center T of the twelve-point sphere also lies on the Euler line. Unlike its triangular counterpart, this center lies one third of the way from the Monge point M towards the circumcenter. Also, an orthogonal line through T to a chosen face is coplanar with two other orthogonal lines to the same face. The first is an orthogonal line passing through the corresponding Euler point to the chosen face. The second is an orthogonal line passing through the centroid of the chosen face. This orthogonal line through the twelve-point center lies midway between the Euler point orthogonal line and the centroidal orthogonal line. Furthermore, for any face, the twelve-point center lies at the midpoint of the corresponding Euler point and the orthocenter for that face.
The radius of the twelve-point sphere is one third of the circumradius of the reference tetrahedron.
There is a relation among the angles made by the faces of a general tetrahedron given by[24]
where αij is the angle between the faces i and j.
The geometric median of the vertex position coordinates of a tetrahedron and its isogonic center are associated, under circumstances analogous to those observed for a triangle. Lorenz Lindelöf found that, corresponding to any given tetrahedron is a point now known as an isogonic center, O, at which the solid angles subtended by the faces are equal, having a common value of π sr, and at which the angles subtended by opposite edges are equal.[25] A solid angle of π sr is one quarter of that subtended by all of space. When all the solid angles at the vertices of a tetrahedron are smaller than π sr, O lies inside the tetrahedron, and because the sum of distances from O to the vertices is a minimum, O coincides with the geometric median, M, of the vertices. In the event that the solid angle at one of the vertices, v, measures exactly π sr, then O and M coincide with v. If however, a tetrahedron has a vertex, v, with solid angle greater than π sr, M still corresponds to v, but O lies outside the tetrahedron.
Geometric relations[edit]
A tetrahedron is a 3-simplex. Unlike the case of the other Platonic solids, all the vertices of a regular tetrahedron are equidistant from each other (they are the only possible arrangement of four equidistant points in 3-dimensional space).
A tetrahedron is a triangular pyramid, and the regular tetrahedron is self-dual.
A regular tetrahedron can be embedded inside a cube in two ways such that each vertex is a vertex of the cube, and each edge is a diagonal of one of the cube’s faces. For one such embedding, the Cartesian coordinates of the vertices are
- (+1, +1, +1);
- (−1, −1, +1);
- (−1, +1, −1);
- (+1, −1, −1).
This yields a tetrahedron with edge-length 2√2, centered at the origin. For the other tetrahedron (which is dual to the first), reverse all the signs. These two tetrahedra’s vertices combined are the vertices of a cube, demonstrating that the regular tetrahedron is the 3-demicube.
The volume of this tetrahedron is one-third the volume of the cube. Combining both tetrahedra gives a regular polyhedral compound called the compound of two tetrahedra or stella octangula.
The interior of the stella octangula is an octahedron, and correspondingly, a regular octahedron is the result of cutting off, from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e., rectifying the tetrahedron).
The above embedding divides the cube into five tetrahedra, one of which is regular. In fact, five is the minimum number of tetrahedra required to compose a cube. To see this, starting from a base tetrahedron with 4 vertices, each added tetrahedra adds at most 1 new vertex, so at least 4 more must be added to make a cube, which has 8 vertices.
Inscribing tetrahedra inside the regular compound of five cubes gives two more regular compounds, containing five and ten tetrahedra.
Regular tetrahedra cannot tessellate space by themselves, although this result seems likely enough that Aristotle claimed it was possible. However, two regular tetrahedra can be combined with an octahedron, giving a rhombohedron that can tile space as the tetrahedral-octahedral honeycomb.
However, several irregular tetrahedra are known, of which copies can tile space, for instance the characteristic orthoscheme of the cube and the disphenoid of the disphenoid tetrahedral honeycomb. The complete list remains an open problem.[26]
If one relaxes the requirement that the tetrahedra be all the same shape, one can tile space using only tetrahedra in many different ways. For example, one can divide an octahedron into four identical tetrahedra and combine them again with two regular ones. (As a side-note: these two kinds of tetrahedron have the same volume.)
The tetrahedron is unique among the uniform polyhedra in possessing no parallel faces.
A law of sines for tetrahedra and the space of all shapes of tetrahedra[edit]
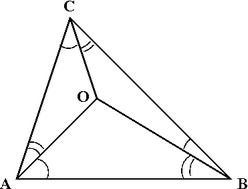
A corollary of the usual law of sines is that in a tetrahedron with vertices O, A, B, C, we have
One may view the two sides of this identity as corresponding to clockwise and counterclockwise orientations of the surface.
Putting any of the four vertices in the role of O yields four such identities, but at most three of them are independent: If the «clockwise» sides of three of them are multiplied and the product is inferred to be equal to the product of the «counterclockwise» sides of the same three identities, and then common factors are cancelled from both sides, the result is the fourth identity.
Three angles are the angles of some triangle if and only if their sum is 180° (π radians). What condition on 12 angles is necessary and sufficient for them to be the 12 angles of some tetrahedron? Clearly the sum of the angles of any side of the tetrahedron must be 180°. Since there are four such triangles, there are four such constraints on sums of angles, and the number of degrees of freedom is thereby reduced from 12 to 8. The four relations given by this sine law further reduce the number of degrees of freedom, from 8 down to not 4 but 5, since the fourth constraint is not independent of the first three. Thus the space of all shapes of tetrahedra is 5-dimensional.[27]
Law of cosines for tetrahedra[edit]
Let {P1 ,P2, P3, P4} be the points of a tetrahedron. Let Δi be the area of the face opposite vertex Pi and let θij be the dihedral angle between the two faces of the tetrahedron adjacent to the edge PiPj.
The law of cosines for this tetrahedron,[28] which relates the areas of the faces of the tetrahedron to the dihedral angles about a vertex, is given by the following relation:
Interior point[edit]
Let P be any interior point of a tetrahedron of volume V for which the vertices are A, B, C, and D, and for which the areas of the opposite faces are Fa, Fb, Fc, and Fd. Then[29]: p.62, #1609
For vertices A, B, C, and D, interior point P, and feet J, K, L, and M of the perpendiculars from P to the faces, and suppose the faces have equal areas, then[29]: p.226, #215
Inradius[edit]
Denoting the inradius of a tetrahedron as r and the inradii of its triangular faces as ri for i = 1, 2, 3, 4, we have[29]: p.81, #1990
with equality if and only if the tetrahedron is regular.
If A1, A2, A3 and A4 denote the area of each faces, the value of r is given by
.
This formula is obtained from dividing the tetrahedron into four tetrahedra whose points are the three points of one of the original faces and the incenter. Since the four subtetrahedra fill the volume, we have 
Circumradius[edit]
Denote the circumradius of a tetrahedron as R. Let a, b, c be the lengths of the three edges that meet at a vertex, and A, B, C the length of the opposite edges. Let V be the volume of the tetrahedron. Then[30][31]
Circumcenter[edit]
The circumcenter of a tetrahedron can be found as intersection of three bisector planes. A bisector plane is defined as the plane centered on, and orthogonal to an edge of the tetrahedron.
With this definition, the circumcenter C of a tetrahedron with vertices x0,x1,x2,x3 can be formulated as matrix-vector product:[32]
In contrast to the centroid, the circumcenter may not always lay on the inside of a tetrahedron.
Analogously to an obtuse triangle, the circumcenter is outside of the object for an obtuse tetrahedron.
Centroid[edit]
The tetrahedron’s center of mass computes as the arithmetic mean of its four vertices, see Centroid.
Faces[edit]
The sum of the areas of any three faces is greater than the area of the fourth face.[29]: p.225, #159
Integer tetrahedra[edit]
There exist tetrahedra having integer-valued edge lengths, face areas and volume. These are called Heronian tetrahedra. One example has one edge of 896, the opposite edge of 990 and the other four edges of 1073; two faces are isosceles triangles with areas of 436800 and the other two are isosceles with areas of 47120, while the volume is 124185600.[33]
A tetrahedron can have integer volume and consecutive integers as edges, an example being the one with edges 6, 7, 8, 9, 10, and 11 and volume 48.[34]
Related polyhedra and compounds[edit]
A regular tetrahedron can be seen as a triangular pyramid.
| Regular pyramids | ||||||||
|---|---|---|---|---|---|---|---|---|
| Digonal | Triangular | Square | Pentagonal | Hexagonal | Heptagonal | Octagonal | Enneagonal | Decagonal… |
| Improper | Regular | Equilateral | Isosceles | |||||

|

|

|

|
|||||

|

|

|

|

|

|

|

|
A regular tetrahedron can be seen as a degenerate polyhedron, a uniform digonal antiprism, where base polygons are reduced digons.
| Antiprism name | Digonal antiprism | (Trigonal) Triangular antiprism |
(Tetragonal) Square antiprism |
Pentagonal antiprism | Hexagonal antiprism | Heptagonal antiprism | Octagonal antiprism | Enneagonal antiprism | Decagonal antiprism | Hendecagonal antiprism | Dodecagonal antiprism | … | Apeirogonal antiprism |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image | … | ||||||||||||
| Spherical tiling image | Plane tiling image | ||||||||||||
| Vertex config. | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | … | ∞.3.3.3 |
A regular tetrahedron can be seen as a degenerate polyhedron, a uniform dual digonal trapezohedron, containing 6 vertices, in two sets of colinear edges.
| Trapezohedron name | Digonal trapezohedron (Tetrahedron) |
Trigonal trapezohedron | Tetragonal trapezohedron | Pentagonal trapezohedron | Hexagonal trapezohedron | Heptagonal trapezohedron | Octagonal trapezohedron | Decagonal trapezohedron | Dodecagonal trapezohedron | … | Apeirogonal trapezohedron |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image | 
|

|

|

|

|

|
|

|
… | ||
| Spherical tiling image | 
|

|

|

|

|

|

|

|
Plane tiling image | ||
| Face configuration | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | … | V∞.3.3.3 |
A truncation process applied to the tetrahedron produces a series of uniform polyhedra. Truncating edges down to points produces the octahedron as a rectified tetrahedron. The process completes as a birectification, reducing the original faces down to points, and producing the self-dual tetrahedron once again.
| Family of uniform tetrahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [3,3], (*332) | [3,3]+, (332) | ||||||

|

|

|

|
||||
| {3,3} | t{3,3} | r{3,3} | t{3,3} | {3,3} | rr{3,3} | tr{3,3} | sr{3,3} |
| Duals to uniform polyhedra | |||||||
|

|

|

|
||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
This polyhedron is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane.
*n32 symmetry mutation of regular tilings: {3,n}
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical | Euclid. | Compact hyper. | Paraco. | Noncompact hyperbolic | |||||||

|

|

|

|

|

|

|

|

|

|

|

|
| 3.3 | 33 | 34 | 35 | 36 | 37 | 38 | 3∞ | 312i | 39i | 36i | 33i |
The tetrahedron is topologically related to a series of regular polyhedra and tilings with order-3 vertex figures.
*n32 symmetry mutation of regular tilings: {n,3}
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||

|

|

|

|

|

|

|

|
|

|

|

|
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} | {12i,3} | {9i,3} | {6i,3} | {3i,3} |
- Compounds of tetrahedra
-
-
-
An interesting polyhedron can be constructed from five intersecting tetrahedra. This compound of five tetrahedra has been known for hundreds of years. It comes up regularly in the world of origami. Joining the twenty vertices would form a regular dodecahedron. There are both left-handed and right-handed forms, which are mirror images of each other. Superimposing both forms gives a compound of ten tetrahedra, in which the ten tetrahedra are arranged as five pairs of stellae octangulae. A stella octangula is a compound of two tetrahedra in dual position and its eight vertices define a cube as their convex hull.
The square hosohedron is another polyhedron with four faces, but it does not have triangular faces.
The Szilassi polyhedron and the tetrahedron are the only two known polyhedra in which each face shares an edge with each other face. Furthermore, the Császár polyhedron (itself is the dual of Szilassi polyhedron) and the tetrahedron are the only two known polyhedra in which every diagonal lies on the sides.
Applications[edit]
Numerical analysis[edit]
An irregular volume in space can be approximated by an irregular triangulated surface, and irregular tetrahedral volume elements.
In numerical analysis, complicated three-dimensional shapes are commonly broken down into, or approximated by, a polygonal mesh of irregular tetrahedra in the process of setting up the equations for finite element analysis especially in the numerical solution of partial differential equations. These methods have wide applications in practical applications in computational fluid dynamics, aerodynamics, electromagnetic fields, civil engineering, chemical engineering, naval architecture and engineering, and related fields.
Structural engineering[edit]
A tetrahedron having stiff edges is inherently rigid. For this reason it is often used to stiffen frame structures such as spaceframes.
Aviation[edit]
At some airfields, a large frame in the shape of a tetrahedron with two sides covered with a thin material is mounted on a rotating pivot and always points into the wind. It is built big enough to be seen from the air and is sometimes illuminated. Its purpose is to serve as a reference to pilots indicating wind direction.[35]
Chemistry[edit]
The tetrahedron shape is seen in nature in covalently bonded molecules. All sp3-hybridized atoms are surrounded by atoms (or lone electron pairs) at the four corners of a tetrahedron. For instance in a methane molecule (CH
4) or an ammonium ion (NH+
4), four hydrogen atoms surround a central carbon or nitrogen atom with tetrahedral symmetry. For this reason, one of the leading journals in organic chemistry is called Tetrahedron. The central angle between any two vertices of a perfect tetrahedron is arccos(−1/3), or approximately 109.47°.[5]
Water, H
2O, also has a tetrahedral structure, with two hydrogen atoms and two lone pairs of electrons around the central oxygen atoms. Its tetrahedral symmetry is not perfect, however, because the lone pairs repel more than the single O–H bonds.
Quaternary phase diagrams of mixtures of chemical substances are represented graphically as tetrahedra.
However, quaternary phase diagrams in communication engineering are represented graphically on a two-dimensional plane.
Electricity and electronics[edit]
If six equal resistors are soldered together to form a tetrahedron, then the resistance measured between any two vertices is half that of one resistor.[36][37]
Since silicon is the most common semiconductor used in solid-state electronics, and silicon has a valence of four, the tetrahedral shape of the four chemical bonds in silicon is a strong influence on how crystals of silicon form and what shapes they assume.
Color space[edit]
Tetrahedra are used in color space conversion algorithms specifically for cases in which the luminance axis diagonally segments the color space (e.g. RGB, CMY).[38]
Games[edit]
The Royal Game of Ur, dating from 2600 BC, was played with a set of tetrahedral dice.
Especially in roleplaying, this solid is known as a 4-sided die, one of the more common polyhedral dice, with the number rolled appearing around the bottom or on the top vertex. Some Rubik’s Cube-like puzzles are tetrahedral, such as the Pyraminx and Pyramorphix.
Geology[edit]
The tetrahedral hypothesis, originally published by William Lowthian Green to explain the formation of the Earth,[39] was popular through the early 20th century.[40][41]
Popular culture[edit]
Stanley Kubrick originally intended the monolith in 2001: A Space Odyssey to be a tetrahedron, according to Marvin Minsky, a cognitive scientist and expert on artificial intelligence who advised Kubrick on the HAL 9000 computer and other aspects of the movie. Kubrick scrapped the idea of using the tetrahedron as a visitor who saw footage of it did not recognize what it was and he did not want anything in the movie regular people did not understand.[42]
Tetrahedral graph[edit]
| Tetrahedral graph | |
|---|---|
 |
|
| Vertices | 4 |
| Edges | 6 |
| Radius | 1 |
| Diameter | 1 |
| Girth | 3 |
| Automorphisms | 24 |
| Chromatic number | 4 |
| Properties | Hamiltonian, regular, symmetric, distance-regular, distance-transitive, 3-vertex-connected, planar graph |
| Table of graphs and parameters |
The skeleton of the tetrahedron (comprising the vertices and edges) forms a graph, with 4 vertices, and 6 edges. It is a special case of the complete graph, K4, and wheel graph, W4.[43] It is one of 5 Platonic graphs, each a skeleton of its Platonic solid.
3-fold symmetry
See also[edit]
- Boerdijk–Coxeter helix
- Möbius configuration
- Caltrop
- Demihypercube and simplex – n-dimensional analogues
- Pentachoron – 4-dimensional analogue
- Synergetics (Fuller)
- Tetrahedral kite
- Tetrahedral number
- Tetrahedron packing
- Triangular dipyramid – constructed by joining two tetrahedra along one face
- Trirectangular tetrahedron
- Orthoscheme
Notes[edit]
- ^ A 3-orthoscheme is not a disphenoid, because its opposite edges are not of equal length. It is not possible to construct a disphenoid with right triangle or obtuse triangle faces.
- ^ For a regular k-polytope, the Coxeter-Dynkin diagram of the characteristic k-orthoscheme is the k-polytope’s diagram without the generating point ring. The regular k-polytope is subdivided by its symmetry (k-1)-elements into g instances of its characteristic k-orthoscheme that surround its center, where g is the order of the k-polytope’s symmetry group.[11]
- ^ A regular polytope of dimension k has a characteristic k-orthoscheme, and also a characteristic (k-1)-orthoscheme. A regular polyhedron has a characteristic tetrahedron (3-orthoscheme) into which it is subdivided by its planes of symmetry, and also a characteristic triangle (2-orthoscheme) into which its surface is subdivided by its faces’ lines of symmetry. After subdividing its surface into characteristic right triangles surrounding each face center, its interior can be subdivided into characteristic tetrahedra by adding radii joining the vertices of the surface right triangles to the polyhedron’s center.[12] The interior triangles thus formed will also be right triangles.
- ^ The 24 characteristic tetrahedra of the regular tetrahedron occur in two mirror-image forms, 12 of each.
- ^ The characteristic orthoscheme of the cube is one of the Hill tetrahedra, a family of space-filling tetrahedra. All space-filling tetrahedra are scissors-congruent to a cube. Every convex polyhedron is scissors-congruent to an orthoscheme. Every regular convex polyhedron (Platonic solid) can be dissected into some even number of instances of its characteristic orthoscheme.
- ^ The tetrahedral-octahedral honeycomb fills space with alternating regular tetrahedron cells and regular octahedron cells in a ratio of 2:1.
- ^ The Coxeter-Dynkin diagram of the generated polyhedron contains three nodes representing the three mirrors. The dihedral angle between each pair of mirrors is encoded in the diagram, as well as the location of a single generating point which is multiplied by mirror reflections into the vertices of the polyhedron. For a regular polyhedron, the Coxeter-Dynkin diagram of the generating characteristic orthoscheme is the generated polyhedron’s diagram without the generating point marking.
References[edit]
- ^ a b Weisstein, Eric W. «Tetrahedron». MathWorld.
- ^ Ford, Walter Burton; Ammerman, Charles (1913), Plane and Solid Geometry, Macmillan, pp. 294–295
- ^ a b c d e f Coxeter, Harold Scott MacDonald; Regular Polytopes, Methuen and Co., 1948, Table I(i)
- ^ Köller, Jürgen, «Tetrahedron», Mathematische Basteleien, 2001
- ^ a b Brittin, W. E. (1945). «Valence angle of the tetrahedral carbon atom». Journal of Chemical Education. 22 (3): 145. Bibcode:1945JChEd..22..145B. doi:10.1021/ed022p145.
- ^ Park, Poo-Sung. «Regular polytope distances», Forum Geometricorum 16, 2016, 227–232. http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf
- ^ «Sections of a Tetrahedron».
- ^ Kepler 1619, p. 181.
- ^ Coxeter, H.S.M. (1989). «Trisecting an Orthoscheme». Computers Math. Applic. 17 (1–3): 59–71. doi:10.1016/0898-1221(89)90148-X.
- ^ a b Coxeter 1973, pp. 71–72, §4.7 Characteristic tetrahedra.
- ^ Coxeter 1973, pp. 130–133, §7.6 The symmetry group of the general regular polytope.
- ^ Coxeter 1973, p. 130, §7.6; «simplicial subdivision».
- ^ Coxeter 1973, pp. 292–293, Table I(i); «Tetrahedron, 𝛼3«.
- ^ Coxeter 1973, pp. 33–34, §3.1 Congruent transformations.
- ^ Coxeter 1973, p. 63, §4.3 Rotation groups in two dimensions; notion of a fundamental region.
- ^ «Simplex Volumes and the Cayley-Menger Determinant», MathPages.com
- ^ Kahan, William M. (3 April 2012), What has the Volume of a Tetrahedron to do with Computer Programming Languages? (PDF), p. 11
- ^ Kahan, William M. (3 April 2012), What has the Volume of a Tetrahedron to do with Computer Programming Languages? (PDF), pp. 16–17
- ^ Bottema, O. «A Theorem of Bobillier on the Tetrahedron.» Elemente der Mathematik 24 (1969): 6-10.
- ^ Murakami, Jun; Yano, Masakazu (2005), «On the volume of a hyperbolic and spherical tetrahedron», Communications in Analysis and Geometry, 13 (2): 379–400, doi:10.4310/cag.2005.v13.n2.a5, ISSN 1019-8385, MR 2154824
- ^ Havlicek, Hans; Weiß, Gunter (2003). «Altitudes of a tetrahedron and traceless quadratic forms» (PDF). American Mathematical Monthly. 110 (8): 679–693. arXiv:1304.0179. doi:10.2307/3647851. JSTOR 3647851.
- ^ Leung, Kam-tim; and Suen, Suk-nam; «Vectors, matrices and geometry», Hong Kong University Press, 1994, pp. 53–54
- ^ Outudee, Somluck; New, Stephen. The Various Kinds of Centres of Simplices (PDF). Dept of Mathematics, Chulalongkorn University, Bangkok. Archived from the original on 27 February 2009.
{{cite book}}: CS1 maint: bot: original URL status unknown (link) - ^ Audet, Daniel (May 2011). «Déterminants sphérique et hyperbolique de Cayley-Menger» (PDF). Bulletin AMQ.
- ^ Lindelof, L. (1867). «Sur les maxima et minima d’une fonction des rayons vecteurs menés d’un point mobile à plusieurs centres fixes». Acta Societatis Scientiarum Fennicae. 8 (Part 1): 189–203.
- ^ Senechal, Marjorie (1981). «Which tetrahedra fill space?». Mathematics Magazine. Mathematical Association of America. 54 (5): 227–243. doi:10.2307/2689983. JSTOR 2689983.
- ^ Rassat, André; Fowler, Patrick W. (2004). «Is There a «Most Chiral Tetrahedron»?». Chemistry: A European Journal. 10 (24): 6575–6580. doi:10.1002/chem.200400869. PMID 15558830.
- ^ Lee, Jung Rye (June 1997). «The Law of Cosines in a Tetrahedron». J. Korea Soc. Math. Educ. Ser. B: Pure Appl. Math.
- ^ a b c d Inequalities proposed in “Crux Mathematicorum”, [1].
- ^ Crelle, A. L. (1821). «Einige Bemerkungen über die dreiseitige Pyramide». Sammlung mathematischer Aufsätze u. Bemerkungen 1 (in German). Berlin: Maurer. pp. 105–132. Retrieved 7 August 2018.
- ^ Todhunter, I. (1886), Spherical Trigonometry: For the Use of Colleges and Schools, p. 129 ( Art. 163 )
- ^ Lévy, Bruno; Liu, Yang (2010). «Lp Centroidal Voronoi Tessellation and its applications». ACM: 119.
- ^ «Problem 930» (PDF), Solutions, Crux Mathematicorum, 11 (5): 162–166, May 1985
- ^ Wacław Sierpiński, Pythagorean Triangles, Dover Publications, 2003 (orig. ed. 1962), p. 107. Note however that Sierpiński repeats an erroneous calculation of the volume of the Heronian tetrahedron example above.
- ^ Federal Aviation Administration (2009), Pilot’s Handbook of Aeronautical Knowledge, U. S. Government Printing Office, p. 13-10, ISBN 9780160876110.
- ^ Klein, Douglas J. (2002). «Resistance-Distance Sum Rules» (PDF). Croatica Chemica Acta. 75 (2): 633–649. Archived from the original (PDF) on 10 June 2007. Retrieved 15 September 2006.
- ^ Záležák, Tomáš (18 October 2007); «Resistance of a regular tetrahedron»[permanent dead link] (PDF), retrieved 25 January 2011
- ^ Vondran, Gary L. (April 1998). «Radial and Pruned Tetrahedral Interpolation Techniques» (PDF). HP Technical Report. HPL-98-95: 1–32. Archived from the original (PDF) on 7 June 2011. Retrieved 11 November 2009.
- ^ Green, William Lowthian (1875). Vestiges of the Molten Globe, as exhibited in the figure of the earth, volcanic action and physiography. Vol. Part I. London: E. Stanford. Bibcode:1875vmge.book…..G. OCLC 3571917.
- ^ Holmes, Arthur (1965). Principles of physical geology. Nelson. p. 32. ISBN 9780177612992.
- ^ Hitchcock, Charles Henry (January 1900). Winchell, Newton Horace (ed.). «William Lowthian Green and his Theory of the Evolution of the Earth’s Features». The American Geologist. Vol. XXV. Geological Publishing Company. pp. 1–10.
- ^ «Marvin Minsky: Stanley Kubrick Scraps the Tetrahedron». Web of Stories. Retrieved 20 February 2012.
- ^ Weisstein, Eric W. «Tetrahedral graph». MathWorld.
Bibliography[edit]
- Kepler, Johannes (1619). Harmonices Mundi (The Harmony of the World). Johann Planck.
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.
External links[edit]
- Weisstein, Eric W. «Tetrahedron». MathWorld.
- Free paper models of a tetrahedron and many other polyhedra
- An Amazing, Space Filling, Non-regular Tetrahedron that also includes a description of a «rotating ring of tetrahedra», also known as a kaleidocycle.
Fundamental convex regular and uniform polytopes in dimensions 2–10 |
|||||
|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn |
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon |
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | |
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell |
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | ||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | |
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | |
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | |
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | ||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | ||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope |
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds |
Тетраэдр в переводе с греческого означает «четырехгранник». Эта геометрическая фигура обладает четырьмя гранями, четырьмя вершинами и шестью ребрами. Грани представляют собой треугольники. По сути, тетраэдр — это Первые упоминания о многогранниках появились еще задолго до существования Платона.
Сегодня поговорим об элементах и свойствах тетраэдра, а также узнаем формулы нахождения у этих элементов площади, объема и других параметров.
Элементы четырехгранника
Отрезок, выпущенный из любой вершины тетраэдра и опущенный на точку пересечения медиан грани, являющейся противоположной, называется медианой.
Высота многоугольника представляет собой нормальный отрезок, опущенный из вершины напротив.
Бимедианой называется отрезок, соединяющий центры скрещивающихся ребер.
Свойства тетраэдра
1) Параллельные плоскости, которые проходят через два скрещивающихся ребра, образуют описанный параллелепипед.
2) Отличительным свойством тетраэдра является то, что медианы и бимедианы фигуры встречаются в одной точке. Важно, что последняя делит медианы в отношении 3:1, а бимедианы — пополам.
3) Плоскость разделяет тетраэдр на две равные по объему части, если проходит через середину двух скрещивающихся ребер.
Виды тетраэдра
Видовое разнообразие фигуры достаточно широко. Тетраэдр может быть:
- правильным, то есть в основании равносторонний треугольник;
- равногранным, у которого все грани одинаковы по длине;
- ортоцентрическим, когда высоты имеют общую точку пересечения;
- прямоугольным, если плоские углы при вершине нормальные;
- соразмерным, все би высоты равны;
- каркасным, если присутствует сфера, которая касается ребер;
- инцентрическим, то есть отрезки, опущенные из вершины в центр вписанной окружности противоположной грани, имеют общую точку пересечения; эту точку именуют центром тяжести тетраэдра.
Остановимся подробно на правильном тетраэдре, свойства которого практически не отличаются.
Исходя из названия, можно понять, что так он называется потому, что грани являют собой правильные треугольники. Все ребра этой фигуры конгруэнтны по длине, а грани — по площади. Правильный тетраэдр — это один из пяти аналогичных многогранников.
Формулы четырехгранника
Высота тетраэдра равна произведению корня из 2/3 и длины ребра.
Объем тетраэдра находится так же, как объем пирамиды: корень квадратный из 2 разделить на 12 и умножить на длину ребра в кубе.
Остальные формулы для расчета площади и радиусов окружностей представлены выше.
На этом уроке мы рассмотрим тетраэдр и его элементы (ребро тетраэдра, поверхность, грани, вершины). И решим несколько задач на построение сечений в тетраэдре, используя общий метод для построения сечений.
Тема: Параллельность прямых и плоскостей
Урок: Тетраэдр. Задачи на построение сечений в тетраэдре
Как построить тетраэдр? Возьмем произвольный треугольник АВС
. Произвольную точку D
, не лежащую в плоскости этого треугольника. Получим 4 треугольника. Поверхность, образованная этими 4 треугольниками, и называется тетраэдром (Рис. 1.). Внутренние точки, ограниченные этой поверхностью, также входят в состав тетраэдра.
Рис. 1. Тетраэдр АВСD
Элементы тетраэдра
А,
B
,
C
,
D
— вершины тетраэдра
.
AB
,
AC
,
AD
,
BC
,
BD
,
CD
— ребра тетраэдра
.
ABC
,
ABD
,
BDC
,
ADC
— грани тетраэдра
.
Замечание:
можно принять плоскость АВС
за основание тетраэдра
, и тогда точка D
является вершиной тетраэдра
. Каждое ребро тетраэдра является пересечением двух плоскостей. Например, ребро АВ
— это пересечение плоскостей АВ
D
и АВС
. Каждая вершина тетраэдра — это пересечение трех плоскостей. Вершина А
лежит в плоскостях АВС
, АВ
D
, А
D
С
. Точка А
— это пересечение трех означенных плоскостей. Этот факт записывается следующим образом: А
= АВС
∩ АВ
D
∩ АС
D
.
Тетраэдр определение
Итак, тетраэдр
— это поверхность, образованная четырмя треугольниками.
Ребро тетраэдра
— линия перечесения двух плоскостей тетраэдра.
Составьте из 6 спичек 4 равных треугольника. На плоскости решить задачу не получается. А в пространстве это сделать легко. Возьмем тетраэдр. 6 спичек — это его ребра, четыре грани тетраэдра и будут четырьмя равными треугольниками. Задача решена.
Дан тетраэдр АВС
D
.
Точка M
принадлежит ребру тетраэдра АВ
, точка N
принадлежит ребру тетраэдра В
D
и точка Р
принадлежит ребру D
С
(Рис. 2.). Постройте сечение тетраэдра плоскостью MNP
.
Рис. 2. Рисунок к задаче 2 — Построить сечение тетраэдра плоскостью
Решение
:
Рассмотрим грань тетраэдра D
ВС
. В этой грани точки N
и P
принадлежат грани D
ВС
, а значит, и тетраэдру. Но по условию точки N, P
принадлежат секущей плоскости. Значит, NP
— это линия пересечения двух плоскостей: плоскости грани D
ВС
и секущей плоскости. Предположим, что прямые NP
и ВС
не параллельны. Они лежат в одной плоскости D
ВС.
Найдем точку пересечения прямых NP
и ВС
. Обозначим ее Е
(Рис. 3.).
Рис. 3. Рисунок к задаче 2. Нахождение точки Е
Точка Е
принадлежит плоскости сечения MNP
, так как она лежит на прямой NР
, а прямая NР
целиком лежит в плоскости сечения MNP
.
Также точка Е
лежит в плоскости АВС
, потому что она лежит на прямой ВС
из плоскости АВС
.
Получаем, что ЕМ
— линия пересечения плоскостей АВС
и MNP,
так как точки Е
и М
лежат одновременно в двух плоскостях — АВС
и MNP.
Соединим точки М
и Е
, и продолжим прямую ЕМ
до пересечения с прямой АС
. Точку пересечения прямых ЕМ
и АС
обозначим Q
.
Итак, в этом случае NPQМ
— искомое сечение.
Рис. 4. Рисунок к задаче 2.Решение задачи 2
Рассмотрим теперь случай, когда NP
параллельна BC
. Если прямая NP
параллельна какой-нибудь прямой, например, прямой ВС
из плоскости АВС
, то прямая NP
параллельна всей плоскости АВС
.
Искомая плоскость сечения проходит через прямую NP
, параллельную плоскости АВС
, и пересекает плоскость по прямой МQ
. Значит, линия пересечения МQ
параллельна прямой NP
. Получаем, NPQМ
— искомое сечение.
Точка М
лежит на боковой грани А
D
В
тетраэдра АВС
D
. Постройте сечение тетраэдра плоскостью, которое проходит через точку М
параллельно основанию АВС
.
Рис. 5. Рисунок к задаче 3 Построить сечение тетраэдра плоскостью
Решение:
Секущая плоскость φ
параллельна плоскости АВС
по условию, значит, эта плоскость φ
параллельна прямым АВ
, АС
, ВС
.
В плоскости АВ
D
через точку М
проведем прямую PQ
параллельно АВ
(рис. 5). Прямая PQ
лежит в плоскости АВ
D
. Аналогично в плоскости АС
D
через точку Р
проведем прямую РR
параллельно АС
. Получили точку R
. Две пересекающиеся прямые PQ
и РR
плоскости РQR
соответственно параллельны двум пересекающимся прямым АВ
и АС
плоскости АВС
, значит, плоскости АВС
и РQR
параллельны. РQR
— искомое сечение. Задача решена.
Дан тетраэдр АВС
D
. Точка М
— точка внутренняя, точка грани тетраэдра АВ
D
. N
— внутренняя точка отрезка D
С
(Рис. 6.). Построить точку пересечения прямой NM
и плоскости АВС
.
Рис. 6. Рисунок к задаче 4
Решение:
Для решения построим вспомогательную плоскость D
МN
. Пусть прямая D
М
пересекает прямую АВ в точке К
(Рис. 7.). Тогда, СК
D
— это сечение плоскости D
МN
и тетраэдра. В плоскости D
МN
лежит и прямая NM
, и полученная прямая СК
. Значит, если NM
не параллельна СК
, то они пересекутся в некоторой точке Р
. Точка Р
и будет искомая точка пересечения прямой NM
и плоскости АВС
.
Рис. 7. Рисунок к задаче 4. Решение задачи 4
Дан тетраэдр АВС
D
. М
— внутренняя точка грани АВ
D
. Р
— внутренняя точка грани АВС
. N
— внутренняя точка ребра D
С
(Рис. 8.). Построить сечение тетраэдра плоскостью, проходящей через точки М
, N
и Р
.
Рис. 8. Рисунок к задаче 5 Построить сечение тетраэдра плоскостью
Решение:
Рассмотрим первый случай, когда прямая MN
не параллельна плоскости АВС
. В прошлой задаче мы нашли точку пересечения прямой MN
и плоскости АВС
. Это точка К
, она получена с помощью вспомогательной плоскости D
МN
, т.е. мы проводим D
М
и получаем точку F
. Проводим СF
и на пересечении MN
получаем точку К
.
Рис. 9. Рисунок к задаче 5. Нахождение точки К
Проведем прямую КР
. Прямая КР
лежит и в плоскости сечения, и в плоскости АВС
. Получаем точки Р 1
и Р 2
. Соединяем Р 1
и М
и на продолжении получаем точку М 1
. Соединяем точку Р 2
и N
. В результате получаем искомое сечение Р 1 Р 2 NМ 1
. Задача в первом случае решена.
Рассмотрим второй случай, когда прямая MN
параллельна плоскости АВС
. Плоскость МNР
проходит через прямую МN
параллельную плоскости АВС
и пересекает плоскость АВС
по некоторой прямой Р 1 Р 2
, тогда прямая Р 1 Р 2
параллельна данной прямой MN
(Рис. 10.).
Рис. 10. Рисунок к задаче 5. Искомое сечение
Теперь проведем прямую Р 1 М
и получим точку М 1
. Р 1 Р 2 NМ 1
— искомое сечение.
Итак, мы рассмотрели тетраэдр, решили некоторые типовые задачи на тетраэдр. На следующем уроке мы рассмотрим параллелепипед.
1. И. М. Смирнова, В. А. Смирнов. — 5-е издание, исправленное и дополненное — М. : Мнемозина, 2008. — 288 с. : ил. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни)
2. Шарыгин И. Ф. — М.: Дрофа, 1999. — 208 с.: ил. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений
3. Е. В. Потоскуев, Л. И. Звалич. — 6-е издание, стереотип. — М. : Дрофа, 008. — 233 с. :ил. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики
Дополнительные веб-ресурсы
2. Как построить сечение тетраэдра. Математика ().
3. Фестиваль педагогических идей ().
Сделай дома задачи по теме «Тетраэдр», как находить ребро тетраэдра, грани тетраэдра, вершины и поверхность тетраэдра
1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) И. М. Смирнова, В. А. Смирнов. — 5-е издание, исправленное и дополненное — М.: Мнемозина, 2008. — 288 с.: ил. Задания 18, 19, 20 стр. 50
2. Точка Е
середина ребра МА
тетраэдра МАВС
. Постройте сечение тетраэдра плоскостью, проходящей через точки В, С
и Е
.
3. В тетраэдре МАВС точка М принадлежит грани АМВ, точка Р — грани ВМС, точка К — ребру АС. Постройте сечение тетраэдра плоскостью, проходящей через точки М, Р, К.
4. Какие фигуры могут получиться в результате пересечения плоскостью тетраэдра?
Все грани его представляют собой равные между собой треугольники. Разверткой равногранного тетраэдра является треугольник, разделенный тремя средними линиями на четыре равных треугольника . В равногранном тетраэдре основания высот, середины высот и точки пересечения высот граней лежат на поверхности одной сферы (сферы 12 точек) (Аналог окружности Эйлера для треугольника).
Свойства равногранного тетраэдра:
- Все его грани равны (конгруэнтны).
- Скрещивающиеся ребра попарно равны.
- Трехгранные углы равны.
- Противолежащие двугранные углы равны.
- Два плоских угла, опирающихся на одно ребро, равны.
- Сумма плоских углов при каждой вершине равна 180°.
- Развертка тетраэдра — треугольник или параллелограмм.
- Описанный параллелепипед прямоугольный.
- Тетраэдр имеет три оси симметрии.
- Общие перпендикуляры скрещивающихся ребер попарно перпендикулярны.
- Средние линии попарно перпендикулярны.
- Периметры граней равны.
- Площади граней равны.
- Высоты тетраэдра равны.
- Отрезки, соединяющие вершины с центрами тяжести противоположных граней, равны.
- Радиусы описанных около граней окружностей равны.
- Центр тяжести тетраэдра совпадает с центром описанной сферы.
- Центр тяжести совпадает с центром вписанной сферы.
- Центр описанной сферы совпадает с центром вписанной.
- Вписанная сфера касается граней в центрах описанных около этих граней окружностей.
- Сумма внешних единичных нормалей (единичных векторов, перпендикулярных к граням), равна нулю.
- Сумма всех двугранных углов равна нулю.
Ортоцентрический тетраэдр
Все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.
Свойства ортоцентрического тетраэдра:
- Высоты тетраэдра пересекаются в одной точке.
- Основания высот тетраэдра являются ортоцентрами граней.
- Каждые два противоположных ребра тетраэдра перпендикулярны.
- Суммы квадратов противоположных ребер тетраэдра равны.
- Отрезки, соединяющие середины противоположных ребер тетраэдра, равны.
- Произведения косинусов противоположных двугранных углов равны.
- Сумма квадратов площадей граней вчетверо меньше суммы квадратов произведений противоположных ребер.
- У ортоцентрического тетраэдра
окружности 9 точек (окружности Эйлера) каждой грани принадлежат одной сфере (сфере 24 точек). - У ортоцентрического тетраэдра
центры тяжести и точки пересечения высот граней, а также точки, делящие отрезки каждой высоты тетраэдра от вершины до точки пересечения высот в отношении 2:1, лежат на одной сфере (сфере 12 точек).
Прямоугольный тетраэдр
Все ребра, прилежащие к одной из вершин, перпендикулярны между собой. Прямоугольный тетраэдр получается отсечением тетраэдра плоскостью от прямоугольного параллелепипеда .
Каркасный тетраэдр
Это тетраэдр, отвечающий любому из следующих условий :
- существует сфера, касающаяся всех ребер,
- суммы длин скрещивающихся ребер равны,
- суммы двугранных углов при противоположных ребрах равны,
- окружности, вписанные в грани, попарно касаются,
- все четырёхугольники, получающиеся на развертке тетраэдра, — описанные,
- перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.
Соразмерный тетраэдр
Свойства соразмерного тетраэдра:
- Бивысоты равны. Бивысотами тетраэдра называют общие перпендикуляры к двум скрещивающимся его ребрам (ребрам, не имеющим общих вершин).
- Проекция тетраэдра на плоскость, перпендикулярную любой бимедиане
, есть ромб . Бимедианами
тетраэдра называют отрезки, соединяющие середины его скрещивающихся ребер (не имеющих общих вершин). - Грани описанного параллелепипеда равновелики.
- Выполняются соотношения: 4a^2{a_1}^2- (b^2+{b_1}^2-c^2-{c_1}^2)^2=4b^2{b_1}^2- (c^2+{c_1}^2-a^2-{a_1}^2)^2=4c^2{c_1}^2- (a^2+{a_1}^2-b^2-(b_1)^2)^2, где a и a_1, b и b_1, c и c_1 — длины противоположных ребер.
- Для каждой пары противоположных ребер тетраэдра плоскости, проведенные через одно из них и середину второго, перпендикулярны.
- В описанный параллелепипед соразмерного тетраэдра можно вписать сферу.
Инцентрический тетраэдр
У этого типа отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Свойства инцентрического тетраэдра:
- Отрезки, соединяющие центры тяжести граней тетраэдра с противоположными вершинами (медианы тетраэдра), всегда пересекаются в одной точке. Эта точка — центр тяжести тетраэдра.
- Замечание
. Если в последнем условии заменить центры тяжести граней на ортоцентры граней, то оно превратится в новое определение ортоцентрического тетраэдра
. Если же заменить их на центры вписанных в грани окружностей, называемых иногда инцентрами , мы получим определение нового класса тетраэдров — инцентрических
. - Отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
- Биссектрисы углов двух граней, проведенному к общему ребру этих граней, имеют общее основание.
- Произведения длин противоположных ребер равны.
- Треугольник, образованный вторыми точками пересечения трех ребер, выходящих из одной вершины, с любой сферой, проходящей через три конца этих ребер, является равносторонним.
Правильный тетраэдр
Это равногранный тетраэдр, у которого все грани правильные треугольники . Является одним из пяти тел Платона .
Свойства правильного тетраэдра:
- все ребра тетраэдра равны между собой,
- все грани тетраэдра равны между собой,
- периметры и площади всех граней равны между собой.
- Правильный тетраэдр является одновременно ортоцентрическим, каркасным, равногранным, инцентрическим и соразмерным.
- Тетраэдр является правильным, если он принадлежит к двум любым видам тетраэдров из перечисленных: ортоцентрический, каркасный, инцентрический, соразмерный, равногранный
. - Тетраэдр является правильным, если он является равногранным
и принадлежит к одному из следующих видов тетраэдров: ортоцентрический, каркасный, инцентрический, соразмерный
. - В правильный тетраэдр можно вписать октаэдр, притом четыре (из восьми) грани октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
- Правильный тетраэдр состоит из одного вписанного октаэдра (в центре) и четырёх тетраэдров (по вершинам), причем ребра этих тетраэдров и октаэдра вдвое меньше ребер правильного тетраэдра.
- Правильный тетраэдр можно вписать в куб двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба.
- Правильный тетраэдр можно вписать в икосаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
- Скрещивающиеся ребра правильного тетраэдра взаимно перпендикулярны.
Объём тетраэдра
- Объём тетраэдра (с учётом знака), вершины которого находятся в точках mathbf{r}_1 (x_1,y_1,z_1), mathbf{r}_2 (x_2,y_2,z_2), mathbf{r}_3 (x_3,y_3,z_3), mathbf{r}_4 (x_4,y_4,z_4), равен
V = frac16
begin{vmatrix}
1 & x_1 & y_1 & z_1 \
1 & x_2 & y_2 & z_2 \
1 & x_3 & y_3 & z_3 \
1 & x_4 & y_4 & z_4
end{vmatrix} = frac16 begin{vmatrix}
x_2 — x_1 & y_2 — y_1& z_2 — z_1\
x_3 — x_1 & y_3 — y_1& z_3 — z_1\
x_4 — x_1 & y_4 — y_1& z_4 — z_1
end{vmatrix},
или
V = frac{1}{3} S H,
где S – площадь любой грани, а H – высота, опущенная на эту грань.
- Объём тетраэдра через длины рёбер выражается с помощью определителя Кэли-Менгера :
288 cdot V^2 =
0 & 1 & 1 & 1 & 1 \
1 & 0 & d_{12}^2 & d_{13}^2 & d_{14}^2 \
1 & d_{12}^2 & 0 & d_{23}^2 & d_{24}^2 \
1 & d_{13}^2 & d_{23}^2 & 0 & d_{34}^2 \
1 & d_{14}^2 & d_{24}^2 & d_{34}^2 & 0
end{vmatrix}.
- Эта формула имеет плоский аналог для площади треугольника в виде варианта формулы Герона через аналогичный определитель.
- Объём тетраэдра через длины двух противоположных рёбер a
и b
, как скрещивающихся линий, которые удалены на расстояние h
друг от друга и образуют друг с другом угол phi , находится по формуле:
V = frac{1}{6} ab h sin phi .
V = frac{1}{3} abc sqrt {D} ,
где
D=
begin{vmatrix}
1 & cos gamma & cos beta \
cos gamma & 1 & cos alpha \
cos beta & cos alpha & 1
end{vmatrix}.
- Аналогом для плоскости последней формулы является формула площади треугольника через длины двух его сторон a
и b
, выходящих из одной вершины и образующих между собой угол gamma :
S = frac{1}{2} ab sqrt {D} ,
где
D=
begin{vmatrix}
1 & cos gamma \
cos gamma & 1 \
end{vmatrix}.
Тетраэдры в микромире
- Правильный тетраэдр образуется при sp 3 -гибридизации атомных орбиталей (их оси направлены в вершины правильного тетраэдра, а ядро центрального атома расположено в центре описанной сферы правильного тетраэдра), поэтому немало молекул, в которых такая гибридизация центрального атома имеет место, имеют вид этого многогранника
- Молекула метана СН 4
- Сульфат-ион SO 4 2- , фосфат-ион PO 4 3- , перхлорат-ион ClO 4 — и многие другие ионы
- Алмаз C — тетраэдр с ребром равным 2,5220 ангстрем
- Флюорит CaF 2 , тетраэдр с ребром равным 3, 8626 ангстрем
- Сфалерит , ZnS, тетраэдр с ребром равным 3,823 ангстрем
- Комплексные ионы — , 2- , 2- , 2+
- Силикаты , в основе структур которых лежит кремнекислородный тетраэдр 4-
Тетраэдры в живой природе
Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи .
Тетраэдры в технике
См. также
- Симплекс — n-мерный тетраэдр
Напишите отзыв о статье «Тетраэдр»
Примечания
Литература
- Матизен В. Э., Дубровский. Из геометрии тетраэдра «Квант» , № 9, 1988 г. С.66.
- Заславский А. А. // Математическое просвещение, сер. 3 (2004), № 8, стр. 78-92.
| Правильные |
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Правильные невыпуклые |
|||||||||||
| Выпуклые |
|
||||||||||
| Формулы , теоремы , теории |
|||||||||||
| Прочее |
Отрывок, характеризующий Тетраэдр
На четвертый день пожары начались на Зубовском валу.
Пьера с тринадцатью другими отвели на Крымский Брод, в каретный сарай купеческого дома. Проходя по улицам, Пьер задыхался от дыма, который, казалось, стоял над всем городом. С разных сторон виднелись пожары. Пьер тогда еще не понимал значения сожженной Москвы и с ужасом смотрел на эти пожары.
В каретном сарае одного дома у Крымского Брода Пьер пробыл еще четыре дня и во время этих дней из разговора французских солдат узнал, что все содержащиеся здесь ожидали с каждым днем решения маршала. Какого маршала, Пьер не мог узнать от солдат. Для солдата, очевидно, маршал представлялся высшим и несколько таинственным звеном власти.
Эти первые дни, до 8 го сентября, – дня, в который пленных повели на вторичный допрос, были самые тяжелые для Пьера.
Х
8 го сентября в сарай к пленным вошел очень важный офицер, судя по почтительности, с которой с ним обращались караульные. Офицер этот, вероятно, штабный, с списком в руках, сделал перекличку всем русским, назвав Пьера: celui qui n»avoue pas son nom [тот, который не говорит своего имени]. И, равнодушно и лениво оглядев всех пленных, он приказал караульному офицеру прилично одеть и прибрать их, прежде чем вести к маршалу. Через час прибыла рота солдат, и Пьера с другими тринадцатью повели на Девичье поле. День был ясный, солнечный после дождя, и воздух был необыкновенно чист. Дым не стлался низом, как в тот день, когда Пьера вывели из гауптвахты Зубовского вала; дым поднимался столбами в чистом воздухе. Огня пожаров нигде не было видно, но со всех сторон поднимались столбы дыма, и вся Москва, все, что только мог видеть Пьер, было одно пожарище. Со всех сторон виднелись пустыри с печами и трубами и изредка обгорелые стены каменных домов. Пьер приглядывался к пожарищам и не узнавал знакомых кварталов города. Кое где виднелись уцелевшие церкви. Кремль, неразрушенный, белел издалека с своими башнями и Иваном Великим. Вблизи весело блестел купол Ново Девичьего монастыря, и особенно звонко слышался оттуда благовест. Благовест этот напомнил Пьеру, что было воскресенье и праздник рождества богородицы. Но казалось, некому было праздновать этот праздник: везде было разоренье пожарища, и из русского народа встречались только изредка оборванные, испуганные люди, которые прятались при виде французов.
Очевидно, русское гнездо было разорено и уничтожено; но за уничтожением этого русского порядка жизни Пьер бессознательно чувствовал, что над этим разоренным гнездом установился свой, совсем другой, но твердый французский порядок. Он чувствовал это по виду тех, бодро и весело, правильными рядами шедших солдат, которые конвоировали его с другими преступниками; он чувствовал это по виду какого то важного французского чиновника в парной коляске, управляемой солдатом, проехавшего ему навстречу. Он это чувствовал по веселым звукам полковой музыки, доносившимся с левой стороны поля, и в особенности он чувствовал и понимал это по тому списку, который, перекликая пленных, прочел нынче утром приезжавший французский офицер. Пьер был взят одними солдатами, отведен в одно, в другое место с десятками других людей; казалось, они могли бы забыть про него, смешать его с другими. Но нет: ответы его, данные на допросе, вернулись к нему в форме наименования его: celui qui n»avoue pas son nom. И под этим названием, которое страшно было Пьеру, его теперь вели куда то, с несомненной уверенностью, написанною на их лицах, что все остальные пленные и он были те самые, которых нужно, и что их ведут туда, куда нужно. Пьер чувствовал себя ничтожной щепкой, попавшей в колеса неизвестной ему, но правильно действующей машины.
Пьера с другими преступниками привели на правую сторону Девичьего поля, недалеко от монастыря, к большому белому дому с огромным садом. Это был дом князя Щербатова, в котором Пьер часто прежде бывал у хозяина и в котором теперь, как он узнал из разговора солдат, стоял маршал, герцог Экмюльский.
Их подвели к крыльцу и по одному стали вводить в дом. Пьера ввели шестым. Через стеклянную галерею, сени, переднюю, знакомые Пьеру, его ввели в длинный низкий кабинет, у дверей которого стоял адъютант.
Даву сидел на конце комнаты над столом, с очками на носу. Пьер близко подошел к нему. Даву, не поднимая глаз, видимо справлялся с какой то бумагой, лежавшей перед ним. Не поднимая же глаз, он тихо спросил:
– Qui etes vous? [Кто вы такой?]
Пьер молчал оттого, что не в силах был выговорить слова. Даву для Пьера не был просто французский генерал; для Пьера Даву был известный своей жестокостью человек. Глядя на холодное лицо Даву, который, как строгий учитель, соглашался до времени иметь терпение и ждать ответа, Пьер чувствовал, что всякая секунда промедления могла стоить ему жизни; но он не знал, что сказать. Сказать то же, что он говорил на первом допросе, он не решался; открыть свое звание и положение было и опасно и стыдно. Пьер молчал. Но прежде чем Пьер успел на что нибудь решиться, Даву приподнял голову, приподнял очки на лоб, прищурил глаза и пристально посмотрел на Пьера.
– Я знаю этого человека, – мерным, холодным голосом, очевидно рассчитанным для того, чтобы испугать Пьера, сказал он. Холод, пробежавший прежде по спине Пьера, охватил его голову, как тисками.
– Mon general, vous ne pouvez pas me connaitre, je ne vous ai jamais vu… [Вы не могли меня знать, генерал, я никогда не видал вас.]
– C»est un espion russe, [Это русский шпион,] – перебил его Даву, обращаясь к другому генералу, бывшему в комнате и которого не заметил Пьер. И Даву отвернулся. С неожиданным раскатом в голосе Пьер вдруг быстро заговорил.
– Non, Monseigneur, – сказал он, неожиданно вспомнив, что Даву был герцог. – Non, Monseigneur, vous n»avez pas pu me connaitre. Je suis un officier militionnaire et je n»ai pas quitte Moscou. [Нет, ваше высочество… Нет, ваше высочество, вы не могли меня знать. Я офицер милиции, и я не выезжал из Москвы.]
– Votre nom? [Ваше имя?] – повторил Даву.
– Besouhof. [Безухов.]
– Qu»est ce qui me prouvera que vous ne mentez pas? [Кто мне докажет, что вы не лжете?]
– Monseigneur! [Ваше высочество!] – вскрикнул Пьер не обиженным, но умоляющим голосом.
Даву поднял глаза и пристально посмотрел на Пьера. Несколько секунд они смотрели друг на друга, и этот взгляд спас Пьера. В этом взгляде, помимо всех условий войны и суда, между этими двумя людьми установились человеческие отношения. Оба они в эту одну минуту смутно перечувствовали бесчисленное количество вещей и поняли, что они оба дети человечества, что они братья.
В первом взгляде для Даву, приподнявшего только голову от своего списка, где людские дела и жизнь назывались нумерами, Пьер был только обстоятельство; и, не взяв на совесть дурного поступка, Даву застрелил бы его; но теперь уже он видел в нем человека. Он задумался на мгновение.
– Comment me prouverez vous la verite de ce que vous me dites? [Чем вы докажете мне справедливость ваших слов?] – сказал Даву холодно.
Пьер вспомнил Рамбаля и назвал его полк, и фамилию, и улицу, на которой был дом.
– Vous n»etes pas ce que vous dites, [Вы не то, что вы говорите.] – опять сказал Даву.
Пьер дрожащим, прерывающимся голосом стал приводить доказательства справедливости своего показания.
Но в это время вошел адъютант и что то доложил Даву.
Даву вдруг просиял при известии, сообщенном адъютантом, и стал застегиваться. Он, видимо, совсем забыл о Пьере.
Когда адъютант напомнил ему о пленном, он, нахмурившись, кивнул в сторону Пьера и сказал, чтобы его вели. Но куда должны были его вести – Пьер не знал: назад в балаган или на приготовленное место казни, которое, проходя по Девичьему полю, ему показывали товарищи.
Он обернул голову и видел, что адъютант переспрашивал что то.
– Oui, sans doute! [Да, разумеется!] – сказал Даву, но что «да», Пьер не знал.
Пьер не помнил, как, долго ли он шел и куда. Он, в состоянии совершенного бессмыслия и отупления, ничего не видя вокруг себя, передвигал ногами вместе с другими до тех пор, пока все остановились, и он остановился. Одна мысль за все это время была в голове Пьера. Это была мысль о том: кто, кто же, наконец, приговорил его к казни. Это были не те люди, которые допрашивали его в комиссии: из них ни один не хотел и, очевидно, не мог этого сделать. Это был не Даву, который так человечески посмотрел на него. Еще бы одна минута, и Даву понял бы, что они делают дурно, но этой минуте помешал адъютант, который вошел. И адъютант этот, очевидно, не хотел ничего худого, но он мог бы не войти. Кто же это, наконец, казнил, убивал, лишал жизни его – Пьера со всеми его воспоминаниями, стремлениями, надеждами, мыслями? Кто делал это? И Пьер чувствовал, что это был никто.
Это был порядок, склад обстоятельств.
Порядок какой то убивал его – Пьера, лишал его жизни, всего, уничтожал его.
От дома князя Щербатова пленных повели прямо вниз по Девичьему полю, левее Девичьего монастыря и подвели к огороду, на котором стоял столб. За столбом была вырыта большая яма с свежевыкопанной землей, и около ямы и столба полукругом стояла большая толпа народа. Толпа состояла из малого числа русских и большого числа наполеоновских войск вне строя: немцев, итальянцев и французов в разнородных мундирах. Справа и слева столба стояли фронты французских войск в синих мундирах с красными эполетами, в штиблетах и киверах.
Преступников расставили по известному порядку, который был в списке (Пьер стоял шестым), и подвели к столбу. Несколько барабанов вдруг ударили с двух сторон, и Пьер почувствовал, что с этим звуком как будто оторвалась часть его души. Он потерял способность думать и соображать. Он только мог видеть и слышать. И только одно желание было у него – желание, чтобы поскорее сделалось что то страшное, что должно было быть сделано. Пьер оглядывался на своих товарищей и рассматривал их.
Два человека с края были бритые острожные. Один высокий, худой; другой черный, мохнатый, мускулистый, с приплюснутым носом. Третий был дворовый, лет сорока пяти, с седеющими волосами и полным, хорошо откормленным телом. Четвертый был мужик, очень красивый, с окладистой русой бородой и черными глазами. Пятый был фабричный, желтый, худой малый, лет восемнадцати, в халате.
Пьер слышал, что французы совещались, как стрелять – по одному или по два? «По два», – холодно спокойно отвечал старший офицер. Сделалось передвижение в рядах солдат, и заметно было, что все торопились, – и торопились не так, как торопятся, чтобы сделать понятное для всех дело, но так, как торопятся, чтобы окончить необходимое, но неприятное и непостижимое дело.
Чиновник француз в шарфе подошел к правой стороне шеренги преступников в прочел по русски и по французски приговор.
Потом две пары французов подошли к преступникам и взяли, по указанию офицера, двух острожных, стоявших с края. Острожные, подойдя к столбу, остановились и, пока принесли мешки, молча смотрели вокруг себя, как смотрит подбитый зверь на подходящего охотника. Один все крестился, другой чесал спину и делал губами движение, подобное улыбке. Солдаты, торопясь руками, стали завязывать им глаза, надевать мешки и привязывать к столбу.
Двенадцать человек стрелков с ружьями мерным, твердым шагом вышли из за рядов и остановились в восьми шагах от столба. Пьер отвернулся, чтобы не видать того, что будет. Вдруг послышался треск и грохот, показавшиеся Пьеру громче самых страшных ударов грома, и он оглянулся. Был дым, и французы с бледными лицами и дрожащими руками что то делали у ямы. Повели других двух. Так же, такими же глазами и эти двое смотрели на всех, тщетно, одними глазами, молча, прося защиты и, видимо, не понимая и не веря тому, что будет. Они не могли верить, потому что они одни знали, что такое была для них их жизнь, и потому не понимали и не верили, чтобы можно было отнять ее.
Пьер хотел не смотреть и опять отвернулся; но опять как будто ужасный взрыв поразил его слух, и вместе с этими звуками он увидал дым, чью то кровь и бледные испуганные лица французов, опять что то делавших у столба, дрожащими руками толкая друг друга. Пьер, тяжело дыша, оглядывался вокруг себя, как будто спрашивая: что это такое? Тот же вопрос был и во всех взглядах, которые встречались со взглядом Пьера.

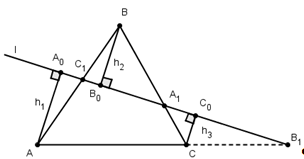
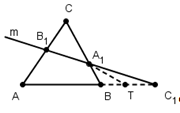

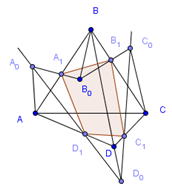
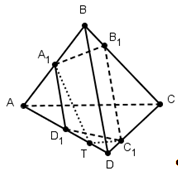
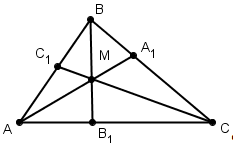
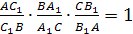
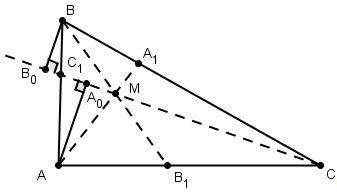
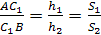
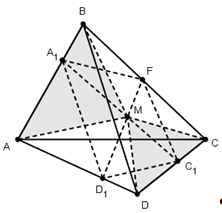
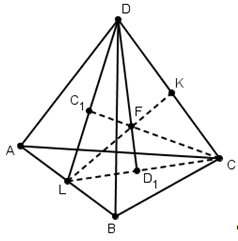
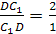
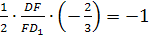
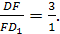
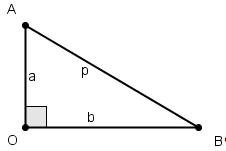
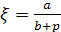
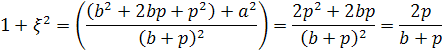
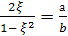
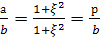
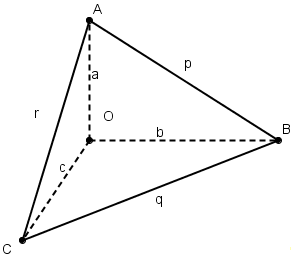
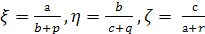
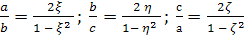
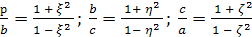
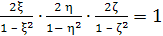
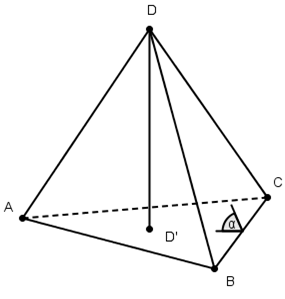
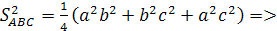
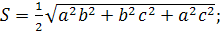
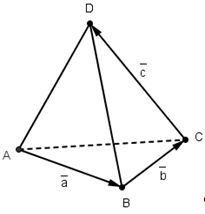
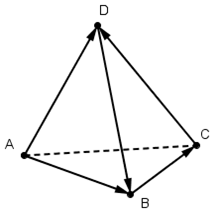
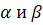
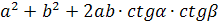
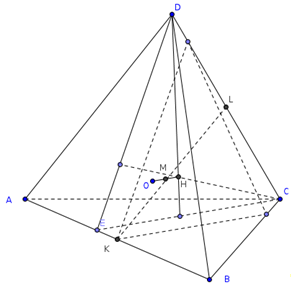
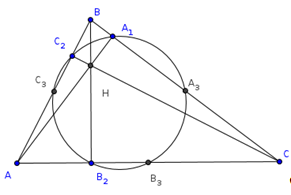
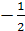
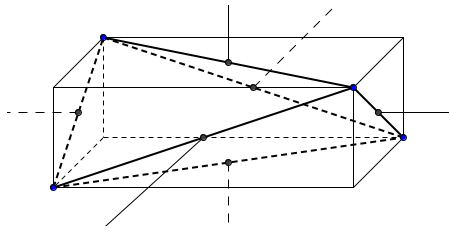
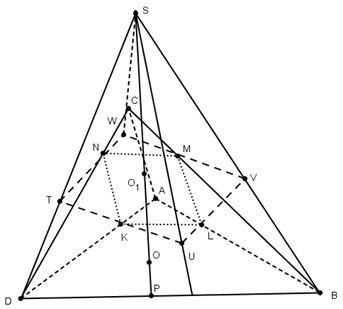
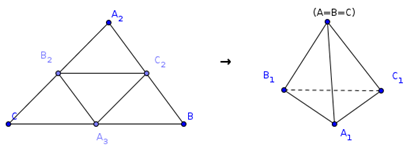
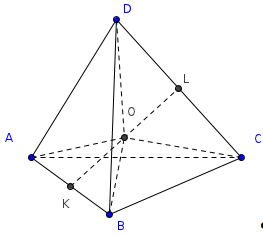
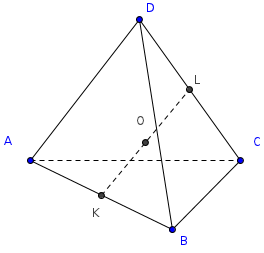
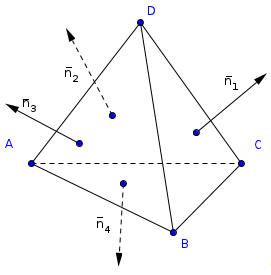
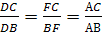
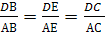
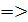
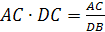
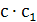
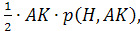
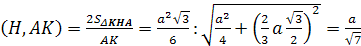
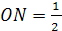
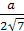
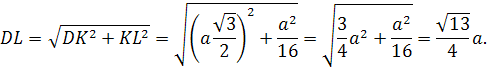
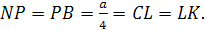
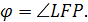
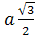
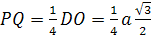
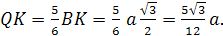
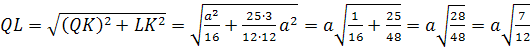
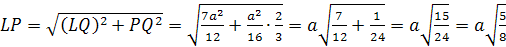
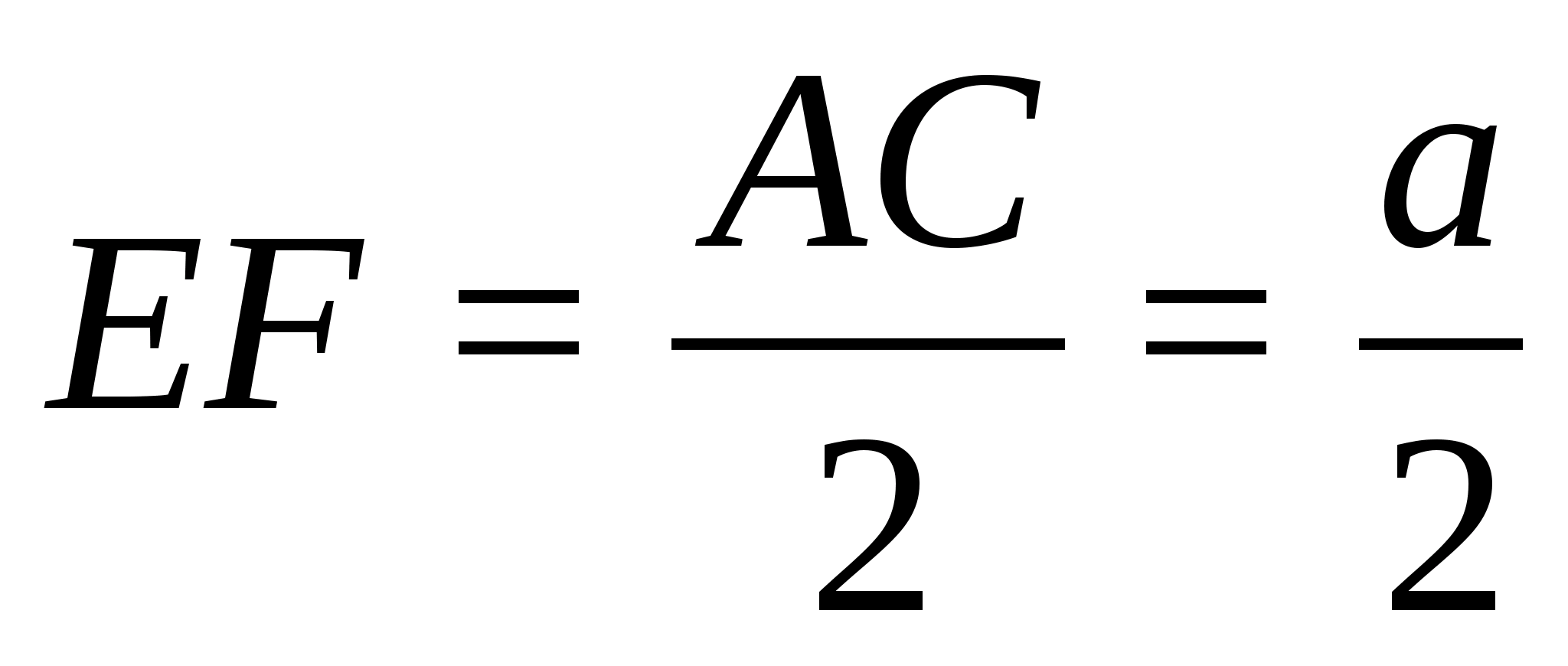
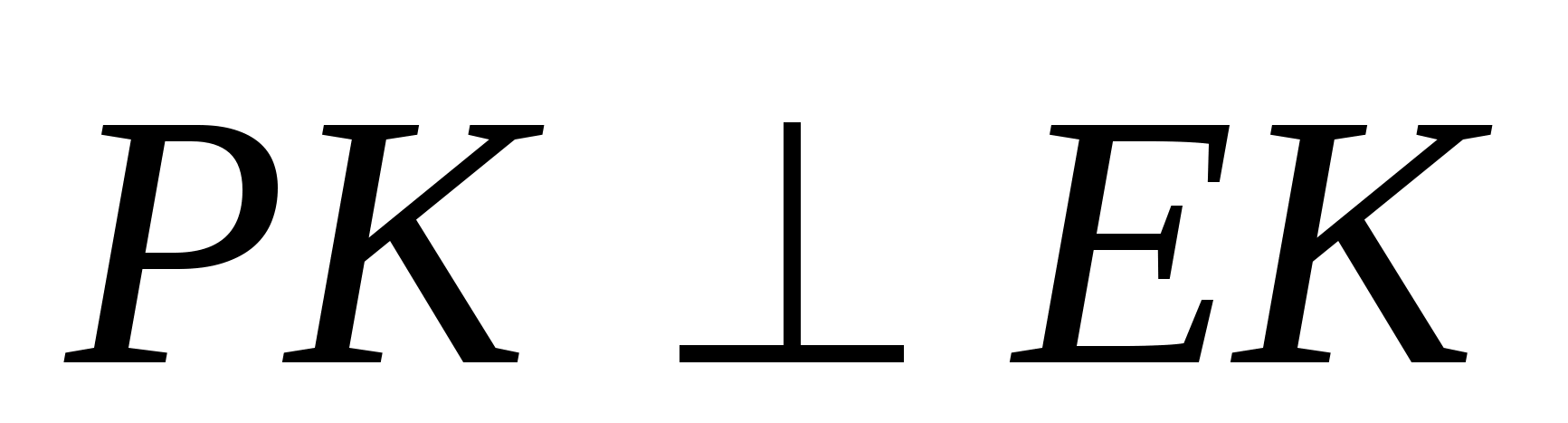
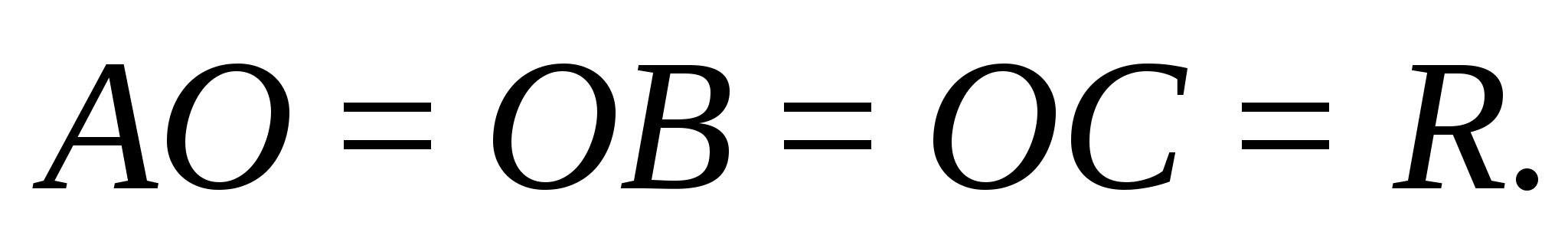
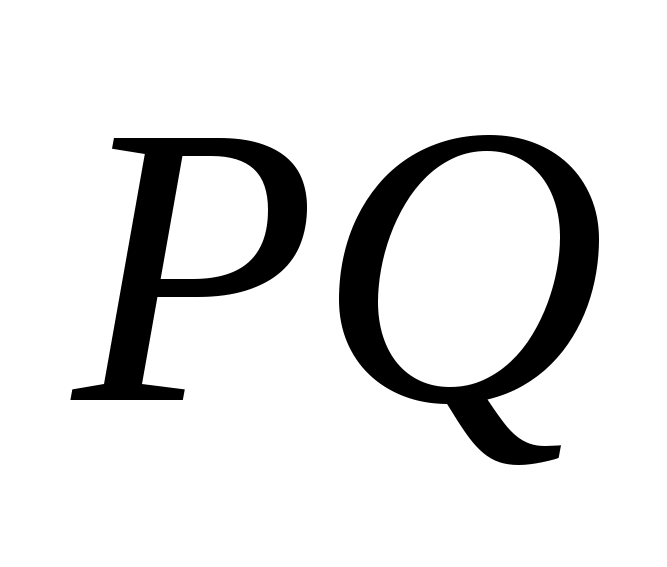
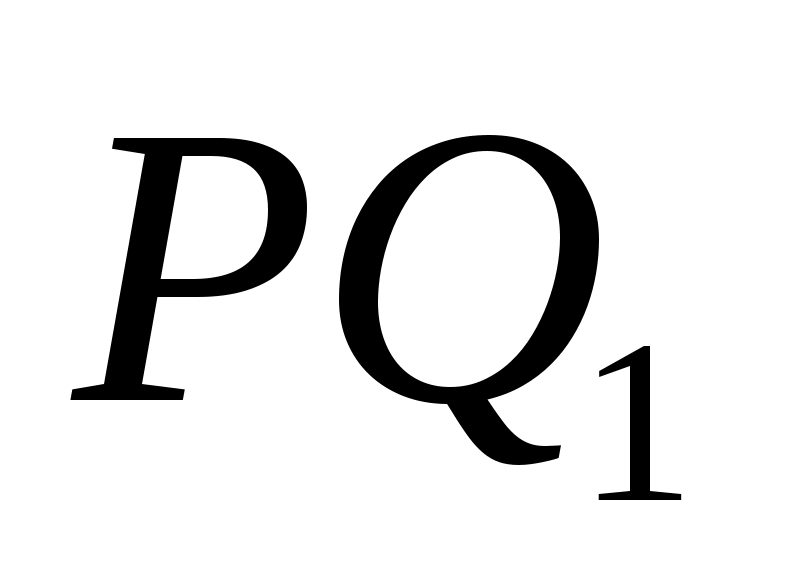
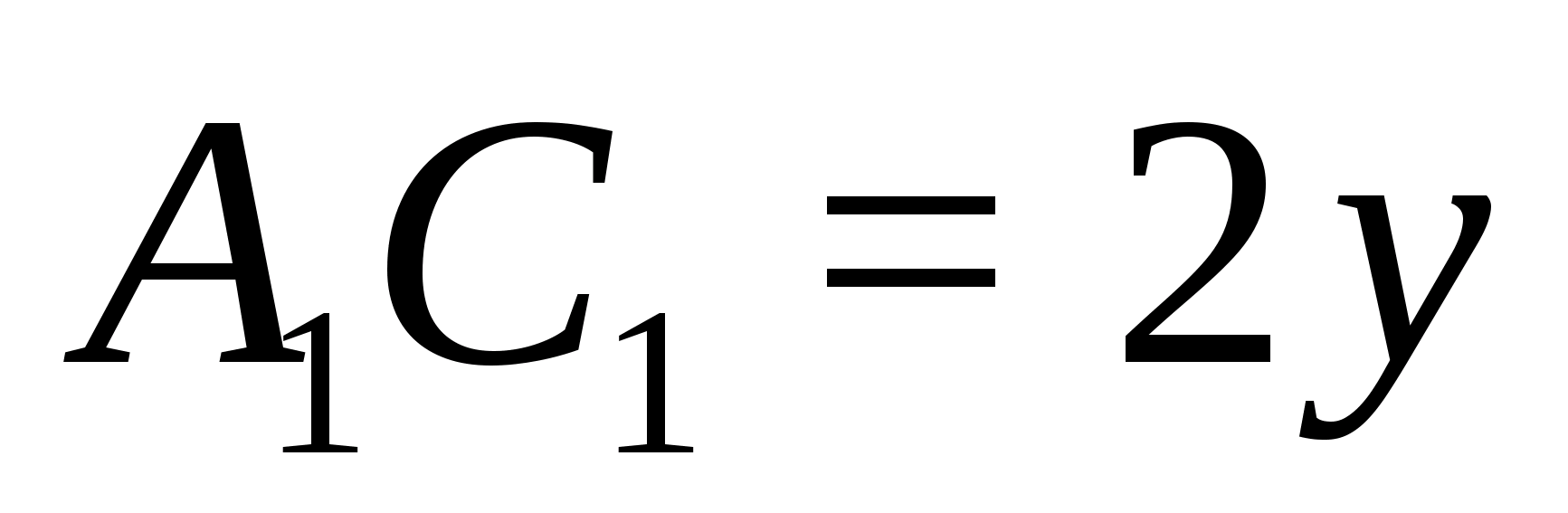
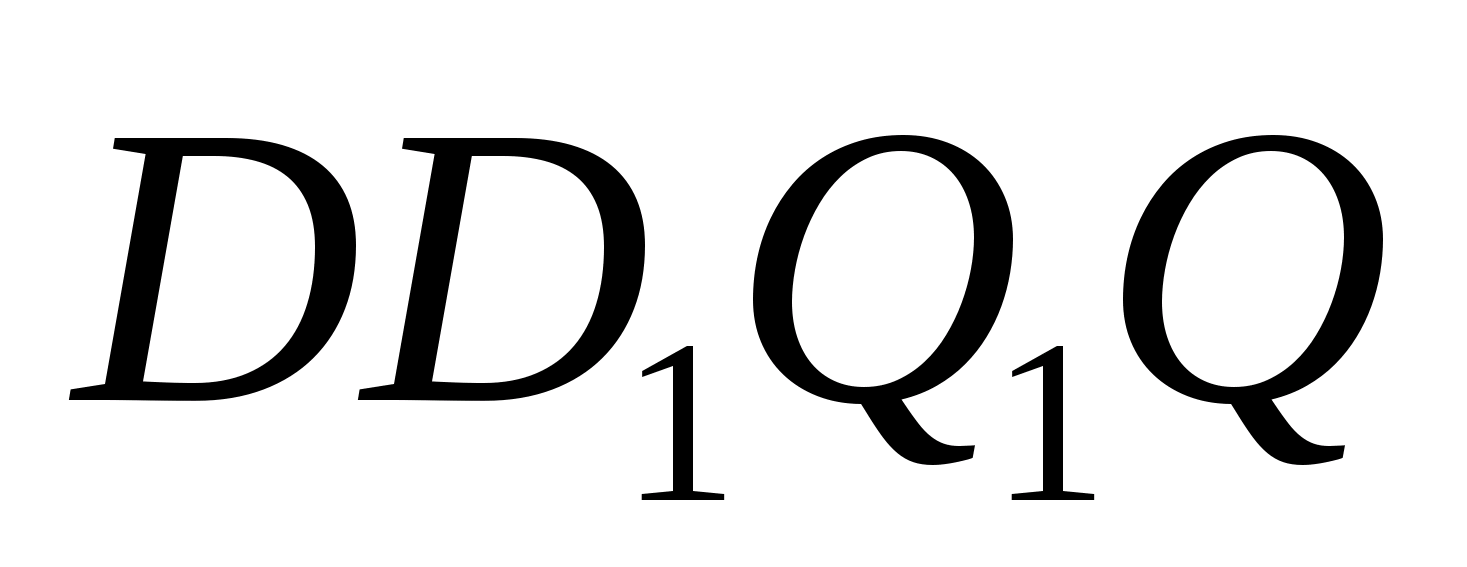
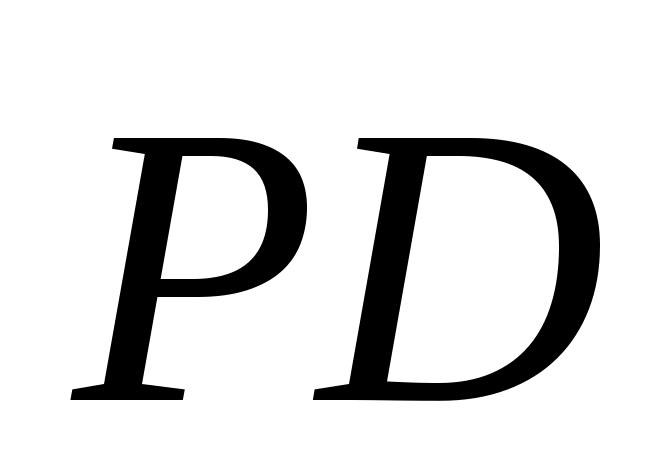

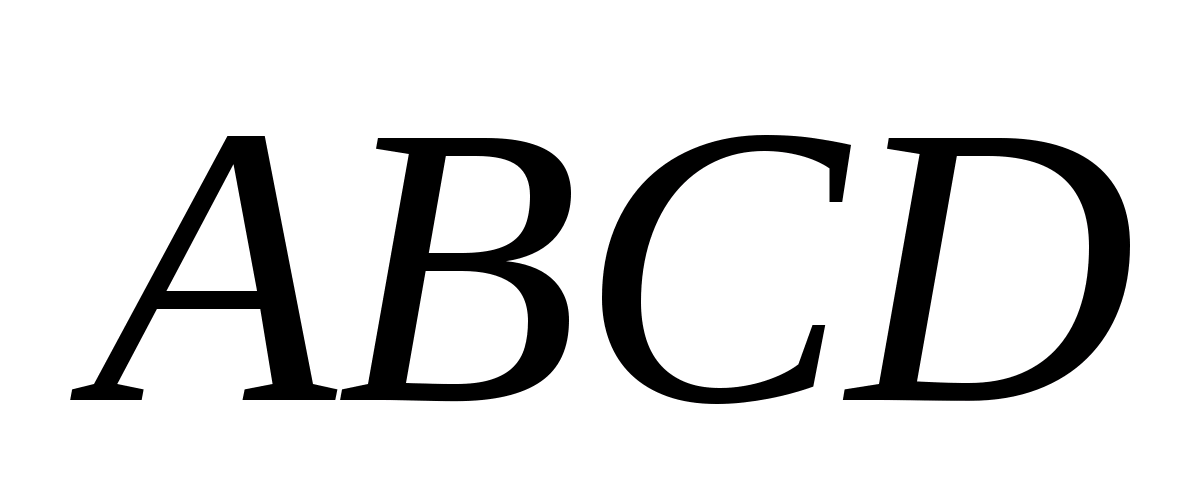
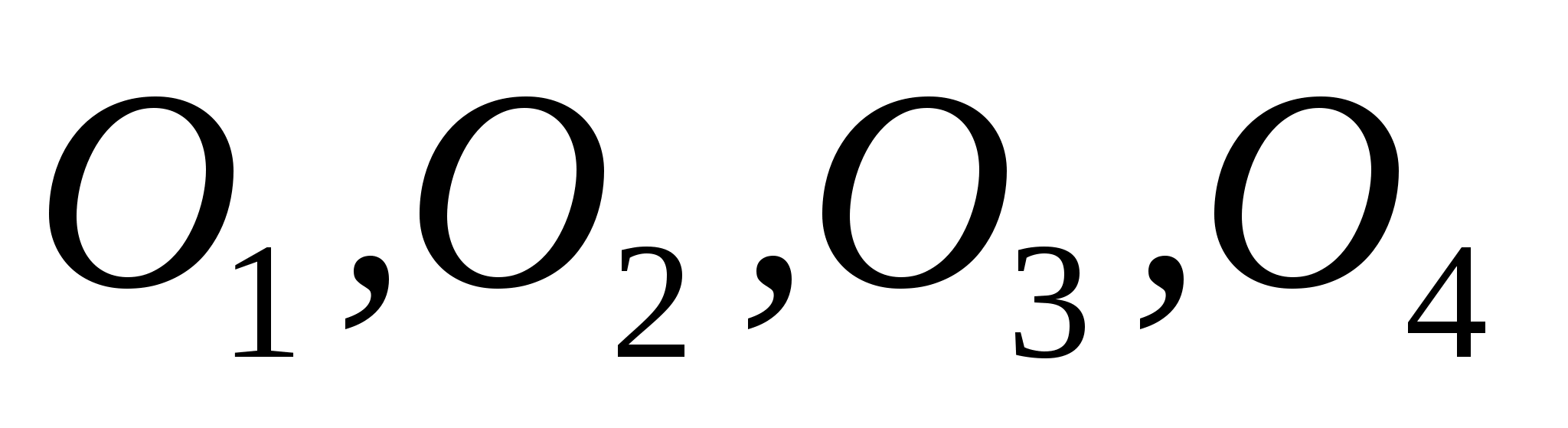

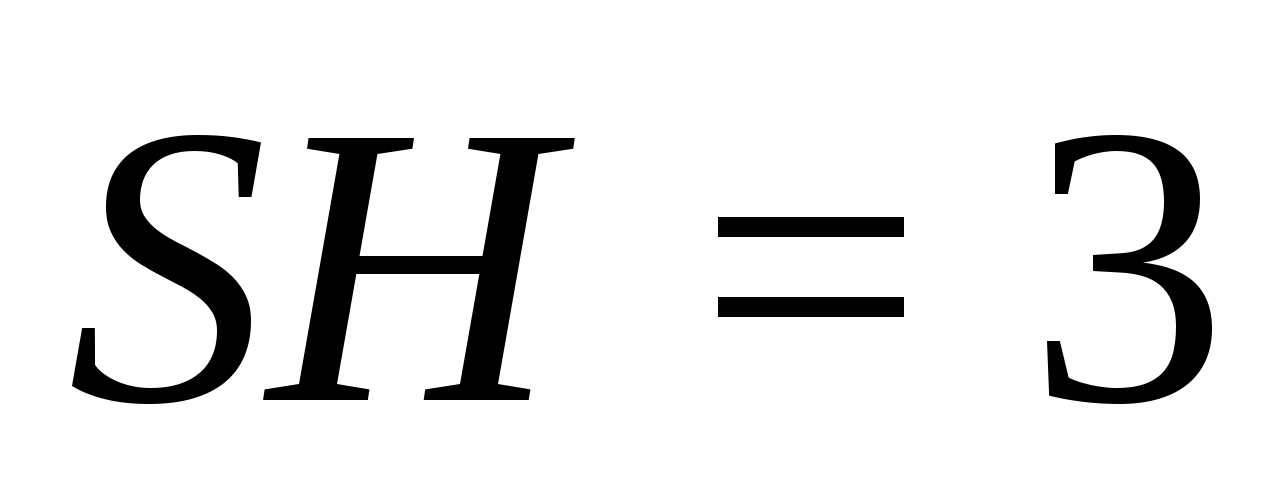







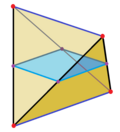



















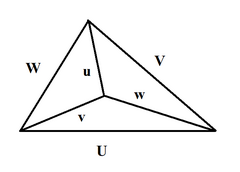













![{displaystyle {begin{aligned}C&=A^{-1}B&{text{where}}& &A=left({begin{matrix}left[x_{1}-x_{0}right]^{T}\left[x_{2}-x_{0}right]^{T}\left[x_{3}-x_{0}right]^{T}end{matrix}}right)& &{text{and}}& &B={frac {1}{2}}left({begin{matrix}|x_{1}|^{2}-|x_{0}|^{2}\|x_{2}|^{2}-|x_{0}|^{2}\|x_{3}|^{2}-|x_{0}|^{2}end{matrix}}right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bb507beee2d2141b350ce111b961c20b502e219)