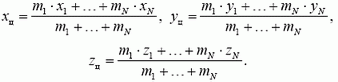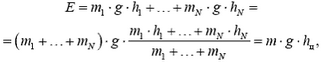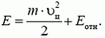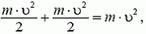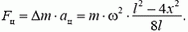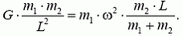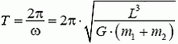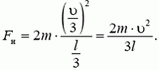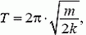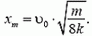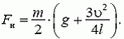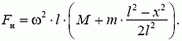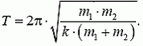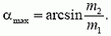Как найти центр масс веревки

Черноуцан А.И. Задачи на центр масс // Квант

Черноуцан А. Задачи на центр масс // Квант. — 1996. — № 2. — С. 43-45.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

При решении механических задач неоценимую помощь может оказать использование понятия центра масс системы материальных точек. Одни задачи просто невозможно решить, не прибегая к этому понятию, решение других с его помощью может стать гораздо проще и нагляднее.

Перед тем как обсуждать конкретные задачи, напомним основные свойства центра масс и проиллюстрируем их примерами.

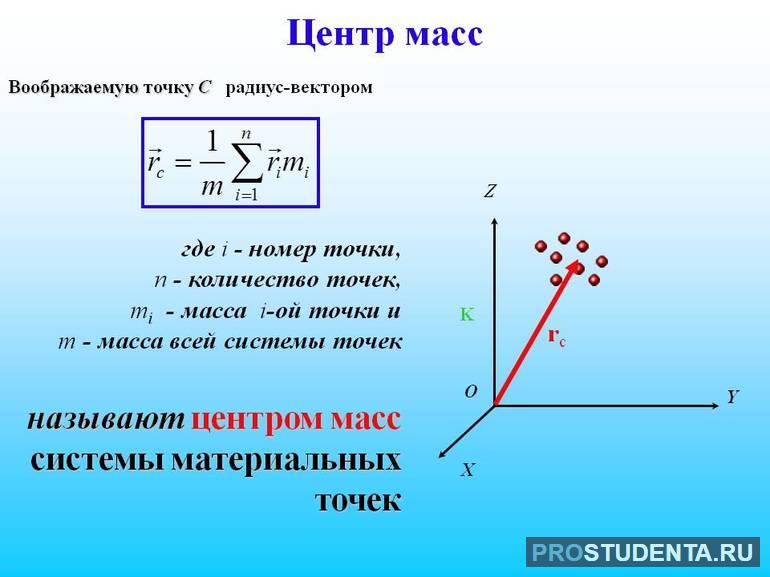
Центром масс (центром инерции) системы материальных точек назовем точку, характеризующую распределение масс в системе, координаты которой определяются формулами

Здесь m_i — массы материальных точек, образующих систему, x_i, y_i, z_i — координаты этих точек. Читатели, знакомые с понятием радиуса-вектора, предпочтут векторную запись:

(1)

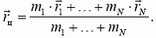
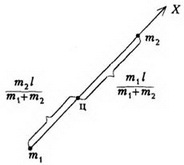
Пример 1. Найдем положение центра масс, простейшей системы, состоящей из двух точек, массы которых m₁ и m₂ и расстояние между ними l (рис. 1).

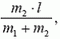
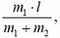
Направив ось X от первой точки ко второй, получим, что расстояние от первой точки до центра масс (т.е. координата центра масс) равно а расстояние от центра масс до второй точки равно т.е. отношение расстояний обратно отношению масс. Значит, в этом случае положение центра масс совпадает с центром тяжести.

Обсудим некоторые свойства центра масс, что, как нам кажется, наполнит физическим содержанием приведенное выше несколько формальное определение этого понятия.

1) Положение центра масс не изменится, если какую-то часть системы заменить одной точкой с массой, равной массе этой подсистемы, и находящейся в ее центре масс.

Пример 2. Рассмотрим плоский однородный треугольник и найдем положение его центра масс. Разделим треугольник на тонкие полоски, параллельные одной из сторон, и заменим каждую полоску точкой, расположенной в ее середине. Так как все такие точки лежат на медиане треугольника, центр масс тоже должен лежать на медиане. Повторяя рассуждения для каждой из сторон, получаем, что центр масс находится на пересечении медиан.

2) Скорость центра масс можно найти, взяв производную по времени от обеих частей равенства (1):

(2)

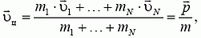
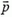
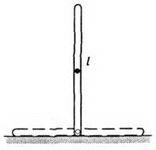
где — импульс системы, m — полная масса системы. Видно, что скорость центра масс замкнутой системы постоянна. Значит, если связать с центром масс поступательно движущуюся систему отсчета, то она будет инерциальной.

Пример 3. Поставим однородный стержень длиной l вертикально на гладкую плоскость (рис. 2) и отпустим. В процессе падения как горизонтальная составляющая его импульса, так и горизонтальная составляющая скорости центра масс будут оставаться равными нулю. Поэтому в момент падения центр стержня окажется в том месте, где первоначально стоял стержень, а концы стержня сместятся по горизонтали на .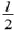

3) Ускорение центра масс равно производной от его скорости по времени:

(3)

где в правой части равенства стоят только внешние силы, так как все внутренние силы сокращаются по третьему закону Ньютона. Получаем, что центр масс, движется так, как двигалась бы воображаемая точка с массой, равной массе системы, под действием результирующей внешней силы. Наверное, это самое физическое свойство центра масс.

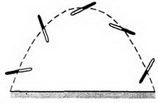
Пример 4. Если бросить палку, приведя ее при этом во вращение, то центр масс палки (ее середина) будет двигаться с постоянным ускорением 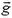по параболе (рис. 3).

4) Пусть система точек находится в однородном поле тяжести. Тогда суммарный момент сил тяжести относительно любой оси, проходящей через центр масс, равен нулю. Это значит, что равнодействующая сил тяжести проходит через центр масс, т.е. центр масс является также центром тяжести.

5) Потенциальная энергия системы точек в однородном поле тяжести вычисляется по формуле

где h_ц — высота центра масс системы.

Пример 5. При выкапывании в однородном фунте ямы глубиной h и разбрасывании грунта по поверхности его потенциальная энергия возрастает на 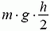, где m — масса извлеченного грунта.

6) И еще одно полезное свойство центра масс. Кинетическая энергия системы точек может быть представлена в виде суммы двух слагаемых: кинетической энергии общего поступательного движения системы, равной 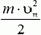, и кинетической энергии E_отн движения относительно системы отсчета, связанной с центром масс:

Пример 6. Кинетическая энергия обруча, катящегося без проскальзывания по горизонтальной поверхности со скоростью υ, равна

так как относительное движение в этом случае представляет собой чистое вращение, для которого линейная скорость точек обруча равна υ (полная скорость нижней точки должна быть равна нулю).

Теперь приступим к разбору задач на использование центра масс.

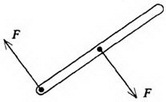
Задача 1. Однородный стержень лежит на гладкой горизонтальной поверхности. К стержню прикладывают две одинаковые по величине, но противоположные по направлению горизонтальные силы: одна сила приложена к середине стержня, другая — к его концу (рис. 4). Относительно какой точки начнет поворачиваться стержень?

На первый взгляд может показаться, что осью вращения будет точка, лежащая посередине между точками приложения сил. Однако уравнение (3) показывает, что поскольку сумма внешних сил равна нулю, то равно нулю и ускорение центра масс. Значит, центр стержня будет оставаться в покое, т.е. служить осью вращения.

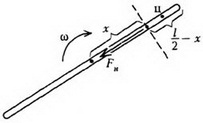
Задача 2. Тонкий однородный стержень длиной l и массой m привели в движение вдоль гладкой горизонтальной поверхности так, что он движется поступательно и одновременно вращается с угловой скоростью ω. Найдите, натяжение стержня в зависимости от расстояния x до его центра.

Перейдем в инерциальную систему отсчета, связанную с центром стержня. Рассмотрим движение куска стержня, заключенного между рассматриваемой точкой стержня (расположенной на расстоянии x от центра) и его концом (рис. 5).

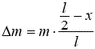
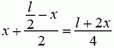
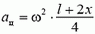
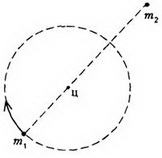
Единственной внешней силой для этого куска является искомая сила натяжения F_н, масса равна , а его центр масс движется по окружности радиусом с ускорением . Записывая уравнение движения центра масс выделенного куска, получим

Задача 3. Двойная звезда состоит из двух звезд-компонентов массами m₁ и m₂, расстояние между которыми не меняется и остается равным L. Найдите период вращения двойной звезды.

Рассмотрим движение звезд-компонентов в инерциальной системе отсчета, связанной с центром масс двойной звезды. В этой системе отсчета звезды движутся с одной и той же угловой скоростью по окружностям разных радиусов (рис. 6).

Радиус вращения звезды массой m₁ равен 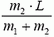(см. Пример 1), а ее центростремительное ускорение создается силой притяжения к другой звезде:

Видим, что период вращения двойной звезды равен

и определяется полной массой двойной звезды, независимо от того, как она распределена между звездами-компонентами.

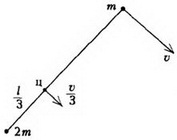
Задача 4. Две точечные массы m и 2m связаны невесомой нитью длиной l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорость массы 2m равна нулю, а скорость массы m равна υ и направлена перпендикулярно нити (рис. 7). Найдите натяжение нити и период вращения системы.

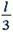
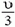
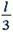
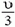
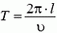
Центр масс системы находится на расстоянии от массы 2m и движется со скоростью . В системе отсчета, связанной с центром масс, точка массой 2m движется по окружности радиусом со скоростью . Значит, период вращения равен (проверьте, что такой же ответ получается, если рассмотреть точку массой m). Натяжение нити найдем из уравнения движения любой из двух точек:

Задача 5. На гладкой горизонтальной плоскости лежат два одинаковых бруска массой m каждый, связанных легкой пружиной жесткостью k (рис. 8). Первому бруску сообщают скорость υ₀ в направлении от второго бруска. Опишите движение системы. Через какое время деформация пружины впервые достигнет максимального значения?

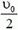
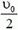
Центр масс системы будет перемещаться с постоянной скоростью . В системе отсчета центра масс начальная скорость каждого бруска равна , а жесткость половинной пружины, которая соединяет его с неподвижным центром масс, составляет 2k (жесткость пружины обратно пропорциональна ее длине). Период таких колебаний равен

а амплитуда колебаний каждого бруска, которую можно найти из закона сохранения энергии, составляет

В первый раз деформация станет максимальной через четверть периода, т.е. через время .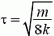

Задача 6. Шар массой m налетает со скоростью υ на покоящийся шар массой 2m. Найдите скорости обоих шаров после упругого центрального удара.

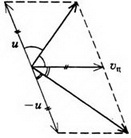
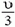
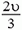
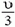
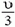
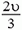
В системе отсчета, связанной с центром масс, полный импульс двух шаров равен нулю как до, так и после coyдарения. Легко догадаться, какой ответ для конечных скоростей удовлетворяет одновременно и этому условию, и закону сохранения энергии: скорости останутся такими же, как до удара, по величине, но изменят свои направления на противоположные. Скорость центра масс системы равна . В системе центра масс первый шар движется со скоростью , а второй шар движется навстречу первому со скоростью . После удара шары будут разлетаться с такими же скоростями. Осталось вернуться в первоначальную систему отсчета. Применяя закон сложения скоростей, находим, что конечная скорость шара массой m равна и направлена назад, а скорость покоившегося раньше шара массой 2m равна и направлена вперед.

Отметим, что в системе центра масс очевидным является утверждение, что при ударе относительная скорость шаров не меняется по величине, но меняется по направлению. А так как разность скоростей при переходе в другую инерциальную систему отсчета не изменяется, можно считать, что мы вывели это важное соотношение и для первоначальной системы отсчета:

где буква υ используется для обозначения начальных скоростей, а u — для конечных. Это уравнение можно решать совместно с законом сохранения импульса вместо закона сохранения энергии (куда скорости входят во второй степени).

Задача 7. Известно, что при упругом нецентральном ударе двух одинаковых шаров, один из которых до удара покоился, угол разлета равен 90°. Докажите это утверждение.

В системе центра масс нецентральный удар можно описать следующим образом. До удара шары сближаются с одинаковыми импульсами, после удара они разлетаются с такими же по величине, но противоположно направленными импульсами, а прямая разлета поворачивается на некоторый угол относительно прямой сближения. Чтобы перейти обратно в начальную систему отсчета, надо каждую конечную скорость сложить (векторно!) со скоростью центра масс. 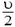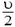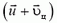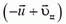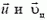В случае одинаковых шаров скорость центра масс равна , где υ — скорость налетающего шара, и в системе отсчета центра масс шары сближаются и разлетаются с одинаковыми скоростями . В том, что после сложения каждой конечной скорости со скоростью центра масс получаются взаимно перпендикулярные векторы, можно убедиться из рисунка 9. А можно и просто проверить, что скалярное произведение векторов и обращается в ноль в силу того, что модули векторов равны друг другу.

1. Стержень массой m и длиной l шарнирно закреплен за один из концов. Стержень отклонили на некоторый угол от вертикального положения и отпустили. В момент прохождения вертикального положения скорость нижней точки равна υ. Найдите натяжение в средней точке стержня в этот момент времени.

2. Стержень массой m и длиной l вращают в горизонтальной плоскости с угловой скоростью ω вокруг одного из его концов. Найдите зависимость натяжения стержня от расстояния x до оси вращения, если на другом конце закреплен маленький грузик массой М.

3. Найдите период колебаний для системы, описанной в задаче 5 статьи, но для брусков различных масс m₁ и m₂.

4. Выведите известные общие формулы для упругого центрального удара двух шаров, используя переход в систему отсчета центра масс.

5. Шар массой m₁ налетает на покоящийся шар меньшей массы m₂. Найдите максимально возможный угол отклонения налетающего шара при упругом нецентральном ударе.

1.

2.

3.

5.

Источник

If $rho$ is the density mass and $S$ is the surface of the rope, the mass $M$ is
$$
M=iint_Srho,mathrm dA
$$
and the moments are
$$
M_x=iint_Srho,y,mathrm dAqquad M_y=iint_Srho,x,mathrm dA
$$
Hence the center of mass coordinates are
$$
begin{align}
bar x&=frac{M_y}{M}=frac{iint_S x,mathrm dA}{iint_Smathrm dA}\
bar y&=frac{M_x}{M}=frac{iint_S y,mathrm dA}{iint_Smathrm dA}
end{align}
$$
If the rope is between $f(x)$ and $g(x)$ and between $a$ and $b$
the center of mass coordinates are
$$
begin{align}
bar x&=frac{M_y}{M}=frac{int_{a}^b int_{g(x)}^{f(x)} x,mathrm dy,mathrm dx}{int_{a}^b int_{g(x)}^{f(x)} mathrm dy,mathrm dx}=frac{int_{a}^b xleft[f(x)-g(x)right]mathrm dx}{int_{a}^b left[f(x)-g(x)right]mathrm dx}=frac{1}{S}int_{a}^b xleft[f(x)-g(x)right]mathrm dx\
\
bar y&=frac{M_x}{M}=frac{int_{a}^b int_{g(x)}^{f(x)} y,mathrm dy,mathrm dx}{int_{a}^b int_{g(x)}^{f(x)} mathrm dy,mathrm dx}=frac{int_{a}^b frac{1}{2}left[f^2(x)-g^2(x)right]mathrm dx}{int_{a}^b left[f(x)-g(x)right]mathrm dx}=frac{1}{S}int_{a}^b frac{1}{2}left[f^2(x)-g^2(x)right]mathrm dx
end{align}
$$
where $S=int_{a}^b left[f(x)-g(x)right]mathrm dx$ is the area of the rope.

If the rope is the surface between $y=f(x)$ even, $y=0$, $x=-a$ and $x=a$
we have
$$
begin{align}
bar x&=frac{M_y}{M}=frac{int_{-a}^a xf(x)mathrm dx}{int_{-a}^a f(x)mathrm dx}=frac{int_{-a}^a xf(x)mathrm dx}{2int_{0}^a f(x)mathrm dx}=0\
\
bar y&=frac{M_x}{M}=frac{int_{-a}^a frac{1}{2}f^2(x)mathrm dx}{int_{-a}^a f(x)mathrm dx}=frac{1}{2}frac{int_{0}^a f^2(x)mathrm dx}{int_{0}^a f(x)mathrm dx}
end{align}
$$

А так ли хорошо знаком вам центр масс? // Квант. — 1999. — № 3. — С. 32-33.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Центром тяжести каждого тела является некоторая расположенная
внутри его точка — такая, что если за нее мысленно подвесить тело,
то оно остается в покое и сохраняет первоначальное положение.
Архимед
Два тяжелых тела, связанных друг с другом, не могут сами па себе
прийти в движение без того, чтобы их общий центр тяжести не опускался.
Эванджеписта Торричелли
Я заметил удивительный закон природы… «общий центр тяжести
двух или трех или скольких угодно тел продолжает двигаться
равномерно в туже сторону по прямой линии как да, так и после удара».
Христиан Гюйгенс
Ведь из того положения, что брошенная в пустоте тачка описывает
параболу, можно также сделать вывод, что всякое конечное тело,
если оно будет брошено, должно двигаться по параболе.
Леонард Эйлер

Не удивляйтесь тому, что это словосочетание не встречается в эпиграфах, хотя именно о нем идет в них речь. Просто долгое время исследователям этого понятия не приходилось сталкиваться с обстоятельствами, в которых необходимо отличать «центр тяжести» тела от его «центра масс». В одной из задач мы предложим вам такую ситуацию, однако в подавляющем большинстве случаев один термин безболезненно можно заменять другим.

Изучение замечательных свойств «центров», которому более двух тысячелетий, оказалось полезным не только для механики — например, при конструировании транспортных средств и военной техники, расчете устойчивости сооружений или для вывода уравнений движения реактивных аппаратов. С помощью этих свойств стало возможным доказывать новые математические факты, находить решения некоторых трудных геометрических проблем, а впоследствии — строить плодотворные модели в таких областях знания, как химия, генетика, статистика, металлургия, теория цветного зрения… Вряд ли Архимед мог даже помыслить о том, что понятие центра масс окажется весьма удобным для исследований в ядерной физике или в физике элементарных частиц.

Многочисленные достоинства центра масс позволяют поместить его сегодня в центр вашего внимания.

Вопросы и задачи

1. При перемещении тела с экватора на полюс действующая на него сила тяжести меняется. Отражается ли это на положении центра тяжести тела?
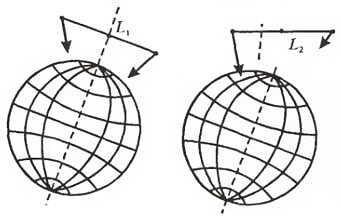
2. Можно ли найти центр тяжести «гантели», состоящей из двух массивных шариков, соединенных невесомым стержнем, при условии, что длина «гантели» сравнима с диаметром Земли?
3. Почему при резком торможении автомобиля его передняя часть опускается?
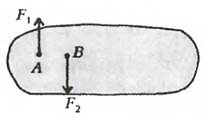
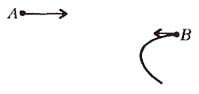
4. Однородное тело находится в покое. К точкам А и В приложили две равные и противоположно направленные силы, как показано на рисунке. В каком направлении станет двигаться точка В?

   

5. Отчего автобус, совершая поворот на относительно большой скорости, наклоняется в сторону, противоположную повороту?
6. Канат длиной L и массой m лежит на земле. Один его конец подняли на высоту L. Какая при этом была совершена работа?
7. Где находится центр тяжести бублика?
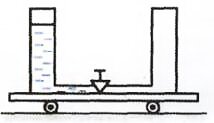
8. В цилиндрический стакан понемногу наливают воду. Как будет изменяться положение центра тяжести системы стакан — вода?
9. Какой длины конец надо отрезать от однородного стержня, чтобы его центр тяжести сместился на Δl?
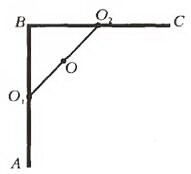
10. Однородный стержень согнули посередине под прямым углом. Где оказался теперь его центр тяжести?
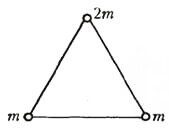
11. Найдите центр тяжести системы шаров, находящихся в вершинах равностороннего невесомого треугольника, изображенного на рисунке.

    

12. Невысокий деревянный цилиндр, обточенный с одного конца в форме полушара, остается в покое, если его поставить на горизонтальную плоскость любой точкой закругления. Где находится его центр тяжести?
13. Неподвижная космическая станция представляет собой цилиндр. Космонавт начинает круговой обход станции по ее поверхности. Что произойдет со станцией?
14. Как будет двигаться изображенная на рисунке тележка после открывания крана? Трением колес о плоскость пренебречь.

    

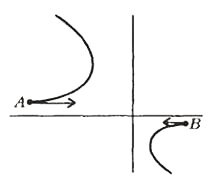
15. Две заряженные частицы массами m и 2m, которые взаимодействуют только между собой, одновременно вылетают навстречу друг другу из точек А и В, имея равные по величине импульсы. По траектории частицы массой 2m, приведенной на рисунке, восстановите траекторию другой частицы.

    

16. Почему трудно передвигаться на ходулях?
17. Когда канатоходцу легче удержать равновесие — при обычном передвижении по канату или при переносе сильно изогнутого коромысла, нагруженного ведрами с водой?
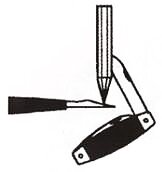
18. Как объяснить сохранение равновесия в случае, показанном на рисунке?

    

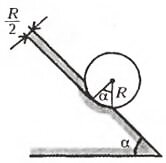
19. Глубина лунки в доске, в которую вставлен шар, в два раза меньше радиуса шара. При каком угле наклона доски к горизонту шар выскочит из лунки?

Микроопыт

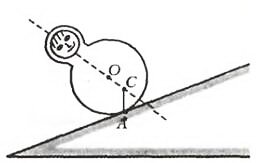
Поставьте детскую игрушку неваляшку (Ваньку-Встаньку) на шероховатую доску и приподнимите правый край доски. В какую сторону отклонится «голова» игрушки при сохранении ее равновесия?

Любопытно, что…

…в своем труде «О равновесии плоских тел» Архимед употреблял понятие центра тяжести, фактически не определяя его. Видимо, оно впервые было введено неизвестным предшественником Архимеда или же им самим, но в более ранней, не дошедшей до нас работе.

…должно было пройти долгих семнадцать столетий, прежде чем наука прибавила к исследованиям Архимеда о центрах тяжести новые результаты. Это произошло, когда Леонардо да Винчи сумел найти центр тяжести тетраэдра. Он же, размышляя об устойчивости итальянских наклонных башен, в том числе — Пизанской, пришел к «теореме об опорном многоугольнике».

…представленный в эпиграфах принцип Торричелли (а его имя носят и формулы для расчета центра масс), оказывается, был предвосхищен его учителем Галилеем. В свою очередь, этот принцип лег в основу классического труда Гюйгенса о маятниковых часах, а также был использован в знаменитых гидростатических исследованиях Паскаля.

…выясненные еще Архимедом условия равновесия плавающих тел впоследствии пришлось переоткрывать. Занимался этим в конце XVI века голландский ученый Симон Стевин, применявший, наряду с понятием центра тяжести, и понятие «центр давления» — точку приложения силы давления окружающей тело воды.

…метод, позволивший Эйлеру изучать движение твердого тела под действием любых сил, состоял в разложении этого движения на перемещение центра масс тела и вращение вокруг проходящих через него осей.

…для сохранения в неизменном положении предметов при движении их опоры уже несколько столетий применяется так называемый карданов подвес — устройство, в котором центр тяжести тела располагают ниже осей, вокруг которых оно может вращаться. Примером может служить показанная на рисунке корабельная керосиновая лампа.

…хотя на Луне сила тяжести в шесть раз меньше, чем на Земле, увеличить там рекорд по прыжкам в высоту удалось бы «всего» лишь в четыре раза. К такому выводу приводят расчеты по изменению высоты центра тяжести тела спортсмена.

…помимо суточного вращения вокруг своей оси и годового обращения вокруг Солнца, Земля принимает участие еще в одном круговом движении. Вместе с Луной она «крутится» вокруг общего центра масс, расположенного примерно в 4700 километрах от центра Земли.

…некоторые искусственные спутники Земли снабжены складной штангой в несколько или даже в десятки метров, утяжеленной на конце (так называемый гравитационный стабилизатор). Дело в том, что спутник вытянутой формы стремится при движении по орбите повернуться вокруг своего центра масс так, чтобы его продольная ось расположилась вертикально. Тогда он, подобно Луне, будет все время обращен к Земле одной стороной.

…движение центра масс системы из разгоняемой в ускорителе частицы и мишени, с которой она затем сталкивается, приводит лишь к неоправданным потерям энергии. Эффективно использовать энергию относительного движения налетающих друг на друга частиц удается в ускорителях на встречных пучках, где центр масс системы остается в покое. Для ультрарелятивистских частиц выигрыш в энергии может быть очень большим — в тысячи или даже в миллионы раз (для классических частиц в случае одинаковых масс выигрыш всего лишь четырехкратный).

…наблюдения за движением некоторых видимых звезд свидетельствуют о том, что они входят в двойные системы, в которых происходит вращение «небесных партнеров» вокруг общего центра масс. Одним из невидимых компаньонов в такой системе может быть нейтронная звезда или, возможно, черная дыра.

Что читать в «Кванте» о центре масс

1. «Системы отсчета в механике» — 1994, Приложение № 3, с. 103;
2. «Что такое центр масс?» — 1995, Приложение № 4, с. 35;
3. «Почему не лежится Ваньке-Встаньке» — 1996, № 1, с. 38;
4. «Задачи на центр масс» — 1996, № 2, с. 43;
5. Калейдоскоп «Кванта» — 1998, № 1, с. 32;
6. «Задачи с распределенной массой» — 1998, № 2, с. 46;
7. «Куда проскользнет палочка?» — 1998, № 4, с. 41;
8. «Палочка продолжает падать…» — 1999, № 2, с. 26.

Ответы

1. Нет, так как относительные изменения силы тяжести всех элементов тела одинаковы.
2. Нет. Условие существования центра тяжести — однородность поля тяготения. В неоднородном гравитационном поле повороты «гантели» вокруг ее центра масс приводят к тому, что линии действия L₁ и L₂ равнодействующих сил тяжести, приложенных к шарикам, не имеют общей точки.

   

3. При торможении на колеса со стороны дороги действует сила трения, создающая вращающий момент вокруг центра масс автомобиля.
4. Пара сил (~vec F_1) и (~vec F_2) сообщает телу вращение по часовой стрелке вокруг его центра масс, лежащего правее точки В. Следовательно, точка В станет двигаться против направления силы (~vec F_2).
5. Силы трения, сообщающие автобусу центростремительное ускорение, приложены не к его центру масс, а к нижним точкам колес, поэтому кузов автобуса движется по кривой большего радиуса, чем колеса.
6. Работа равна (~frac{mgL}{2}), так как центр тяжести каната оказался поднят на высоту (~frac{L}{2}).
7. В дырке!
8. Центр тяжести системы сначала будет понижаться, а потом — повышаться.
9. Длиной Δl.
10. В точке O — середине отрезка O₁O₂, соединяющего середины участков АВ и ВС стержня.

    

11. Центр тяжести лежит на середине биссектрисы угла, в вершине которого находится шар массой 2m.
12. В центре шара.
13. Станция придет во вращение в противоположную сторону, причем ее центр будет описывать окружность вокруг общего с космонавтом центра масс.
14. Тележка и находящаяся в сосудах вода будут совершать колебания вокруг общего центра масс. После того как уровни воды в сосудах окончательно сравняются, движение тележки прекратится.
15. Траектория частицы массой m получается растяжением с коэффициентом подобия 2 траектории частицы массой 2m.

    

16. Центр тяжести человека на ходулях значительно повышается, а площадь его опоры на землю уменьшается.
17. Во втором случае, так как центр масс канатоходца с ведрами лежит ниже, т.е. ближе к опоре — канату.
18. Центр тяжести системы карандаш — нож лежит ниже точки опоры.
19. При (~alpha > frac{pi}{2}) .

    

Микроопыт

Центр тяжести С неваляшки находится ниже геометрического центра О шарообразной поверхности «туловища». В положении равновесия точка С и точка касания А игрушки с наклонной плоскостью должны находиться на одной вертикали; следовательно «голова» неваляшки отклонится влево.

Материал подготовил А.Леонович

Точку, в которой происходит равное распределение величины, определяющей инерционные и гравитационные свойства, называют центром масс. Формула для определения параметра зависит от радиус-вектора частиц системы и их полной энергии. Эту характеристику тела отличают от тяжести, при этом в трудах советских учёных Ландау, Лифшица для неё используется термин «центр инерции».

Оглавление:

• Общие сведения
• Связь с центром тяжести
• Вычисление положения
• Геометрический способ определения

Общие сведения

Допустим, имеется тело, на которое действуют скомпенсированные силы. В этом случае оно будет в состоянии покоя или прямолинейного равномерного движения. Пусть тело будет неподвижным. Например, лодка на воде. К ней можно приложить воздействие F1 в районе её кормы. Под действием силы она начнёт разворачиваться. Аналогично если воздействовать на её нос F2, то она тоже будет поворачиваться, но при этом разворот будет происходить в другую сторону.

Получается, что можно подобрать такую линию, на которой действие сил приведёт её к ускоренно поступательному движению. Пусть это будет F3. На самом деле таких сил может быть несколько. При этом их можно перемещать вдоль линии их воздействия. Если все такие силы изобразить в виде линий, то они пересекутся в одной точке. Такое место и называют центром масс тела (ЦМ). То есть точку, в которой пересекаются линии действия сил, вызывающие только ускоренное поступательное механическое движение.

Эта важная точка в теле и движется она довольно просто. Перемещение любого тела можно представить, как комбинацию двух видов движения:

• центра масс;
• вращения.

Существует теорема: ЦМ тела движется так, как перемещалась бы материальная точка, в которой сосредоточена вся масса и к которой приложены все воздействия, действующие на объект. Таким образом, различные виды изменения положения точек в пространстве можно описать с помощью законов Ньютона. Согласно же теореме их можно применять и к телу, если считать, что все силы приложены к центру масс.

Рассматривая объект, можно не учитывать его размер, форму, а брать во внимание только инерцию, ускорение и принцип парного взаимодействия. Фактически в механике перемещение сколь угодно сложного вида рассматривается по принципу суперпозиции и закона сохранении энергии. При этом довольно удобно изучать изменение положения в системе отсчёта связанной с этим центром. В ней полный импульс всегда будет равным нулю, что позволяет упростить уравнение движения.

Связь с центром тяжести

Пусть имеется объект, находящийся на Земле. Говорят, что на него действует сила тяжести. Но на самом деле она воздействует не на вещество, а на каждый его атом, частичку. Если предположить, что ускорение свободного падения буде одинаковым, то на объект действует очень множество сил тяжести. Рассматривать такую систему неудобно. Поэтому все воздействия заменяют равнодействующей. И считают, что действует одна сила, которая приложена к центру тяжести твёрдого тела.

Для того чтобы найти взаимосвязь между тяжестью и массой нужно представить, что объект вдруг распался на отдельные равные кусочки. Они держатся вместе, но не прикреплены друг к другу. Если тело отпустить, то они будут падать вместе, так как ускорение свободного падения не зависит от массы. При этом движение будет поступательным. Значит, сила, приложенная к телу в целом, будет приложена к центру масс.

Получается, что центральная точка является общей как для тяжести, так и для масс. Это две точки положение которых совпадает несмотря на разный их принцип определения в физике. Но существуют условия, когда это правило не выполняется. Например, если система материальных точек неоднородна по объёму плотности в гравитационном поле, то центры не совпадут.

Для примера можно привести список однородных фигур с указанием их центральной точки:

• отрезок — середина;
• параллелограмм — место пересечения диагоналей;
• треугольник — точка пересечения медиан (центроид);
• любой правильный многоугольник — центр поворотной симметрии;
• полукруг — точка, в которой перпендикулярный радиус делится в отношении 4:3p считая от центра круга.

Чтобы найти координату центра масс объекта, который можно представить, как совокупность связанных материальных точек используют два метода: аналитический и геометрический. Но второй способ не всегда можно применить. В однородном гравитационном поле центры тяжести и масс всегда совпадают. И это часто подтверждается на практике, из-за того, что внешнее гравитационное поле в задачах, связанных с действиями на Земле, считают постоянным в пределах объёма тела.

Поэтому эти термины объединяют в геометрии, статике и так далее. То есть в тех областях, где применение определения можно назвать метафорическим и предполагается ситуация их эквивалентности.

При таком понимании оба термина синонимичны, но при этом чаще предпочитают использовать термин, связанный с тяжестью. Это происходит в силу того, что исторически он появился раньше.

Вычисление положения

Пусть тело представляет собой совокупность материальных точек, лежащих на одной прямой при этом их массы разные. Задача состоит в нахождении его центра. Для этого следует вести систему координат с осью икс, которая будет совпадать с линией расположения точек. При этом тело пусть подвешено на невесомой опоре и находится под действием Земного тяготения. Это условие даёт возможность воспользоваться тем фактом, что положения центров масс и тяжести совпадают.

На каждую из материальных точек действует своя сила: m1g, m2g… mng. Если предоставить это тело самому себе, то оно будет в состоянии свободного падения. Остановить тело — подпереть, но при этом так, чтобы оно находилось в равновесии. Это значит, что сила реакции опоры должна проходить через центр тяжести, так как равнодействующая тоже её пересекает.

Получится, что сила реакции опоры будет лежать на одной прямой с силой тяжести действующей на тело в совокупности и их моменты тоже будут проходить через неё. С помощью координатной оси точкам можно присвоить положение, x1, x2… xn, а ЦМ xц. Чтобы тело находилось в равновесии необходимо выполнение двух условий:

• векторная сумма всех сил должна быть равной нулю: m1g + m2g +…+mng + F = 0;
• сумма моментов равняться нулю: Mm 1 g + Mm 2 g +…+ Mmng + MF = 0.

Из первого условия можно найти силу реакции опоры: F = (m1 + m2 +…+mn) * g. Если вращение выбрать против часовой стрелки, тогда относительно оси все моменты силы тяжести будут отрицательными, а опоры — положительные. Тогда справедливо записать: F * хц = (m1 x 1 + m2 x 2 +…+mn xn) * g.

Из последнего равенства можно выразить координату ЦМ: xц = ((m1 x 1 + m2 x 2 +…+mn xn) * g) / F. В эту формулу можно подставить выражение для F. В результате ускорение свободного падения сократится и получится: xц = (m1 x 1 + m2 x 2 +…+mn xn) / (m1 + m2 +…+mn). Это формула выглядит громоздко, но запомнить её легко. В числителе стоят произведения масс материальных точек на их координаты, а в знаменателе — вес всего тела.

Если точки не будут лежать на одной прямой, то координата ЦМ тоже не изменится. То есть приведённая формула справедлива для любого положения тела относительно координаты y.

При этом её можно применять и для рассмотрения предметов в пространстве, так как все направления в существующем мире равноправные.

Геометрический способ определения

Для простейших симметричных фигур ЦМ можно определить геометрическим методом. Для этого используются свойства диагоналей и медиан. Пусть имеется произвольной формы четырёхугольник. Изготовлен он из однородного материала.

Идея вычисления состоит в том, что эту фигуру необходимо разбить на два треугольника. Для этого нужно провести диагональ, которая разделит фигуру на два тела. Затем провести в каждом треугольном теле три медианы. Точка их пересечения и будет ЦМ. В результате вместо четырёхугольника можно рассматривать две материальные точки.

Несмотря на то что масса у них разная ЦМ будет находиться на соединяющем их отрезке. Теперь четырёхугольник можно разбить на два других треугольника и выполнить аналогичные действия уже для них. Получится два отрезка, на которых одновременно расположен ЦМ. Значит, его положение будет определяться точкой их пересечения.

Для более сложной фигуры, например, шести или восьмиугольника можно использовать такой же подход. Сначала нужно разделить тело на прямоугольники, а затем треугольники. Найти ЦМ для полученных фигур и определить точку пересечения. Следует понимать, что ЦМ может находиться и за пределами объекта.

Но в реальных ситуациях бывают фигуры, которые имеют неправильную форму. Для них нельзя применить расчёт или геометрический метод. Поэтому выясняют, где расположен ЦМ экспериментальным путём.

Например, пусть имеется тело сложной неправильной формы. Чтобы найти ЦМ необходимо фигуру подвесить в пространстве. На неё действует две силы: тяжести и реакции оси. Первая заставляет фигуру поворачиваться с определённой скоростью до тех пор, пока момент силы тяжести относительно оси крепления не станет равным нулю. То есть точка опоры, ось и центр тяжести окажутся на одной вертикале.

Чтобы узнать, где же находится ЦМ, тело нужно подвесить, используя другую точку. При этом на самой фигуре следует отметить, как проходит вертикаль.

Повторяя такой опыт минимум три раза, можно увидеть точку пересечения осей, которая и будет искомым ЦМ. Причём чем будет больше экспериментов, тем точнее он будет определён.

Сущность понятия «центр масс»

Понятие «центр масс» широко используется в физике для решения задач, связанных с движением тел. Например, математический маятник удобно представить себе как подвешенное на нити тело, вся масса которого сконцентрирована в единой точке. В законе всемирного тяготения тоже речь идет о расстоянии не между телами, а между центрами тел, под каковыми подразумеваются именно центры масс, а не геометрические центры.

Признаком центра масс является то, что если тело подвесить, закрепив за эту точку, оно останется в покое, т.е. не будет раскачиваться или вращаться относительно этого центра. В простейшем случае, если речь идет о симметричном теле с равномерной плотностью, центр масс находится на пересечении осей симметрии рассматриваемого тела. Например, если взять линейку длиной 30 см, то ее центр масс будет расположен на отметке «15 см». Подложив карандаш под эту отметку, легко привести линейку в положение равновесия.

На практике далеко не все тела, центр масс которых нужно найти, являются симметричными и однородными по плотности. Более того, многие исследуемые объекты представляют собой системы из нескольких тел с различными геометрическими и химическими характеристиками. Для расчетов их разбивают на элементарные фрагменты и производят вычисления поэтапно.

Нахождение координат центра масс

Отсюда следует, что чем массивнее тело в такой элементарной системе, тем ближе оно к общему центру масс.

Расстояние между точечными телами равно:

$Delta x = x_2 — x_1$

Пропорция между массами и расстояниями, согласно определению:

$frac{l_1}{l_2} = frac{m_2}{m_1}$,

где $l_1$, $l_2$ — расстояния от соответствующих тел до центра масс.

Выразив, длины через координаты

$l_1 = x_c — x_1; l_2 = x_2 — x_c$,

центр масс можно определить как

$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$.

где $x_c$ — координата центра тяжести.

Разложив любую сложную систему на множество элементарных тел с точечными массами, можно обобщить изложенный принцип в виде формулы (для оси абсцисс):

$x_c = frac{sumlimits^N_{i=1}{m_i cdot x_i}}{sumlimits^N_{i=1}{m_i}}$

В большинстве случаев центр масс требуется найти не на координатной прямой, а в двух- или трехмерной системе координат. Для дополнительных осей координаты центра масс ($y_c$, $z_c$) находят по аналогичному принципу.