Дроби, у которых числитель меньше знаменателя, называются правильные дроби.
Дроби, у которых числитель больше либо равен знаменателю, называются неправильные дроби.
Для неправильных дробей действует негласное правило, согласно которому необходимо в конце решения в обязательном порядке выделить целую часть. Для того чтобы выделить целую часть из неправильной дроби, нужно разделить числитель на знаменатель, записать целую часть перед дробью, посередине, остаток записать в числитель, а знаменатель оставить тем же.
Пример:

Некоторые действия с дробями требуют, наоборот, исключительно неправильных дробей. Среди них, в первую очередь – умножение и деление дробей. Для того чтобы превратить смешанную дробь (дробь, в которой присутствует целая часть) в неправильную дробь, необходимо целую часть умножить на знаменатель, прибавить к ней текущий числитель дроби – это и станет новым числителем. Знаменатель останется тем же.
Пример:
В обоих случаях, если изначальная дробь была несократимой, то в результате у числителя и знаменателя также не найдется общих множителей.
Перевод неправильной дроби в смешанное число и обратно
- Главная
- /
- Математика
- /
- Арифметика
- /
- Перевод неправильной дроби в смешанное число и обратно
Если вам необходимо перевести неправильную дробь в смешанное число или наоборот воспользуйтесь нашим онлайн калькулятором:
Перевод неправильной дроби в смешанное число
Перевод смешанного числа в неправильную дробь
Просто заполните необходимые поля и получите ответ и подробное решение.
Теория
Как перевести неправильную дробь в смешанное число
Для того чтобы перевести неправильную дробь в смешанное число, то есть выделить целую часть из неправильной дроби, нужно произвести следующие действия:
- Сократить дробь, если это возможно
- Разделить в столбик числитель на знаменатель
- Полученное целое число записать в целую часть смешанного числа
- Полученный остаток записать в числитель, а знаменатель оставить прежним
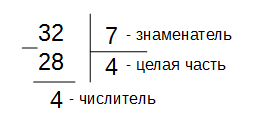
Пример №1
Преобразуем 146 в смешанное число:
146=7⋅23⋅2=73
| 7 | 3 |
| 6 | 2 |
| 1 | |
73=213
Всё решение можно ещё записать так:
146=7⋅23⋅2=73=2⋅3+13=2⋅33 + 13=213
Тут мы раскладываем число 7 на 2⋅3+1 и далее путём сокращения получаем результат.
Пример №2
Преобразуем 83 в смешанное число:
83=2⋅3+23=2⋅33 + 23=223
Как перевести смешанное число в неправильную дробь
Для того чтобы перевести смешанное число (смешенную дробь) в неправильную дробь следует воспользоваться следующей формулой:
Формула
a bc=b+a⋅cc
Пример
Преобразуем 213 в неправильную дробь:
213=1+2⋅33=73
См. также
Онлайн калькулятор поможет определить долю от числа. Для вычисления доли из числа, необходимо разделить число на знаменатель, а затем умножить на числитель.
Или чтобы найти часть от числа, необходимо разделить это число на значение, находящееся под чертой, и умножить на значение, находящееся над чертой.
Формула для нахождения доли от числа: [ x = frac{c}{b} sdot a ]
Где: [ frac{a}{b} ] — доля, а с — число.
| AC | 7 | 8 | 9 | ← |
| C | 4 | 5 | 6 | / |
| % | 1 | 2 | 3 | × |
| xy | . | 0 | = | — |
| x2 | √ | ( | ) | + |
Пример: продолжительность жизни собкаи – 15 лет. [ frac{1}{5} ] часть жизни она растёт. Сколько лет растёт собака?
Решение: разделим пятнадцать на пять и умножим на один: 15 : 5 × 1 = 3 года.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также
Как преобразовать неправильную дробь в смешанную
На данной странице калькулятор онлайн для преобразования неправильную дробь в смешанную, выделить целую часть. При переводе выводится описание решения.
Преобразовать дробь
У неправильной дроби числитель больше знаменателя или равен знаменателю.
Что выделить целую часть из неправильной дроби нужно:
- Разделить числитель на знаменатель.
- Полученное целое число запишем в целую часть дроби.
- Остаток от деления запишем в числитель.
- Знаменатель оставим прежним.
Пример
Преобразуем дробь .
Разделим в столбик числитель на знаменатель:
Получим дробь: .
…что я вам собственно вам пудрю мозги, занимаюсь тавтологией, лучше уж сразу предметно о том, что если мы имеем какое-то число, знаем часть от него выраженную в дроби, то мы всегда найдем и количественное значение. Именно об этом и будет моя статья. Об этом я напишу, расскажу, «разжую», а вот выводы останутся с вами! Начинаем!
Если у нас есть целое
Давайте наверное опять начну с аксиом (истин). Ведь строить выводы без догм (истин), это все равно, что дом без фундамента. Нам известно о том, что есть целое, то есть что-то единое, что мы привыкли считать по 1, применять к нему термин 100 процентов, представлять как нечто обособленное, отдельное если хотите.
Заметьте, что не смотря на то, что мы имеем что-то целое, это не значит, что его нельзя разобрать на части. Я думаю так делали многие дети, а в прошлом их родители, когда отрывали колесики от целой машинки или руки от пластиковых пупсиков… Ну, а опять же самый ходовой пример, это откусить часть от яблока.
И именно здесь пришло то самое время, дабы поговорить уже о частях целого!
Часть от целого
Итак, не смотря на то, что некоторые вещи мы привыкли видеть обособленно целыми, практически все можно разбить на части. Есть небольшие исключения для физического мира, о чем по программе начальной школы еще рано знать… А вот если чисто теоретически, то есть в математических подсчетах, то тут и вовсе без исключений! Любое из чисел можно всегда разбить на части, будь то 1, 100 или 25489.
Собственно именно для такого «расчленения», ладно скажу более умеренно, для разделения на части, и применяются наши дроби! Если вы уже знаете, что 1/2 это половина, а 1/3 это третья часть то замечательно! Ведь теперь самое время перейти к логике нахождения, сколько же будет в количественном значении эта часть в виде дроби от целого.
Как найти значение дроби (части) от целого
Теперь, когда мы понимаем, что дробь нам указывает на какую-то часть от целого, то есть 1/2 читается как одна вторая, а 23/56, — как двадцать три пятьдесят шестых, то нам хотелось бы манипулировать не просто понятиями как частями от целого, а именно их количественным значением. То есть скажем ваши родители, когда им говорят, что они получат премию в размере 2/3 от оклада всегда хотят знать, а сколько это в рублях, а именно не в частях.
Когда вы слышите от бабушек, что часть своей пенсии она потратит на ваши услады, всегда хотите больше знать не то, что это 1/10 часть, а то сколько это будет в рублях, ведь именно на них вы сможете купить мороженое и проиграть в игровых автоматах.
Так вот и в этом случае, находим конечную часть именно выраженную в тех же значениях, что и целое. То есть если это были рубли в виде целого оклада, то нам интересны именно рубли, а не части. Если это была вишня в кг, то лучше знать сколько это именно килограммов вишни, а не часть от того. что было. Именно с такими знаниями и я бы сказал нашими хотелками, ладно желаниями, мы и подходим к апогею нашей статьи. Так как же посчитать значение части выраженной в дроби от целого!
Смотрите, опять к нашим яблокам. У нас есть корзинка с яблоками, и это условно целое, то есть корзинка это наша «полная часть». И нам скажем необходимо найти 2/5 от нее.
При этом мы знаем, что в корзине 20 яблок или это можно сказать как 5 частей по 4 яблока. Все это показано на рисунке. Однако нам надо найти лишь 2 части из 5, те которые подчеркнуты красной линией. Вы визуально можете уже посчитать, что это будет 8 яблок. Однако как же это можно было найти не столь наглядным образом, а именно исходя из расчетов? Легко!
Необходимо было наше целое, то есть 20 яблок, разделить на 5 частей, так как мы ищем значение именно из 5 частей и умножить на 2, так как именно две части нас интересуют.То есть 2/5 от 20 это 20/5*2=8 яблок.
Мне кажется все понятно. Теперь немного практики, в виде задачи, а потом перейдем к наглядным обучающим пособиям в виде онлайн — калькулятора для нахождения значения части в виде дроби от какого-то числа условно нашего целого.
Задачи на нахождение значения дроби от числа
Первую задачу можно сказать мы уже разобрали выше. Это с корзинкой и яблоками. Теперь давайте другую.
Задача:
Туристы за 2 дня прошли 25 км по маршруту, при этом в первый день они прошли 3/5 пути. Сколько км туристы прошли в первый день?
Решение:
25:5*3=5*3=15 (км) — прошли туристы в первый день.
Ответ: 15 км.
Онлайн калькулятор нахождения значения дроби от числа
Хорошо, очень надеюсь, что вы поняли о чем я вам объяснял. Теперь же хочу представить вам онлайн калькулятор, который поможет вам очень быстро исходя из значения исходного числа и из его части в виде дроби, найти эту самую часть в виде значений эквивалентных исходному числу! Пробуем!
Введите значения дроби для вычисления ее в виде части от исходного:
Дробь
Находим то число, где дробь часть от «исходного числа»
Находим то число, где известно, что его часть равна дроби, а дробь по количественному значению -«исходному числу»