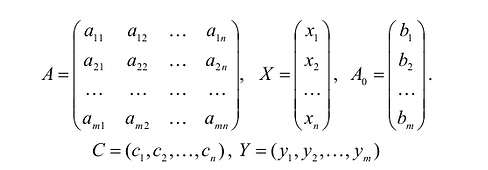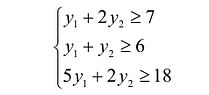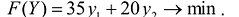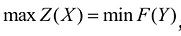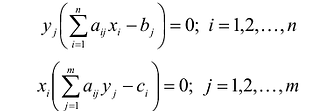Подробный разбор симплекс-метода
Время на прочтение
6 мин
Количество просмотров 192K
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение:
Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
Замечание:
Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
- Неравенства с отрицательными
умножаем на (-1).
- Если неравенство вида (≤), то к левой части добавляем
– добавочную переменную, и получаем равенство.
- Если неравенство вида (≥), то из левой части вычитаем
, и получаем равенство.
- Делаем замену переменных:
Замечание:
Будем нумеровать
по номеру неравенства, в которое мы его добавили.
Замечание:
≥0.
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Определение:
Точка
называется угловой точкой, если представление
возможно только при
.
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит
(т.е.
– не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение:
Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.
§4. Симплекс-метод
Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.
Необходимые условия для применения симплекс-метода:
- Задача должна иметь каноническую форму.
- У задачи должен быть явно выделенный базис.
Определение:
Явно выделенным базисом будем называть вектора вида:
, т.е. только одна координата вектора ненулевая и равна 1.
Замечание:
Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.
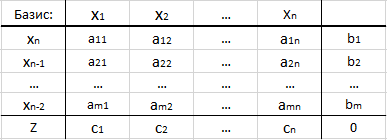
Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:
- В первой строке указывают «наименование» всех переменных.
- В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
- В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
- Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
- Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.
Замечание:
Базис – переменные, коэффициенты в матрице ограничений при которых образуют базисные вектора.
Замечание:
Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.
Замечание:
Коэффициенты в строке функционала берутся со знаком “-”.
Алгоритм симплекс-метода:
1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:
- Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
- Если задача на максимум – выбираем минимальный отрицательный.
Такой выбор, действительно, соответствует упомянутому выше принципу: если задача на минимум, то чем большее число вычитаем – тем быстрее убывает функционал; для максимума наоборот – чем большее число добавляем, тем быстрее функционал растет.
Замечание:
Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.
Определение:
Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.
2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:
- Вектор правых частей почленно делится на ведущий столбец
- Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)
Определение:
Такая строка называется ведущей строкой и отвечает переменной, которую нужно вывести из базиса.
Замечание:
Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.
3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.
Определение:
Такой элемент называется ведущим элементом.
4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.
5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.
- Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
- Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка
Замечание:
Преобразование такого вида направлено на введение выбранной переменной в базис, т.е. представление ведущего столбца в виде базисного вектора.
6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.
§5. Интерпретация результата работы симплекс-метода
1. Оптимальность
Условие оптимальности полученного решения:
- Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
- Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).
2. Неограниченность функционала
Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:
При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.
Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.
3. Альтернативные решения
При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).
Алгебраический признак существования альтернативы:
После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.
Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.
Эпилог
Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.
Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.
Спасибо за внимание!
P.S.
Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.

В результате получена игра размерностью 2×2 (табл. 36). Она по-прежнему не имеет седловой точки, но может быть решена на основе полученных выше расчетных соотношений:
|
p* = |
3 |
− 4 |
= |
−1 |
= 0,33 |
, p* =1 |
− p* = 0,67 ; |
|
1 |
3 + 3 |
− 5 − 4 |
− 3 |
4 |
1 |
||
q1* = 3−−35 = 0,67 , q2* =1−q1* = 0,33 ; V=3,67.
Решение примера 40 с учетом всего исходного набора чистых стратегий: P*=(0,33; 0; 0; 0,67), Q*=(0,67; 0,33), V=3,67.
В отличие от рассмотренных выше, следующий пример демонстрирует ограниченность метода упрощения и требует для своего решения других методов.
|
Таблица 36 |
|||
|
Страте- |
В1 |
В2 |
α |
|
гии |
|||
|
А1 |
3 |
5 |
3 |
|
А4 |
4 |
3 |
3 |
|
β |
4 |
7 |
|
Таблица 37
|
Страте- |
В1 |
В2 |
В3 |
α |
|
гии |
||||
|
А1 |
2 |
-3 |
4 |
−3 |
|
А2 |
-3 |
4 |
-5 |
-5 |
|
А3 |
4 |
-5 |
6 |
-5 |
|
β |
4 |
4 |
6 |
|
Пример 41. В игре, матрица которой представлена в табл. 37,
нижняя цена α=–3, верхняя цена β=4, седловая точка отсутствует. Заведомо невыгодные и дублирующие стратегии, симметрич-
ные фрагменты также отсутствуют. Размерность игры 3×3, что исключает возможность применения графического способа упрощения. Таким образом, методом упрощения решить данную игру не удается.
Сведение стратегической матричной игры без седловой точки к задаче линейного программирования обеспечивается при условии положительности цены игры V. Для этого в соответствии с (57)
достаточно α≥0.
Отметим сразу, что если такое условие для рассматриваемой игры не выполняется, достаточно в процессе ее решения найти минимальный элемент матрицы (очевидно, он будет отрицатель-
138
ным) и вычесть его величину из всех элементов матрицы, тем самым сдвигая их в положительном направлении. Полученная матрица игры будет содержать только неотрицательные элементы ai j , включая, очевидно и нижнюю цену игры. Анализируя соотношения (58)…(64), нетрудно убедиться, что такой прием не повлияет на величины оптимальных частот и приведет лишь к смещению величины цены игры V. Эту поправку необходимо будет учесть при записи окончательного результата.
Обратимся к неравенству (63) и условиям, которым подчиняются значения частот применения стороной А ее чистых страте-
m
гий: 0 ≤ pi ≤1, i=1,2,…,т; ∑ pi =1. Введем новые переменные:
i=1
xi = pi /V , i=1,2,…,т. С учетом pi ≥ 0 и V>0 на все переменные
xi накладывается требование неотрицательности, традиционное для аргументов задачи линейного программирования.
m
Разделим обе части уравнения ∑ pi =1 и неравенств (63) на
i=1
положительную переменную V:
|
m |
p |
i |
m |
1 |
|||
|
∑ |
= ∑xi = |
, |
(65) |
||||
|
V |
|||||||
|
i=1 V |
i=1 |
||||||
|
m |
|||||||
|
∑xiaij ≥1 |
, j=1,2,…,n. |
(66) |
i=1
Целью решения стратегической матричной игры для стороны А является нахождение таких значений частот pi, а следовательно, и связанных с ними значений переменных xi, которые доставят стороне А наибольший средний выигрыш V.
Введем на основе (65) целевую функцию
|
1 |
m |
|||
|
q = − |
= −∑xi → max . |
(67) |
||
|
V |
||||
|
i=1 |
Теперь задача поиска оптимальной стратегии стороны А может быть сформулирована как задача линейного программирования: определить неотрицательные значения переменных x1 ,x2 ,…,xm , доставляющие максимум целевой функции (67) и удовлетворяющие системе ограничений (66). Эта задача сводится к форме ОЗЛП с m свободными (в их качестве выступают исходные переменные задачи xi) и n базисными переменными:
139

|
m |
|||
|
q = −∑xi′′→ max ; |
|||
|
i=1 |
|||
|
x′j = xm+ j = −1 |
m |
||
|
+ ∑aij xi′′≥ 0 |
, i=1,2,…,n. |
(68) |
i=1
Матрица коэффициентов для данной задачи в соответствии с (44), (45) будет иметь вид
|
0 |
1 |
… |
1 |
|||||
|
−1 |
−a11 … |
−a1m |
. |
(69) |
||||
|
… |
… … |
… |
||||||
|
−1 |
−an1 … |
−anm |
Решение полученной задачи линейного программирования позволит найти V = –1/q и частоты, определяющие оптимальную смешанную стратегию стороны А: p*i =xi V, i=1,2,…,т.
Отметим, что дополнительно удается установить и полезные стратегии стороны В: для них переменные xm+j в решении ОЗЛП будут равны нулю, что соответствуют равенствам в (68) и в (63).
Теперь обратимся к неравенству (64) и условиям, которым подчиняются значения частот применения стороной В ее чистых
|
n |
|||
|
стратегий: |
0 |
≤ q j ≤1, j=1,2,…,n; ∑q j =1 |
. Введем новые пере- |
j=1
менные: u j = qi /V , j=1,2,…,n. С учетом qi ≥0 и V>0 на все переменные ui накладывается требование неотрицательности.
n
Разделим обе части уравнения ∑q j =1 и неравенств (64) на V
j=1
и учтя, что цель решения стратегической матричной игры для стороны В – нахождение таких значений частот qj, (и значений переменных uj), которые доставят стороне В наименьший средний проигрыш V, введем целевую функцию. Сведем задачу к форме ОЗЛП введением m дополнительных переменных:
|
n |
|||
|
q = −∑u′′j → min ; |
|||
|
i=1 |
|||
|
ui′ = un+i =1 |
n |
||
|
− ∑aiju′′j ≥ 0 |
, i=1,2,…,m. |
(70) |
j=1
140
Решение полученной задачи линейного программирования позволит найти V = –1/q и частоты, определяющие оптимальную смешанную стратегию стороны В: q*j =uj V, j=1,2,…,n. Нулевым значениям переменных xn+i будут соответствовать полезные стратегии стороны А.
Сопоставляя запись задачи (70) с матрицей (69), можно убедиться, что критерий оптимальности и ограничения здесь соответствуют столбцам матрицы, что аналогично связи задачи (46) с матрицей (45).
Таким образом, задача (70) является двойственной по отношению к задаче (68). Следовательно, для получения полного решения игровой задачи достаточно решить одну из получаемых задач линейного программирования. Например, после решения задачи (68), помимо цены игры V и оптимальной смешанной стратегии стороны А, может быть найдена и оптимальная стратегия стороны В – на основе коэффициентов первой строки полученного оптимального линейного плана.
Пример 39 (продолжение). Вернемся к примеру, решенному выше методом упрощения. Матрица игры представлена в табл. 33.
Составим для данной игры систему неравенств (63):
3p1 +8 p2 ≥V , 8 p1 +3p2 ≥V , 4 p1 + 6 p2 ≥V , 7 p1 + 5 p2 ≥V .
Введем, как это показано выше, целевую функцию, свободные и базисные переменные ОЗЛП:
x1 = p1 /V ≥ 0 , x2 = p2 /V ≥ 0 ; q = −1/V = −x1 − x2 → max ; 3x1 +8x2 ≥1 , 8x1 +3x2 ≥1 ,
|
4x1 +6x2 ≥1, 7x1 +5x2 ≥1 ; |
(71) |
x3 = −1+3x1 +8x2 ≥ 0 , x4 = −1+8x1 +3x2 ≥ 0 , x5 = −1 + 4x1 + 6x2 ≥ 0 ,
x6 = −1 + 7x1 + 5x2 ≥ 0 .
Исходный линейный план представлен в табл. 38. Решение задачи симплекс-методом отражено в табл. 39…41.
141
|
Таблица 38 |
||||||||||||
|
Базис |
1 |
—x1 |
—x2 |
|||||||||
|
q |
0 |
1 |
1 |
|||||||||
|
–1/3 |
1/3 |
–8/3 |
||||||||||
|
x3 |
-1 |
-3 |
-8 |
|||||||||
|
1/3 |
–1/3 |
8/3 |
||||||||||
|
x4 |
-1 |
-8 |
-3 |
|||||||||
|
8/3 |
–8/3 |
64/3 |
||||||||||
|
x5 |
-1 |
-4 |
-6 |
|||||||||
|
4/3 |
–4/3 |
32/3 |
||||||||||
|
x6 |
-1 |
-7 |
-5 |
|||||||||
|
7/3 |
–7/3 |
56/3 |
||||||||||
|
Таблица 39 |
||||||||||||
|
Базис |
1 |
—x3 |
—x2 |
|||||||||
|
q |
–1/3 |
1/3 |
–5/3 |
|||||||||
|
5/42 |
–10/21 |
5/14 |
||||||||||
|
x1 |
1/3 |
–1/3 |
8/3 |
|||||||||
|
–4/21 |
16/21 |
–4/7 |
||||||||||
|
x4 |
5/3 |
–8/3 |
55/3 |
|||||||||
|
–55/42 |
110/21 |
–55/14 |
||||||||||
|
x5 |
1/3 |
–4/3 |
14/3 |
|||||||||
|
1/14 |
–2/7 |
3/14 |
||||||||||
|
x6 |
4/3 |
–7/3 |
41/3 |
|||||||||
|
–41/42 |
82/21 |
–41/14 |
||||||||||
|
Таблица 40 |
||||||||||||
|
Базис |
1 |
—x3 |
—x5 |
|||||||||
|
q |
–3/14 |
–1/7 |
5/14 |
|||||||||
|
5/252 |
1/18 |
–55/252 |
||||||||||
|
x1 |
1/7 |
3/7 |
–4/7 |
|||||||||
|
–5/84 |
–1/6 |
55/84 |
||||||||||
|
x4 |
5/14 |
18/7 |
–55/14 |
|||||||||
|
5/36 |
7/18 |
–55/36 |
||||||||||
|
x2 |
1/14 |
–2/7 |
3/14 |
|||||||||
|
5/126 |
1/9 |
–55/126 |
||||||||||
|
x6 |
5/14 |
11/7 |
–41/14 |
|||||||||
|
–55/252 |
–11/18 |
605/252 |
||||||||||
142
|
Таблица 41 |
||||
|
Базис |
1 |
—x4 |
—x5 |
|
|
q |
–7/36 |
1/18 |
5/36 |
|
|
x1 |
1/12 |
–1/6 |
1/12 |
|
|
x3 |
5/36 |
7/18 |
–55/36 |
|
|
x2 |
1/9 |
1/9 |
–2/9 |
|
|
x6 |
5/36 |
–11/18 |
–19/36 |
|
|
В |
результате цена |
игры |
V = −1/ q = |
36 |
≈ 5,14 , оптимальные |
||||||
|
7 |
|||||||||||
|
частоты |
применения |
стратегий |
стороны |
А |
|||||||
|
p* = x V = |
1 |
36 ≈ 0,43 |
, p* = x V = 1 |
36 |
≈ 0,57 . |
||||||
|
1 |
1 |
12 |
7 |
2 |
2 |
9 |
7 |
Обратим внимание на то, что базисные переменные исходного плана (табл. 38) соответствуют столбцам матрицы игры (табл. 33),
|
а следовательно, |
чистым стратегиям стороны В: x3 → B1 , |
|
x4 → B2 , x5 → B3 , |
x6 → B4 . Решение ОЗЛП дает x4 =x5 =0 (сво- |
бодные переменные). Следовательно, неравенства, соответствующие В2 и В3 в системах (71) и (63) для рассматриваемой задачи обращаются в равенства, что является признаком полезных стратегий.
Учитывая же двойственность задач линейного программирования, получаемых на основе стратегической матричной игры, отметим, что для двойственной задачи на основе оптимального плана ОЗЛП (табл. 4 1) u1 =u4 =0, u2 =1/18, u3 =5/36. Остается рассчитать оптимальные частоты применения стратегий стороны
|
В: |
q |
* = u V =1/18 36 / 7 ≈ 0,29 , |
p* = x V =1/12 36 / 7 ≈ 0,43, |
||
|
2 |
2 |
1 |
1 |
||
|
q* = q* = 0 . |
|||||
|
1 |
4 |
Результаты совпадают с полученным выше решением рассматриваемого примера.
Следует также отметить, что исходный линейный план ОЗЛП, формируемый на соотношениях (63), может быть получен непосредственно на основе матрицы игры без представленных выше промежуточных преобразований. А именно:
143
−коэффициент на пересечении первых строки и столбца всегда равен нулю;
−все остальные коэффициенты первой строки равны едини-
це;
−все остальные коэффициенты первого столбца равны «–1»;
−в оставшиеся части строк, начиная со второй заносятся выигрыши из столбцов матрицы игры с противоположным знаком.
Если ОЗЛП формируется на основе соотношений (64), правила составления исходного плана будут следующими:
−коэффициент на пересечении первых строки и столбца всегда равен нулю;
−все остальные коэффициенты первой строки равны «-1»;
−все остальные коэффициенты первого столбца равны еди-
нице;
−в оставшиеся части строк, начиная со второй непосредственно заносится матрица игры.
Воспользуемся сформулированными правилами и рассмотрим другой представленный выше пример.
Пример 41 (продолжение). Матрица игры представлена в
табл. 37. Для метода линейного программирования обеспечим неотрицательность элементов матрицы. Минимальный выигрыш, содержащийся в матрице игры a23= –5. Вычитание его из всех элементов матрицы игры приводит к получению новой матрицы, представленной в табл. 42.
Таблица 42
|
Стратегия |
В1 |
В2 |
В3 |
α |
|
А1 |
7 |
2 |
9 |
2 |
|
А2 |
2 |
9 |
0 |
0 |
|
А3 |
9 |
0 |
11 |
0 |
|
β |
9 |
9 |
11 |
|
Используя неравенства (64), сведем данную игровую задачу к задаче линейного программирования. Исходный линейный план приведен в табл. 43. Решение задачи симплекс-методом отражено в табл. 44…46.
144
|
Таблица 43 |
||||||||||||||||||||||
|
Базис |
1 |
—u1 |
—u2 |
—u3 |
||||||||||||||||||
|
q |
0 |
1/9 |
-1 |
1/9 |
-1 |
0 |
-1 |
11/9 |
||||||||||||||
|
u4 |
1 |
7 |
2 |
9 |
||||||||||||||||||
|
–7/9 |
–7/9 |
0 |
–77/9 |
|||||||||||||||||||
|
u5 |
1 |
2 |
9 |
0 |
||||||||||||||||||
|
–2/9 |
–2/9 |
0 |
–22/9 |
|||||||||||||||||||
|
u6 |
1 |
1/9 |
9 |
1/9 |
0 |
0 |
11 |
11/9 |
||||||||||||||
|
Таблица 44 |
||||||||||||||||||||||
|
Базис |
1 |
—u6 |
—u2 |
—u3 |
||||||||||||||||||
|
q |
1/9 |
1/9 |
-1 |
2/9 |
||||||||||||||||||
|
7/81 |
–2/81 |
1/9 |
–22/81 |
|||||||||||||||||||
|
u4 |
2/9 |
–7/9 |
2 |
4/9 |
||||||||||||||||||
|
–14/81 |
4/81 |
–2/9 |
44/81 |
|||||||||||||||||||
|
u5 |
7/9 |
–2/9 |
9 |
–22/9 |
||||||||||||||||||
|
7/81 |
–2/81 |
1/9 |
–22/81 |
|||||||||||||||||||
|
u1 |
1/9 |
1/9 |
0 |
11/9 |
||||||||||||||||||
|
0 |
0 |
0 |
0 |
|||||||||||||||||||
|
Таблица 45 |
||||||||||||||||||||||
|
Базис |
1 |
—u6 |
—u5 |
—u3 |
||||||||||||||||||
|
q |
16/81 |
7/81 |
1/9 |
–4/81 |
||||||||||||||||||
|
1/405 |
–59/1620 |
–1/90 |
1/20 |
|||||||||||||||||||
|
u4 |
4/81 |
–59/81 |
–2/9 |
80/81 |
||||||||||||||||||
|
1/20 |
–59/80 |
–9/40 |
81/80 |
|||||||||||||||||||
|
u2 |
7/81 |
–2/81 |
1/9 |
–22/81 |
||||||||||||||||||
|
11/810 |
–649/3240 |
–11/180 |
11/40 |
|||||||||||||||||||
|
u1 |
1/9 |
1/9 |
0 |
11/9 |
||||||||||||||||||
|
–11/180 |
649/720 |
11/40 |
–99/80 |
|||||||||||||||||||
|
Таблица 46 |
||||||||||||||||||||||
|
Базис |
1 |
—u6 |
—u5 |
—u4 |
||||||||||||||||||
|
q |
1/5 |
1/20 |
1/10 |
1/20 |
||||||||||||||||||
|
u3 |
1/20 |
–59/80 |
–9/40 |
81/80 |
||||||||||||||||||
|
u2 |
1/10 |
–9/40 |
1/20 |
11/40 |
||||||||||||||||||
|
u1 |
1/20 |
81/80 |
11/40 |
–99/80 |
||||||||||||||||||
145
Соседние файлы в папке metods
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т.е. отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих процессах выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т.д.). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» или математические методы исследования операций.
Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же относят и стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.
Математическое программирование — это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных, при наличии ограничений на переменные.
Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразования, транспортные задачи и т.д.
Построение математической модели экономической задачи включает следующие этапы:
- выбор переменных задачи;
- составление системы ограничений;
- выбор целевой функции.
Переменными задачи называются величины
Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т.п.
Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.
Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции: 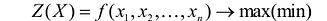
Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования и в общем виде может быть записана следующим образом:
Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные X = (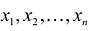
Допустимым решением (планом) задачи линейного программирования называется любойX = (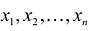
Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума.
Задача линейного программирования
В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:
Используя знак суммирования эту задачу можно записать следующим образом:
Каноническая задача линейного программирования в векторной форме имеет вид:
В данном случае введены векторы:
Здесь С — X — скалярное произведение векторов С и X.
Каноническая задача линейного программирования в матричной форме записи имеет вид:
где:
Здесь А — матрица коэффициентов системы уравнений, X -матрица-столбец переменных задачи; 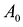
Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:
Приведение общей задачи линейного программирования к канонической форме
В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:
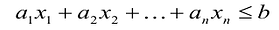
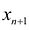
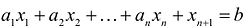
Неотрицательная переменная 
Основания для возможности такого преобразования дает следующая теорема.
Теорема. Каждому решению 
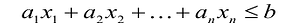
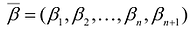
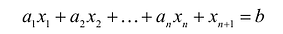
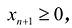

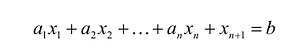

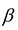
Доказательство. Пусть 
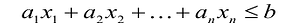
Если в уравнение 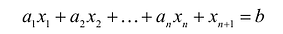
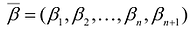
Таким образом, решение 
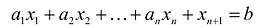

Доказана первая часть теоремы.
Пусть 
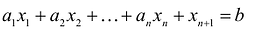

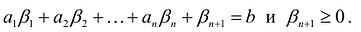
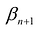
т.е. 
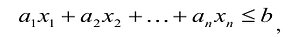
Если в левую часть неравенств системы ограничений вида
добавить переменную 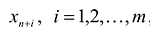
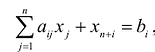
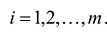
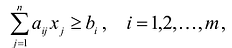
Полученная таким образом система уравнений-ограничений, вместе с условиями неотрицательности переменных, т.е. 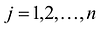
Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.
В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах 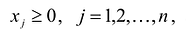
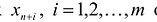
Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.
Множества допустимых решений
Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит их произвольную выпуклую линейную комбинацию.
Выпуклой линейной комбинацией произвольных точек 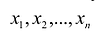
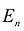
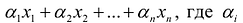
Геометрически это означает, что если множеству с любыми двумя его произвольными точками полностью принадлежит и отрезок, соединяющий эти точки, то оно будет выпуклым. Например, выпуклыми множествами являются прямолинейный отрезок, прямая, круг, шар, куб, полуплоскость, полупространство и др.
Точка множества называется граничной, если любая окрестность этой точки сколь угодно малого размера содержит точки, как принадлежащие множеству, так и не принадлежащие ему.
Граничные точки множества образуют его границу. Множество называется замкнутым, если оно содержит все свои граничные точки.
Ограниченным называется множество, если существует шар с радиусом конечной длины и центром в любой точке множества, содержащий полностью в себе данное множество. В противном случае множество будет неограниченным.
Пересечение двух или более выпуклых множеств будет выпуклым множеством, так как оно отвечает определению выпуклого множества.
Точка выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации двух других различных точек этого множества.
Так, угловые точки треугольника — его вершины, круга — точки окружности, ее ограничивающие, а прямая, полуплоскость, плоскость, полупространство, пространство не имеют угловых точек.
Выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек, называется выпуклым многоугольником, а замкнутое выпуклое ограниченное множество в трехмерном пространстве, имеющее конечное число угловых точек, называется выпуклым многогранником.
Теорема. Любая тонка многоугольника является выпуклой линейной комбинацией его угловых точек.
Теорема. Область допустимых решений задачи линейного программирования является выпуклым множеством.
Уравнение целевой функции при фиксированных значениях самой функции является уравнением прямой линии (плоскости, гиперплоскости и т.д.). Прямая, уравнение которой получено из целевой функции при равенстве ее постоянной величине, называется линией уровня.
Линия уровня, имеющая общие точки с областью допустимых решений и расположенная так, что область допустимых решений находится целиком в одной из полуплоскостей, называется опорной прямой.
Теорема. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали и убывают при перемещении в противоположном направлении.
Теорема. Целевая функция задачи линейного программирования достигает экстремума в угловой точке области допустимых решений; причем, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, она также достигает экстремума в любой выпуклой комбинации этих точек.
Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками
Каноническая задача линейного программирования в векторной форме имеет вид:
Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.
Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное 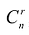
Опорным решением задачи линейного программирования называется такое допустимое решение 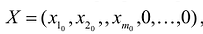
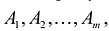
Число отличных от нуля координат опорного решения не может превосходить ранга r системы векторов условий (т.е. числа линейно независимых уравнений системы ограничений).
Если число отличных от нуля координат опорного решения равно m, то такое решение называется невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше т, такое решение называется вырожденным.
Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.
Теорема. Любое опорное решение является угловой точкой области допустимых решений.
Теорема. Любая угловая точка области допустимых решений является опорным решением.
Пример:
Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при n = 2.
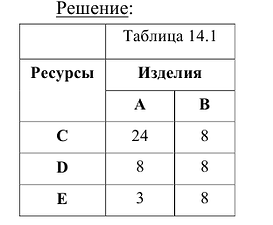
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1
Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В — 50 млн.руб. Требуется найти объемы производства изделий А и В, обеспечивающие максимальную прибыль.
Построим математическую модель задачи, для чего обозначим 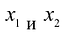
Тогда прибыль предприятия от реализации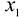
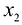
Ограничения по ресурсам будут иметь вид:
Естественно, объемы производства должны быть неотрицательными
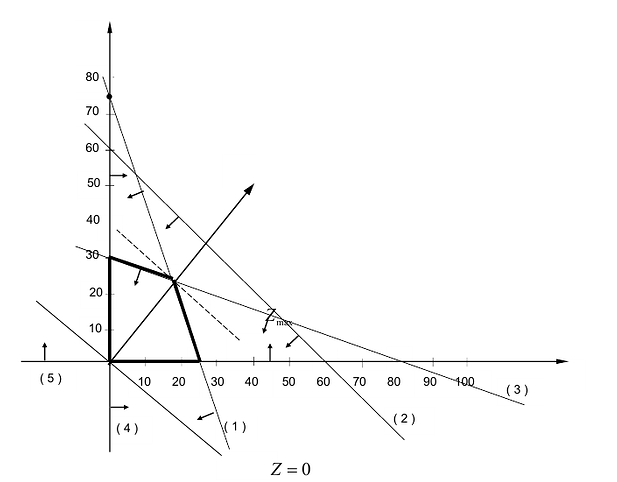
Решение сформулированной задами найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:
Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.
Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: 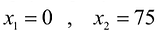
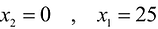
Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку O(0,0) подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка O(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой
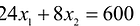
Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям 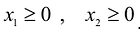
Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т.е. моговариантпа. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.
Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор-градиент прямой функции
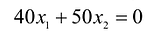
Рис. 14.1
Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.
Решив эту систему, получаем, что
Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:
Алгоритм решения задачи линейного программирования графическим методом таков:
- Строится область допустимых решений;
- Строится вектор нормали к линии уровня с точкой приложении в начале координат;
- Перпендикулярно вектору нормали проводится одна из линий уровня, проходящая через начало координат;
- Линия уровня перемещается до положения опорной прямой. На этой прямой и будут находиться максимум или минимум функции.
В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.
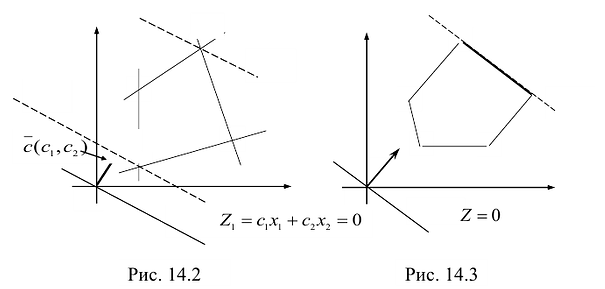
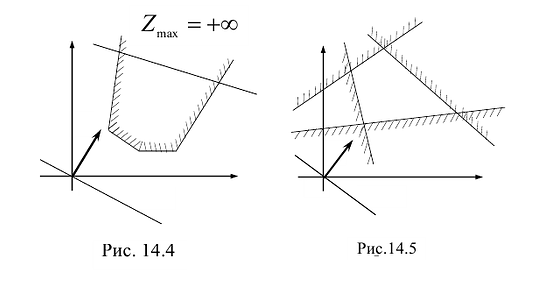
На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции Z достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т.к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.
На рисунке 14.4 изображен случай, когда система ограничений образует неограниченное сверху множество. Функция Z в данном случае стремится к бесконечности, так как прямую функции можно передвигать в направлении вектора градиента как угодно далеко, а на рисунке 14.5 представлен случай несовместной системы ограничений.
Основные понятия симплексного метода решения задачи линейного программирования.
Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж.Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.
Симплекс-метод основан на следующих свойствах задачи линейного программирования:
- Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
- Множество всех планов задачи линейного программирования выпукло.
- Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
- Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.
Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).
- Заказать решение задач по высшей математике
Симплекс-метод с естественным базисом
Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью mхm. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).
Для определенности предположим, что первые m векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план:
Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.
Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.
Признак оптимальности заключается в следующих двух теоремах.
Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:
то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:
- если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
- если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.
Теорема 2. Если для всех векторов выполняется условие 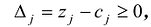
На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс-разности:
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор 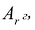
Строка 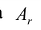
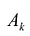
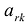
Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:
а элементы любой другой i-й строки пересчитываются по формулам:
Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:
Если наименьшее значение Q достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.
Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение Q на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.
Для использования приведенной выше процедуры симплекс -метода к минимизации линейной формы 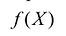
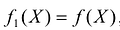
Симплексный метод с искусственным базисом (М-метод)
Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.
М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М — достаточно большое положительное число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки А, теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М — достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения M-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.
Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.
Теория двойственности
Любой задаче линейного программирования можно сопоставить сопряженную или двойственную ей задачу. Причем, совместное исследование этих задач дает, как правило, значительно больше информации, чем исследование каждой из них в отдельности.
Любую задачу линейного программирования можно записать в виде:
Первоначальная задача называется исходной или прямой.
Модель двойственной задачи имеет вид:
Переменные двойственной задачи 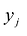
Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.
Двойственная задача по отношению к исходной составляется согласно следующим правилам:
- Целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи — на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид <, а в задаче на минимум — вид
- Матрица
, составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица
, в двойственной задаче получаются друг из друга транспонированием;
- Число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи — числу переменных в исходной задаче;
- Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи — коэффициенты при неизвестных в целевой функции исходной задачи;
- Каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства <, соответствует переменная, связанная условием неотрицательности.
Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.
Математические модели пары двойственных задач могут быть симметричными и несимметричными. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной — в виде неравенств, причем переменные в двойственной задаче могут быть и отрицательными. В симметричных двойственных задачах система ограничений как исходной, так и двойственной задачи задается в виде неравенств, причем на двойственные переменные налагается условие неотрицательности.
где:
Рассмотрим пример, показывающий, как в реальной экономической ситуации появляются взаимно двойственные задачи линейного программирования.
На некотором предприятии после выполнения годового плана возник вопрос: как поступить с остатками сырья? Из оставшегося сырья можно наладить производство продукции и реализовать его или продать сырье.
Предположим, что имеется два вида сырья 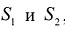
При исследовании первой возможности (наладить выпуск товаров 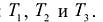
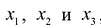
Прибыль, которую получит предприятие от реализации товара, составит:
В интересах предприятия эту прибыль максимизировать.
Это прямая задача.
Объективно обусловленными оценками двойственной задачи 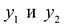
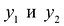
Справедливое требование со стороны продающего предприятия состоит в следующем: если взять сырье, идущее на производство единицы товара 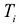
Это требование можно представить в виде системы неравенств:
В левой части каждого неравенства предполагаемая выручка от продажи сырья, необходимого для производства единицы товара 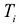
Что касается покупателя, то он заинтересован в минимизации расходов на покупку сырья, т.е. величины
Теоремы двойственности
Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач: можно либо найти оптимальное решение другой задачи, не решая ее, либо установить его отсутствие.
Возможны следующие случаи:
- обе задачи из пары двойственных имеют оптимальные решения;
- одна из задач не имеет решения ввиду неограниченности целевой функции, а другая — ввиду несовместности системы ограничений.
Первая теорема двойственности.
Для двойственных задач линейного программирования имеет место один из взаимоисключающих случаев:
- В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают:
- В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.
- В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым;
- Обе из рассматриваемых задач имеют пустые допустимые множества.
Вторая теорема двойственностн (теорема о дополняющей нежесткости):
Пусть 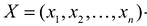
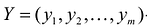
Для того, чтобы они были оптимальными решениями соответствующих взаимодвойственных задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:
Эти условия устанавливают связь между оптимальными значениями прямой и двойственной задач и позволяют, зная решение одной из них, находить решение другой задачи.
Теорема об оценках:
Значения переменных 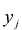
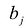
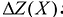
Диапазон изменения компонент вектора В, в котором сохраняется оптимальный базис, называется областью устойчивости оптимальных оценок.
Экономический смысл первой теоремы двойственности следующий. План производства X и набор ресурсов Y оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции 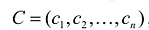
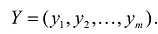
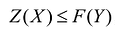
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Пространство R»
- Неопределённый интеграл
- Линейный оператор — свойства и определение
- Многочлен — виды, определение с примерами
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами

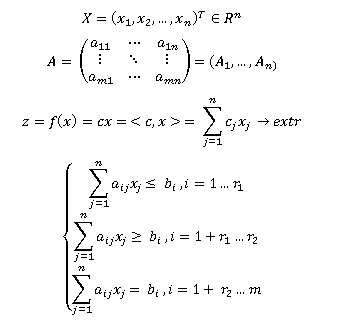
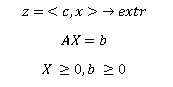
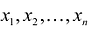
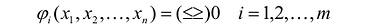
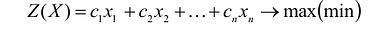
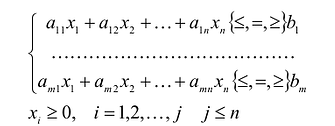
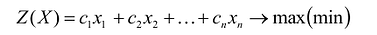
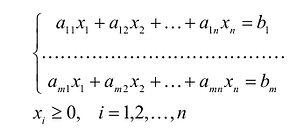
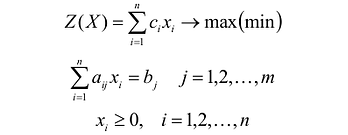
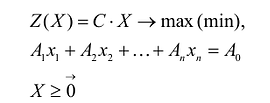
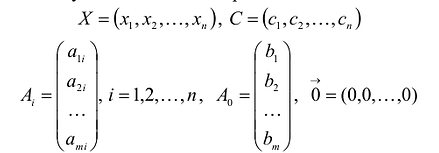
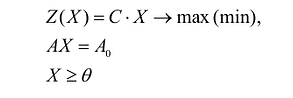
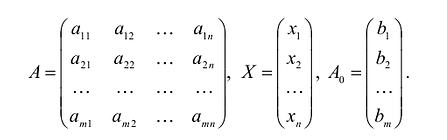
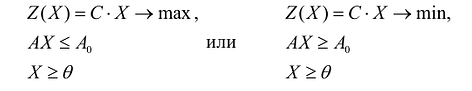
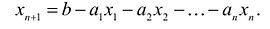
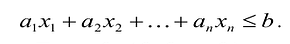
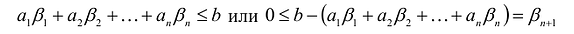
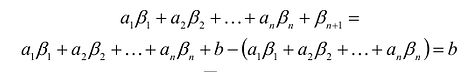
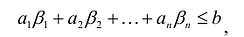
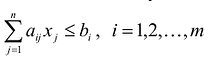
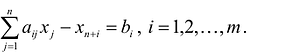
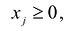
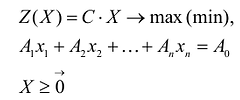
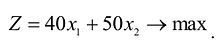
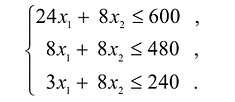
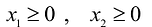
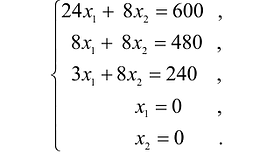
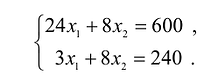
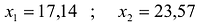
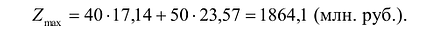
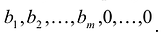
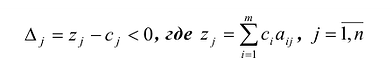
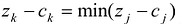
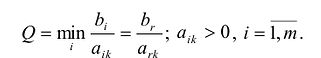
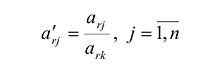
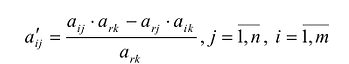
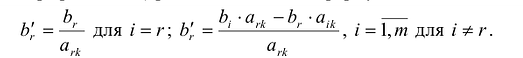
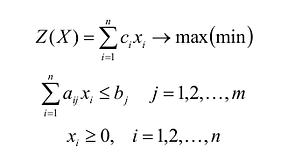
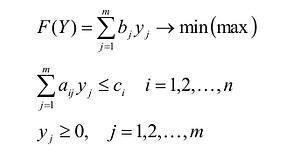
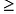
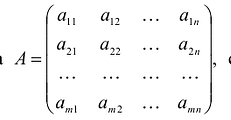 , составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица
, составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица 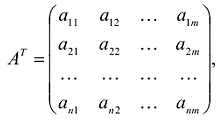 , в двойственной задаче получаются друг из друга транспонированием;
, в двойственной задаче получаются друг из друга транспонированием;