В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Введение в графический метод
Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно.
Возможно эта страница вам будет полезна:
Задача линейного программирования в стандартной форме с двумя переменными имеет вид:
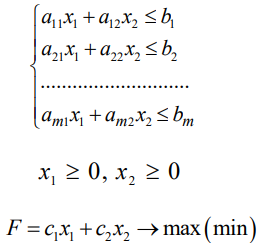
Эти задачи допускают простое геометрическое истолкование.
Рассмотрим вначале геометрическое истолкование системы ограничений задачи. Каждую совокупность значений переменных 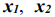


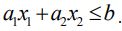
Рассмотрим прямую на плоскости с уравнением:
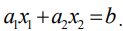
Эта прямая делит плоскость на две полуплоскости, в одной из которых справедливо наше неравенство, а в другой — противоположное. Для того чтобы проверить, какая из полуплоскостей состоит из решений нашего неравенства, следует взять точку из какой-либо полуплоскости и проверить, выполняется ли наше неравенство в этой точке. Множество решений отдельно взятого линейного неравенства представляет собой полуплоскость. Для системы из нескольких таких неравенств точки, координаты которых удовлетворяют всем неравенствам одновременно, должны находиться во всех соответствующих полуплоскостях, т. е. принадлежать теоретико-множественному пересечению этих полуплоскостей. Множество точек на плоскости, удовлетворяющих системе ограничений, составляет, таким образом, некоторую выпуклую многоугольную область (область допустимых решений). Условия неотрицательности переменных 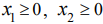
При решении двумерных задач линейного программирования возможны следующие ситуации (ОДР — область допустимых решений):
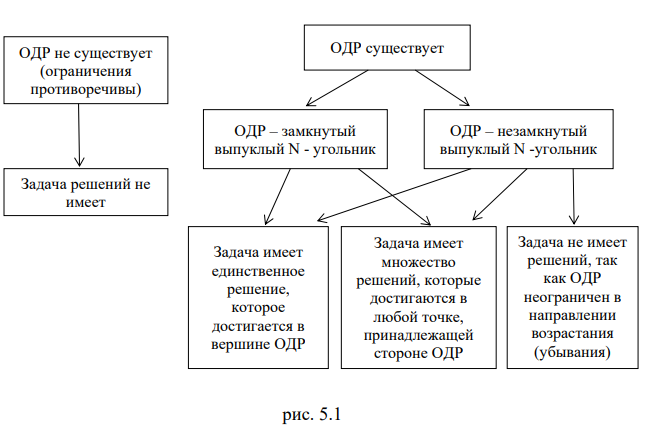
Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция 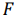
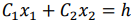
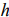
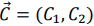
Отметим, что при нахождении решения задачи (5.1)-(5.3) могут встретиться случаи, изображенные на рис. 5.2- 5.5. Рис.5.2 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке 
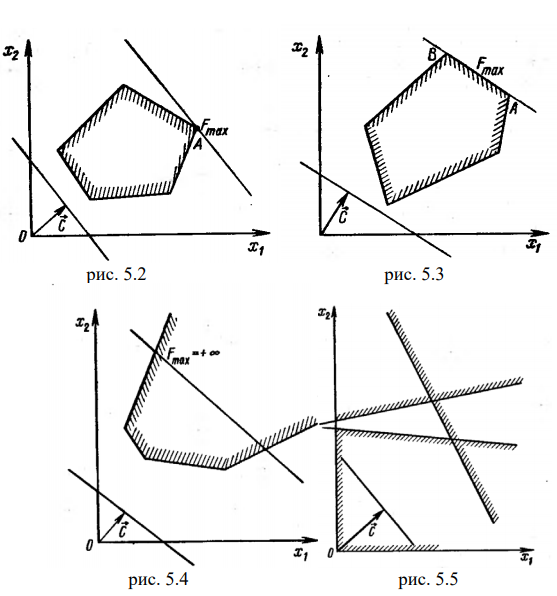
Также отметим, что нахождение минимального значения линейной функции при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня 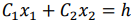
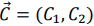
Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
Алгоритм графического метода решении задач линейного программирования
- Построить область допустимых решений.
- Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений.
- Если область допустимых решений является непустым множеством, построить нормаль линий уровня
и одну из линий уровня, имеющую общие точки с этой областью.
- Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум — в противоположном направлении.
- Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.
- Если задача линейного программирования имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычислить значение целевой функции на этих решениях.
Пример задачи №1
Пусть имеется два станка 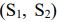
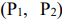
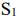

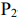
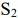

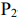
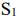
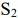

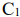
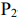
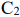

Решение:
Для наглядности сведем условие задачи в таблицу 5.1.
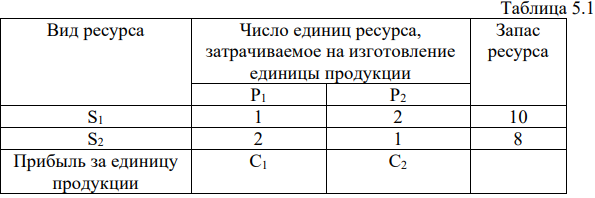
Составим математическую модель задачи. Обозначим через 


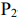
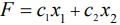


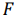
Переменные 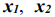

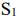
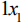
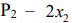
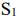


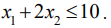
Аналогично можно получить неравенство для станка 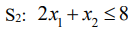


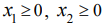
по смыслу задачи. Такие задачи кратко записываются следующим образом:
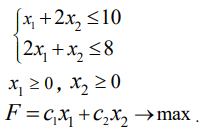
Итак, математическая модель задачи: найти такой план выпуска продукции 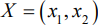
Решения, удовлетворяющие системе ограничений (5.4) и требованиям неотрицательности (5.5), являются допустимыми, а решения, удовлетворяющие одновременно и требованию (5.6) — оптимальными.
Рассмотрим геометрическое истолкование задачи:
Возьмем 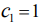
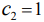
Математическая модель задачи:
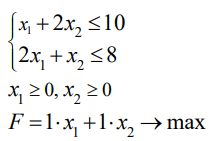
Построение области допустимых решений целевой функции 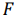
1.Построим прямоугольную систему координат. Так как, 

Рассмотрим первое ограничение:
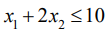
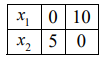
Рассмотрим второе ограничение:
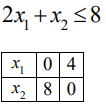
Отложим полученные точки на числовых осях и найдем полуплоскости, которые соответствуют данным ограничениям.
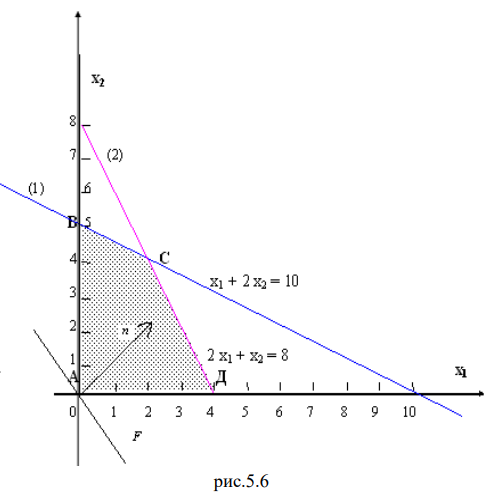
Двумерные задачи линейного программирования решаются графически.
Для случая 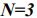
В общем виде, когда в задаче участвуют 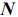
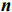
Для решения ЗЛП любой размерности существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.
Графический метод решения задач линейного программирования
Множество решений системы ограничений задачи ЛП образует область допустимых решений (ОДР).
Графический метод решения задач ЛП основывается на возможности графического изображения ОДР и нахождении среди них оптимального решения. Этот метод применяется для задач ЛП с одной, двумя или тремя переменными, для которых система ограничений стандартна (состоит из неравенств), и задач со многими переменными, для которых система ограничений содержит 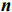
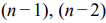
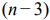
ОДР задачи строится как пересечение областей решений каждого из ограничений и представляет собой выпуклый многогранник (многоугольник, интервал). Область допустимых решений может содержать бесконечное число точек. Для того чтобы найти решение ЗЛП, нужно рассмотреть поведение целевой функции в ОДР.
I. Одномерное пространство переменных
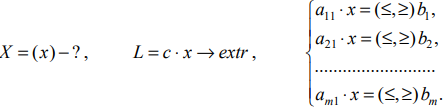
Решение системы ограничений есть пересечение лучей, что определяет интервал решений (ОДР): точку, отрезок, луч или всю числовую прямую.
Значения целевой функции в угловых точках интервала решений определяют наименьшее (наибольшее) значение исследуемой целевой функции, монотонно убывающей (если 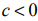
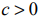
В случае неограниченности ОДР задача ЛП может и не иметь оптимума.
II. Двумерное пространство переменных
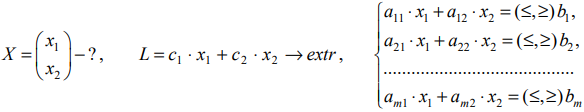
Областью решений линейного неравенства
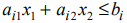
является одна из полуплоскостей, на которые прямая делит всю координатную плоскость. Для того, чтобы определить, какая из двух координатных полуплоскостей является областью допустимых решений неравенства, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство: если оно удовлетворяется, то областью решений является полуплоскость, содержащая данную точку; если же неравенство не удовлетворяется, то областью решений является полуплоскость, не содержащая данную точку.
Решение системы ограничений есть пересечение полуплоскостей с граничными прямыми
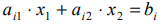
многоугольник решений (ОДР).
Линией уровня называется прямая, на которой целевая функция задачи принимает постоянное значение. Уравнение
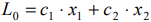
задаёт семейство линий уровня исследуемой целевой функции 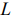
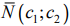
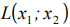
Замечание.
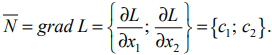
Т. о., если линию уровня 


• Прямая
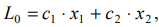
имеющая с многоугольником решений, расположенным по одну сторону от неё, хотя бы одну общую точку, называется опорной. ОДР любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение.
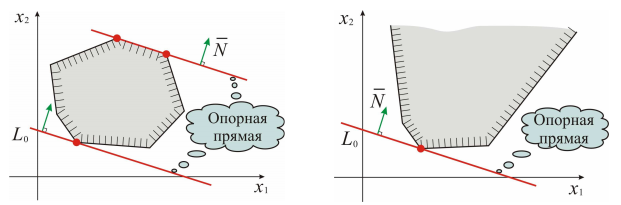
Значение 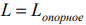
Графически опорная прямая определяет оптимум целевой функции в угловой точке многоугольника решений. Поэтому перебором значений целевой функции во всех угловых точках можно так же выбрать искомый оптимум.
Замечание. Если заданы ограничения неотрицательности переменных, то все построения проводятся в первой четверти.
Особые случаи

Алгоритм графического метода решения задач линейного программирования с двумя переменными
- Находим область допустимых решений из системы ограничений. Если ОДР является пустым множеством, то задача ЛП неразрешима (не имеет решения) в виду несовместности системы ограничений.
- Если область допустимых решений является непустым множеством, строим направляющий вектор
прямой
и параллельно ему проводим линию уровня
.
- Строим вектор нормали
перпендикулярно прямой
.
- Линию уровня
перемещаем до положения опорной прямой в направлении вектора
для задач на максимум или в направлении, противоположном
для задач на минимум. Т. е. перемещение проводится до тех пор, пока линия уровня не коснется области допустимых решений. Общая точка (точки) будет точкой экстремума (оптимума) целевой функции в ОДР.
- Находим координаты точки экстремума и значение целевой функции в ней, т. е. оптимум задачи ЛП.
Пример задачи №2
Найти 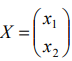
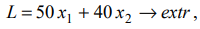
если имеются ограничения:
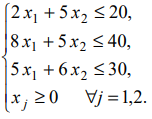
Решение:
Система ограничений определяет граничные прямые:
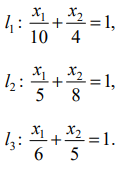
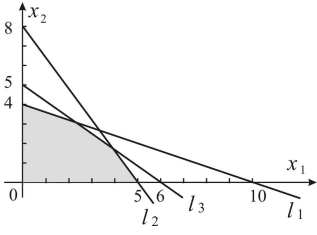
С учётом исходной системы неравенств строим ОДР.
Прямая
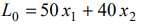
имеет вектор нормали 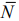
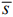
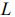
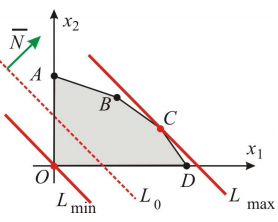
Т. о. имеем:
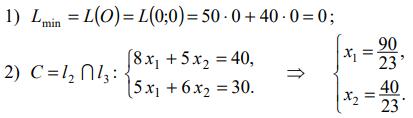
Тогда
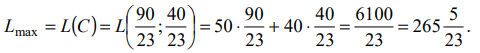
Ответ:
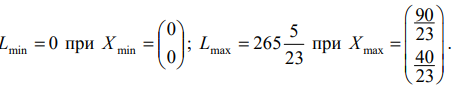
Пример задачи №3
Найти план
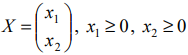
при котором:
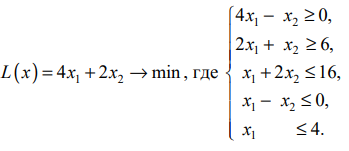
Решение:
Строим ОДР, проводим линии уровня 
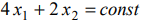
и вектор 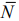
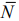
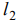
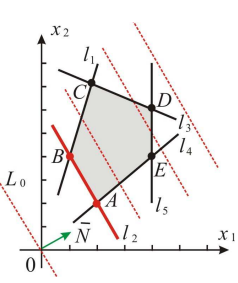
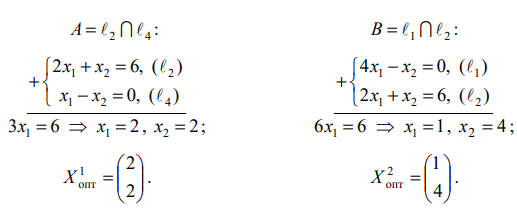
Общее решение (выпуклая линейная комбинация точек отрезка 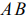
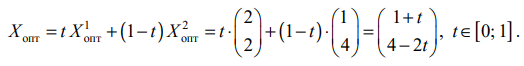
Вычисляем
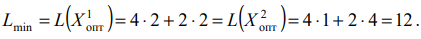
Ответ:
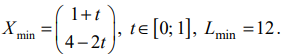
Пример задачи №4
Найти план
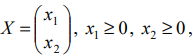
при котором
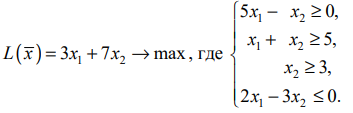
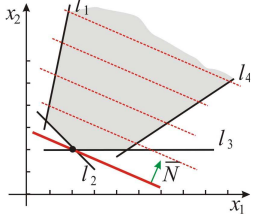
Решение:
Строим ОДР, проводим линию уровня 
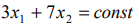
и вектор 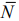
Таким образом, задача ЛП не имеет решения в виду неограниченности целевой функции.
Пример задачи №5
Найти план
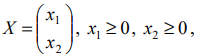
при котором
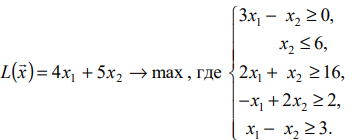
Решение:
Строим прямые линии, соответствующие неравенствам системы ограничений и находим полуплоскости, являющиеся областями решений этих неравенств. Область допустимых решений задачи является пустым множеством. Задача не имеет решения в виду несовместности системы ограничений.
III. Трёхмерное пространство переменных
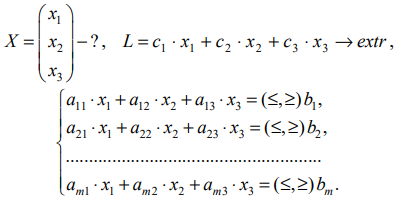
Решение системы ограничений — многогранник решений (ОДР) — пересечение полупространств с граничными плоскостями
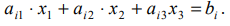
Уравнение
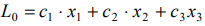
задаёт семейство поверхностей уровня функции 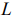
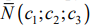
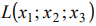
Плоскость
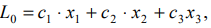
имеющая с многогранником решений, расположенным по одну сторону от нее, хотя бы одну общую точку, называется опорной. Значение 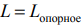
Графический метод в виду большой размерности реальных практических задач ЛП достаточно редко применяется, однако он позволяет уяснить одно из основных свойств ЛП- если в задаче ЛП существует оптимальное решение, то, по крайней мере, одна из вершин допустимой области определяет собой оптимальное решение.
IV. С помощью графического метода может быть решена основная ЗЛП, система ограничений (уравнений) которой удовлетворяет условию 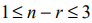
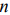
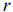
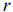
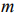
Основной случай: система ограничений содержит 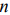
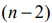
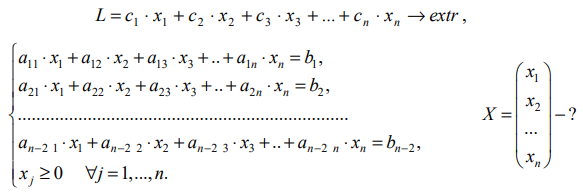
Расширенную матрицу системы с помощью элементарных преобразований строк можно привести к виду:
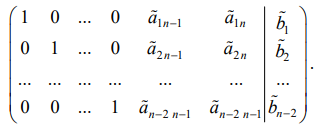
Тогда соответствующая система уравнений примет вид:
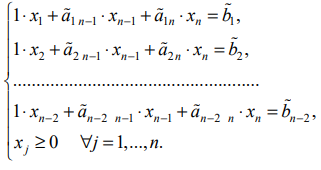
Выражая базисные неизвестные 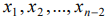
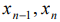
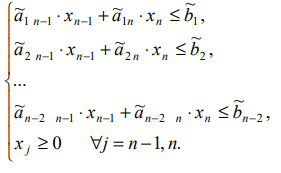
Подставляя полученные выражения для базисных неизвестных в целевую функцию, получим:
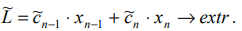
Преобразованная задача ЛП содержит только два неизвестных. Следовательно, возможен графический способ её решения на плоскости.
Найденное решение 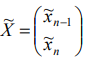
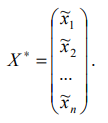
При этом оптимум:
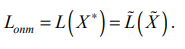
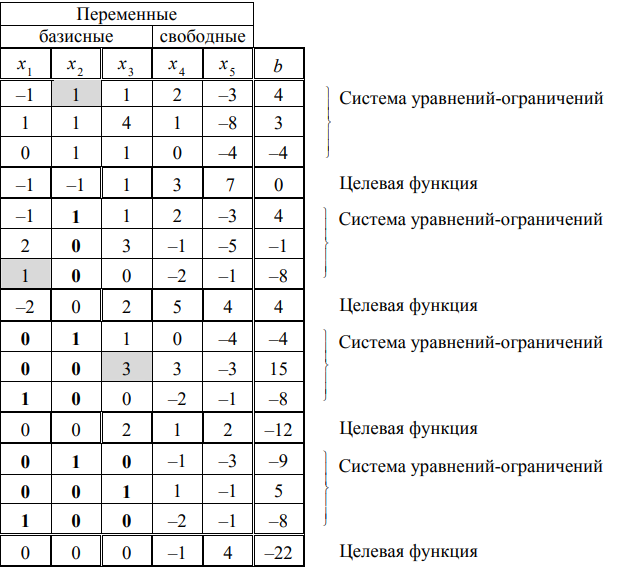
Пример. Решить задачу ЛП:
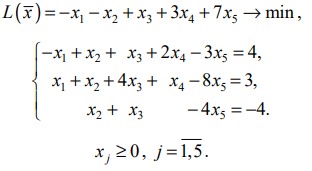
Решение. Метод применим,так как 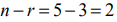
Используя последнюю часть табл., запишем задачу ЛП в преобразованном виде:
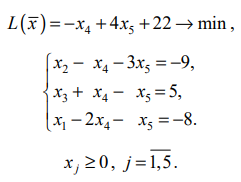
Отбросим в уравнениях-ограничениях неотрицательные базисные переменные 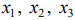
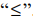
Получим вспомогательную задачу ЛП с двумя переменными:

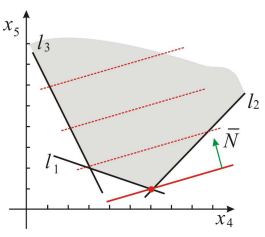
Решаем задачу графическим методом. Свободный член 22 в целевой функции не влияет на отыскание оптимального решения и учитывается только при вычислении значения целевой функции.
Находим оптимальное решение вспомогательной задачи 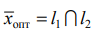
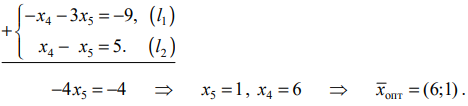
Вычисляем минимальное значение целевой функции
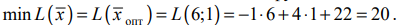
Находим оптимальное решение исходной задачи:
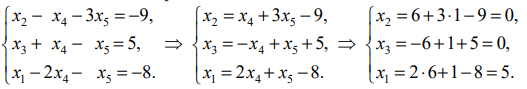
Т. о., получаем:
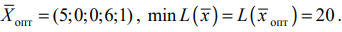
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюЛинейное программирование в ExcelКурсовая работа по линейному программированию
Графический метод решения задачи линейного программирования.
В
линейном программировании используется
графический метод, с помощью которого
определяют выпуклые множества
(многогранник решений). Если основная
задача линейного программирования
имеет оптимальный план, то целевая
функция принимает значение в одной из
вершин многогранника решений (см.
рисунок).
-
На
плоскости X10X2 строят
прямые. -
Определяются
полуплоскости. -
Определяют
многоугольник решений; -
Строят
вектор N(c1,c2),
который указывает направление целевой
функции; -
Передвигают
прямую целевую функцию c1x2 +
c2x2 =
0 в направлении вектора N до крайней
точки многоугольника решений.
Вычисляют
координаты точки и значение целевой
функции в этой точке.
Алгоритмический метод.
Для
усвоения симплексного метода, а также
других алгоритмов, рассмотренных в
последующих главах, полезно иметь
представление о некоторых основных
моментах, учитываемых при использовании
любой вычислительной процедуры. Оценивая
тот или иной вычислительный алгоритм,
необходимо, в частности, рассмотреть
следующие его характеристики:
Рассмотренные
выше методы служат для сбора информации
о субъекте труда или профессиональной
среде. Вместе с тем существует ряд
методов упорядочения полученной
информации. Одним из таких методов
является алгоритмический анализ. Алгоритм —
строгая последовательность действий,
которая неизбежно приводит к решению
задачи определенного класса. Эта
последовательность действий может
иметь словесное описание, в котором
представлены все элементарные действия
и логические условия, определяющие
порядок этих действий, а может быть
описана в символической форме или в
виде графика. Метод дает возможность
представить совокупность действий в
компактной форме и понять их закономерные
связи. Благодаря своей полноценности,
конкретности и систематичности алгоритмы
позволяют постепенно проследить характер
операций, выполняемых работниками, и
установить те звенья процесса, в которых
наиболее часты аварии и брак и которые
необходимо рационализировать или
автоматизировать в первую очередь, либо
функции, требующие перераспределения
или изменения.
Существуют
также возможности применения
алгоритмического подхода при изучении
и распространении передового опыта, в
процессе обучения рабочих и повышения
их квалификации на производстве, для
оценки рациональности размещения
оборудования, для повышения качества
нормирования труда и т. д.
Введение в симплексный алгоритм.
Для
решения задач линейного программирования
предложено немало различных алгоритмов.
Однако наиболее эффективным среди них
оказался алгоритм, рассмотренный ниже.
При этом следует подчеркнуть, что при
решении некоторых частных задач (как,
например, задач, связанных с оптимизацией
потоков в сетях) могут оказаться более
эффективными другие алгоритмы.
Попытаемся ход рассуждений, который
был в каком-то разделе учебника выше,
описать словесно. Упомянутая модель
содержит два уравнения. Пробные решения
выбирались следующим образом: допускалось,
что две переменные принимают
некоторые положительные значения, а
остальные переменные предполагались
тождественно равными нулю. Стремясь к
обобщению, можно предположить, что
в тех случаях, когда модель содержит т
уравнений, для построения пробных
решений используются т переменных,
принимающих некоторые положительные
значения при нулевых значениях остальных
переменных. Вначале допустим, что решение
существует, причем оптимальное значение
целевой функции конечно ). В этом
случае вычислительная процедура будет
выглядеть следующим образом:
Шаг 1. Выберем
т переменных,
задающих допустимое пробное решение.
Исключим эти переменные из выражения
для целевой функции.
Шаг 2. Проверим, нельзя ли за счет
одной из переменных, приравненной
вначале к нулю, улучшить значение целевой
функции, придавая ей отличные от нуля
(причем положительные) значения. Если
это возможно, перейдем к шагу 3. В противном
случае прекратим вычисления.
Шаг 3. Найдем
предельное значение переменной, за счет
которой можно улучшить значение
целевой функции. Увеличение значения
этой переменной
допустимо до тех пор, пока одна из т
переменных,
вошедших в пробное решение, не обратится
в нуль. Исключим из выражения для
целевой функции только что упомянутую
переменную и введем
в пробное решение ту переменную, за счет
которой результат может быть улучшен.
Шаг 4. Разрешим
систему т
уравнений
относительно переменных, вошедших
в новое пробное решение. Исключим эти
переменные из выражения для целевой
функции. Вернемся к шагу 2.
Важно отметить, что
при однозначном понимании данного
предписания предложенный алгоритм
действительно приводит к оптимальному
решению для любой модели линейного
программирования за конечное число
итераций. Такой способ решения задач
линейного программирования часто
называют симплексным алгоритмом.
Обратимся вначале к одной простой
задаче, не имеющей никаких «аномалий»,
и попытаемся с ее помощью получить общее
представление о симплексном методе.
К более подробному анализу данного
метода вернемся несколько позже.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Графический способ решения производственной задачи
Условие
Сначала запишем условие производственной задачи из предыдущей главы:
| Ресурс | Изделие A | Изделие B | Сколько ресурса на складах |
| R1 | 1 | 3 | 15 |
| R2 | 2 | 1 | 20 |
| R3 | 3 | 2 | 35 |
| Прибыль | 5 | 10 |
У нас получилась система ограничений и целевая функция следующего вида:
$$begin{array}{l}
left{ {begin{array}{*{20}{c}}
{{x_A} + 3{x_B} le 15}\
{2{x_A} + {x_B} le 20}\
{3{x_A} + 2{x_B} le 35}
end{array}} right.\
{x_A},{x_B} ge 0\
F({x_A},{x_B}) = 5{x_A} + 10{x_B} to max
end{array}$$
Лучшее спасибо — порекомендовать эту страницу
Строим область допустимых решений
Чтобы решить данную задачу линейного программирования графическим методом, необходимо
сначала превратить (мысленно) все неравенства в равенства, и на время забыть про целевую
функцию. То есть, получить следующую систему:
$$left{ {begin{array}{*{20}{c}}
{{x_A} + 3{x_B} = 15}\
{2{x_A} + {x_B} = 20}\
{3{x_A} + 2{x_B} = 35}\
{{x_A} = 0}\
{{x_B} = 0}
end{array}} right.$$
Мы получили пять уравнений с двумя переменными, следовательно, мы можем построить
их графики. Например, мы можем направить ось с переменной $x_A$ вправо (где обычно у нас
ось абсцисс) и ось с переменной $x_B$ вверх (где обычно у нас ось ординат). Для построения
графиков нужно лишь выразить из этих уравнений $x_B$. Сделаем это:
$$left{ {begin{array}{*{20}{c}}
{3{x_B} = 15 — {x_A}}\
{{x_B} = 20 — 2{x_A}}\
{2{x_B} = 35 — 3{x_A}}\
{{x_A} = 0}\
{{x_B} = 0}
end{array}} right.$$
$$left{ {begin{array}{*{20}{c}}
{{x_B} = 5 — frac{1}{3}{x_A}}\
{{x_B} = 20 — 2{x_A}}\
{{x_B} = 17,5 — 1,5{x_A}}\
{{x_A} = 0}\
{{x_B} = 0}
end{array}} right.$$
Прежде чем строить графики, разберемся с последними двумя уравнениями, $x_A=0$ и
$x_B=0$. Эти уравнения выражают сами оси — абсцисс и ординат. А так как в исходных
ограничениях были неравенства $x_Ageq0$ и $x_Bgeq0$, то точка нашего решения должна
быть правее и выше, чем эти оси — то есть, находиться в первой четверти. Поэтому эти
две линии можно не строить, а просто учитывать, что решение в первой четверти.
Остальные линии мы построим на графике, и получим следующую картину (естественно,
на нормальном графике не нужно рисовать такие стрелки, они лишь для наглядности,
чтобы не перепутать линии друг с другом):
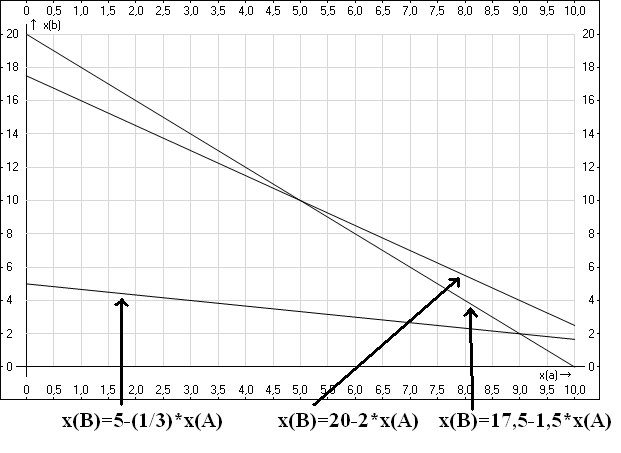
Каждая из этих линий разбивает область допустимых решений на две — одна находится
правее и выше каждой из этих линий, вторая — левее и ниже. Какая из них нужна нам?
Та, которая левее и ниже. Во-первых, в исходных неравенствах у нас был знак «меньше
или равно», а левее и ниже как раз более маленькие значения переменных. А во-вторых,
как мы говорили в предыдущем пункте, решение (0,0) вполне удовлетворяет условию задачи,
хоть и не является оптимальным. А точка (0,0) — начало координат — расположена как
раз левее и ниже каждой из прямых.
То есть, нам нужно найти область, расположенную левее и ниже, чем каждая из наших
прямых. Отобразим ее:
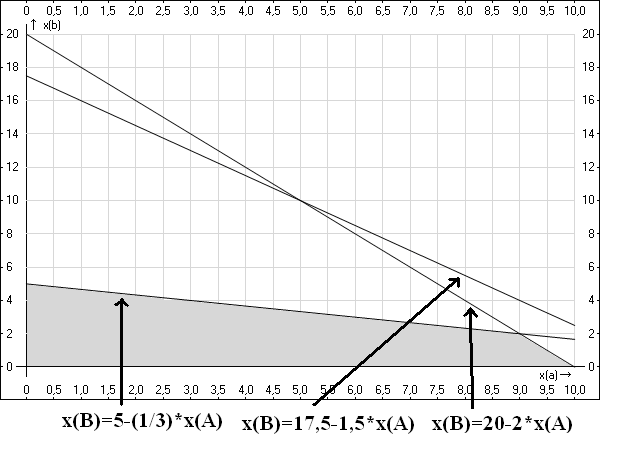
Эта область, во-первых, расположена в первой четверти, как и должно быть, во-вторых,
левее и ниже прямых $x_B=5-frac{1}{3}x_A$ и $x_B=20-2x_A$. Прямая $x_B=17,5-1,5x_A$
оказалась не участвующей в решении, так иногда бывает, это не страшно.
Далее задачу можно решать двумя способами.
Основной способ
Рассмотрим первый из них. Для него
нужно нарисовать линию нулевого дохода, то есть, линию, при которой целевая функция
равна нулю: $5x_A+10x_B=0$. Если упростить данное выражение, получим $x_B=-0,5x_A$.
Построим эту функцию красным цветом, и уберем подписи. Она будет расположена не в первой
четверти, это нормально.
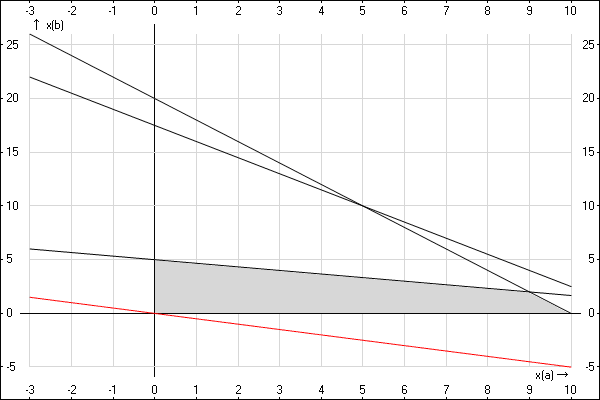
Эта линия состоит из точек, каждая из которых является решением, применяя которое, мы
получим нулевой доход. Однако с тем условием, что $x_A,x_Bgeq0$, такое решение мы получаем
всего одно — в точке (0,0) — остальные точки лежат во второй и четвертой четверти.
Что будет, если эту линию поднимать выше (параллельным переносом)? Мы получим линии,
которые будут давать больший, чем 0 доход. Получается, чем выше мы поднимем данную линию,
тем лучше. Однако совсем до бесконечности поднимать ее не получится, ведь она должна
хотя бы касаться разрешенной области, обозначенной серым цветом (сейчас она касается только
в точке (0,0)). Попробуем провести (пока на глаз) линии, параллельные данной, через
оставшиеся три точки многоугольника:
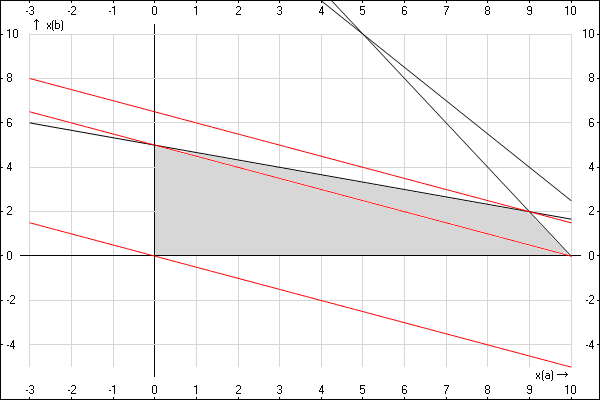
Мы нарисовали еще две линии, параллельные линии нулевого дохода, но расположенные выше.
Средняя из них проходит через две точки нашего многоугольника с решениями, а самая высокая —
через еще одну точку многоугольника. Кроме того, она вообще пересекает наш многоугольник
в одной-единственной точке. И еще выше данную линию поднять нельзя — она вообще перестанет
пересекать наш многоугольник. Следовательно, эта линия и есть «линия максимального дохода»,
а наше решение находится, как раз, в той точке, в которой эта линия пересекает нашу область
допустимых решений — в точке пересечения линий $x_B=5-frac{1}{3}x_A$ и $x_B=20-2x_A$.
Найдем координаты данной точки. Для этого приравняем эти два значения для $x_B$:
$$5-frac{1}{3}x_A=20-2x_A$$
$$-frac{1}{3}x_A+2x_A=20-5$$
$$frac{5}{3}x_A=15$$
$$5x_A=45$$
$$x_A=9$$
$$x_B=20-2cdot9=20-18=2$$
Итак, наше решение находится в точке (9,2). Это означает, что необходимо производить
9 единиц изделия A и 2 единицы изделия B. При этом мы получим прибыль
$$F(x_A,x_B)=5cdot9+10cdot2=45+20=65$$
Во всех остальных точках многоугольника решений прибыль будет меньше.
Другой способ
Второй способ заключается в том, что нужно просто проверить значение целевой функции в
каждой точке многоугольника. Всего их четыре. Обозначим их буквами:
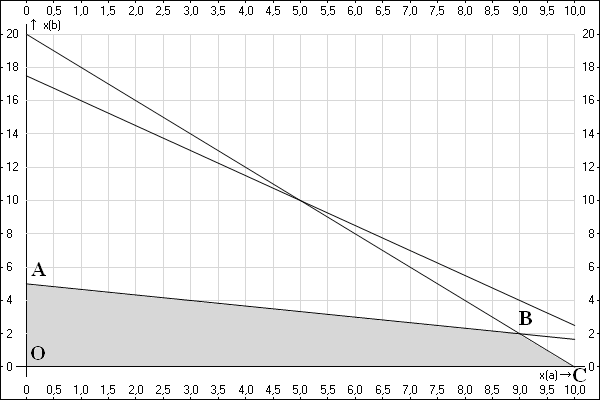
Найдем координаты каждой из них. Координаты точки O мы знаем — (0,0). Координаты
точки B мы нашли выше (по первому способу) — (9,2). Точка A — это точка на прямой
$x_B=5-frac{1}{3}x_A$, причем $x_A=0$. Следовательно $x_B=5$. То есть, ее координаты
(0,5). Точка C — это точка на прямой $x_B=20-2x_A$, причем $x_B=0$. То есть,
$20-2x_A=0$, $2x_A=20$, $x_A=10$. Следовательно, ее координаты (10,0).
Теперь найдем значение целевой функции в каждой из данных точек:
$$F(O)=F(0,0)=5cdot0+10cdot0=0+0=0$$
$$F(A)=F(0,5)=5cdot0+10cdot5=0+50=50$$
$$F(B)=F(9,2)=5cdot9+10cdot2=45+20=65$$
$$F(C)=F(10,0)=5cdot10+10cdot0=50+0=50$$
Действительно, в точке B наша функция принимает максимальное значение, равное 65. Это
и есть максимальная прибыль, которую можно получить в данном случае.
А если товаров больше?
Как говорилось в предыдущем разделе, графическим способом можно решать только задачу
для двух производимых товаров. Это потому, что если товаров будет больше двух, то и
переменных будет больше двух, например, три — $x_A, x_B, x_C$. И тогда придется строить
трехмерный график, в котором запросто можно запутаться. А если переменных больше трех,
то график не построить вообще. Однако специально для этих случаев был разработан еще
один метод решения задач линейного программирования, и, в частности, производственной
задачи — симплекс-метод, который мы рассмотрим в следующей главе.
Далее: 2.1.1. Симплексный способ решения
Полезное по теме
- Примеры решений задач ЛП графическим способом
- Решенные контрольные по линейному программированию
- Заказать свою работу по ЛП


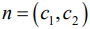 и одну из линий уровня, имеющую общие точки с этой областью.
и одну из линий уровня, имеющую общие точки с этой областью.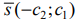 прямой
прямой 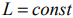 и параллельно ему проводим линию уровня
и параллельно ему проводим линию уровня 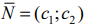 перпендикулярно прямой
перпендикулярно прямой