Ответ мой будет аналогичным ответу на похожий вопрос (см. здесь).
Из основного тригонометрического тождества:
выразим косинус в квадрате угла а:
Значит косинус угла равен либо корню квадратному из этого выражения, либо ему же, только со знаком -.
Знак перед корнем зависит от ограничения, которое накладывается для определенности в условии задачи.
Если дано положительное значение синуса,то угол находится в 1-й или во 2-й четверти. В первой четверти (0< a< 90) значение косинуса будет положительным. Здесь выбираем знак плюс. Во второй четверти (90< a< 180) значение косинуса будет отрицательным. Тогда перед корнем выбираем знак минус.
Если значение синуса отрицательное, то угол расположен в 3-й или 4-й четверти. В 3 четверти (180< a< 270) косинус угла будет меньше нуля.
В 4 четверти (270< a< 360) косинус угла будет больше нуля.
Примеры.
Пример 1. Найти косинус угла, если sina = -0,6. 180<a<270 (в градусах)
Решение. Находим разность 1 и квадрата значения sina, т.е. квадрата (-0,6).
-0,6 в квадрате находится так: (-0,6)*(-0,6) = 0,36. Подставим его в искомую разность:
1-0,36=0,64
Получили квадрат значения косинуса. Для нахождения значения самого косинуса, извлечем корень квадратный из 0,64 и возьмем его со знаком + или со знаком — . Получим 0,8 или -0,8.
Так как по условию угол находится в 3 четверти, то искомое значение косинуса будет также меньше нуля. Значит выбираем -0,8.
Ответ: cos a =-0,8.
Рассмотрим пример для случая, когда угол находится в 4 четверти:
Пример 2. Найти косинус угла, если sina = -0,6. 270<a<360 (в градусах)
Решение такое же (см. пример 1).
Перед выбором ответа рассуждаем так:
Т. к. по условию угол расположен в 4 четверти, то значение косинуса будет больше нуля. Значит выбираем 0,8.
Ответ: cos a =0,8.
Таблица косинусов, найти значения угла косинусов
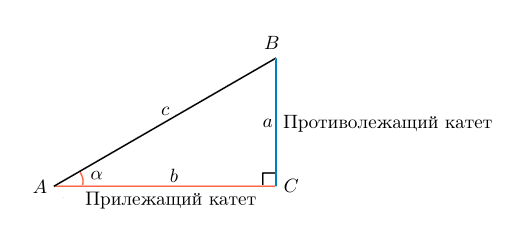
Косинус угла представляет собой одну из тригонометрических функций. Является соотношением ближнего к углу прямоугольного треугольника катета к гипотенузе. Записывается следующим образом: cos (А) = АС/АВ, где АС – ближний катет угла (А), АВ – гипотенуза.
Зачем необходимо производить такие сложные на первый взгляд вычисления? Еще с древних времен известна аксиома: знаю угол – знаю его тригонометрическую функцию. Соответственно, если известен cos любого угла, в таблице Брадиса можно найти этот угол. И наоборот – зная угол, не сложно вычислить косинус. Отсюда можно найти следующие данные: длина катетов и гипотенузы.
Эти данные используются не только в голых математических вычислениях. Невозможно составить даже элементарный план местности, не зная тригонометрических функций. Посредством онлайн калькулятора можно облегчить задачу и получать требуемые данные за доли секунды.
Таблица косинусов от 0° — 360°
|
|
|
|
|
|
|
|
|
|
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Перевести косинус в синус и обратно
Перевести косинус в синус (cos в sin) и обратно
Перевести:
Значение cos(x):
Угол, градусы:
Значение sin(x):
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн — косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о «Использование сердечного индекса Руфье в медико-спортивном контроле». Проба Руфье — представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор — онлайн tg φ: cos φ: ± Поделиться в соц сетях:
Косинусом угла в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе.
Для простоты запоминания можно дать такое определение: косинус угла — это отношение ближнего от рассматриваемого угла катета к гипотенузе.
В случае с рисунком, описанным выше: cosα=bccosalpha=frac{b}{c}
Гипотенуза прямоугольного треугольника равна 10 см10text{ см}. Один из катетов равен 6 см6text{ см}. Найдите косинус угла, прилежащего к наибольшему катету.
Решение
Пользуясь теоремой Пифагора вычислим длину неизвестного нам катета.
a2+b2=c2a^2+b^2=c^2
62+b2=1026^2+b^2=10^2
36+b2=10036+b^2=100
b2=64b^2=64
b=8b=8
Катет bb длиннее катета aa. Нам нужно найти косинус угла, прилежащего к наибольшему катету, то есть, к катету bb:
cosα=bc=810=0.8cosalpha=frac{b}{c}=frac{8}{10}=0.8
Ответ
0.8
Две стороны треугольника равны 4 см4text{ см} и 9 см9text{ см}. Периметр его равен 25 см25text{ см}.
Найдите косинус угла, прилежащего к неизвестной стороне и стороне с длиной 4 см4text{ см}.
Решение
Найдем третью сторону треугольника. Так как известен периметр, это будет легко сделать:
P=a+b+cP=a+b+c
25=9+4+c25=9+4+c
c=12c=12
При нахождении косинуса угла нам поможет следствие из теоремы косинусов, которое выглядит так:
cosα=b2+c2−a22⋅b⋅c=42+122−922⋅4⋅12=16+144−8196=7996≈0.82cosalpha=frac{b^2+c^2-a^2}{2cdot bcdot c}=frac{4^2+12^2-9^2}{2cdot 4cdot 12}=frac{16+144-81}{96}=frac{79}{96}approx0.82
Ответ
0.820.82
Решение задач по математике от экспертов сайта Студворк!
Тест по теме “Вычисление косинуса”
Найти угол, зная косинус угла: примеры решения
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Имея на руках значение косинуса угла, выяснить угол, которому он принадлежит, совсем не сложно.
Существует специальная тригонометрическая функция, которой можно воспользоваться для этого и называется она арккосинусом (записывается как $arccos$).
Замечание 1
Для того чтобы воспользоваться ей и узнать значение угла, можно применить специальную расширенную таблицу со значениями углов и соответствующих им тригонометрических функций. Эта таблица называется таблицей Брадиса.
Также наиболее часто встречающиеся значения углов и соответствующих им синусов-косинусов собраны в небольшую таблицу внизу:
Рисунок 1. Зная косинус или синус, найти угол. Автор24 — интернет-биржа студенческих работ
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Но есть и другой, более современный вариант нахождения угла по значению косинуса: достаточно включить режим Scientific (Научный) и найти кнопку переключения функций на калькуляторе.
В Windows 10 она обозначается стрелкой как показано на рисунке. При её нажатии кнопка $sin$ поменяется на $sin^{-1}$, а $cos$ на $cos^{-1}$. Теперь для того чтобы узнать значение угла по косинусу — просто набираете значение функции и жмёте кнопку $cos^{-1}$. Не забудьте выбрать нужную единицу измерения — градусы или радианы.
Рисунок 2. Как узнать угол, зная косинус угла. Автор24 — интернет-биржа студенческих работ
Пример 1
Найдите, чему равен $arccos 0,456$.
Решение:
Воспользуемся калькулятором в Научном режиме, на рисунке представлен калькулятор Mac OC, кнопка переключения между $sin$ и $sin^{-1}$ обведена красным:
Рисунок 3. Как по косинусу угла найти угол. Автор24 — интернет-биржа студенческих работ
После нажатия кнопки мы получили значение $α = 27,129°$.
Пример 2
Определите, чему равен угол, если известен его косинус, и он равен $0,95$.
Решение:
Воспользуемся вновь калькулятором и получим, что $α = 18,19°$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 07.05.2023