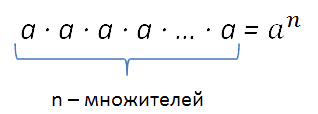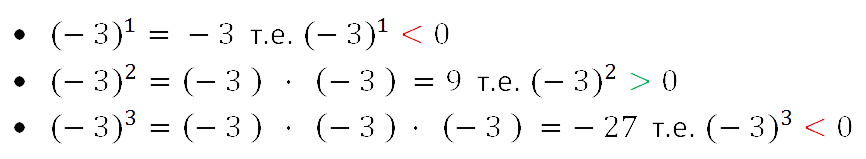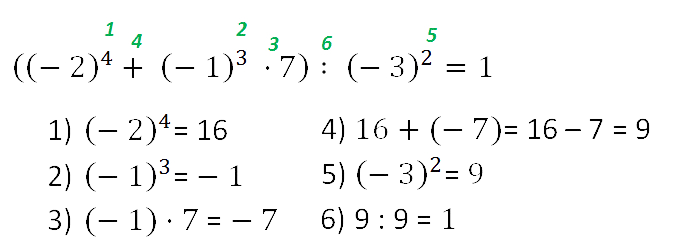Действия, обратные возведению в степень
7. В виду последней особенности действий возведения в степень для него можно составить 2 обратных задачи. Напр.:
1) Я задумал число, возвел его в третью степень (или: в куб), получилось 64; какое число я задумал?
Эту задачу можно записать в виде
(?)3 = 64
2) Я взял число 3, возвел его в некоторую степень, – получилось 81. В какую степень было возведено число 3.
Эту задачу можно записать в виде:
3? = 81
Теперь уже, так как возведение в степень не обладает переместительным законом, эти две задачи следует считать совершенно различными.
Сначала решать их можно подбором: попробуем число 1, 13 = 1, а не 64, след., 1 не годится; 23 = 8, а не 64, след., 2 не годится, 33 = 27, а не 64, след., 3 не годится; 43 = 64, след., в 1 задаче было задумано число 4. Также выясним, что во второй задаче число 3 было возведено в 4-ую степень.
Так как таких задач можно составить очень много, то для их решения необходимо изобрести новые действия. Эти действия обратны возведению в степень. Итак, для возведения в степень существуют два обратных действия: первое из них называется извлечением корня и служит для решения вопросов, подобных первой из наших задач; второе называется нахождением логарифма и служит для решения вопросов, подобных второй задаче.
Если мы обратим внимание на то, что в первой задаче нам даны степень 64 и показатель степени 3, то мы установим определение:
Извлечением корня называется действие, обратное возведению в степень, при помощи которого по данной степени и по данному показателю находят основание степени.
Также точно: во второй задаче даны степень (81) и основание степени (3), а надо найти показателя степени. Поэтому
нахождением логарифма называется действие, обратное возведению в степень, при помощи которого по данной степени и по данному основанию находится показатель степени.
Возведение в степень – это такая же математическая операция, как сложение, вычитание, умножение или деление.
Сейчас объясню все человеческим языком на очень простых примерах. Будь внимателен. Примеры элементарные, но объясняющий важные вещи. Начнем со сложения.
Сложение
( 2+2+2+2+2+2+2+2=16 )
Объяснять тут нечего. Ты и так все знаешь: нас восемь человек. У каждого по две бутылки колы. Сколько всего колы? Правильно – 16 бутылок. Теперь умножение.
Умножение
Тот же самый пример с колой можно записать по-другому: (displaystyle 2cdot 8=16).
Математики — люди хитрые и ленивые. Они сначала замечают какие-то закономерности, а потом придумывают способ как быстрее их «считать».
В нашем случае они заметили, что у каждого из восьми человек одинаковое количество бутылок колы и придумали прием, который называется умножением.
Согласись, (displaystyle 2cdot 8=16) считается легче и быстрее, чем (displaystyle 2+2+2+2+2+2+2+2=16).
И еще одна важная деталь. Ошибок при таком счете делается гораздо меньше. Математики из Стэнфорда, кстати, считают, что человек, знающий приемы счета, делает это в два раза легче и быстрее и совершает в два раза меньше ошибок. Работы меньше, а результат лучше.
Круто, да?
Итак, чтобы считать быстрее, легче и без ошибок, нужно всего лишь запомнить таблицу умножения. Ты, конечно, можешь делать все медленнее, труднее и с ошибками, но лучше ее запомнить! Вот таблица умножения. Выучи ее наизусть.
И другая таблица, красивее:
А какие еще хитрые приемы счета придумали ленивые математики? Правильно – возведение числа в степень.
Далее, почему говорят «степень числа с натуральным показателем»?
Ты уже наверное, догадался: потому что показатель степени – это натуральное число. Да, но что такое натуральное число? Элементарно! Натуральные это те числа, которые используются в счете при перечислении предметов: один, два, три… Мы же когда считаем предметы не говорим: «минус пять», «минус шесть», «минус семь». Мы так же не говорим: «одна третья», или «ноль целых, пять десятых». Это не натуральные числа. А какие это числа как ты думаешь?
Числа типа «минус пять», «минус шесть», «минус семь» относятся к целым числам.
Вообще, к целым числам относятся все натуральные числа, числа противоположные натуральным (то есть взятые со знаком минус), и число ( displaystyle 0) . Ноль понять легко – это когда ничего нет.
А что означают отрицательные («минусовые») числа? А вот их придумали в первую очередь для обозначения долгов: если у тебя баланс на телефоне ( displaystyle -100) рублей, это значит, что ты должен оператору ( displaystyle 100) рублей.
Всякие дроби — это рациональные числа. Как они возникли, как думаешь? Очень просто. Несколько тысяч лет назад наши предки обнаружили, что им не хватает натуральных чисел для измерения длинны, веса, площади и т.п. И они придумали рациональные числа… Интересно, правда ведь?
Есть еще иррациональные числа. Что это за числа? Если коротко, то бесконечная десятичная дробь. Например, если длину окружности разделить на ее диаметр, то в получится иррациональное число ( displaystyle 3,141592…).
Итак…
Откуда взялись, например, первые два свойства? Сейчас покажу.
1. ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}})
Посмотрим: что такое ( displaystyle {{a}^{n}}) и ( displaystyle {{a}^{m}}) ?
По определению:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{a}^{m}}=underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }end{array} right|Rightarrow text{ }{{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }leftarrow )
Сколько здесь множителей всего?
Очень просто: к ( displaystyle n) множителям мы дописали ( displaystyle m) множителей, итого получилось ( displaystyle n+m) множителей.
Итак, в правой части этого выражения получается такое произведение:
( displaystyle {{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{n+mtext{ множителей}})
Но по определению это степень числа ( displaystyle a) с показателем ( displaystyle n+m) , то есть: ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) , что и требовалось доказать.
Пример: Упростите выражение ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}) .
Решение: ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}={{5}^{4+7+9}}={{5}^{20}})
Пример: Упростите выражение ( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}) .
Решение:
Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания!
Поэтому степени с основанием ( displaystyle 3) мы объединяем, а ( displaystyle {{5}^{7}}) остается отдельным множителем:
( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}={{3}^{5+8}}cdot {{5}^{7}}={{3}^{13}}cdot {{5}^{7}})
Еще одно важное замечание: это правило – только для произведения степеней!
Ни в коем случае нельзя написать, что ( displaystyle {{2}^{4}}+{{2}^{6}}={{2}^{10}}).
Начнем с показателя, равного ( displaystyle 0) .
Любое число в нулевой степени равно единице:
( displaystyle {{a}^{0}}=1, ane 0)
Как всегда, зададимся вопросом: почему это так?
Рассмотрим какую-нибудь степень с основанием ( displaystyle 3). Возьмем, например ( displaystyle {{3}^{5}}), и домножим на ( displaystyle {{3}^{0}}):
( displaystyle {{3}^{5}}cdot {{3}^{0}}underset{text{по правилу умножения}}{mathop{=}},{{3}^{5+0}}={{3}^{5}})
Итак, мы умножили число ( displaystyle {{3}^{5}}) на ( displaystyle {{3}^{0}}) и получили то же, что и было – ( displaystyle {{3}^{5}}). А на какое число надо умножить, чтобы ничего не изменилось? Правильно, на ( displaystyle 1) . Значит ( displaystyle {{3}^{0}}=1) .
Можем проделать то же самое уже с произвольным числом ( displaystyle a):
( displaystyle {{a}^{n}}cdot {{a}^{0}}underset{по правилу умножения}{mathop{=}},{{a}^{n+0}}={{a}^{n}}={{a}^{n}}cdot 1text{ }Rightarrow text{ }{{a}^{0}}=1)
Повторим правило:
Любое число в нулевой степени равно единице.
Но из многих правил есть исключения. И здесь оно тоже есть – это число ( displaystyle 0) (в качестве основания).
С одной стороны, ( displaystyle 0) в любой степени должен равняться ( displaystyle 0) – сколько ноль сам на себя ни умножай, все-равно получишь ноль, это ясно. Но с другой стороны, ( displaystyle {{0}^{0}}) , как и любое число в нулевой степени, должен равняться ( displaystyle 1) . Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень.
То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень.
Поехали дальше. Кроме натуральных чисел и числа ( displaystyle 0) к целым относятся отрицательные числа.
Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: домножим какое-нибудь нормальное число на такое же в отрицательной степени:
( displaystyle {{3}^{5}}cdot {{3}^{-5}}underset{text{по правилу умножения}}{mathop{=}},{{3}^{5+left( -5 right)}}={{3}^{5-5}}={{3}^{0}}=1)
Отсюда уже несложно выразить искомое ( displaystyle {{3}^{-5}}) :
( displaystyle {{3}^{5}}cdot {{3}^{-5}}=1text{ }Rightarrow text{ }{{3}^{-5}}=frac{1}{{{3}^{5}}})
Теперь распространим полученное правило на произвольную степень:
( displaystyle {{a}^{n}}cdot {{a}^{-n}}={{a}^{n+left( -n right)}}={{a}^{0}}=1text{ }Rightarrow text{ }{{a}^{-n}}=frac{1}{{{a}^{n}}})
Итак, сформулируем правило:
Число в отрицательной степени обратно такому же числу в положительной степени. Но при этом основание не может быть нулевым: ( displaystyle ane 0) (т.к. на ( displaystyle 0) делить нельзя).
( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0)
( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0)
( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0)
Подведем итоги:
I. Выражение ( {{0}^{k}}) не определено в случае ( kle 0) . Если ( k>0) , то ( {{0}^{k}}=0) .
II. Любое число в нулевой степени равно единице: ( displaystyle {{a}^{0}}=1, ane 0) .
III. Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: ( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0).
( displaystyle {{6}^{-1}}=frac{1}{6})
( displaystyle {{left( frac{3}{2} right)}^{-2}}=frac{4}{9})
Чтобы понять, что такое «дробная степень», рассмотрим дробь ( displaystyle frac{1}{n}) :
пусть ( displaystyle {{3}^{frac{1}{n}}}=x) .
Возведем обе части уравнения в степень ( displaystyle n) :
( displaystyle {{left( {{3}^{frac{1}{n}}} right)}^{n}}={{x}^{n}})
Теперь вспомним правило про «степень в степени»:
( displaystyle {{x}^{n}}={{left( {{3}^{frac{1}{n}}} right)}^{n}}={{3}^{frac{1}{n}cdot n}}={{3}^{1}}=3)
Какое число надо возвести в степень ( displaystyle n) , чтобы получить ( displaystyle 3) ?
Эта формулировка – определение корня ( displaystyle n) -ой степени.
Напомню: корнем ( displaystyle n) -ой степени числа ( displaystyle a) (( displaystyle sqrt[n]{a}) ) называется число, которое при возведении в степень ( displaystyle n) равно ( displaystyle a) .
То есть, корень ( displaystyle n) -ой степени – это операция, обратная возведению в ( displaystyle n) степень: ( displaystyle sqrt[n]{a}=btext{ }Leftrightarrow text{ }a={{b}^{n}}) .
Получается, что ( displaystyle x={{3}^{frac{1}{n}}}=sqrt[n]{3}) . Очевидно, этот частный случай можно расширить: ( displaystyle {{a}^{frac{1}{n}}}=sqrt[n]{a}) .
Теперь добавляем числитель: что такое ( displaystyle {{a}^{frac{m}{n}}}) ? Ответ легко получить с помощью правила «степень в степени»:
( displaystyle {{a}^{frac{m}{n}}}={{a}^{frac{1}{n}cdot m}}={{left( {{a}^{frac{1}{n}}} right)}^{m}}={{left( sqrt[n]{a} right)}^{m}}) или ( displaystyle sqrt[n]{{{a}^{m}}}) .
Но может ли основание ( displaystyle a) быть любым числом? Ведь корень можно извлекать не из всех чисел.
Например, можно ли посчитать число ( displaystyle sqrt[4]{-16}) ? То есть, какое число нужно возвести в ( displaystyle 4) степень, чтобы получить ( displaystyle -16) ?
Никакое!
Вспоминаем правило: любое число, возведенное в четную степень – число положительное. То есть, извлекать корни четной степени из отрицательных чисел нельзя!
А это значит, что нельзя такие числа возводить в дробную степень с четным знаменателем, то есть выражение ( displaystyle {{left( -1 right)}^{frac{1}{2}}}) не имеет смысла.
А что насчет выражения ( displaystyle {{left( -1 right)}^{frac{1}{3}}}) ?
Его уже вроде бы можно посчитать: это ( displaystyle sqrt[3]{-1}=-1) .
Но тут возникает проблема.
Число ( displaystyle frac{1}{3}) можно представить в виде дргих, сократимых дробей, например, ( displaystyle frac{2}{6}) или ( displaystyle frac{4}{12}) .
И получается, что ( displaystyle {{left( -1 right)}^{frac{1}{3}}}) существует, но ( displaystyle {{left( -1 right)}^{frac{2}{6}}}) не существует, а ведь это просто две разные записи одного и того же числа.
Или другой пример: раз ( displaystyle sqrt[3]{-8}=-2) , то можно записать ( displaystyle {{left( -8 right)}^{frac{1}{3}}}=-2) . Но стоит нам по-другому записать показатель, и снова получим неприятность: ( displaystyle {{left( -8 right)}^{frac{1}{3}}}={{left( -8 right)}^{frac{2}{6}}}=sqrt[6]{{{left( -8 right)}^{2}}}=sqrt[6]{64}=2) (то есть, получили совсем другой результат!).
Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем.
Итак, если:
- ( a>0);
- ( m) – натуральное число;
- ( n) – целое число;
Тогда:
( {{a}^{frac{n}{m}}}=sqrt[m]{a^n})
Примеры:
( {{a}^{frac{1}{2}}}=sqrt{a})
( {{a}^{frac{1}{5}}}=sqrt[5]{a})
( {{a}^{-frac{3}{4}}}=frac{1}{sqrt[4]{a^3}})
( displaystyle frac{{{5}^{-frac{1}{2}}}cdot {{left( {{5}^{frac{5}{6}}} right)}^{frac{3}{10}}}cdot {{3}^{-frac{5}{4}}}}{{{3}^{-frac{3}{2}}}}={{5}^{-frac{1}{2}}}cdot {{5}^{frac{5}{6}cdot frac{3}{10}}}cdot {{3}^{left( -frac{5}{4}+frac{3}{2} right)}}=)
( displaystyle={{5}^{left( -frac{1}{2}+frac{1}{4} right)}}cdot {{3}^{frac{1}{4}}}={{5}^{-frac{1}{4}}}cdot {{3}^{frac{1}{4}}}={{left( frac{3}{5} right)}^{frac{1}{4}}}=sqrt[4]{frac{3}{5}})
Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:
( displaystyle frac{sqrt[9]{6}cdot sqrt[18]{6}}{sqrt[6]{6}}=frac{{{6}^{frac{1}{9}}}cdot {{6}^{frac{1}{18}}}}{{{6}^{frac{1}{6}}}}={{6}^{frac{1}{9}+frac{1}{18}-frac{1}{6}}}={{6}^{frac{2+1-3}{18}}}={{6}^{0}}=1)
При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах.
Например, степень с натуральным показателем – это число, несколько раз умноженное само на себя; число в нулевой степени – это как-бы число, умноженное само на себя ( 0) раз, то есть его еще не начали умножать, значит, само число еще даже не появилось – поэтому результатом является только некая «заготовка числа», а именно число ( 1) ; степень с целым отрицательным показателем – это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.
Вообразить степень с иррациональным показателем крайне сложно (так же, как сложно представить 4-мерное пространство). Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел.
Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель – это даже не действительное число. Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.
Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!:)
Например: ( {{3}^{sqrt{2}}}cdot {{3}^{1-sqrt{2}}}={{3}^{sqrt{2}+1-sqrt{2}}}=3)
Или: ( frac{{{2}^{3sqrt{3}}}}{{{8}^{sqrt{3}-1}}}=frac{{{2}^{3sqrt{3}}}}{{{2}^{3left( sqrt{3}-1 right)}}}={{2}^{3sqrt{3}-3sqrt{3}+3}}=8)
И еще: ( {{left( {{5}^{sqrt[3]{4}}} right)}^{sqrt[3]{2}}}={{5}^{sqrt[3]{8}}}={{5}^{2}}=25).
Определение степени
Степенью называется выражение вида: ( {{a}^{b}}), где ( a) – основание степени и ( b) – показатель степени.
Степень с натуральным показателем {n = 1, 2, 3,…}
- ( {{a}^{1}}=a)
- ( {{a}^{2}}=acdot a)
- ( {{a}^{3}}=acdot acdot a)
Возвести число в натуральную степень n — значит умножить число само на себя ( n) раз:
- ( {{a}^{n}}=underbrace{acdot acdot acdot …a}_{n})
Степень с целым показателем {0, ±1, ±2,…}
Если показателем степени является целое положительное число:
( {{a}^{n}}={{a}^{n}}, n>0)
Возведение в нулевую степень:
( {{a}^{0}}=1, ane 0) . ( {{0}^{0}}) – выражение неопределенное, т.к., с одной стороны, ( 0) в любой степени – это ( 0) , а с другой – любое число в ( 0) -ой степени – это ( 1) .
Если показателем степени является целое отрицательное число:
( {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0) (т.к. на ( 0) делить нельзя).
Еще раз о нулях: выражение ( {{0}^{k}}) не определено в случае ( kle 0). Если ( k>0) , то ( {{0}^{k}}=0) .
Примеры:
( {{6}^{-1}}=frac{1}{6})
( {{left( frac{3}{2} right)}^{-2}}=frac{4}{9})
Степень с рациональным показателем
Если,
- ( a>0);
- ( m) – натуральное число;
- ( n) – целое число;
Тогда:
- ( {{a}^{frac{n}{m}}}=sqrt[m]{{{a}^{n}}})
Примеры:
( {{a}^{frac{1}{2}}}=sqrt{a})
( {{a}^{frac{1}{5}}}=sqrt[5]{a})
( {{a}^{-frac{3}{4}}}=frac{1}{sqrt[4]{{{a}^{3}}}})
Свойства степеней
| Произведение степеней | ( {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) ( {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}}) |
| Деление степеней | ( frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}}) ( frac{{{a}^{n}}}{{{b}^{n}}}={{left( frac{a}{b} right)}^{n}}) |
| Возведение степени в степень | ( {{left( {{a}^{m}} right)}^{n}}={{a}^{mcdot n}}) |
Чтобы проще было решать задачи, попробуем понять: откуда эти свойства взялись? Докажем их.
Доказательства свойств степени
1. ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}})
Посмотрим: что такое ( displaystyle {{a}^{n}}) и ( displaystyle {{a}^{m}}) ?
По определению:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{a}^{m}}=underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }end{array} right|Rightarrow text{ }{{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{acdot acdot …cdot a}_{mtext{ множителей}})
Сколько здесь множителей всего? Очень просто: к ( displaystyle n) множителям мы дописали ( displaystyle m) множителей, итого получилось ( displaystyle n+m) множителей.
Итак, в правой части этого выражения получается такое произведение:
( displaystyle {{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{n+mtext{ множителей}})
Но по определению это степень числа ( displaystyle mathbf{a}) с показателем ( displaystyle mathbf{n}+mathbf{m}), то есть:
( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) , что и требовалось доказать.
Пример: Упростите выражение ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}) .
Решение: ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}={{5}^{4+7+9}}={{5}^{20}}) .
Пример: Упростите выражение ( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}) .
Решение: Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания. Поэтому степени с основанием ( displaystyle 3) мы объединяем, а ( displaystyle {{5}^{7}}) остается отдельным множителем:
( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}={{3}^{5+8}}cdot {{5}^{7}}={{3}^{13}}cdot {{5}^{7}}) .
Еще одно важное замечание: это правило – только для произведения степеней!
Ни в коем случае нелья написать, что ( displaystyle {{2}^{4}}+{{2}^{6}}={{2}^{10}}) .
2. ( displaystyle {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}})
Так же, как и с предыдущим свойством, обратимся к определению степени:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{b}^{n}}=underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}end{array} right|Rightarrow text{ }{{a}^{n}}cdot {{b}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}) .
Перегруппируем это произведение так:
( displaystyle {{a}^{n}}cdot {{b}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}=underbrace{left( acdot b right)cdot left( acdot b right)cdot …cdot left( acdot b right)}_{ntext{ множителей}}).
Получается, что выражение ( displaystyle acdot b) умножается само на себя ( displaystyle n) раз, то есть, согласно определению, это и есть ( displaystyle n) -я степень числа ( displaystyle acdot b) :
( displaystyle {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}}), ч.т.д.
По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме: ( displaystyle {{2}^{4}}+{{3}^{4}}ne {{left( 2+3 right)}^{4}}) !
Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать ( displaystyle {{left( a+b right)}^{2}}={{a}^{2}}+{{b}^{2}}) ? Но это неверно, ведь ( displaystyle {{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}) .
3. ( displaystyle frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}})
И снова используем определение степени:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{a}^{m}}=underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }end{array} right|Rightarrow text{ }frac{{{a}^{n}}}{{{a}^{m}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{acdot acdot …cdot a}_{mtext{ множителей}}})
Здесь, очевидно, можем сократить. Но с одной оговоркой: чтобы степень получилась натуральная, нам придется предположить, что ( displaystyle n>m) (то есть, в числителе множителей должно быть больше, чем в знаменателе). Тогда ( displaystyle m) множителей числителя сокращаются со всеми ( displaystyle m) множителями знаменателя. Таким образом множители остаются только в числителе, причем в количестве ( displaystyle n-m) штук:
( displaystyle frac{{{a}^{n}}}{{{a}^{m}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{acdot acdot …cdot a}_{mtext{ множителей}}}=frac{underbrace{acdot acdot …cdot a}_{n-mtext{ множителей}}}{1}={{a}^{n-m}}) , ч.т.д.
4. ( displaystyle frac{{{a}^{n}}}{{{b}^{n}}}={{left( frac{a}{b} right)}^{n}})
Все как обычно – записываем определение степеней ( displaystyle {{a}^{n}}) и ( displaystyle {{b}^{n}}) , делим их друг на друга, разбиваем на пары ( displaystyle frac{a}{b}) и получаем:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{b}^{n}}=underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}end{array} right|Rightarrow text{ }frac{{{a}^{n}}}{{{b}^{n}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}}=underbrace{frac{a}{b}cdot frac{a}{b}cdot …cdot frac{a}{b}}_{ntext{ множителей}}={{left( frac{a}{b} right)}^{n}}) , ч.т.д.
Прежде чем разобрать последнее правило, решим несколько примеров.
Степень числа
- Возведение в степень
- Выражения со степенями. Порядок действий
- Калькулятор возведения в степень
Степень числа — это выражение, обозначающее краткую запись произведения одинаковых сомножителей.
Рассмотрим умножение одинаковых чисел, например:
5 · 5 · 5 = 125.
Произведение 5 · 5 · 5 можно записать так: 53 (пять в третьей степени). Выражение 53 — это степень. Следовательно,
5 · 5 · 5 = 53 = 125.
Рассмотрим выражение 53 . В этом выражении число 5 — основание степени, а число 3 — показатель степени.
Основание степени — это повторяющийся множитель. Показатель степени — это число, указывающее количество повторений, то есть показатель степени показывает сколько одинаковых множителей содержится в произведении.
Читаются степени так:
- 72 —
семь во второй степени
.Вторую степень числа также называют квадратом этого числа. Следовательно, выражение 72 можно прочесть так:
семь в квадрате
иликвадрат числа семь
. - 23 —
два в третьей степени
.Третью степень числа также называют кубом этого числа. Следовательно, выражение 23 можно прочесть так:
два в кубе
илидва куб
. - 64 —
шесть в четвёртой степени
. - 1015 —
десять в пятнадцатой степени
. - an —
a в энной степени
илиa в степени эн
.
Пример. Записать в виде степени:
a) 5 · 5;
б) 10 · 10 · 10 · 10;
в) 8 · 8 · 8.
Решение:
a) 5 · 5 = 52;
б) 10 · 10 · 10 · 10 = 104;
в) 8 · 8 · 8 = 83.
Возведение в степень
Возведение числа в степень — это вычисление произведения одинаковых множителей. Например, возвести число 2 в третью степень (23) — это значит найти произведение 2 · 2 · 2 , то есть
23 = 2 · 2 · 2 = 8.
Результат возведения в степень называется степенью (также как и само выражение, значение которого вычисляется). В выражении:
23 = 8,
2 — это основание степени, 3 — показатель степени, 8 — степень.
Пример. Вычислите:
a) 112;
б) 25;
в) 104.
Решение:
a) 112 = 11 · 11 = 121;
б) 25 = 2 · 2 · 2 · 2 · 2 = 32;
в) 104 = 10 · 10 · 10 · 10 = 10000.
Выражения со степенями. Порядок действий
Если выражение не содержит скобки и содержит степени, то сначала выполняется возведение в степень в порядке следования степеней (слева направо), а затем все остальные арифметические действия. Если выражение содержит скобки, то сначала выполняются действия в скобках, с учётом всех правил порядка выполнения действий.
Рассмотрим два выражения:
52 + 22
и
(5 + 2)2
В соответствии с порядком выполнения действий в первом случае сначала выполняется возведение в степень, а затем вычисляется сумма. Во втором случае сначала вычисляется сумма, а затем результат возводится в квадрат.
52 + 22 = 25 + 4 = 29,
(5 + 2)2 = 72 = 49.
Пример 1. Найти значение выражения:
5 · (10 — 
Решение: Сначала выполняется действие, заключённое в скобки:
1) 10 — 8 = 2.
Затем, по правилам порядка действий, выполняется возведение в степень:
2) 23 = 2 · 2 · 2 = 8.
И последним действием вычисляется произведение:
3) 5 · 8 = 40.
Ответ: 5 · (10 — 
Пример 2. Вычислить:
a) (4 + 2) · 32;
б) 3 · 52 — 50;
в) 3 · 4 + 62.
Решение:
a) (4 + 2) · 32 = 54
- 4 + 2 = 6
- 32 = 9
- 6 · 9 = 54
б) 3 · 52 — 50 = 25
- 52 = 25
- 3 · 25 = 75
- 75 — 50 = 25
в) 3 · 4 + 62 = 48
- 62 = 36
- 3 · 4 = 12
- 12 + 36 = 48
Калькулятор возведения в степень
Данный калькулятор поможет вам выполнить возведение в степень. Просто введите основание с показателем степени и нажмите кнопку Вычислить
.
☰
Что обратно возведению в степень?
Возведению в степень обратны два действия:
- извлечение корня,
- нахождение логарифма.
Во-первых, сначала надо разобраться, что значит обратное действие. Так деление есть обратное действие умножению, а вычитание — сложению. Это вытекает из рассуждений, что произведение, получившееся от перемножения двух множителей, позволяет найти один из множителей, если известен другой. Например, 5 * 3 = 15. Если нам неизвестен второй множитель (5 * ? = 15), то его можно найти, выполнив деление: 15 : 5 = 3. Операция не меняется, если неизвестен первый множитель: ? * 3 = 15, 15 : 3 = 5. Это связано с тем, что умножение подчиняется переместительному закону (от перемены мест множителей произведение не меняется).
Аналогично и для вычитания: ? + 10 = 33, 33 — 10 = 23 или ? + 23 = 33, 33 — 23 = 10. Неважно, какое слагаемое неизвесто, его всегда находят вычитанием.
Но не все так просто с возведением в степень. Здесь от перестановки основания степени и показателя степени результат изменяется, т.е. возведение в степень не подчиняется переместительному закону: 43 = 64, но 34 = 81. (Хотя есть исключения: 24 = 16 и 42 = 16.)
Поэтому, если нам известен результат операции возведения в степень и показатель степени, то, чтобы найти основание степени, надо извлечь корень известной по показателю степени из результа возведения в степень:
?3 = 125, следовательно 3√125 = 5.
Если же известны основание степени и результат возведения в степень, а надо найти показатель степени, то используется такая операция как нахождение логарифма:
2? = 64, отсюда log264 = 6
Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.
Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.
Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.
Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 46 и произносят «четыре в шестой степени».
4 · 4 · 4 · 4 · 4 · 4 = 46
Выражение 46 называют степенью числа, где:
- 4 — основание степени;
- 6— показатель степени.
В общем виде степень с основанием «a» и показателем «n» записывается с помощью выражения:
Запомните!
Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».
Запись «an» читается так: «а в степени n» или «n-ая степень числа a».
Исключение составляют записи:
- a2 — её можно произносить как «а в квадрате»;
- a3 — её можно произносить как «а в кубе».
Конечно, выражения выше можно читать и по определению степени:
- a2 — «а во второй степени»;
- a3 — «а в третьей степени».
Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).
Запомните!Степенью числа «а» с показателем n = 1 является само это число:
a1 = a
Любое число в нулевой степени равно единице.
a0 = 1
Ноль в любой натуральной степени равен нулю.
0n = 0
Единица в любой степени равна 1.
1n = 1
Выражение 00 (ноль в нулевой степени) считают лишённым смысла.
- (−32)0 = 1
- 0253 = 0
- 14 = 1
При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.
Пример. Возвести в степень.
- 53 = 5 · 5 · 5 = 125
- 2,52 = 2,5 · 2,5 = 6,25
- (3/4)4 = 3/4 * 3/4 * 3/4 * 3/4 = 81/256
Возведение в степень отрицательного числа
Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.
Запомните!При возведении в степень положительного числа получается положительное число.
При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.
Рассмотрим примеры возведения в степень отрицательных чисел.
Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.
Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.
Запомните!Отрицательное число, возведённое в чётную степень, есть число положительное.
Отрицательное число, возведённое в нечётную степень, — число отрицательное.
Квадрат любого числа есть положительное число или нуль, то есть:
a2 ≥ 0 при любом a.
- 2 · (−3)2 = 2 · (−3) · (−3) = 2 · 9 = 18
- −5 · (−2)3 = −5 · (−8) = 40
Обратите внимание!
При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5)4 и −54 это разные выражения. Результаты возведения в степень данных выражений будут разные.
Вычислить (−5)4 означает найти значение четвёртой степени отрицательного числа.
(−5)4 = (−5) · (−5) · (−5) · (−5) = 625
В то время как найти «−54» означает, что пример нужно решать в 2 действия:
- Возвести в четвёртую степень положительное число 5.
54 = 5 · 5 · 5 · 5 = 625 - Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание).
−54 = −625
Пример. Вычислить: −62 − (−1)4
−62 − (−1)4 = −37
- 62 = 6 · 6 = 36
- −62 = −36
- (−1)4 = (−1) · (−1) · (−1) · (−1) = 1
- −(−1)4 = −1
- −36 − 1 = −37
Порядок действий в примерах со степенями
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
Запомните!В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление, а в конце сложение и вычитание.
Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.
Пример. Вычислить:
Домашнее задание
Стр. 66 — 67 читать
Упр. 133, 135, 137, 139, 141, 143, 145