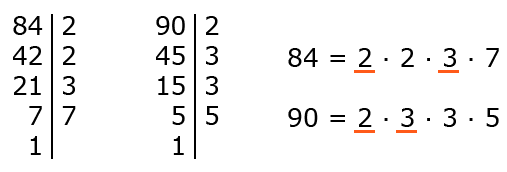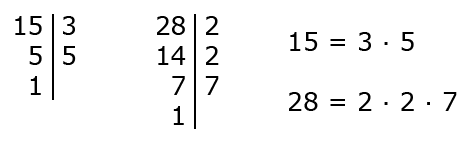Как найти число с наибольшим количеством делителей

Общие соображения

Заметим, что:

  1. Величины
    С = lg (X * p1 * p2 * … * pk) и П = cnt(X) * lg p1 * lg p2 * … * lg pk
    — это сумма и произведение величин (a1+1) lg p1, (a2+1) lg p2,…, (ak+1) lg pk.
    Не будь задача дискретной, в соответствии с теоремами о средних оптимум достигался бы при равенстве этих величин, (а с учётом потенцирования — и величин вида piai+1).

  2. Наш случай — дискретное приближение к оптимуму, так что эти величины должны хотя бы стремиться к равенству. А поскольку основания растут, то показатели не должны возрастать (a1>=a2>=…>=ak).

  3. Сумма и произведение величин идут «в одном флаконе», и алгоритмы линейного динамического программирования здесь неприменимы.

  4. Так как показатели степеней канонического разложения не возрастают, то требуемое оптимальное число X можно представить в виде произведения X=Pk…P2P1, где Pk=p1p2…pk— это произведения последовательных простых чисел (праймориалы), которые могут повторяться и которые можно протабулировать.
    И поскольку праймориал при возрастании k растёт быстрее факториала, то их произведение для числа X подбирается очень быстро.

_Известно, что

Every highly composite number is a product of primorials_

Алгоритм и анализ результатов

Алгоритм по п.4 рекурсивный, параметром является частное от деления числа на уже готовую часть цепочки.
Для поиска текущего оптимального праймориала (звена цепочки) ведётся перебор по убыванию в границах от «жадного» звена для текущего частного до «жадного» звена для квадратного корня из этого частного.
Перебор обрывается, когда целевая функция (количество множителей) начинает падать.
Такая схема обеспечивает решение задачи.

Дополнительный контроль невозрастания звеньев в цепочке избавляет от повторения пройденного.

Для случая N=1018 оптимальное решение нашлось за 118 шагов и совпало с предыдущим ответом:
X = P12P4P2P2P1P1P1P1 = 28 * 34 * 52 * 72 * 11 * 13 … 37 = 897612484786617600,
cnt(X) = (8+1) (4+1) (2+1)2 (1+1)8 = 103680.

При этом порядок величин 29=512, 35=243, 53=125, 73=343, 112=121, …, 372=1369 примерно одинаков, что подтверждает теорию оптимума.

Для случая N=1036 (cnt(X)=127401984 множителей) понадобилось всего 168 шагов. Т.е. сложность алгоритма возрастает не быстрее логарифма. Хотя разрядность данных меняется.

Исходный код на PHP использует библиотеку BCMath. границу возможностей не тестировал (скорее всего, первым подведёт int для cnt(X)):

function prods(&$prod){
    $p = array( "2", "3", "5", "7", "11",       "13", "17", "19", "23", "29", 
            "31", "37", "41", "43", "47",   "53", "59", "61", "67", "71",
            "73", "79", "83", "89", "97",);
    $str="1"; 
    foreach($p as $val){
        $str = bcmul($str,$val);
        array_push($prod,$str);
    } 
    return 1;
}

function greedy_prod($n){
    global $p_prod;
    foreach($p_prod as $key=>$val){
        if(bccomp($val,$n)>0) break;
        $i_m=$key+1;
    }
    if (!isset($i_m)) $i_m=0;
    return $i_m;    
}

function show_chain($chain){
    $s = "[";
    foreach($chain as $len) $s = $s . sprintf("%d.",$len);  
    $s = $s."]";
    return $s; 
}

function multi_prod($chain){
    global $p_prod;     
    $m_prod = "1";
    foreach($chain as $val) $m_prod= bcmul($m_prod, $p_prod[$val-1]);
    return $m_prod;
}

function multi_count($chain){
    $cnt = array();
    for ($i=0; $i<$chain[0]; $i++)  array_push($cnt, 0);
    foreach($chain as $key=>$val){
        for ($i=0; $i<$val; $i++)   $cnt[$i]++;
    }
    $count=1;
    foreach($cnt as $val) $count *= $val+1;
    return $count;
}

function maxi_count($n, &$main_chain, &$latch_chain){
    global  $maxi_counter, $p_prod;
    $maxi_counter++;

    $m_prod = multi_prod($main_chain);
    $nn = bcdiv($n,$m_prod);

    $long_chain  = greedy_prod($nn);
    if(count($main_chain)>0){
        $last = array_pop($main_chain); array_push($main_chain,$last);
        $long_chain = min($long_chain, $last);
    }
    $short_chain = greedy_prod(bcsqrt($nn));
    $short_chain = max($short_chain,1);

    if ($long_chain==0) {
        $max_count = multi_count($main_chain);
        if($max_count> multi_count($latch_chain)) $latch_chain=$main_chain;
    }
    else {
        $max_count = 0;
        for ($cur_chain=$long_chain; $cur_chain>$short_chain-1; $cur_chain--){
            array_push($main_chain,$cur_chain);     
            $counter = maxi_count($n, $main_chain, $latch_chain);
            array_pop($main_chain);
            if($counter>$max_count) $max_count = $counter;
            else break;
        }
    }       
    $s1 = show_chain($main_chain);  $s2=show_chain($latch_chain);
    print("<tr><td align="right">&emsp;$m_prod</td><td align="right">$max_count</td><td>$s2</td><td>$s1</td></tr>");
    return $max_count;
}   

//$N="1000000000000000000";     
$N="1000000000000000000000000000000000000";
$p_prod = array();
if (prods($p_prod)>0){
    print("<br>p_prod:<br>");   
    foreach($p_prod as $key=>$val) printf("&emsp;%d=>%s", $key, $val); 
}

$maxi_counter = 0; $chain=array(); $optimal_chain=array();
print("<br><br>maxi_count:<br>N=$N");
print('<table border="2">');
print('<tr><th>current number</th><th>multi_prod</th><th>optimal chain</th><th>current chain</th></tr>');
$max_count=maxi_count($N, $chain, $optimal_chain);
print('</table>');
printf("<br>Количество последовательностей = %d<br>Цепочка произведений = %s,<br>Kоличество множителей = %d<br>Минимальное число = %s", $maxi_counter, show_chain($optimal_chain), $max_count, multi_prod($optimal_chain));

Результаты для N = 1036: 

<pre>
p_prod:
 0=>2 1=>6 2=>30 3=>210 4=>2310 5=>30030 6=>510510 7=>9699690 8=>223092870
 9=>6469693230 10=>200560490130 11=>7420738134810 12=>304250263527210
 13=>13082761331670030 14=>614889782588491410 15=>32589158477190044730
 16=>1922760350154212639070 17=>117288381359406970983270
 18=>7858321551080267055879090 19=>557940830126698960967415390
 20=>40729680599249024150621323470 21=>3217644767340672907899084554130
 22=>267064515689275851355624017992790 23=>23768741896345550770650537601358310
 24=>2305567963945518424753102147331756070

maxi_count:
N=1000000000000000000000000000000000000
    current number	                 multi_prod	optimal chain	current chain
 713062256890366523119516128040749300	56623104	[24.3.]	[24.3.]
 855674708268439827743419353648899160	67108864	[24.2.2.]	[24.2.2.]
 570449805512293218495612902432599440	62914560	[24.2.2.]	[24.2.1.1.]
 285224902756146609247806451216299720	62914560	[24.2.2.]	[24.2.1.]
 142612451378073304623903225608149860	67108864	[24.2.2.]	[24.2.]
 23768741896345550770650537601358310	67108864	[24.2.2.]	[24.]
 616919031242227216631491481563344900	63700992	[24.2.2.]	[23.5.]
 673002579536975145416172525341830800	94371840	[23.4.2.1.]	[23.4.2.1.]
 336501289768487572708086262670915400	94371840	[23.4.2.1.]	[23.4.2.]
 897336772715966860554896700455774400	99090432	[23.4.1.1.1.1.]	[23.4.1.1.1.1.]
 448668386357983430277448350227887200	99090432	[23.4.1.1.1.1.]	[23.4.1.1.1.]
 224334193178991715138724175113943600	99090432	[23.4.1.1.1.1.]	[23.4.1.1.]
 112167096589495857569362087556971800	99090432	[23.4.1.1.1.1.]	[23.4.1.]
 56083548294747928784681043778485900	99090432	[23.4.1.1.1.1.]	[23.4.]
 961432256481393064880246464774044000	100663296	[23.3.3.1.1.]	[23.3.3.1.1.]
 480716128240696532440123232387022000	100663296	[23.3.3.1.1.]	[23.3.3.1.]
 240358064120348266220061616193511000	100663296	[23.3.3.1.1.]	[23.3.3.]
 576859353888835838928147878864426400	94371840	[23.3.3.1.1.]	[23.3.2.2.1.]
 288429676944417919464073939432213200	94371840	[23.3.3.1.1.]	[23.3.2.2.]
 769145805185114451904197171819235200	100663296	[23.3.3.1.1.]	[23.3.2.1.1.1.1.]
 384572902592557225952098585909617600	100663296	[23.3.3.1.1.]	[23.3.2.1.1.1.]
 192286451296278612976049292954808800	100663296	[23.3.3.1.1.]	[23.3.2.1.1.]
 96143225648139306488024646477404400	100663296	[23.3.3.1.1.]	[23.3.2.1.]
 48071612824069653244012323238702200	100663296	[23.3.3.1.1.]	[23.3.2.]
 8011935470678275540668720539783700	100663296	[23.3.3.1.1.]	[23.3.]
 267064515689275851355624017992790	100663296	[23.3.3.1.1.]	[23.]
 579755234179442444545257054963143400	84934656	[23.3.3.1.1.]	[22.6.2.]
 773006978905923259393676073284191200	95551488	[23.3.3.1.1.]	[22.6.1.1.1.]
 386503489452961629696838036642095600	95551488	[23.3.3.1.1.]	[22.6.1.1.]
 193251744726480814848419018321047800	95551488	[23.3.3.1.1.]	[22.6.1.]
 96625872363240407424209509160523900	95551488	[23.3.3.1.1.]	[22.6.]
 891931129506834530069626238404836000	113246208	[22.5.3.1.1.]	[22.5.3.1.1.]
 445965564753417265034813119202418000	113246208	[22.5.3.1.1.]	[22.5.3.1.]
 222982782376708632517406559601209000	113246208	[22.5.3.1.1.]	[22.5.3.]
 535158677704100718041775743042901600	106168320	[22.5.3.1.1.]	[22.5.2.2.1.]
 267579338852050359020887871521450800	106168320	[22.5.3.1.1.]	[22.5.2.2.]
 713544903605467624055700990723868800	113246208	[22.5.3.1.1.]	[22.5.2.1.1.1.1.]
 356772451802733812027850495361934400	113246208	[22.5.3.1.1.]	[22.5.2.1.1.1.]
 178386225901366906013925247680967200	113246208	[22.5.3.1.1.]	[22.5.2.1.1.]
 89193112950683453006962623840483600	113246208	[22.5.3.1.1.]	[22.5.2.1.]
 44596556475341726503481311920241800	113246208	[22.5.3.1.1.]	[22.5.2.]
 7432759412556954417246885320040300	113246208	[22.5.3.1.1.]	[22.5.]
 851388805438342051430097773022798000	104857600	[22.5.3.1.1.]	[22.4.4.2.]
 567592536958894700953398515348532000	100663296	[22.5.3.1.1.]	[22.4.4.1.1.]
 283796268479447350476699257674266000	100663296	[22.5.3.1.1.]	[22.4.4.1.]
 141898134239723675238349628837133000	104857600	[22.5.3.1.1.]	[22.4.4.]
 608134861027387179592926980730570000	98304000	[22.5.3.1.1.]	[22.4.3.3.]
 729761833232864615511512376876684000	113246208	[22.5.3.1.1.]	[22.4.3.2.2.]
 973015777643819487348683169168912000	125829120	[22.4.3.2.1.1.1.]	[22.4.3.2.1.1.1.]
 486507888821909743674341584584456000	125829120	[22.4.3.2.1.1.1.]	[22.4.3.2.1.1.]
 243253944410954871837170792292228000	125829120	[22.4.3.2.1.1.1.]	[22.4.3.2.1.]
 121626972205477435918585396146114000	125829120	[22.4.3.2.1.1.1.]	[22.4.3.2.]
 20271162034246239319764232691019000	125829120	[22.4.3.2.1.1.1.]	[22.4.3.]
 675705401141541310658807756367300	125829120	[22.4.3.2.1.1.1.]	[22.4.]
 3217644767340672907899084554130	125829120	[22.4.3.2.1.1.1.]	[22.]
 790130551223459534127080290097448600	71663616	[22.4.3.2.1.1.1.]	[21.8.1.]
 395065275611729767063540145048724300	71663616	[22.4.3.2.1.1.1.]	[21.8.]
 623787277281678579574010755340091000	84934656	[22.4.3.2.1.1.1.]	[21.7.3.]
 748544732738014295488812906408109200	99532800	[22.4.3.2.1.1.1.]	[21.7.2.2.]
 998059643650685727318417208544145600	111476736	[22.4.3.2.1.1.1.]	[21.7.2.1.1.1.]
 499029821825342863659208604272072800	111476736	[22.4.3.2.1.1.1.]	[21.7.2.1.1.]
 249514910912671431829604302136036400	111476736	[22.4.3.2.1.1.1.]	[21.7.2.1.]
 124757455456335715914802151068018200	111476736	[22.4.3.2.1.1.1.]	[21.7.2.]
 20792909242722619319133691844669700	111476736	[22.4.3.2.1.1.1.]	[21.7.]
 513707169526088242002126504397722000	94371840	[22.4.3.2.1.1.1.]	[21.6.4.1.]
 256853584763044121001063252198861000	94371840	[22.4.3.2.1.1.1.]	[21.6.4.]
 880640862044722700575074007538952000	123863040	[22.4.3.2.1.1.1.]	[21.6.3.2.1.1.]
 440320431022361350287537003769476000	123863040	[22.4.3.2.1.1.1.]	[21.6.3.2.1.]
 220160215511180675143768501884738000	123863040	[22.4.3.2.1.1.1.]	[21.6.3.2.]
 587093908029815133716716005025968000	113246208	[22.4.3.2.1.1.1.]	[21.6.3.1.1.1.1.]
 293546954014907566858358002512984000	113246208	[22.4.3.2.1.1.1.]	[21.6.3.1.1.1.]
 146773477007453783429179001256492000	113246208	[22.4.3.2.1.1.1.]	[21.6.3.1.1.]
 73386738503726891714589500628246000	113246208	[22.4.3.2.1.1.1.]	[21.6.3.1.]
 36693369251863445857294750314123000	123863040	[22.4.3.2.1.1.1.]	[21.6.3.]
 528384517226833620345044404523371200	111476736	[22.4.3.2.1.1.1.]	[21.6.2.2.2.1.]
 264192258613416810172522202261685600	111476736	[22.4.3.2.1.1.1.]	[21.6.2.2.2.]
 704512689635778160460059206031161600	119439360	[22.4.3.2.1.1.1.]	[21.6.2.2.1.1.1.1.]
 352256344817889080230029603015580800	119439360	[22.4.3.2.1.1.1.]	[21.6.2.2.1.1.1.]
 176128172408944540115014801507790400	119439360	[22.4.3.2.1.1.1.]	[21.6.2.2.1.1.]
 88064086204472270057507400753895200	119439360	[22.4.3.2.1.1.1.]	[21.6.2.2.1.]
 44032043102236135028753700376947600	119439360	[22.4.3.2.1.1.1.]	[21.6.2.2.]
 7338673850372689171458950062824600	119439360	[22.4.3.2.1.1.1.]	[21.6.2.]
 1223112308395448195243158343804100	123863040	[22.4.3.2.1.1.1.]	[21.6.]
 869350594582610871080521776673068000	100663296	[22.4.3.2.1.1.1.]	[21.5.5.1.1.]
 434675297291305435540260888336534000	100663296	[22.4.3.2.1.1.1.]	[21.5.5.1.]
 217337648645652717770130444168267000	100663296	[22.4.3.2.1.1.1.]	[21.5.5.]
 592739041760871048463992120458910000	98304000	[22.4.3.2.1.1.1.]	[21.5.4.3.]
 711286850113045258156790544550692000	113246208	[22.4.3.2.1.1.1.]	[21.5.4.2.2.]
 948382466817393677542387392734256000	125829120	[22.4.3.2.1.1.1.]	[21.5.4.2.1.1.1.]
 474191233408696838771193696367128000	125829120	[22.4.3.2.1.1.1.]	[21.5.4.2.1.1.]
 237095616704348419385596848183564000	125829120	[22.4.3.2.1.1.1.]	[21.5.4.2.1.]
 118547808352174209692798424091782000	125829120	[22.4.3.2.1.1.1.]	[21.5.4.2.]
 19757968058695701615466404015297000	125829120	[22.4.3.2.1.1.1.]	[21.5.4.]
 508062035795032327254850388964780000	106168320	[22.4.3.2.1.1.1.]	[21.5.3.3.2.]
 677416047726709769673133851953040000	117964800	[22.4.3.2.1.1.1.]	[21.5.3.3.1.1.1.]
 338708023863354884836566925976520000	117964800	[22.4.3.2.1.1.1.]	[21.5.3.3.1.1.]
 169354011931677442418283462988260000	117964800	[22.4.3.2.1.1.1.]	[21.5.3.3.1.]
 84677005965838721209141731494130000	117964800	[22.4.3.2.1.1.1.]	[21.5.3.3.]
 609674442954038792705820466757736000	115605504	[22.4.3.2.1.1.1.]	[21.5.3.2.2.2.]
 812899257272051723607760622343648000	127401984	[21.5.3.2.2.1.1.1.]	[21.5.3.2.2.1.1.1.]
 406449628636025861803880311171824000	127401984	[21.5.3.2.2.1.1.1.]	[21.5.3.2.2.1.1.]
 203224814318012930901940155585912000	127401984	[21.5.3.2.2.1.1.1.]	[21.5.3.2.2.1.]
 101612407159006465450970077792956000	127401984	[21.5.3.2.2.1.1.1.]	[21.5.3.2.2.]
 16935401193167744241828346298826000	127401984	[21.5.3.2.2.1.1.1.]	[21.5.3.2.]
 2822566865527957373638057716471000	127401984	[21.5.3.2.2.1.1.1.]	[21.5.3.]
 94085562184265245787935257215700	127401984	[21.5.3.2.2.1.1.1.]	[21.5.]
 40729680599249024150621323470	    127401984	[21.5.3.2.2.1.1.1.]	[21.]
 746835726498886408969432055023615800	71663616	[21.5.3.2.2.1.1.1.]	[20.9.2.]
 995780968665181878625909406698154400	80621568	[21.5.3.2.2.1.1.1.]	[20.9.1.1.1.]
 497890484332590939312954703349077200	80621568	[21.5.3.2.2.1.1.1.]	[20.9.1.1.]
 248945242166295469656477351674538600	80621568	[21.5.3.2.2.1.1.1.]	[20.9.1.]
 124472621083147734828238675837269300	80621568	[21.5.3.2.2.1.1.1.]	[20.9.]
 974133556302895316047085289161238000	99532800	[21.5.3.2.2.1.1.1.]	[20.8.3.2.]
 649422370868596877364723526107492000	95551488	[21.5.3.2.2.1.1.1.]	[20.8.3.1.1.]
 324711185434298438682361763053746000	95551488	[21.5.3.2.2.1.1.1.]	[20.8.3.1.]
 162355592717149219341180881526873000	99532800	[21.5.3.2.2.1.1.1.]	[20.8.3.]
 779306845042316252837668231328990400	104509440	[21.5.3.2.2.1.1.1.]	[20.8.2.2.1.1.]
 389653422521158126418834115664495200	104509440	[21.5.3.2.2.1.1.1.]	[20.8.2.2.1.]
 194826711260579063209417057832247600	104509440	[21.5.3.2.2.1.1.1.]	[20.8.2.2.]
 519537896694877501891778820885993600	95551488	[21.5.3.2.2.1.1.1.]	[20.8.2.1.1.1.1.]
 259768948347438750945889410442996800	95551488	[21.5.3.2.2.1.1.1.]	[20.8.2.1.1.1.]
 129884474173719375472944705221498400	95551488	[21.5.3.2.2.1.1.1.]	[20.8.2.1.1.]
 64942237086859687736472352610749200	95551488	[21.5.3.2.2.1.1.1.]	[20.8.2.1.]
 32471118543429843868236176305374600	104509440	[21.5.3.2.2.1.1.1.]	[20.8.2.]
 5411853090571640644706029384229100	104509440	[21.5.3.2.2.1.1.1.]	[20.8.]
 657967402064236309961627783029959000	75497472	[21.5.3.2.2.1.1.1.]	[20.7.5.]
 717782620433712338139957581487228000	106168320	[21.5.3.2.2.1.1.1.]	[20.7.4.2.1.]
 358891310216856169069978790743614000	106168320	[21.5.3.2.2.1.1.1.]	[20.7.4.2.]
 957043493911616450853276775316304000	113246208	[21.5.3.2.2.1.1.1.]	[20.7.4.1.1.1.1.]
 478521746955808225426638387658152000	113246208	[21.5.3.2.2.1.1.1.]	[20.7.4.1.1.1.]
 239260873477904112713319193829076000	113246208	[21.5.3.2.2.1.1.1.]	[20.7.4.1.1.]
 119630436738952056356659596914538000	113246208	[21.5.3.2.2.1.1.1.]	[20.7.4.1.]
 59815218369476028178329798457269000	113246208	[21.5.3.2.2.1.1.1.]	[20.7.4.]
 512701871738365955814255415348020000	99532800	[21.5.3.2.2.1.1.1.]	[20.7.3.3.1.]
 256350935869182977907127707674010000	99532800	[21.5.3.2.2.1.1.1.]	[20.7.3.3.]
 615242246086039146977106498417624000	111476736	[21.5.3.2.2.1.1.1.]	[20.7.3.2.2.1.]
 307621123043019573488553249208812000	111476736	[21.5.3.2.2.1.1.1.]	[20.7.3.2.2.]
 820322994781385529302808664556832000	119439360	[21.5.3.2.2.1.1.1.]	[20.7.3.2.1.1.1.1.]
 410161497390692764651404332278416000	119439360	[21.5.3.2.2.1.1.1.]	[20.7.3.2.1.1.1.]
 205080748695346382325702166139208000	119439360	[21.5.3.2.2.1.1.1.]	[20.7.3.2.1.1.]
 102540374347673191162851083069604000	119439360	[21.5.3.2.2.1.1.1.]	[20.7.3.2.1.]
 51270187173836595581425541534802000	119439360	[21.5.3.2.2.1.1.1.]	[20.7.3.2.]
 8545031195639432596904256922467000	119439360	[21.5.3.2.2.1.1.1.]	[20.7.3.]
 284834373187981086563475230748900	119439360	[21.5.3.2.2.1.1.1.]	[20.7.]
 503151542755004237029480069375851000	67108864	[21.5.3.2.2.1.1.1.]	[20.6.6.]
 928895155855392437592886281924648000	110100480	[21.5.3.2.2.1.1.1.]	[20.6.5.2.1.1.]
 464447577927696218796443140962324000	110100480	[21.5.3.2.2.1.1.1.]	[20.6.5.2.1.]
 232223788963848109398221570481162000	110100480	[21.5.3.2.2.1.1.1.]	[20.6.5.2.]
 619263437236928291728590854616432000	100663296	[21.5.3.2.2.1.1.1.]	[20.6.5.1.1.1.1.]
 309631718618464145864295427308216000	100663296	[21.5.3.2.2.1.1.1.]	[20.6.5.1.1.1.]
 154815859309232072932147713654108000	100663296	[21.5.3.2.2.1.1.1.]	[20.6.5.1.1.]
 77407929654616036466073856827054000	100663296	[21.5.3.2.2.1.1.1.]	[20.6.5.1.]
 38703964827308018233036928413527000	110100480	[21.5.3.2.2.1.1.1.]	[20.6.5.]
 738893873975880348085250451530970000	92160000	[21.5.3.2.2.1.1.1.]	[20.6.4.4.]
 633337606265040298358786101312260000	106168320	[21.5.3.2.2.1.1.1.]	[20.6.4.3.2.]
 844450141686720397811714801749680000	117964800	[21.5.3.2.2.1.1.1.]	[20.6.4.3.1.1.1.]
 422225070843360198905857400874840000	117964800	[21.5.3.2.2.1.1.1.]	[20.6.4.3.1.1.]
 211112535421680099452928700437420000	117964800	[21.5.3.2.2.1.1.1.]	[20.6.4.3.1.]
 105556267710840049726464350218710000	117964800	[21.5.3.2.2.1.1.1.]	[20.6.4.3.]
 760005127518048358030543321574712000	115605504	[21.5.3.2.2.1.1.1.]	[20.6.4.2.2.2.]
 506670085012032238687028881049808000	113246208	[21.5.3.2.2.1.1.1.]	[20.6.4.2.2.1.1.]
 253335042506016119343514440524904000	113246208	[21.5.3.2.2.1.1.1.]	[20.6.4.2.2.1.]
 126667521253008059671757220262452000	115605504	[21.5.3.2.2.1.1.1.]	[20.6.4.2.2.]
 21111253542168009945292870043742000	115605504	[21.5.3.2.2.1.1.1.]	[20.6.4.2.]
 3518542257028001657548811673957000	117964800	[21.5.3.2.2.1.1.1.]	[20.6.4.]
 16754963128704769797851484161700	117964800	[21.5.3.2.2.1.1.1.]	[20.6.]
 557940830126698960967415390	119439360	[21.5.3.2.2.1.1.1.]	[20.]
 1	127401984	[21.5.3.2.2.1.1.1.]	[]

Количество последовательностей = 168
Цепочка произведений = [21.5.3.2.2.1.1.1.],
Kоличество множителей = 127401984
Минимальное число = 812899257272051723607760622343648000 

</pre>

Расширенная постановка задачи

Итак, мы нашли оптимальное решение задачи, которому соответствует минимальное среди n<N. В приведённом примере отношение N/n=1.23. Но если бы потребовалось найти все возможные числа до N с полученным количеством делителей, то возникла бы комбинаторная задача на тему возможных обменов простых множителей.

Источник

I think this problem can be solved by algorithm similar to Hamming Number, indeed your original concept is very similar to Hamming Number as well.

Hamming Number is a problem to generate number x, where x = 2^i * 3*j * 5*k, from small to large in O(N) where N is the number of hamming number to be generated.

Here, I think similar concept can be used but we have to use the set of prime which is below your upper bound instead of {2,3,5}, we just need to also count the maximum # of prime factors when generating the number, and output it after the number generated is larger than N.

For example, here is the list of hamming number(using {2,3,5} for demo purpose) < 100:

1 2 3 4 5 6 8 9 10 12 15 16 18 20 24 25 27 30 32 36 40 45 48 50 54 60 64 72 75 80 81 90 96 100

60 = 2^2 * 3^1 * 5^1, total factors = 3*2*2 = 12 or

96 = 2^5 * 3^1, total factors = 6*2 = 12

So there may be multiple answer but you should be able to capture them while generating hamming number.

One can show that it is logically correct because

  1. The numbers are generated by prime numbers (prime factors)
  2. The numbers are generated in order

Note that in your case, basically you are generating all positive numbers from 1 to your upper bound.

Here is a site with tons of example in different language implementing this algorithm to generate hamming numbers: https://rosettacode.org/wiki/Hamming_numbers

Источник

ProgramerPython

0 / 0 / 0

Регистрация: 09.02.2019

Сообщений: 19

1

14.04.2019, 18:26. Показов 8386. Ответов 1

Метки нет (Все метки)

Студворк — интернет-сервис помощи студентам

Всем добрый день
Прошу помочь переписать или исправить код так, чтобы он работал для больших чисел(1 ⩽ a ⩽ b ⩽ 1 млн). Сам просто в питоне не силен.
Исходный смысл задачи: найти число с самым большим кол-вом делителей в интервале от а до b включительно и вывести его.
Требования к задаче: Ограничение по времени: 2 секунды

Мой код:

Python 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def sea(a, b):
    nums = range(a, b+1)
    result = []
    maximal = [0, 0]
    for i in nums:
        dev = 0
        for z in range(1, i+1):
            if not i % z:
                dev += 1
        result.append([i, dev])
    for i in result:
        if i[1] > maximal[1]:
            maximal = i
    print(max(maximal))
    return maximal
 
sea(int(input()),int(input()))



0

m0nte-cr1st0

1040 / 575 / 242

Регистрация: 15.01.2019

Сообщений: 2,178

Записей в блоге: 1

14.04.2019, 18:35

2

Лучший ответ Сообщение было отмечено ProgramerPython как решение

Решение

ProgramerPython,

Python 
1
2
3
4
5
6
7
8
9
10
11
12
13
14

i = n = D = 0
while D < 500:
    i += 1
    n += i
    if n % (2*3*5*7) != 0: 
        continue
    d = 2
    for j in range(2, int(n**0.5) + 1):
        if n % j == 0: 
            d += 2
        if j * j == n: 
            d -= 1
    D = max(D, d)
print(i, n, D)



1
Источник

Понятие наибольшего общего делителя

Для начала разберемся, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.

Делитель натурального числа — это такое целое натуральное число, на которое делится данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.

Общий делитель нескольких целых чисел — это такое число, которое может быть делителем каждого числа из указанного множества. Например, у чисел 12 и 8 общими делителями будут 4 и 1. Чтобы это проверить, напишем верные равенства: 8 = 4 * 2 и 12 = 3 * 4.

Любое число можно разделить на 1 и на само себя. Значит, у любого набора целых чисел будет как минимум два общих делителя.

Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).

Например, для 4 и 16 НОД будет 4. Как мы к этому пришли:

  1. Зафиксируем все делители четырех: 4, 2, 1.

  2. А теперь все делители шестнадцати: 16, 8, 4 и 1.

  3. Выбираем общие: это 4, 2, 1. Самое большое общее число: 4. Вот и ответ.

Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.

Найдем наибольший общий делитель нескольких целых чисел: 12, 6, 42, 18. Он будет равен шести. Ответ можно записать так: НОД (12, 6, 42, 18) = 6. А чтобы проверить правильность ответа, нужно записать все делители и выбрать из них самые большие.

Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.

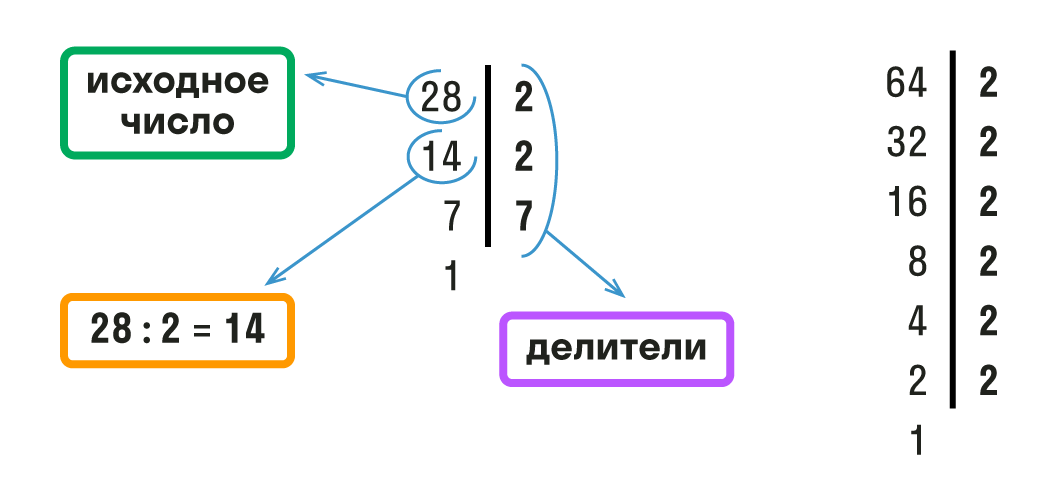
Еще один пример. Рассчитаем НОД для 28 и 64.

Как находим:

 

  1. Распишем простые множители для каждого числа и подчеркнем одинаковые

    Д (28) = 2 * 2 * 7

    Д (64) = 2 * 2 * 2 * 2 * 2 * 2

  2. Найдем произведение одинаковых простых множителей и запишем ответ

    НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Альтернативный текст для изображения

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Узнай, какие профессии будущего тебе подойдут

Способы нахождения наибольшего общего делителя

Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.

1. Разложение на множители

Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.

Пример 1. Найти НОД (84, 90).

Как решаем:

 

  1. Разложим числа 84 и 90 на простые множители:

    Пример разложения чисел 84 и 90

  2. Подчеркнем все общие множители и перемножим их между собой:

    2 * 3 = 6.

 

Ответ: НОД (84, 90) = 6.

Пример 2. Найти НОД (15, 28).

Как решаем:

 

  1. Разложим 15 и 28 на простые множители:

    пример разложения чисел 15 и 28

  2. Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель — единица.

 

Ответ: НОД (15, 28) = 1.

Пример 3. Найти НОД для 24 и 18.

Как решаем:

 

  1. Разложим оба числа на простые множители:

    Разложение чисел на простые множители

  2. Найдем общие множители чисел 24 и 18: 2 и 3. Для удобства общие множители можно подчеркнуть.

    Находим общие множители

  3. Перемножим общие множители:

    НОД (24, 18) =2 * 3 = 6

 

Ответ: НОД (24, 18) = 6

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

2. Алгоритм Евклида

Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.

Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.

Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.

Пример 1. Найти НОД для 24 и 8.

Как рассуждаем:

Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, 8) = 8.

В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:

 

  1. Большее число поделить на меньшее.

  2. Меньшее число поделить на остаток, который получается после деления.

  3. Первый остаток поделить на второй остаток.

  4. Второй остаток поделить на третий и т. д.

  5. Деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель и есть наибольший общий делитель.

Пример 2. Найти наибольший общий делитель чисел 140 и 96:

Как решаем:

 

  1. 140 : 96 = 1 (остаток 44)

  2. 96 : 44 = 2 (остаток 8)

  3. 44 : 8 = 5 (остаток 4)

  4. 8 : 4 = 2

Последний делитель равен 4 — это значит: НОД (140, 96) = 4.

Ответ: НОД (140, 96) = 4

Пошаговое деление можно записать столбиком:

пошаговое деление солбиком

Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:

 

  1. Найти наибольший общий делитель любых двух чисел из данных.

  2. Найти НОД найденного делителя и третьего числа.

  3. Найти НОД последнего найденного делителя и четвёртого числа и т. д.

Свойства наибольшего общего делителя

У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.

Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.

Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.

Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.

Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.

Доказательство

 

Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Из этого следует, что любой делитель числа b является общим делителем чисел а и b.

 

Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b.

 

В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.

  • Например, НОД (25, 25) = 25.

Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.

  • Например, НОД (4, 40) = 4, так как 40 кратно 4.

Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.

Доказательство

 

Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c.

 

Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым.

Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).

Доказательство

Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители.

Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.

Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.

Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.

Источник


Загрузить PDF


Загрузить PDF

Нахождение наибольшего общего делителя (НОД) для определенного количества чисел может быть легкой задачей, если вы умеете это делать.

  1. Изображение с названием Find the Greatest Common Factor Step 1

    1

    Найдите делители чисел. Начните с поиска всех делителей первого и второго числа.

  2. Изображение с названием Find the Greatest Common Factor Step 2

    2

    Сравните делители обоих чисел и найдите самое большое число, которое есть в списке делителей как первого, так и второго числа. Это число равно НОД.

    Реклама

  1. Изображение с названием Find the Greatest Common Factor Step 3

    1

    Разложите каждое число на простые множители. Простое число — это число, большее 1 и которое делится только на 1 и на само себя. Примеры простых чисел: 5, 17, 97, 331.

  2. Изображение с названием Find the Greatest Common Factor Step 4

    2

    Найдите общие простые множители. Общий простой множитель может быть только один, или их может быть несколько.

  3. Изображение с названием Find the Greatest Common Factor Step 5

    3

    Если у двух чисел есть только один общий простой множитель, то он равен НОД. Если у двух чисел есть несколько общих простых множителей, то их произведение равно НОД.

  4. Изображение с названием Find the Greatest Common Factor Step 6

    4

    Изучите пример. Чтобы продемонстрировать этот метод, изучите пример, приведенный на рисунке.

    Реклама

Советы

  • Простое число — это число, которое делится только на 1 и на само себя.
  • Знаете ли вы, что в третьем веке до н.э. математик Евклид создал алгоритм для вычисления наибольшего общего делителя двух натуральных чисел и двух многочленов?

Реклама

Об этой статье

Эту страницу просматривали 7409 раз.

Была ли эта статья полезной?

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти молярную концентрацию раствора пример
  • Как найти импульс пружины
  • Как составить сложноподчиненное предложение с определительным придаточным
  • Как найти образующую усеченого конуса
  • Как составить пентакли

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии