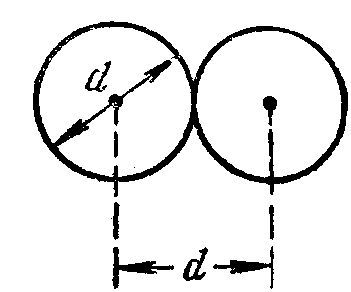Основное уравнение молекулярно-кинетической теории газов
Определение и формула основного уравнения молекулярно-кинетической теории
Изучать процессы, которые протекают в больших системах весьма сложно из за огромного числа частиц и их малых размеров. Рассмотреть отдельно каждую частицу практически невозможно, вводятся статистические величины: средняя скорость частиц, их концентрация, масса частицы. Возникает необходимость, установления математической связи (уравнения) между микро параметрами, которые относят к отдельным частицам (масса молекулы, ее скорость и т.д.) и макро параметрами описывающими систему в целом (температура, давление) Формула, характеризующая состояние системы с учетом микроскопических и макроскопических параметров, называется основным уравнением молекулярно-кинетической теории газов (МКТ).
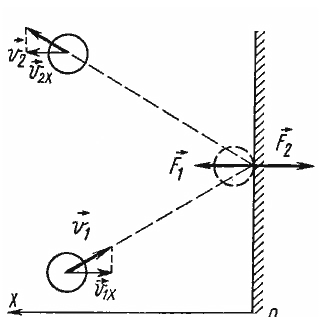
Естественно, что проще всего устанавливается такая связь на простейшей модели — идеальном газе. В газе молекулы совершают свободное (изолированное от других молекул) движение, лишь время от времени сталкиваясь друг с другом или со стенками сосуда. Было сделано предположение, что давление газа является результатом ударений молекул о стенки сосуда. В свою очередь, сила есть импульс, передаваемый от тела к телу в секунду. Значит, чтобы найти давление газа, нужно определить, какой импульс передаёт газ единице площади стенки сосуда в секунду.
рис. 1.
Довольно простой расчет и основные положения молекулярно-кинетической теории позволяют получить уравнение, связывающее давление газа, если известны масса молекулы , среднее значение скорости молекул
и концентрацию молекул в газе n:
это уравнение называют основным уравнением молекулярно-кинетической теории.
Если мы обозначим среднее значение кинетической энергии поступательного движения молекул через , в таком случае уравнение (1) примет вид:
Средняя кинетическая энергия молекулы пpи равновесии идеального газа обладает одной очень важной особенностью: в смеси различных идеальных газов средняя кинетическая энергия молекулы для различных компонентов смеси одна и та же.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Количество молекул продукта, образующихся за 1 секунду Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Квантовая эффективность для продуктов: 99 —> Конверсия не требуется
Количество поглощенных квантов: 51 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
5049 —> Конверсия не требуется
18 Закон Старка-Эйнштейна Калькуляторы
Количество молекул продукта, образующихся за 1 секунду формула
Молекулы продукта, образующиеся в секунду = Квантовая эффективность для продуктов*Количество поглощенных квантов
dNPdt = Φp*Iquanta
Что такое закон фотохимической эквивалентности Штарка-Эйнштейна?
Закон фотохимической эквивалентности Штарка-Эйнштейна можно сформулировать следующим образом: каждая молекула, участвующая в фотохимической реакции, поглощает один квант излучения, вызывающего реакцию. Этот закон применим к первичному акту возбуждения молекулы за счет поглощения света. Этот закон помогает вычислить квантовую эффективность, которая является мерой эффективности использования света в фотохимической реакции.
Что такое закон Гроттуса-Дрейпера?
Согласно этому закону, только свет, который поглощается молекулой, может вызвать в ней фотохимические изменения. Это означает, что недостаточно пропустить свет через вещество, чтобы вызвать химическую реакцию; но свет должен поглощаться им. Закон фотохимической эквивалентности Штарка-Эйнштейна обеспечивает квантово-механическую форму закону Гроттуса-Дрейпера.
-
Средняя длина
свободного пробега
-
Эффективный
диаметр молекулы
Молекулы
газа, находясь в тепловом движении,
непрерывно сталкиваются друг с другом.
Термин «столкновение» применительно
к молекулам не следует понимать буквально
и представлять себе этот процесс подобным
соударению твердых шаров. Под столкновением
молекул подразумевают процесс
взаимодействия между молекулами, в
результате которого молекулы изменяют
направление своего движения.
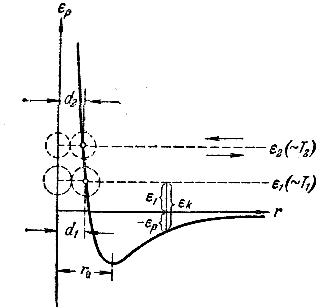
На рис.1 показана кривая, изображающая
взаимную потенциальную энергию двух
молекул как функцию расстояния r
между их центрами.
Рассмотрим с помощью этой кривой
процесс сближения (соударения) молекул.
-
Поместим мысленно центр одной из молекул
в начало координат, а центр второй
молекулы представим перемещающимся
по оси r. -
Пусть вторая молекула летит по направлению
к первой из бесконечности, имея начальный
запас кинетической энергии
. -
Приближаясь к первой молекуле, вторая
под действием силы притяжения движется
с все возрастающей скоростью. В
результате:
— кинетическая энергия молекулы
также растет.
— полная энергия системы, равная
,
остается неизменной (система двух
молекул замкнута) и равной
,
так как одновременно уменьшается
потенциальная энергия
.
-
При прохождении молекулой точки с
координатой
силы притяжения сменяются силами
отталкивания, вследствие чего молекула
начинает быстро терять скорость (в
области отталкивания криваяидет очень круто). В момент, когда
потенциальная энергиястановится равной полной энергии
системы,
скорость молекулы обращается в нуль.
В этот момент имеет место наибольшее
сближение молекул друг с другом. -
После остановки молекулы все явления
протекают в обратной последовательности:
сначала молекула движется с все
возрастающей скоростью под действием
силы отталкивания; миновав расстояние
,
молекула попадает под действие
замедляющей ее движение силы притяжения
и, наконец, удаляется на бесконечность,
имея первоначальный запас кинетической
энергии.
Минимальное расстояние, на которое
сближаются при столкновении центры
двух молекул, называется эффективным
диаметром молекулы d
(рис. 2).
Величина
называется
эффективным сечением молекулы
.
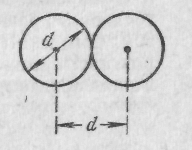
Из рис.1 видно, что в случае, когда
молекула начинает свое движение из
бесконечности с большим запасом энергии,
минимальное расстояние, на которое
сближаются центры молекул, оказывается
меньшим (d1 и d2
на рисунке).
Таким образом, эффективный диаметр
молекул зависит от их энергии, а
следовательно, и от температуры. С
повышением температуры эффективный
диаметр молекул уменьшается.
За время между двумя последовательными
соударениями молекула газа проходит
некоторый путь
,
который называется длиной
свободного пробега.
Длина свободного пробега — случайная
величина. Иной раз молекуле удается
пролететь между соударениями довольно
большой путь, в другой раз этот путь
может оказаться весьма малым.
Найдем вероятность различных значений
.
Вероятность dP
того, что молекула испытает
соударение на отрезке пути ds,
очевидно, пропорциональна величине
этого отрезка и не зависит от того, какой
путь уже прошла молекула без столкновений.
Взяв коэффициент пропорциональности
в виде
,
получим, что
Вероятность — безразмерная
величина, следовательно,
λ- имеет размерность длины.
Пусть из полного числа
молекул путь s пролетели
без столкновения N(s)
молекул.
Из их числа претерпевает соударения на
следующем за s отрезке ds
количество молекул, равное
.
Это количество представляет собой убыль
величины N(s)
на отрезке ds,
т. е. – dN(s).
Таким образом,
Проинтегрировав, получаем
.
Здесь
= N(0) — число
молекул, прошедших без столкновений
путь, равный нулю, т. е. полное число
молекул.
Отношение N(s)
к
дает вероятность P(s)
того, что молекула пролетит, начиная с
некоторого выбранного произвольно
момента времени, путь s
без столкновений:
Найдем среднее значение длины
свободного пробега
.
Для этого нужно знать вероятность dPl
того, что молекула, пролетев без
столкновений путь
,
претерпит соударение на следующем за
отрезке d
.
Оба эти события, т. е. пролет без
столкновений пути
и соударение на отрезке d
,
статистически независимы. Следовательно,
dPl
равна произведению вероятностей двух
указанных событий.
Вероятность первого события равна
.
Вероятность второго события в соответствии
равна
.
Таким образом,
Среднее значение
:
Таким образом, обозначенная нами
буквой λ величина совпадает
со средней длиной свободного пробега.
За секунду молекула проходит в среднем
путь, равный средней скорости
.
Если за секунду она претерпевает в
среднем
столкновений, то средняя длина
свободного пробега будет равна
Д
ля
того чтобы подсчитать среднее число
столкновений
,
-
предположим вначале, что все
молекулы, кроме данной, застыли неподвижно
на своих местах. -
Проследим за движением выделенной
нами молекулы.
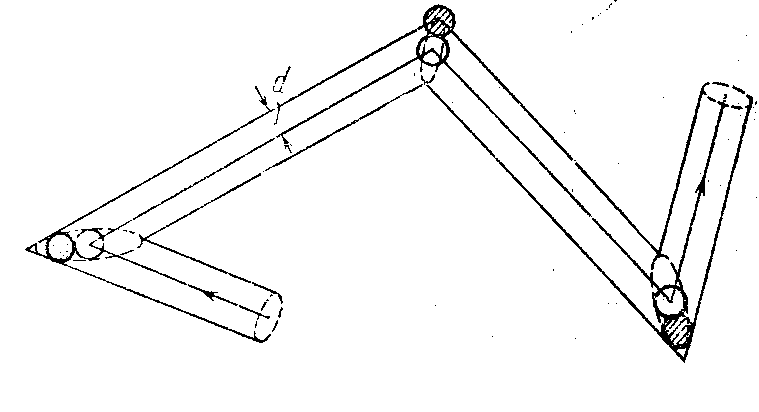
— Ударившись об одну из неподвижных
молекул, она будет лететь прямолинейно
до тех пор, пока не столкнется с какой-либо
другой неподвижной молекулой (рис.3).
— Это соударение произойдет в том случае,
если центр неподвижной молекулы окажется
от прямой, вдоль которой летит молекула,
на расстоянии, меньшем эффективного
диаметра молекулы d.
— В результате столкновения молекула
изменит направление своего движения,
после чего некоторое время опять будет
двигаться прямолинейно, пока на ее пути
снова не встретится молекула, центр
которой будет находиться в пределах
показанного на рис.3 цилиндра радиуса
d.
-
За секунду молекула проходит путь,
равный.
-
Число происходящих за это время
соударений с неподвижными молекулами
равно количеству молекул, центры которых
попадают внутрь коленчатого цилиндра
длиныи радиуса d.
-
Средняя длина свободного пробега много
больше, чем эффективный диаметр молекул
d. -
Поэтому объем цилиндра можно считать
равным πd2
. -
Умножив этот объем на число молекул в
единице объема n,
получим среднее число столкновений
за секунду движущейся молекулы с
неподвижными:
В действительности все молекулы движутся,
и число соударений определяется средней
скоростью движения молекул по отношению
друг к другу, а не средней скоростью
молекул относительно стенок сосуда.
Относительная скорость двух произвольно
взятых молекул равна
Возведя это соотношение в квадрат,
получим
Начало
формы
Конец
формы
(мы воспользовались тем, что
).
Среднее значение суммы нескольких
величин равно сумме средних значений
складываемых величин. Поэтому
События, заключающиеся в том,
что первая молекула имеет скорость
,
а вторая — скорость
,
являются статистически независимыми.
Поэтому
.
Для газа, находящегося в равновесии,
каждый из сомножителей равен нулю. Таким
образом,
(среднее значение квадрата скорости
всех молекул одинаково и равно
).
Среднее число столкновений за секунду
и средняя длина свободного пробега:
Заменив πd2 через
σ (где
эффективное сечение молекулы) ,
получаем
При постоянной температуре n
пропорционально р (р=nkT).
Следовательно, средняя длина свободного
пробега обратно пропорциональна
давлению:
Эффективный диаметр молекул убывает
с ростом температуры, поэтому при
повышении температуры длина свободного
пробега увеличивается.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
За 10 суток полностью
испарилось из стакана 100 г воды. Сколько в среднем вылетало молекул с
поверхности воды за 1,0 с (постоянная Авогадро NA = 6,02•1023 1/моль)?
Решение.
Число молекул воды в
стакане определяется из соотношения N = mNA/M, M –
молярная масса воды. В среднем за 1,0 с с поверхности воды в стакане вылетает N1 молекул. N1 = N/t = mNA/Mt = 3,9•1018.
Ответ: за 1 секунду с
поверхности воды вылетало примерно 3,9•1018 молекул.
Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.
2017-06-30
Оцените число ударов молекул воздуха о поверхность оконного стекла площадью $S = l м^{2}$ со стороны аудитории за интервал времени $Delta t = 1 с$. Температура воздуха в аудитории $t = 27^{ circ} С$, давление $p = 10^{5} Па$, молярная масса воздуха $mu = 29 г/моль$.
Решение:
При заданных условиях ($p = 10^{5} Па$) воздух можно считать идеальным газом, поэтому молекулы воздуха, удаленные от поверхности стекла на расстояние не большее, чем $langle v rangle Delta t$ ($langle v rangle$ — средняя скорость молекул, под которой будем иметь ввиду среднеквадратичную скорость, $Delta t = frac{1}{ nu}$, $nu$ — частота столкновений молекул), будут менять направление своего движения только при столкновениях с поверхностью окна, а не за счет столкновений друг с другом. При этом за время $Delta t$ о поверхность стекла ударятся в среднем
$N = frac{nS langle v rangle Delta t}{6}$
молекул воздуха, т.е. те молекулы, которые находятся в объеме $Sv Delta t$ и движутся в направлении окна, $n$ — концентрация молекул. Это — 1/6 часть (примерно) всех молекул, заключенных в объеме $Sv Delta t$ (рисунок).
Концентрацию молекул можно выразить через давление $p$ и температуру $T = t + 273 К$ из уравнения состояния идеального газа $p = nkT$, а скорость можно найти из соотношения, связывающего среднюю кинетическую энергию поступательного движения молекулы $langle E rangle$ и абсолютную температуру
$langle E rangle = frac{3}{2} kT = m_{0} frac{ langle v^{2} rangle }{2}$,
$m_{0}$ — масса молекулы. Тогда
$N = frac{pS Delta t}{6kT} sqrt{ frac{3kT}{m_{0}}} = frac{pS Delta t N_{A}}{6} sqrt{ frac{3}{R(t + 273) mu}} approx 2 cdot 10^{27}$.
Здесь $N_{A} = 6 cdot 10^{23} frac{1}{моль}$