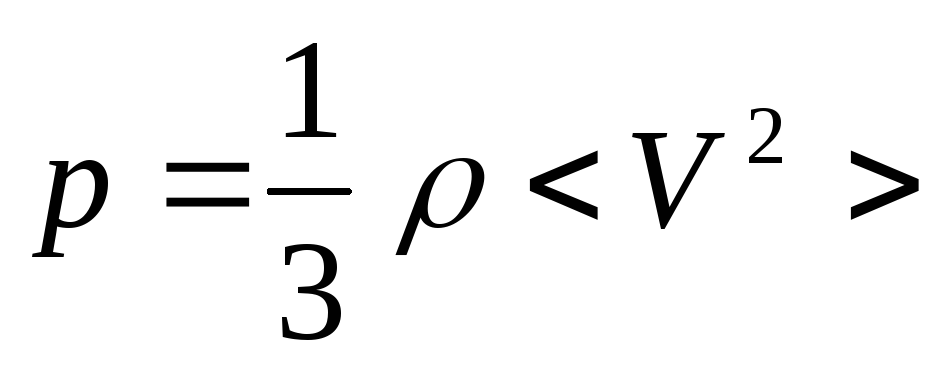Примеры решения задач
Задача 1.
Найти число молекул в 1 см3
водорода, если давление газа равно
2,67.104
Па, а средняя квадратичная скорость его
молекул при данных условиях равна 2400
.
Дано:
Решение
р
В условиях задачи
концентрацию молекул можно найти двумя
способами:
1. Используем
основное уравнение кинетической теории
где
.
= 2,67.104
Па
<Vкв
> = 2400
V
= 1 см3
= 10–6
м3
= 2.10-3
N
— ?
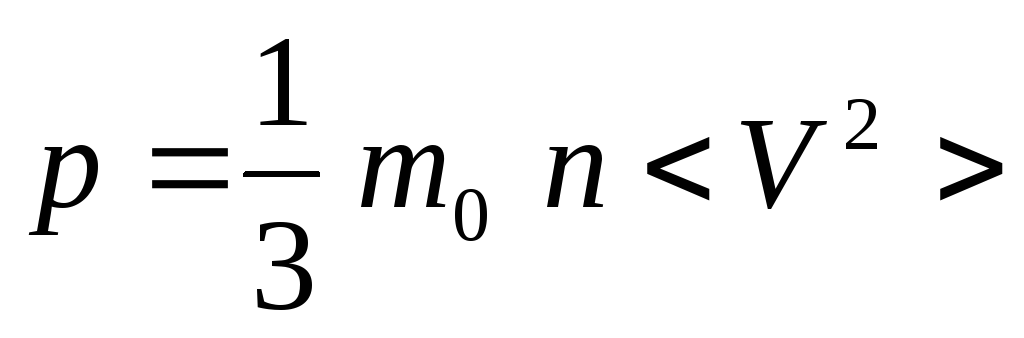
где
.
Отсюда
.
(1)
Массу молекулы
найдем, зная молярную массу и число
Авогадро:
.
Подставляем в
формулу (1):
.
Вычисляем
концентрацию молекул:
= 4,2 .
1024
м –3.
Тогда число молекул
N
= n
.
V
= 4,2 . 1018
(молекул).
2. Используя связь
давления с концентрацией и формулу
средней квадратичной скорости
Получаем ту же
формулу для вычисления п.
Ответ: N
= 4,2 . 1018
молекул содержится в 1 см3.
Задача 2.
Плотность некоторого газа 6.10-2
,
а средняя квадратичная скорость его
молекул <Vкв
> = 500
.
Найти давление, которое газ оказывает
на стенки сосуда.
Д
Запишем основное
уравнение молекулярно-кинетической
теории:
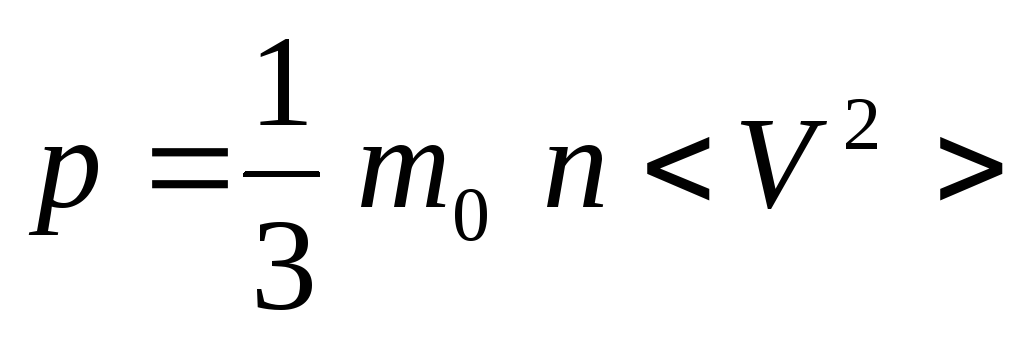
= 6,0 . 10-2
<Vкв
> = 500
p
— ?
Преобразуем
это уравнение:
где N
– число молекул газа, т
– масса газа,
– масса одной молекулы газа.
Тогда — плотность газа равна произведению массы одной молекулы на концентрацию молекул. Получим
= 5 .
103
Па.
Ответ: p
= 5 . 103
Па.
Задача 3.
В колбе емкостью V
= 100 см3
содержится некоторый газ при температуре
t
= 27 0С.
На сколько понизится давление газа в
колбе, если вследствие утечки из колбы
выйдет N
= 1020
молекул?
Д
V
Начальное давление
в колбе
=
k
T.
Конечное давление
= 100 см3
= 10-4 м3
t
= 27 0С,
Т
= 300 К

= 1020
молекул
р
— ?
=
k
T,
где
и
– концентрации молекул газа в колбе.
Отсюда получаем изменение давления при утечке газа
,
.
Тогда
,
= 4,14 .
103
Па.
Ответ: р
= 4,14 Па.
Задача 4.
Определить среднюю кинетическую энергию
теплового движения всех молекул
двухатомного газа, заключенного в сосуд
объемом 2 л при давлении 1,5 .
105
Па?
Решение
Энергия теплового
движения одной молекулы идеального
газа
Д
V
= 2 л = 2 .10-3
м3
р =
1,5 . 105
Па
i
= 5
<
— ?
где i
– число степеней свободы молекулы.
В сосуде объемом
V
находится N
молекул. Полная энергия теплового
движения всех молекул равна
.
Число молекул газа
N
можно найти с помощью числа Авогадро.
Число молекул в одном моле вещества
одинаково для всех веществ и равно
.
Количество вещества
в молях определяется так:
где m
– масса вещества;
— его молярная масса.
Тогда число молекул будет равно
.
Полная энергия
теплового движения всех молекул вещества
.
Это выражение
определяет энергию теплового движения
всех молекул данного количества вещества.
Для идеального газа энергия теплового
движения молекул является его внутренней
энергией. Это следует из определения
идеального газа. Внутренняя энергия
обозначается буквой U:
.
Для условий нашей
задачи
(уравнение
Менделеева — Клапейрона).
Следовательно,
Дж.
Из равенства
видно, что внутренняя энергия идеального
газа зависит только от температуры
газа. Изменение внутренней энергии не
зависит от процесса. Внутренняя энергия
является функцией состояния.
Ответ: <Wк>
= 750 Дж.
Соседние файлы в папке Часть 3
- #
- #
- #
- #
- #
- #
- #
- #
- #
Опубликовано 08.06.2017 по предмету Физика от Гость
>> <<
Определите число молекул газа,содержащегося в трехлитровом сосуде,если средний квадрат скорости движения его молекул 3,6*10 в 5 степени м2/с2,масса молекул газа 4,6*10 -23 степени г,давление газа 920 Па.
Ответ оставил Гость
Дано:
V = 3 л = 0,003 м^3
v^2 = 3,6*10^5 м^2/c^2
mo = 4,6*10^-23 г = 4,6*10^-26 кг
p = 920 Па
___________________________
N — ?
Решение:
По основному уравнению МКТ
p = 1/3 mo*n*v^2, где n = N/V — концентрация молекул, тогда p = 1/3 mo*N/V * v^2
отсюда N = 3pV / (mo*v^2)
N = 3*920 Па*0,003 м^3 / (4,6*10^-26 кг*3,6*10^5 м^2/c^2) = 5*10^20
Оцени ответ
Подпишись на наш канал в телеграм. Там мы даём ещё больше полезной информации для школьников!

Тип 14 № 1056
i
Какое число молекул двухатомного газа содержится в сосуде объемом 20 см3 при давлении Па и температуре 27 °С? Какой энергией теплового движения обладают эти молекулы?
Спрятать решение
Решение.
По закону Авогадро концентрация молекул
Тогда число молекул равно
Средняя кинетическая энергия молекул равна
Ответ: Дж.
Источник: Кирик Л. А. Самостоятельные и контрольные работы для 10 класса, Х.: «Гимназия», 2002 (№ 1 (высок.) стр. 10)
Дано:
t=27°Ct=27°mathrm{C}
ρ=3.0 кПаrho=3.0,mathrm{кПа}
V=1.4 лV=1.4,mathrm{}л
Найти:
NN — ?
СИ:
t=300 К,t=300,К,
ρ=3.0⋅103 Па,rho = 3.0cdot 10^3,Па,
V=1.4⋅10−3 м3.V=1.4cdot 10^{-3}, м^3.
Решение:
Определим число молекул идеального газа по формуле
N=nVN=nV,
где nn — концентрация молекул газа.
Идеальный газ в сосуде создает давление ρ=nkT.rho=nkT.
Тогда n=ρkTn={dfrac{rho}{kT}}.
Следовательно, N=ρVkTN={dfrac{rho V}{kT}}.
N=3.0⋅103⋅1.4⋅10−31.38⋅10−23⋅300=1⋅1021.N={dfrac{3.0 cdot 10^3 cdot 1.4 cdot 10^{-3}}{1.38 cdot 10^{-23} cdot 300}}=1 cdot 10^{21}.
Ответ: N=1⋅1021.N=1 cdot 10^{21}.
Перейти к контенту
Условие задачи:
В сосуде находится газ под давлением 150 кПа при температуре 23° C. Найти концентрацию молекул.
Задача №4.1.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(p=150) кПа, (t=23^circ) C, (n-?)
Решение задачи:
Запишем формулу связи давления (p) идеального газа с концентрацией молекул (n) и абсолютной температурой (T):
[p = nkT]
В этой формуле (k) – постоянная Больцмана, равная 1,38·10-23 Дж/К. Выразим из этой формулы искомую концентрацию (n):
[n = frac{p}{{kT}}]
Обратите свое внимание, что в формуле фигурирует абсолютная температура, поэтому переведем данную в условии температуру в шкалу Кельвина:
[23^circ;C = 296;К]
Произведем вычисления:
[n = frac{{150 cdot {{10}^3}}}{{1,38 cdot {{10}^{ – 23}} cdot 296}} = 3,67 cdot {10^{25}};м^{-3}]
Ответ: 3,67·1025 м-3.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.1.20 Считая, что диаметр молекул водорода составляет около 0,23 нм, подсчитать, какой длины
4.1.22 Определить среднюю квадратичную скорость молекул водорода
4.1.23 Под каким давлением находится кислород в баллоне, если при температуре 27 C
( 13 оценок, среднее 4.08 из 5 )