Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
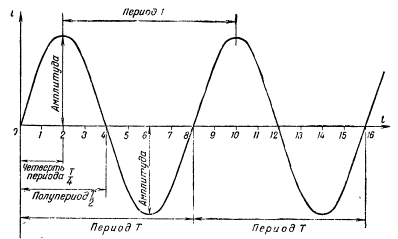
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10-3сек.
1 мкс=0,001 мс = 0,000001сек =10-6сек.
1000 мкс = 1 мс.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 103 Гц = 1 кГц;
1000 000 Гц = 106 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 109 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.
Рисунок 2. Радиан.
Тогда,
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.
Итак,
?= 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Переменный ток, в отличие от тока
постоянного, непрерывно изменяется как
по величине, так и по направлению, причем
изменения эти происходят периодически,
т. е. точно повторяются через равные
промежутки времени.
Чтобы вызвать в цепи такой ток, используются
источники переменного тока, создающие
переменную ЭДС, периодически изменяющуюся
по величине и направлению. Такие
источники называются генераторами
переменного тока.
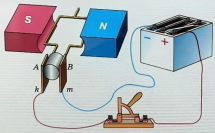
На рис. 1 показана схема устройства
(модель) простейшего генератора
переменного тока.
Прямоугольная рамка, изготовленная из
медной проволоки, укреплена на оси и
при помощи ременной передачи вращается
в поле магнита.
Концы рамки припаяны к медным контактным
кольцам, которые, вращаясь вместе с
рамкой, скользят по контактным пластинам
(щеткам).
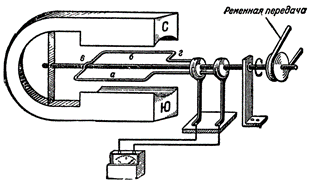
Рисунок 1. Схема простейшего генератора
переменного тока
Такое устройство является источником
переменной ЭДС.
Предположим, что магнит создает между
своими полюсами равномерное
магнитное поле, т. е. такое,
в котором плотность магнитных силовых
линий в любой части поля одинаковая.
Вращаясь, рамка пересекает силовые
линии магнитного поля, и в каждой из ее
сторон а и б индуктируются
ЭДС.
Стороны же в и г рамки — нерабочие,
так как при вращении рамки они не
пересекают силовых линий магнитного
поля и, следовательно, не участвуют в
создании ЭДС.
В любой момент времени ЭДС, возникающая
в стороне а, противоположна по
направлению ЭДС, возникающей в стороне
б, но в рамке обе ЭДС действуют
согласно и в сумме составляют общую
ЭДС, т. е. индуктируемую всей рамкой.
В этом нетрудно убедиться, если
использовать для определения направления
ЭДС известное нам правило правой руки.
Для этого надо ладонь правой руки
расположить так, чтобы она была обращена
в сторону северного полюса магнита, а
большой отогнутый палец совпадал с
направлением движения той стороны
рамки, в которой мы хотим определить
направление ЭДС. Тогда направление ЭДС
в ней укажут вытянутые пальцы руки.
Для какого бы положения рамки мы ни
определяли направление ЭДС в сторонах
а и б, они всегда складываются
и образуют общую ЭДС в рамке. При этом
с каждым оборотом рамки направление
общей ЭДС изменяется в ней на обратное,
так как каждая из рабочих сторон рамки
за один оборот проходит под разными
полюсами магнита.
Величина ЭДС, индуктируемой в рамке,
также изменяется, так как изменяется
скорость, с которой стороны рамки
пересекают силовые линии магнитного
поля. Действительно, в то время, когда
рамка подходит к своему вертикальному
положению и проходит его, скорость
пересечения силовых линий сторонами
рамки бывает наибольшей, и в рамке
индуктируется наибольшая ЭДС. В те
моменты времени, когда рамка проходит
свое горизонтальное положение, ее
стороны как бы скользят вдоль магнитных
силовых линий, не пересекая их, и ЭДС не
индуктируется.
Таким образом, при равномерном вращении
рамки в ней будет индуктироваться ЭДС,
периодически изменяющаяся как по
величине, так и по направлению.
ЭДС, возникающую в рамке, можно измерить
прибором и использовать для создания
тока во внешней цепи.
Используя явление
электромагнитной индукции,
можно получить переменную ЭДС и,
следовательно, переменный ток.
Переменный ток для промышленных
целей и для
освещения вырабатывается
мощными генераторами, приводимыми во
вращение паровыми или водяными турбинами
и двигателями внутреннего сгорания.
Графическое изображение постоянного
и переменного токов
Графический метод дает возможность
наглядно представить процесс изменения
той или иной переменной величины в
зависимости от времени.
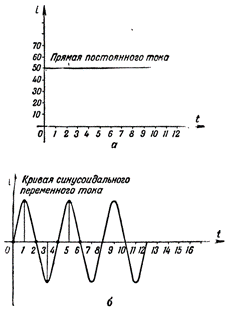
Рисунок 2. Графическое изображение
постоянного и переменного тока
На горизонтальной оси в определенном
масштабе откладывают отрезки времени,
а на вертикальной, также в некотором
масштабе, — значения той величины,
график которой собираются построить
(ЭДС, напряжения или тока).
На рис. 2 графически изображены постоянный
и переменный токи. В данном случае мы
откладываем значения тока, причем вверх
по вертикали от точки пересечения осей
0 откладываются значения тока одного
направления, которое принято называть
положительным, а вниз от этой точки —
противоположного направления, которое
принято называть отрицательным.
Убедиться в правильности построенного
на рис. 2,а графика постоянного тока
величиной 50 мА можно путём проведения
наблюдений.
Так как этот ток постоянный, т. е. не
меняющий с течением времени своей
величины и направления, то различным
моментам времени будут соответствовать
одни и те же значения тока, т. е. 50 мА.
Следовательно, в момент времени, равный
нулю, т. е. в начальный момент нашего
наблюдения за током, он будет равен 50
мА. Отложив по вертикальной оси вверх
отрезок, равный значению тока 50 мА,
получают первую точку графика.
То же самое следует сделать и для
следующего момента времени, соответствующего
точке 1 на оси времени, т. е. отложить от
этой точки вертикально вверх отрезок,
также равный 50 мА. Конец отрезка определит
нам вторую точку графика.
Проделав подобное построение для
нескольких последующих моментов времени,
мы получим ряд точек, соединение которых
даст прямую линию, являющуюся графическим
изображением постоянного тока
величиной 50 мА.
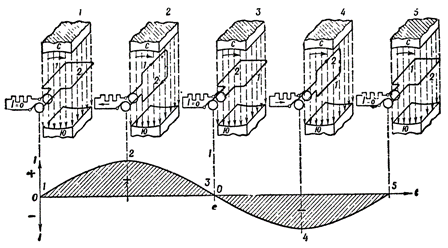
Рисунок 3. Построение графика переменной
ЭДС
Построение графика переменной ЭДС
На рис. 3 в верхней части показана рамка,
вращающаяся в магнитном поле, а внизу
дано графическое изображение возникающей
переменной ЭДС.
При равномерном вращении рамки по
часовой стрелке можно проследить ход
изменения в ней ЭДС, приняв за начальный
момент горизонтальное положение рамки.
В этот начальный момент ЭДС будет равна
нулю, так как стороны рамки не пересекают
магнитных силовых линий. На графике это
нулевое значение ЭДС, соответствующее
моменту t = 0, изобразится
точкой 1.
При дальнейшем вращении рамки в ней
начнет появляться ЭДС и будет возрастать
по величине до тех пор, пока рамка не
достигнет своего вертикального положения.
На графике это возрастание ЭДС изобразится
плавной поднимающейся вверх кривой,
которая достигает своей вершины в точке
2.
По мере приближения рамки к горизонтальному
положению ЭДС в ней будет убывать и
упадет до нуля. На графике это изобразится
спадающей плавной кривой.
Следовательно, за время, соответствующее
половине оборота рамки, ЭДС в ней успела
возрасти от нуля до наибольшей величины
и вновь уменьшиться до нуля в точке 3.
При дальнейшем вращении рамки в ней
вновь возникнет ЭДС и будет постепенно
возрастать по величине, однако направление
ее уже изменится на обратное, в чем можно
убедиться, применив правило правой
руки.
График учитывает изменение направления
ЭДС тем, что кривая, изображающая ЭДС,
пересекает ось времени и располагается
теперь ниже этой оси. ЭДС возрастает
опять-таки до тех пор, пока рамка не
займет вертикальное положение. Затем
начнется убывание ЭДС, и величина ее
станет равной нулю, когда рамка вернется
в свое первоначальное положение, совершив
один полный оборот. На графике это
выразится тем, что кривая ЭДС, достигнув
в обратном направлении своей вершины
в точке 4, встретится затем с осью времени
в точке 5.
На этом заканчивается один цикл изменения
ЭДС, но если продолжать вращение рамки,
тотчас же начинается второй цикл, в
точности повторяющий первый, за которым,
в свою очередь, последует третий, а потом
четвертый, и так до тех пор, пока не
останавливается вращение рамки.
Таким образом, за каждый оборот рамки
ЭДС, возникающая в ней, совершает полный
цикл своего изменения.
Если же рамка будет замкнута на какую-либо
внешнюю цепь, то по цепи потечет переменный
ток, график которого будет по виду таким
же, как и график ЭДС.
Полученная волнообразная кривая
называется синусоидой, а ток, ЭДС
или напряжение, изменяющиеся по такому
закону, называются синусоидальными.
Сама кривая названа синусоидой потому,
что она является графическим изображением
переменной тригонометрической величины,
называемой синусом.
Лекция № 08
Синусоидальный характер изменения
тока — самый распространенный в
электротехнике, поэтому, говоря о
переменном токе, в большинстве случаев
имеют в виду синусоидальный ток.
Для сравнения различных переменных
токов (ЭДС и напряжений) существуют
величины, характеризующие тот или иной
ток. Они называются параметрами
переменного тока.
Период, амплитуда и частота — параметры
переменного тока
Переменный ток характеризуется двумя
параметрами — периодом и амплитудой,
зная которые можно судить, какой это
переменный ток, и построить график тока.
Рисунок 4. Кривая синусоидального тока
Промежуток времени, на протяжении
которого совершается полный цикл
изменения тока, называется периодом.
Период обозначается буквой Т и
измеряется в секундах.
Промежуток времени, на протяжении
которого совершается половина полного
цикла изменения тока, называется
полупериодом. Следовательно, период
изменения тока (ЭДС или напряжения)
состоит из двух полупериодов. Совершенно
очевидно, что все периоды одного и того
же переменного тока равны между собой.
Как видно из графика, в течение одного
периода своего изменения ток достигает
дважды максимального значения.
Максимальное значение переменного
тока (ЭДС или напряжения) называется
его амплитудой или амплитудным значением
тока.
Im, Em и Um — общепринятые обозначения
амплитуд тока, ЭДС и напряжения.
Прежде всего следует обратить внимание
на амплитудное
значение тока, однако, как
это видно из графика, существует
бесчисленное множество промежуточных
его значений, меньших амплитудного.
Значение переменного тока (ЭДС,
напряжения), соответствующее любому
выбранному моменту времени, называется
его мгновенным значением.
i, е и u — общепринятые
обозначения мгновенных значений тока,
ЭДС и напряжения.
Мгновенное значение тока, как и амплитудное
его значение, легко определить с помощью
графика. Для этого из любой точки на
горизонтальной оси, соответствующей
интересующему нас моменту времени,
нужно провести вертикальную линию до
точки пересечения с кривой тока;
полученный отрезок вертикальной прямой
определит значение тока в данный момент,
т. е. мгновенное его значение.
Очевидно, что мгновенное значение тока
по истечении времени Т/2 от начальной
точки графика будет равно нулю, а по
истечении времени — T/4
его амплитудному значению. Ток также
достигает своего амплитудного значения;
но уже в обратном на правлении, по
истечении времени, равного 3/4 Т.
Итак, график показывает, как с течением
времени меняется ток в цепи, и что каждому
моменту времени соответствует только
одно определенное значение как величины,
так и направления тока. При этом значение
тока в данный момент времени в одной
точке цепи будет точно таким же в любой
другой точке этой цепи.
Число полных периодов, совершаемых
током в 1 секунду, называется частотой
переменного тока и обозначается
латинской буквой f.
Чтобы определить частоту переменного
тока, т. е. узнать, сколько периодов
своего изменения ток совершил в течение
1 секунды, необходимо 1 секунду разделить
на время одного периода f
= 1/T. Зная частоту
переменного тока, можно определить
период: T = 1/f.
Частота переменного тока измеряется
единицей, называемой герцем.
Если речь идёт о переменном токе,
частота изменения которого равна 1
герцу, то период такого тока будет равен
1 секунде. И, наоборот, если период
изменения тока равен 1 секунде, то частота
такого тока равна 1 герцу.
Итак, мы определили параметры переменного
тока — период, амплитуду и частоту,
— которые позволяют отличать друг от
друга различные переменные токи, ЭДС и
напряжения и строить, когда это необходимо,
их графики.
При определении сопротивления различных
цепей переменному току использовать
еще одну вспомогательную величину,
характеризующую переменный ток, так
называемую угловую или круговую
частоту.
Круговая частота обозначается
буквой ω и связана с
частотой f соотношением
ω=2πf.
При построении графика переменной ЭДС
можно заметить, что за время одного
полного оборота рамки происходит полный
цикл изменения ЭДС. Иначе говоря, для
того чтобы рамке сделать один оборот,
т. е. повернуться на 360°, необходимо
время, равное одному периоду, т. е. Т
секунд. Тогда за 1 секунду рамка совершает
360°/T оборота. Следовательно, 360°/T
есть угол, на который поворачивается
рамка в 1 секунду, и выражает собой
скорость вращения рамки, которую принято
называть угловой или круговой скоростью.
Но так как период Т связан с частотой
f соотношением f = 1/T, то и круговая
скорость может быть выражена через
частоту и будет равна ω
= 360°f.
Для удобства пользования круговой
частотой при всевозможных расчетах
угол 360°, соответствующий одному обороту,
заменяют его радиальным выражением,
равным 2π радиан,
где π = 3,14. Таким
образом, получается ω
= 2πf. Следовательно,
чтобы определить круговую частоту
переменного тока (ЭДС
или напряжения), надо частоту
в герцах умножить на постоянное число
6,28.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.
Определение
Переменный ток — вынужденные электромагнитные колебания.
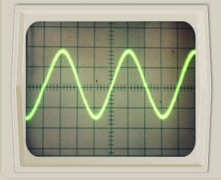
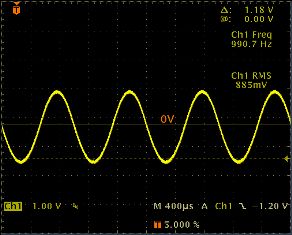
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:
Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.
Определение
Частота переменного тока — это количество колебаний за 1 с.
Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.
Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.
Внимание!
При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙108 м/с).
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).
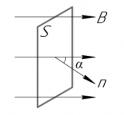
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.
Численно магнитный поток определяется формулой:
Φ=BScosα
При равномерном вращении рамки угол α увеличивается пропорционально времени:
α=2πnt
где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:
Φ=BScos2πnt
Здесь множитель 2πn представляет собой число колебаний магнитного потока за 2π секунд. Это не что иное, как циклическая частота колебаний:
ω=2πn
Следовательно:
Φ=BScosωt
Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:
e=−Φ´=−BS(cosωt)´=BSωsinωt=εmaxsinωt
εmax — амплитуда ЭДС индукции, равная:
εmax=BSω
Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:
u=Umaxsinωt
u=Umaxcosωt
где Umax — амплитуда напряжения (максимальное по модулю значение напряжения).
Сила тока меняется с той частотой, что и напряжение — ω. Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:
i=Imaxsin(ωt+φс)
где Imax — амплитуда силы тока (максимальное по модулю значение силы тока), φс — разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.
u=Umaxcosωt=12cos300,25π=12√22≈8,5 (В).
Активное сопротивление в цепи переменного тока
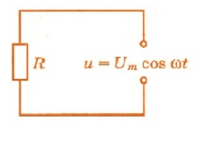
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).
Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:
u=Umaxcosωt
Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:
i=uR=UmaxcosωtR=Imaxcosωt
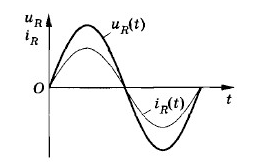
В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:
Imax=UmaxR
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Определение
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
P=I2R
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
p=i2R
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
p=(Imaxcosωt)2R
Вспомним из курса математики:
cos2α=1+cos2α2
Отсюда:
p=I2max2R(1+cos2ωt)=I2maxR2+I2maxR2cos2ωt
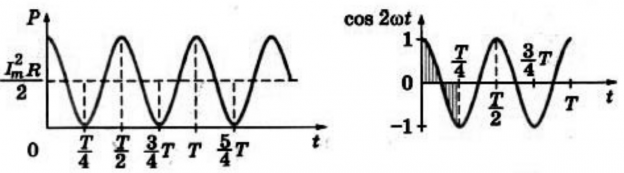
График зависимости мгновенной мощности от времени:
На протяжении первой четверти периода, когда cos2ωt>0, мощность в любой момент времени больше величины I2maxR2. На протяжении второй четверти периода, когда cos2ωt<0, мощность в любой момент времени меньше этой величины. Среднее за период значение cos2ωt=0, следовательно, средняя за период мощность равна I2maxR2.
Средняя мощность −p равна:
−p=I2maxR2=−i2R
Пример №2. Сила переменного тока в цепи меняется по закону i=Imaxcosωt. Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.
p=(Imaxcosωt)2R=10(1·cos(100π·1)2=10 (Дж)
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
−i2=I2max2
Определение
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I=√−i2=Imax√2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
U=√−u2=Umax√2
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
P=I2R=UI
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
P=I2R
I=Imax√2
P=(Imax√2)2R=I2max2R=222·5=10 ⎛⎝Дж⎞⎠
Задание EF22720
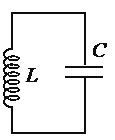
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу Томсона.
3.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• Закон изменения напряжения между обкладками конденсатора: UC=U0cosωt.
• Амплитуда напряжения: U0=5 В.
• Циклическая частота колебаний: ω = 1000π с–1.
Запишем формулу Томсона:
T=2πω=2π1000π=21000=0,002 (с)
Ответ: 0,002
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18735
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Описать, что происходит в момент замыкания и размыкания цепи.
3.Выполнить решение задачи в общем виде.
4.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
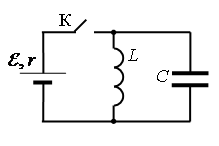
• ЭДС источника тока: ε=5 В.
• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.
• Сопротивление ЭДС источника тока: r = 2 Ом.
• Индуктивность катушки: L = 1 мГн.
1 мГн = 10–3 Гн
Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:
I0=εr
Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.
После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:
u=−UCmaxsinωt
Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.
Циклическую частоту выразим из формулы Томсона:
ω=2πT=1√LC
Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:
W=Li22+Cu22=CU2Cmax2=LI202
Выразим максимальное напряжение на конденсаторе:
CU2Cmax=LI20
UCmax=I0√LC
Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:
UCmax=ε=I0r=I0√LC
Отсюда:
√LC=r
C=Lr2
Период колебаний в контуре определим через формулу Томсона:
T=2π√LC=2π√LLr2=2πLr
Вспомним зависимость напряжения от времени:
u=−UCmaxsinωt
Подставим известные данные для искомого момента времени:
5=−5sinωt
Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:
t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)
Ответ: 7,85
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18116
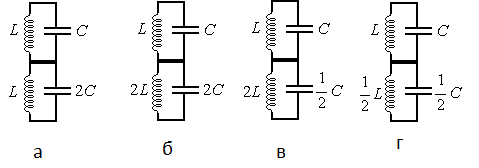
Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?
Алгоритм решения
- Выделить цель эксперимента.
- Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
- Выбрать верную пару контуров
Решение
Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18656
Алгоритм решения
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
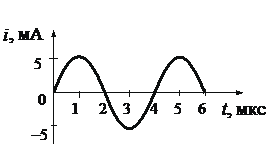
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.6k
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,663 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,987 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
-
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
-
Условие квазистационарности
-
Резистор в цепи переменного тока
-
Конденсатор в цепи переменного тока
-
Катушка в цепи переменного тока
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Переменный ток — это вынужденные электромагнитные колебания, вызываемые в электрической цепи источником переменного (чаще всего синусоидального) напряжения.
Переменный ток присутствует всюду. Он течёт по проводам наших квартир, в промышленных электросетях, в высоковольтных линиях электропередач. И если вам нужен постоянный ток, чтобы зарядить аккумулятор телефона или ноутбука, вы используете специальный адаптер, выпрямляющий переменный ток из розетки.
Почему переменный ток распространён так широко? Оказывается, он прост в получении и идеально приспособлен для передачи электроэнергии на большие расстояния. Подробнее об этом мы поговорим в листке, посвящённом производству, передаче и потреблению электрической энергии.
А сейчас мы рассмотрим простейшие цепи переменного тока. Будем подключать к источнику переменного напряжения поочерёдно: резистор сопротивлением , конденсатор ёмкости
и катушку индуктивности
. Изучив поведение этих элементов, мы в следующем листке «Переменный ток. 2» подключим их одновременно и исследуем прохождение переменного тока через колебательный контур, обладающий сопротивлением.
Напряжение на клеммах источника меняется по закону:
(1)
Как видим, напряжение может быть положительным и отрицательным. Каков смысл знака напряжения?
Всегда подразумевается, что выбрано положительное направление обхода контура. Напряжение считается положительным, если электрическое поле зарядов, образующих ток, имеет положительное направление. В противном случае напряжение считается отрицательным.
Начальная фаза напряжения не играет никакой роли, поскольку мы рассматриваем процессы, установившиеся во времени. При желании вместо синуса в выражении (1) можно было бы взять косинус — принципиально от этого ничего не изменится.
Текущее значение напряжения в момент времени
называется мгновенным значением напряжения.
к оглавлению ▴
Условие квазистационарности
В случае переменного тока возникает один тонкий момент. Предположим, что цепь состоит из нескольких последовательно соединённых элементов.
Если напряжение источника меняется по синусоидальному закону, то сила тока не успевает мгновенно принимать одно и то же значение во всей цепи — на передачу взаимодействий между заряженными частицами вдоль цепи требуется некоторое время.
Между тем, как и в случае постоянного тока, нам хотелось бы считать силу тока одинаковой во всех элементах цепи. К счастью, во многих практически важных случаях мы действительно имеем на это право.
Возьмём, к примеру, переменное напряжение частоты Гц (это промышленный стандарт России и многих других стран). Период колебаний напряжения:
с.
Взаимодействие между зарядами передаётся со скоростью света: м/с. За время, равное периоду колебаний, это взаимодействие распространится на расстояние:
м
км.
Поэтому в тех случаях, когда длина цепи на несколько порядков меньше данного расстояния, мы можем пренебречь временем распространения взаимодействия и считать, что сила тока мгновенно принимает одно и то же значение во всей цепи.
Теперь рассмотрим общий случай, когда напряжение колеблется с циклической частотой . Период колебаний равен
, и за это время взаимодействие между зарядами передаётся на расстояние
. Пусть
— длина цепи. Мы можем пренебречь временем распространения взаимодействия, если
много меньше
:
(2)
Неравенство (2) называется условием квазистационарности. При выполнении этого условия можно считать, что сила тока в цепи мгновенно принимает одно и то же значение во всей цепи. Такой ток называется квазистационарным.
В дальнейшем мы подразумеваем, что переменный ток меняется достаточно медленно и его можно считать квазистационарным. Поэтому сила тока во всех последовательно включённых элементах цепи будет принимать одинаковое значение — своё в каждый момент времени. Оно называется мгновенным значением силы тока.
к оглавлению ▴
Резистор в цепи переменного тока
Простейшая цепь переменного тока получится, если к источнику переменного напряжения подключить обычный резистор (мы полагаем, разумеется, что индуктивность этого резистора пренебрежимо мала, так что эффект самоиндукции можно не принимать во внимание)
, называемый также активным сопротивлением (рис. 1)
Рис. 1. Резистор в цепи переменного тока
Положительное направление обхода цепи выбираем против часовой стрелки, как показано на рисунке. Напомним, что сила тока считается положительной, если ток течёт в положительном направлении; в противном случае сила тока отрицательна.
Оказывается, мгновенные значения силы тока и напряжения связаны формулой, аналогичной закону Ома для постоянного тока:
Таким образом, сила тока в резисторе также меняется по закону синуса:
Амплитуда тока равна отношению амплитуды напряжения
к сопротивлению
:
Мы видим, что сила тока через резистор и напряжение на нём меняются «синхронно», точнее говоря — синфазно (рис. 2).
Рис. 2. Ток через резистор совпадает по фазе с напряжением
Фаза тока равна фазе напряжения, то есть сдвиг фаз между током и напряжением равен нулю.
к оглавлению ▴
Конденсатор в цепи переменного тока
Постоянный ток через конденсатор не течёт — для постоянного тока конденсатор является разрывом цепи. Однако переменному току конденсатор не помеха! Протекание переменного тока через конденсатор обеспечивается периодическим изменением заряда на его пластинах.
Рассмотрим конденсатор ёмкости , подключённый к источнику синусоидального напряжения (рис. 3). Активное сопротивление проводов, как всегда, считаем равным нулю. Положительное направление обхода цепи снова выбираем против часовой стрелки.
Рис. 3. Конденсатор в цепи переменного тока
Как и ранее, обозначим через заряд той пластины конденсатора, на которую течёт положительный ток — в данном случае это будет правая пластина. Тогда знак величины
совпадает со знаком напряжения
. Кроме того, как мы помним из предыдущего листка, при таком согласовании знака заряда и направления тока будет выполнено равенство
.
Напряжение на конденсаторе равно напряжению источника:
Отсюда
Дифференцируя это равенство по времени, находим силу тока через конденсатор:
(3)
Графики тока и напряжения представлены на рис. 4. Мы видим, что сила тока каждый раз достигает максимума на четверть периода раньше, чем напряжение. Это означает, что фаза силы тока на больше фазы напряжения (ток опережает по фазе напряжение на
).
Рис. 4. Ток через конденсатор опережает по фазе напряжение на
Найти сдвиг фаз между током и напряжением можно также с помощью формулы приведения:
Используя её, получим из (3):
И теперь мы чётко видим, что фаза тока больше фазы напряжения на .
Для амплитуды силы тока имеем:
Таким образом, амплитуда силы тока связана с амплитудой напряжения соотношением, аналогичным закону Ома:
где
Величина называется ёмкостным сопротивлением конденсатора. Чем больше ёмкостное сопротивление конденсатора, тем меньше амплитуда тока, протекающего через него, и наоборот.
Ёмкостное сопротивление обратно пропорционально циклической частоте колебаний напряжения (тока) и ёмкости конденсатора. Попробуем понять физическую причину такой зависимости.
1. Чем больше частота колебаний (при фиксированной ёмкости ), тем за меньшее время по цепи проходит заряд
; тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление. При
ёмкостное сопротивление стремится к нулю:
. Это означает, что для тока высокой частоты конденсатор фактически является коротким замыканием цепи.
Наоборот, при уменьшении частоты ёмкостное сопротивление увеличивается, и при имеем
. Это неудивительно: случай
отвечает постоянному току, а конденсатор для постоянного тока представляет собой бесконечное сопротивление (разрыв цепи).
2. Чем больше ёмкость конденсатора (при фиксированной частоте), тем больший заряд проходит по цепи за то же время (за ту же четверть периода); тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление.
Подчеркнём, что, в отличие от ситуации с резистором, мгновенные значения тока и напряжения в одни и те же моменты времени уже не будут удовлетворять соотношению, аналогичному закону Ома. Причина заключается в сдвиге фаз: напряжение меняется по закону синуса, а сила тока — по закону косинуса; эти функции не пропорциональны друг другу. Законом Ома связаны лишь амплитудные значения тока и напряжения.
к оглавлению ▴
Катушка в цепи переменного тока
Теперь подключим к нашему источнику переменного напряжения катушку индуктивности (рис. 5). Активное сопротивление катушки считается равным нулю.
Рис. 5. Катушка в цепи переменного тока
Казалось бы, при нулевом активном (или, как ещё говорят, омическом) сопротивлении через катушку должен потечь бесконечный ток. Однако катушка оказывает переменному току сопротивление иного рода.
Магнитное поле тока, меняющееся во времени, порождает в катушке вихревое электрическое поле , которое, оказывается, в точности уравновешивает кулоновское поле
движущихся зарядов:
(4)
Работа кулоновского поля по перемещению единичного положительного заряда по внешней цепи в положительном направлении — это как раз напряжение
. Аналогичная работа вихревого поля — это ЭДС индукции
.
Поэтому из (4) получаем:
(5)
Равенство (5) можно объяснить и с энергетической точки зрения. Допустим, что оно не выполняется. Тогда при перемещении заряда по цепи совершается ненулевая работа, которая должна превращаться в тепло. Но тепловая мощность равна нулю при нулевом омическом сопротивлении цепи. Возникшее противоречие показывает, что равенство (5) обязано выполняться.
Вспоминая закон Фарадея , переписываем соотношение (5):
откуда
(6)
Остаётся выяснить, какую функцию, меняющуюся по гармоническому закону, надо продифференцировать, чтобы получить правую часть выражения (6). Сообразить это нетрудно (продифференцируйте и проверьте!):
(7)
Мы получили выражение для силы тока через катушку. Графики тока и напряжения представлены на рис. 6.
Рис. 6. Ток через катушку отстаёт по фазе от напряжения на
Как видим, сила тока достигает каждого своего максимума на четверть периода позже, чем напряжение. Это означает, что сила тока отстаёт по фазе от напряжения на .
Определить сдвиг фаз можно и с помощью формулы приведения:
Получаем:
Непосредственно видим, что фаза силы тока меньше фазы напряжения на .
Амплитуда силы тока через катушку равна:
Это можно записать в виде, аналогичном закону Ома:
где
Величина называется индуктивным сопротивлением катушки. Это и есть то самое сопротивление, которое наша катушка оказывает переменному току (при нулевом омическом сопротивлении).
Индуктивное сопротивление катушки пропорционально её индуктивности и частоте колебаний. Обсудим физический смысл этой зависимости.
1. Чем больше индуктивность катушки, тем большая в ней возникает ЭДС индукции, противодействующая нарастанию тока; тем меньшего амплитудного значения достигнет сила тока. Это и означает, что будет больше.
2. Чем больше частота, тем быстрее меняется ток, тем больше скорость изменения магнитного поля в катушке, и тем большая возникает в ней ЭДС индукции, препятствующая возрастанию тока. При имеем
, т. е. высокочастотный ток практически не проходит через катушку.
Наоборот, при имеем
. Для постоянного тока катушка является коротким замыканием цепи.
И снова мы видим, что закону Ома подчиняются лишь амплитудные, но не мгновенные значения тока и напряжения. Причина та же — наличие сдвига фаз.
Резистор, конденсатор и катушка, рассмотренные пока что по отдельности, теперь соберутся вместе в колебательный контур, подключённый к источнику переменного напряжения. Читайте следующий листок — «Переменный ток. 2».
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Переменный ток. 1» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023