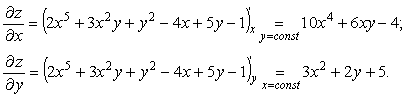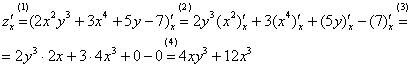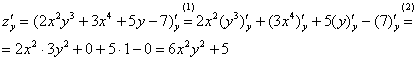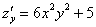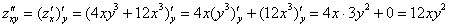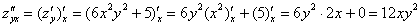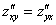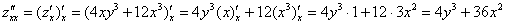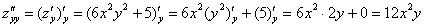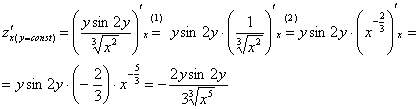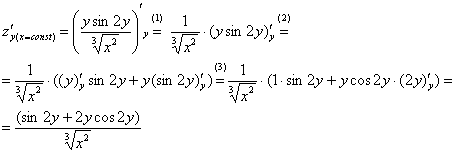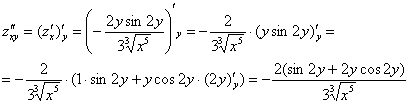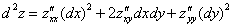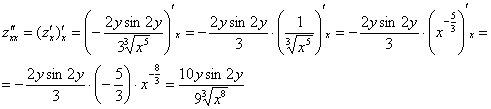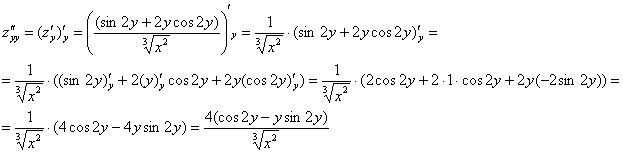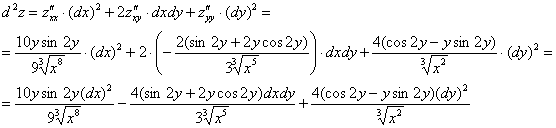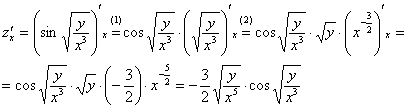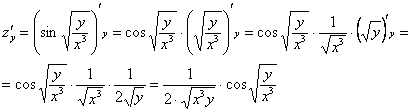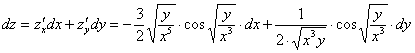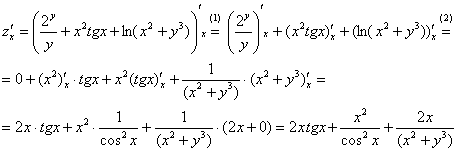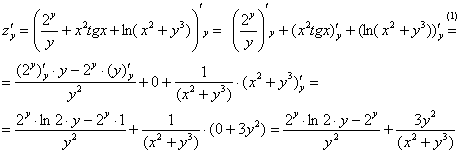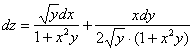Частная производная функции в точке
Как найти значение?
Постановка задачи
Найти значение частной производной функции $ u(x,y,z) $ в точке $ M(x_0,y_0,z_0) $
План решения
Частная производная в точке обозначается и вычисляется по формуле:
$$ frac{partial u}{partial x} bigg |_{M(x_0,y_0,z_0)} = frac{partial u}{partial x} (x_0,y_0,z_0) $$
$$ frac{partial u}{partial y} bigg |_{M(x_0,y_0,z_0)} = frac{partial u}{partial y} (x_0,y_0,z_0) $$
$$ frac{partial u}{partial z} bigg |_{M(x_0,y_0,z_0)} = frac{partial u}{partial z} (x_0,y_0,z_0) $$
- Находим частные производные, к примеру первого порядка:
$$ frac{partial u}{partial x}; frac{partial u}{partial y}; frac{partial u}{partial z} $$ - Подставляем координаты $ x_0,y_0,z_0 $ точки $ M $ в полученные частные производные вместо $ x,y,z $:
$$ frac{partial u}{partial x} (x_0,y_0,z_0); frac{partial u}{partial y} (x_0,y_0,z_0); frac{partial u}{partial z} (x_0,y_0,z_0) $$ - Вычисляем выражения и записываем ответ
Примеры решений
| Пример 1 |
| Найти частную производную $ u = xy + ln(y^3+z^3) $ в точке $ M(1,2,3) $ |
| Решение |
|
Берем частные производные первого порядка: $$ frac{partial u}{partial x} = y $$ $$ frac{partial u}{partial y} = x + frac{3y^2}{y^3+z^3} $$ $$ frac{partial u}{partial z} = frac{3z^2}{y^3+z^3} $$ Подставляем координаты точки $ M $ вместо $ x,y,z $ в полученные выражения и находим значения частных производных в точке: $$ frac{partial u}{partial x} (1,2,3) = 2 $$ $$ frac{partial u}{partial y} (1,2,3) = 1 + frac{3 cdot 4}{8+27} = 1 + frac{12}{35} = 1.34 $$ $$ frac{partial u}{partial z} (1,2,3) = frac{3 cdot 9}{8+27} = frac{27}{35} = 0.77 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ frac{partial u}{partial x} (1,2,3) = 2; frac{partial u}{partial y} (1,2,3) = 1.34; frac{partial u}{partial z} (1,2,3) = 0.77 $$ |
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
36.
Частные производные ФНП, их нахождение.
Частные производные ФДП, их геометрический
смысл. Примеры.
Частные
производные
Частной
производной по x функции z
= f(x,y) в
точке A(x0,y0)
называется предел отношения частного
приращения по x функции
в точке A к
приращению ∆x при
стремлении ∆x к
нулю.
Частные
производные функции z(x,y) находятся
по следующим формулам: Вторые
частные производные функции z(x,y) находятся
по формулам:
Смешанные
частные производные функции z(x,y) находятся
по формулам:
Частные
производные функции нескольких переменных
Ели
одному из аргументов функции z
= f(x,y) придать
приращение, а другой аргумент не изменять,
то функция получит частное
приращение по одному из аргументов: –
эточастное приращение функции z по
аргументу x; –
это частное приращение функции z по
аргументу у.
Частной
производной функции нескольких
переменных по
одному из её аргументов называется
предел отношения частного приращения
функции по этому аргументу к соответствующему
приращению аргумента при условии, что
приращение аргумента стремится к
нулю:
–
это частная производная функции z по
аргументу x;
–
это частная производная функции z по
аргументу у.
Чтобы
вычислить частную производную ФНП по
одному из её аргументов, нужно все другие
её аргументы считать постоянными и
проводить дифференцирование по правилам
дифференцирования функции одного
аргумента.
Пример
1.
z = 2x5 +
3x2y
+ y2 –
4x + 5y — 1
Пример
2.
Найти частные производные функции
z = f(x;y) в точке A(x0;y0).
Находим
частные производные:
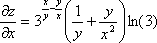

Найдем
частные производные в точке А(1;1)
Находим
вторые частные производные:


Найдем
смешанные частные производные:
Геометрический
смысл частных производных функции двух
переменных
Остановимся
на функции двух переменных.
Если
каждой паре значений x, y из
множества D ставится
в соответствие одно определённое
значение z из
множества E,
то z называется
функцией двух независимых друг от друга
переменных x и y и
обозначается z= f(x, y).
Множество D называется
областью определения функции z,
а множество E –
множеством её значений. Переменные x и y по
отношению к функции z называются
её аргументами.
Частным
значениям аргументов
Соответствует
частное значение функции
Пример
4.Область
определения функции S = xy,
выражающей зависимость площади
многоугольника от длин его сторон, может
быть записана двумя неравенствами
и
которые
определяют I квадрант на плоскости xOy.
Частное значение этой функции при x =
3, y =
5 составляет
В
общем случае область определения функции
двух переменных геометрически может
быть представлена некоторым множеством
точек (x; y)
плоскости xOy.
Подобно
тому, как функция y = f(x)
геометрически изображается графиком,
можно геометрически истолковать и
уравнение z = f(x, y).
Ставя
в соответствие каждой точке
аппликату z = f(x, y),
мы получим некоторое множество точек
(x; y; z)
трёхмерного пространства – чаще всего
некоторую поверхности. Поэтому
равенство z = f(x, y)
называют уравнением поверхности.
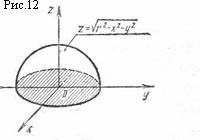
Пример
5. Пусть
задана функция
Её
область определения найдём из равенства
т.е.
Это
круг с центром в начале координат и
радиусом r.
Графиком функции
является
верхняя половина сферы
(разрешив
уравнение сферы относительно z,
получим две однозначные функции z:
и
Соседние файлы в папке Bilety
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Частные производные
- Формула
- Примеры решений
- Частные производные
- Правила ввода функции, заданной в явном виде
- Правила ввода функции, заданной в неявном виде
- Частные производные функции нескольких переменных
- Частные производные функции двух переменных. Понятие и примеры решений
- В чём смысл частных производных?
- Систематизируем элементарные прикладные правила:
Частные производные
Частные производные применяются в заданиях с функциями нескольких переменных. Правила нахождения точно такие же как и для функций одной переменной, с разницей лишь в том, что одну из переменных нужно считать в момент дифференцирования константой (постоянным числом).
Формула
Частные производные для функции двух переменных $ z(x,y) $ записываются в следующем виде $ z’_x, z’_y $ и находятся по формулам:
Частные производные первого порядка
Частные производные второго порядка
Частная производная сложной функции
а) Пусть $ z (t) = f( x(t), y(t) ) $, тогда производная сложной функции определяется по формуле:
б) Пусть $ z (u,v) = z(x(u,v),y(u,v)) $, тогда частные производные функции находится по формуле:
Частные производные неявно заданной функции
а) Пусть $ F(x,y(x)) = 0 $, тогда $$ frac = -frac $$
б) Пусть $ F(x,y,z)=0 $, тогда $$ z’_x = — frac; z’_y = — frac $$
Примеры решений
Для нахождения частной производной по $ x $ будем считать $ y $ постоянной величиной (числом):
$$ z’_x = (x^2-y^2+4xy+10)’_x = 2x — 0 + 4y + 0 = 2x+4y $$
Для нахождения частной производной функции по $ y $ определим $ y $ константой:
$$ z’_y = (x^2-y^2+4xy+10)’_y = -2y+4x $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
| Пример 1 |
| Найти частные производные первого порядка $ z (x,y) = x^2 — y^2 + 4xy + 10 $ |
| Решение |
| Ответ |
| $$ z’_x = 2x+4y; z’_y = -2y+4x $$ |
Сперва нужно найти первый производные, а затем зная их можно найти производные второго порядка.
Полагаем $ y $ константой:
Положим теперь $ x $ постоянной величиной:
Зная первые производные аналогично находим вторые.
Устанавливаем $ y $ постоянной:
Задаем $ x $ постоянной:
Теперь осталось найти смешанную производную. Можно продифференцировать $ z’_x $ по $ y $, а можно $ z’_y $ по $ x $, так как по теореме $ z»_ = z»_ $
| Пример 2 |
| Найти частные производные функции второго порядка $ z = e^ $ |
| Решение |
| Ответ |
| $$ z’_x = ye^; z’_y = xe^; z»_ = yxe^ $$ |
Теперь ищем $ frac
Подставляем всё это в формулу и записываем ответ:
$$ frac
| Пример 3 |
| Найти частную производную сложной функции $ z = x^2 + y^2, x = sin t, y = t^3 $ |
| Решение |
| Ответ |
| $$ frac
|
Записываем функцию в формате: $ F(x,y,z) = 3x^3z — 2z^2 + 3yz^2-4x+z-5 = 0 $ и находим производные:
$$ z’_x (y,z — const) = (x^3 z — 2z^2 + 3yz^2-4x+z-5)’_x = 3 x^2 z — 4 $$
$$ z’_y (x,y — const) = (x^3 z — 2z^2 + 3yz^2-4x+z-5)’_y = 3z^2 $$
Источник
Частные производные
Назначение сервиса . Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word .
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
- Примеры
x 2 +xy ≡ x^2+x*y .
cos 2 (2x+y) ≡ (cos(2*x+y))^2≡ (x-y)^(2/3)
Правила ввода функции, заданной в неявном виде
- Все переменные выражаются через x,y,z
- Примеры
≡ x^2/(z+y)
cos 2 (2x+zy) ≡ (cos(2*x+z*y))^2≡ z+(x-y)^(2/3)
Частные производные функции нескольких переменных
Пример 1 . z=2x 5 +3x 2 y+y 2 –4x+5y-1
Пример 2 . Найти частные производные 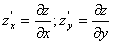
Находим частные производные:
Найдем частные производные в точке А(1;1)
Находим вторые частные производные:
Источник
Частные производные функции двух переменных.
Понятие и примеры решений
На данном уроке мы продолжим знакомство с функцией двух переменных и рассмотрим, пожалуй, самое распространенное тематическое задание – нахождение частных производных первого и второго порядка, а также полного дифференциала функции. Студенты-заочники, как правило, сталкиваются с частными производными на 1 курсе во 2 семестре. Причем, по моим наблюдениям, задание на нахождение частных производных практически всегда встречается на экзамене.
Для эффективного изучения нижеизложенного материала вам необходимо уметь более или менее уверенно находить «обычные» производные функции одной переменной. Научиться правильно обращаться с производными можно на уроках Как найти производную? и Производная сложной функции. Также нам потребуется таблица производных элементарных функций и правил дифференцирования, удобнее всего, если она будет под рукой в распечатанном виде. Раздобыть справочный материал можно на странице Математические формулы и таблицы.
Быстренько повторим понятие функции двух переменных, я постараюсь ограничиться самым минимумом. Функция двух переменных обычно записывается как 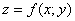
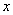
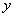
Пример: 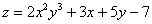
Иногда используют запись 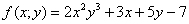
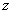
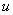
С геометрической точки зрения функция двух переменных 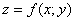
никогда не давал списывать мой вузовский преподаватель является моим «коньком».
Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.
Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас:
…да, кстати, для этой темы я таки создал маленькую pdf-книжку, которая позволит «набить руку» буквально за пару часов. Но, пользуясь сайтом, вы, безусловно, тоже получите результат – только может чуть медленнее:
Найти частные производные первого и второго порядка функции
Сначала найдем частные производные первого порядка. Их две.
Обозначения:
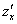
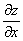
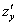
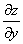
Начнем с 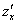
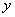
Комментарии к выполненным действиям:
(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом.
Внимание, важно! Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае, если вы где-нибудь нарисуете «штрих» без 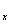
Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.
(2) Используем правила дифференцирования 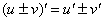
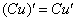
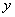
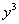
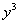
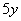
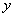
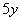
(3) Используем табличные производные 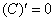
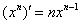
(4) Упрощаем, или, как я люблю говорить, «причесываем» ответ.
Теперь 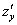
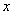
(1) Используем те же правила дифференцирования 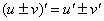
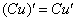
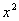
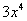
(2) Используем таблицу производных элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица рАвно справедлива и для 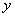
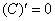
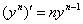
В чём смысл частных производных?
По своей сути частные производные 1-го порядка напоминают «обычную» производную:
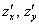
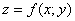
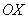
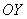
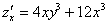
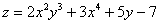
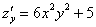
! Примечание: здесь подразумеваются направления, которые параллельны координатным осям.
В целях лучшего понимания рассмотрим конкретную точку 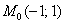
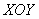
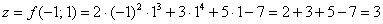
Вычислим частную производную по «икс» в данной точке:
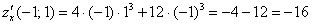
Отрицательный знак «иксовой» производной сообщает нам об убывании функции 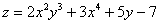
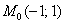
Теперь узнаем характер «местности» по направлению оси ординат: 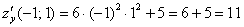
Производная по «игрек» положительна, следовательно, в точке 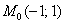
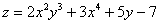
Кроме того, частная производная в точке характеризует скорость изменения функции по соответствующему направлению. Чем полученное значение больше по модулю – тем поверхность круче, и наоборот, чем оно ближе к нулю – тем поверхность более пологая. Так, в нашем примере «склон» по направлению оси абсцисс более крут, чем «гора» в направлении оси ординат.
Но то были два частных пути. Совершенно понятно, что из точки, в которой мы находимся, (и вообще из любой точки данной поверхности) мы можем сдвинуться и в каком-нибудь другом направлении. Таким образом, возникает интерес составить общую «навигационную карту», которая сообщала бы нам о «ландшафте» поверхности 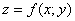
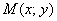
Систематизируем элементарные прикладные правила:
1) Когда мы дифференцируем по 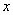
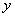
2) Когда же дифференцирование осуществляется по 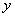
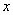
3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной (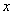
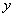
Шаг второй. Находим частные производные второго порядка. Их четыре.
Обозначения:
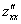
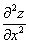
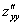
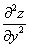
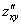
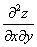
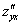
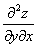
Со второй производной нет никаких проблем. Говоря простым языком, вторая производная – это производная от первой производной.
Для удобства я перепишу уже найденные частные производные первого порядка: 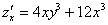
Сначала найдем смешанные производные:
Как видите, всё просто: берем частную производную 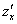
Аналогично:
В практических примерах можно ориентироваться на следующее равенство:
Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.
Находим вторую производную по «икс».
Никаких изобретений, берем 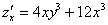
Аналогично:
Следует отметить, что при нахождении 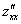
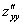
Вторые производные также находят широкое практическое применение, в частности, они используются в задаче отыскания экстремумов функции двух переменных. Но всему своё время:
Вычислить частные производные первого порядка функции 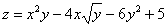
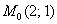
Это пример для самостоятельного решения (ответы в конце урока). Если возникли трудности с дифференцированием корней, вернитесь к уроку Как найти производную? А вообще, довольно скоро вы научитесь находить подобные производные «с лёту».
Набиваем руку на более сложных примерах:
Найти частные производные первого порядка функции 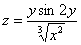
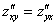
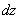
Решение: Находим частные производные первого порядка:
Обратите внимание на подстрочный индекс: 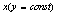
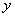
(1) Выносим все константы за знак производной. В данном случае 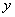
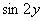
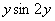
(2) Не забываем, как правильно дифференцировать корни.
(1) Выносим все константы за знак производной, в данной случае константой является 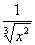
(2) Под штрихом у нас осталось произведение двух функций, следовательно, нужно использовать правило дифференцирования произведения 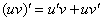
(3) Не забываем, что 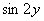
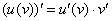
Теперь находим смешанные производные второго порядка:
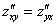
Запишем полный дифференциал 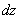
Полный дифференциал первого порядка функции двух переменных имеет вид:
В данном случае:
То есть, в формулу нужно тупо просто подставить уже найденные частные производные первого порядка. Значки дифференциалов 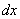
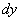
И по неоднократным просьбам читателей, полный дифференциал второго порядка.
Он выглядит так:
ВНИМАТЕЛЬНО найдём «однобуквенные» производные 2-го порядка:
и запишем «монстра», аккуратно «прикрепив» квадраты 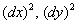
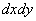
Ничего страшного, если что-то показалось трудным, к производным всегда можно вернуться позже, после того, как поднимите технику дифференцирования:
Найти частные производные первого порядка функции 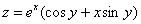
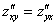
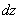
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Рассмотрим серию примеров со сложными функциями:
Найти частные производные первого порядка функции 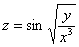
Записать полный дифференциал 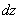
Решение:
(1) Применяем правило дифференцирования сложной функции 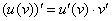
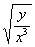
(2) Здесь используем свойство корней: 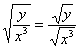
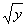
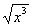
Аналогично:
Запишем полный дифференциал первого порядка:
Найти частные производные первого порядка функции 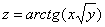
Записать полный дифференциал 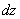
Это пример для самостоятельного решения (ответ в конце урока). Полное решение не привожу, так как оно достаточно простое
Довольно часто все вышерассмотренные правила применяются в комбинации.
Найти частные производные первого порядка функции 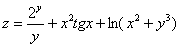
(1) Используем правило дифференцирования суммы
(2) Первое слагаемое в данном случае считается константой, поскольку в выражении 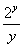
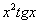
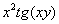
(1) В первом слагаемом и в числителе и в знаменателе содержится «игрек», следовательно, нужно использовать правило дифференцирования частного: 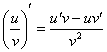
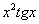
Для тех читателей, которые мужественно добрались почти до конца урока, расскажу старый мехматовский анекдот для разрядки:
Однажды в пространстве функций появилась злобная производная и как пошла всех дифференцировать. Все функции разбегаются кто куда, никому не хочется превращаться! И только одна функция никуда не убегает. Подходит к ней производная и спрашивает:
– А почему это ты от меня никуда не убегаешь?
– Ха. А мне всё равно, ведь я «е в степени икс», и ты со мной ничего не сделаешь!
На что злобная производная с коварной улыбкой отвечает:
– Вот здесь ты ошибаешься, я тебя продифференцирую по «игрек», так что быть тебе нулем.
Кто понял анекдот, тот освоил производные, минимум, на «тройку»).
Найти частные производные первого порядка функции 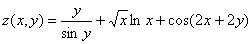
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Ну вот почти и всё. Напоследок не могу не обрадовать любителей математики еще одним примером. Дело даже не в любителях, у всех разный уровень математической подготовки – встречаются люди (и не так уж редко), которые любят потягаться с заданиями посложнее. Хотя, последний на данном уроке пример не столько сложный, сколько громоздкий с точки зрения вычислений.
Дана функция двух переменных 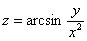
Это пример для самостоятельного решения. Полное решение и образец оформления где-то рядом.
Что дальше? Дальше знакомимся с родственной темой – частными производными функции трёх переменных. После этого я рекомендую ДОБРОСОВЕСТНО (жить будет легче ;)) отработать технику дифференцирования на уроках Производные сложных функций нескольких переменных, Как проверить, удовлетворяет ли функция уравнению? и Частные производные неявно заданной функции. И, наконец, обещанная вкусняшка – Производная по направлению и градиент функции. Стратегия и тактика знакомы – сначала учимся решать, затем вникаем в суть!
Решения и ответы:
Пример 2: 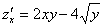
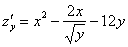
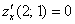
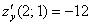
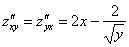
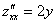
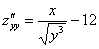
Пример 4: Ссылка для просмотра или скачивания ниже.
Пример 6: 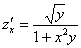
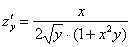
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Источник
Adblock
detector
| Пример 4 |
| Пусть $ 3x^3z — 2z^2 + 3yz^2-4x+z-5 = 0 $ задаёт неявную функцию $ F(x,y,z) = 0 $. Найти частные производные первого порядка. |
| Решение |
Лекция№7. Геометрическое
истолкование функции двух переменных. Понятие непрерывности функции. Частные
производные первого и второго порядков.
1. Определение
функций двух переменных
§
Функцией
двух переменных называется правило (закон,
соответствие) , по которому каждой упорядоченной
паре чисел из некоторого множества на
плоскости поставлено в соответствие
единственное число из множества
. Множество
называется областью
определения, а множество — множеством
значений функции .
§
Для
функции двух переменных областью
определения является некоторое множество точек на плоскости (область), а областью значений —
промежуток на оси .
2. Способы
задания функций двух переменных
Основными
способами задания функций являются аналитический, табличный,
графический. Существует и другие способы задания функций —
алгоритмический, с помощью программы на ЭВМ.
v
Аналитический способ
задания функции.
1) одной формулой,
разрешенной относительно зависимой переменной (например, ), или
2) разными формулами
на определенных числовых промежутках
Функция двух
переменных называется неявной, если она задана уравнением, не
разрешенной относительно зависимой переменной. Например, .
v
Табличный
способ задания функции — с помощью таблицы, в которой указаны
значения аргументов и соответствующие им значения зависимой переменной.
Таблица функции двух переменных
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
v
Графический
способ задания функции.
§
Графиком
функции двух переменных является поверхность
в трехмерном пространстве ХУZ, состоящая
из точек , где пары
принадлежат области определения
функции . Графиком линейной функции
является
плоскость в пространстве.
Пример1. Для
функции график представляет собой плоскость,
проходящую через точки ,
,
.

4
4 y
2
x
3. Частные производные. Ограничимся
случаем функции двух переменных (для большего числа переменных аналогично).
§
Пусть
функция определена в окрестности точки
. Придадим переменной
в точке
приращение
, оставляя значение переменной
неизменным. Соответствующее
приращение функции
называется частным
приращением функции по переменной в точке
.
Аналогично
определяется частное приращение функции по переменной
:
.
Обозначается
частная производная по символами:
,
,
,

§ Частной
производной функции по
переменной называется
предел:

Обозначения:
,
,
,
.
Частные
производные можно рассматривать как скорости изменения функции относительно
одной из переменных (в направлении соответствующей оси координат). Для
нахождения частной производной по переменной
используются правила
дифференцирования функции одной переменной, считая переменную постоянной..
Аналогично, для нахождения частной производной по переменной
постоянной считается
переменная .
Пример 2. Для
функции найти частные производные
,
и вычислить их значения в точке
.
Решение
Частная производная функции по переменной
находится в предположении, что
постоянна:
.
Найдем частную производную функции по , считая постоянной
:
.
Вычислим значения частных производных при ,
:
;
.
4. Частные производные высших
порядков.
Введем понятие частных производных высших
порядков. Пусть функция имеет
частные производные и
в точке
и в каждой точке окрестности точки
.
§
Частными
производными второго порядка функции нескольких переменных называются
частные производные от частных производных первого порядка.
Запишем для все частные
производные второго порядка:




Аналогично определяются и обозначаются частные
производные третьего порядка, например:


§
Производные,
взятые последовательно по разным переменным, называются смешанными
частными производными. Для функции двух переменных смешанные частные
производные есть ,
.
§
Теорема.
Если
смешанные частные производные функции нескольких переменных непрерывны в
некоторой точке , то они равны между собой в этой
точке.
Для функции двух
переменных значения смешанных частных производных не зависят от порядка
дифференцирования: .
Пример 3. Для
функции найти частные производные второго
порядка и
.
Смешанная частная
производная находится последовательным
дифференцированием сначала функции по
(считая
постоянным), затем
дифференцированием производной по
(считая
постоянным).
=
Производная находится дифференцированием
функции сначала по
, затем производной
по
.

Смешанные частные производные равны между
собой: .
5. Дифференциал функции двух
переменных и его применение
Рассмотрим функцию двух переменных . Пусть каждый аргумент
,
получил приращение
и
и стал равным
и
, т.е. точка
«перешла» в точку
. Приращение функции
по переменным
и
называется полным приращением функции в точке
.
Пример 4. Для
функции полное приращение:
Таким образом, в полном приращении функции
можно выделить слагаемые, линейные относительно приращений аргументов и
:
.
Нетрудно видеть, что коэффициенты при
приращениях и
есть частные производные функции
по
и по
:
,

·
Часть
полного приращения функции, линейная относительно приращений аргументов и
, называется полным
дифференциалом функции и обозначается :

Так как для независимых переменных и
их дифференциалы равны приращениям
,
, то полный дифференциал функции
равен 
Дифференциал функции равен
.
·
Функция
, имеющая дифференциал в точке
, называется дифференцируемой в
данной точке .
Итак, если функция дифференцируема в
точке , то она имеет
частные производные в этой точке
Пример 5. Полный
дифференциал для равен
.
Рассмотрим применение полного
дифференциала для приближенных вычислений. При малых приращениях аргументов
,
полное
приращение функции приближенно равно полному
дифференциалу :
, или
.
Выразим значение функции:
.Формула «полных приращений»
позволяет приближенно вычислить значение функции в точке
, если известны значения функции и
ее частных производных в ближайшей точке .
Пример 6. Вычислить
.
Воспользуемся функцией и вычислим ее значение в точке
. Ближайшей точкой является точка
, то есть
,
. Приращение аргументов
и
.
Найдем значения функции и частных
производных в точке :
;
; тогда

; тогда

Подставим найденные значения в формулу
полных приращений, получим .
6. Дифференциал второго порядка.
§
Дифференциалом
второго порядка функции называется
дифференциал от дифференциала первого порядка:
Пример 7. Для
функции найти дифференциал второго
порядка.
Найдем частные производные первого и
второго порядка:
;
;
;
;
;
Дифференциал второго порядка равен .
7. Непрерывность
функций двух переменных.
Пусть дана функция с областью определения G и пусть
– предельная точка множества G.
Определение.
Говорят, что функция непрерывна в точке
, если:
1)
; 2)
, т.е.

Сформулируем определение
непрерывности в эквивалентной форме. С этой целью обозначим ,
. Полным
приращением функции при переходе от точки М0
к точке М называется разность значений функции в этих точках, а именно:
.
Определение.
Говорят, что функция непрерывна в точке
, если выполняется равенство
.
Пример 8. Функция непрерывна в любой точке
плоскости хОу, так как при любых значениях х и у величина
стремиться
к нулю при .
Свойства
непрерывных функций:
Если функции и
непрерывны
в точке , то этим же свойством обладают функции
,
, а
если , то и функция
.
8. Экстремум
функции двух переменных.
Пусть функция определена в некоторой области
и пусть точка
. Точка
называется точкой максимума
функции , если
есть наибольшее значение функции в
окрестности этой точки. Точка называется точкой
минимума функции , если
есть наименьшее значение функции в
окрестности этой точки. Точки максимума и минимума называются точками
экстремума.
Значение функции в
точке максимума называется максимумом функции, а значение функции
в точке минимума – минимумом функции. Максимум и минимум функции
называются экстремумами функции.
Если в точке функция
имеет экстремум, то частные
производные функции в этой точке равны нулю, т.е. и
. Это необходимые условия
экстремума.
Точка, в которой
обе частные производные равны нулю, называется критической точкой
функции . Для отыскания критических точек
функции нужно найти её частные производные, приравнять их нулю и решить систему
двух уравнений с двумя неизвестными: Точки
экстремума, если они есть, находятся среди критических точек функции. Пусть является критической точкой
функции . Вычислим частные производные
второго порядка в этой точке: ,
,
. Составим выражение
и проанализируем его знак:
1) если , то функция
в точке
имеет экстремум: максимум при A<0 и
минимум при A>0;
2) если , то функция
в точке
экстремума не имеет;
3) если , то для определения экстремума
нужны дополнительные исследования.
Рассмотренные
условия называются достаточными условиями экстремума.
Пример.
Исследовать функцию на экстремум.
Решение. Найдём
частные производные ,
и решим систему уравнений
Из второго уравнения 2y(x+1)=0, y=0, x=
1. Подставим у=0
в первое уравнение: , 2x(3x+5)=0, x=0, 3x+5=0,
. Таким образом, найдены две
критические точки ,
. Теперь в первое уравнение
подставим x=1:
,
,
,
. Следовательно, стали известны ещё
две критические точки ,
. Найдём частные производные
второго порядка: ,
,
.
Проверим
достаточные условия для точки :
,
,
,
. Следовательно, в точке
функция имеет экстремум. Так как A>0, то
это минимум. При этом .
Аналогично
установим, что в точке функция имеет
максимум, причём . В точках
и
экстремума нет.
Примеры:
1) Найти
частные производные функции z = ( x 2
+ y 3)exy .
( ( x 2
+ y 3)exy
)/х= 2 xe xy + ( x 2
+ y3
)e xy y = (2 x + x 2
y + y 4)exy,
( ( x 2
+ y 3)exy
)/у= 3 y 2e xy + ( x 2 + y3 )e
xy x = (3 y 2 + x3 + xy 3)exy
2) Найти
частные производные функции z = 5x3
y + 2x2 −
6 y .
|
Решение |
|
|
1. |
z′x |
|
2. |
z′x |
3) Найти
частные производные второго порядка функции .
Решение. ,
,
,
=
,
=
=
,
=
=
.
Задания для
самостоятельной работы
1.
Найти
частные производные первого и второго порядков функций:
а) ; б)
; в)
; г)
.
2.
Исследовать
функции на экстремум:
а) ;
б) ;
в) .



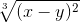 ≡ (x-y)^(2/3)
≡ (x-y)^(2/3) 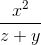 ≡ x^2/(z+y)
≡ x^2/(z+y) 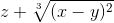 ≡ z+(x-y)^(2/3)
≡ z+(x-y)^(2/3)