Как найти будущую стоимость вклада

Понятие, что деньги обладают временной
стоимостью, является наиболее важной
концепцией в финансовом анализе. Деньги
имеют временную стоимость вследствие
того, что их можно инвестировать на
определенный срок под определенную
процентную ставку. В первых трех разделах
нашего курса лекций мы рассмотрим три
базовых понятий, которые позволят нам
донести слушателям курса основную идею
временной стоимости денег.

Во-первых, мы объясним, как определяется
будущая стоимость инвестированного
капитала. Во-вторых, мы покажем процедуру
расчета количества денег, которые
необходимо инвестировать сегодня с
целью получения определенной суммы
денег в будущем, И, наконец, мы покажем,
как определить доходность любых
инвестиций.

Будущая стоимость
инвестиций

Предположим, что инвестор вкладывает
на депозитный счет в Сбербанк 100 000 руб.
под 8% в год. Через год банк начислит
инвестору процентные платежи в сумме
8000 руб. (100 000×0,08), и на счету у инвестора
будет первоначальная сумма 100 000 руб.
плюс 8000 руб., т.е. 108 000 руб. Если инвестор
примет решение оставить свой вклад в
банке еще на один год под те же проценты
(8% в год), то в конце второго года на
банковском счету инвестора будет уже
116 640 руб. Эта сумма включает:

Сумму денег, которая находится на
счету на начало второго года 108 000
руб.

Процентные платежи за второй год
(108 000×0,08) 8 640 руб.

Итого денег на счету
116 640
руб.

Полученный результат можно представить
и в следующем виде:

Сумма денег, которая была вложена на
счет в начале первого года 100 000
руб.

Процентные платежи за первый год
8000
руб.

Процентные платежи на базовый вклад за
второй год 8000 руб.

Проценты, начисленный на процентные
платежи за первый год (8000×0,08) 640 руб.

Итого
116 640
руб.

Если инвестор решает вложить свои деньги
на депозитный счет сроком на 5 лет, то
его накопления по годам будут равны, в
рублях:

к концу первого года (100 000×1,08)
108000

к концу второго года (108 000×1,08)
116640

к концу третьего года (116 640×1,08)
125971,2

к концу четвертого года (125 971,2×1,08)
136048,9

к концу пятого года (136 048,9×1,08)
146932,8

Таким образом, к концу пятого года вклад
в 100 000 руб. увеличится до 146 932,8 руб.
Полученную конечную сумму обычно
называют будущей стоимостью100 000
руб., вложенных сроком на пять лет под
8% годовых.

Обращаем внимание нашего читателя, что
общая сумма процентных платежей в
течение 5 лет равна 46 932,8 руб., которая
включает доход от процентных платежей
по номинальному вкладу 100 000 руб. в размере
40 000 руб.(8000×5) и доход от реинвестиции
процентных платежей в сумме 6 932,8 руб.
(46 932,8 – 40 000).

В общем виде формула, которая позволяет
определить будущую стоимость (FV)
вклада в суммеP руб. черезTлет,
вложенных подi
процентов в год, имеет следующий вид:

FV = P×(1
+i)^T,
руб.
(1.1)

Выражение (1 + i)^T
называют будущей стоимостью одного
рубля. Оно позволяет определить рост
одного рубля вклада, вложенного подi
процентов в год сроком наТлет.
Табулированные значения будущей
стоимости одного рубля при разных
значенияхiиТприведены в Приложении1.

Рассмотрим ряд примеров, иллюстрирующих
расчеты по определению будущей стоимости
определенной суммы инвестиций.

Пример 1.1.Менеджер пенсионного
фонда вкладывает 20 млн. руб. в финансовый
инструмент, который обеспечит получение
в течение 6 лет процентных платежей в
размере 7,5% в год от номинальной суммы
инвестированного капитала. Определить
будущую стоимость 20 млн. руб.

Задано: P= 20 млн руб.;i= 7,5%;T
= 6 лет.

Будущая стоимость определяется на
основе формулы 1.1 следующим образом:

FV= 20 000
000×(1+0,075)⁶= 20 000 000 ×1,5433 = 30 866
000 руб.

Пример 1.2.Г-н Сидоров застраховал
свою жизнь сроком на 5 лет и внес страховой
взнос в сумме 6 млн. руб. По условиям
страхования страховщик через 5 лет
обязан выплатить страхователю 8,2 млн.
руб. Страховщик планирует вложить
полученный страховой взнос на депозитный
счет в Альфа банк сроком на 5 лет под 8%
в год. Определить будущую стоимость
страховой премии и хватит ли ее для
выполнения обязательства страховщика
перед страхователем?

Задано: P= 6 млн. руб.;i= 8%;T
= 5 лет.

Будущая стоимость 6 млн. руб равна:

FV= 6 000 000
× (1+0,08)⁵= 6 000 000 ×1,4693 = 8 815
800 руб.

Полученный результат свидетельствует,
что страховщик будет иметь через 5 лет
достаточную сумму, которая обеспечит
ему выполнение своего обязательства
по уплате страхователю 8,2 млн. руб.

Пример 1.3.Менеджер необлагаемого
налогом фонда решает инвестировать 5
млн руб. в финансовый проект, который
обеспечит получение ежегодного дохода
в размере 6% в год от вложенной суммы в
течение 4 лет. Полученную через четыре
года сумму менеджер планирует вложить
на депозитный счет сроком на три года
под 7,8% в год. Определить будущую стоимость
фонда.

Задано: P= 5 000 000
руб.;i= 6%;T
= 4 года.

Будущая стоимость 5 млн руб. через 4 года
равна:

FV= 5 000 000
× (1+0,06)⁴= 5 000 000 ×1,2625 = 6 312
500 руб.

Будущая стоимость 6 312 500 руб.,
реинвестированных сроком на три года
под 7,8% в год, будет равна:

FV= 6 312 500
× (1+0,078)³= 6 312 500 ×1,2527 = 7 907
669 руб.

Пример 1.4.Вернемся к предыдущему
примеру и предположим, что менеджер
имеет возможность купить финансовый
инструмент, который позволит ему ежегодно
в течение 7 лет получать доход в размере
6,5% в год от номинальной суммы фонда.
Определить который из альтернативных
вариантов управления фондом принесет
больший доход к концу седьмого года.

Задано: P= 5 000 000
руб.;i= 6,5%;T
= 7 лет.

Будущая стоимость 5 млн руб. через 7 лет
равна:

FV= 5 000
000×(1+0,065)⁷= 5 000 000×1,554 = 7 770 000
руб.

Сравнение полученных результатов
позволяет сделать вывод, что первый
вариант управления фондом обеспечит к
концу 7 года большую величину будущей
стоимости 5 млн руб. Следовательно, при
условии одинаковых рисков по дефолту
первый вариант управления фондом
эффективнее второго варианта управления.

Нецелочисленные
периоды

В примерах, рассмотренных выше, мы
исходили из условия, что будущая стоимость
сегодняшних денежных вложений,
определяемая по формуле 1.1, рассчитывается
для периодов, выражавшихся в целых
годах. Эта формула применима и для
случая, когда период выражается частью
года. Например, инвестор свои свободные
денежные ресурсы в сумме 2 млн. руб.
инвестирует сроком на 4 года и 6 месяцев,
т.е. на 4,5 года под 7 % в год. Тогда в формуле
1.1 показатель степени будет равен 4,5.

Для нашего примера мы будем иметь: PV= 2 000 000 руб.;i= 7 %;T = 4,5 года.

Будущая стоимость указанных инвестиций
будет равна:

FV= 2 000
000×(1+0,07)^4,5= 2 000 000
× 1,3559 = 2 711 800
руб.

Процентные платежи по инвестированному
капиталу могут выплачиваться более чем
один раз в год: например каждые полгода,
или ежеквартально, или ежемесячно. В
этом случае мы должны скорректировать
число периодов начисления процентных
платежей и величину процентных платежей
за период. Скорректированное число
периодов (n) определяется
как произведение количества процентных
платежей за год (m) на
число лет (T), в течение
которых выплачиваются процентные
платежи. Величина процентных платежей
за период (r) определяется
как отношение значения процентного
платежа за год на число выплат процентных
платежей в год (i/m).

В этом случае формула 1.1, используемая
для определения будущей стоимости
инвестированного капитала, примет
следующий вид:

FV = P×(1+i/m)^T×m
или FV =
P×(1+r)ⁿ,
руб. (1.2)

Пример 1.5. Инвестор вкладывает 3 000
000 руб. в финансовый инструмент, по
которому в течение 5 лет выплачиваются
процентные платежи два раза в год исходя
из доходности этого инструмента 8% в
год. Определить будущую стоимость
инвестированного капитала.

Задано: P= 3000 000 руб.;i= 8%;T
= 5 лет;m= 2 раза в год.

Откуда: r = i/m
= 8/2 = 4%; n = T×m
= 5×2 = 10.

Будущая стоимость 3 000 000 руб. равна:

FV = P×(1+r)ⁿ
=3 000 000
× (1 + 0,04)¹⁰= 4 440
730 руб.

Если бы процентные платежи выплачивались
только один раз в год, то будущая стоимость
равнялась бы:

FV= 3 000 000
× (1+0,08)⁵= 3 000 000 × 1,4693 = 4 407
900 руб.

Большая величина будущей стоимости
инвестированного капитала при начислении
процентных платежей два раза в год
обусловлена большей величиной дохода
от реинвестирования процентных платежей,
что подтверждается следующим расчетом..

Пример 1.6.Вернемся к предыдущему
примеру и предположим, что процентные
платежи выплачиваются ежеквартально,
а прочие показатели останутся без
изменения. В этом случае исходные данные
будут следующие:P=
3000 000 руб.;i= 8%;T
= 5 лет;m= 4 раза в
год.

Откуда: r = i/m
= 8/4 = 2%; n = T×m
= 5×4 = 20.

Будущая стоимость 3 000 0000 руб. составит:

FV= 3 000 000
× (1+0,02)²⁰= 3 000 000 × 1,4859 = 4 457 700
руб.

Полученная величина будущей стоимости
3 000 000 руб. больше в сравнении с
условием выплаты процентных платежей
два раза в год на 16 970 руб. (4 457 700
— 4 440 730).

Будущая стоимость
простых аннуитетов

В некоторых случаях инвестор при вложении
своего капитала через определенные
промежутки времени может получать
определенные суммы в виде равных по
величине денежных потоков. Если денежные
потоки поступают (вкладывают) равными
сумами через равные промежутки времени,
то они называются аннуитетами. Аннуитет,
по условиям которого выплата или
получение очередного платежа осуществляются
в конце каждого периода, называются
простыми аннуитетами или аннуитетами
постнумерандо. В наших дальнейших
расчетах мы будем использовать простые
аннуитеты.

Пример 1.7.Инвестор при инвестировании
определенной суммы денег ожидает
получать ежегодно в течение 5 лет денежный
поток в размере 50 000 руб. При получении
этой суммы инвестор планирует
реинвестировать ее под 8% в год. Тогда
встает вопрос: а какова будет будущая
стоимость аннуитетов, получаемых
инвестором в течение 5 лет?

Через год инвестор получит 50 000 руб.
и реинвестирует их сроком на 4 года под
8% в год. Следовательно, будущая стоимость
этих 50 000 руб. составит:

FV₄= 50 000 × (1+0,08)⁴= 50 000 × 1,3605 = 68
025 руб.

Через два года инвестор вновь получает
50 000 руб. и реинвестирует их уже сроком
на три года, и будущая стоимость этой
суммы будет равна:

FV₃
= 50 000 × (1+0,08)³= 50 000 × 1,2597 =
62 985 руб.

Через три года инвестор вновь получает
50 000 руб. и реинвестирует их уже сроком
на два года, и будущая стоимость этой
суммы будет равна:

FV₂
= 50 000 × (1+0,08)²= 50 000 × 1,1664=
58 320 руб.

Через четыре года инвестор вновь получает
50 000 руб. и реинвестирует их уже сроком
на один год, и будущая стоимость этой
суммы будет равна:

FV₁
= 50 000 × (1+0,08) = 50 000 × 1,08 = 54 000 руб.

Через пять лет инвестор получает
последний денежный поток в размере FV₀
=50 000 руб. и не реинвестирует их.

Таким образом, будущая стоимость всех
денежных потоков (FV_Σ),
полученных инвестором за пять лет, будет
равна:

FV_Σ
= 68 025 + 62 985 + 58 320 + 54 000 + 50 000
= 293 330 руб.

Полученная сумма включает пять ежегодных
платежей по 50 000 руб. в размере 250 000
руб. и процентные платежи от реинвестирования
ежегодных денежных потоков под 8% в год
в сумме 43 330 руб. (293 330 — 250 000).

В рассмотренном примере мы определяли
будущую стоимость денежного потока для
каждого года его получения, а затем
полученные результаты суммировали.
Такой алгоритм определения будущей
стоимости всех аннуитетов не удобен.
Поэтому в практике расчета будущей
стоимости простых аннуитетов применяется
следующая формула:

а) аннуитеты выплачивают (получают)
один раз в год:

FV = А×((1+
i) —1)^T
/i), руб.,(1.3)

где А– величина ежегодного
аннуитета, руб.;

i– годовая
процентная ставка реинвестирования
аннуитета, доли ед.;

Т– период, в течение которого
выплачивают (получают) аннуитеты, лет.

б) аннуитеты выплачивают (получают)
mраз в год:

FV =(А/m)×((1+ r)
-1)ⁿ /r,
руб., (1.4)

где m– количество
платежей в виде аннуитета в год;

r = i/m
– процентная ставка реинвестирования
аннуитета, доли ед. за период;

n=Т×m
– число периодов, в течение которых
выплачивают (получают) аннуитеты.

Пример 1.8.Рассмотрим вновь данные
примера 1.7. В этом случае исходные данные
представим в виде:А = 50 000 руб.;i= 0,08;Т= 5 лет.

Будущую стоимость аннуитетов определим
по формуле 1.3:

FV = А×((1+i)
-1)^T /i)
= 50 000 × ((1 + 0,08)⁵– 1)/0,08 = 293 330
руб.

А теперь определим будущую стоимость
аннуитетов, выплачиваемых mраз в год.

Пример 1.9.Вернемся к примеру 1.8. и
предположим, что платежи в виде аннуитетов
выплачиваются каждое полугодие.
Следовательно, процентные платежи при
реинвестировании аннуитетов начисляются
два раза в год. В этом случае число
периодов выплаты аннуитетов (n)
будет равно 10 (5×2), а r
= i/m
= 0,08/2 = 0,04. Подставим наши данные в
формулу (1.4), и будущая стоимость
аннуитетов будет равна:

FV = (А/m)×((1+ r) -1)ⁿ
/r = (50 000/2)×((1
+ 0,04)¹⁰-1) / 0,04 = 300 153 руб.

Пример 1.10.Инвестор купил облигацию
по номинальной цене, которая равна 1,0
млн. руб. Купонные платежи производятся
один раз в год по процентной ставке 10%,
которые реинвестируются под 7% в год.
Срок обращения облигации 8 лет. Определить
будущую стоимость денежных потоков,
генерируемых этой облигацией за весь
срок обращения.

Задано: P_N= 1 000 000 руб.;g=
0,1;i = 0,07;T
= 8.

Определяем ежегодный купонный доход,
получаемый инвестором в течение 8 лет:

СР = P_N
× g= 1 000 000
× 0,1 = 100 000 руб.

Таким образом, к концу восьмого года
инвестор получит:

• 8 купонных платежей, которые в сумме
  будут равны 8×100 000 = 800 000 руб.

• доход от реинвестиции купонных платежей;

• по истечении 8 лет номинальную стоимость
  облигации 1 000 000 руб.

1. Определим по формуле 1.3 сумму дохода
инвестора, включающую купонные платежи
и процентные платежи при инвестировании
купонного дохода:

FV = А×((1+i)
-1)^T /i
= 100 000×((1+0,07)⁸-1)/0,07=100 000×10,2598 =1 025
980 руб.

2. Следовательно, доход от реинвестирования
купонных платежей (RI)
будет равен:

RI =
1 025 980
– 800 000 = 225 980 руб.

3. Номинальная стоимость облигации –
1 000 000 руб.

Общая сумма платежей (E_Total),
полученная инвестором в течение 8 лет
равна:

E_Total
= 800 000 + 225 980 + 1 000 000 = 2 025
980 руб.

Пример 1.11.Обратимся к данным примера
1.10 и предположим, что купонные платежи
по облигации выплачиваются каждые шесть
месяцев, а все остальные данные оставим
без изменения. Необходимо определить
будущую стоимость всех платежей,
получаемой инвестором в течение срока
обращения облигации.

Задано: P_N
= 1 000 000 руб.; g
= 0,1; i =
0,07; T =
8; m = 2;
r = i/m
= 0,07/2 = 0,035.

1. Определяем количество периодов, в
течение которых эмитент выплачивает
держателю облигации купонные платежи:

n = T×m= 8×2 = 16.

2. Определяем купонный доход, получаемый
инвестором каждые 6 месяцев в течение
8 лет:

СР = P_N
×g/2= 1 000 000
× 0,1/2 = 50 000 руб.

Таким образом, к концу восьмого года
инвестор получит:

• 16 купонных платежей, которые в сумме
  будут равны 16×50 000 = 800 000 руб.

• доход от реинвестиции купонных платежей;

• по истечении 8 лет номинальную стоимость
  облигации 1 000 000 руб.

3. Определим по формуле 1.4 сумму дохода
инвестора, включающую купонные платежи
и процентные платежи при инвестировании
купонного дохода:

FV = А×((1+r)
-1)ⁿ/r
= 50 000×((1+0,035)¹⁶-1)/0,035
= 50 000×20,971 = 1 048 550 руб.

4. Следовательно, доход от реинвестирования
купонных платежей (RI)
будет равен:

RI= 1 048
550 – 800 000 = 248 550 руб.

5. Номинальная стоимость облигации –
1 000 000 руб.

Общая сумма платежей (E_Total),
полученная инвестором в течение 8 лет,
равна:

E_Total
= 800 000 + 248 550 + 1 000 000 = 2 048
550руб.

Полученные результаты указывают, что
при увеличении частоты получения
купонных платежей держатель облигации
получит большую сумму в период до срока
погашения облигации.

Резюме

Будущая стоимость купонных доходов по
облигации зависит от номинальной
стоимости и срока обращения облигации,
ставки купонного дохода, количества
выплат купонного дохода в течение года
и ставки рефинансирования купонных
платежей.

Основные формулы,
применяемые при определении будущей
стоимости

1. Будущая стоимость капитала,
инвестированного сроком на Тлет:

FV = P×(1
+ i)^T,

где FV – будущая
стоимость, руб.;

P – сумма
инвестированного капитала, руб.;

i– процентная
ставка (доли ед);

Т– период, на который инвестирован
капитал, годы.

2. Будущая стоимость капитала,
инвестированного на n
периодов:

FV = P×(1
+r)ⁿ,

где r– годовая
процентная ставка, деленная наm(i/m);

m– число
платежей в год;

n– число
периодов платежей (n=m×T).

3. Будущая стоимость простых аннуитетов
для Т лет:

,

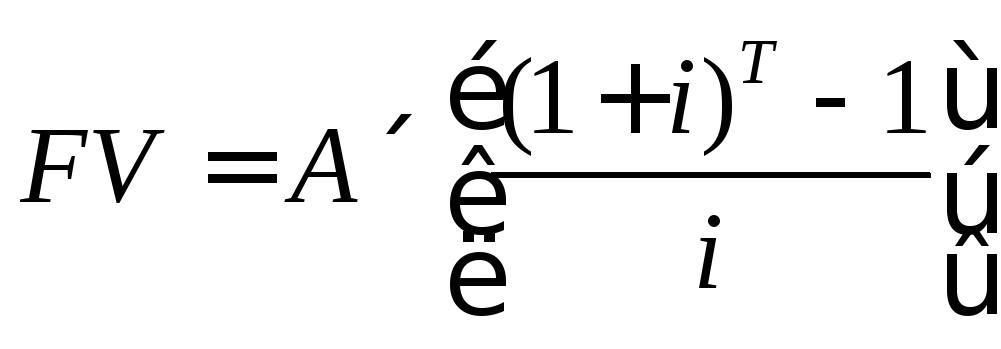
где А– величина аннуитета, руб.;

i– годовая
процентная ставка, доли ед.

4. Будущая стоимость простых аннуитетов
для nпериодов:

,

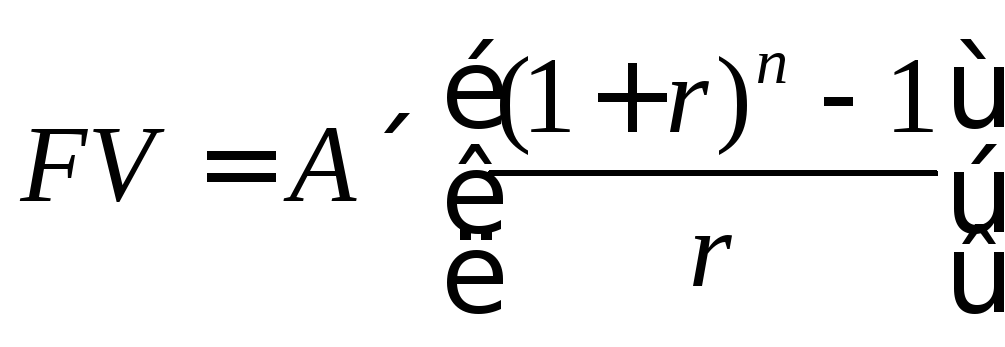
где A– величина аннуитета,
руб.;

r– годовая
процентная ставка, деленная наm(i/m);

m– число платежей
в год;

n– число периодов
платежей (n=m×T).

5. Величина аннуитета при известной
будущей стоимости через Т лет:

,

где FV— будущая
стоимость инвестиций, руб.;

i – годовая
процентная ставка, доли ед.;

Т– число лет.

Контрольные вопросы
и задачи

1. Почему деньги имеют временную стоимость?

2. Какие факторы определяют значение
временной стоимости?

3. Как определяется будущая стоимость
денег при условии начисления процентных
платежей один раз в год?

4. Как определяется будущая стоимость
денег при условии начисления процентных
платежей несколько раз в год?

5. Какие факторы влияют на величину
будущей стоимости аннуитетов?

6. Инвестор вложил 3,0 млн. руб. в покупку
финансового инструмента, по которому
он будет получать ежегодно 6% в год в
течение 10 лет. Чему равна будущая
стоимость всех денежных потоков, которые
получит инвестор?

7. Инвестор купил облигацию стоимостью
100 000 руб. за 80 000 руб. Срок обращения
облигации 3 года. Купонные платежи
выплачиваются ежеквартально исходя из
ставки10% в год. Чему равна будущая
стоимость всех денежных потоков,
полученной инвестором?

8. Инвестор купил облигацию стоимостью
100 000 руб. за 90 000 руб. Срок обращения
облигации 15 лет. Купонные платежи
выплачиваются два раза в год исходя из
ставки 12% в год. Чему равна будущая
стоимость купонных выплат, полученных
инвестором за первые 10 лет, если ставка
рефинансирования купонных платежей
принять равной 8% в год?

Будущая стоимость инвестиций – это сумма, до которой возрастет первоначальный вклад с учетом капитализации на основе сложных процентов, в течение периода хранения средств на счете.

Расчет будущей стоимости инвестиций осуществляется с использованием стандартных формул.

Чтобы их усвоить, достаточно попрактиковаться на простом примере.

Допустим, у нас имеется вклад в размере 1000 долл. под 7% годовых. Будущая стоимость инвестиций в данном случае может быть рассчитана по следующей формуле:

Будущая стоимость на конец 1-го периода = 1000 долл. * (1 + 0,07) = 1070 долл.

В случае продления срока действия вклада на тех же условиях еще на год будущую стоимость вклада следует рассчитывать по той же формуле с учетом полученного результата:

Будущая стоимость на конец 2-го периода = 1070 долл. * (1 + 0,07) = 1144,9 долл.

Понятно, что этот процесс может быть продолжен сколь угодно долго.

Формула расчета будущей стоимости инвестиций

Было бы удобно, не производя промежуточных расчетов, сразу получать значения будущей стоимости денег (инвестиций) на некоторый период времени, располагая данными о [1] размере первоначального вклада и [2] размере процентной ставки.

Для этого выведем общую формулу.

Для сокращения записи обозначим будущую стоимость инвестиций на конец n-го периода буквой S_n, размер первоначального вклада – буквой N, размер процентной ставки – k.

Тогда наша формула примет вид:

S_n = N*(1+k/100)ⁿ.

В частности, будущая стоимость инвестиций на конец 2-го периода с учетом наших первоначальных данных будет рассчитана по формуле 1000 долл. * (1+7/100)² = 1000 долл. * 1,1449 = 1144,9 долл., что соответствует полученному нами ранее результату.

Таблица расчета будущей стоимости инвестиций

На практике производить вручную приведенные выше расчеты бывает крайне утомительным.

Рассчитать будущую стоимость инвестиций на конец хотя бы 10-го периода способны разве что истинные фанаты счетного дела.

Попробуйте, к примеру, возвести в 10-ю степень число 1,07; лично я сразу начинаю искать калькулятор или что-то в этом роде…

До изобретения калькуляторов и компьютеров широко использовались таблицы с уже готовыми результатами.

На практике такие таблицы могут оказаться очень удобными в использовании.

Чтобы было понятно, о чем идет речь, предлагаю взглянуть на таблицу ниже:

Таблица содержит коэффициенты для 1 долл. (значения коэффициентов округлены до 3-го знака после запятой).

В частности, по истечению 2-го периода (года) при 7-процентной ставке размер вклада составит 1,145 долл. Если первоначальная сумма вклада составляла 1000 долл., то для расчета будущей стоимости вклада нужно его первоначальный размер умножить на соответствующий коэффициент из таблицы (1000 долл. * 1,145 = 1145 долл.).

Будущая стоимость инвестиций: важные закономерности

Внимательно присмотревшись к таблице, можно сделать несколько основополагающих выводов относительно формирования будущей стоимости инвестиций.

Во-первых, чем выше процентная ставка по вкладу, тем выше размер будущей стоимости.

Во-вторых, для каждой процентной ставки характерно увеличение размера будущей стоимости инвестиций с течением времени.

Наконец, в-третьих, коэффициент наращения будущей стоимости, как правило, всегда больше 1; он может быть равен 1 лишь в случае, когда процентная ставка равна 0.

В таком случае будущая стоимость инвестиций оказывается равной первоначальному вкладу, что случается, например, когда, вы просто одалживаете деньги на некоторый срок своим знакомым без взимания процентов за пользование одолженными средствами.

Конечно, использование таблиц не лишено недостатков.

Их расширение может представлять определенные трудности.

Если нам понадобится узнать размер капитала через 100 периодов, потребуется довольно обширная таблица, пользование которой окажется не таким уж простым делом.

На сегодняшний момент оптимальным следует признать использование так называемых инвестиционных калькуляторов, позволяющих в режиме онлайн производить соответствующие расчеты и мгновенно получать интересующие нас результаты.

Резюме

Сегодняшняя статья не охватывает всех аспектов, касающихся описания концепции сложных процентов и концепции будущей стоимости, а также связанных с этими концепциями расчетов.

Существует ряд формул, позволяющих рассчитывать будущую стоимость аннуитета (потока равных сумм денежных средств), приведенной стоимости, которые будет полезно усвоить каждому вдумчивому инвестору.

Но обо всем об этом мы поговорим в другой раз. Так что до скорой встречи и удачных инвестиций!

Подробнее про формулу

Банки в своей практике руководствуются несколькими формулами, позволяющими рассчитывать простые % и сложные. При их начислении применяется фиксированный и плавающий вид ставок. Фиксированную закрепляют договором при размещении вклада, она не меняется до конца периода его действия. Она может измениться в случае автоматических пролонгаций действия договора. Также она изменится в случае досрочного разрыва соглашения между клиентом и банком с выплатой % за фактический период размещения вложений, если вклад был размещен до востребования. Эти нюансы должны быть описаны в договорах.

В случае плавающих ставок, установленных изначально, их размер может изменяться на протяжении действия договоров.

При каких условиях и в каком порядке будет осуществляться этот процесс, нужно описывать в договорах. Изменение процентов привязано к изменениям:

• ключевой ставки;
• валютного курса;
• переводом депозита в иную категорию и др.

Для расчетов указываются все требуемые формой данные:

• сумма вклада;
• размер % ставки конкретного вклада;
• периодичность начислений % (поквартально, помесячно, ежедневно и др.);
• срок заключения договора;
• иногда нужно знать вид применяемой ставки – она может плавать или быть зафиксированной.

Общая формула расчета процентов по вкладу

Использование формулы простых процентов целесообразно в случае начисления процентов в конце срока размещения депозита или если они будут переводиться на отдельный счет – если капитализация договором не предусмотрена.

Выбирая вклад, клиент банка должен обратить внимание на порядок, который применяется при начислении процентов.

Формула расчета простых:

S = (P x I x t / K) / 100

Обозначения:

• S – прибыль со вклада (только проценты, без тела вклада);
• P – сумма, изначально внесенная на депозит;
• I – размер % ставки (за год);
• t – кол-во дней начисления %;
• K – кол-во дней за год по календарю.

A = P * (1 + r/n)^(n*t)

Здесь все более сложно, поскольку нужно высчитывать степень (^ – знак степени). Остальные обозначения:

• A – общая сумма денег (тело вклада + проценты), которую вы получите после того, как срок вклада закончится.
• P – стартовая сумма, которую вы кладете на счет вклада.
• r – процентная ставка по вкладу.
• n – количество расчетов прибыль в году, для ежедневной капитализации – 365 или 366, для ежемесячной – 12 и так далее.
• t – количество лет вклада. 6 месяцев – это 0.5 года.

Формула для вкладов с ежемесячной капитализацией

Чтобы рассчитать возможную прибыль в случае выбора вида депозита с капитализацией % с ежемесячным начислением % подойдет такая формула:

S = Р * (1 + (N/100)/12)^n, здесь используются следующие обозначения:

n – количество проведенных операций перевода процентов в тело вклада на протяжении полного срока действия договора (то есть месяцев вклада);

S – сумма вклада на дату окончания действия депозита, которую вкладчик получит на руки;

Р – изначально внесенная сумма на депозит с возможностью капитализации;

N — % ставка (годовая).

Формула для вкладов с ежедневной капитализацией

Если выбрана форма начисления % с ежедневной капитализацией, применяется следующая формула:

S = P * (1 + (N/100)/K)^T, где:

S – суммарный доход (тело вклада + проценты);

Р – внесенная при заключении договора сумма;

N – годовая % ставка;

К – 365 или 366 дней;

Т – кол-во дней, на которые открыт депозит.

Формула для вкладов с ежеквартальной капитализацией

В данном случае расчет процентов будет выглядеть следующим образом:

S=Р * (1+ (N/100)/4)^Т, где:

S — получаемый в конце срока доход (тело вклада + проценты);

Р – изначально размещенная сумма на депозите;

N — годовой %;

Т – количество кварталов, на протяжении которых открыт вклад.

Что такое эффективная ставка по депозиту?

Эффективная ставка = фактическая ставка + прибыль от капитализации. Если вклад – без капитализации, то эффективная ставка равна фактической ставке (указана в договоре); если вклад – с капитализацией, то эффективная ставка будет выше фактической, поскольку капитализация будет увеличивать тело вклада.

Как рассчитать через Excel?

Рассчитать в Excel доход от депозита можно на примере. Если необходимо положить на депозит 50 000 руб. с процентной ставкой 8% на три года с ежемесячной капитализацией и просчитать размер дохода через 24 месяца, нужно составить таблицу:

• A1-A24 – указываем месяцы, то есть 1,2,3…
• D1 – указываем сумму тела кредита.
• D2 – указываем ставку в процентах

Теперь нужно в ячейку B1 вставить специальную формулу для подсчета сложного процента: =БС($D$2/12;A1;;-$D$1). Первый аргумент ($D$2/12) – проценты, нужно делать на 12, поскольку считаем ежемесячное начисление. Второй аргумент (A1) – месяц, за который считаем. Третий аргумент оставляем пустым (комиссии/сборы). Четвертый (-$D$1) – тело вклада, ввиду некоторых особенностей работы функции БС его нужно указывать с минусом. Теперь выделяем ячейку B1, растягиваем ее содержимое на ячейки ниже, до B24. Получаем суммарное количество денег на счете в каждом месяце, через 24 месяца получим 58 644 рубля.

Как рассчитать онлайн?

Онлайн расчет процентов можно осуществлять на сайте банка, выбранного для размещения депозита. Для этого нужно найти на странице банка онлайн калькулятор вкладов, ввести в него требуемые данные и рассчитать:

• сумму;
• срок;
• дату начала размещения вклада;
• % ставку;
• период капитализации;
• пополнение (если возможно).

Пример расчета

Расчет при ежемесячной капитализации:

Исходные данные:

Сумма вклада – 50 000 руб.;

Годовая ставка — 8%;

Срок вклада – 12 мес.

50 000 х(1+0,08/12)^12= 54 150 руб.

Налоги на доход по вкладам

За 2021 и 2022 годы налог по вкладам не начисляли вовсе. На доход со вкладов, полученный с 1 января 2023 года, начисляется НДФЛ в размере 13%, но – только на доход, превышающий определенный порог. Порог рассчитывается так: берут максимальную ключевую ставку ЦБ РФ за год, после чего умножают ее на 1 000 000 рублей. Например, максимальная ключевая ставка составила 6% – значит, налогом не будет облагаться доход за год в 60 000 рублей. Если ваш доход за год превысил эту сумму – на сумму превышения начисляется 13%. Если вы получили за год 90 000 рублей дохода со вкладов – с 30 000 рублей нужно будет заплатить 13% НДФЛ, то есть 3 900 рублей. Налог рассчитывается автоматически, в 2024 году вам пришлют уведомление за 2023-й год. Это работает как для резидентов, так и для нерезидентов РФ.