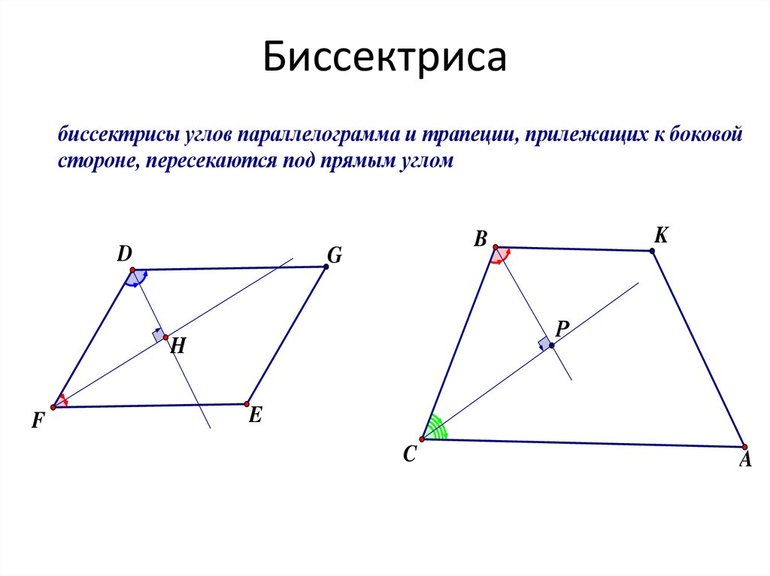
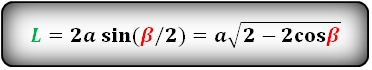Выпускники, которые рассчитывают успешно сдать ЕГЭ, в обязательном порядке должны повторить тему «Свойства биссектрисы параллелограмма». Как показывает статистика, при прохождении аттестационного испытания задачи по данному разделу планиметрии вызывают сложности у большого количества учащихся. При этом задания, в которых необходимо применить свойства биссектрисы угла параллелограмма, встречаются в ЕГЭ ежегодно. Таким образом, справляться с ними должны все учащиеся.
Образовательный портал «Школково» предлагает выстроить процесс подготовки к прохождению аттестационного испытания по-новому. Занимаясь вместе с нашим ресурсом, выпускники смогут определить наиболее сложные для себя темы и ликвидировать пробелы в знаниях.
Чтобы задания ЕГЭ не вызывали трудностей, рекомендуем вначале повторить основные понятия и свойства биссектрисы параллелограмма. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».
Для того чтобы окончательно понять принцип решения задач по данному разделу планиметрии, мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий различного уровня сложности представлена в разделе «Каталог». Для каждого упражнения на сайте приведен алгоритм решения и дан правильный ответ. Последовательно выполняя их, учащиеся смогут понять, как правильно применять свойства биссектрисы внутреннего угла параллелограмма.
Получать новые знания и оттачивать собственные навыки по данной теме или, например, в решении задач на тему «Прямоугольник» в ЕГЭ учащиеся могут в онлайн-режиме, находясь в Москве или любом другом российском городе. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
Равнобедренный треугольник в параллелограмме
Биссектриса параллелограмма может быть проведена из вершины острого или тупого угла фигуры. Доказательство теоремы о равнобедренности образуемых прямой треугольников в этих случаях имеет аналогичный порядок. Чтобы доказать утверждение, нужно знать признак равнобедренности треугольника:
- Согласно условию, проведенная из острого угла А биссектриса AF делит одну из сторон ABCD на 2 отрезка.
- Свойство биссектрисы позволяет утверждать, что углы FAD и BAF равны между собой.
- Определение внутренних накрест лежащих углов, которые образует секущая AF с прямыми ВС и AD, приводит к выводу о равенстве FAD и BFA.
- Поскольку углы BFA и BAF равны, этот признак свидетельствует о равнобедренности треугольника ABF.
- Стороны АВ и BF являются равными и соответствуют отрезку m, который образован при делении ВС биссектрисой.
С помощью аналогичных рассуждений можно доказать, что биссектриса тупого угла параллелограмма делит противоположную сторону на отрезки и отсекает от него равнобедренный треугольник.
Точка пересечения прямых
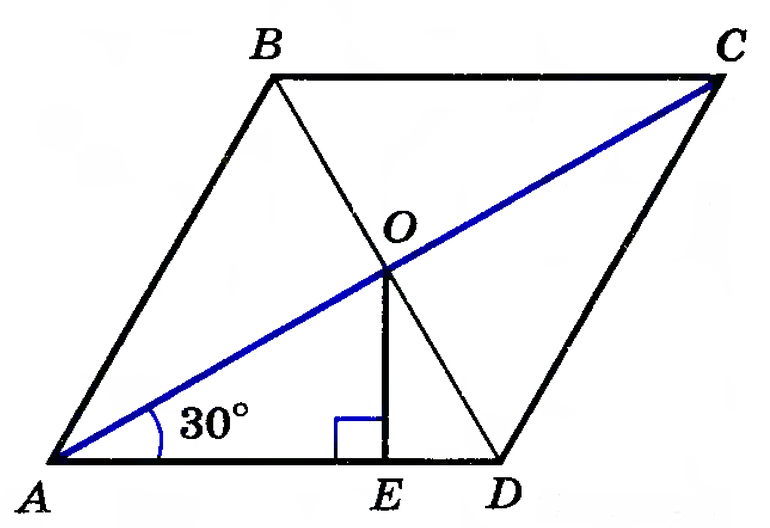
Согласно свойству, проведенные из смежных углов параллелограмма биссектрисы пересекаются в точке на противоположной стороне, если она в 2 раза больше меньшей. Доказать это утверждение можно следующим способом:
- В равнобедренном треугольнике АВО сторона АО является биссектрисой четырехугольника АВСD.
- Признак равнобедренности предполагает равенство АВ и ВО.
- Согласно свойству, равенство СО и СD свидетельствует о равнобедренности треугольника СDО.
- Стороны АВ и СD равны как противолежащие, из чего следует равенство ВО и СО.
- Поскольку АВ и ВО равны, то ВО = СО, поэтому АВ равна половине ВС, значит большая сторона фигуры в 2 раза превышает величину меньшей.
Доказательство свойства позволяет предположить, что биссектрисы смежных углов пересекаются внутри либо вне параллелограмма. При этом одна сторона больше или меньше половины другой. Если ее величина больше половины соседней, значит прямые пересекутся внутри фигуры.
Биссектрисы, проведенные через смежные углы, пересекаются с продолжением противоположных сторон параллелограмма в вершинах ромба. В зависимости от величины другой стороны, ромб совпадает с ним либо обладает большим или меньшим периметром. Если частить с построением этой фигуры, то длины сторон параллелограмма будут бесконечными.
Свойства односторонних углов
Параллелограмм АВСД имеет смежные углы при параллельных прямых АВ и СД, обозначенные а1 и а2. Для доказательства теоремы о перпендикулярности биссектрис нужно знать свойства смежных углов, сумма которых равна 180 градусам.
Поскольку биссектрисы можно провести внутри острого или тупого угла параллелограмма, то величину смежного с ним внешнего угла можно сложить, получив 180 градусов. Если обозначить их через АО и ДЕ, то углы ОАВ и ЕДС будут равны половинам а1 и а2 соответственно. Так как а1 + а2 = 180, то (а1 + а2) / 2 = 90, значит АО и ДЕ образуют прямой угол АКД.
Применять свойство биссектрис можно при нахождении периметра фигуры. Должны быть известны данные о соотношениях или длинах отрезков, образованных при пересечении противолежащей стороны биссектрисой. Например, она делит на отрезки ВК и КС сторону параллелограмма ABCD, величины которых известны.
Формула определения периметра будет иметь вид: P=2 (n+n+m). Где ВС=BК+КC=n+m, а АВ=ВК=n по свойству биссектрисы. С учетом признака равнобедренности треугольника можно построить эту прямую, дополнив рисунок фигуры без транспортира с помощью циркуля.
Противолежащие углы и биссектрисы
Согласно свойству параллельных прямых, биссектрисы a и b проходят параллельно друг другу. Они образуют внутри фигуры со сторонами mnkp другой параллелограмм, следовательно, он обладает параллельными противоположными сторонами. Прямые, на которых они лежат, соответствуют сторонам исходной фигуры, поэтому ее биссектрисы a и b являются равными.
Углы, которые образованы отрезками a и m, а также b и k, согласно свойствам биссектрис и параллелограммов, равны. Противолежащие равные по величине углы, образованные отрезками mp и nk, можно разделить пополам. Прямая b, пересекающая отрезки n и p, образует с ними накрест лежащие углы, признак которых состоит в их равенстве. Они равны разделенным пополам противоположным и являются соответственными при параллельных прямых n и p.
Вершины образуемого прямоугольника
Биссектрисы параллелограмма пересекаются в точках, представляющих собой вершины прямоугольника, что можно доказать следующим образом:
- Согласно исходным данным, параллелограмм ABCД имеет внешние углы, через вершины которых В и С проведены прямые, разделяющие их пополам.
- Если К, М, Р и О представляют собой точки пересечения биссектрис, исходящей из вершин фигуры, то они образуют четырехугольник.
- По свойству смежных внутренних углов, образуемых параллельными прямыми и секущей, все стороны четырехугольника КМРО перпендикулярны между собой.
- Если через середину ВС фигуры провести медиану треугольника ВКС в параллелограмме, то эта точка Х разделит ВС на равные отрезки ВХ и СХ.
- Отсюда следует равенство углов ХКС, КСХ и КСТ, где Т — это точка, принадлежащая прямой СД.
- Вывод из доказательства: прямые СД и КХ параллельны.
Аналогичным способом можно доказать параллельность других сторон прямой СД. Следовательно, диагональ КР образованного биссектрисами параллелограмма прямоугольника КМРО содержит точки Х и Т. Доказательство предполагает следующее равенство: КР = КХ + ХТ + ТР = ХС + СД + ТД = ВС + СД, поэтому величина диагонали равна сумме двух смежных сторон параллелограмма.
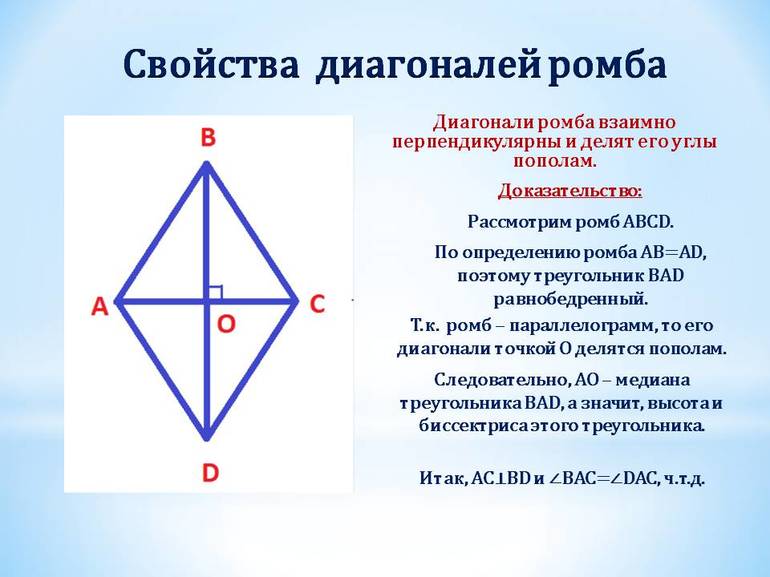
Ромб и его диагонали
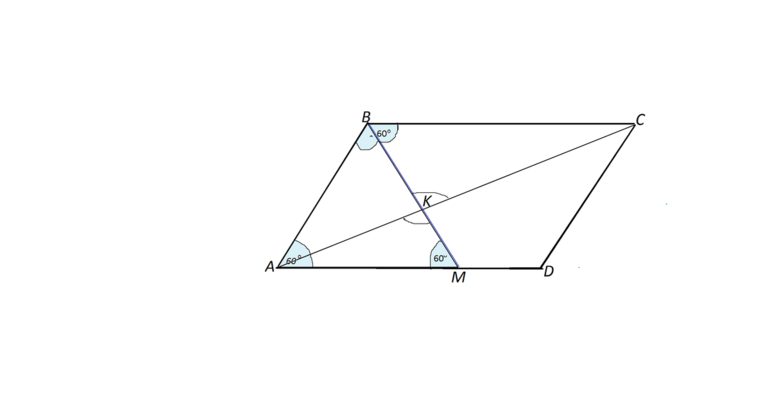
Параллелограмм, имеющий биссектрису, которая совпадает с его диагональю, представляет собой ромб. Чтобы доказать это, нужно провести диагональ AC, соединяющую противоположные вершины ABCD. Способ доказательства теоремы основан на равенстве противолежащих углов параллелограмма.
Согласно свойству биссектрисы, отрезок АС делит пополам углы BCD и BAD. Они имеют одинаковую величину, поскольку противоположные углы равны. Диагональ АС — основание треугольников ACB и ACD. Согласно признаку равнобедренности АВ и АС, а также AD и CD, равны между собой. По свойству равенства противоположных сторон параллелограмма AB = CD и AD = BC.
Фигура ABCD, представляющая собой по условию параллелограмм, имеет равные по величине AB, AD, BC и CD в соответствии с доказательством. Отсюда следует, что параллелограмм ABCD по определению ромб. В нем биссектриса АС — это его диагональ.
Примеры решения задач
Биссектрисы смежных углов параллелограмма пересеклись в точке на его противолежащей стороне. Зная его меньшую сторону, можно найти большую, а также наоборот. Допустим, что длина меньшей стороны фигуры составляет 5 сантиметров.
Обозначив вершины фигуры A, B, C, D, а точку на AD буквой Р, достаточно иметь в виду, что AD=AР+РD=AB+CD. Это доказывает признак равенства накрест лежащих углов СВР и АРВ, а также ВСР и СРD при параллельных прямых. Формула для нахождения большей стороны будет иметь вид: AD=2AB=10, поскольку AB = CD. При необходимости найти меньшую можно по формуле: AD=AB/2.
По условию задачи биссектриса, исходящая из острого угла параллелограмма, разделяет его противоположную сторону на отрезки 73 мм и 54 мм, если считать от вершины тупого угла. Требуется вычислить периметр параллелограмма ABCD. Точка Е делит сторону ВС на отрезки заданной длины, поскольку АЕ — биссектриса угла ВАD. Эта прямая представляет собой секущую для параллельных AD и BC.
Отсекая равнобедренный треугольник АВЕ, биссектриса ВЕ является его основанием, поэтому сторона параллелограмма АВ равна отрезку ВЕ, длина которого по условию 73 мм. В сумме ВЕ и ЕС равны ВС, что составляет 127 мм. Отсюда периметр ABCD соответствует удвоенной сумме его сторон: Р = 2 (73+127) = 400 мм. Чтобы найти большую сторону параллелограмма ABCD при известном периметре 128 мм, можно использовать аналогичное доказательство равнобедренности треугольника.
По условию соотношение отрезков, образуемых точкой пересечения биссектрисы DЕ с противоположной стороной ВС, равно 4:3, если считать от острого угла при вершине А. Из равенства противоположных сторон ABCD и признака равнобедренного треугольника следует AD=BC=АЕ=4х, а ЕВ=3х, поэтому CD=АЕ+ЕВ=4х+3х=7х. Зная периметр ABCD, можно составить уравнение Р=2 (7х+4х)=128. Отсюда 22х=128, а х=32, поэтому большая сторона параллелограмма CD=32*7=224 мм.
Свойства биссектрисы параллелограмма
— Биссектриса по определению делит угол пополам
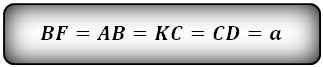
— Биссектриса отсекает равнобедренный треугольник (в данном случае треугольники ABF и DKC)
— Биссектрисы смежных углов, пересекаются под прямым углом (90°)
— Биссектрисы противоположных углов, равны и параллельны
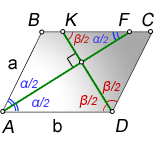
DK — биссектриса из тупого угла
α — острый угол
β — тупой угол
a — меньшая сторона
b — большая сторона
Так как треугольники ABF и DKC, равнобедренные, следовательно справедливы тождества:
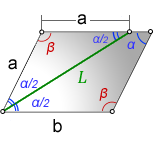
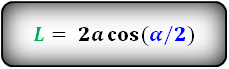
Длина биссектрисы параллелограмма
L — биссектриса параллелограмма
a, b — стороны
α, β — углы
Формулы длины биссектрисы через сторону и углы, (L):
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 07 ноября 2011
-
Обновлено: 13 августа 2021
На этой странице вы узнаете
- Чем отличаются признаки от свойств?
- Сколько крыс у биссектрисы?
- Гибридом чего будет квадрат?
Когда мы видим изображение с множеством деталей, наш мозг автоматически раскладывает их на простые фигуры. Этот процесс занимает доли секунды. Разные геометрические фигуры вызывают у нас разные ощущения, эмоции и ассоциации.А что будет, если мы задержим взгляд на одной из них и разберем подробнее? Давайте сделаем так с параллелограммом.
Параллелограмм
Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.

Параллелограмм мы видим достаточно часто.


Признаки параллелограмма
У параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.
Признаки параллелограмма:
- Две противоположные стороны четырехугольника параллельны и равны.
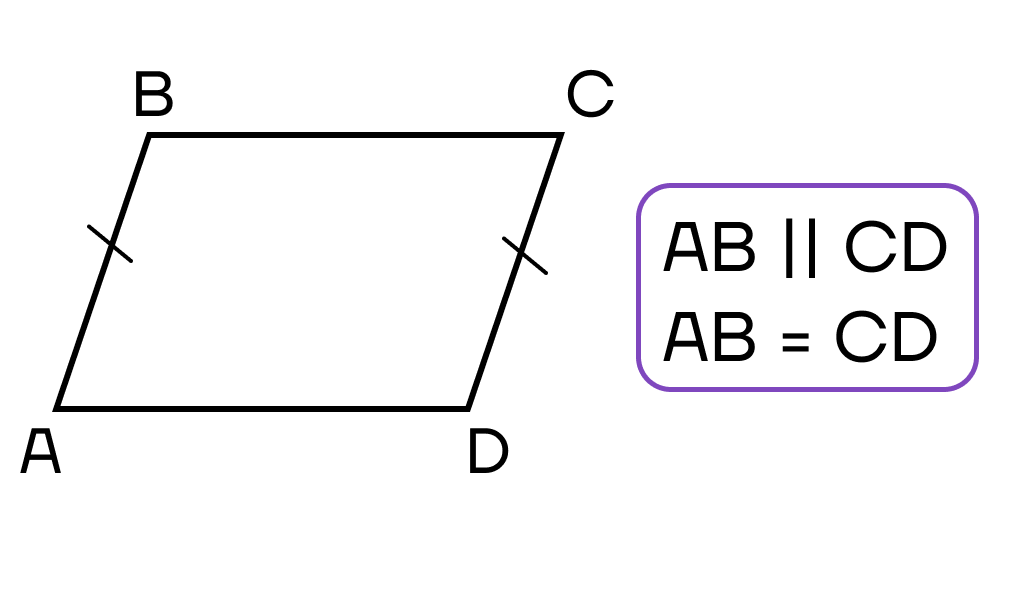
- Противоположные стороны четырехугольника попарно равны.
- Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.

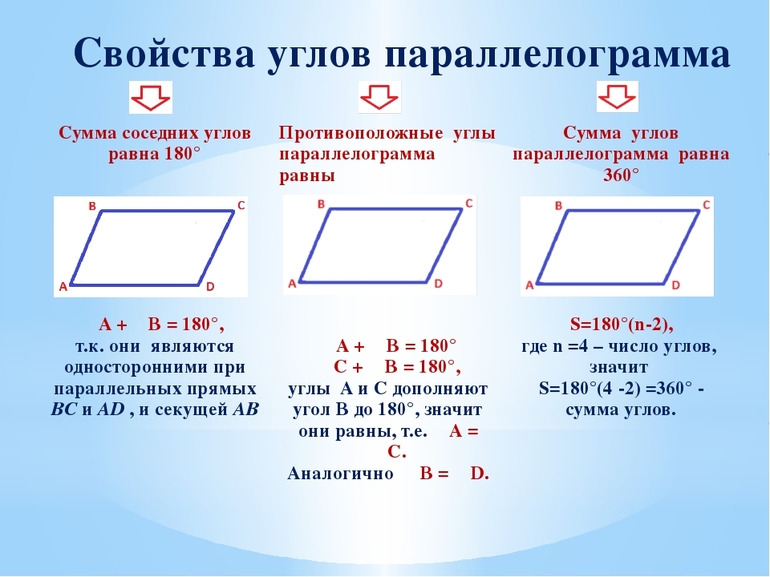
Свойства параллелограмма
Свойства нельзя путать с признаками, хоть они и очень похожи. Свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, тогда как признаки предназначены для выявления параллелограммов среди четырехугольников.
Свойства параллелограмма:
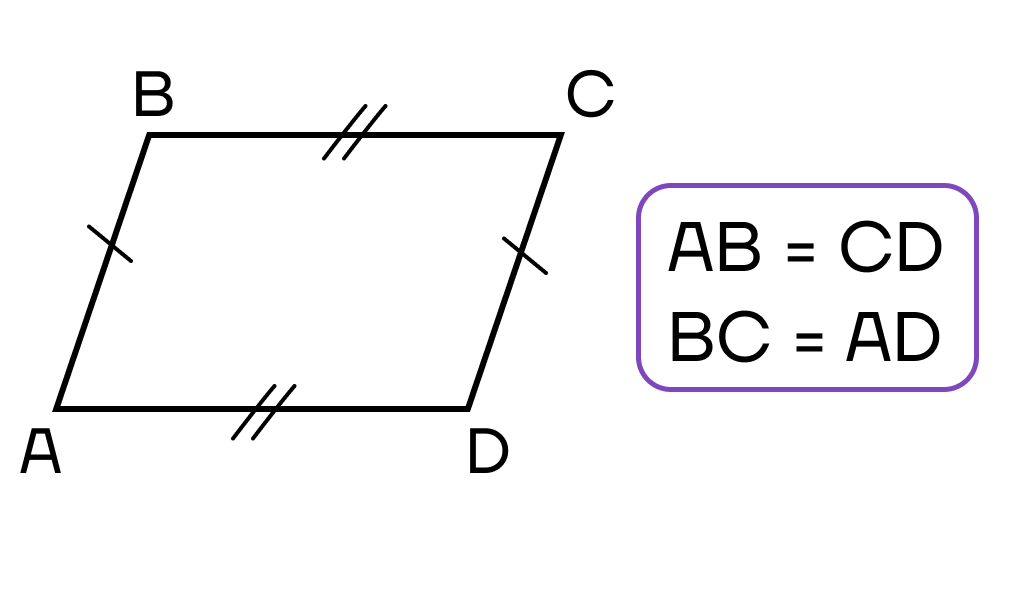
- Противолежащие стороны равны.

- Противолежащие стороны параллельны.
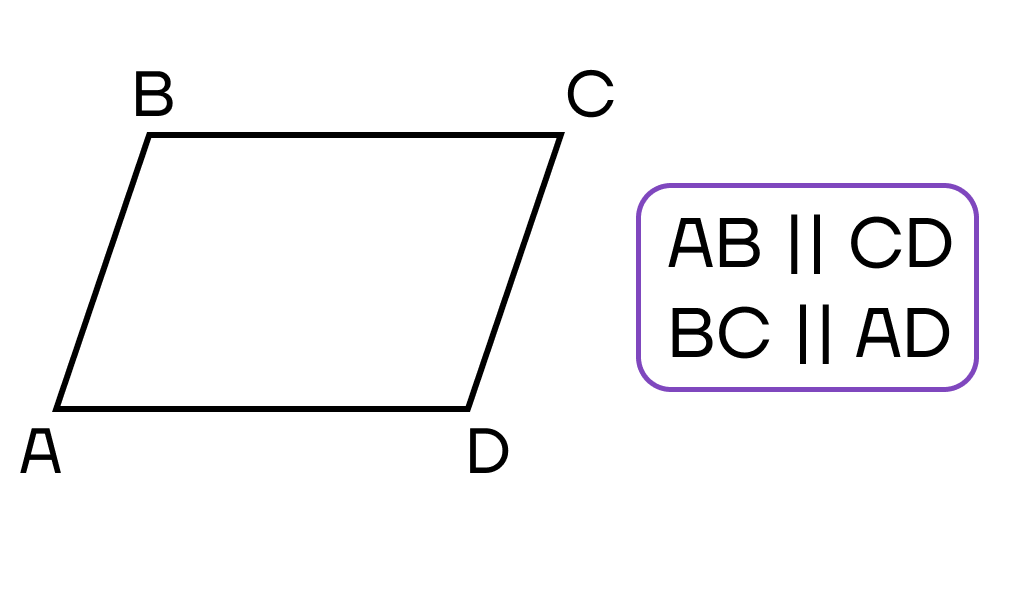
- Противолежащие углы равны.
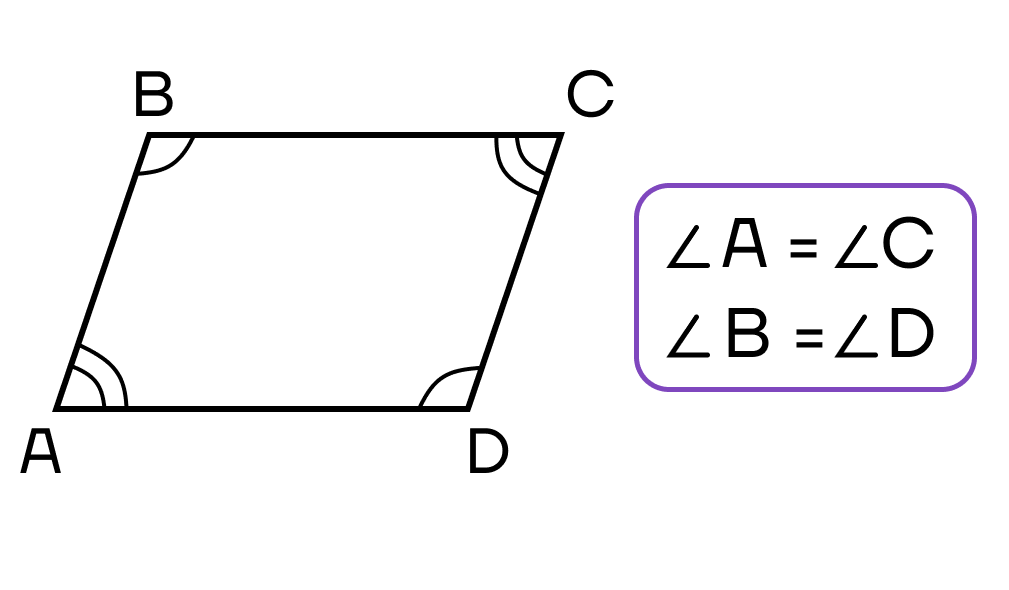
- Сумма всех углов 3600.
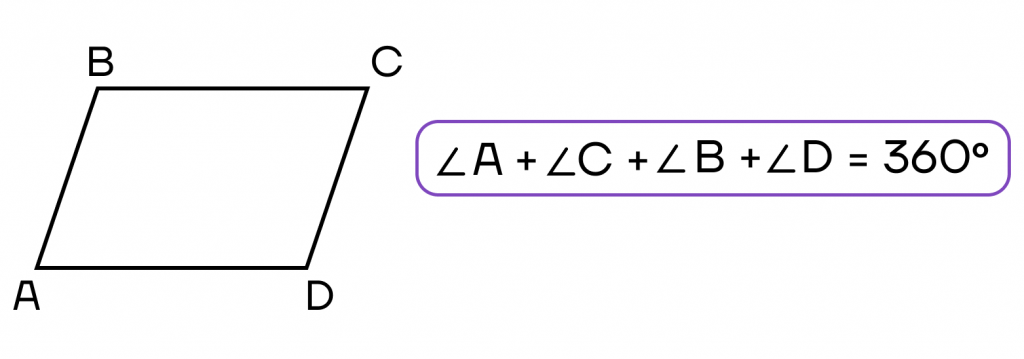
- Диагонали пересекаются и точкой пересечения делятся пополам.
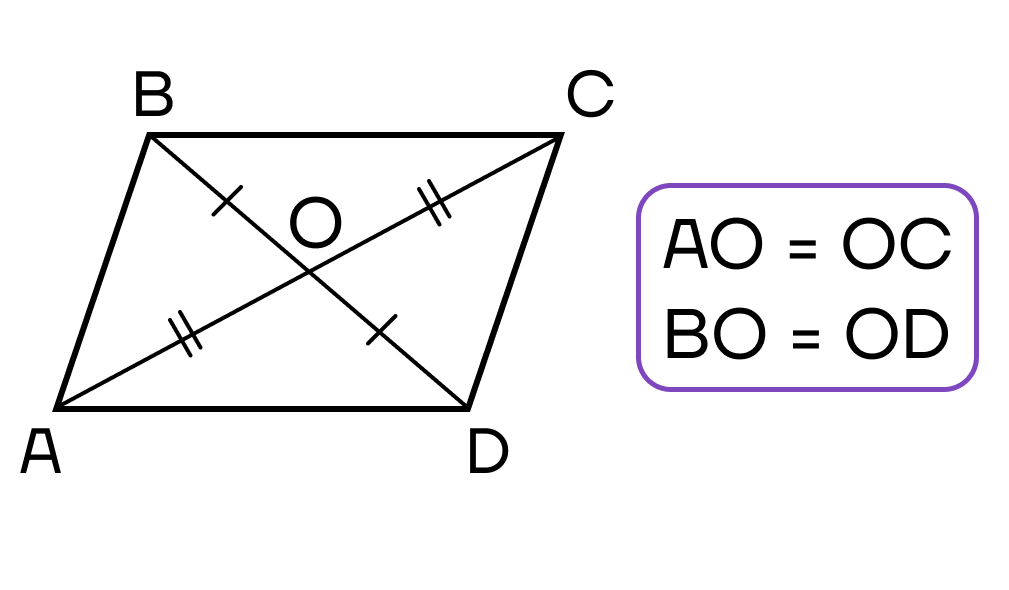
- Сумма углов, прилежащих к любой стороне, равна 1800.
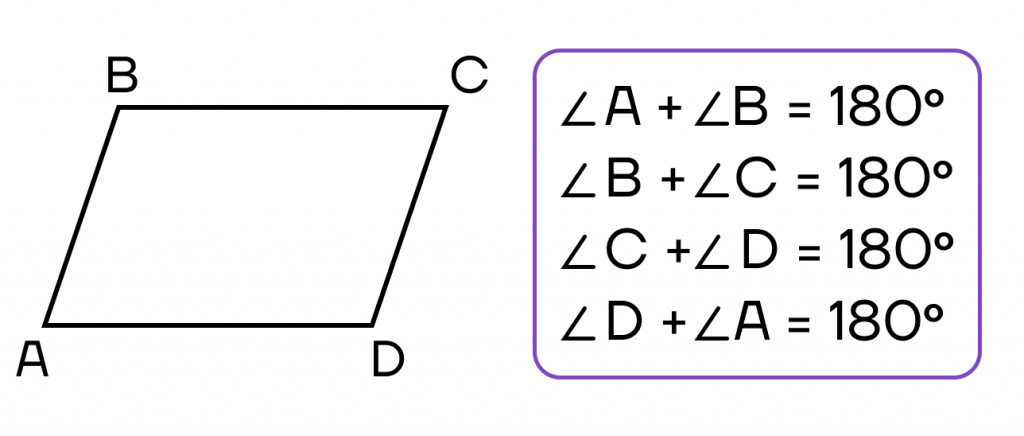
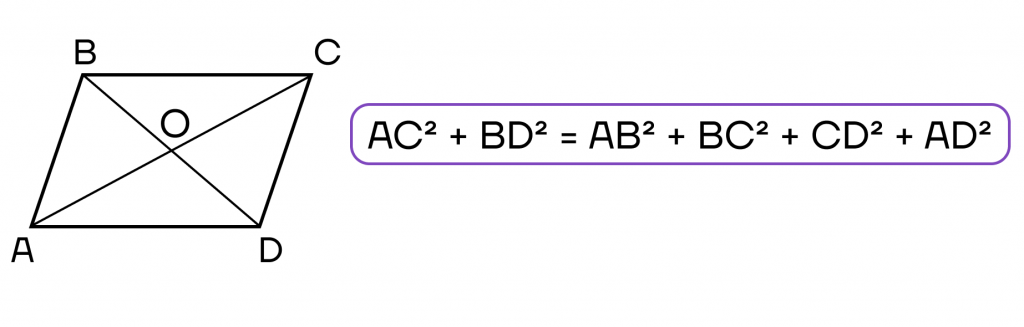
- Сумма квадратов диагоналей равна сумме квадратов всех сторон.
- Диагонали делят параллелограмм на четыре треугольника с одинаковой площадью.

- Каждая диагональ делит параллелограмм на два равных треугольника

Биссектриса в параллелограмме
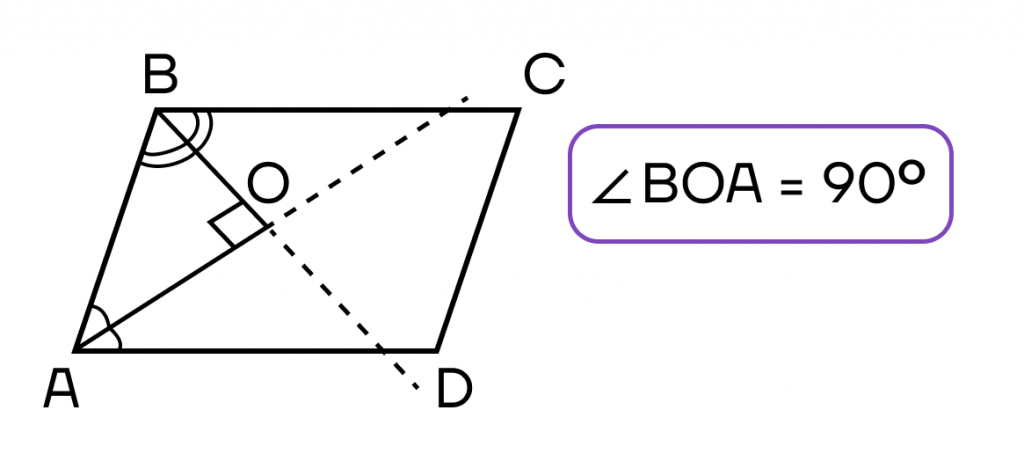
Можно ли провести биссектрису в параллелограмме? Да. Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.

Значение биссектрисы легко запомнить, используя фразу “Биссектриса – это крыса, она бегает по углам и делит угол пополам”.
Так как у треугольника три угла – соответственно, и крыс-биссектрис тоже три.
Два факта связанные с биссектрисой в параллелограмме:
- Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник.

- Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.
Площадь параллелограмма
Есть три формулы площади параллелограмма, которые применяются в зависимости от известных величин
- Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
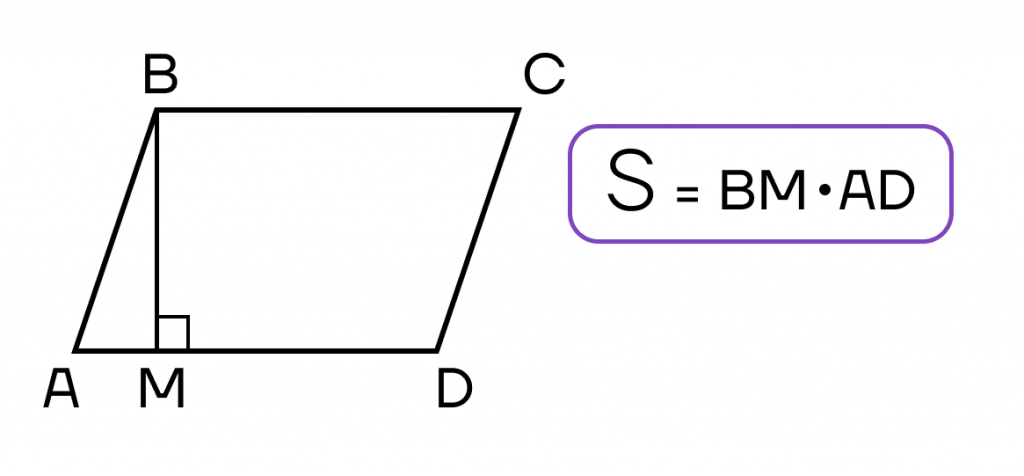
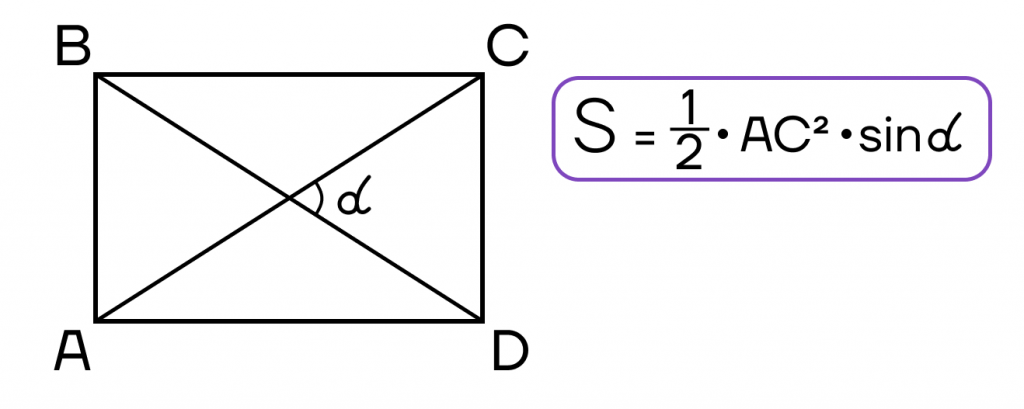
- Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.

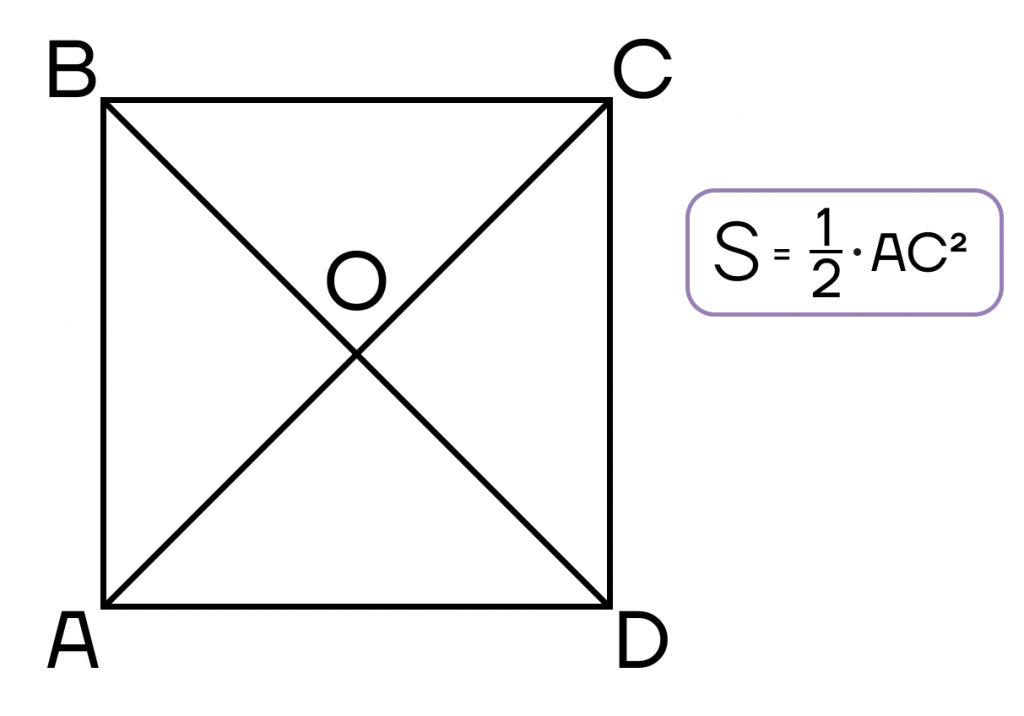
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.

Прямоугольник
Как параллелограмм связан с прямоугольником?
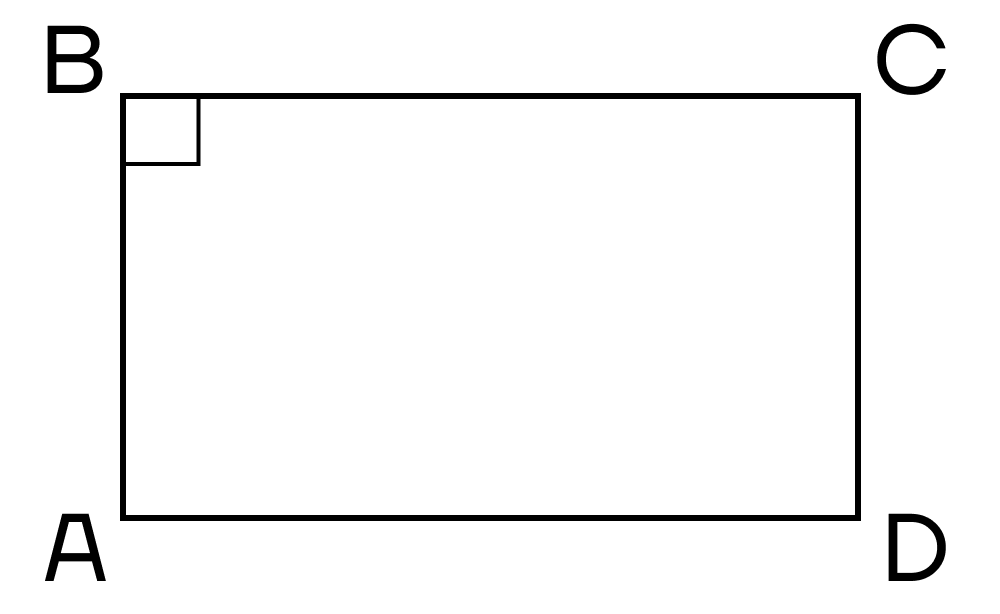
Прямоугольник – это параллелограмм, углы которого по 900.
Данную фигуру часто называют частным случаем параллелограмма. Из этого следует, что для прямоугольника применимы те же признаки и свойства, что для параллелограмма, но и имеется ряд собственных.
В жизни прямоугольником можно назвать дверь, картину или фотографию:
Признаки прямоугольника
- Параллелограмм, имеющий хотя бы один прямой угол.
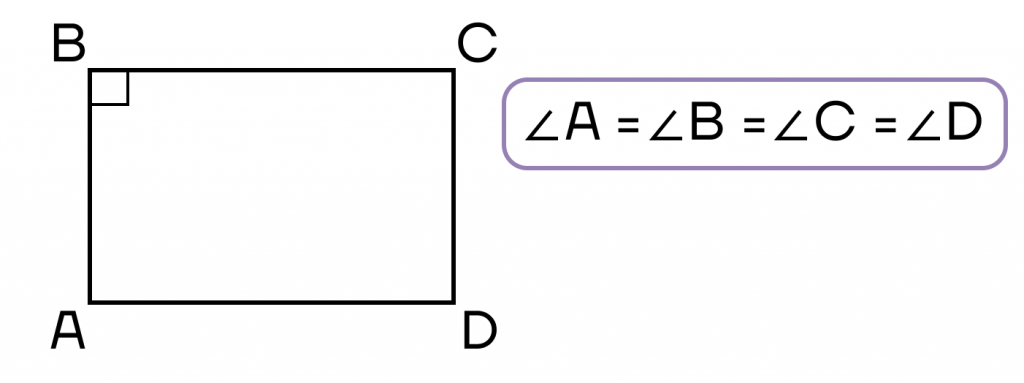
- Параллелограмм, все углы которого равны.
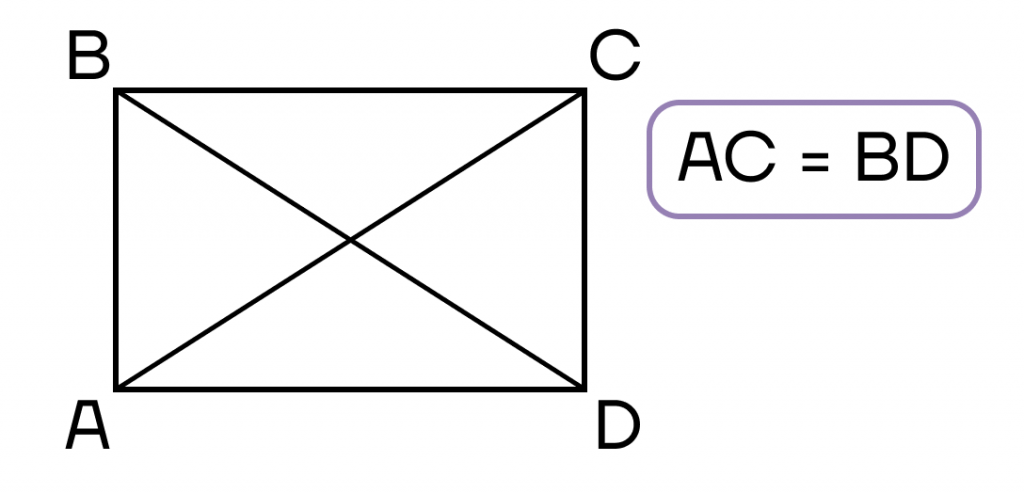
- Параллелограмм, диагонали которого равны.
- Четырехугольник, у которого три прямых угла.

Свойства прямоугольника
- Все углы прямые.

- Диагонали равны.

- Стороны прямоугольника одновременно являются и его высотами.
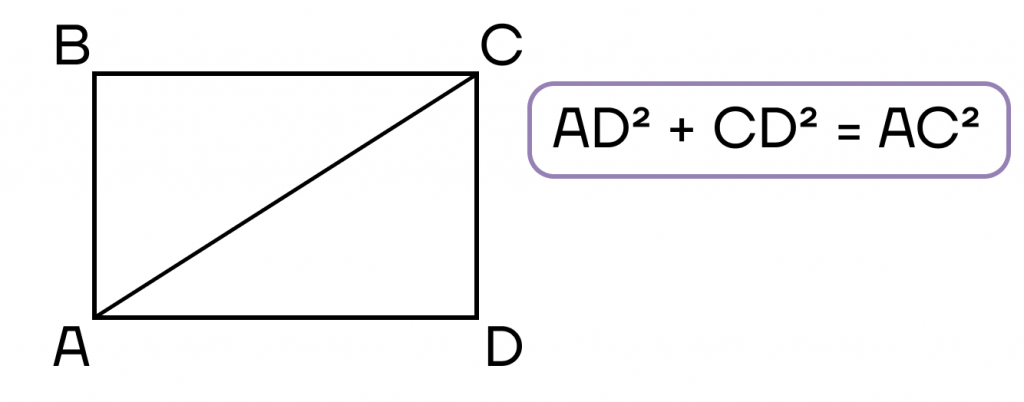
- Сумма квадратов двух прилежащих сторон равна квадрату диагонали.
Биссектриса и площадь прямоугольника
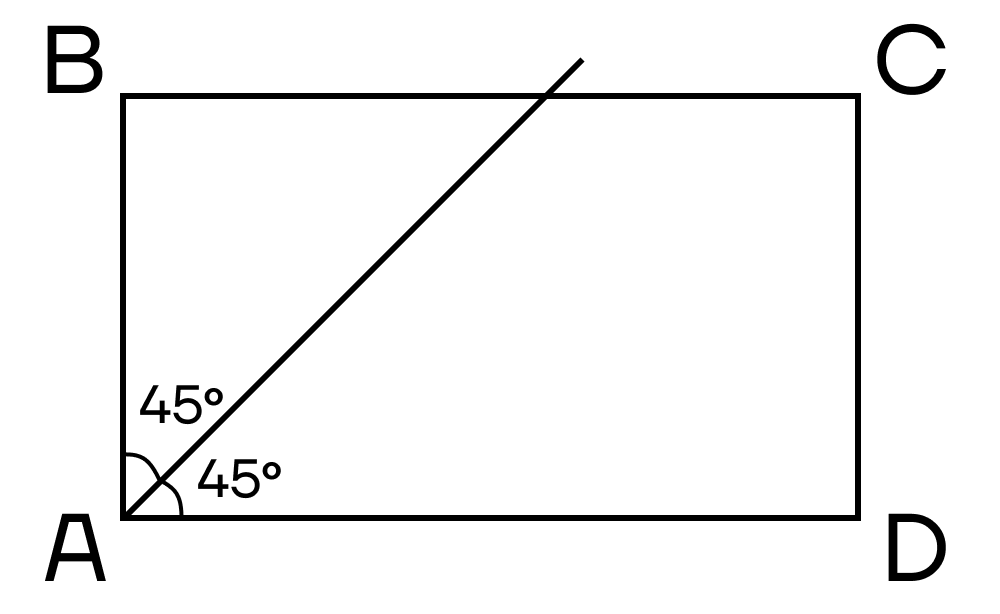
Биссектриса делит угол прямоугольника на два угла по 450 и пересекает одну из сторон прямоугольника.
Теперь рассмотрим два способа нахождения площади прямоугольника:
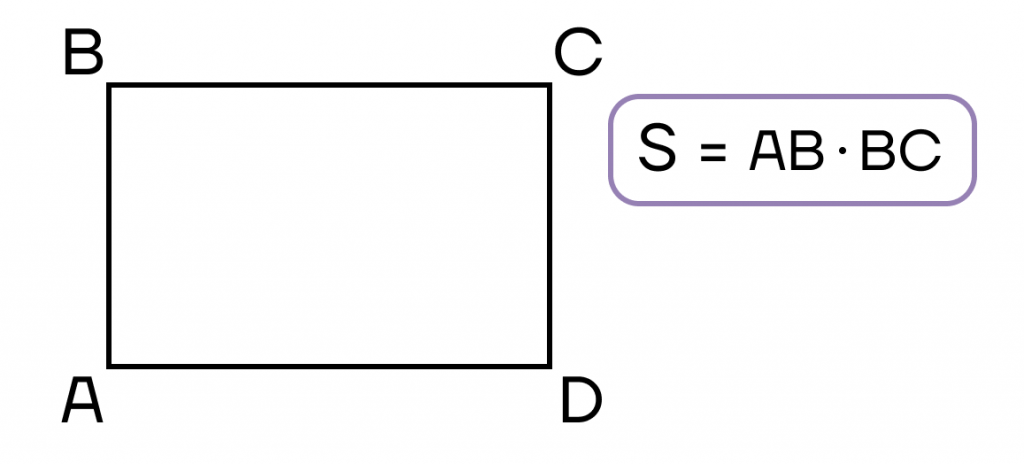
- Площадь прямоугольника равна произведению двух соседних сторон.
- Площадь прямоугольника равна половине произведения квадрата диагонали на синус угла между диагоналями.
Ромб
Пожалуй, это самая неустойчивая фигура.

Ромб – это параллелограмм, у которого все стороны равны.

Ромб можно увидеть на знаке машины “Митсубиси”, их там целых три.
А также в игровых наградах:

Также является частным случаем параллелограмма и обладает его признаками и свойствами, но имеет и собственные.
Всё о ромбе
Признаки ромба:
- Две смежные стороны параллелограмма равны.
- Диагонали параллелограмма пересекаются под прямым углом.
- Диагональ параллелограмма делит каждый угол пополам.
- Четырехугольник, у которого все стороны равны.
Свойства ромба:
- Все стороны равны.

- Диагонали пересекаются под прямым углом и точкой пересечения делятся пополам.

- Диагонали являются биссектрисами.

- Высоты в ромбе равны.
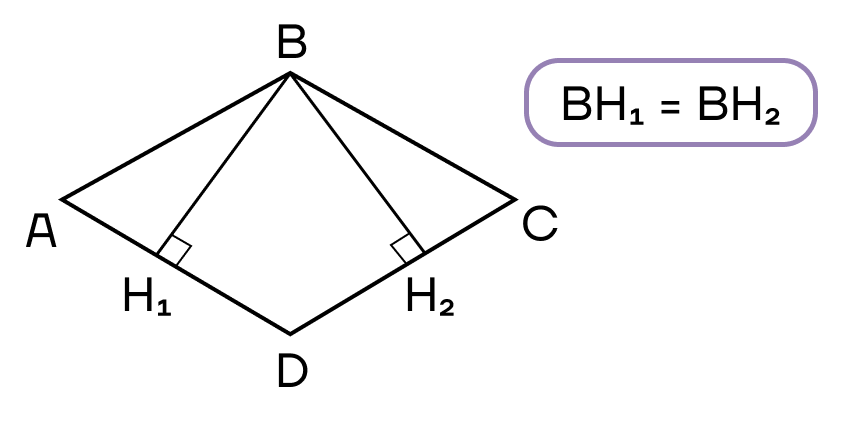
Как уже отмечено в свойствах ромба, биссектрисой ромба является диагональ.
Как найти площадь ромба?
Для нахождения площади ромба есть три разные формулы:
- Площадь ромба равна произведению стороны и высоты ромба.
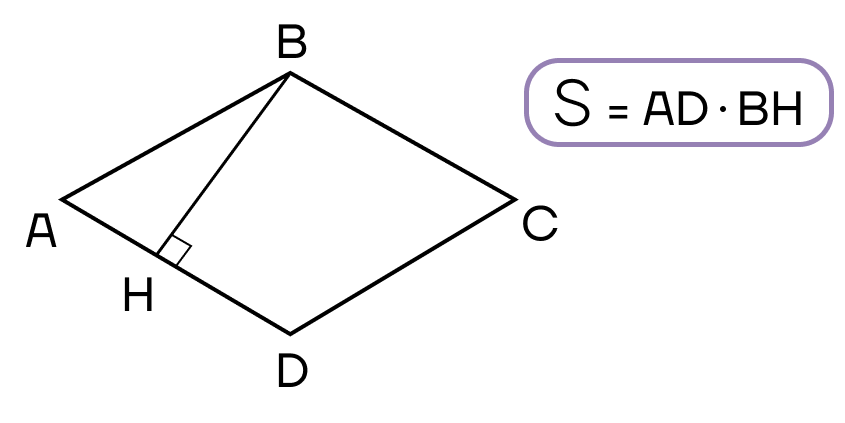
- Площадь ромба равна половине произведения его диагоналей.
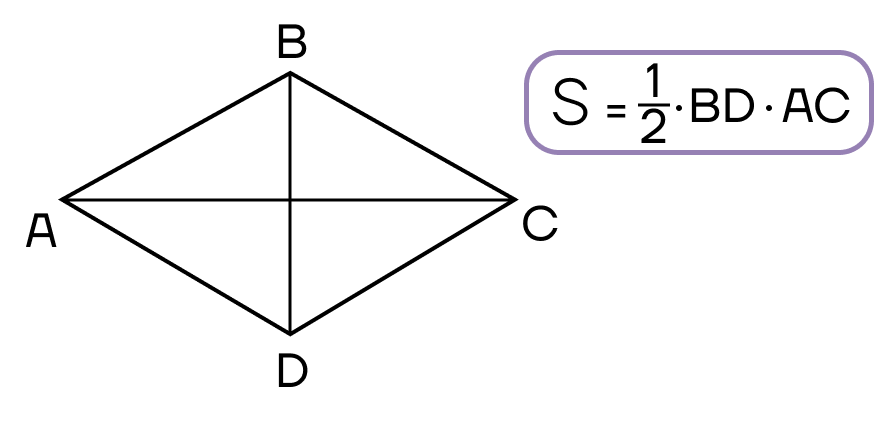
- Площадь ромба равна произведению квадрата стороны на синус угла ромба.
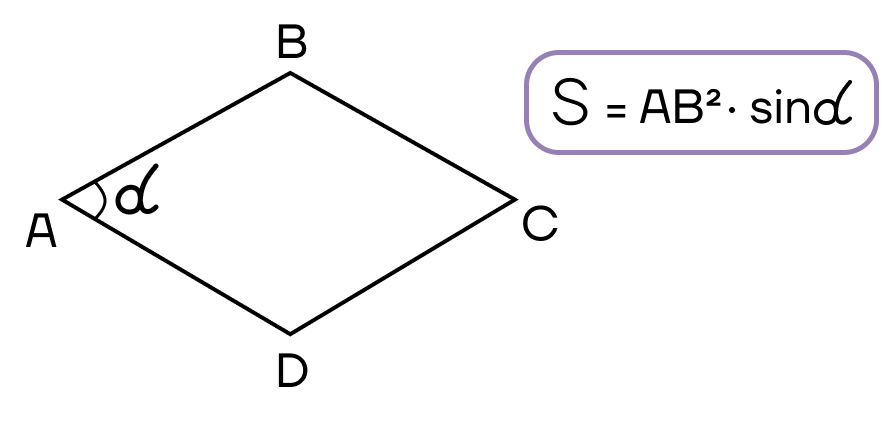
Квадрат
А вот квадрат, наоборот, достаточно устойчив.

Квадрат – это четырехугольник, у которого все углы и стороны равны.
Если внимательно посмотреть на определение, то можно заметить, что квадрат объединяет в себе и параллелограмм, и прямоугольник, и ромб.
Нечто, сочетающее в себе разнородные элементы, называют гибридом. Квадрат будет иметь все признаки и свойства родительских фигур:параллелограмма, прямоугольника и ромба.

Квадратом может быть крышка подарочной коробки или окно.


Рассмотрим признаки и свойства данной фигуры.
Всё о квадрате
Признаки квадрата:
- Ромб, у которого хотя бы один угол прямой.
- Ромб, у которого все углы равны.
- Ромб, у которого диагонали равны.
- Четырехугольник, диагонали которого равны и перпендикулярны.
Свойства квадрата:
- Диагональ квадрата равна 2 стороны квадрата.
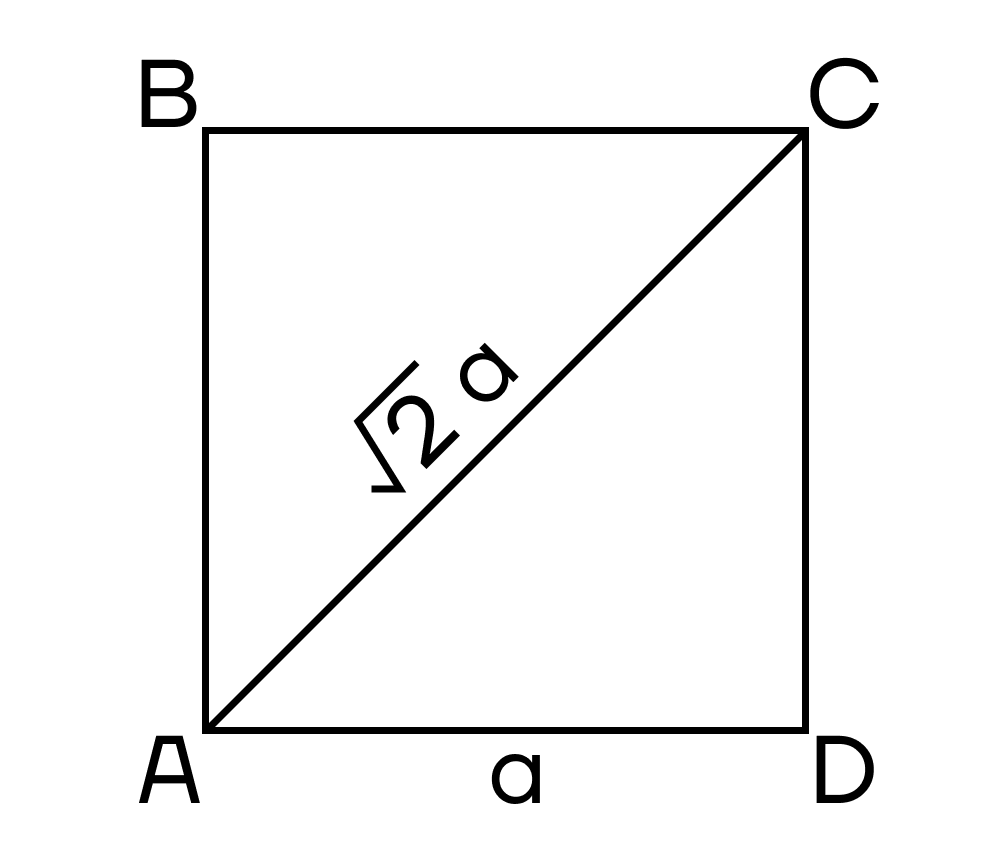
- Диагонали делят квадрат на четыре равных треугольника.

Биссектрисой квадрата, как и у ромба, является диагональ.
Рассмотрим формулы для нахождения площади квадрата:
- Площадь квадрата равна квадрату его стороны.
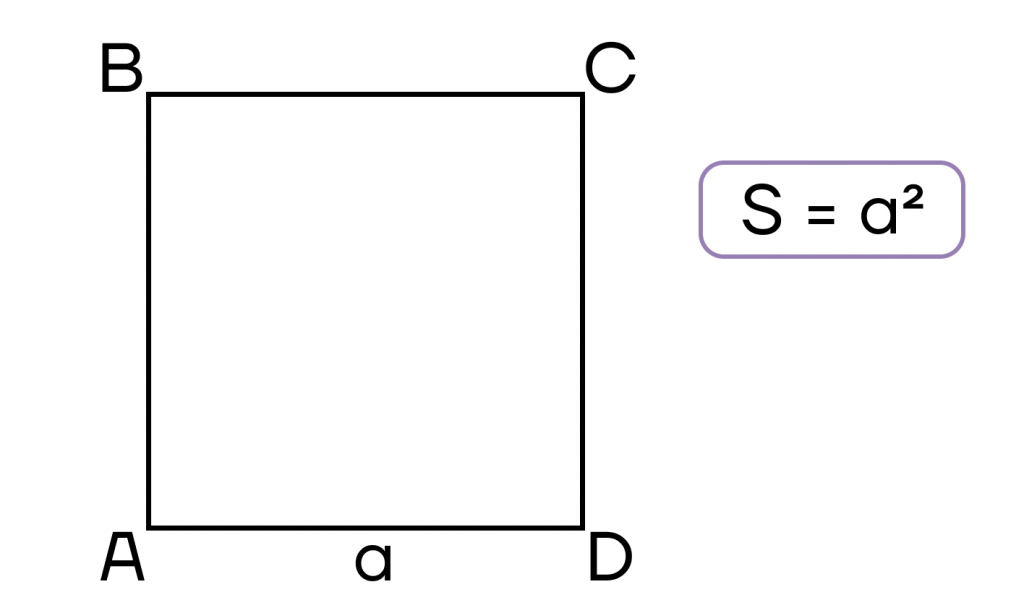
- Площадь квадрата равна половине квадрата диагонали.
Фактчек
- Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.
- Прямоугольник – это параллелограмм, углы которого по 900 и диагонали которого равны.
- Ромб – это параллелограмм, у которого все стороны равны, а также диагонали перпендикулярны друг другу
- Квадрат – это четырехугольник, у которого все углы и стороны равны. Квадрат является гибридом параллелограмма, прямоугольника и ромба.
Проверь себя
Задание 1.
Найдите площадь параллелограмма, если его стороны 5 и 8, а угол между ними 300
- 40
- 20
- 10
- 25
Задание 2.
Найдите площадь прямоугольника, если его диагональ 12, а угол между диагоналями 600
- 83
- 6
- 63
- 4
Задание 3.
Найдите площадь ромба, если его диагонали 6 и 10
- 30
- 60
- 15
- 25
Задание 4.
У четырехугольника диагонали пересекаются под углом 300, а его стороны попарно параллельны и равны. Что это за фигура?
- Квадрат
- Ромб
- Прямоугольник
- Параллелограмм
Задание 5.
У четырехугольника две противоположные стороны параллельны и равны и есть один прямой угол. Что это за фигура?
- Квадрат
- Ромб
- Прямоугольник
- Параллелограмм
Ответы: 1. – 2; 2. – 3; 3. – 1; 4. – 4; 5. – 3
Аксиома параллельности прямых, которая приведена Евклидом в книге «Начала», служит основой для доказательства многих свойств биссектрисы параллелограмма. О них знали пифагорейцы. Но понятие о самой фигуре ввел именно Евклид. Она представляет собой четырехугольник с параллельными противоположными сторонами.

Содержание
- Равнобедренный треугольник в параллелограмме
- Точка пересечения прямых
- Свойства односторонних углов
- Противолежащие углы и биссектрисы
- Вершины образуемого прямоугольника
- Ромб и его диагонали
- Примеры решения задач
Равнобедренный треугольник в параллелограмме
Биссектриса параллелограмма может быть проведена из вершины острого или тупого угла фигуры. Доказательство теоремы о равнобедренности образуемых прямой треугольников в этих случаях имеет аналогичный порядок. Чтобы доказать утверждение, нужно знать признак равнобедренности треугольника:

С помощью аналогичных рассуждений можно доказать, что биссектриса тупого угла параллелограмма делит противоположную сторону на отрезки и отсекает от него равнобедренный треугольник.
Точка пересечения прямых
Согласно свойству, проведенные из смежных углов параллелограмма биссектрисы пересекаются в точке на противоположной стороне, если она в 2 раза больше меньшей. Доказать это утверждение можно следующим способом:

Доказательство свойства позволяет предположить, что биссектрисы смежных углов пересекаются внутри либо вне параллелограмма. При этом одна сторона больше или меньше половины другой. Если ее величина больше половины соседней, значит прямые пересекутся внутри фигуры.
Биссектрисы, проведенные через смежные углы, пересекаются с продолжением противоположных сторон параллелограмма в вершинах ромба. В зависимости от величины другой стороны, ромб совпадает с ним либо обладает большим или меньшим периметром. Если частить с построением этой фигуры, то длины сторон параллелограмма будут бесконечными.
Свойства односторонних углов
Параллелограмм АВСД имеет смежные углы при параллельных прямых АВ и СД, обозначенные а1 и а2. Для доказательства теоремы о перпендикулярности биссектрис нужно знать свойства смежных углов, сумма которых равна 180 градусам.
Поскольку биссектрисы можно провести внутри острого или тупого угла параллелограмма, то величину смежного с ним внешнего угла можно сложить, получив 180 градусов. Если обозначить их через АО и ДЕ, то углы ОАВ и ЕДС будут равны половинам а1 и а2 соответственно. Так как а1 + а2 = 180, то (а1 + а2) / 2 = 90, значит АО и ДЕ образуют прямой угол АКД.

Применять свойство биссектрис можно при нахождении периметра фигуры. Должны быть известны данные о соотношениях или длинах отрезков, образованных при пересечении противолежащей стороны биссектрисой. Например, она делит на отрезки ВК и КС сторону параллелограмма ABCD, величины которых известны.
Формула определения периметра будет иметь вид: P=2 (n+n+m). Где ВС=BК+КC=n+m, а АВ=ВК=n по свойству биссектрисы. С учетом признака равнобедренности треугольника можно построить эту прямую, дополнив рисунок фигуры без транспортира с помощью циркуля.
Противолежащие углы и биссектрисы
Согласно свойству параллельных прямых, биссектрисы a и b проходят параллельно друг другу. Они образуют внутри фигуры со сторонами mnkp другой параллелограмм, следовательно, он обладает параллельными противоположными сторонами. Прямые, на которых они лежат, соответствуют сторонам исходной фигуры, поэтому ее биссектрисы a и b являются равными.
Углы, которые образованы отрезками a и m, а также b и k, согласно свойствам биссектрис и параллелограммов, равны. Противолежащие равные по величине углы, образованные отрезками mp и nk, можно разделить пополам. Прямая b, пересекающая отрезки n и p, образует с ними накрест лежащие углы, признак которых состоит в их равенстве. Они равны разделенным пополам противоположным и являются соответственными при параллельных прямых n и p.
Вершины образуемого прямоугольника
Биссектрисы параллелограмма пересекаются в точках, представляющих собой вершины прямоугольника, что можно доказать следующим образом:

Аналогичным способом можно доказать параллельность других сторон прямой СД. Следовательно, диагональ КР образованного биссектрисами параллелограмма прямоугольника КМРО содержит точки Х и Т. Доказательство предполагает следующее равенство: КР = КХ + ХТ + ТР = ХС + СД + ТД = ВС + СД, поэтому величина диагонали равна сумме двух смежных сторон параллелограмма.
Ромб и его диагонали
Параллелограмм, имеющий биссектрису, которая совпадает с его диагональю, представляет собой ромб. Чтобы доказать это, нужно провести диагональ AC, соединяющую противоположные вершины ABCD. Способ доказательства теоремы основан на равенстве противолежащих углов параллелограмма.

Согласно свойству биссектрисы, отрезок АС делит пополам углы BCD и BAD. Они имеют одинаковую величину, поскольку противоположные углы равны. Диагональ АС — основание треугольников ACB и ACD. Согласно признаку равнобедренности АВ и АС, а также AD и CD, равны между собой. По свойству равенства противоположных сторон параллелограмма AB = CD и AD = BC.
Фигура ABCD, представляющая собой по условию параллелограмм, имеет равные по величине AB, AD, BC и CD в соответствии с доказательством. Отсюда следует, что параллелограмм ABCD по определению ромб. В нем биссектриса АС — это его диагональ.
Примеры решения задач
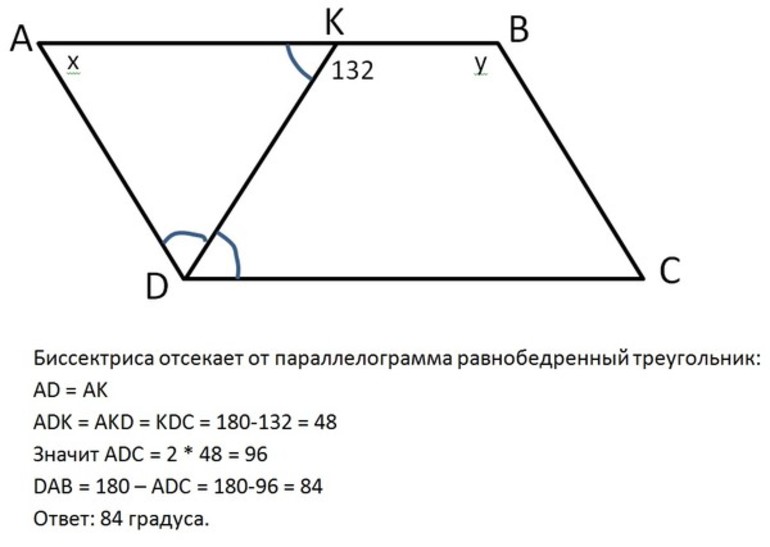
Биссектрисы смежных углов параллелограмма пересеклись в точке на его противолежащей стороне. Зная его меньшую сторону, можно найти большую, а также наоборот. Допустим, что длина меньшей стороны фигуры составляет 5 сантиметров.
Обозначив вершины фигуры A, B, C, D, а точку на AD буквой Р, достаточно иметь в виду, что AD=AР+РD=AB+CD. Это доказывает признак равенства накрест лежащих углов СВР и АРВ, а также ВСР и СРD при параллельных прямых. Формула для нахождения большей стороны будет иметь вид: AD=2AB=10, поскольку AB = CD. При необходимости найти меньшую можно по формуле: AD=AB/2.

По условию задачи биссектриса, исходящая из острого угла параллелограмма, разделяет его противоположную сторону на отрезки 73 мм и 54 мм, если считать от вершины тупого угла. Требуется вычислить периметр параллелограмма ABCD. Точка Е делит сторону ВС на отрезки заданной длины, поскольку АЕ — биссектриса угла ВАD. Эта прямая представляет собой секущую для параллельных AD и BC.
Отсекая равнобедренный треугольник АВЕ, биссектриса ВЕ является его основанием, поэтому сторона параллелограмма АВ равна отрезку ВЕ, длина которого по условию 73 мм. В сумме ВЕ и ЕС равны ВС, что составляет 127 мм. Отсюда периметр ABCD соответствует удвоенной сумме его сторон: Р = 2 (73+127) = 400 мм. Чтобы найти большую сторону параллелограмма ABCD при известном периметре 128 мм, можно использовать аналогичное доказательство равнобедренности треугольника.
По условию соотношение отрезков, образуемых точкой пересечения биссектрисы DЕ с противоположной стороной ВС, равно 4:3, если считать от острого угла при вершине А. Из равенства противоположных сторон ABCD и признака равнобедренного треугольника следует AD=BC=АЕ=4х, а ЕВ=3х, поэтому CD=АЕ+ЕВ=4х+3х=7х. Зная периметр ABCD, можно составить уравнение Р=2 (7х+4х)=128. Отсюда 22х=128, а х=32, поэтому большая сторона параллелограмма CD=32*7=224 мм.
Предыдущая
ГеометрияСредняя линия трапеции — свойства, теоремы и задачи
Следующая
ГеометрияКак построить высоту треугольника — основные способы