ЛЕКЦИЯ 11.
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ
УРАВНЕНИЙ
Задача 1.
Решить систему
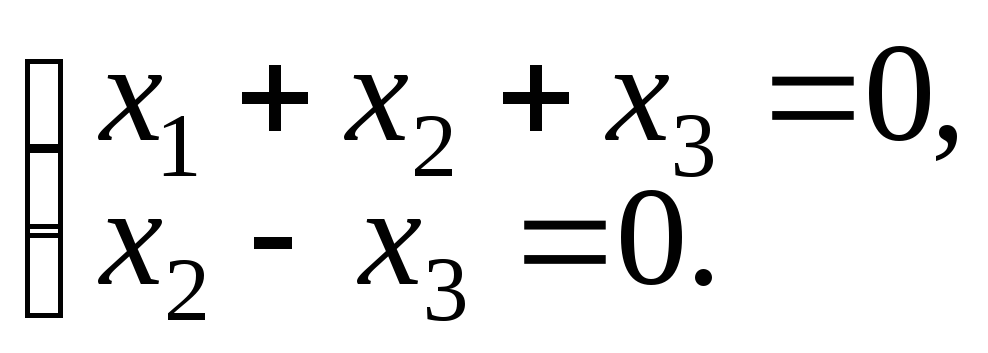
Решение.
Системе двух уравнений с тремя неизвестными
соответствует матрица системы

Матрица А
имеет ступенчатый вид, угловые элементы
выделены жирным шрифтом
прямой ход метода Гаусса выполнять не
надо. Каждый столбец матрицы состоит
из коэффициентов при переменных, которые
написаны сверху над столбцами. Переменные
,
в столбцах которых есть угловые элементы,
являются главными или зависимыми;
— свободная или независимая переменная.
Положим
и выразим главные переменные
через параметр
:
Мы нашли общее
решение в координатной форме.
Размерность
подпространстве решений однородной
системы равна количеству независимых
переменных, т.е. одному. Базис (ФСР) в
подпространстве решений однородной
системы состоит из одного вектора,
который можно получить, выбрав
и записывая решение в виде вектора:
Общее решение
однородной системы в векторной форме
– разложение общего решения по ФСР
имеет вид
.
Задача 2.
Найти общее решение и фундаментальную
систему решений однородной системы
.
Разложить общее решение по Ф.С.Р.
Матрица
задана.
Решение.
Выпишем систему уравнений в координатной
форме
Поскольку вектор
правых частей равен нулевому вектору,
т. е. ,
то система уравнений является однородной.
Методом Гаусса
приведем систему уравнений к ступенчатому
виду. Выпишем матрицу
и преобразуем ее:
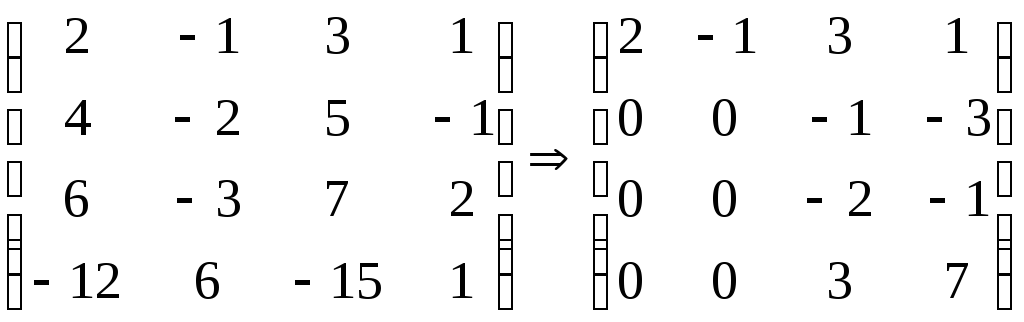
На первом шаге
первую строку не меняем (в верхнем левом
углу стоит ведущий элемент
);
из второй строки вычитаем первую,
умноженную на 2,
и результат запишем во вторую строку;
из третьей строки вычитаем первую,
умноженную на 3, и результат запишем в
третью строку; к четвертой строке
прибавляем первую, умноженную на 6,
результат запишем в четвертую строку.
Условно эти элементарные операции можно
записать так:
.
Далее применим
элементарные операции:
.
Получаем:

После чего к
четвертой строке, умноженную на 5,
прибавим третью строку, умноженную на
2, результат запишем в четвертую строку,
т. е.
:
Матрица
приведена к ступенчатому виду. Мы
выполнили прямой
ход метода Гаусса.
Число угловых
элементов (отмечены) равно трем,
следовательно, ранг матрицы
.
Находим общее
решение однородной системы в координатной
форме:
а) Главными
(зависимыми) назовем переменные х1,
х3
и х4,
так как угловые элементы являются
коэффициентами перед х1,
х3
и х4
в ступенчатой
системе, переменная х2
– свободная
(независимая). Свободную переменную
обозначим как
.
б) Выпишем
ступенчатую систему уравнений,
эквивалентную исходной:
в) Выразим
зависимые переменные через свободную
из ступенчатой системы (обратный
ход метода Гаусса),
начиная с последнего уравнения и
подымаясь “вверх” по системе уравнений.
Из третьего уравнения получим:
.
Из второго уравнения имеем:
.
Из первого уравнения получим:
.
Формулы
выражающие главные
переменные х1,
х3
и х4
через
свободную переменную (параметры),
определяют параметрическую запись
решения системы. Эти формулы задают
общее решение системы в координатной
форме.
Теперь получим
решение однородной системы в векторной
форме. Поскольку ранг матрицы
,
а размерность системы n=4,
система имеет бесконечное множество
решений. Решения однородной системы
образуют подпространство V
пространства R4
размерности
.
Базис подпространства
решений однородной системы состоит из
одного вектора
.
Базис подпространства V
решений однородной системы называется
фундаментальной
системой решений.
Пусть свободная
переменная принимает значение
,
получим вектор-решение
.
Этот вектор может служить фундаментальной
системой решений однородной системы
уравнений. Тогда любой вектор-решение
запишется в виде:
где
– произвольная константа. Формула
определяет общее решение однородной
системы
в векторном виде.
Задача 3.
Решить систему (найти общее решение в
координатной и векторной форме)
Решение.
Расширенная матрица имеет вид:
.
Вычитая из 2-й
строки 1-ю, умноженную на 2, получаем
ступенчатый вид этой матрицы
,
.
Следовательно,
система совместна:
х1,
х2
– зависимые переменные, х3,
х4
– свободные.
Новая система
имеет вид:
Переносим члены
со свободными переменными вправо:
Закончился прямой
ход метода Гаусса. Теперь – обратный
ход. Из последнего уравнения получаем
.
Подставляем в
первое:
откуда
.
Итак,
– общее решение
в координатной форме неоднородной
системы.
Найдем векторную
форму. Для этого заменим в общем решении
свободные члены нулями:
Получаем общее
решение однородной системы
1) Пусть
,

2) Пусть
,

Следовательно,

Найдем частное
решение неоднородной системы. Полагая
в общем решении неоднородной
системы
,
получаем:
.
Следовательно,

Итак,
– общее решение
в векторной форме.
Задача 4.
Решить систему
Решение.
Выпишем расширенную матрицу системы и
приведем ее к ступенчатому виду:
Получили систему
ступенчатого вида эквивалентную исходной
системе. Все три переменные главные,
свободных переменных нет. Решение
единственно:
.
Задача 5.
Исследовать совместность системы, и в
случае совместности найти общее или
единственное решение системы уравнений
в координатной и векторной формах.
Матрица А
и вектор
заданы.

Решение.
Методом Гаусса приведем систему уравнений
к ступенчатому виду. Выпишем расширенную
матрицу и преобразуем ее:

На первом шаге
первую строку не меняем (в верхнем левом
углу стоит ведущий элемент
);
вторую строку не меняем (в первом столбце
стоит
нуль); из третьей строки вычитаем первую,
умноженную на 2, и результат запишем в
третью строку; из четвертой строки
вычитаем первую, умноженную на 3, результат
запишем в четвертую строку. Обратите
внимание, что последний столбец меняется
аналогично другим столбцам. Условно
эти операции можно записать так:
.
Далее применим
элементарные операции:
.
Получаем:

Угловые элементы
(отмечены) определяют, что ранги матрицы
системы и расширенной матрицы совпадают:
по теореме
Кронекера-Капелли система уравнений
совместна, а так как
,
то система имеет бесконечное множество
решений.
Закончился прямой
ход метода Гаусса. Найдем общее решение
системы в координатной форме:
а) Главными
(зависимыми) назовем переменные х1
и х2,
так как угловые элементы являются
коэффициентами перед х1
и х2
в ступенчатой
системе, остальные переменные х3,
х4
– свободные
(независимые). Свободные переменные
обозначим как
,
.
б) Выпишем ступенчатую
систему уравнений, эквивалентную
исходной:
в) Выразим зависимые
переменные через свободные из ступенчатой
системы (обратный ход метода Гаусса),
начиная с последнего уравнения и
подымаясь “вверх” по системе уравнений.
Из второго уравнения получим:
,
из первого уравнения имеем:
.
Формулы
выражающие главные
переменные х1,
х2
через свободные переменные (параметры),
определяют параметрическую запись
решения системы. Давая свободным
переменным любые значения и вычисляя
х1
и х2,
получим решение системы
,
причем любое решение системы можно
получить по этим формулам. Мы нашли
общее
решение системы в координатной форме.
Теперь найдем
общее решение неоднородной системы в
векторной форме. Для этого нужно найти
общее решение соответствующей однородной
системы и прибавить к нему некоторое
частное решение неоднородной системы.
а) Выпишем
соответствующую однородную систему
уравнений
,
приведенную к ступенчатому виду. Она
только свободными членами отличается
от ступенчатой неоднородной системы
Ранг системы r
равен 2, размерность системы n
равна 4, система имеет бесконечное
множество решений. Решения однородной
системы образуют подпространство V
пространства R4
размерности
.
Базис подпространства
решений однородной системы состоит из
двух векторов
.
Это могут быть любые два линейно
независимые решения системы
.
Напомним, что базис подпространства V
решений однородной системы называется
фундаментальной
системой решений.
б) Выразим зависимые
переменные х1,
х2
через
независимые х3,
х4
в) Пусть, например,
свободные переменные принимают значения
,
тогда
,
получим вектор-решение
;
если
,
то получим вектор-решение
.
Пара линейно независимых векторов
может служить фундаментальной системой
решений однородной системы уравнений.
Тогда любой вектор-решение
запишется как линейная комбинация
базисных решений:
,
где
– произвольные константы.
Последняя формула
определяет общее решение однородной
системы
в векторном виде.
г) Найдем
какой-нибудь вектор-решение неоднородной
системы
.
Используем для этого параметрическую
(координатную) запись решения неоднородной
системы
Положим, например,
,
тогда
.
Вектор
является некоторым частным решением
неоднородной системы.
д) Теперь запишем
общее решение
неоднородной системы в виде
.
Эта последняя
запись является векторной записью
общего решения неоднородной системы
в виде суммы частного решения неоднородной
системы
и общего решения однородной системы
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решебник.Ру / Кузнецов Л.А. Линейная алгебра. Задача 3
Системы линейных однородных уравнений
Постановка задачи. Найти какой-нибудь базис и определить размерность линейного пространства решений системы
1. Записываем матрицу системы:
и с помощью элементарных преобразований преобразуем матрицу к треугольному виду, т.е. к такому виду, когда все элементы, находящиеся ниже главной диагонали равны нулю. Ранг матрицы системы равен числу линейно независимых строк, т.е., в нашем случае, числу строк, в которых остались ненулевые элементы:
.
Размерность пространства решений равна . Если , то однородная система имеет единственное нулевое решение, если , то система имеет бесчисленное множество решений.
2. Выбираем базисных и свободных переменных. Свободные переменные обозначаем . Затем базисные переменные выражаем через свободные, получив таким образом общее решение однородной системы линейных уравнений.
3. Записываем базис пространства решений системы полагая последовательно одну из свободных переменных равной единице, а остальные нулю. Размерность линейного пространства решений системы равна количеству векторов базиса.
Примечание. К элементарным преобразованиям матрицы относят:
1. умножение (деление) строки на множитель, отличный от нуля;
2. прибавление к какой-либо строке другой строки, умноженной на любое число;
3. перестановка строк местами;
4. преобразования 1–3 для столбцов (в случае решения систем линейных уравнений элементарные преобразования столбцов не используются).
Задача 3. Найти какой-нибудь базис и определить размерность линейного пространства решений системы.
Выписываем матрицу системы и с помощью элементарных преобразований приводим ее к треугольному виду:
Полагаем , тогда
.
Размерность линейного пространства решений равна 3.
:: Рекомендуемая литература. Ремендуем покупать учебную литературу в интернет-магазине Озон
Системы линейных однородных уравнений
Назначение сервиса . Онлайн-калькулятор предназначен для нахождения нетривиального и фундаментального решения СЛАУ. Полученное решение сохраняется в файле Word (см. пример решения).
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Свойства систем линейных однородных уравнений
Теорема. Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.
Теорема. Любая линейная комбинация решений системы также является решением этой системы.
Определение. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.
Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из ( n-r ) решений.
Лекция № 5 (02.03.10)
Лекция № 5 (02.03.10)
5.4.2. Фундаментальная система решений
Определение. Фундаментальной системой решений (сокращённо ФСР) данной однородной линейной системы уравнений называется любой базис её подпространства решений.
5.4.3. Размерность подпространства решений
Лемма 1. При элементарных преобразованиях над строками матрицы линейно зависимые столбцы переходят в линейно зависимые.
Пусть A = (a1, a2, …, an) − векторная запись данной матрицы. После совершения нескольких элементарных преобразований матрицу А мы привели к матрице В. Пусть aj1, aj2, …, ajk − линейно зависимые столбцы данной матрицы, где 1 ≤ j1
http://math.semestr.ru/gauss/equations.php
http://pandia.ru/text/78/375/777.php
Способы описания подпространств линейного пространства
Рассмотрим два важных способа описания линейных подпространств, которые условно будем называть внутренним и внешним. В первом (внутреннем) способе используется понятие линейной оболочки векторов, когда все элементы подпространства выражаются через некоторые его элементы (образующие). При втором (внешнем) способе применяются однородные системы уравнений. В этом случае подпространство описывается как пересечение некоторых содержащих его множеств. Для каждого способа описания подпространств укажем методики на хождения размерностей, базисов, алгебраических дополнений, пересечений и сумм подпространств.
Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству
. Чтобы установить изоморфизм
, достаточно выбрать в пространстве
базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства
.
Первый (внутренний) способ. Пусть в пространстве заданы столбцы
. Напомним, что для систем столбцов
были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.
Рассматривая линейную оболочку столбцов
как линейное подпространство
, заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства
.
Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:
1) составить из данных столбцов матрицу размеров
;
2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;
3) определить размерность и базис подпространства
– количество ненулевых строк в матрице равняется размерности подпространства, т.е.
,
– столбцы матрицы , содержащие единичные элементы (в начале каждой «ступеньки»), определяют номера линейно независимых столбцов матрицы
, т.е. искомый базис.
Таким образом, если подпространство задано своими образующими
, то его размерность равна рангу системы столбцов
, т.е.
, а базисом
служит максимальная линейно независимая подсистема образующих.
Второй (внешний) способ. Пусть подпространство задано как множество
решений однородной системы
уравнений с
неизвестными. Множество решений системы уравнений можно рассматривать как пересечение
подпространств
, где
— множество решений i-го уравнения системы
. Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства
, а базисом
служит фундаментальная система решений однородной системы
. Способы нахождения фундаментальной системы решений рассмотрены ранее.
Переход от одного способа описания подпространств к другому
Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов
. Требуется составить такую однородную систему
уравнений, множество решений которой совпадает с
, т.е.
. Для этого нужно выполнить следующие действия.
1. Из данных столбцов составить матрицу размеров
, а затем блочную матрицу
, приписав к матрице
единичную матрицу
n-го порядка.
2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу
к виду
, где
— простейший вид матрицы
.
3. Из последних строк матрицы
составить матрицу
.
4. Записать искомую систему уравнений .
Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид
. Решаемую задачу можно сформулировать так: для каких векторов
найдутся такие числа
, чтобы выполнялось равенство
. Другими словами, при каких
неоднородная система
(
уравнений с
неизвестными
) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство
. Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.
Пример 8.8. Подпространство задано линейной оболочкой столбцов
. Составить систему уравнений, определяющую подпространство
.
Решение. 1. Составляем матрицу и блочную матрицу:
2. Приводим левый блок к простейшему виду. Вычитаем первую строку из остальных, а затем к четвертой строке прибавляем вторую, умноженную на (-2):
Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер вый, умноженный на (-1), к третьему столбцу прибавим первый, умноженный на (-3), а затем второй, умноженный на (-1). Эти преобразования не изменяют правый блок полученной матрицы. Находим простейший вид Л матрицы и матрицу
3. Из последних строк матрицы
составляем матрицу
искомой системы.
4. Записываем систему уравнений Заданные в условии примера столбцы
являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо
.
Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными:
. Требуется найти размерность
и базис
этого подпространства, т.е. представить его в виде линейной оболочки
. Для этого нужно выполнить следующие действия.
1. Найти фундаментальную систему решений однородной системы
. Искомая размерность
.
2. Представить заданное пространство как линейную оболочку .
Первый пункт алгоритма удобно выполнять следующим образом:
– составить блочную матрицу , приписав к матрице
единичную матрицу
n-го порядка;
– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу
к виду
, где
— простейший вид матрицы
;
– из последних столбцов матрицы
составить фундаментальную матрицу
.
Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.
Заметим, что решение поставленной задачи неоднозначно, так как существует много базисов одного и того же линейного подпространства.
Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений
Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6
Ее столбцы образуют фундаментальную систему решений. Размерность подпространства
равна
,
.
2. Столбцы являются искомым базисом, так как они линейно независимы
и
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Тема: Найти размерность и базис подпространства решений однородной СЛУ (Прочитано 23789 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Натолкните меня пожалуйста, голова сломана %)
Найти размерность и базис подпространства решений однородной системы линейных уравнений.
х1 + 2х2 + 3х3 + х4 = 0
2х1 + 3х2 + х3 + х4 = 0
3х1 + 2х2 + х3 + х4 = 0
7х1 + 9х2 + 8х3 + 4х4 = 0
ранг матрицы равен 3.
значит размерность = n(число неизвестных) — r(ранг матрицы)= 4-3=1
1 — это получается и есть размерность?
а базис? что и как с ним?
и если честно условие задачи я на 100% не пойму ещё никак
в интернете не нашёл подобных примеров решений(
помогите, уже 6 утра почти, а я всё сижу %)
« Последнее редактирование: 10 Декабря 2010, 00:58:52 от Asix »
вот что я получил:
1 2 3 1|0
0 -1 -5 -1|0
0 0 6 1|0
0 0 0 0|0
соответственно нашёл, что:
х1= -1/6х4
х2= -1/6х4
х3= -1/6х4
х4= свободная неизвестная
И допустим х4=1, то базис = (-1/6, -1/6, -1/6, 1)
и как требовалось по условию ответ такой? :
Размерность подпространства: 1
Базис подпространства: (-1/6, -1/6, -1/6, 1)
так что ли?
пожалуйста, ответьте, мне очень важно ваше мнение, бред я решил или нормально)
« Последнее редактирование: 10 Декабря 2010, 00:58:58 от Asix »
ребятки, ну не серьёзно как то, форум для помощи, а тут молчок…
прошу прощения, за 3ий пост подряд
« Последнее редактирование: 10 Декабря 2010, 00:59:07 от Asix »
ребятки, ну не серьёзно как то, форум для помощи, а тут молчок…
прошу прощения, за 3ий пост подряд
Вы бы еще все посты ночью написали и требовали бы ответ.
Люди либо в такое время спят, либо утром ушли на работу. На форуме круглосуточно никто не работает и не круглосуточно тоже.
« Последнее редактирование: 10 Декабря 2010, 00:59:13 от Asix »
вот что я получил:
1 2 3 1|0
0 -1 -5 -1|0
0 0 6 1|0
0 0 0 0|0соответственно нашёл, что:
х1= -1/6х4
х2= -1/6х4
х3= -1/6х4
х4= свободная неизвестная
Если хотите проверку, то показывайте все преобразования сначала.
И допустим х4=1, то базис = (-1/6, -1/6, -1/6, 1)
и как требовалось по условию ответ такой? :
Размерность подпространства: 1
Базис подпространства: (-1/6, -1/6, -1/6, 1)
Если поверить вашим вычислениям, то похоже на правду.
« Последнее редактирование: 10 Декабря 2010, 00:59:20 от Asix »
Извините, после трудовой, бессонной ночи за линейкой, я не очень злой был)
преобразования правильны, Гаусса проверял по калькулятору с этого сайта. да и преобразования то там плёвые
в принципе мне и нужно было узнать, похоже на правду или нет. а то особа я не понял, что требовалось от меня. но потом додумал
сдал уже, видно будет, думаю ночь не зря прошла)
Спасибо
« Последнее редактирование: 10 Декабря 2010, 00:59:28 от Asix »
« Последнее редактирование: 10 Декабря 2010, 00:59:35 от Asix »
Размерность пространства решений однородной системы линейных уравнений
Как мы отметили ранее, совокупность решений Xодн однородной системы линейных уравнений с матрицей 
Теорема 9.17.1. Если r=r(A)<n, то 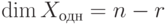
Доказательство. Для удобства записи переупорядочим неизвестные, если это необходимо, так, чтобы
Пусть 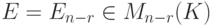

Эта система n-r строк-решений линейно независима (поскольку строки единичной матрицы, конечно, линейно независимы). Если
произвольное решение, то
Однако, конечно,
при этом 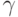
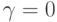
Итак, мы построили базис 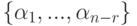
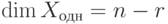
Замечание 9.17.2. Если вместо строк единичной матрицы En-r для свободных неизвестных брать строки всевозможных матриц 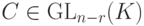
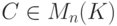
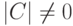
Замечание 9.17.2. Любой базис линейного пространства решений Xодн однородной системы линейных уравнений называется в ряде алгебраических текстов » фундаментальной системой решений однородной системы линейных уравнений «.
Задание любого подпространства в _K V = K^n как пространства решений однородной системы линейных уравнений
Пусть K — поле, 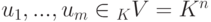
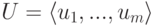
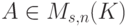
совпадает с U.
Если U — нулевое подпространство, то в качестве A мы можем взять любую матрицу 
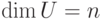




Рассмотрим матрицу 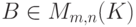

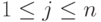
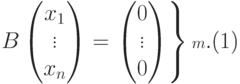 |
( 9.2) |
Ясно, что 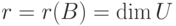
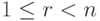
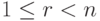
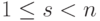
Пусть строки 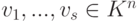
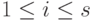
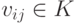
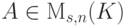
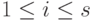
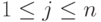
Действительно, по построению матрицы A любая строка из U (как линейная комбинация строк u1,…,um ) является решением однородной системы уравнений
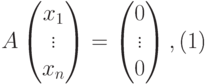 |
( 9.3) |
т. е. 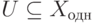
Следовательно, U=Xодн.
В заключение отметим, что матрица A определена неоднозначно. Например, другая матрица A’ может быть получена с помощью другой фундаментальной системы решений системы (9.2).
Полученное задание линейных подпространств оказывается полезным при решении ряда практических задач. Например, пусть 
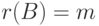
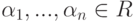
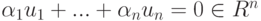
имеем 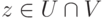
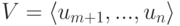
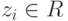

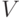
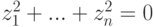
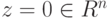
Но u1,…,um — линейно независимые строки, поэтому 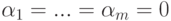
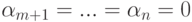
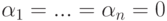
Таким образом, мы рассмотрели два способа задания линейных подпространств в K V=Kn :
- как множество решений Xодн однородной системы линейных уравнений;
- как линейную оболочку
строк
.
При этом мы научились переходить от первого задания ко второму (фундаментальная система решений) и от второго задания к первому. Первый способ задания удобен для задания пересечения 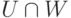
В следующем примере мы увидим комбинацию этих приемов.
Пример 9.18.1. Пусть 
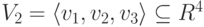

Решение Запишем строки u1, u2, u3, v1, v2, v3 по столбцам и приведем полученную матрицу к ступенчатому виду с помощью элементарных преобразований строк:
Поскольку 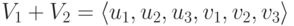

Поэтому v’_2=u’_1+u’_2+u’_3-v’_1 и, следовательно, v2=u1+u2+u3-v1. Для v’3 мы видим, что v’3+v’1=(2,0,2,0)*=2u’1+2u’3, поэтому v3=2u1+2u3-v1. Проведенные вычисления равносильны завершению приведения матрицы к главному ступенчатому виду:
Рассмотрим теперь 
Для V1:
система уже имеет ступенчатый вид, x1, x2, x3 — главные неизвестные, x4 — свободная. Фундаментальная система решений состоит из одной строки (-1,1,-1,1). Итак, подпространство V1 совпадает с пространством решений однородной системы линейных уравнений
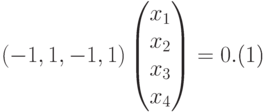 |
( 9.4) |
Для V2 :
и мы приходим к ступенчатому виду, при этом x1, x2, x3 — главные неизвестные, а x4 — свободная. Фундаментальная система решений состоит из одной строки (-1,-1,1,1). Значит, однородная система линейных уравнений
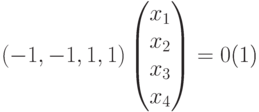 |
( 9.5) |
задает подпространство V2.
Ясно, что система
задает подпространство 
Решим эту систему:
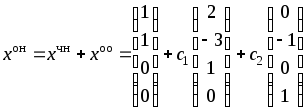
x1, x2 — главные неизвестные, x3, x4 — свободные неизвестные. Фундаментальная система решений состоит из двух строк
Следовательно, {u,v} — базис линейного подпространства 




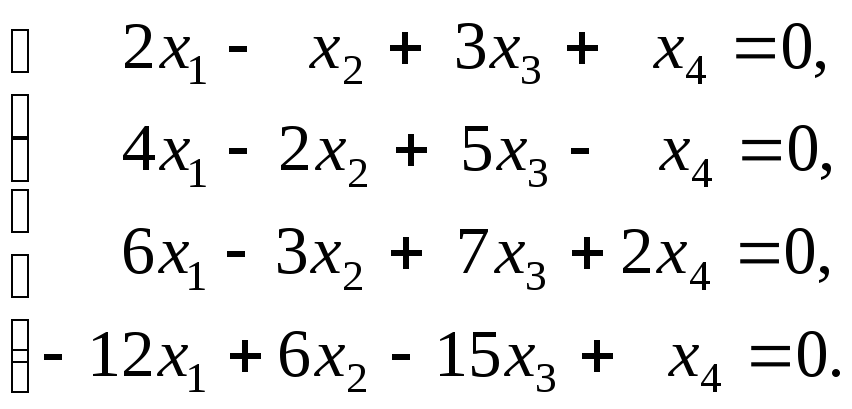



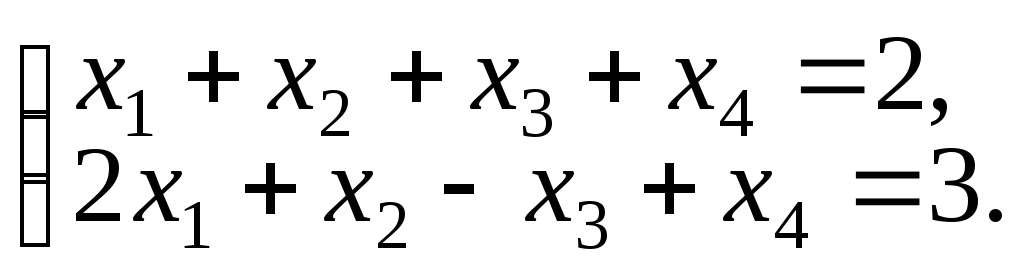
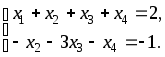
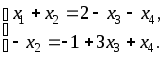
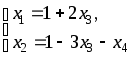
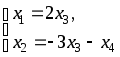


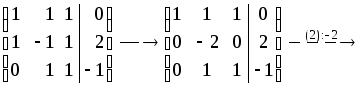

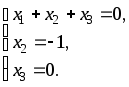

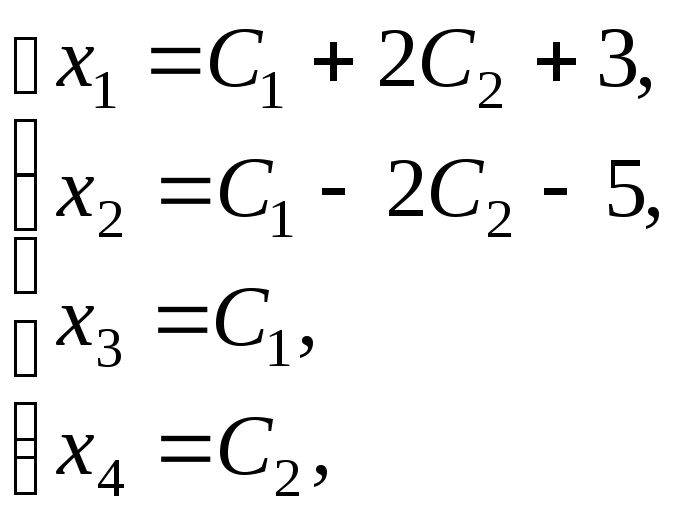
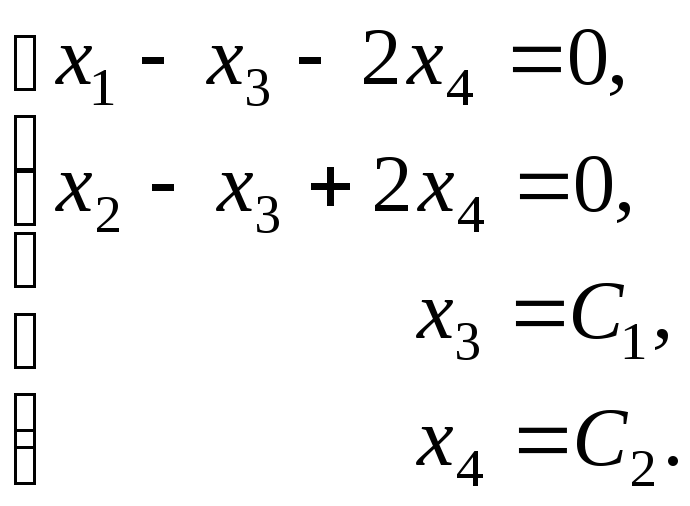
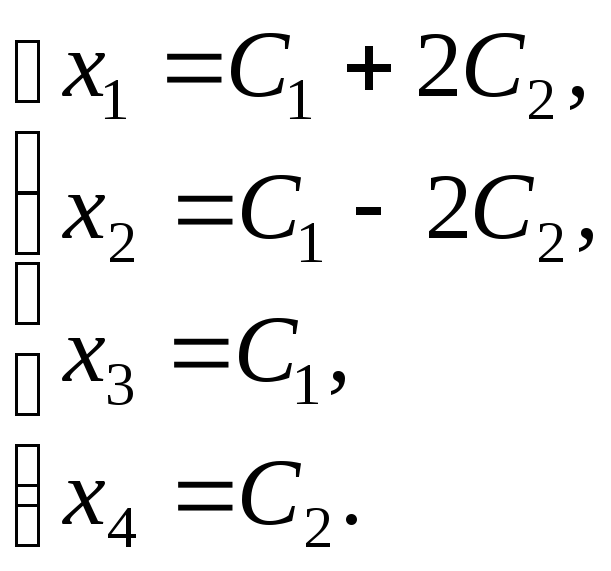





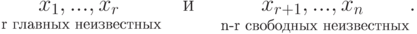
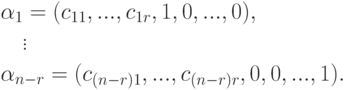
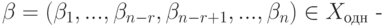
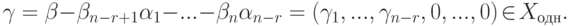
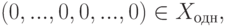
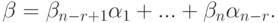
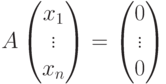
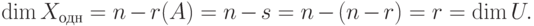
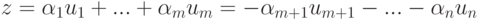
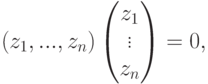

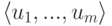 строк
строк 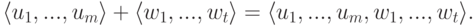
![begin{mult}
begin{gathered}
u_1 u_2 u_3,, ! v_1 v_2 v_3 kern53mm
\
left(
begin{array}{cccccc}
1 & 0 & 0 & 1 & 0 & 1\
1 & 1 & 0 & 0 & 2 & 2\
0 & 1 & 1 & 1 & 1 & 1\
0 & 0 & 1 & 0 & 1 & 2
end{array}right)to
left(
begin{array}{cccccc}
1 & 0 & 0 & phm 1 & 0 & 1\
0 & 1 & 0 & -1 & 2 & 1\
0 & 1 & 1 & phm 1 & 1 & 1\
0 & 0 & 1 & phm 0 & 1 & 2
end{array}right)to{}
end{gathered}
\[3mm]
begin{gathered}
kern55mm u'_1, u'_2, u'_3 v'_1; v'_2; v'_3
\
{}to
left(
begin{array}{cccccc}
1 & 0 & 0 & phm 1 & phm 0 & 1\
0 & 1 & 0 & -1 & phm 2 & 1\
0 & 0 & 1 & phm 2 & -1 & 0\
0 & 0 & 1 & phm 0 & phm 1 & 2
end{array}right)to
left(
begin{array}{cccccc}
multicolumn{1}{|c}{1} & 0 & 0 & phm 1 & phm 0 & phm 1\
cline{1-1}
0 & multicolumn{1}{|c}{1} & 0 & -1 & phm 2 & phm 1\
cline{2-2}
0 & 0 & multicolumn{1}{|c}{1} & phm 2 & -1 & phm 0\
cline{3-3}
0 & 0 & 0 & multicolumn{1}{|c}{phm 1} & -1 & -1\
cline{4-6}
end{array}right).
end{gathered}
end{mult}](https://intuit.ru/sites/default/files/tex_cache/dd0dbbb69869493ca81113a368c90d5a.png)
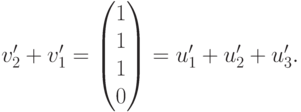

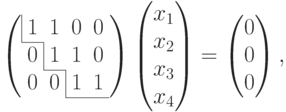
![begin{align*} & begin{pmatrix}
1 & 0 & 1 & 0\
0 & 2 & 1 & 1\
1 & 2 & 1 & 2
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0\
0
end{pmatrix} to
begin{pmatrix}
1 & 0 & 1 & 0\
0 & 2 & 1 & 1\
0 & 2 & 0 & 2
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
begin{pmatrix}
1 & 0 & 1 & 0\
0 & 2 & 1 & 1\
0 & 1 & 0 & 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} !=!
begin{pmatrix}
0\
0\
0
end{pmatrix} to!
%{}
%\[3mm]
%& quad {}to
begin{pmatrix}
1 & 0 & 1 & 0\
0 & 1 & 0 & 1\
0 & 2 & 1 & 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} !=!
begin{pmatrix}
0\
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
left(
begin{array}{cccc}
multicolumn{1}{|c}{1} & 0 & 1 & phm 0\
cline{1-1}
0 & multicolumn{1}{|c}{1} & 0 & phm 1\
cline{2-2}
0 & 0 & multicolumn{1}{|c}{1} & -1\
cline{3-4}
end{array}right)
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0\
0
end{pmatrix},
end{align*}](https://intuit.ru/sites/default/files/tex_cache/9b3e5cd07c99c5ba9b0cfe865a6061bc.png)
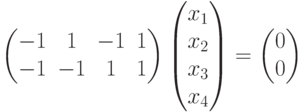
![begin{align*} & begin{pmatrix}
-1 & phm 1 & -1 & 1\
-1 & -1 & phm 1 & 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
begin{pmatrix}
phm 1 & -1 & 1 & -1\
-1 & -1 & 1 & phm 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
left(
begin{array}{cccc}
multicolumn{1}{|c}{1} & -1 & 1 & -1\
cline{1-1}
0 & multicolumn{1}{|c}{-2} & 2 & phm 0\
cline{2-4}
end{array}right)
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0
end{pmatrix},
end{align*}](https://intuit.ru/sites/default/files/tex_cache/514a0838571b1cf6b55788bbade81424.png)