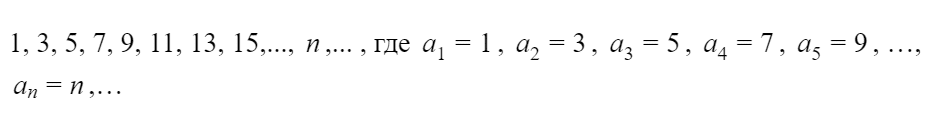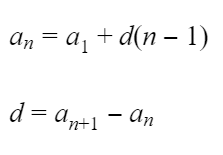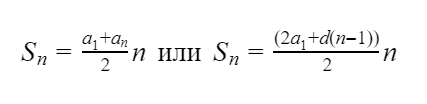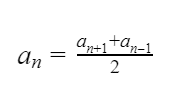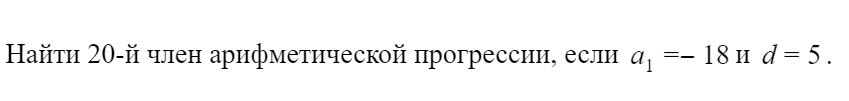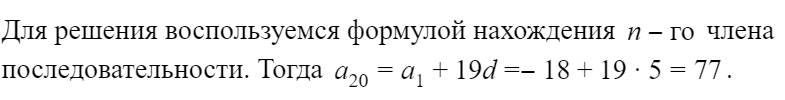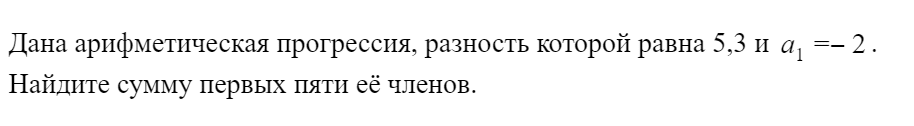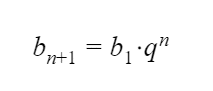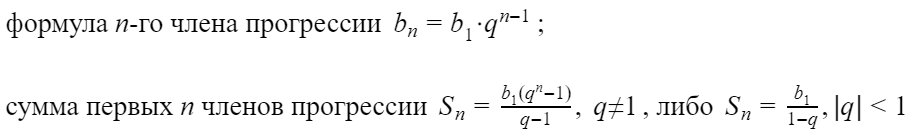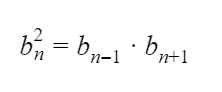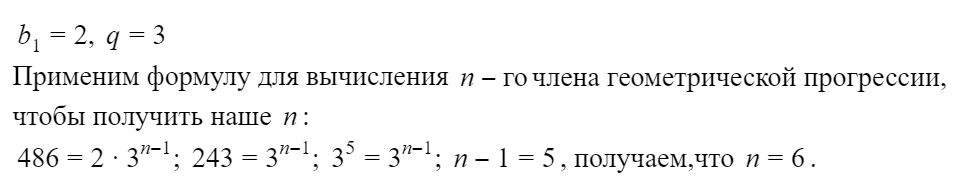Как найти арифметическую прогрессию 9 класс огэ - Avtoru.top

Прогрессии и последовательности: решаем ОГЭ по математике

04.06.2020
20374

Тема «прогрессии» на ОГЭ тесно связана с понятием «последовательность». Если ученики понимают, как числа в последовательности связаны друг с другом, они легко справляются с заданиями. Сейчас мы разберем прогрессии — одну из самых коварных тем ОГЭ по математике. Обратите внимание: в этом материале все самое главное для решения ОГЭ, никакой воды!

В этой статье:

Что такое последовательность?Какие виды последовательности бывают?Что такое арифметическая прогрессия?Как решать задачи ОГЭ на арифметическую прогрессию?Что такое геометрическая прогрессия?Как решать задачи ОГЭ на геометрическую прогрессию?В каком задании ОГЭ могут встретиться прогрессии?

Что такое последовательность?

В жизни мы очень часто сталкиваемся с математическими последовательностями и прогрессиями, буквально, каждый день, сами того не замечая. Однако встреча не всегда может быть приятной, особенно если она происходит на экзамене.

Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:

для каждого натурального числа существует элемент данного множества;
это число является номером элемента и обозначает позицию данного элемента в последовательности;
для любого элемента последовательности можно указать следующий за ним элемент.

Хочешь круто подготовится к ОГЭ? Тебе поможет учебный центр MAXIMUM! Все наши преподаватели сами сдавали этот экзамен на хороший балл. Мы ежегодно изучаем изменения ФИПИ и корректируем курсы, исходя из этого. Читай подробнее про наши курсы и выбирай подходящий!

Какие виды последовательности бывают?

Различают следующие виды последовательности:

постоянную, или монотонную последовательность: 1, 1, 1, 1, 1..;
возрастающую последовательность, в которой каждый следующий элемент больше предыдущего;
убывающую последовательность, в которой каждый следующий элемент меньше предыдущего.

Что такое арифметическая прогрессия?

Давайте посмотрим на следующий ряд чисел:

Что же у них может быть общего? Во-первых, все они нечетные, во-вторых, каждое следующее число мы можем получить из предыдущего, прибавляя к нему одно и то же число. Назовем это число d. В нашем случае d=2.

Описанная выше последовательность называется арифметической прогрессией. Получаем определение:

Приведем основные формулы:

Сумма первых n членов прогрессии можно вычислить по формуле:

Также арифметическая прогрессия обладает характерным свойством:

Как решать задачи ОГЭ на арифметическую прогрессию?

Теория — это прекрасно, но каждую теоретическую тему необходимо закреплять на практике. Сейчас мы разберем пару заданий ОГЭ по арифметической прогрессии.

Например, на ОГЭ может попасться вот такое задание:

Решение:

Ура! Первый прототип задания, который может встретиться на реальном экзамене, успешно выполнен. Идем дальше.

Решение:

Вот и все! Ничего сложного, учитывая то, что формула суммы первых n членов прогрессии есть в справочных материалах, которые выдаются на экзамене.

Что такое геометрическая прогрессия?

Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии можно задать соотношением:

Вот основные формулы для геометрической прогрессии:

Также геометрическая прогрессия, как и арифметическая, обладает характерным свойством:

Как решать задачи ОГЭ на геометрическую прогрессию?

Закрепим материал на практике и разберем две задачи ОГЭ по геометрической прогрессии.

Дана геометрическая прогрессия 3, 6, 12, … . Найти сумму первых 10 членов.

Решение:

Число 486 является членом геометрической прогрессии 2, 6, 18, … . Найдите его номер.

Решение:

Как видите, со знанием формул любое задание становится несложным!

В каком задании ОГЭ могут встретиться прогрессии?

Тема «Прогрессия» встречается в задании ОГЭ под номером 12. Выполнение этого задания экзаменуемым зависит от уровня сложности самого задания. В среднем с ним справляется всего 47% школьников. Как видите, сама тема не очень сложная. Все можно решить — достаточно правильно и хорошо подготовиться.

Напомним, что в КИМах с инструкцией и заданиями есть вспомогательные формулы, которые помогут при решении нашей задачи на прогрессию.

Теперь вы знаете теорию по теме прогрессии на ОГЭ. Можете смело оттачивать знания на практике. Пусть ваша встреча с прогрессиями на экзамене будет не печальной, а победной!

Хотите разобраться в других темах ОГЭ? Боитесь, что экзамены уже в следующем году, а вы даже не открывали учебники? Начните готовиться к ОГЭ-2021 уже сейчас на курсах с MAXIMUM. Мы поможем закрыть пробелы и сдать все на отлично. Правильная и интересная подготовка — залог успеха на экзаменах. Консультация бесплатно!

Лайфхаки экзамена

К рубрике

Источник

Анна Малкова

Арифметическая прогрессия — это последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и некоторого фиксированного числа d:

$a_{n+1}= a_n+d, , , (n = 1,2,...).$

Фиксированное число d называется разностью арифметической прогрессии.

Формула n-го члена арифметической прогрессии:

Сумма первых n членов арифметической прогрессии

вычисляется по формуле:

$S_n=frac{(a_1+a_n)}{2}cdot n=frac{2a_1+(n-1)d}{2}cdot n$

Каждый член арифметической прогрессии, начиная со второго, есть среднее арифметическое соседних: $a_n=frac{a_{n-1}+a_{n+1}}{2}.$

1. Студент Василий задумал стать репетитором. Он рассчитал, что будет проводить ровно 4 занятия в месяц с каждым учеником и стоимость каждого занятия составит 1000 рублей.

а) Если в первый месяц у Василия 2 ученика и каждый месяц число учеников увеличивается на 1, то сколько заработает Василий за 12-й месяц работы?

б) Сколько всего заработает Василий за год (то есть за 12 месяцев работы)?

В первый месяц у Василия два ученика. Во второй – три ученика, в третий – четыре, в каждый следующий – на одного ученика больше. Число учеников Василия образует арифметическую прогрессию, где a_1=2 – первый член прогрессии, d = 1 – разность прогрессии.

По формуле n-ного члена арифметической прогрессии,

Получим:

$a_{12}=2+(12-1)cdot 1=2+11=13.$

а) Работая 12-й месяц, Василий обучает 13 учеников.

Проводя с каждым 4 занятия по 1000 рублей в месяц, Василий заработает за 12-й месяц тысячи рублей.

б) Сколько всего заработает Василий за год? Суммы, которые Василий зарабатывает ежемесячно, также образуют арифметическую прогрессию, в которой тысяч рублей, а $c_{12} =52$ тысячи рублей.

По формуле суммы арифметической прогрессии, $S_n=frac{(c_1+c_n)}{2}cdot n$ .

$S_{12}=frac{left(8+52right)}{2}cdot 12=360$ тысяч рублей.

2. Проработав год репетитором, студент Василий обнаружил, что вместе с количеством учеников растут и его расходы на транспорт. В первый месяц Василий потратил на поездки к ученикам 800 рублей и каждый следующий месяц эта сумма увеличивалась на 300 рублей

Сколько денег потратил Василий на поездки к ученикам за весь год?

По условию, суммы денег, которые Василий тратит на поездки к ученикам, образуют арифметическую прогрессию, в которой a_1=800 и d=300 .

По формуле суммы арифметической прогрессии, $S_n=frac{{2a}_1+left(n-1right)d}{2}cdot n$

Получим: $S_{12}=frac{1600+left(12-1right)cdot 300}{2}cdot 12=29400$ рублей.

3. Ученица Маша хочет сдать тест не менее чем на 88 баллов. Студент Василий заметил, что каждый месяц результат Маши увеличивается на 7 баллов. За сколько месяцев занятий Маша достигнет результата, если ее результат до начала занятий составлял 43 балла?

После первого месяца занятий результат Маши улучшается на 7 баллов и составляет 43 + 7 = 50 баллов. Еще через месяц 50 + 7 = 57 баллов.

Мы имеем дело с арифметической прогрессией, в которой

Пусть результат не ниже 88 баллов достигнут через n месяцев. Получим:

$n-1geq frac{45}{7}$

$ngeq frac{52}{7}$

Так как n – целое, ngeq 8. Осталось ответить на вопрос задачи.

Результаты теста Маши составляют арифметическую прогрессию, в которой

Значит, через 1 месяц занятий результат Маши увеличится до 50, через два – до 57, а через семь – до 92.

Семь месяцев занятий нужно Маше, чтобы достичь результата.

Задачи ОГЭ на тему «Арифметическая прогрессия»

4. (Задача ОГЭ)

В первом ряду кинозала 30 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в ряду с номером n?

1) 28 + 2n 2) 30 + 2n 3) 32+2n 4) 2n

Количество мест в рядах кинозала образуют арифметическую прогрессию. По формуле для нахождения n-го члена арифметической прогрессии:

В нашей прогрессии

Значит,

Правильный ответ: 1.

5. (Задача ОГЭ) Выписаны первые несколько членов арифметической прогрессии: −87 ; −76; −65; … Найдите первый положительный член этой прогрессии.

Найдем разность прогрессии:

По формуле для нахождения n-го члена арифметической прогрессии:

Мы хотим найти первый положительный член этой прогрессии. Это значит, что мы находим номер n, начиная с которого выполняется неравенство .

Получим:

Отсюда

Значит, a_9 – первый положительный член прогрессии. Он равен:

Задачи ОГЭ для самостоятельного решения:

1. Найдите сумму всех отрицательных членов арифметической прогрессии –7,2; –6,9; …

2. Выписано несколько последовательных членов арифметической прогрессии: …; −9; x; −13; −15; … Найдите член прогрессии, обозначенный буквой x .

Ответы к задачам:

1. Ответ: -90

2. Ответ: -11.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Арифметическая прогрессия в задачах ОГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

В задании № (14) ОГЭ нужно работать с арифметической или геометрической прогрессией.

Пример:

Вася решил делать зарядку. В первый день он сделал 12 отжиманий, а каждый следующий день выполнял на одно и то же число отжиманий больше, чем в предыдущий. За 20 дней он сделал 1000 отжиманий. Сколько отжиманий сделал Вася на четвёртый день?

За правильное выполнение задания даётся (1) первичный балл. За неправильное ставится (0) баллов.

Алгоритм выполнения задания

Определи вид прогрессии.
Определи необходимую формулу для вычислений.
Выполни необходимые вычисления.
Запиши ответ на вопрос задачи.

Обрати внимание!

Ответом является число или последовательность цифр, которую необходимо записать без пробелов, запятых и других дополнительных символов. Если получилась обыкновенная дробь, то ответ запиши в виде десятичной.

Как решить задание из примера?

Данная задача относится к типу арифметической прогрессии.

Нам известен первый член прогрессии

a1=12

и сумма

S20=1000

Найдём разность прогрессии, используя формулу суммы

Sn=2a1+d⋅n−12⋅n

Подставим и вычислим:

d=76:19=4

отжимания в день.

Найдём количество отжиманий на четвёртый день по формуле:

an=a1+d⋅(n−1)

a4=12+4⋅(4−1)=24

отжимания.

В ответе записываем только значение без единицы измерения.

Ответ: 24.

Источник

Каталог заданий.
Арифметическая прогрессия

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задания Д12 № 35

Дана арифметическая прогрессия: Найдите сумму первых десяти её членов.

Аналоги к заданию № 35: 165 139 383602 … Все

Источники:

Демонстрационная версия ГИА—2013 по математике;

Демонстрационная версия ГИА—2014 по математике.

Решение

Помощь

Задания Д12 № 113

Дана арифметическая прогрессия Найдите a_16.

Аналоги к заданию № 113: 341378 392898 392925 … Все

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1309

Решение

Помощь

Задания Д12 № 165

Дана арифметическая прогрессия Найдите сумму первых десяти её членов.

Аналоги к заданию № 35: 165 139 383602 … Все

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1317

Решение

Помощь

Задания Д12 № 137301

Выписаны первые несколько членов арифметической прогрессии: 3; 6; 9; 12;… Какое из следующих чисел есть среди членов этой прогрессии?

1) 83

2) 95

3) 100

4) 102

Аналоги к заданию № 137301: 169551 169553 169555 … Все

Решение

Помощь

Задания Д12 № 137302

Арифметические прогрессии и заданы формулами n-го члена: y_n=4n,

Укажите те из них, у которых разность d равна 4.

левая круглая скобка x_n правая круглая скобка

левая круглая скобка y_n правая круглая скобка

левая круглая скобка z_n правая круглая скобка

Аналоги к заданию № 137302: 169581 169583 169585 … Все

Решение

Помощь

Пройти тестирование по этим заданиям

Источник

Появились трудностями с прогрессиями при подготовке к экзаменам? Напомним, что такое прогрессия, и как бороться с задачами этой темы ОГЭ по математике.

388

Что такое последовательность

Последовательность — это набор элементов, расположенных в определенном порядке. Каждый элемент в последовательности имеет свой индекс, который определяет его место в порядке следования.

Например, последовательность целых чисел может быть представлена в таком виде: 1, 2, 3, 4, 5, 6 и далее. В этом случае каждое число имеет свой индекс, например, a₁ = 1, a₂ = 2 до конечного элемента а_n, где n — это количество элементов в последовательности.

В задачах ОГЭ по математике 9 класса последовательности представлены арифметическими и геометрическими прогрессиями.

Школьникам часто задают задания, которые требуют определения элемента последовательности, нахождения суммы первых n элементов или нахождения количества элементов в последовательности.

Чтобы решать такие задачи, необходимо знать свойства и характеристики прогрессий, уметь применять формулы и методы для решения задач на последовательности.

Что такое арифметическая прогрессия

Арифметическая прогрессия — это разновидность числовой последовательности, в которой каждый новый компонент на фиксированное значение отличается от предшествующего. Это значение называют разностью.

Прогрессия описывается правилом a_n+1 = a_n + d.

Можно представить ее как: а₁, а₂, а₃, …, a_n, где a₁ будет первым элементом, а_n — n-м элементом, а разность d можно определить разницей между двумя соседними членами a₂ — a₁ = a₃ — a₂ = … = a_n — a_n-1.

Например, последовательность чисел 3, 7, 11, 15, 19 может называться арифметической прогрессией, так как каждый последующий член отличается от предыдущего на фиксированное значение 4. Элемент a₁ = 3, разность d = 4.

Характеристическое свойство арифметической прогрессии

Такая последовательность имеет определенную закономерность в построении. Элемент n — это всегда среднее арифметическое значение от соседних членов прогрессии. Исключение составляют первый и последний члены, которые не имеет соседнего с одной из сторон.

a_n = (a_n-1 + a_n+1) / 2
Условие: n > 1.

Как решать задачи с арифметической прогрессией на ОГЭ

Для решения задач экзамена после 9 класса нужно знать основные формулы и правила, которые применяются для арифметических прогрессий. Задания могут включать в себя поиск суммы, определения конкретного элемента и прочее.

Разность d равна разнице между любыми двумя соседними элементами последовательности: d = a_n — a_n-1.
Если нужно найти определенный член a_n, используй формулу: a_n = a₁ + (n — 1) * d.
a₁ — первый член прогрессии, n — номер искомого члена, d — разность.
Сумму n членов прогрессии можно вычислить по формуле: S_n = (a₁ + a_n) * n / 2.
a₁ — первый элемент, a_n — n-й элемент, n — количество элементов.
Если необходимо найти номер члена, который соответствует заданному значению, подойдет формула: n = (a_n — a₁) / d + 1.
a₁ — первый член, a_n — искомый член, d — разность.

Важно внимательно читать условие задачи, чтобы понимать, какие данные уже имеются, и что конкретно тебя просят найти.

Что такое геометрическая прогрессия

Геометрическая прогрессия — это разновидность числовой последовательности, в которой каждый новый компонент получается умножением предшествующего на фиксированное значение. Это значение называют знаменателем.

Прогрессия описывается правилом: b_n = b_n-1 * q, где q — знаменатель, n — номер члена прогрессии.

Например, последовательность чисел 3, 9, 27, 81, 243 может называться геометрической прогрессией, так как каждый последующий член отличается от предыдущего в фиксированные 3 раза. Элемент b₁ = 3, знаменатель q = 3.

Характеристическое свойство геометрической прогрессии

Последовательность тоже имеет определенную закономерность в построении. Квадрат элемента n — это всегда произведением предыдущего и последующего элемента. Исключение составляет первый элемент, который не имеет соседнего с одной из сторон.

a_n² = (a_n-1 * a_n+1)

Как решать задачи с геометрической прогрессией на ОГЭ

Для решения задач на ОГЭ также нужно знать формулы и правила, которые описывают свойства прогрессии. Задания могут включать в себя нахождение суммы компонентов, нахождение n-го члена и прочее.

Знаменатель q равен частному от деления члена прогрессии на предыдущий член: q = b_n / b_n-1.
Если нужно найти определенный член b_n, используй формулу: b_n = b₁ * q^(n-1).
b₁ — первый компонент, q — знаменатель, n — номер компонента.
Сумму n членов прогрессии можно вычислить по формуле: S_n = b₁ * ((1 — qⁿ) / (1 — q)),
b₁ — первый компонент, q — знаменатель, n — количество элементов в последовательности.

При решении задач нужно внимательно читать условия и уметь работать со степенями и извлечениями корней.

В каких заданиях ОГЭ есть задачи на арифметическую и геометрическую прогрессию

На этапе 9-го класса, задачи на арифметическую и геометрическую прогрессии могут встречаться в разделе «Алгебра и начала анализа». В демонстрационном варианте ОГЭ по математике 2023 года задание на знание свойств прогрессии встречается под номером 14. Скачать демонстрационный вариант можно на сайте ФИПИ.

Задачи на арифметическую и геометрическую прогрессии могут иметь разный уровень сложности, поэтому для успешного решения на ОГЭ нужно иметь хорошее понимание основных понятий и формул, связанных с арифметическими и геометрическими прогрессиями.

Если прогрессии все еще кажутся тебе сложными, то начинай подготовку в «СОТКЕ». Наши преподаватели объяснят так, чтобы ты понял абсолютно все. А разнообразные практические задания и качественная проверка с работой над ошибками помогут закрепить твои знания и повысить уверенность в себе.

Записывайся на бесплатный вводный урок, в «СОТКЕ» ты сможешь подготовиться к 4-м предметами по цене одного.

Источник

Прогрессии и последовательности: решаем ОГЭ по математике

Что такое последовательность?

Какие виды последовательности бывают?

Что такое арифметическая прогрессия?

Как решать задачи ОГЭ на арифметическую прогрессию?

Что такое геометрическая прогрессия?

Как решать задачи ОГЭ на геометрическую прогрессию?

В каком задании ОГЭ могут встретиться прогрессии?

Лайфхаки экзамена

Что такое последовательность

Что такое арифметическая прогрессия

Характеристическое свойство арифметической прогрессии

Как решать задачи с арифметической прогрессией на ОГЭ

Что такое геометрическая прогрессия

Характеристическое свойство геометрической прогрессии

Как решать задачи с геометрической прогрессией на ОГЭ

В каких заданиях ОГЭ есть задачи на арифметическую и геометрическую прогрессию

Не пропустите также: