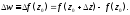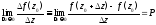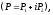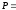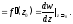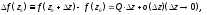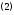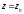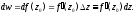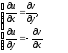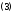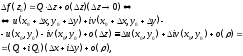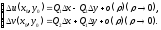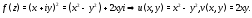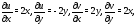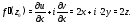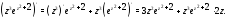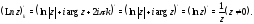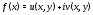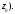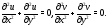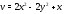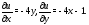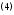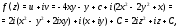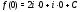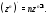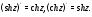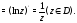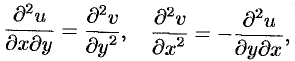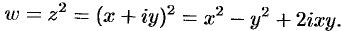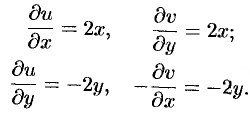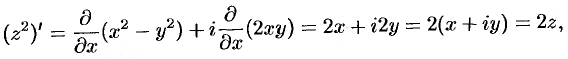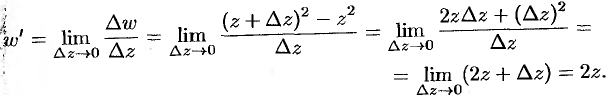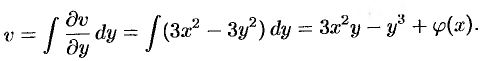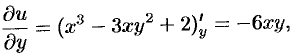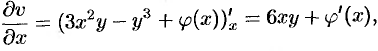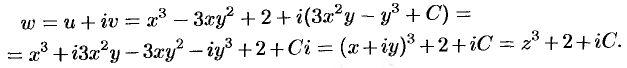Определение
Условия Коши-Римана, которые также в некоторых источниках называются условиями Даламбера-Эйлера —
соотношения, связывающие вещественную $u=u(x;y)$ и мнимую
$v=v(x;y)$ части всякой дифференцируемой функции
комплексного переменного $f(z)=u(x ; y)+i v(x ; y)$, где
$z=x+iy$ .
Для того чтобы функция $f=f(z)$, которая определена
в некоторой области комплексной плоскости $D$,
была дифференцируема в точке $z_{0}=x_{0}+i y_{0}$, необходимо и достаточно,
чтобы её вещественная и мнимая части
$u=u(x;y)$ и
$v=v(x;y)$ были дифференцируемы в точке $(x_0;y_0)$ как функции вещественных переменных $x$ и $y$ и в этой точке выполнялись условия Коши-Римана:
$$begin{aligned} frac{partial u}{partial x} &=frac{partial v}{partial y} \ frac{partial u}{partial y} &=-frac{partial v}{partial x} end{aligned}$$
Эти условия впервые появились в работе французского ученого-энциклопедиста, философа, математика и
механика Жана Лерона Даламбера (1717 — 1783) в 1752 году. В работе швейцарского, немецкого и российского математика и
механика Леонардо Эйлера (1707 — 1783), доложенной Петербургской академии наук в 1777 году, условия получили впервые
характер общего признака аналитичности функций. Великий французский математик и механик Огюстен Луи Коши (178 9- 1857)
пользовался этими соотношениями для построения теории функций.
Пусть задана действительная часть
$u(x;y)$ функции комплексной переменной $f(z)$. Требуется найти мнимую часть
$v(x;y)$ этой функции. Найти саму функцию
$f=f(z)$, используя некоторое начальное условие.
Алгоритм решения состоит в следующем:
1) Используя условия Коши-Римана, находим мнимую часть
$v(x;y)$ .
2) Когда и действительная, и мнимая части функции
$f(z)$ известны, составляем функцию
$f(z)=u(x ; y)+i v(x ; y)$ . Далее в полученном выражении надо произвести
такие преобразования, чтобы выделить переменную $z=x+iy$ или
$$bar{z}=x-i y$$, то есть «избавиться» от переменных
$x$ и $y$.
Замечание 1
На практике будут полезны соотношения:
$$x+i y=z$$
$$x^{2}+2 x y i-y^{2}=(x+i y)^{2}=z^{2}$$
$$x^{3}+3 x^{2} y i-3 x y^{2}-y^{3} i=(x+i y)^{3}=z^{3}$$
Замечание 2
Поделить на мнимую единицу
$i$ равносильно умножению на
$-i$.
3) В конечном итоге будет получена функция
$f(z)$, выражение которой содержит только комплексную переменную
$z$ и константы. Используя начальное условие,
если оно задано, находим значение константы и окончательно получаем искомую функцию.
Аналогично по известной мнимой части
$v(x;y)$ можно найти действительную часть
$u(x;y)$. Алгоритм решения практически идентичен.
Пример
Задание. По действительной часть
$u(x ; y)=-x^{2}+y^{2}-5 y$ функции комплексной переменной восстановить
мнимую часть $v(x;y)$ данной функции и составить саму функцию, которая удовлетворяет начальному условию $f(0)=0$ .
Решение. 1) Сначала найдем мнимую часть
$v(x;y)$ функции
$f(z)$. Из первого условия Коши-Римана имеем, что
$$frac{partial u}{partial x}=frac{partial v}{partial y}$$
то есть
$$frac{partial v}{partial y}=frac{partial}{partial x}left(-x^{2}+y^{2}-5 yright)=-2 x$$
Тогда
$$v(x ; y)=int(-2 x) d y+phi(x)$$
Если мы продифференцируем последнее равенство по
$y$ (то есть найдем $frac{partial v}{partial y}$ ), то как раз получим
$-2x$. Отсюда
$$v(x ; y)=int(-2 x) d y+phi(x)=-2 x y+phi(x)$$
Неизвестной остается функция $phi (x)$.
Согласно второму условию Коши-Римана имеем:
$$frac{partial u}{partial y}=-frac{partial v}{partial x}$$
то есть
$$2 y-5=-left(-2 y+phi^{prime}(x)right) Leftrightarrow 2 y-5=2 y-phi^{prime}(x)$$
Из последнего равенства определяем, что
$$phi^{prime}(x)=5 Rightarrow phi(x)=int 5 d x=5 x+C$$
Итак,
$$v(x ; y)=-2 x y+5 x+C$$
2) Мнимая часть искомой функции $f(z)$
восстановлена, тогда можем записать саму функцию:
$$f(z)=u(x ; y)+i v(x ; y)=-x^{2}+y^{2}-5 y+i(-2 x y+5 x+C)$$
Далее наша задача так сгруппировать слагаемые, чтобы выделить переменную
$z$ или какую-либо ее степень.
Раскроем скобки и перепишем полученное выражение следующим образом:
$$f(z)=-x^{2}+y^{2}-5 y-2 x y i+5 x i+C i=$$
$$=left(-x^{2}+y^{2}-2 x y iright)+(-5 y+5 x i)+C i=$$
$$=-left(x^{2}+2 x y i-y^{2}right)+5 ileft(x-frac{y}{i}right)+C i$$
Тогда согласно замечанию 1 первую скобку свернем как квадрат суммы, а согласно замечанию 2
во вторых скобках преобразуем выражение. Имеем, что:
$$f(z)=-(x+y i)^{2}+5 i(x+y i)+C i=-z^{2}+5 z i+C i$$
Итак, получили, что в выражении искомой функции
$f(z)$ присутствует только переменная
$z$ и константа.
3) Используя начальное условие
$f(0)=0$, найдём значение константы
$C$ . Для этого в выражении функции
$z$ заменим на 0,
$f(z)$ также равно 0, будем иметь:
$$f(0)=0=-0^{2}+5 cdot 0 cdot i+C i Rightarrow C i=0 Rightarrow C=0$$
Таким образом,
$$f(z)=-z^{2}+5 z i$$
С учетом того, что $C=0$, запишем, что мнимая часть
$v(x ; y)=-2 x y+5 x$ .
Ответ. $v(x ; y)=-2 x y+5 x, f(z)=-z^{2}+5 z i$
Читать первую тему — понятие комплексного числа,
раздела комплексные числа.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Так же, как и в
действительном анализе, для функций
комплексного переменного вводится
понятие производной. Однако здесь это
понятие более глубокое, чем в действительном
анализе. Например, всякая линейная
действительная функция дифференцируема
в любой точке. Для комплексных функций
это не так. Например, функция
изучению этого понятия.
Пусть функция
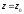
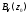
Сместимся из точки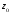
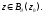
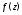
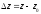
а сама функция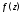
приращение
Определение 1.
Если существует конечный предел
то его называют
производной
функции
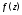
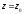
С понятием
производной тесно связано понятие
дифференцируемости функции в точке
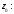
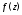
в точке
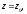
представляется в виде
где
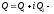
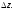
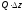
функции
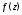
и обозначается
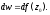
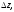
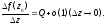
существует предел (1), т.е. что существует
производная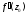
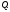
функции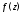
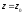
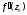
При этом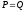
Как уже отмечалось выше, не любая
(даже очень простая) функция дифференцируема
в точке

части должны быть определенным образом
подчинены друг другу в следующем смысле.
Теорема
Коши-Римана.
Для того чтобы
функция
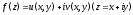
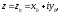
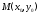
дифференцируемы (как функции действительных
переменных) и чтобы в этой точке имели
место равенства
(равенства (3)
называются условиями Коши-Римана).
Доказательство.
Пусть функция
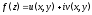
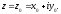
разложение (2). Запишем его более подробно:
где
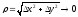
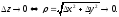
Отделяя здесь мнимые и действительные
части, получим
Эти равенства
означают, во-первых, что функции
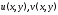
переменных
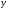
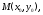
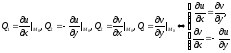
Таким образом, если
функция
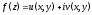
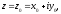
имеют место условия Коши-Римана (3).
Рассуждая обратным ходом, покажем, что
при выполнении условий (3) функция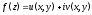
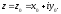
доказана.
Замечание 1.Из доказательства
теоремы следует, что если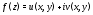
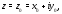
ее производную в этой точке можно
вычислять по формуле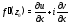
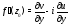
Пример 1. Проверить, будет ли
функция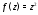
производную.
Решение. Выделим сначала в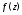
Теперь проверим условия Коши-Римана.
Имеем
значит, условия (3) Коши-Римана выполняются
для всех
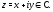
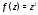
в любой точке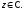
Таким образом, как и ожидалось, мы
получили, что
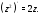
всех элементарных однозначных комплексных
функций находятся по тем же правилам,
что и производные действительных
функций. Например,
То же замечание справедливо и для
отдельных ветвей многозначных функций.
Например,
Введём теперь следующее важное понятие.
Определение 2. Функция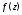
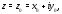
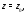
Аналитичность функции
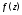
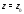
удовлетворяет условиям Коши-Римана (3)
в некоторой окрестности точки
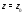
Определение 3. Функция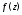
голоморфной) в области
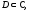
этой области.
Заметим, что действительная и мнимая
части аналитической функции удовлетворяют
уравнению Лапласа:
Это непосредственно вытекает из
условий Коши-Римана. Функции, удовлетворяющие
уравнению Лапласа, называютсягармоническими.
Пример 2. Является
ли функция
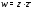
Решение. Так
как
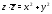
то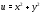
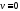
Условия Коши–Римана имеют вид: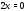
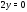
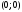
Следовательно, функция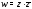
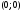
(44) запишем: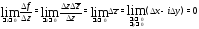
Таким образом, производная
Так как мнимая и
действительная части аналитической
функции
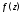
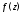
слагаемого) либо своей действительной,
либо мнимой частью. Покажем это на
примере.
Пример 3.
Найти
аналитическую функцию, если известна
ее мнимая часть
при дополнительном
условии
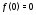
Решение. Так
как
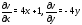
то из условий Коши-Римана (3) находим
производные действительной части:
Решив первое из этих
уравнений, находим
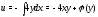
где
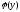

Для определения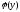

и подставляем
в (2):
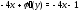
откуда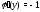
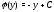
Следовательно,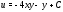
т.е. действительная
часть восстанавливается с точностью
до постоянного слагаемого. Условие
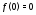
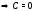
Таким образом,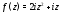
Имеют место следующие
утверждения.
1. Степенная
функция с натуральным показателем
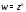
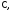
2. Каждая ветвь
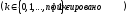
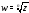
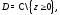
3. Комплексная
экспонента
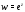
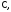
4. Комплексные
тригонометрические функции
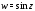
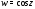
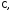
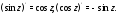
гиперболических функций, причем
5. Каждая ветвь

области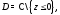
Все эти утверждения
проверяются с помощью соотношений
Коши-Римана.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аналитическая функция. Дифференциал
Фундаментальным понятием в теории функций комплексного переменного является понятие аналитической функции.
Однозначная функция 


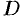
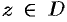
Как видно из этого определения, условие аналитичности в точке не совпадает с условием дифференцируемости функции в этой же точке (первое условие — более сильное).
Точки плоскости 



Пусть функция 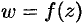

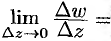
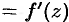
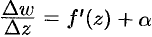
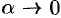
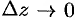
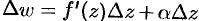
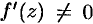
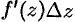
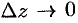
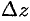
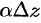
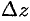
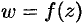
Дифференциалом 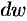
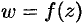

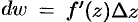
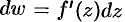
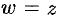
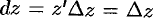
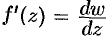
Замечание. Если функция 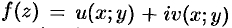
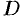
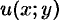
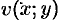
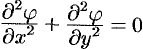
Действительно, дифференцируя первое из равенств Эйлера-Даламбера по 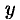
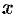
откуда 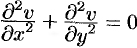
Функции 
Пример №74.3.
Проверить, является ли функция 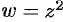
Решение:
Находим действительную 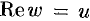
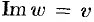
Таким образом, 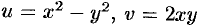
Условия (74.5) выполняются во всех точках комплексной плоскости 
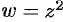
т. е. 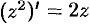
Заметим, что производную функции 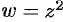
Пример №74.4.
Найти аналитическую функцию 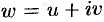
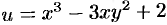
Решение:
Отметим, что функция и является гармонической функцией (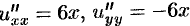
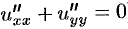
Для определения мнимой части 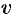
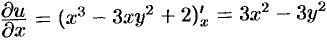
то, согласно первому условию, 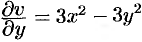
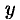
Для определения функции 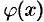
а
то 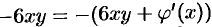

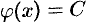
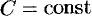
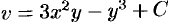
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны: