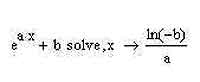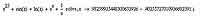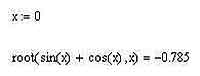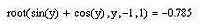Как найти аналитическое решение уравнения

Решение уравнений на бумаге — это задача, с которой каждый знаком еще со школьной скамьи. Сначала мы учились решать простые линейные уравнения, деля а на b и получая x, потом — системы уравнений, затем переходили к квадратным уравнениям. Находим дискриминант, извлекаем корень, делим, складываем… Все это вам знакомо, не так ли? Знакомы, наверное, и трансцендентные уравнения: тригонометрические, логарифмические (они же показательные), смешанные…

Системы трансцендентных уравнений — это вообще песня, причем песня из серии «этот стон у нас песней зовется». Люди давно уже пришли к выводу, что решать уравнения с помощью компьютера — отнюдь не роскошь, а вполне разумный подход к делу. Только раньше каждый, кто желал решить уравнение, должен был уметь программировать и владеть при этом какими-нибудь численными методами — например, методом Гаусса для решения систем линейных уравнений или методом Зейделя для решения трансцендентных. Сейчас эти все методы, конечно, тоже используются, но большая часть пользователей могут забыть их как страшный сон — все эти вычисления возможны в MathCAD’е, и именно о том, как их выполнять в этом замечательном математическом пакете, я сейчас и расскажу.

Аналитическое решение уравнений

Довольно значительное число уравнений поддаются аналитическому решению — т.е. решению в обобщенном виде, когда корни уравнения представляются в виде какой-то формулы, выражающей их зависимость от входящих в уравнение функций и различных коэффициентов перед ними. При этом, однако, надо заметить, что такой подход применим отнюдь не ко всем уравнениям — большая часть трансцендентных уравнений не может быть решена аналитически. Поэтому мы сейчас будем говорить преимущественно о полиномиальных уравнениях, известных также под названием алгебраических. Алгебраическим называется уравнение, которое можно преобразовать так, что в левой части будет многочлен от одной или нескольких неизвестных, а в правой — нуль. Степень многочлена называется степенью уравнения. Простейшие алгебраические уравнения: линейное уравнение — уравнение 1-й степени с одним неизвестным ax + b = 0, имеющее один действительный корень; квадратное уравнение — уравнение 2-й степени ax2 + bx + c = 0, которое в зависимости от значения коэффициентов может иметь либо два различных, либо два совпадающих действительных корня либо не иметь действительных корней. Вообще алгебраическое уравнение степени n не может иметь более n корней, что доказывается в рамках основной теоремы алгебры, которую в ВУЗах проходят в курсе математического анализа.

Что ж, давайте, пожалуй, перейдем к практике. То есть запустим MathCAD, включим панель символьных вычислений (Symbolic) — о том, как это сделать, уже было рассказано ранее в первой статье про MathCAD. На этой панели нам с вами понадобится оператор solve — именно он отвечает за аналитическое решение уравнений. Общий вид этого оператора такой: уравнение solve, переменная > решение. Здесь уравнение — это именно то уравнение, решение которого мы хотим найти в общем виде, а переменная — это символ, обозначающий в нашем уравнении переменную величину. Его нужно указывать для того, чтобы MathCAD (не такой уж он умный, как иногда кажется!) мог отличить переменную от коэффициентов. Давайте попробуем найти решение обычного квадратного уравнения ax2 + bx + c = 0. Для этого нажмите на кнопку Solve на панели инструментов символьных вычислений и на то место, где должно быть записано уравнение, введите наше квадратное уравнение. Здесь есть два тонких момента. Во-первых, чтобы записать «x2», нужно после x нажать Shift + 6 — тогда вы перейдете от записи переменных к записи показателя степени. Чтобы затем переключиться в режим записи других слагаемых в уравнении, достаточно нажать на клавиатуре стрелку вправо. Вообще навигация по записям в MathCAD при помощи стрелок вполне прозрачная — вы передвигаетесь стабильно в том направлении, куда указывает стрелка, и перескакиваете в показатели степени и индексы автоматически. Во-вторых, при записи уравнения в операторе solve «равно» нужно не обычное, а логическое — оно записывается с клавиатуры комбинацией Ctrl + =. При этом, если правая часть вашего уравнения равна нулю, то и ноль, и знак равенства можно опускать — MathCAD посчитает, что уравнение записано в стандартном виде, и успешно (если это, конечно, возможно) решит его. Итак, давайте посмотрим, что получилось от «скармливания» оператору solve нашего с вами квадратного уравнения.

Как видите, ничего неожиданного не произошло: MathCAD честно воспользовался известными всем еще из школьного курса алгебры формулами Виета, а решения уравнения записал в виде вектора-столбца. Несложно самостоятельно убедиться в том, что MathCAD знает и формулы Кордано для решения кубических уравнений — их он также может решать с произвольными коэффициентами. Правда, конечно, решения получаются несравненно более громоздкими, а потому я их здесь не буду приводить. Это же справедливо и для уравнений четвертой степени, для которых также существуют аналитические решения. Решение других видов уравнений (например, показательных) в аналитическом виде также вполне возможно. Например, если мы запишем уравнение eax + b = 0, то MathCAD совершенно справедливо сообщит, что решением этого уравнения будет выражение ln(-b)/a. Точно так же можно решать простые тригонометрические уравнения.

Численное решение уравнений с помощью функции solve

Но, конечно, такие красивые результаты в максимально обобщенной форме мы сможем получать далеко не всегда. Уже на уравнениях пятой степени MathCAD спотыкается, и произвольные коэффициенты приходится заменять постоянными. Впрочем, в этом ничего страшного нет — даже уравнения третьей степени со всеми произвольными коэффициентами решать вряд ли имеет смысл, поскольку гораздо проще подставить коэффициенты и получить нормальные числа в решении — в конце концов, общие формулы для решения алгебраических выражений используются именно из-за того, что живому человеку гораздо проще подставить числа в готовую формулу, чем подбирать каждый раз корни уравнения. С компьютерами дело обстоит в большинстве случаев с точностью до наоборот — получить численное решение уравнения зачастую гораздо проще, чем аналитическое. Оператор solve умеет находить и численные решения уравнений. Если аналитическое решение получить не удается, он автоматически подключает систему нахождения численных решений уравнений. Так что, если мы запишем совершенно невообразимое для нормального человека уравнение x25 + sin(x) + ln(x) + ex + 1/x = 0, то MathCAD, и глазом не моргнув, выдаст нам результат вычислений.

Но численное решение уравнений с помощью функции solve — честно говоря, не лучшая идея. Некоторые виды уравнений она решает из рук вон плохо — в первую очередь, конечно же, это относится к уравнениям тригонометрическим. Начнем с того, что эта функция выдает решение только для одного периода в то время, как большая часть решений тригонометрических уравнений описывается с помощью специального целочисленного параметра, выражающего номер периода. Но это, в общем-то, не самое худшее, поскольку иногда использование solve приводит к получению совершенно неверного результата, который при подстановке его в уравнение дает совершенно неверное значение. Конечно, это является минусом MathCAD’а, но положение дел совсем не фатально. Если использовать специальные методы решения трансцендентных уравнений, то численные результаты будут совершенно адекватными. Можно также пойти по другому пути, например, преобразуя выражения с помощью символьного процессора MathCAD (о том, как это делается, я еще расскажу в дальнейшем), а затем уже решая с помощью solve более простые уравнения, получившиеся в результате этих преобразований. Численное решение уравнений требует от пользователя понимания того, что он ожидает в результате этого решения получить. Поэтому прежде, чем приступать к рассказу о самом процессе численного решения, я расскажу об одной полезной функции, которая пригодится для численного решения простых трансцендентных уравнений.

Решение уравнений с помощью функции root

Эта очень хорошая и полезная во всех смыслах функция имеет лишь одно ограничение — она может найти всего один корень. К сожалению, несущественным это ограничение назвать, честно говоря, сложно. Впрочем, вы увидите, что и его запросто можно обойти — разработчики MathCAD, по крайней мере, предусмотрели такую возможность, и ею вполне можно воспользоваться, если, конечно, в этом есть необходимость. Функция root имеет следующий вид: root(функция, переменная). Функция — это фактически левая часть уравнения в стандартном виде, т.е. уравнения, в котором левая часть равна нулю. Переменная — это, конечно же, тот символ, который обозначает в функции переменную величину. Для использования функции root нужно задать начальное приближение — то есть число, отталкиваясь от которого, функция root будет искать корни нашего уравнения. От начального приближения может весьма существенно зависеть и сам результат работы функции root, особенно если искомые корни уравнения находятся сравнительно близко. Начальное приближение задается очень просто: набираем имя нашей переменной до функции root, ставим двоеточие (MathCAD самостоятельно преобразует его в знак присвоения «:=»), пишем число, соответствующее нашему начальному приближению.

В принципе, вместо начального приближения можно задать интервал, в пределах которого должно лежать решение, отыскиваемое нами с помощью функции root. Для этого после имени переменной в списке параметров функции нужно (через запятую, конечно же) указать начало и конец интервала, на котором должно располагаться решение. У этого способа есть только одно существенное но: числа, определяющие начало и конец этого интервала, должны иметь разные знаки. При этом, если уравнение не имеет действительных корней, то и интервал нужно задавать в комплексной форме. Мнимая единица при этом записывается как i или как j.

Как видите, для численного нахождения уравнений с помощью функции root необходимо довольно точно представлять, где именно должны располагаться корни уравнения — сделать это можно, например, с помощью графика функции, на котором с помощью трассировки можно определить нули функции. Но о том, как строить графики и как ими потом пользоваться, как-нибудь в другой раз.

SF, spaceflyer@tut.by

1. Аналитическое решение уравнения

Аналитическое
решение допускают уравнения f(x)=0
с левой частью в виде многочлена степени
не выше четырех. Так же аналитическое
решение допускают простейшие
трансцендентные уравнения, содержащие
тригонометрические функции и экспоненты.
Фактически почти все случаи аналитического
решения уравнений изучаются в средней
школе.

Любая
электронная таблица легко описывает,
например, решение квадратного уравнения
с действительными корнями:

Ax²+Bx+C=0.

Рис.
10.4. Решение квадратного уравнения

Формулы
в строке 6 очевидны.

Существуют
таблицы, в которых так же легко можно
описать решение произвольного квадратного
уравнения, например Excel.

1. Аналитическое решение системы линейных уравнений

Уже
в ранних версиях 1-2-3 и Quattro существовали
команды умножения и обращения матриц.

В
Excel с первых версий существовали функции
для матричных операций и для вычисления
определителя матрицы.

Поэтому
системы линейных уравнений невысокой
размерности с хорошими определителями
легко решаются в электронных таблицах.

Пусть
дана система линейных уравнений

Ax=b.

Тогда
ее решение можно записать так:

x=A^-1b

или
так

x₁=∆_A1/∆_A;x₂=∆_A2/∆_A

где,
∆_A– определитель матрицы А;
∆_Ai– соответствующий минор.

Рис.
10.5. Аналитическое решение системы
линейных уравнений

Для
вычисления определителей в столбце А
используется функция МОПРЕД. Остальные
формулы очевидны.

Ограничения,
налагаемые на систему уравнений
конкретной таблицей, следует смотреть
в документации.

Например,
ранние версии 1-2-3 работали с квадратными
матрицами с числом строк меньшим 80,
Excel’97 работает с матрицами размерностью
меньше 75.

1. Итеративное решение уравнения

Уравнение
x ²— x-1=0 допускает аналитическое решение.

Поэтому
численное решение является исключительно
методическим.

Преобразуем
уравнение в систему.

x=√y

y=x+1

Откроем
окно команды Параметры из меню Сервис.
Установим автоматический режим вычислений
и включим итерации.

Введем
в ячейки В3 и В4 соответствующие формулы.

И
получим результат.

Рис.
10.6. Итеративное решение уравнения

Рассмотрим
уравнение x³—x-1=0.

Возможно
два варианта записи системы уравнений
соответствующей данному уравнению. Оба
показаны на рис. 10.6. Первый сходится,
второй расходится.

Рассмотрим
классическое уравнение Кардано
x³-15x-4=0. Оно, очевидно,
обладает корнемx=4.
Остальные два корня отрицательны, как
видно из графика.

Рис.
10.7. График функции y=
x³-15x-4

Для
этого уравнения также возможны два
варианта систем уравнений.

Как
видно из рис. 10.6, они приводят к разным
результатам. А если во второй системе
поменять местами уравнения, то можно
получить расходящуюся систему.

Несколько
слов о задании начальных значений.

Все
вышеперечисленные модели вводились на
чистый лист, точнее — в первоначально
пустые ячейки. Согласно правилам
вычислений в электронных таблицах
пустая ячейка эквивалентна ячейке, в
которую записано число 0. Фактически
это и задавало начальные значения.

Если
же до ввода формул ввести в ячейки
числовые значения, то задание начальных
значений для неизвестных будет иным.
И, возможно, система сойдется к другому
решению.

1. Итеративное решение системы линейных уравнений

Итерационный
метод Гаусса–Зейделя представляет
собой многомерную разновидность метода
последовательных приближений, описанного
выше для решения уравнений. Для применения
этого метода следует разрешить каждое
уравнение относительно некоторой
неизвестной, своей в каждом уравнении.
Затем начинается привычный ход метода:
задается приближение, подставляется в
правую часть и находится следующее
приближение. Процесс продолжается до
тех пор, пока не будет достигнута
удовлетворительная точность или пока
расходимость не станет очевидной.

Классический
метод последовательных приближений в
применении к системам уравнений требует,
чтобы следующее приближение, все
компоненты вектора решения, вычислялось
строго на основе предыдущего приближения,
опять же всех компонент вектора. Но
компоненты вектора вычисляются поочередно
и при вычислении очередного компонента
часть новых значений уже известна, и
может использоваться в расчете. В методе
Гаусса–Зейделя так и происходит. Такой
подход к расчету компонент приближения
еще легче реализуется в электронных
таблицах. Для реализации классического
метода последовательных приближений
при использовании электронных таблиц
как минимум потребуется вспомогательный
диапазон. А как максимум вспомогательный
диапазон и простая программа для
копирования вычисленного приближения
на место предыдущего.

Для
лучшей сходимости следует выбирать в
каждом уравнении переменную с максимальной
абсолютной величиной.

Решим
методом Гаусса–Зейделя простую систему
линейных уравнений:

2x₁+x₂—x₃=-1

x₁+2x₂+x₃=1

x₁+x₂—x₃=-2

Преобразуем
систему.

x₁
=(-1-x₂+x₃)/2

x₂
=(1-x₁—x₃)/2

x₃=2+
x₁+x₂

Рис.
10.8. Итеративное решение системы линейных
уравнений

Формулы
в диапазоне В7:В9 очевидны.

Соседние файлы в папке Konspekt

• #

  22.08.20131.06 Кб26.listing

• #
• #
• #
• #
• #
• #
• #

Аналитические методы решения линейных уравнений с параметрами.
консультация по алгебре (11 класс) на тему

В работа рассмотрены различные подходы к решению линейных уравнений с параметрами.

Скачать:

Предварительный просмотр:

Аналитические методы решения линейных уравнений с параметрами.

В работе рассмотрены различные подходы к решению линейных уравнений с параметрами. Данная тема необходима учащимся для первичного ознакомления с методами решения уравнений с параметрами, которая является опорным пунктом подготовки к ЕГЭ (решение заданий части «С5»).

1. Понятие уравнений с параметрами.
2. Различные виды и методы решений линейных уравнений с параметрами.
3. Задания для самостоятельной работы.

Рассмотрим уравнения, в которых некоторые коэффициенты заданы не конкретными числами, а обозначены буквами. Такие уравнения называются уравнениями с параметрами, а буквы – параметрами. Предполагается, что эти параметры могут принимать любые числовые значения.

Решить уравнение с параметрами – значит, найти множество всех корней данного уравнения в зависимости от допустимого значения параметра. (Т.е. указать, при каких значениях параметра существуют решения, и каковы они, затем исследовать его относительно параметра)

Алгоритм решения уравнений с параметрами примерно таков:

• Разбить область изменения параметра на промежутки, где при изменении параметра в каждом из них полученные уравнения решаются одним и тем же методом.(Границами промежутков служат те значения параметра, в которых, или при переходе через которые, происходит качественное изменение уравнения. Такие значения параметра называют «особыми» или контрольными).
• Отдельно на каждом промежутке находятся корни уравнения, выраженные через значения параметра.
• Ответ уравнения состоит из списков изменения параметра с указанием всех корней для каждого промежутка (или конкретных значений параметра).

Основные методы решения уравнений с параметрами.

1. Решение простейших линейных уравнений с параметрами.

Исследуем линейное уравнение вида: ax =b (1)

1. а 0, b R, то уравнение (1) имеет единственный корень х= .
2. а=0, b=0, уравнение (1) имеет корнем любое действительное число, т.е. х R.
3. а 0, 0, уравнение (1) не имеет корней.

Пример №1: ax = 5; при a=0 имеем 0х=5, чего не может быть,

тогда х , при а 0 х= .

Пример №2: 0х=а; при а=0 получим 0х=0 х R, при а 0 х .

Пример №3 : Iхl=а, при а=0 х=0; при а>0 х= а, при а х .

Приведем уравнение к виду: х(а-1)=6;

если а=1, то 0х=6, нет решений;

Ответ: при а 1 х = ; при а=1 нет решений.

1. Более сложные линейные уравнения с параметром, при решении которых требуется дополнительная проверка, связанная с ограничением на ОДЗ.

Алгоритм решения таких уравнений:

1. Найти ОДЗ.
2. Решить уравнение относительно х.
3. Определить контрольные значения параметра (к.з.п.)
4. Проверить, нет ли таких значений параметра, при которых значение х было бы равно числу, не входящему в ОДЗ.

1. ОДЗ: х 2
2. К.з.п. а=0.
3. Решим уравнение относительно х:

• При а=0 уравнение имеет вид =3. Уравнение корней не имеет.
• При а 0 уравнение имеет вид а=3(х-2), отсюда х=

1. Проверим, нет ли таких значений параметра а, при которых х=2, т.е. решим уравнение: =2, а=0 ( т.е. приа=0 нет решений)

Ответ: при а 0 х= ; при а=0 нет решений.

2. Решим уравнение относительно х. Умножим обе части уравнения на а 0: 2(а-1)х=(х-1)а +5;

2ах -2х – ах = 5 – а;

1. К.з.п. а = 2, т.к. коэффициент при х обращается в 0 при а=2

• Если а=2, то 0х=3, нет решений;
• Если а 2, то х = .

Ответ: при а=2 нет решений; при а 2 и при а 0 х = ; при а=0 уравнение не имеет смысла.

Примечание. Если при каком-нибудь значении параметра а=а 0 данное уравнение не имеет смысла, то нет и решений при а=а 0. Обратное утверждение не верно. Бывает, что при контрольном значении параметра уравнение имеет корни, но они не входят в ОДЗ.

3.Уравнения, сводящиеся к линейным

Пример №1 Решить уравнение: m = +

1. ОДЗ: т 0, х 1.
2. Решим уравнение относительно х. Умножим обе части уравнения на т(х-1) 0, получим т 2 (х-1) = х – 1 + т – 1;

Х( т 2 – 1) = т 2 + т – 2;

1. К.з.п. т= 1

• Если т=1, то 0х=0, следовательно, х-любое действительное число, где х 1.
• Если т=-1, то 0х=-2, нет решений.
• Если т 1 и т то х= .
• Если т = 0, то нет решений.

1. Проверим, нет ли значений параметра а, при которых найденное значение х равно 1:

= 1, т+2=т+1, 0т=1, нет решений.

Ответ: при т=0 и т=-1 нет решений; при т=1 х (-∞;1) (1;+∞); при т 1 и

Пример №2 Решить уравнение: = .

2)Решим уравнение относительно х: (a+b)х = a – b.

3) К.з.п.: a+b = 0, a = -b.

• Если a = -b, то нет решений.
• Если a -b, то х = .

1. Найдем значения параметров а и b, при которых полученное значение х=1:

1 = , 2b = 0, b = 0. Следовательно, при b = 0 нет решений.

Ответ: при a -b и b 0 х = ; при a = -b и b=0 нет решений.

Пример №3 (МГУ, 2002) При каких значениях параметра b уравнение

9х+ b 2 – (2 — )b — 2 = b 4 х – b 2 (b + ) не имеет корней?

1. ОДЗ: х .
2. Решим уравнение относительно х:

(b 4 – 9)х = b 3 + (1+ ) b 2 – (2 — )b -2 ,

Линейное уравнение не имеет корней тогда и только тогда, когда

Первое уравнение системы имеет два корня: b 1 = , b 2 = — .

1. Подставим во второе уравнение системы b 1 = , получим: 2 +6 ;

b 2 = — , получим 0=0. Т.е. второму условию удовлетворяет b 1 = .

Ответ: при b= уравнение корней не имеет.

Решить самостоятельно уравнения

1) (а+5)(а-3)х=а 2 — 25 ( при а и а х= ; при а=3 ; при а=-5 х ∊ R)

2) а 2 х = а(х+2) – 2 ( при а и а х= ; при а=0 ∅ ; при а=1 х ∊ R)

3) = — ( при а=-3, а=-2, а=1/2 ∅ ; при а и а х= )

4)1+ = — ( при а и а х= ; при а=-3, а=0, а=1 ∅ )

5) Для каких значений а решение уравнения 10х-15а = 13- 5ах = 2а больше 2? (МГУ, 1982)

• Г.А. Ястребинецкий. Уравнения и неравенства, содержащие параметры. М. Просвещение.1972.
• А.Г. Корянов. Задачи с параметрами. Брянск.2010.
• М.А. Галицкий, А.М.Гольдман, Л.И. Звавич. Сборник задач по алгебре для 8-9 классов. Углубленное изучение математики. М. Просвещение. 1992.

По теме: методические разработки, презентации и конспекты

Рабочая программа элективного курса по математике 10 класс «Методы решения задач с параметром».

Предлагаемый курс «Методы решения задач с параметром» предназначен для реализации в 10 классах для расширения теоретичес.

Координатно-параметрический метод решения задач с параметрами

Решение задач с параметрами систематизирует знание основных разделов школьной математики, повышает уровень математического и логического мышления, формирует первоначальные навыки исследовательской дея.

Аналитические методы решения задач с параметрами Составитель: Е.М .Чернова МКОУ КГ№ 1

Одними из наиболее сложных задач для учащихся в курсе математики — это задачи с параметрами, так как требуют от них умения рассуждать логически и анализировать полученные решения. С одной сторон.

Графические методы решения уравнений с параметрами

урок в 11 классе.

Применение различных способов и методов решения задач с параметрами

Задачи с параметрами являются сложными потому, что не существует единого алгоритма их решения. Спецификой подобных задач является то, что наряду с неизвестными величинами в них фигурируют параметры, ч.

Основные методы решения задач с параметрами

В действующем формате ЕГЭ по математике (профильный уровень) задания №18 содержат параметры и предполагают исследование свойств различных элементарных функций. Поэтому подготовку к и.

Аналитический способ решения задач с параметром.

Данный материал предназначен для обучающихся 10-11 классов и содержит задания для подготовки к ЕГЭ по теме «Задание №18. Решение задач с параметром». Он направлен на совершенствование умений.

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ И ИХ СИСТЕМ В ПАКЕТАХ СИМВОЛЬНОЙ МАТЕМАТИКИ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ М.Е. ЕВСЕВЬЕВА»

Кафедра информатики и вычислительной техники

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ И ИХ СИСТЕМ В ПАКЕТАХ СИМВОЛЬНОЙ МАТЕМАТИКИ

Автор работы _____________________________________И. Ю. Добрынькина

Направление подготовки 44.03.05 Педагогическое образование

Профиль Информатика. Математика

Руководитель работы_______________________________ Т. В. Кормилицына

Введение

Одним из факторов, определяющих уровень развития современного общества и его интеллектуальные возможности, является оснащенность его средствами вычислительной техники. Сфера использования ЭВМ в настоящее время настолько широка, что нет такой области, где ее применение было бы нецелесообразным.

Развитие вычислительной техники повлекло за собой создание и совершенствование языков программирования, а вследствие этого и программного обеспечения. Однако совершенствование программного обеспечения связано с увеличением его сложности. Поэтому процесс разработки программ становится трудоемким, а их модификация и сопровождение затруднительным.

Традиционная инженерная деятельность связана с решением совокупности разнообразных задач расчета, проведением экспериментов, оформление документации. Развитие современных методов и компьютерной технологии существенно изменяет деятельность специалиста.

В начале 90-х гг. на смену универсальным языкам программирования пришли специализированные системы компьютерной математики (СКМ). Среди них наибольшую известность получили системы Eureka, Mercury, Mathcad, Derive, Mathematica 2/3/4, Maple V R3/R4/R5 и Maple 6 и др.

Научное программное обеспечение и математические пакеты играют важную роль в современном естествознании и технике. Такие пакеты как Axiom, Derive, Maсsyma, Maple, MatLab, MathCAD, Mathematica широко распространились в университетах, исследовательских центрах и компаниях развитых стран. Владение одним или несколькими математическими пакетами и регулярное использование их в работе будь то исследовательская или преподавательская задача быстро становится нормой для специалиста.

1. Mathematica . Решение простейших дифференциальных уравнений

Для решения дифференциальных уравнений в аналитической форме в пакете Mathematica используется функция DSolve, дифференциальное уравнение 29 относительно функции y(x). Функция y и все ее производные должны быть записаны с аргументом, заключенным в квадратные скобки: y[x], y’[x]

Функция DSolve стремится найти общее решение ДУ в явном виде и выдает результат в виде списка правил замены, причем каждое решение заключается в фигурные скобки. Для ДУ порядка n общее решение содержит n произвольных констант, которые обозначаются C[1], C[2],…,C[n]. Для получения частного решения необходимо в качестве первого аргумента DSolve указать список, состоящий из самого уравнения и начальных или граничных условий:

Найденные с помощью DSolve решения можно подставить в любое выражение, содержащее y(x). Однако это решение не определяет правил замены производных y’(x), y’’(x) и так далее, например:

Чтобы получить решение, не имеющее этого недостатка, нужно в качестве второго аргумента функции DSolve записать только имя искомой функции, не указывая ее аргумент. В этом случае решение представляется в виде чистой функции («purefunction»-объекта), в котором роль аргумента x, в некоторых случаях, играет символ «#1», а признаком этого объекта является символ «&». Полученное решение можно подставить в любое выражение, содержащее как функцию y(x), так и ее производные:

Для решения систем уравнений в качестве первого аргумента функции указывается список уравнений, а в качестве второго аргумента – список искомых функций:

Если в список уравнений включить необходимое количество начальных или граничных условий, то будет найдено частное решение системы ДУ, не содержащее произвольных постоянных:

Для некоторых уравнений решение может быть выражено через спецфункции, встроенные в пакет Mathematica. Если же DSolve не может найти аналитического решения ДУ, то Mathematica просто перепечатывает введенные данные в выходную ячейку:

В этом случае нужно преобразовать ДУ к более простому виду, используя правила, известные из теории дифференциальных уравнений. Если же аналитически решить уравнение не удается, можно попробовать решить его численно.

1.2 Примеры из математического анализа

Разумеется, роль систем символьной математики далеко не исчерпывается приведенными выше примерами. Эти системы способны преобразовывать сложнейшие алгебраические выражения, находить аналитические решения сложных систем линейных, нелинейных и дифференциальных уравнений, манипулировать со степенными многочленами, вычислять производные и интегралы, анализировать функции, находить их пределы и т. д. Это видно уже из примеров, представленных на рис. 1.6 .

В этих примерах функция D (как приятное исключение из правил, обозначенная одной буквой) вычисляет производную, функция Integrate — интеграл, функция Solve решает нелинейное уравнение (в данном случае квадратное), а функция Series разлагает выражение в ряд относительно заданной переменной и при заданных начальном значении переменной и максимальной степени ряда. В фигурных скобках задаются списки некоторых входных и выходных параметров (аргументов).

Системы символьной математики являются справочниками по многим специальным функциям. При этом они способны давать результаты вычислений в виде специальных функций, что демонстрируют следующие примеры:

Здесь специальные функции получаются в результате вычисления суммы, символьного интегрирования и решения в аналитическом виде дифференциального уравнения. Соответствующие функции будут более подробно описаны в дальнейшем. Обратите внимание на то, что эти примеры даны прямо в тексте книги. Мы будем часто использовать такой прием для представления небольших примеров.

DSolve [Derivative [1] [у] [х] ==2*а*х^3, у[х], х]

DSolve [у» [х] — у’ [х] — 6 у [х] == 0, у [х] , х] <<У[х] ->| е-4хС[1] + С[2] -Cos[2x] -|sin[2x]>>

DSolve [у» [х] + 4 у'[х] == 10 Sin [2 х] , у [х] , х]

DSolve[y'[x] == Sin[Ex] , y[x] , x]

DSolvefz2 w»[z] +zw'[z] — (z2 + l)w[z] ==0, w[z], z]

<BesselI[l, z] C[l] +BesselK[l, z] C[2] >>

Как нетрудно заметить, аналитические решения дифференциальных уравнений могут содержать не только элементарные, но и специальные математические функции, что заметно расширяет возможности применения системы Mathematica в решении задач динамического моделирования.

1. 3 Аналитическое решение дифференциальных уравнений

Общее решение дифференциальных уравнений.

Для нахождения аналитических решений дифференциальных уравнений в Maple применяется команда dsolve(eq,var,options),где eq – дифференциальное уравнение, var – неизвестные функции, options – параметры. Параметры могут указывать метод решения задачи, например, по умолчанию ищется аналитическое решение: type=exact. При составлении дифференциальных уравнений для обозначения производной применяется команда diff, например, дифференциальное уравнение y»+y=x записывается в виде: diff(y(x),x$2)+y(x)=x.

Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения. В Maple такие постоянные, как правило, обозначаются как _С1, _С2, и т.д.

Общее решение неоднородного линейного дифференциального уравнения всегда выводится так, чтобы была четко видна, структура этого решения. Как известно, общее решение неоднородного линейного дифференциального уравнения равно сумме общего решения соответствующего однородного дифференциального уравнения и частного решения этого же неоднородного дифференциального уравнения. Поэтому в строке вывода решение неоднородного линейного дифференциального уравнения всегда состоит из слагаемых, которые содержат произвольные постоянные (это общее решения соответствующего однородного дифференциального уравнения), и слагаемых без произвольных постоянных (это частное решения этого же неоднородного дифференциального уравнения).

Команда dsolve выдает решение дифференциального уравнения в невычисляемом формате. Для того, чтобы с решением можно было бы работать далее (например, построить график решения) следует отделить правую часть полученного решения командой rhs(%).

eq:=<2*x-3*y+5*z+7*t=1, 4*x-6*y+2*z+3*t=2, 2*x-3*y-11*z-15*t=1>: > s:=solve(eq,); s:= < z=-11/8 t , y=y , x=3/2 y — 1/16 t+1/2 >Для нахождения частного решения следует выполнить подстановку конкретного значения одной из переменных при помощи команды subs: > subs(,s); < z=(-11)/8, x=31/16 , 1=1>»>

2. Аналитические вычисления в Mathcad

С помощью аналитических вычислений находят аналитические или полные решения уравнений и систем, вычисляют в производные и неопределенные интегралы, а также проводят преобразования сложных выражений (например, упрощение). Иначе говоря, при таком подходе можно получить результат в виде некоторой функции. В программе Mathcad при проведении символьных преобразований конкретные значения, присвоенные переменным, игнорируются – переменные рассматриваются как неопределенные параметры.

Команды для выполнения аналитических вычислений в основном сосредоточены в меню Символика (Symbolics) и продублированы на аналогичной панели инструментов.

Чтобы упростить выражение (или часть выражения), надо выбрать его при помощи уголкового курсора и дать команду Символика > Упростить (Symbolics > Simplify). При этом выполняются арифметические действия, сокращаются общие множители и приводятся подобные члены, применяются тригонометрические тождества, упрощаются выражения с радикалами, а также выражения, содержащие прямую и обратную функции. Некоторые действия по раскрытию скобок и упрощению сложных тригонометрических выражений требуют применения команды Символика > Раскрыть/Расширить (Symbolics > Expand).

В меню Символика (Symbolics) предусмотрен ряд операций, ориентированных на выделенную переменную, использованную в выражении. Например, команда Solve (Решить) ищет корни функции, заданной данным выражением. В примере в аналитической форме получены все корни полинома второй степени: сначала применена команда solve для решения, а затем simplify для упрощения результата:

Другие возможности использования этого меню включают:

аналитическое дифференцирование и интегрирование: Символика > Переменная > Дифференцировать (Symbolics > Variable > Differentiate) и Символика > Переменная > Интегрировать (Symbolics > Variable > Integrate);

замена переменной: Символика > Переменная > Подставить (Symbolics > Variable > Substitute) – вместо переменной подставляется содержимое буфера обмена;

Механизм аналитических вычислений можно использовать для аналитического решения уравнений и систем уравнений и неравенств. Для этого задается блок решения Given, в который помещаются уравния и неравенства, а последняя формула блока должна выглядеть как

где в скобках приведен список искомых величин, а далее следует знак аналитического вычисления, отображаемый в виде стрелки, направленной вправо:

Отметим, что функция Find пытается найти решение в аналитической форме. В том случае, если до блока Given задать численно значения всех параметров, входящих в уравнения, а также начальные приближения для корней, то получим решение в числовом виде.

Примеры использования функции Find для решения уравнений и систем уравнений различного типа приведены в соответствующих разделах пособия.

Любое аналитическое вычисление можно применить с помощью ключевого слова. Cписок ключевых слов

3. Решение систем дифференциальных уравнений в символьном виде в системе MATLAB

Для решения дифференциальных уравнений в форме Коши MatLAB имеет функцию dsolve(‘eqn1’,’eqn2’, …), которая возвращает аналитическое решение системы дифференциальных уравнений с начальными условиями. Они задаются равенствами eqni(вначале задаются уравнения, затем начальные условия).

По умолчанию независимой переменной считается ‘t’ . Можно использовать и другую переменную, включив ее в конец списка параметров функции dsolve. Символ D обозначает производную по независимой переменной, то есть d/dt, при этом D2 означает d^2/dt^2 и т.д.

Начальные условия задаются в виде равенств ‘y(a) = b’ или ‘Dy(a) = b’, где y — независимая переменная, a и b – константы. Если число начальных условий меньше, чем число дифференциальных уравнений, то в решений будут присутствовать произвольные постоянные С1, С2 и т.д. Вывод осуществляется в виде массива записей.

Обратите внимание, что уравнение, которое требуется решить, задано как строка, то есть взято в одинарные кавычки. Ответ представляет собой точное (символьное) решение 1+корень(5). Для получения числовых решений введите double (ans) или vpa (ans), чтобы отобразить больше знаков. Ввод с командой solve может также быть символьным выражением, но в этом случае программа MATLAB потребует, чтобы правая часть выражения была заключена в скобки, и фактически синтаксис решения уравнения х 2 — Зх = -7 будет выглядеть так:

Ответ представляет собой точное (символьное) решение (3 + корень(19i))/2 (сложные числа, где буква i в ответе ставится для мнимой единицы V-1). Для получения числовых решений введите double (ans) или vpa (ans), чтобы отобразить больше знаков.

Заключение

В настоящее время научное программирование претерпевает серьезную трансформацию: развиваются интегрированные среды, основанные на алгоритмических языках, и растет применение универсальных математических систем (Maple, Mathematica, MATLAB, MatCad и др.). Эти системы имеют дружественный интерфейс, реализуют множество стандартных и специальных математических операций, снабжены мощными графическими средствами и обладают собственными языками программирования. Все это предоставляет широкие возможности для эффективной работы специалистов разных профилей, о чем говорит активное применение математических пакетов в научных исследованиях и в преподавании. С помощью этих пакетов проще готовить и выполнять задания, устраивать демонстрации и гораздо быстрее решать исследовательские и инженерные задачи.

Конечным продуктом исследования выступают публикации, подготовка, распространение и использование которых в настоящее время требует квалифицированного применения компьютера. Это касается редактирования текста, изготовления графических материалов, ведения библиографии, размещения электронных версий в Интернет, поиска статей и их просмотра. Де-факто сейчас стандартными системами подготовки научно-технических публикаций являются различные реализации пакета TeX и текстовый редактор Word. Кроме того, необходимы минимальные знания о стандартных форматах файлов, конверторах, программах и утилитах, используемых при подготовке публикаций.

Математические пакеты Maple и MATLAB — интеллектуальные лидеры в своих классах и образцы, определяющие развитие компьютерной математики. Компьютерная алгебра Maple вошла составной частью в ряд современных пакетов, численный анализ от MATLAB и наборы инструментов (Toolboxes) уникальны. Сами пакеты постоянно совершенствуются, развивая аппарат и пополняя ресурсы. Пакет Maple и вычислительная среда MATLAB — мощные и хорошо организованные системы, надежные и простые в работе. Освоение даже части их возможностей даст несомненный эффект, а по мере накопления опыта придет настоящая эффективность от взаимодействия с ними.

В заключение, отметим, что пользователь пакетов компьютерной математики должен иметь представление об основных численных методах. Вообще говоря, появление современных вычислительных систем значительно облегчает доступ к компьютеру непрофессионалам в области программирования, и поддерживает постоянное стремление к их усовершенствованию и освоению новых компьютерных технологий.

Список литературы

1. Дьяконов В.П. Справочник по применению системы PC MATLAB. — М.: «Физматлит» , 1993. — С. 112. — ISBN 5-02-015101-7

2. Дьяконов В.П. Компьютерная математика. Теория и практика. — СПб: «Питер» , 1999, 2001. — С. 1296. — ISBN 5-89251-065-4

3. Дьяконов В.П. MATLAB 5 — система символьной математики. — М.: «Нолидж» , 1999. — С. 640. — ISBN 5-89251-069-7

4. Дьяконов В.П., Абраменкова И.В. MATLAB. Обработка сигналов и изображений. Специальный справочник. — СПб.: «Питер» , 2002. — С. 608. — ISBN 5-318-00667-608

5. Дьяконов В.П., Круглов В.В. MATLAB. Анализ, идентификация и моделирование систем. Специальный справочник. — СПб.: «Питер» , 2002. — С. 448. — ISBN 5-318-00359-1

6. Дьяконов В. П. Simulink 4. Специальный справочник. — СПб.: «Питер» , 2002. — С. 528. — ISBN 5-318-00551-9

7. Дьяконов В . П . MATLAB 6/6.1/6.5 + Simulink 4/5. Основы применения. Полное руководство пользователя. — Москва.: «СОЛОН-Пресс» , 2002. — С. 768. — ISBN 5-98003-007-7

8. Дьяконов В.П. MATLAB 6/6.1/6.5 + Simulink 4/5 в математике и моделировании. Основы применения. Полное руководство пользователя. — Москва.: «СОЛОН-Пресс» , 2003. — С. 576. — ISBN 5-93455-177-9

9. Дьяконов В . П . MATLAB 6.0/6.1/6.5/6.5+SP1 + Simulink 4/5. Обработка сигналов и изображений. Полное руководство пользователя. — Москва.: «СОЛОН-Пресс» , 2005. — С. 592. — ISBN 5-93003-158-8

10. Дьяконов В . П . MATLAB 6.5/7.0 + Simulink 5/6. Основы применения. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2005. — С. 800. — ISBN 5-98003-181-2

11. Дьяконов В.П. MATLAB 6.5/7.0 + Simulink 5/6 в математике и моделировании. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2005. — С. 576. — ISBN 5-98003-209-6

12. Дьяконов В . П . MATLAB 6.5/7.0 + Simulink 5/6. Обработка сигналов и проектирование фильтров. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2005. — С. 576. — ISBN 5-98003-206-1

13. Дьяконов В . П . MATLAB 6.5/7.0/7 SP1 + Simulink 5/6. Работа с изображениями и видеопотоками. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2005. — С. 400. — ISBN 5-98003-205-3

14. Дьяконов В . П . MATLAB 6.5/7.0/7 SP1/7 SP2 + Simulink 5/6. Инструменты искусственного интеллекта и биоинформатики. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2005. — С. 456. — ISBN 5-98003-255-X

15. Дьяконов В . П . MATLAB R2006/2007/2008 + Simulink 5/6/7. Основы применения. Изд-е 2-е, переработанное и дополненное. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2008. — С. 800. — ISBN 978-5-91359-042-8

16. Дьяконов В.П. MATLAB 7.*/R2006/2007. Самоучитель. — Москва: «ДМК-Пресс» , 2008. — С. 768. — ISBN 978-5-94074-424-5

17. Дьяконов В.П. SIMULINK 5/6/7. Самоучитель. — Москва: «ДМК-Пресс» , 2008. — С. 784. — ISBN 978-5-94074-423-8

18. Дьяконов В.П. Вейвлеты. От теории к практике. Полное руководство пользователя. Изд-е 2-е переработанное и дополненное. — Москва: «СОЛОН-Пресс» , 2004. — С. 400. — ISBN 5-98003-171-5

19. Чарльз Генри Эдвардс, Дэвид Э. Пенни Дифференциальные уравнения и проблема собственных значений: моделирование и вычисление с помощью Mathematica, Maple и MATLAB = Differential Equations and Boundary Value Problems: Computing and Modeling. — 3- е изд . — М .: « Вильямс » , 2007. — ISBN 978-5-8459-1166-7

20. Алексеев Е.Р., Чеснокова О.В MATLAB 7. Самоучитель.. — Пресс , 2005. — С. 464.

21. Курбатова Екатерина Анатольевна MATLAB 7. Самоучитель. — М.: «Диалектика» , 2005. — С. 256. — ISBN 5-8459-0904-X

22. Джон Г. Мэтьюз, Куртис Д. Финк Численные методы. Использование MATLAB = Numerical Methods: Using MATLAB. — 3- е изд . — М .: « Вильямс » , 2001. — С . 720. — ISBN 0-13-270042-5 u

Аналитические методы решения уравнений в частных производных

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К курсовой работе по дисциплине

«ЧИСЛЕННЫЕ МЕТОДЫ»

Рецензент – доцент В.В. Луценко

Составитель Бондаренко А.И.

Методические указания к курсовой работе по дисциплине «Численные методы»/ Сост. А.И. Бондаренко; Шахтинский ин-т (филиал) ЮРГТУ (НПИ). – Новочеркасск: ЮРГТУ, 2008. — 12 с.

Методические указания содержат теоретический материал, примеры выполнения и требования к оформлению курсовой работы по дисциплине «Численные методы».

Предназначены для студентов второго курса специальностей 230201«Информационные системы и технологии» и 0808001 «Прикладная информатика».

© Шахтинский институт ЮРГТУ, 2008

© Бондаренко А.И., 2008

ВВЕДЕНИЕ

Изучение различных процессов требует наряду с глубоким пониманием физики происходящих явлений совершенного владения современными методами вычислительной математики.

Обычно математическая модель записывается в форме как угодно сложных математических структур и, как правило, получить аналитическое решение такой задачи не удаётся. Приходится использовать численные методы вычислительной математики, реализация которых на ЭВМ требует соответствующего программного обеспечения. Результаты моделирования объекта на ЭВМ позволяют “проиграть” его поведение в самых разных, под­час экстремальных условиях. Значение такого вычислительного экспери­мента трудно переоценить, особенно если натурный эксперимент опасен, дорог или просто невозможен.

Большинство физических процессов можно сформулировать на языке дифференциальных уравнений с частными производными. Производные в этих уравнениях описывают важнейшие физические величины: скорость, ускорение, силу, температуру, трение, ток, потенциал и т.д.). Многие из таких уравнений не имеют аналитического решения и, чтобы их решить, приходится прибегать к численным методам.

В курсовой работе рассматривается одно из самых важных уравнений математической физики — уравнение Лапласа на примере решения задачи Дирихле в заданной плоской области. Отсутствие аналитического решения поставленной задачи требует выбора численного метода и его реализации на ЭВМ.

Курсовая работа является завершающим этапом изучения курса “Численные методы”. Цель курсовой работы:

· систематизация, закрепление и расширение теоретических и практических знаний по компьютерному моделированию типовых вычислительных алгоритмов и анализа полученной информации;

· выявление степени подготовленности студентов к самостоятельной работе в ходе решения поставленных задач.

Аналитические методы решения уравнений в частных производных

Существует целый арсенал методов для решения уравнений в частных производных. Перечислим некоторые аналитические методы решения таких уравнений.

Метод разделения переменных. Уравнение с частными производными с n независимыми переменными сводится к n обыкновенным дифференциальным уравнениям. Решение краевых задач для уравнения Лапласа может быть найдено методом разделения переменных (методом Фурье) лишь для простейших областей (круг, прямоугольник, шар цилиндр и др.).

Метод преобразования координат. Исходное уравнение с частными производными сводится к обыкновенному дифференциальному уравнению или к другому, более простому уравнению с частными производными с помощью соответствующего преобразования координат (например, поворота координатных осей и т.п.).

Введение новых переменных. Исходное уравнение с частными производными преобразуется к такому уравнению с частными производными для другой неизвестной функции, которое решается легче, чем исходное.

Метод интегральных уравнений. Уравнение с частными производными сводится к интегральному уравнению (уравнение, в котором неизвестная функция стоит под знаком интеграла).

Вариационные методы. Вместо уравнения с частными производными решается некоторая задача минимизации. Оказывается, что функция, доставляющая минимум некоторому выражению, является решением исходного уравнения.

Метод разложения по собственным функциям. Эти собственные функции находятся как решения так называемой задачи на собственные значения, которые соответствуют исходной задаче для уравнения с частными производными.

Метод функций Грина. Начальные и граничные условия заменяются системой простейших источников, и задача решается для каждого простейшего источника. Полное решение исходной задачи получается в результате суммирования решений для элементарных источников.

Содержание:

1. Правила решения аналитических уравнений
2. Решение дифференциального уравнения

Дифференциальным уравнением называется уравнение, связывающее независимую переменную , неизвестную функцию этой независимой переменной и ее производные

где — функция указанных аргументов, заданная в некоторой области их изменения.

Правила решения аналитических уравнений

Порядком дифференциального уравнения называется порядок старшей Производной, входящей в уравнение.

Уравнение (1.1) является уравнением л-го порядка, уравнения могут быть записаны в виде дифференциального уравнения первого порядка:

а уравнения (В.3)-(В.7) — в виде дифференциального уравнения второго порядка:

где — заданные величины, — известная функция.

Если в соотношении (1.1) функция Fтакова, что его можно представить в виде

то уравнение называется ОДУ -го порядка, разрешенным относительно старшей производной.

В Уравнения (В.1)-(В.7) могут быть записаны в форме (1.4), а например, уравнение — нет; оно относится к типу уравнений, не разрешенных относительно старшей производной.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Уравнение называется линейным, если функция F линейна относительно искомой функции и ее производных, то есть если уравнение может быть записано в виде

где — известные функции.

Если все функции не зависят от то есть , то уравнение

называется линейным уравнением с постоянными коэффициентами.

Уравнения (В.1)-(В.7) относятся к типу (1.6).

Уравнение

называется однородным уравнением, соответствующим неоднородному уравнению (1.5).

Уравнения (В.4),(В.5) — однородные, причем уравнение (В.4) является однородным уравнением, соответствующим неоднородному уравнению (В.З). Таким образом, однородное уравнение получится из неоднородного, если положить .

Решение дифференциального уравнения

Решением дифференциального уравнения n-го порядка называется функция непрерывная на некотором интервале (а,Ь) вместе со своими про; изводными до -го порядка включительно, имеющая производную и такая, что подстановка в уравнение обращает его в тождество.

Рассмотрим, например, функцию где С — произвольная постоянная. Путем непосредственной подстановки этой функции в уравнения можно убедиться в том, что она является их решением. Аналогично, функции и вообще — произвольные постоянные, являются решениями уравнения

Возможно вам будут полезны данные страницы:

Отметим еще, что процедура решения простейшего дифференциального уравнения означает нахождение функции по ее производной, то есть сводится к нахождению неопределенного интедеала Данный факт и приведенные примеры показывают, что дифференциальные уравнения имеют бесконечные множества решений.

Вернемся к уравнению (В.6). Его решение можно найти непосредственно методами математического анализа. Действительно, из уравнения следует

Таким образом, решения уравнения (В.6) образуют совокупность функций, зависящую от двух произвольных постоянных . Конкретные значения произвольных постоянных определяются начальной скоростью и начальным положением , которые позволят выбрать из указанной совокупности конкретное решение. В результате может быть найден закон движения тела, брошенного вертикально вверх.

График решения дифференциального уравнения называется интегральной кривой. Совокупность интегральных кривых, зависящая от набора произвольных постоянных, называется семейством интегральных кривых.

Например, решения уравнения (В.6) образуют двухпараметрическое семейство парабол каждая из которых является интегральной кривой.