Алгоритмы поиска в строке
Время на прочтение
4 мин
Количество просмотров 176K
Постановка задачи поиска в строке
Часто приходится сталкиваться со специфическим поиском, так называемым поиском строки (поиском в строке). Пусть есть некоторый текст Т и слово (или образ) W. Необходимо найти первое вхождение этого слова в указанном тексте. Это действие типично для любых систем обработки текстов. (Элементы массивов Т и W – символы некоторого конечного алфавита – например, {0, 1}, или {a, …, z}, или {а, …, я}.)
Наиболее типичным приложением такой задачи является документальный поиск: задан фонд документов, состоящих из последовательности библиографических ссылок, каждая ссылка сопровождается «дескриптором», указывающим тему соответствующей ссылки. Надо найти некоторые ключевые слова, встречающиеся среди дескрипторов. Мог бы иметь место, например, запрос «Программирование» и «Java». Такой запрос можно трактовать следующим образом: существуют ли статьи, обладающие дескрипторами «Программирование» и «Java».
Поиск строки формально определяется следующим образом. Пусть задан массив Т из N элементов и массив W из M элементов, причем 0<M≤N. Поиск строки обнаруживает первое вхождение W в Т, результатом будем считать индекс i, указывающий на первое с начала строки (с начала массива Т) совпадение с образом (словом).
Пример. Требуется найти все вхождения образца W = abaa в текст T=abcabaabcabca.
Образец входит в текст только один раз, со сдвигом S=3, индекс i=4.
Алгоритм прямого поиска
Идея алгоритма:
1. I=1,
2. сравнить I-й символ массива T с первым символом массива W,
3. совпадение → сравнить вторые символы и так далее,
4. несовпадение → I:=I+1 и переход на пункт 2,
Условие окончания алгоритма:
1. подряд М сравнений удачны,
2. I+M>N, то есть слово не найдено.
Сложность алгоритма:
Худший случай. Пусть массив T→{AAA….AAAB}, длина │T│=N, образец W→{A….AB}, длина │W│=M. Очевидно, что для обнаружения совпадения в конце строки потребуется произвести порядка N*M сравнений, то есть O(N*M).
Недостатки алгоритма:
1. высокая сложность — O(N*M), в худшем случае – Θ((N-M+1)*M);
2. после несовпадения просмотр всегда начинается с первого символа образца и поэтому может включать символы T, которые ранее уже просматривались (если строка читается из вторичной памяти, то такие возвраты занимают много времени);
3. информация о тексте T, получаемая при проверке данного сдвига S, никак не используется при проверке последующих сдвигов.
Алгоритм Д. Кнута, Д. Мориса и В. Пратта (КМП-поиск)
Алгоритм КМП-поиска фактически требует только порядка N сравнений даже в самом плохом случае.
Пример.
(Символы, подвергшиеся сравнению, подчеркнуты.)
После частичного совпадения начальной части образа W с соответствующими символами строки Т мы фактически знаем пройденную часть строки и может «вычислить» некоторые сведения (на основе самого образа W), с помощью которых потом быстро продвинемся по тексту.
Идея КМП-поиска – при каждом несовпадении двух символов текста и образа образ сдвигается на все пройденное расстояние, так как меньшие сдвиги не могут привести к полному совпадению.
Особенности КМП-поиска:
1. требуется порядка (N+M) сравнений символов для получения результата;
2. схема КМП-поиска дает подлинный выигрыш только тогда, когда неудаче предшествовало некоторое число совпадений. Лишь в этом случае образ сдвигается более чем на единицу. К несчастью совпадения встречаются значительно реже чем несовпадения. Поэтому выигрыш от КМП-поиска в большинстве случаев текстов весьма незначителен.
Алгоритм Р. Боуера и Д. Мура (БМ-поиск)
На практике алгоритм БМ-поиска наиболее эффективен, если образец W длинный, а мощность алфавита достаточно велика.
Идея БМ-поиска – сравнение символов начинается с конца образца, а не с начала, то есть сравнение отдельных символов происходит справа налево. Затем с помощью некоторой эвристической процедуры вычисляется величина сдвига вправо s. И снова производится сравнение символов, начиная с конца образца.
Этот метод не только улучшает обработку самого плохого случая, но и даёт выигрыш в промежуточных ситуациях.
Почти всегда, кроме специально построенных примеров, БМ-поиск требует значительно меньше N сравнений. В самых же благоприятных обстоятельствах, когда последний символ образца всегда попадает на несовпадающий символ текста, число сравнений равно (N / M), в худшем же случае – О((N-M+1)*M+ p), где p – мощность алфавита.
Алгоритм Рабина-Карпа (РК-поиск)
Пусть алфавит D={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, то есть каждый символ в алфавите есть d–ичная цифра, где d=│D│.
Пример. Пусть образец имеет вид W = 3 1 4 1 5
Вычисляем значения чисел из окна длины |W|=5 по mod q, q — простое число.
23590(mod 13)=8, 35902(mod 13)=9, 59023(mod 13)=9, …
k1=314157(mod 13) – вхождение образца,
k2=673997(mod 13) – холостое срабатывание.
Из равенства ki= kj (mod q) не следует, что ki= kj (например, 31415=67399(mod 13), но это не значит, что 31415=67399). Если ki= kj (mod q), то ещё надо проверить, совпадают ли строки W[1…m] и T[s+1…s+m] на самом деле.
Если простое число q достаточно велико, то дополнительные затраты на анализ холостых срабатываний будут невелики.
В худшем случае время работы алгоритма РК — Θ((N-M+1)*M), в среднем же он работает достаточно быстро – за время О(N+M).
Пример: Сколько холостых срабатываний k сделает алгоритм РК, если
q= 11, 13, 17. Пусть W={2 6}
26 mod 11=4 → k =3 холостых срабатывания,
26 mod 13=0 → k =1 холостое срабатывание,
26 mod 17=9 → k =0 холостых срабатываний.
Очевидно, что количество холостых срабатываний k является функцией от величины простого числа q (если функция обработки образца mod q) и, в общем случае, от вида функции для обработки образца W и текста Т.
Мы начнем с наивного алгоритма текстового поиска, который является наиболее интуитивным и помогает обнаружить другие сложные проблемы, связанные с этой задачей.
2.1. Вспомогательные методы
Прежде чем мы начнем, давайте определим простые методы вычисления простых чисел, которые мы используем в алгоритме Рабина Карпа:
public static long getBiggerPrime(int m) {
BigInteger prime = BigInteger.probablePrime(getNumberOfBits(m) + 1, new Random());
return prime.longValue();
}
private static int getNumberOfBits(int number) {
return Integer.SIZE - Integer.numberOfLeadingZeros(number);
}2.2. Простой текстовый поиск
Название этого алгоритма описывает его лучше, чем любое другое объяснение. Это наиболее естественное решение:
public static int simpleTextSearch(char[] pattern, char[] text) {
int patternSize = pattern.length;
int textSize = text.length;
int i = 0;
while ((i + patternSize) <= textSize) {
int j = 0;
while (text[i + j] == pattern[j]) {
j += 1;
if (j >= patternSize)
return i;
}
i += 1;
}
return -1;
}Идея этого алгоритма проста: переберите текст и, если есть совпадение для первой буквы шаблона, проверьте, все ли буквы шаблона соответствуют тексту.
Еслиm — это количество букв в шаблоне, аn — это количество букв в тексте, временная сложность этого алгоритма составляетO(m(n-m + 1)).
Наихудший сценарий имеет место в случае, когдаString имеет много частичных вхождений:
Text: baeldunbaeldunbaeldunbaeldun
Pattern: example2.3. Алгоритм Рабина Карпа
Как упомянуто выше, алгоритм простого текстового поиска очень неэффективен, когда шаблоны длинные и когда в шаблоне много повторяющихся элементов.
Идея алгоритма Рабина Карпа заключается в использовании хеширования для поиска шаблона в тексте. В начале алгоритма нам нужно вычислить хэш шаблона, который позже будет использован в алгоритме. Этот процесс называется вычислением отпечатка пальца, и мы можем найти подробное объяснениеhere.
Важным моментом в этапе предварительной обработки является то, что его временная сложность составляетO(m), а итерация по тексту займетO(n), что дает временную сложность всего алгоритмаO(m+n).
Код алгоритма:
public static int RabinKarpMethod(char[] pattern, char[] text) {
int patternSize = pattern.length;
int textSize = text.length;
long prime = getBiggerPrime(patternSize);
long r = 1;
for (int i = 0; i < patternSize - 1; i++) {
r *= 2;
r = r % prime;
}
long[] t = new long[textSize];
t[0] = 0;
long pfinger = 0;
for (int j = 0; j < patternSize; j++) {
t[0] = (2 * t[0] + text[j]) % prime;
pfinger = (2 * pfinger + pattern[j]) % prime;
}
int i = 0;
boolean passed = false;
int diff = textSize - patternSize;
for (i = 0; i <= diff; i++) {
if (t[i] == pfinger) {
passed = true;
for (int k = 0; k < patternSize; k++) {
if (text[i + k] != pattern[k]) {
passed = false;
break;
}
}
if (passed) {
return i;
}
}
if (i < diff) {
long value = 2 * (t[i] - r * text[i]) + text[i + patternSize];
t[i + 1] = ((value % prime) + prime) % prime;
}
}
return -1;
}В худшем случае временная сложность этого алгоритма составляетO(m(n-m+1)). Однако в среднем этот алгоритм имеет временную сложностьO(n+m).
Кроме того, существует версия алгоритма Монте-Карло, которая работает быстрее, но может привести к неправильным совпадениям (ложным срабатываниям).
2.4 Knuth-Morris-Pratt Algorithm
В алгоритме простого текстового поиска мы увидели, как алгоритм может быть медленным, если есть много частей текста, которые соответствуют шаблону.
Идея алгоритма Кнута-Морриса-Пратта заключается в расчете таблицы сдвигов, которая предоставляет нам информацию, в которой мы должны искать кандидатов-паттернов. Мы можем узнать больше о таблице сдвигаhere.
Java-реализация алгоритма KMP:
public static int KnuthMorrisPrattSearch(char[] pattern, char[] text) {
int patternSize = pattern.length;
int textSize = text.length;
int i = 0, j = 0;
int[] shift = KnuthMorrisPrattShift(pattern);
while ((i + patternSize) <= textSize) {
while (text[i + j] == pattern[j]) {
j += 1;
if (j >= patternSize)
return i;
}
if (j > 0) {
i += shift[j - 1];
j = Math.max(j - shift[j - 1], 0);
} else {
i++;
j = 0;
}
}
return -1;
}А вот как мы рассчитываем таблицу сдвигов:
public static int[] KnuthMorrisPrattShift(char[] pattern) {
int patternSize = pattern.length;
int[] shift = new int[patternSize];
shift[0] = 1;
int i = 1, j = 0;
while ((i + j) < patternSize) {
if (pattern[i + j] == pattern[j]) {
shift[i + j] = i;
j++;
} else {
if (j == 0)
shift[i] = i + 1;
if (j > 0) {
i = i + shift[j - 1];
j = Math.max(j - shift[j - 1], 0);
} else {
i = i + 1;
j = 0;
}
}
}
return shift;
}Временная сложность этого алгоритма также составляетO(m+n).
2.5. Простой алгоритм Бойера-Мура
Два ученых, Бойер и Мур, пришли с другой идеей. Почему бы не сравнить шаблон с текстом справа налево, а не слева направо, сохраняя при этом направление смещения:
public static int BoyerMooreHorspoolSimpleSearch(char[] pattern, char[] text) {
int patternSize = pattern.length;
int textSize = text.length;
int i = 0, j = 0;
while ((i + patternSize) <= textSize) {
j = patternSize - 1;
while (text[i + j] == pattern[j]) {
j--;
if (j < 0)
return i;
}
i++;
}
return -1;
}Как и ожидалось, это займетO(m * n) времени. Но этот алгоритм привел к реализации вхождения и эвристики соответствия, что значительно ускоряет алгоритм. Мы можем найти ещеhere.
2.6. Алгоритм Бойера-Мура-Хорспула
Существует много вариантов эвристической реализации алгоритма Бойера-Мура, и самым простым из них является вариант Хорсула.
Эта версия алгоритма называется Бойер-Мур-Хорспул, и эта вариация решила проблему отрицательных сдвигов (о проблеме отрицательных сдвигов можно прочитать в описании алгоритма Бойера-Мура).
Как и алгоритм Бойера-Мура, временная сложность наихудшего сценария составляетO(m * n), а средняя сложность — O (n). Использование пространства не зависит от размера шаблона, а только от размера алфавита, который равен 256, поскольку это максимальное значение символа ASCII в английском алфавите:
public static int BoyerMooreHorspoolSearch(char[] pattern, char[] text) {
int shift[] = new int[256];
for (int k = 0; k < 256; k++) {
shift[k] = pattern.length;
}
for (int k = 0; k < pattern.length - 1; k++){
shift[pattern[k]] = pattern.length - 1 - k;
}
int i = 0, j = 0;
while ((i + pattern.length) <= text.length) {
j = pattern.length - 1;
while (text[i + j] == pattern[j]) {
j -= 1;
if (j < 0)
return i;
}
i = i + shift[text[i + pattern.length - 1]];
}
return -1;
}Поиск подстроки в строке (англ. String searching algorithm) — класс алгоритмов над строками, которые позволяют найти паттерн (pattern) в тексте (text).
Содержание
- 1 Классификация алгоритмов поиска подстроки в строке
- 1.1 Сравнение — «чёрный ящик»
- 1.2 По порядку сравнения паттерна в тексте
- 1.2.1 Прямой
- 1.2.2 Обратный
- 1.2.3 Сравнение в необычном порядке
- 1.3 По количеству поисковых шаблонов
- 1.4 По необходимости препроцессинга текста
- 2 Сравнение алгоритмов
- 3 Примечания
- 4 Источники информации
Классификация алгоритмов поиска подстроки в строке
Сравнение — «чёрный ящик»
Во всех алгоритмах этого типа сравнение является «чёрным ящиком» для программиста.
Преимущества:
- позволяет использовать стандартные функции сравнения участков памяти (man *cmp(3)), которые, зачастую, оптимизированы под конкретное железо.
Недостатки:
- не выдается точка, в которой произошло несовпадение.
По порядку сравнения паттерна в тексте
Прямой
Преимущества:
- отсутствие регрессии на «плохих» данных.
Недостатки:
- не самая хорошая средняя асимптотическая сложность.
Обратный
Паттерн движется по тексту слева направо, но сравнение подстрок происходит справа налево.
Преимущества:
- при несовпадении позволяет перемещать паттерн по строке сразу на несколько символов.
Недостатки:
- производительность сильно зависит от данных.
Сравнение в необычном порядке
Специфические алгоритмы, основанные, как правило, на некоторых эмпирических наблюдениях над словарём.[1]
По количеству поисковых шаблонов
Сколько поисковых шаблонов может обработать алгоритм за один раз.
- один шаблон (англ. single pattern algorithms)
- конечное количество шаблонов (англ. finite set of patterns)
- бесконечное количество шаблонов (англ. infinite number of patterns) (см. Теория формальных языков)
По необходимости препроцессинга текста
Виды препроцессинга:
- Префикс-функция
- Z-функция
- Бор
- Суффиксный массив
Алгоритмы, использующие препроцессинг — одни из самых быстрых в этом классе.
Сравнение алгоритмов
- — размер алфавита
- — длина текста
- — длина паттерна
- — размер ответа(кол-во пар)
- — суммарная длина всех паттернов
| Название | Среднее | Худшее | Препроцессинг | Дополнительная память | Кол-во поисковых шаблонов | Порядок сравнения | Описание |
|---|---|---|---|---|---|---|---|
| Наивный алгоритм (Brute Force algorithm) |
Single | Прямой | Сравнение — «чёрный ящик». Если достаточно мало по сравнению с , то асимптотика будет близкой к , что позволяет использовать его на практике в случаях, когда паттерн много меньше текста (например, Ctrl+F в браузерах) | ||||
| Поиск подстроки в строке с помощью Z-функции | Single | Прямой | |||||
| Алгоритм Рабина-Карпа (Karp-Rabin algorithm) |
Single / Finite | Прямой | Данный алгоритм использует хэширование, что снижает скорость в среднем. Можно модифицировать для поиска нескольких паттернов | ||||
| Алгоритм Кнута-Морриса-Пратта (Knuth-Morris-Pratt algorith) |
Single | Прямой | Использует префикс-функцию | ||||
| Алгоритм Колусси (Colussi algorithm) |
Single | Прямой / Обратный | Оптимизация Алгоритма Кнута-Морриса-Пратта использует как прямой, так и обратный обход | ||||
| Алгоритм Ахо-Корасик (Aho–Corasick string matching algorithm) |
Finite | Прямой | Строит конечный автомат. Можно хранить таблицу переходов как индексный массив (array), а можно как Красно-черное дерево. В последнем случае уменьшится расход памяти, но ухудшится асимптотика | ||||
| Алгоритм Shift-Or | — размер машинного слова | Single | Прямой | Использует тот факт, что в современных процессорах битовые сдвиг и или являются атомарными. Эффективен, если . Иначе деградирует и по памяти, и по сложности | |||
| Алгоритм Бойера-Мура (Boyer-Moore algorithm) |
Single | Обратный | Считается наиболее быстрым из алгоритмов общего назначения. Использует эвристики. Существует большое количество оптимизаций[2] | ||||
| Поиск подстроки в строке с помощью суффиксного массива (Suffix array) |
Single | Прямой | Использует Суффиксный массив. Если использовать Largest common prefix (lcp), то можно уменьшить асимптотику до . Суффиксный массив можно строить стандартными способами или алгоритмом Карккайнена-Сандерса. Асимптотика приведена для построения суффиксного массива с помощью алгоритма Карккайнена-Сандерса | ||||
| Поиск подстроки в строке с помощью суффиксного дерева (Suffix tree) |
Single | Прямой | Позволяет выполнять поиск подстроки в строке за линейное время | ||||
| Алгоритм Апостолико-Крочемора ( Apostolico-Crochemore algorithm) |
Single | Прямой | В худшем случае выполнит сравнений. |
Примечания
- ↑ Например, Алгоритм Райты (англ.)
- ↑ Например, Турбо-алгоритм Бойера-Мура
(Turbo-BM algorithm)
Источники информации
- Википедия — Поиск подстроки
- Википедия — String searching algorithm
- ESMAJ — (англ.) Большое количество разных алгоритмов поиска подстроки в строке. Многие из них в данной статье не описаны.
Аннотация: В лекции рассматриваются основные понятия и алгоритмы, используемые в задачах поиска в тексте и приводятся примеры реализации основных алгоритмов поиска в тексте.
Цель лекции: изучить основные алгоритмы поиска в тексте и научиться решать задачи поиска в тексте на основе алгоритмов прямого поиска; Кнута, Морриса и Пратта; Боуера и Мура.
Работа в текстовом редакторе, поисковые запросы в базе данных, задачи в биоинформатике, лексический анализ программ требуют эффективных алгоритмов работы с текстом. Задачи поиска слова в тексте используются в криптографии, различных разделах физики, сжатии данных, распознавании речи и других сферах человеческой деятельности.
Введем ряд определений, которые будут использоваться далее в изложении материала.
Алфавит – конечное множество символов.
Строка (слово) – это последовательность символов из некоторого алфавита. Длина строки – количество символов в строке.
Строку будем обозначать символами алфавита, например X=x[1]x[2]…x[n] – строка длиной n, где x[i] – i -ый символ строки Х, принадлежащий алфавиту. Строка, не содержащая ни одного символа, называется пустой.
Строка X называется подстрокой строки Y, если найдутся такие строки Z1 и Z2, что Y=Z1XZ2. При этом Z1 называют левым, а Z2 – правым крылом подстроки. Подстрокой может быть и сама строка. Иногда при этом строку X называют вхождением в строку Y. Например, строки hrf и fhr является подстроками строки abhrfhr.
Подстрока X называется префиксом строки Y, если есть такая подстрока Z, что Y=XZ. Причем сама строка является префиксом для себя самой (так как найдется нулевая строка L, что X=XL ). Например, подстрока ab является префиксом строки abcfa.
Подстрока X называется суффиксом строки Y, если есть такая подстрока Z, что Y=ZX. Аналогично, строка является суффиксом себя самой. Например, подстрока bfg является суффиксом строки vsenfbfg.
Поставим задачу поиска подстроки в строке. Пусть задана строка, состоящая из некоторого количества символов. Проверим, входит ли заданная подстрока в данную строку. Если входит, то найдем номер, начиная с какого символа строки, то есть, определим первое вхождение заданной подстроки в исходной строке.
Рассмотрим несколько известных алгоритмов поиска подстроки в строке более подробно.
Прямой поиск
Данный алгоритм еще называется алгоритмом последовательного поиска, он является самым простым и очевидным.
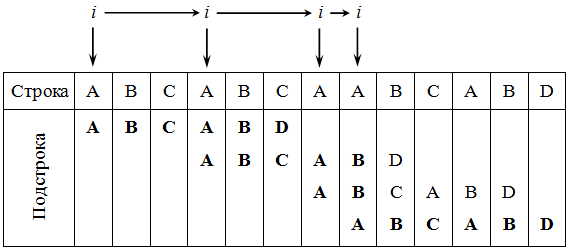
Основная идея алгоритма прямым поиском заключается в посимвольном сравнении строки с подстрокой. В начальный момент происходит сравнение первого символа строки с первым символом подстроки, второго символа строки со вторым символом подстроки и т. д. Если произошло совпадение всех символов, то фиксируется факт нахождения подстроки. В противном случае производится сдвиг подстроки на одну позицию вправо и повторяется посимвольное сравнение, то есть сравнивается второй символ строки с первым символом подстроки, третий символ строки со вторым символом подстроки и т. д. (
рис.
39.1) Символы, которые сравниваются, на рисунке выделены жирным. Рассматриваемые сдвиги подстроки повторяются до тех пор, пока конец подстроки не достиг конца строки или не произошло полное совпадение символов подстроки со строкой, то есть найдется подстрока.
Рис.
39.1.
Демонстрация алгоритма прямого поиска
//Описание функции прямого поиска подстроки в строке
int DirectSearch(char *string, char *substring){
int sl, ssl;
int res = -1;
sl = strlen(string);
ssl = strlen(substring);
if ( sl == 0 )
cout << "Неверно задана строкаn";
else if ( ssl == 0 )
cout << "Неверно задана подстрокаn";
else
for (int i = 0; i < sl - ssl + 1; i++)
for (int j = 0; j < ssl; j++)
if ( substring[j] != string[i+j] )
break;
else if ( j == ssl - 1 ){
res = i;
break;
}
return res;
}
Данный алгоритм является малозатратным и не нуждается в предварительной обработке и в дополнительном пространстве. Большинство сравнений алгоритма прямого поиска являются лишними. Поэтому в худшем случае алгоритм будет малоэффективен, так как его сложность будет пропорциональна O((n-m+1)xm), где n и m – длины строки и подстроки соответственно.
Алгоритм Кнута, Морриса и Пратта
Алгоритм был открыт Д. Кнутом и В. Праттом и, независимо от них, Д. Моррисом. Результаты своей работы они совместно опубликовали в 1977 году. Алгоритм Кнута, Морриса и Пратта (КМП-алгоритм) является алгоритмом, который фактически требует только O(n) сравнений даже в самом худшем случае. Рассматриваемый алгоритм основывается на том, что после частичного совпадения начальной части подстроки с соответствующими символами строки фактически известна пройденная часть строки и можно, вычислить некоторые сведения, с помощью которых затем быстро продвинуться по строке.
Основным отличием алгоритма Кнута, Морриса и Пратта от алгоритма прямого поиска заключается в том, что сдвиг подстроки выполняется не на один символ на каждом шаге алгоритма, а на некоторое переменное количество символов. Следовательно, перед тем как осуществлять очередной сдвиг, необходимо определить величину сдвига. Для повышения эффективности алгоритма необходимо, чтобы сдвиг на каждом шаге был бы как можно большим (
рис.
39.2). На рисунке символы, подвергшиеся сравнению, выделены жирным шрифтом.
Если для произвольной подстроки определить все ее начала, одновременно являющиеся ее концами, и выбрать из них самую длинную (не считая, конечно, саму строку), то такую процедуру принято называть префикс-функцией. В реализации алгоритма Кнута, Морриса и Пратта используется предобработка искомой подстроки, которая заключается в создании префикс-функции на ее основе. При этом используется следующая идея: если префикс (он же суффикс) строки длиной i длиннее одного символа, то он одновременно и префикс подстроки длиной i-1. Таким образом, проверяем префикс предыдущей подстроки, если же тот не подходит, то префикс ее префикса, и т.д. Действуя так, находим наибольший искомый префикс.
Рис.
39.2.
Демонстрация алгоритма Кнута, Морриса и Пратта
//описание функции алгоритма Кнута, Морриса и Пратта
int KMPSearch(char *string, char *substring){
int sl, ssl;
int res = -1;
sl = strlen(string);
ssl = strlen(substring);
if ( sl == 0 )
cout << "Неверно задана строкаn";
else if ( ssl == 0 )
cout << "Неверно задана подстрокаn";
else {
int i, j = 0, k = -1;
int *d;
d = new int[1000];
d[0] = -1;
while ( j < ssl - 1 ) {
while ( k >= 0 && substring[j] != substring[k] )
k = d[k];
j++;
k++;
if ( substring[j] == substring[k] )
d[j] = d[k];
else
d[j] = k;
}
i = 0;
j = 0;
while ( j < ssl && i < sl ){
while ( j >= 0 && string[i] != substring[j] )
j = d[j];
i++;
j++;
}
delete [] d;
res = j == ssl ? i - ssl : -1;
}
return res;
}
Точный анализ рассматриваемого алгоритма весьма сложен. Д. Кнут, Д. Моррис и В. Пратт доказывают, что для данного алгоритма требуется порядка O(m+n) сравнений символов (где n и m – длины строки и подстроки соответственно), что значительно лучше, чем при прямом поиске.
Поиск – распространённое действие, выполняемое в бизнес-приложениях. Под катом лежат реализации известных алгоритмов поиска на Java.
Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
Интересно, хочу попробовать
Программирование на Java – всегда интересный экспириенс. Но куда интереснее работать, применяя правильные для конкретных ситуаций алгоритмы.
Реализуем алгоритмы на Java и проанализируем производительность с помощью параметров временной и пространственной сложности.
Линейный поиск
Линейный или последовательный поиск – простейший алгоритм поиска. Он редко используется из-за своей неэффективности. По сути, это метод полного перебора, и он уступает другим алгоритмам.
У линейного поиска нет предварительных условий к состоянию структуры данных.
Объяснение
Алгоритм ищет элемент в заданной структуре данных, пока не достигнет конца структуры.
При нахождении элемента возвращается его позиция в структуре данных. Если элемент не найден, возвращаем -1.
Реализация
Теперь посмотрим, как реализовать линейный поиск в Java:
public static int linearSearch(int arr[], int elementToSearch) {
for (int index = 0; index < arr.length; index++) {
if (arr[index] == elementToSearch)
return index;
}
return -1;
}
Для проверки используем целочисленный массив:
int index = linearSearch(new int[]{89, 57, 91, 47, 95, 3, 27, 22, 67, 99}, 67);
print(67, index);
Простой метод для вывода результата:
public static void print(int elementToSearch, int index) {
if (index == -1){
System.out.println(elementToSearch + " not found.");
}
else {
System.out.println(elementToSearch + " found at index: " + index);
}
}
Вывод:
67 found at index: 8
Временная сложность
Для получения позиции искомого элемента перебирается набор из N элементов. В худшем сценарии для этого алгоритма искомый элемент оказывается последним в массиве.
В этом случае потребуется N итераций для нахождения элемента.
Следовательно, временная сложность линейного поиска равна O(N).
Пространственная сложность
Этот поиск требует всего одну единицу памяти для хранения искомого элемента. Это не относится к размеру входного массива.
Следовательно, пространственная сложность линейного поиска равна O(1).
Применение
Линейный поиск можно использовать для малого, несортированного набора данных, который не увеличивается в размерах.
Несмотря на простоту, алгоритм не находит применения в проектах из-за линейного увеличения временной сложности.
Двоичный поиск
Двоичный или логарифмический поиск часто используется из-за быстрого времени поиска.
Объяснение
Этот вид поиска использует подход «Разделяй и властвуй», требует предварительной сортировки набора данных.
Алгоритм делит входную коллекцию на равные половины, и с каждой итерацией сравнивает целевой элемент с элементом в середине. Поиск заканчивается при нахождении элемента. Иначе продолжаем искать элемент, разделяя и выбирая соответствующий раздел массива. Целевой элемент сравнивается со средним.
Вот почему важно иметь отсортированную коллекцию при использовании двоичного поиска.
Поиск заканчивается, когда firstIndex (указатель) достигает lastIndex (последнего элемента). Значит мы проверили весь массив Java и не нашли элемента.
Есть два способа реализации этого алгоритма: итеративный и рекурсивный.
Временная и пространственная сложности одинаковы для обоих способов в реализации на Java.
Реализация
Итеративный подход
Посмотрим:
public static int binarySearch(int arr[], int elementToSearch) {
int firstIndex = 0;
int lastIndex = arr.length - 1;
// условие прекращения (элемент не представлен)
while(firstIndex <= lastIndex) {
int middleIndex = (firstIndex + lastIndex) / 2;
// если средний элемент - целевой элемент, вернуть его индекс
if (arr[middleIndex] == elementToSearch) {
return middleIndex;
}
// если средний элемент меньше
// направляем наш индекс в middle+1, убирая первую часть из рассмотрения
else if (arr[middleIndex] < elementToSearch)
firstIndex = middleIndex + 1;
// если средний элемент больше
// направляем наш индекс в middle-1, убирая вторую часть из рассмотрения
else if (arr[middleIndex] > elementToSearch)
lastIndex = middleIndex - 1;
}
return -1;
}
Используем алгоритм:
int index = binarySearch(new int[]{89, 57, 91, 47, 95, 3, 27, 22, 67, 99}, 67);
print(67, index);
Вывод:
67 found at index: 5
Рекурсивный подход
Теперь посмотрим на рекурсивную реализацию:
public static int recursiveBinarySearch(int arr[], int firstElement, int lastElement, int elementToSearch) {
// условие прекращения
if (lastElement >= firstElement) {
int mid = firstElement + (lastElement - firstElement) / 2;
// если средний элемент - целевой элемент, вернуть его индекс
if (arr[mid] == elementToSearch)
return mid;
// если средний элемент больше целевого
// вызываем метод рекурсивно по суженным данным
if (arr[mid] > elementToSearch)
return recursiveBinarySearch(arr, firstElement, mid - 1, elementToSearch);
// также, вызываем метод рекурсивно по суженным данным
return recursiveBinarySearch(arr, mid + 1, lastElement, elementToSearch);
}
return -1;
}
Рекурсивный подход отличается вызовом самого метода при получении нового раздела. В итеративном подходе всякий раз, когда мы определяли новый раздел, мы изменяли первый и последний элементы, повторяя процесс в том же цикле.
Другое отличие – рекурсивные вызовы помещаются в стек и занимают одну единицу пространства за вызов.
Используем алгоритм следующим способом:
int index = binarySearch(new int[]{3, 22, 27, 47, 57, 67, 89, 91, 95, 99}, 0, 10, 67);
print(67, index);
Вывод:
67 found at index: 5
Временная сложность
Временная сложность алгоритма двоичного поиска равна O(log (N)) из-за деления массива пополам. Она превосходит O(N) линейного алгоритма.
Пространственная сложность
Одна единица пространства требуется для хранения искомого элемента. Следовательно, пространственная сложность равна O(1).
Рекурсивный двоичный поиск хранит вызов метода в стеке. В худшем случае пространственная сложность потребует O(log (N)).
Применение
Этот алгоритм используется в большинстве библиотек и используется с отсортированными структурами данных.
Двоичный поиск реализован в методе Arrays.binarySearch Java API.
Алгоритм Кнута – Морриса – Пратта
Алгоритм КМП осуществляет поиск текста по заданному шаблону. Он разработан Дональдом Кнутом, Воном Праттом и Джеймсом Моррисом: отсюда и название.
Объяснение
В этом поиске сначала компилируется заданный шаблон. Компилируя шаблон, мы пытаемся найти префикс и суффикс строки шаблона. Это поможет в случае несоответствия – не придётся искать следующее совпадение с начального индекса.
Вместо этого мы пропускаем часть текстовой строки, которую уже сравнили, и начинаем сравнивать следующую. Необходимая часть определяется по префиксу и суффиксу, поэтому известно, какая часть уже прошла проверку и может быть безопасно пропущена.
КМП работает быстрее алгоритма перебора благодаря пропускам.
Реализация
Итак, пишем метод compilePatternArray(), который позже будет использоваться алгоритмом поиска КМП:
public static int[] compilePatternArray(String pattern) {
int patternLength = pattern.length();
int len = 0;
int i = 1;
int[] compliedPatternArray = new int[patternLength];
compliedPatternArray[0] = 0;
while (i < patternLength) {
if (pattern.charAt(i) == pattern.charAt(len)) {
len++;
compliedPatternArray[i] = len;
i++;
} else {
if (len != 0) {
len = compliedPatternArray[len - 1];
} else {
compliedPatternArray[i] = len;
i++;
}
}
}
System.out.println("Compiled Pattern Array " + Arrays.toString(compliedPatternArray));
return compliedPatternArray;
}
Скомпилированный массив Java можно рассматривать как массив, хранящий шаблон символов. Цель – найти префикс и суффикс в шаблоне. Зная эти элементы, можно избежать сравнения с начала текста после несоответствия и приступать к сравнению следующего символа.
Скомпилированный массив сохраняет позицию предыдущего местонахождения текущего символа в массив шаблонов.
Давайте реализуем сам алгоритм:
public static List<Integer> performKMPSearch(String text, String pattern) {
int[] compliedPatternArray = compilePatternArray(pattern);
int textIndex = 0;
int patternIndex = 0;
List<Integer> foundIndexes = new ArrayList<>();
while (textIndex < text.length()) {
if (pattern.charAt(patternIndex) == text.charAt(textIndex)) {
patternIndex++;
textIndex++;
}
if (patternIndex == pattern.length()) {
foundIndexes.add(textIndex - patternIndex);
patternIndex = compliedPatternArray[patternIndex - 1];
}
else if (textIndex < text.length() && pattern.charAt(patternIndex) != text.charAt(textIndex)) {
if (patternIndex != 0)
patternIndex = compliedPatternArray[patternIndex - 1];
else
textIndex = textIndex + 1;
}
}
return foundIndexes;
}
Здесь мы последовательно сравниваем символы в шаблоне и текстовом массиве. Мы продолжаем двигаться вперёд, пока не получим совпадение. Достижение конца массива при сопоставлении означает нахождение шаблона в тексте.
Но! Есть один момент.
Если обнаружено несоответствие при сравнении двух массивов, индекс символьного массива перемещается в значение compiledPatternArray(). Затем мы переходим к следующему символу в текстовом массиве. КМП превосходит метод грубой силы однократным сравнением текстовых символов при несоответствии.
Запустите алгоритм:
String pattern = "AAABAAA";
String text = "ASBNSAAAAAABAAAAABAAAAAGAHUHDJKDDKSHAAJF";
List<Integer> foundIndexes = KnuthMorrisPrathPatternSearch.performKMPSearch(text, pattern);
if (foundIndexes.isEmpty()) {
System.out.println("Pattern not found in the given text String");
} else {
System.out.println("Pattern found in the given text String at positions: " + .stream().map(Object::toString).collect(Collectors.joining(", ")));
}
В текстовом шаблоне AAABAAA наблюдается и кодируется в массив шаблонов следующий шаблон:
- Шаблон
A(Одиночная A) повторяется в 1 и 4 индексах. - Паттерн
AA(Двойная A) повторяется во 2 и 5 индексах. - Шаблон
AAA(Тройная A) повторяется в индексе 6.
В подтверждение наших расчётов:
Compiled Pattern Array [0, 1, 2, 0, 1, 2, 3] Pattern found in the given text String at positions: 8, 14
Описанный выше шаблон ясно показан в скомпилированном массиве.
С помощью этого массива КМП ищет заданный шаблон в тексте, не возвращаясь в начало текстового массива.
Временная сложность
Для поиска шаблона алгоритму нужно сравнить все элементы в заданном тексте. Необходимое для этого время составляет O(N). Для составления строки шаблона нам нужно проверить каждый символ в шаблоне – это еще одна итерация O(M).
O (M + N) – общее время алгоритма.
Пространственная сложность
O(M) пространства необходимо для хранения скомпилированного шаблона для заданного шаблона размера M.
Применение
Этот алгоритм используется в текстовых инструментах для поиска шаблонов в текстовых файлах.
Поиск прыжками
От двоичного поиска этот алгоритм отличает движение исключительно вперёд. Имейте в виду, что такой поиск требует отсортированной коллекции.
Мы прыгаем вперёд на интервал sqrt(arraylength), пока не достигнем элемента большего, чем текущий элемент или конца массива. При каждом прыжке записывается предыдущий шаг.
Прыжки прекращаются, когда найден элемент больше искомого. Затем запускаем линейный поиск между предыдущим и текущим шагами.
Это уменьшает поле поиска и делает линейный поиск жизнеспособным вариантом.
Реализация
public static int jumpSearch(int[] integers, int elementToSearch) {
int arrayLength = integers.length;
int jumpStep = (int) Math.sqrt(integers.length);
int previousStep = 0;
while (integers[Math.min(jumpStep, arrayLength) - 1] < elementToSearch) {
previousStep = jumpStep;
jumpStep += (int)(Math.sqrt(arrayLength));
if (previousStep >= arrayLength)
return -1;
}
while (integers[previousStep] < elementToSearch) {
previousStep++;
if (previousStep == Math.min(jumpStep, arrayLength))
return -1;
}
if (integers[previousStep] == elementToSearch)
return previousStep;
return -1;
}
Мы начинаем с jumpstep размером с корень квадратный от длины массива и продолжаем прыгать вперёд с тем же размером, пока не найдём элемент, который будет таким же или больше искомого элемента.
Сначала проверяется элемент integers[jumpStep], затем integers[2jumpStep], integers[3jumpStep] и так далее. Проверенный элемент сохраняется в переменной previousStep.
Когда найдено значение, при котором integers[previousStep] < elementToSearch < integers[jumpStep], производится линейный поиск между integers[previousStep] и integers[jumpStep] или элементом большим, чем elementToSearch.
Вот так используется алгоритм:
int index = jumpSearch(new int[]{3, 22, 27, 47, 57, 67, 89, 91, 95, 99}, 67);
print(67, index);
Вывод:
67 found at Index 5
Временная сложность
Поскольку в каждой итерации мы перепрыгиваем на шаг, равный sqrt(arraylength), временная сложность этого поиска составляет O(sqrt (N)).
Пространственная сложность
Искомый элемент занимает одну единицу пространства, поэтому пространственная сложность алгоритма составляет O(1).
Применение
Этот поиск используется поверх бинарного поиска, когда прыжки в обратную сторону затратны.
С ограничением сталкиваются при работе с вращающейся средой. Когда при легком поиске по направлению вперёд многократные прыжки в разных направлениях становятся затратными.
Интерполяционный поиск
Интерполяционный поиск используется для поиска элементов в отсортированном массиве. Он полезен для равномерно распределенных в структуре данных.
При равномерно распределенных данных местонахождение элемента определяется точнее. Тут и вскрывается отличие алгоритма от бинарного поиска, где мы пытаемся найти элемент в середине массива.
Для поиска элементов в массиве алгоритм использует формулы интерполяции. Эффективнее применять эти формула для больших массивов. В противном случае алгоритм работает как линейный поиск.
Реализация
public static int interpolationSearch(int[] integers, int elementToSearch) {
int startIndex = 0;
int lastIndex = (integers.length - 1);
while ((startIndex <= lastIndex) && (elementToSearch >= integers[startIndex]) &&
(elementToSearch <= integers[lastIndex])) {
// используем формулу интерполяции для поиска возможной лучшей позиции для существующего элемента
int pos = startIndex + (((lastIndex-startIndex) /
(integers[lastIndex]-integers[startIndex]))*
(elementToSearch - integers[startIndex]));
if (integers[pos] == elementToSearch)
return pos;
if (integers[pos] < elementToSearch)
startIndex = pos + 1;
else
lastIndex = pos - 1;
}
return -1;
}
Используем алгоритм так:
int index = interpolationSearch(new int[]{1,2,3,4,5,6,7,8}, 6);
print(67, index);
Вывод:
6 found at Index 5
Смотрите, как работают формулы интерполяции, чтобы найти 6:
startIndex = 0 lastIndex = 7 integers[lastIndex] = 8 integers[startIndex] = 1 elementToSearch = 6
Теперь давайте применим эти значения к формулам для оценки индекса элемента поиска:
index=0+(7−0)/(8−1)∗(6−1)=5
Элемент integers[5] равен 6 — это элемент, который мы искали. Индекс для элемента рассчитывается за один шаг из-за равномерной распределенности данных.
Временная сложность
В лучшем случае временная сложность такого алгоритма – O(log log N). При неравномерном распределении элементов сложность сопоставима с временной сложностью линейного алгоритма, которая = O(N).
Пространственная сложность
Алгоритм требует одну единицу пространства для хранения элемента для поиска. Его пространственная сложность = O(1).
Применение
Алгоритм полезно применять для равномерно распределенных данных вроде телефонной книги.
Экспоненциальный поиск
Экспоненциальный поиск используется для поиска элементов путём перехода в экспоненциальные позиции, то есть во вторую степень.
В этом поиске мы пытаемся найти сравнительно меньший диапазон и применяем на нем двоичный алгоритм для поиска элемента.
Для работы алгоритма коллекция должна быть отсортирована.
Реализация
public static int exponentialSearch(int[] integers, int elementToSearch) {
if (integers[0] == elementToSearch)
return 0;
if (integers[integers.length - 1] == elementToSearch)
return integers.length;
int range = 1;
while (range < integers.length && integers[range] <= elementToSearch) {
range = range * 2;
}
return Arrays.binarySearch(integers, range / 2, Math.min(range, integers.length), elementToSearch);
}
Применяем алгоритм Java:
int index = exponentialSearch(new int[]{3, 22, 27, 47, 57, 67, 89, 91, 95, 99}, 67);
print(67, index);
Мы пытаемся найти элемент больше искомого. Зачем? Для минимизации диапазона поиска. Увеличиваем диапазон, умножая его на 2, и снова проверяем, достигли ли мы элемента больше искомого или конца массива. При нахождении элемента мы выходим из цикла. Затем выполняем бинарный поиск с startIndex в качестве range/2 и lastIndex в качестве range.
В нашем случае значение диапазона достигается в элементе 8, а элемент в integers[8] равен 95. Таким образом, диапазон, в котором выполняется бинарный поиск:
startIndex = range/2 = 4 lastIndex = range = 8
При этом вызываем бинарный поиск:
Arrays.binarySearch(integers, 4, 8, 6);
Вывод:
67 found at Index 5
Здесь важно отметить, что можно ускорить умножение на 2, используя оператор левого сдвига range << 1 вместо *.
Временная сложность
В худшем случае временная сложность этого поиска составит O(log (N)).
Пространственная сложность
Итеративный алгоритм двоичного поиска требует O(1) места для хранения искомого элемента.
Для рекурсивного двоичного поиска пространственная сложность становится равной O(log (N)).
Применение
Экспоненциальный поиск используется с большими массивами, когда бинарный поиск затратен. Экспоненциальный поиск разделяет данные на более доступные для поиска разделы.
Заключение
Каждая система содержит набор ограничений и требований. Правильно подобранный алгоритм поиска, учитывающий эти ограничениях, играет определяющую роль в производительности системы.
В этой статье мы рассмотрели работу алгоритмов поиска Java и случаи их применения.
Описанные алгоритмы доступны на Github.
Источник
- 25 самых используемых регулярных выражений в Java
- Создаём приложение с чистой архитектурой на Java 11
- ТОП-10 лучших книг по Java для программистов