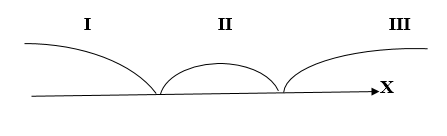
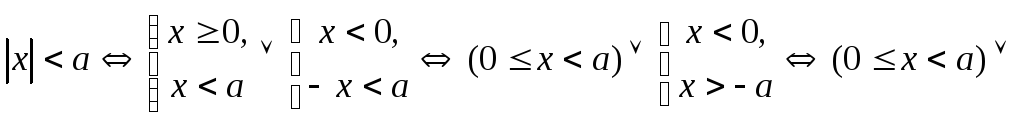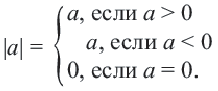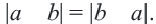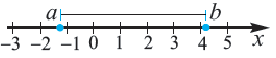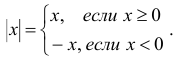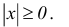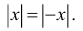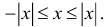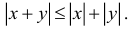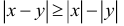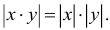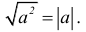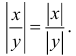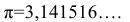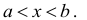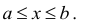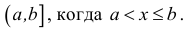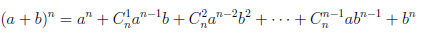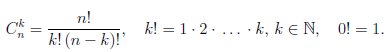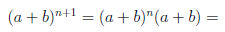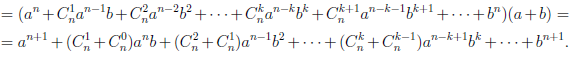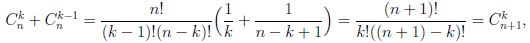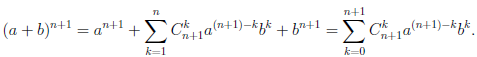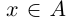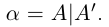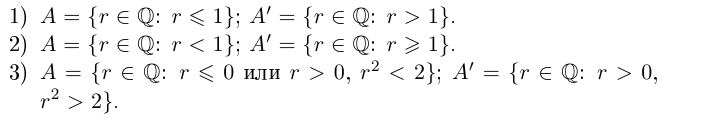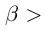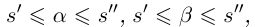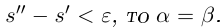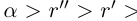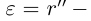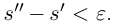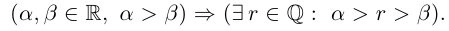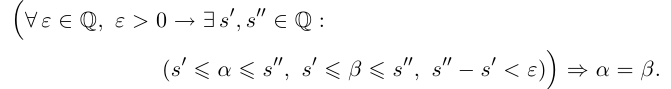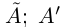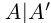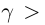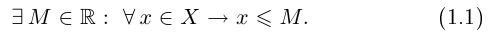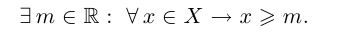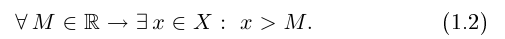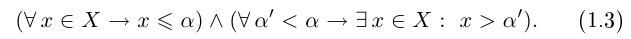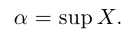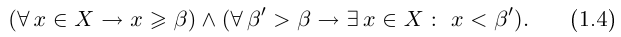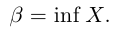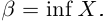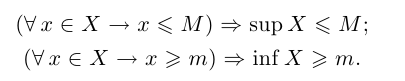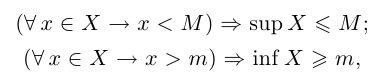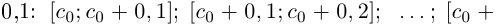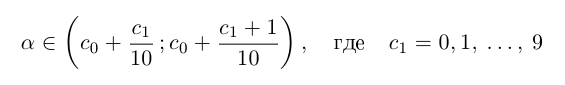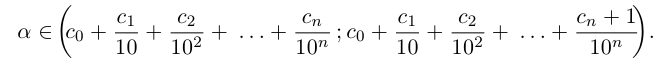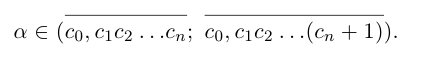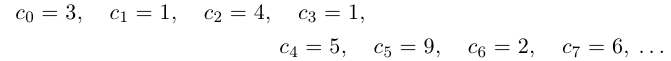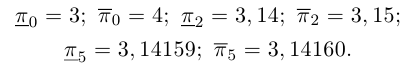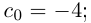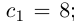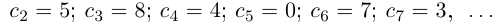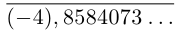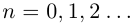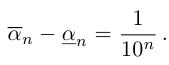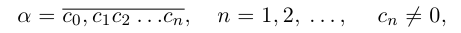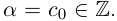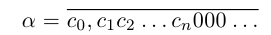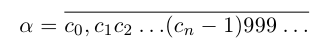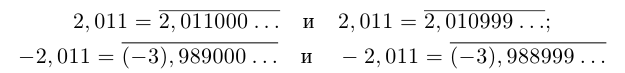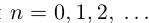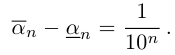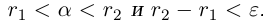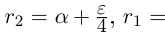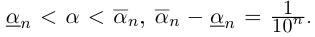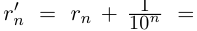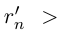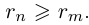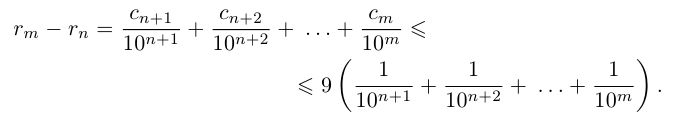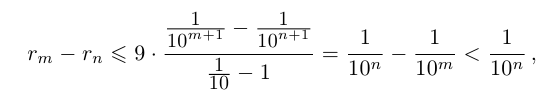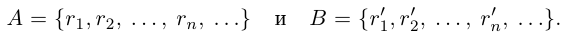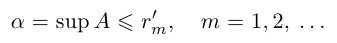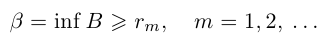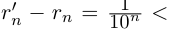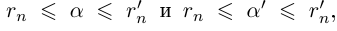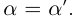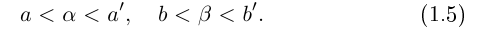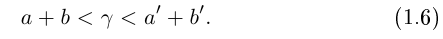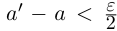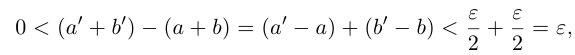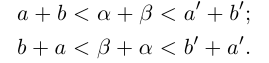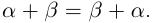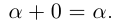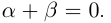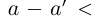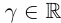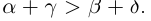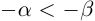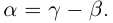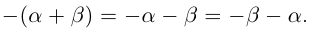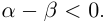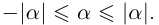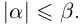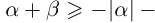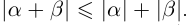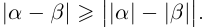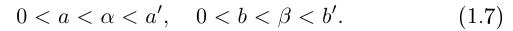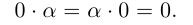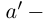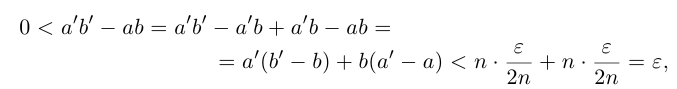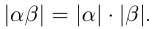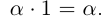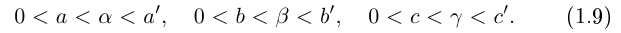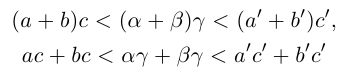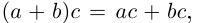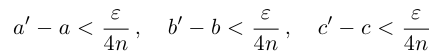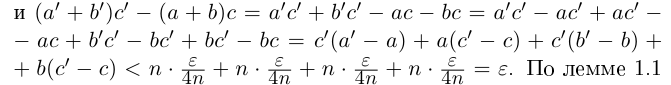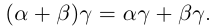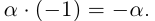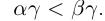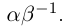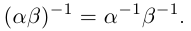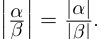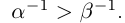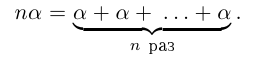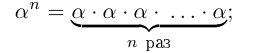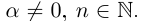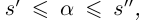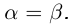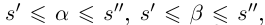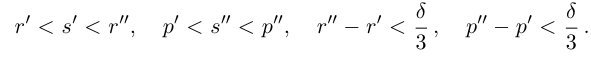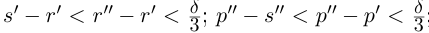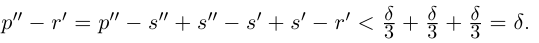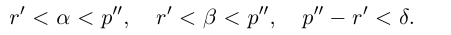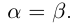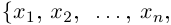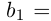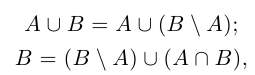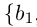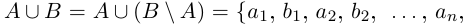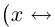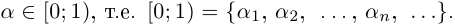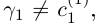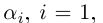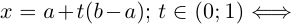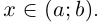The graph of the absolute value function for real numbers
The absolute value of a number may be thought of as its distance from zero.
In mathematics, the absolute value or modulus of a real number 









Generalisations of the absolute value for real numbers occur in a wide variety of mathematical settings. For example, an absolute value is also defined for the complex numbers, the quaternions, ordered rings, fields and vector spaces. The absolute value is closely related to the notions of magnitude, distance, and norm in various mathematical and physical contexts.
Terminology and notation[edit]
In 1806, Jean-Robert Argand introduced the term module, meaning unit of measure in French, specifically for the complex absolute value,[1][2] and it was borrowed into English in 1866 as the Latin equivalent modulus.[1] The term absolute value has been used in this sense from at least 1806 in French[3] and 1857 in English.[4] The notation |x|, with a vertical bar on each side, was introduced by Karl Weierstrass in 1841.[5] Other names for absolute value include numerical value[1] and magnitude.[1] In programming languages and computational software packages, the absolute value of x is generally represented by abs(x), or a similar expression.
The vertical bar notation also appears in a number of other mathematical contexts: for example, when applied to a set, it denotes its cardinality; when applied to a matrix, it denotes its determinant. Vertical bars denote the absolute value only for algebraic objects for which the notion of an absolute value is defined, notably an element of a normed division algebra, for example a real number, a complex number, or a quaternion. A closely related but distinct notation is the use of vertical bars for either the Euclidean norm[6] or sup norm[7] of a vector in 


Definition and properties[edit]
Real numbers[edit]
For any real number 


The absolute value of 



From an analytic geometry point of view, the absolute value of a real number is that number’s distance from zero along the real number line, and more generally the absolute value of the difference of two real numbers (their absolute difference) is the distance between them.[9] The notion of an abstract distance function in mathematics can be seen to be a generalisation of the absolute value of the difference (see «Distance» below).
Since the square root symbol represents the unique positive square root, when applied to a positive number, it follows that
This is equivalent to the definition above, and may be used as an alternative definition of the absolute value of real numbers.[10]
The absolute value has the following four fundamental properties (a, b are real numbers), that are used for generalization of this notion to other domains:
Non-negativity, positive definiteness, and multiplicativity are readily apparent from the definition. To see that subadditivity holds, first note that 








Some additional useful properties are given below. These are either immediate consequences of the definition or implied by the four fundamental properties above.

|
Idempotence (the absolute value of the absolute value is the absolute value) |

|
Evenness (reflection symmetry of the graph) |

|
Identity of indiscernibles (equivalent to positive-definiteness) |

|
Triangle inequality (equivalent to subadditivity) |
 (if (if  ) )
|
Preservation of division (equivalent to multiplicativity) |

|
Reverse triangle inequality (equivalent to subadditivity) |
Two other useful properties concerning inequalities are:
These relations may be used to solve inequalities involving absolute values. For example:
The absolute value, as «distance from zero», is used to define the absolute difference between arbitrary real numbers, the standard metric on the real numbers.
Complex numbers[edit]
Since the complex numbers are not ordered, the definition given at the top for the real absolute value cannot be directly applied to complex numbers. However, the geometric interpretation of the absolute value of a real number as its distance from 0 can be generalised. The absolute value of a complex number is defined by the Euclidean distance of its corresponding point in the complex plane from the origin. This can be computed using the Pythagorean theorem: for any complex number
where 



the Pythagorean addition of 






When a complex number 


Since the product of any complex number 





This generalizes the alternative definition for reals: 
The complex absolute value shares the four fundamental properties given above for the real absolute value. The identity 
Absolute value function[edit]
The graph of the absolute value function for real numbers
The real absolute value function is continuous everywhere. It is differentiable everywhere except for x = 0. It is monotonically decreasing on the interval (−∞, 0] and monotonically increasing on the interval [0, +∞). Since a real number and its opposite have the same absolute value, it is an even function, and is hence not invertible. The real absolute value function is a piecewise linear, convex function.
For both real and complex numbers the absolute value function is idempotent (meaning that the absolute value of any absolute value is itself).
Relationship to the sign function[edit]
The absolute value function of a real number returns its value irrespective of its sign, whereas the sign (or signum) function returns a number’s sign irrespective of its value. The following equations show the relationship between these two functions:
or
and for x ≠ 0,
Derivative[edit]
The real absolute value function has a derivative for every x ≠ 0, but is not differentiable at x = 0. Its derivative for x ≠ 0 is given by the step function:[12][13]
The real absolute value function is an example of a continuous function that achieves a global minimum where the derivative does not exist.
The subdifferential of |x| at x = 0 is the interval [−1, 1].[14]
The complex absolute value function is continuous everywhere but complex differentiable nowhere because it violates the Cauchy–Riemann equations.[12]
The second derivative of |x| with respect to x is zero everywhere except zero, where it does not exist. As a generalised function, the second derivative may be taken as two times the Dirac delta function.
Antiderivative[edit]
The antiderivative (indefinite integral) of the real absolute value function is
where C is an arbitrary constant of integration. This is not a complex antiderivative because complex antiderivatives can only exist for complex-differentiable (holomorphic) functions, which the complex absolute value function is not.
Distance[edit]
The absolute value is closely related to the idea of distance. As noted above, the absolute value of a real or complex number is the distance from that number to the origin, along the real number line, for real numbers, or in the complex plane, for complex numbers, and more generally, the absolute value of the difference of two real or complex numbers is the distance between them.
The standard Euclidean distance between two points
and
in Euclidean n-space is defined as:
This can be seen as a generalisation, since for 

and for 

The above shows that the «absolute value»-distance, for real and complex numbers, agrees with the standard Euclidean distance, which they inherit as a result of considering them as one and two-dimensional Euclidean spaces, respectively.
The properties of the absolute value of the difference of two real or complex numbers: non-negativity, identity of indiscernibles, symmetry and the triangle inequality given above, can be seen to motivate the more general notion of a distance function as follows:
A real valued function d on a set X × X is called a metric (or a distance function) on X, if it satisfies the following four axioms:[15]
Generalizations[edit]
Ordered rings[edit]
The definition of absolute value given for real numbers above can be extended to any ordered ring. That is, if a is an element of an ordered ring R, then the absolute value of a, denoted by |a|, is defined to be:[16]
where −a is the additive inverse of a, 0 is the additive identity, and < and ≥ have the usual meaning with respect to the ordering in the ring.
Fields[edit]
The four fundamental properties of the absolute value for real numbers can be used to generalise the notion of absolute value to an arbitrary field, as follows.
A real-valued function v on a field F is called an absolute value (also a modulus, magnitude, value, or valuation)[17] if it satisfies the following four axioms:
Where 0 denotes the additive identity of F. It follows from positive-definiteness and multiplicativity that v(1) = 1, where 1 denotes the multiplicative identity of F. The real and complex absolute values defined above are examples of absolute values for an arbitrary field.
If v is an absolute value on F, then the function d on F × F, defined by d(a, b) = v(a − b), is a metric and the following are equivalent:
An absolute value which satisfies any (hence all) of the above conditions is said to be non-Archimedean, otherwise it is said to be Archimedean.[18]
Vector spaces[edit]
Again the fundamental properties of the absolute value for real numbers can be used, with a slight modification, to generalise the notion to an arbitrary vector space.
A real-valued function on a vector space V over a field F, represented as ‖ · ‖, is called an absolute value, but more usually a norm, if it satisfies the following axioms:
For all a in F, and v, u in V,
The norm of a vector is also called its length or magnitude.
In the case of Euclidean space 
is a norm called the Euclidean norm. When the real numbers 



The complex absolute value is a special case of the norm in an inner product space, which is identical to the Euclidean norm when the complex plane is identified as the Euclidean plane 
Composition algebras[edit]
Every composition algebra A has an involution x → x* called its conjugation. The product in A of an element x and its conjugate x* is written N(x) = x x* and called the norm of x.
The real numbers 


In general the norm of a composition algebra may be a quadratic form that is not definite and has null vectors. However, as in the case of division algebras, when an element x has a non-zero norm, then x has a multiplicative inverse given by x*/N(x).
See also[edit]
- Least absolute values
Notes[edit]
- ^ a b c d Oxford English Dictionary, Draft Revision, June 2008
- ^ Nahin, O’Connor and Robertson, and functions.Wolfram.com.; for the French sense, see Littré, 1877
- ^ Lazare Nicolas M. Carnot, Mémoire sur la relation qui existe entre les distances respectives de cinq point quelconques pris dans l’espace, p. 105 at Google Books
- ^ James Mill Peirce, A Text-book of Analytic Geometry at Internet Archive. The oldest citation in the 2nd edition of the Oxford English Dictionary is from 1907. The term absolute value is also used in contrast to relative value.
- ^ Nicholas J. Higham, Handbook of writing for the mathematical sciences, SIAM. ISBN 0-89871-420-6, p. 25
- ^ Spivak, Michael (1965). Calculus on Manifolds. Boulder, CO: Westview. p. 1. ISBN 0805390219.
- ^ Munkres, James (1991). Analysis on Manifolds. Boulder, CO: Westview. p. 4. ISBN 0201510359.
- ^ Mendelson, p. 2.
- ^ Smith, Karl (2013). Precalculus: A Functional Approach to Graphing and Problem Solving. Jones & Bartlett Publishers. p. 8. ISBN 978-0-7637-5177-7.
- ^ Stewart, James B. (2001). Calculus: concepts and contexts. Australia: Brooks/Cole. p. A5. ISBN 0-534-37718-1.
- ^ González, Mario O. (1992). Classical Complex Analysis. CRC Press. p. 19. ISBN 9780824784157.
- ^ a b «Weisstein, Eric W. Absolute Value. From MathWorld – A Wolfram Web Resource».
- ^ Bartle and Sherbert, p. 163
- ^ Peter Wriggers, Panagiotis Panatiotopoulos, eds., New Developments in Contact Problems, 1999, ISBN 3-211-83154-1, p. 31–32
- ^ These axioms are not minimal; for instance, non-negativity can be derived from the other three: 0 = d(a, a) ≤ d(a, b) + d(b, a) = 2d(a, b).
- ^ Mac Lane, p. 264.
- ^ Shechter, p. 260. This meaning of valuation is rare. Usually, a valuation is the logarithm of the inverse of an absolute value
- ^ Shechter, pp. 260–261.
References[edit]
- Bartle; Sherbert; Introduction to real analysis (4th ed.), John Wiley & Sons, 2011 ISBN 978-0-471-43331-6.
- Nahin, Paul J.; An Imaginary Tale; Princeton University Press; (hardcover, 1998). ISBN 0-691-02795-1.
- Mac Lane, Saunders, Garrett Birkhoff, Algebra, American Mathematical Soc., 1999. ISBN 978-0-8218-1646-2.
- Mendelson, Elliott, Schaum’s Outline of Beginning Calculus, McGraw-Hill Professional, 2008. ISBN 978-0-07-148754-2.
- O’Connor, J.J. and Robertson, E.F.; «Jean Robert Argand».
- Schechter, Eric; Handbook of Analysis and Its Foundations, pp. 259–263, «Absolute Values», Academic Press (1997) ISBN 0-12-622760-8.
External links[edit]
- «Absolute value». Encyclopedia of Mathematics. EMS Press. 2001 [1994].
- absolute value at PlanetMath.
- Weisstein, Eric W. «Absolute Value». MathWorld.
Определение.Абсолютной величиной(илимодулем) действительного
числа(обозначается
)
называется неотрицательное число,
удовлетворяющее условиям:
Ясно, что всегда
.
(3.1)
Свойства абсолютных величин:
1)
;
2);
3);
4).
Доказательство.1) Если,
тов силу (3.1). Если
,
то.
Первое свойство доказано.
2) Имеем
,
отсюда.
Второе свойство доказано.
3)
,
третье свойство доказано.
Четвертое свойство доказывается так
же, как свойство 3).
Замечание. Свойство 1) распространяется
на любое число слагаемых, свойство 3) –
на любое число сомножителей.
Отметим также, что
,
т.е.худовлетворяет неравенствутогда и только тогда, когда принадлежит
интервалу.
Геометрический смысл модуля действительного
числа состоит в том, что
равен расстоянию от точкихна
числовой прямой до нуля.
§ 4. Понятие числовой последовательности. Бесконечно большая и бесконечно малая последовательности, их свойства
Определение 1. Если каждому значениюn из множества
натуральных чиселставится в соответствие по определенному
закону некоторое действительное число,
то множество занумерованных действительных
чисел называетсячисловой
последовательностью .
– члены последовательности,
–
сокращенная запись последовательности.
Например,.
Определение 2. Пусть даны две
последовательностии
.
Последовательностиназываются соответственно суммой,
разностью, произведением и частным
последовательностейи
.
Определение 3. Последовательностьназываетсяограниченной, если
множество ее членов ограничено, т.е.
существует число,
такое, что.
Последовательностьназываетсяограниченной сверху
(снизу), если существует
числоМ, такое, что.
Если последовательность
неограниченна, то для любого числа
найдется номерnтакой, что.
Ясно, что если последовательность
ограничена только снизу или только
сверху, то она неограниченна. Среди
неограниченных последовательностей
выберем бесконечно большие
последовательности.
Определение 4. Последовательностьназываетсябесконечно большой,
если для любогонайдется номерN,
такой, чтодля всех
.
Всякая бесконечно большая последовательность
неограниченна, но не всякая неограниченная
последовательность бесконечно большая.
Примером этого может служить
последовательность
.
Определение 5. Последовательностьназываетсябесконечно малой,
если для любогонайдется номерN,
такой, чтодля всех
.
Установим основные свойства бесконечно
малых последовательностей.
Теорема 1. Сумма двух бесконечно
малых последовательностей есть бесконечно
малая последовательность.
Доказательство. Пустьи
– бесконечно малые последовательности.
Возьмемпроизвольно и положим
.
По определению 5 длянайдутся номера
и
,
такие, чтодля всех
и
для всех
.
Положим.
Тогда для всехи по определению 5 последовательность
бесконечно
малая. Теорема доказана.
Аналогично доказываются
Теорема 2. Разность двух бесконечно
малых последовательностей есть бесконечно
малая последовательность.
Следствие. Алгебраическая сумма
любого конечного числа бесконечно малых
последовательностей есть бесконечно
малая последовательность.
Теорема 3. Произведение ограниченной
последовательности на бесконечно малую
последовательность есть бесконечно
малая последовательность.
(Можно поручить студентам доказать
теоремы 2, 3 и следствие самостоятельно).
Теорема 4. Всякая бесконечно малая
последовательность ограничена.
Доказательство. Пусть– бесконечно малая последовательность.
Положим.
По определению 5 найдется номерN,
такой, чтодля всех
.
Обозначим.
Тогдадля всехn. Теорема
доказана.
Следствие теорем 3и 4. Произведение
двух (любого конечного числа) бесконечно
малых последовательностей есть бесконечно
малая последовательность.
Теорема 5. Если все члены бесконечно
малой последовательности равны одному
и тому же числус, то.
Доказательство. Предположим
противное, т.е. что.
Возьмем.
По определению 5 найдется номерN,
такой, чтодля всех
,
т.е.для всех
,
а этого не может быть, так какдля всехn. Противоречие
доказывает утверждение теоремы.
Теорема 6. Если– бесконечно большая последовательность,
то–
бесконечно малая последовательность.
Доказательство. Возьмемпроизвольно и положим
.
Тогда по определению 4 найдется номерN, такой, чтодля всех значений
.
Отсюдадля всех
,
т.е.–
бесконечно малая последовательность
по определению 5. Теорема доказана.
Теорема 7. Если–
бесконечно малая последовательность
и все члены этой последовательности
отличны от нуля, то последовательность–
бесконечно большая (доказать
самостоятельно).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Действительные числа
В основе применения математических методов при решении практических задач лежат вычисления и измерения. При счете используются натуральные числа. При делении целого на части натуральных чисел недостаточно. Поэтому вводятся дробные числа. Длину отрезка можно выразить с помощью рационального числа с любой точностью. В теоретических вычислениях приходится рассматривать отрезки, длины которых не выражаются с помощью рациональных чисел. По этой причине вводится понятие иррационального числа. Изменение значений величины в противоположном направлении удобнее показать отрицательными числами.
Действительные числа
Рациональные и иррациональные числа образуют множество действительных чисел. Любое действительное число можно представить в виде бесконечной десятичной дроби. Для любого действительного числа
Два действительных числа, отличающиеся только знаками, называются противоположными числами. 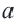
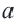
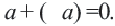
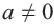
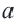
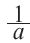
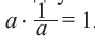
Для любых действительных чисел 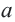
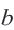
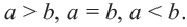
Абсолютная величина действительного числа показывает расстояние на числовой оси от точки, соответствующей этому числу, до начала отсчета.
Расстояние между двумя точками числовой оси равно абсолютной величине разности их координат 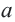
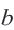

Действительные (вещественные числа)
Числа рациональные и иррациональные, положительные и отрицательные, получили название действительных или вещественных чисел. Геометрически действительные числа изображаются точками числовой оси — прямой, на которой указано положительное направление, масштаб и начальная точка (т.е. точки, изображающие 0 и 1).
Комплексные числа. Однако не успело ещё закрепиться новое расширенное понятие числа, как в процессе развития математики обнаружилось, что и новое понятие является также неудовлетворительным. В частности, решение квадратных уравнений уже на самой ранней ступени развития алгебры привело в области действительных чисел операции извлечения корня из отрицательного числа. Выяснилось, что среди действительных чисел нет ни одного такого, квадрат которого был бы величиной отрицательной, следовательно, и корень
квадратный из отрицательной величины 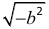
Мнимое число имеет вид 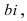
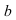
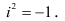
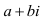
Абсолютная величина действительного числа
Абсолютной величиной (или модулем) действительного числа х (обозначается |х|) называется неотрицательное действительное число,
удовлетворяющее условиям:
Свойства абсолютных величин:
1.
2.
3.
4. Пусть 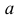
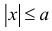
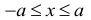
5. Для любых двух действительных чисел справедливы неравенства
6. Для любых двух действительных чисел справедливы неравенства
7.
8.
9.
Постоянные и переменные величины
Постоянной величиной называется величина, численные значения которой не меняются.
Величина с одним и тем же названием может быть постоянной (скорость равномерного движения) или переменной (скорость равномерно ускоренного движения).
Величины, которые сохраняют своё значение в любом явлении, называются абсолютными постоянными, например число
Переменной величиной называется величина, которая принимает различные числовые значения.
Совокупность всех числовых значений переменной величины называется областью изменения этой величины.
Промежутком или открытым интервалом (а,b) называется совокупность всех чисел х, заключенных между данными числами 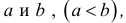
Отрезком или закрытым интервалом 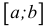
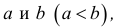
Естественным образом определяются полуоткрытые интервалы, т.е. промежутки, открытые с одной стороны. Например: 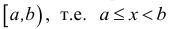
Определения интервалов можно сформулировать, используя вместо понятия «число» понятие «точка».
Окрестностью данной точки 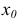
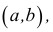
—————
Действительные числа
Число является одной из основных математических абстракций, изучению которой может быть посвящен самостоятельный курс. Из многих концепций построения множества действительных чисел приведем аксиоматическую.
Определение 1.17. Множество R называется множеством вещественных чисел, а его элементы — вещественными (действительными) числами, если выполнен следующий комплекс условий, называемый аксиоматикой вещественных чисел:
1. Аксиомы сложения
Определено отображение (операция сложения: + ), действующее из 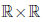
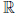
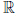
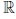
(a) x + y = y + x, ∀x, y ∈ 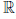
(b) в 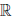
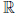
(c) для любого элемента x ∈ 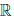
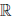
(d) x + (y + z) = (x + y) + z, ∀x, y, z ∈ 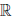
2. Аксиомы умножения
Определено отображение (операция умножения: •), действующее из 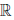
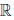
(a) x ∙ y = y ∙ x, ∀x,y ∈ 
(b) в 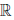
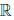
(c) для любого элемента x ∈ 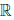
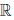
(d) x ∙ (y ∙ z) = (x ∙ y) ∙ z, ∀x,y,z ∈ 
(e) (x + y) ∙ z = x ∙ z + y ∙ z, ∀x,y., z ∈ 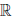
Множество, на котором определены обе операции, и которые удовлетворяют группам аксиом 1 и 2, называется алгебраическим полем.
(Часто знак операции умножения в математических выражениях опускают и вместо x ∙ y пишут xy.)
3. Аксиомы порядка
Для любых элементов x, y ∈ 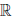



(a) x 

(b) если x, y ∈ 


(c) если x, y, z ∈ 



(d) если x, y, z ∈ 


(e) если x,y ∈ 


Отношение 


4. Аксиома полноты (непрерывности)
Если X и Y — непустые подмножества множества 

x 

Эту аксиому часто называют принципом отделимости.
Можно доказать, что во введенном множестве R имеют место все, известные из школьного курса математики, свойства чисел. Желающие могут получить их самостоятельно или изучить соответствующий раздел в книгах [2] или [6].
Важнейшие подмножества действительных чисел
Определение 1.18. Множество X ⊂ 
Множество натуральных чисел обозначают через 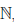
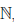
0 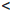
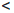
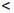
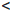
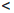
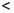
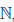
Прямым следствием определения 1.18 является принцип математической индукции.
Если подмножество E множества натуральных чисел 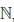
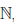
Иллюстрируя этот принцип в действии, докажем с его помощью формулу, называемую формулой бинома Ньютона:
или коротко
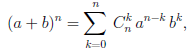
В этой формуле a, b — произвольные действительные числа, n — произвольное натуральное число,
Пусть E — множество тех натуральных чисел n, для которых справедлива формула (1.1). При 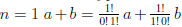
Покажем, что если n ∈ E , то n + 1 ∈ E :
Но 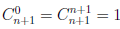
поэтому
Таким образом, n + 1 ∈ E и, следовательно, E = 
Числа 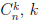
Определение 1.19. Множество, состоящее из всех натуральных чисел, им противоположных и нуля называют множеством целых чисел и обозначают символом Z.
Определение 1.20. Множество {m/n ∈ 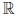
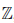
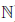
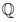
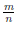
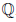
Можно доказать, что 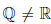
Определение 1.21. Действительные числа, которые не являются рациональными, называются иррациональными.
Часто полезна «геометрическая терминология в которой множество 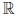
Пусть a, b ∈ 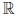
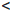

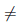
[a, b] := {x ∈ 


(a, b) := {x ∈ 
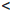
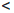
(a, b] := {x ∈ 
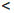

[a, b) := {x ∈ 

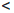
Введенные множества называют промежутками, числа a и b — их концами, число b — a — длиной промежутка.
Часто удобно дополнить множество 
-∞ 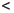
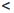
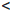
+∞ + (+∞) = +∞; a + (+∞) = +∞,
-∞ + (-∞) = -∞; a + (-∞) = -∞,
+∞ ∙ (+∞) = +∞, -∞ ∙ (-∞) = +∞,
±∞ ∙ a = ±∞, если a > 0,
±∞ ∙ a = ±∞, если a 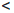
Множество 


[a, +∞) = {x ∈ 

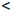
(-∞, a] = {x ∈ 


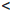
В этих обозначениях часто пишут: 
——————
Действительные числа
Определение действительного числа по Дедекинду
Одним из основных понятий, изучаемых в курсе математического анализа, является понятие действительного числа. Оно возникает в школьном курсе элементарной алгебры фактически на интуитивном уровне как развитие понятия о числе — от натуральных чисел к целым, от целых к рациональным, от рациональных к действительным. В нашу задачу не входит сейчас аккуратное выведение этой цепочки из основных представлений о натуральных числах и их свойствах. Будем считать, что понятие рационального числа и основные свойства рациональных чисел, а также другие вопросы школьного курса элементарной алгебры (в частности, основная символика теории множеств) хорошо известны. Напомним, что множество натуральных чисел обозначается N, множество целых чисел — Z. множество рациональных чисел — Q.
При переходе к действительным числам (множество которых обозначается R) возникает качественно новое понятие непрерывности, присущее именно математическому анализу Поэтому этот шаг будет разобран подробно и аккуратно.
Определение 1.1. Сечением а множества рациональных чисел Q называется такое разбиение Q на два непустых множества 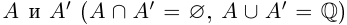
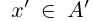
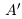
Применяется обозначение
Приведём простейшие примеры сечений.
Напомним, что не существует рационального числа такого, что г2 = 2.
Легко видеть, что в примере 1) в нижнем классе А есть наибольший элемент в верхнем классе А’ нет наименьшего элемента. В примере 2) в A нет наибольшего элемента, в А’ есть наименьший. В примере 3) в A нет наибольшего элемента, в А’ нет наименьшего.
Докажем, например, что в примере 3) в A нет наибольшего элемента (значком □ будем обозначать начало доказательства, значком ■ — конец доказательства).
□ Доказательство от противного. Пусть в А есть наибольший элемент г. Тогда г > 0, г2 < 2. Но легко заметить, что найдётся рациональное число 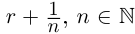
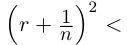
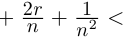
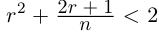
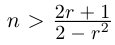
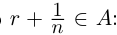
Докажем теперь, что невозможен случай, когда в А есть наибольший элемент, в А’ есть наименьший.
□ Пусть существуют 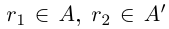
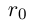
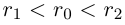
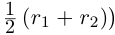
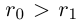
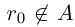
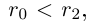
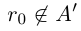
Итак, существуют сечения трёх типов.
I. В нижнем классе есть наибольший элемент, в верхнем нет наименьшего.
II. В нижнем классе нет наибольшего элемента, в верхнем есть наименьший.
III. В нижнем классе нет наибольшего элемента, в верхнем нет наименьшего.
Определение 1.2. Иррациональным числом называется сечением III типа.
В случаях I и II говорят, что сечение производится рациональным числом (соответствующим наибольшему элементу в нижнем классе или наименьшему в верхнем). Сечения I и II типов отождествляются с соответствующими рациональными числами. Чтобы соответствие было взаимно однозначным, сечения типа I в дальнейшем не рассматриваются.
Например, сечение в примере 1) мы не будем рассматривать. Сечение в примере 2) — это рациональное число 1. Сечение в примере 3) — это иррациональное число (которое естественно объявить корнем квадратным из 2, не придавая пока этому термину строгого смысла).
Определение 1.3. Действительным (вещественным) числом называется любое сечение II или III типов. Множество действительных чисел обозначается R. Сечения II типа отождествляются с соответствующими рациональными числами.
У сечений, соответствующих действительным числам, в нижнем классе нет наибольшего элемента. Если в верхнем классе есть наименьший элемент — сечение является рациональным числом, если нет — иррациональным.
Определение 1.4. Два действительных числа 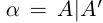
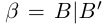
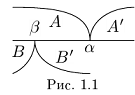
Определение 1.5. Рассмотрим два неравных действительных числа 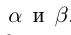
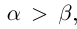
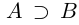
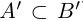
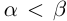
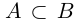
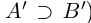
Символ > читается «больше», символ < читается «меньше». На рис. 1.1 изображена ситуация, возникающая при 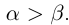
Из свойств числовых множеств очевидно следует, что:
1) 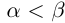
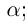
2) если 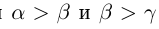
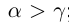
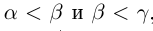

Теорема 1.1. Если действительные числа 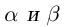
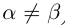
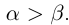
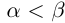
□ Пусть А и В — нижние классы сечений 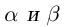
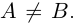
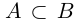
Но если включение 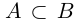
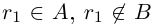
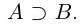
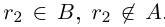
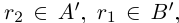
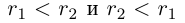
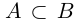
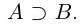
Доказанная теорема выражает свойство упорядоченности множества действительных чисел (если два числа не равны, то одно из них больше другого).
Теорема 1.2 (плотность рациональных чисел во множестве действительных чисел). Для любых действительных чисел 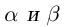
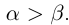
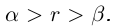
□ Так как 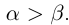
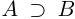
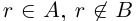
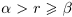
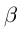
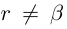
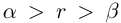
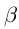
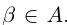
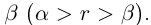
3амечание. Таких рациональных чисел г между 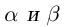
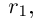
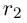
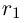
Теорема 1.3 (принцип Архимеда). Для любого действительного числа а существует натуральное число n, большее а.
□ Пусть 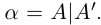
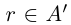
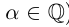
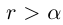
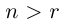
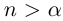
Следующее утверждение мы назовём леммой. Принципиального различия между теоремами и леммами нет, и то, и другое — утверждения, доказываемые в настоящем курсе. Теоремами обычно называют более фундаментальные утверждения, обладающие достаточной общностью формулировки, часто используемые в дальнейшем. Леммы обычно имеют более специальные формулировки и не так широко применяются в последующем изложении.
Лемма 1.1. Пусть 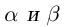
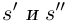
(Иными словами, если два действительных числа можно зажать между двумя сколь угодно близкими рациональными числами, то они равны.)
Как и в школьной программе, знак 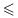
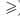
□Пусть 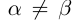
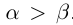
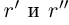
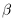
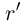
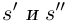
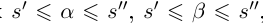
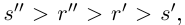
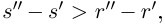
3амeчание. При формулировке подобных утверждений рекомендуется применять сокращённые записи, содержащие кванторы 
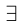
Лемма 1.1 может быть сформулирована так:
Такие записи являются лишь удобным сокращением словесных формулировок, и не следует считать, что в каждом конкретном случае данная запись является единственно возможной. Конечно, можно поставить вопрос о формальном языке, необходимом для таких записей, и довести их до логического совершенства. При этом придётся ввести символы 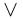


Во множестве действительных чисел можно строить сечения так же, как и во множестве рациональных чисел.
Определение 1.6. Сечением множества действительных чисел R называется такое разбиение R на два непустых множества 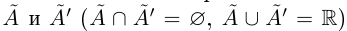
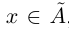
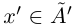
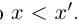
Одновременное существование наибольшего элемента в нижнем классе 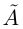
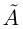
Теорема 1.4 (Дедекинда). Для любого сечения 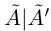
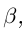
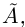
□ Пусть А — множество всех рациональных чисел из
—множество всех рациональных чисел из 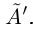
—сечение в Q, которое определяет некоторое действительное число 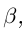
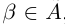
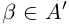
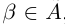
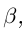
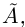
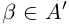
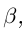
Предположим, что 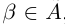
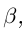
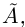
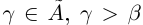
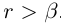
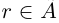
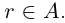
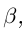
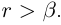
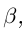
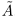
Заметим, что здесь не игнорируются сечения такие, что в нижнем классе есть наибольший элемент. В своё время это нужно было для установления взаимно однозначного соответствия между сечениями в Q и множеством R, здесь похожей необходимости нет.
Теорема Дедекинда отражает свойство полноты или непрерывности множества действительных чисел. Иррациональные числа, как сечения III типа, фактически являлись «дырками» во множестве рациональных чисел. Введение действительных чисел заполнило эти дырки. Теорема Дедекинда показывает, что во множестве действительных чисел таких дырок нет.
Свойство непрерывности показывает существенное отличие множества R от множества Q. Рассмотренные ранее свойства — упорядоченность, плотность, принцип Архимеда — имели место и во множестве Q.
Ограниченные множества. Точные верхние и нижние грани
Определение 1.7. Множество X, состоящее из действительных чисел, называется ограниченным сверху, если найдётся действительное число М такое, что для всех элементов х множества X выполняется неравенство 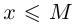

На языке кванторов ограниченность множества X сверху описывается следующей сокращённой записью:
Ограниченность снизу описывается так:
Пример 1.1. Пусть 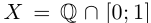
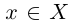
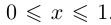
Таким образом, верхняя и нижняя границы множества определены неоднозначно.
Попытаемся сформулировать высказывание «Множество X, состоящее из действительных чисел, не является ограниченным сверху», не применяя частиц и приставок типа «не» и «нет», т.е. в позитивном смысле. Что означает невыполнение (1.1)? Это значит, что для любого действительного числа М не выполняется высказывание 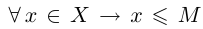
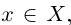
Запишем окончательно на языке кванторов, что означает неограниченность множества X сверху:
Наблюдая преобразование (1.1) в (1.2), мы можем сформулировать формальное правило построения отрицаний в позитивном смысле:
1) кванторы меняются друг на друга, т.е. 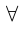
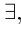
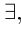
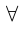
2)высказывания, стоящие при кванторах, не меняются;
3)существенные высказывания, не стоящие при кванторах, меняются на противоположные.
Пример 1.2. Множество N натуральных чисел ограничено снизу 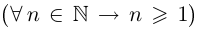
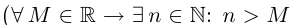
Определение 1.8. Действительное число л называется точной верхней гранью множества 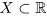
На языке кванторов это описывается как конъюнкция (т.е. одновременное выполнение) двух высказываний:
Логический символ 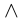
Точная верхняя грань обозначается sup («supremum»):
Определение 1.9. Действительное число 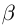
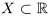
На языке кванторов записывается конъюнкция двух высказываний:
Точная нижняя грань обозначается inf («infimum»):
Из определений следует, что sup X — это наименьшая из верхних границ множества X, a inf X — это наибольшая из нижних границ. Пока ниоткуда не следует, что эти наименьшая из верхних и наибольшая из нижних границ существуют. Дело в том, что ограниченное сверху множество может иметь наибольший элемент, а может и не иметь; ограниченное снизу множество может иметь наименьший элемент, а может и не иметь.
Лемма 1.2. Если множество 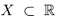
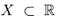
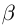
□ Доказательство приведём для наибольшего элемента, вторая часть доказывается аналогично.
Так как а — наибольший элемент X, то для всех 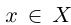
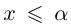
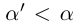
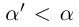
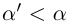
Но может быть и так, что во множестве нет наибольшего (наименьшего) элемента, а точная верхняя (нижняя) грань существует. В этом случае говорят, что точная верхняя (нижняя) грань не достигается.
Пример 1.3. Пусть 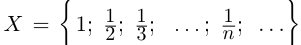
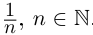
С другой стороны, ясно, что при всех 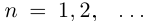
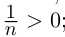
□ В самом деле, для всех 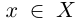
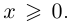
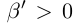
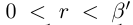
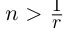
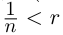
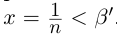
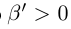
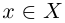
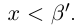
Теорема 1.5 (о точной верхней (нижней) грани). Для любого непустого множества действительных чисел, ограниченного сверху, существует и единственна точная верхняя грань. Для любого непустого множества действительных чисел, ограниченного снизу, существует и единственна точная нижняя грань.
□ Доказательство проведём для точной верхней грани, вторая часть доказывается аналогично (отметим, что пустое множество формально является ограниченным сверху и снизу, но говорить о точных верхней и нижней гранях бессмысленно).
Пусть сначала ограниченное сверху множество 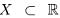
Пусть теперь в X нет наибольшего элемента. Проведём сечение во множестве К так, что А’ — это все верхние границы X (они существуют в силу ограниченности X сверху), а 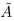
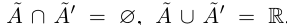
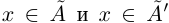
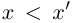
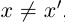
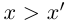
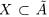
По теореме Дедекинда существует действительное число a либо наибольшее в 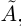
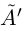
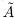
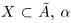
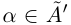
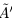
Докажем теперь, что точная верхняя грань единственна. Пусть a = supX и 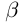
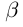
Отмстим ещё раз, что sup X — это наименьшая из верхних границ множества X, a inf X — это наибольшая из нижних границ X (теорема 1.5 утверждает, что во множестве верхних границ, существует наименьший элемент, а во множестве нижних границ существует наибольший элемент). Отсюда следует также
Лемма 1.3. Если число М является верхней границей множества X, то и sup 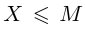
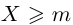
Запишем формулировку этой леммы на языке кванторов:
Отметим, кстати, что
т.е. при переходе к точной верхней (нижней) грани строгое неравенство может превратиться в нестрогое. В примере 1.3 для всех 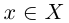
Определение 1.10. Если множество 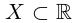
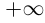
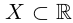
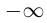
Представление действительных чисел бесконечными десятичными дробями
Пусть действительное число а не является целым числом или конечной десятичной дробью. Рассмотрим соответствующее сечение во множестве рациональных чисел 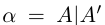
Обозначим через со наибольшее целое число в А. Тогда 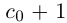
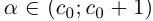
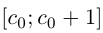
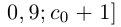
(a не совпадает с концом отрезка, так как не является конечной десятичной дробью).
Снова разбиваем полученный отрезок на 10 отрезков равной длины 0,01 и т.д., на n-м шагу получим
Здесь 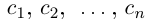
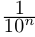
Естественно, что если сn = 9, то при переходе к правому концу отрезка предыдущую цифру 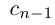

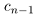
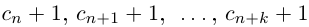
Так как а не является конечной десятичной дробью, то процесс никогда не оборвётся, и мы получим бесконечную последовательность цифр 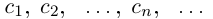
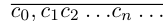
Например, для числа 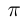
Описанная выше конструкция даст следующие интервалы:
Левый конец соответствующего интервала длины 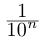
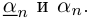
Бесконечная десятичная дробь 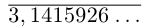
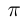
Интересно отмстить, что в такой конструкции для числа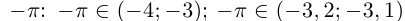
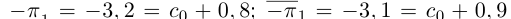
Представлением числа 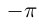
Легко видеть, что для любого
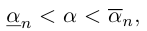
Особое значение имеет случай, когда а — конечная десятичная дробь с n знаками после запятой:
или целое число:
Случай целого a можно рассматривать как частный случай конечной десятичной дроби при n = 0.
В описанной выше конструкции после n-го шага процесс оборвётся. Число ft будет являться общим концом двух отрезков длины 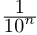
(для иллюстрации общности процесса мы дополнили её бесконечной последовательностью нулей). Если же a рассматривать как правый конец левого из двух возникших отрезков, то а представляется как бесконечная дробь, в которой начиная с (n + 1)-го места после запятой идут девятки:
Таким образом, конечная десятичная дробь имеет два десятичных представления (с нулями, начиная с некоторого места, и с девятками, начиная с некоторого места). Например:
В любом случае при
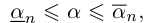
Докажем теперь очень важную лемму, которая неоднократно будет использоваться в дальнейшем в теории действительных чисел.
Лемма 1.4. Пусть a —действительное число. Тогда для любого рационального положительного числа s найдутся paциональные числа 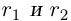
Иными словами, любое действительное число может быть зажато между двумя сколь угодно близкими рациональными числами.
□ Если a — рациональное число, то возьмём 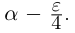
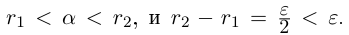
Поэтому можно взять 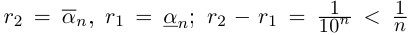
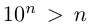
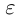
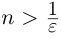
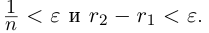
Мы видели, что любое действительное число представляется бесконечной десятичной дробью. Это представление единственно, если действительное число не является целым или конечной десятичной дробью, в противном случае таких представлений два. Докажем обратное утверждение.
Теорема 1.6. Любая бесконечная десятичная дробь является представлением некоторого действительного числа, причем это число определяется единственным образом.
□ Пусть 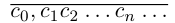

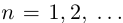
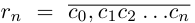

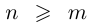
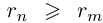
Пусть теперь 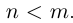
Применяя формулу суммы членов геометрической прогрессии, получим
поэтому 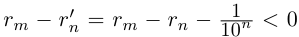
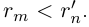
Рассмотрим множества рациональных чисел
При фиксированном 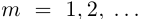
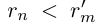
Аналогично, при фиксированном 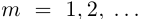
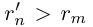
Из леммы 1.3 и последнего неравенства, верного при всех 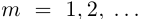
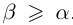
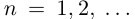
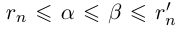
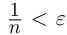
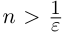
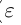
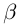
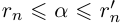
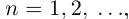
Единственность искомого действительного числа следует из леммы 1.1. В самом деле, если два числа 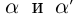
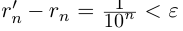
- Заказать решение задач по высшей математике
Арифметические операции с действительными числами
Нам предстоит определить для действительных чисел арифметические операции (сложение, вычитание, умножение, деление) так, чтобы сохранялись привычные свойства этих операций, а для рациональных чисел результаты операций не отличались от обычных.
Пусть 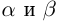
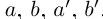
Определение 1.11. Суммой 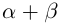
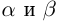
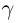
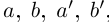
Докажем корректность этого определения. Иными словами, докажем, что такое действительное число 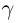
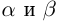
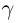
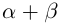
□ I) Существование. Рассмотрим множество всевозможных сумм {а + b} в условиях (1.5). Оно ограничено сверху некоторой суммой 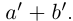
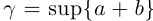
Тогда при выполнении условий (1.5) 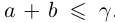
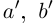
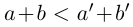
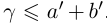
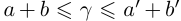
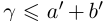
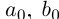
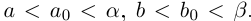
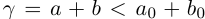
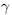
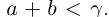
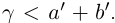
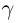
II) Единственность. По лемме 1.4 для любого положительного рационального числа 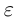
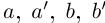
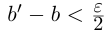
и эта разность может быть сделана сколь угодно малой. По лемме 1.1 существует единственное действительное число 7, удовлетворяющее условиям (1.6).
III) Преемственность. Если 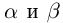
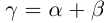
Теперь нужно показать, что привычные свойства операции сложения сохраняются для определённого таким образом сложения действительных чисел. Ввиду большого количества этих свойств будут проведены доказательства лишь некоторых из них; доказать остальные читатели смогут самостоятельно (наиболее существенные моменты будут показаны в доказательствах, приведённых здесь).
Свойства сложения действительных чисел
1)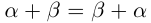
□ Рассмотрим рациональные числа 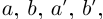
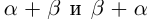
Так как сложение рациональных чисел коммутативно, то а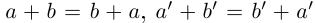
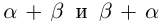
2)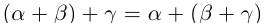
3)
4)Для любого действительного числа а найдётся число 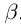
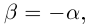
□ Если а — рациональное число, то 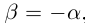
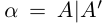
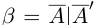
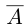
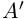
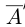
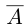
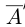
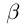
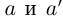
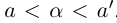
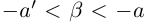
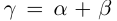
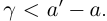
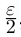
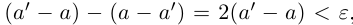
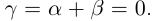
Так как операция сложения во множестве действительных чисел удовлетворяет условиям 1) — 4), то на языке высшей алгебры «действительные числа образуют коммутативную группу по сложению». В такой группе противоположный элемент всегда определён единственным образом.
5)Если 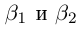
□ С одной стороны, 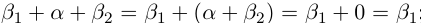
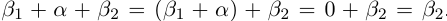
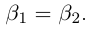
6)Если 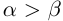

□ По лемме 1.2 найдутся рациональные числа 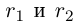
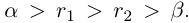
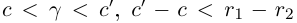
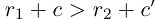
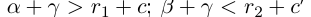
Значит, 
7)Если 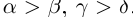
□ Двукратное применение предыдущего свойства. ■
8)Если 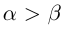
9)Если а > 0, то —а < 0.
Определение 1.12. Разностью 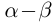
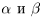
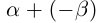
10)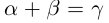
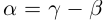
□ С одной стороны, 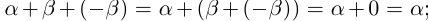
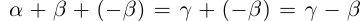
11)
12)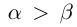
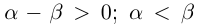
Определение 1.13. Модулем (абсолютной величиной) действительного числа а называется число, обозначаемое 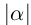
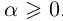
13)
14)Если 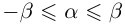
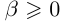
15)
□ Так как 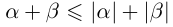
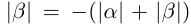
16)
Определим теперь умножение действительных чисел.
Определение 1.14. I. Пусть 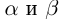
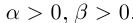
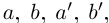
Произведением 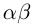
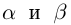
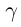
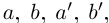
II.Для любого действительного числа а
III.Если действительные числа 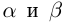
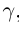
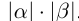
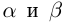
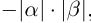
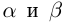
Корректность части I определения 1.14 доказывается аналогично корректности определения 1.11. При этом доказательства существования и преемственности сохраняются дословно с заменой там, где нужно, суммы на произведение. Доказательство единственности чуть сложнее.
□ Пусть n — некоторое натуральное число, большее чисел 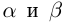
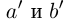
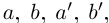
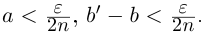
и эта разность может быть сделана сколь угодно малой (мы считаем, что 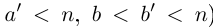
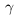
Свойства умножения действительных чисел аналогичны соответствующим свойствам сложения. Они здесь приводятся без доказательств, которые аналогичны доказательствам свойств сложения.
17)
18)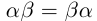
19)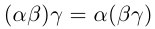
20)
21)Для любого ненулевого действительного числа а найдётся число 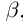
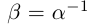
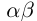
Свойства 18) — 21) означают на языке высшей алгебры, что «ненулевые действительные числа образуют коммутативную группу по умножению». Свойства 1) — 4) и 18) — 21) вместе означают что «действительные числа образуют поле относительно операций сложения и умножения».
22)Обратный элемент для любого ненулевого действительного числа определён единственным образом.
23)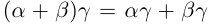
□ Рассмотрим сначала случай, когда все числа 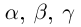
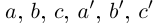
Если n — некоторое натуральное число, большее чисел 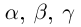
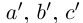
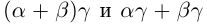
(по определению суммы и произведения положительных действительных чисел). В силу дистрибутивности умножения рациональных чисел относительно сложения 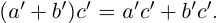
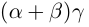
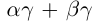
В самом деле, по лемме 1.4 найдутся рациональные числа 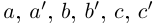
существует единственное такое действительное число, откуда
К случаю положительных 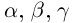
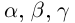
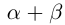
24)
25)Если 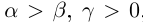
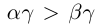
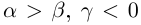
Определение 1.15. Частным 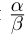
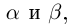
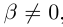
26)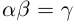
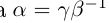
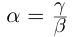
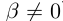
27)Если 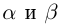
28)Если 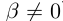
29)Если 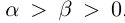
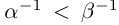
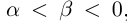
30)Если а — действительное число, a n — натуральное число, то число па равно сумме п слагаемых, равных а:
Вывод. Для действительных чисел имеют место все правила элементарной алгебры, относящиеся к четырём арифметическим действиям, равенствам и неравенствам.
Естественным образом определяется аn, где а — действительное, n — натуральное число:
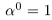
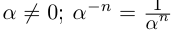
Сохраняются все свойства степеней с целым показателем (доказательства ничем не отличаются от доказательств в школьном курсе алгебры).
Обратим теперь внимание на то, что в лемме 1.1 действительное число зажималось между рациональными потому, что у нас ещё не было понятия разности действительных чисел. Приведём теперь более общий вариант этого утверждения.
Лемма 1.5. Пусть 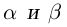
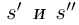
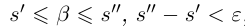
□ Пусть 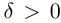
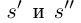
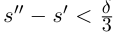
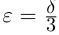
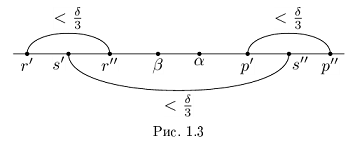
По лемме 1.4 найдутся рациональные числа 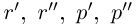
Тогда (см. рис. 1.3):
Итак, для любого рационального положительного числа 6 найдутся рациональные числа 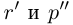
По лемме 1.1
Счётные и несчётные множества
Определение 1.16. Два множества А и В называются эквивалентными (равномощными), если между А и В можно установить взаимно однозначное (биективное) соответствие.
Здесь мы фактически имеем дело с переводом русскоязычного термина на латинский язык (равномощный — эквивалентный, взаимно однозначное — биективное и т.д.). В принципе вполне можно было бы ограничиться русскоязычными терминами, но, поскольку их переводы очень распространены в отечественной научной и учебной литературе, их игнорировать нельзя.
Пример 1.4. Множество натуральных чисел эквивалентно множеству чётных натуральных чисел (взаимно однозначное соответствие устанавливается зависимостью 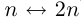
Определение 1.17. Множество называется счётным, если оно эквивалентно множеству натуральных чисел (т.е. если его элементы можно занумеровать в виде бесконечной последовательности).
Лемма 1.6. Любое бесконечное множество содержит счётное подмножество.
□ Выберем некоторый элемент х1, принадлежащий данному бесконечному множеству А. Так как множество бесконечно, то можно выбрать элемент х2 среди оставшихся элементов, х3 среди оставшихся и т.д. Процесс не оборвётся в силу бесконечности А. Построенное счётное множество 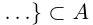
Лемма 1.7. Любое бесконечное подмножество счётного множества счётно.
□ Пусть 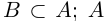
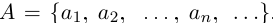
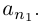
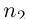
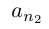
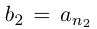
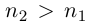
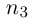
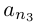
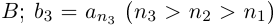
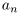
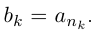
Лемма 1.8. Сумма конечного и счётного множеств, двух счётных множеств — счётна.
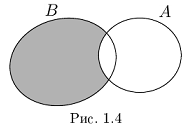
□ Напомним, что в теории множеств разностью множеств В А называется множество тех и только тех элементов, которые принадлежат В, но не принадлежат А (на диаграмме Эйлера заштрихована разность В А — см. рис. 1.4).
Из рис. 1.4 очевидны равенства
причём множества, объединяемые в правых частях этих равенств, имеют пустые пересечения.
1) Пусть А — счётно, В — конечно.
Если 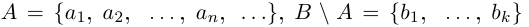
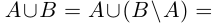
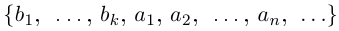
2) Пусть А и В счётны. Если В А конечно, то доказательство проходит, как в первом случае. Если В А бесконечно, т.е. счётно, то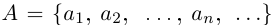
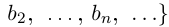
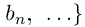
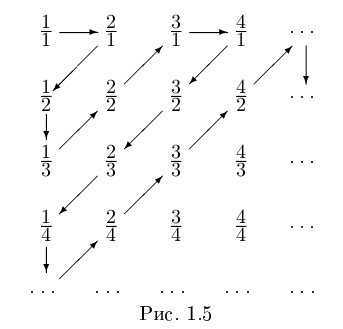
Теорема 1.7. Множество рациональных чисел Q счётно.
□ Достаточно доказать, что счётно множество положительных рациональных чисел Q+, так как в этом случае множество отрицательных рациональных чисел, эквивалентное ему 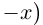
Занумерованы все положительные рациональные числа, причём каждое число встречается много раз 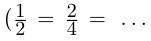
Следствие. Множество целых чисел Z счётно (принадлежит Q).
Теорема 1.8. Множество действительных чисел К несчётно (т.е. действительных чисел «значительно больше», чем рациональных).
□ Достаточно доказать, что несчётным является множество действительных чисел полуинтервала [0; 1) (если R — счётно, то [0; 1) 
Выпишем десятичные представления этих чисел:
при этом конечная десятичная дробь записывается с нулями, начиная с некоторого номера (а не с девятками).
Рассмотрим число 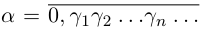

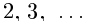
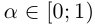
Следствие 1. Множество иррациональных чисел несчётно (иначе вместе с Q получилось бы счётное множество R).
Следствие 2. Множество чисел любого конечного интервала несчётно.
□ Множество (0; 1) несчётно, так как иначе при добавлении одной точки 0 получилось бы счётное множество [0; 1).
Несчётность произвольного интервала (а;b) следует из того, что между (0; 1) и (a: b) можно установить взаимно однозначное соответствие по формуле
Замечание к главе I. При помощи сечений были определены лишь арифметические операции с действительными числами. Развивая этот метод, можно определить арифметический корень n-й степени из положительного действительного числа, степень положительного числа с произвольным действительным показателем, логарифмы и другие элементарные функции, известные из школьного курса алгебры. Но если этим вопросам уделить внимание в лекционном курсе математического анализа, то возникнет нехватка времени для изложения последующих очень существенных глав.
Представляется удобным и разумным пойти путём наименьшего сопротивления — не вводить пока эти элементарные функции, ограничившись в главах II и III (теория пределов последовательностей и функций) арифметическими свойствами действительных чисел. И только в главе III, после изучения свойств непрерывных функций, ввести корень n-й степени как обратную функцию к хn на соответствующем промежутке, аккуратно определить степень с действительным показателем, логарифм как обратную функцию и т.д. Этот путь имеет один недостаток — обедняется практическая сторона курса, при решении иллюстрирующих примеров приходится ограничиваться арифметическими операциями. Конечно, на практических занятиях следует решать примеры с корнями, логарифмами, тригонометрическими функциями и т.д., но при этом понимать, что всё, выходящее за рамки арифметики, пока является «незаконным» и чисто иллюстративным.
- Решение уравнений высших степеней
- Системы неравенств
- Квадратные неравенства
- Точка, прямая и плоскость в пространстве
- Уравнение
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
Абсолютная величина – это модуль действительного числа (неотрицательное число), определение которого зависит от типа числа.
Абсолютная величина и свойства модуля
Абсолютная величина или модуль (обозначается
) называется отрицательное число, что совпадает с
, если
и взятое со знаком минус, если
, то есть
(1)
В первом уравнении , если
, а во втором уравнении
, если
.
Например, ,
,
.
Есть такие свойства модулей:
(2)
, тогда согласно (1)
. В это же время
, поэтому из первого свойства получается
Значит
. Теперь пусть
, тогда из (1) имеем
. В то же время
, поэтому
. Значит
.
,
(3)
Доказательство неравенства (3).
а) Если , тогда в первом соотношении
, а во втором –
.
б) Если же , тогда
, а
.
(4)
Аналогично можно доказать (4).
Пусть:
а) тогда согласно (1)
, а согласно (3) дальше у нас получается
.
б) , поэтому снова согласно (1), (3), и (2) имеем:
.
Свойство доказано.
(5)
Доказательство неравенства (5).
[согласно (4)]
.
Аналогично:
.
Так как , тогда из полученных соотношений получается неравенство (5).
(6)
По определению модуль произведения чисел и
равен либо
x
, если
, либо -(
x
), если
x
. Из правил умножения действительных чисел следует, что произведение модулей чисел
и
равно либо
x
.
, либо
, если
. что доказывает рассматриваемое свойство.
Рассмотрим (7) свойство:
Модуль частного от деления на
= частному от деления модуля числа
на модуль числа
, где
(7)
Так как частное =
, тогда
Определение и свойство вышеперечисленных модулей применяются при исследовании функций, построения их графиков, решения уравнений и неравенств с модулями.
Геометрические свойства абсолютной величины
Если смотреть с точки зрения геометрической абсолютной величины, тогда модуль вещественного (действительного) или комплексного чисел находится расстояние между числом и началом координат. Рассмотрим комплексные и вещественные (действительные числа.
Вещественные числа
Комплексные числа
- Область определения, то есть, вся комплексная плоскость.
- Область значений –
.
- Модуль как комплексная функция ни в одной точке не дифференцируема
Обратим внимание, что абсолютной величине можно дать геометрическое объяснение: если задать на числовой оси точку с абсциссой
, тогда
– это расстояние этой точки
к точке
.
Алгебраические свойства абсолютной величины
Для любых вещественных чисел имеют место такие соотношения:
Примеры решения задач с модулем
Задача
1) Построить график функции .
2) Решить уравнение .
3) Решить неравенство .
4) Решить неравенство .
Решение
Сначала построим график функции , а за основу берём (1) неравенство:
(8)
При этом в первом уравнении , если
, а
, если
. Поэтому графиком функции
будет ломаная, см. рис. 1.
Рис. 1
2) Первую часть задания выполнили, то есть, график построили а теперь нам необходимо решить уравнение .
Пользуясь изображением выше (рис. 1) по формуле (8) решим сначала уравнение на интервале
. Так как
, тогда
.
Если же , тогда
, поэтому
.
Если , тогда у нас получается единственное решения
.
Решили уравнение и получилось, что ,
.
Обратим ваше внимание, что решения и
легко понять по рис. 1. А если выходить из геометрического содержания абсолютной величины, тогда очевидно, что на расстоянии
от точки
на оси
находятся две точки
и
.
3) Решаем неравенство .
Можно осуществить на каждом из интервалов и
или проще воспользоваться нашим уже построенным рисунком, из которого видно, что график ломаной
находится не выше прямой
для
, то есть
, где
(9)
4) Итак, решаем последнее неравенство .
Запишем, согласно с рис. 1:
.
(10)
Соотношение (9) и (10) будут использоваться и в дальнейшем.
Ответ
Решили уравнение и у нас получилось: ,
;
Из первого неравенства получилось, что , где
.
Второе неравенство – .
Задача
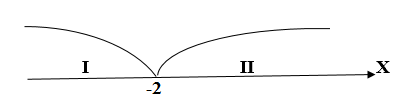
Записать без знака модуля для функции . Построить её график.
Решение
Приравняем подмодульное выражение к нулю .
Теперь разделим ось на два интервала и
.
Если , тогда
, поэтому, согласно с (1)
.
Если же , тогда
, поэтому
. Значит
Строим отдельно графики: для
и
для
. (см. рис. 2)
Рис. 2
Мы видим, что график функции можно получить параллельным переносом графика
влево вдоль оси
на две единицы.
Очевидно, что по большому счёту график функции можно получить параллельным переносом графика
по направлению оси
на
единиц вправо, если
и влево, если
.
Как и в примере 1 после построения графика можно легко найти решение уравнения
, а также неравенств
.
Ответ
Запишем: =
и неравенство
.
Задача
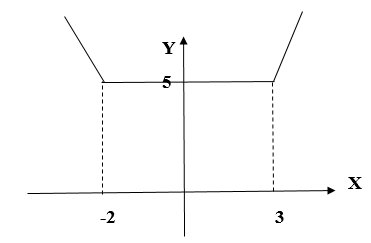
Построить график функции .
Решение
Аналогично предыдущему примеру, приравняем к нулю подмодульное выражение: .
Разбиваем на три интервала:
1. Если , тогда
, поэтому
,
.
2. Если , тогда
и
, а
и
, поэтому
.
3. Если , тогда
, поэтому
.
Значит, для нашей функции имеем:
её график см. на рис. 3.
Рис. 3
Абсолютная величина или модуль, вещественного числа x есть расстояние от x до нуля.
Более точно: абсолютная величина x есть неотрицательное число, обозначаемое |x|, определяемое следующим образом: если x ≥ 0, то |x|=x; если x < 0, то |x| = −x.
Для абсолютной величины имеют место следующие соотношения:
Альтернативные определения
Абсолютная величина комплексного числа
Абсолютная величина или модуль комплексного числа z = x + iy (x и y — вещественные числа) — неотрицательное число (обозначаемое |z|), определяемое по формуле 
История
Считают, что термин предложил использовать Котс, ученик Ньютона.
Знак модуля введен в 19 веке Вейерштрассом.
Для комплексных чисел это понятие ввели Коши и Арган в 19 веке.
См. также
- Нормированное векторное пространство.
bg:Абсолютна стойност
ca:Valor absolut
cs:Absolutní hodnota
eo:Absoluta valoro
et:Absoluutväärtus
fa:قدر مطلق (ریاضی)
gl:Valor absoluto
he:ערך מוחלט
hu:Abszolútérték-függvény
is:Algildi
nl:Absolute waarde
no:Absoluttverdi
pl:Wartość bezwzględna
sk:Absolútna hodnota
sl:Absolutna vrednost
sr:Апсолутна вредност
sv:Absolutbelopp
th:ค่าสัมบูรณ์
uk:Абсолютна величина
vi:Giá trị tuyệt đối