Страница 2 из 8
Абсолютная и относительная сила
Абсолютная сила – предельное, максимальное усилие, которое спортсмен может развить в динамическом или статическом режиме. Примером проявления абсолютной силы в динамическом режиме является поднимание штанги или приседание со штангой предельного веса. В статическом режиме абсолютная сила может быть проявлена, например, когда максимальное усилие прилагается к неподвижному объекту («выжимание» неподвижно закрепленной штанги).
Относительная сила — величина силы, приходящаяся на 1 кг веса спортсмена. Этот показатель применяется в основном для того, чтобы объективно сравнить силовую подготовленность различных спортсменов.
Между этими двумя понятиями имеются определенные соотношения, которые выражаются формулой:
Относительная сила = (Абсолютная сила)/(Собственный вес)
Из этой формулы следуют два вывода:
1) с увеличением веса показатели относительной силы у людей примерно равного уровня подготовленности будут различаться, и проигрывать в этом случае будет атлет с большим весом;
2) относительно сильнее спортсмен будет тогда, когда станет развивать абсолютную силу одновременно стремясь удержать свой вес стабильным.
В видах спорта, где приходится иметь дело с перемещением снарядов предельного веса или другими отягощениями, результат особенно или в большей мере зависит от показателей абсолютной силы. Высокие же показатели относительной силы имеют определяющее значение в видах спорта, включающих перемещение спортсменом своего тела в пространстве без дополнительных внешних отягощений, а также в тех видах спорта, где нужно ограничивать свой вес в рамках установленных весовых категорий.
Результаты исследований позволяют утверждать, что уровень абсолютной силы человека в большей степени обусловлен факторами среды (тренировка, самостоятельные занятия и др.). В то же время показатели относительной силы в большей мере испытывают на себе влияние генотипа (В. И. Лях, 1997; цит. по: Ж. К. Холодов, В. С. Кузнецов, 2003).
Абсолютная сила
Предмет
Физическая культура
Разместил
🤓 ritulya.fomina.95
👍 Проверено Автор24
суммарная сила всех мышечных групп, участвующая в данном движении.
Научные статьи на тему «Абсолютная сила»
Гауссова система единиц (СГС)
Единицей силы в СГС, например, является дина:
$1,дин=frac{гbullet см}{с^{2}}$
В абсолютной электростатической…
Если заряды выразить в абсолютных электростатических единицах, сила будет в динах, расстояние в сантиметрах…
она абсолютной электромагнитной единицей силы тока), то получится система СГСМ….
Абсолютную электромагнитную единицу силы тока обозначают $СГСМ_i.$
$1 СГСМ_i=1sqrt{дин}.$
Единица силы…
Абсолютная электростатическая система и абсолютная электромагнитная система — это две разные системы,

Статья от экспертов
Об абсолютной юридической силе обязательства
В статье рассматриваются последние законодательные изменения, позволяющие расширить общепринятое представление об обязательстве как относительном правоотношении. Основываясь на судебной практике и позициях известных цивилистов, автор приходит к выводу о том, что обязательство не только связывает должника с кредитором, но и порождает у всех субъектов правопорядка пассивную обязанность воздержаться от создания препятствий кредитору в осуществлении его субъективного права. При этом сам кредитор вправе защищать свое субъективное право от нарушений со стороны не только должника, но и любых третьих лиц. Однако в целом ряде установленных законом случаев кредитор может быть лишен возможности ссылаться на обязательство в отношениях с третьими лицами. Подобные юридические последствия наступают, в частности, при неисполнении законодательных предписаний о необходимости государственной регистрации договора, а также при нарушении правил уведомления о залоге движимого имущества. Юридическую значим…
Основные аксиомы статики
С точки зрения статики все тела считаются абсолютно твердыми….
Согласно определению аксиомы, данное положение принимается абсолютно истинным в рамках теории статики…
Если на абсолютно твердое тело действуют два усилия, то такое тело может находиться в равновесии лишь…
нарушено, если тело считать абсолютно твердым….
Третья аксиома может быть применена к абсолютно любым телам.

Статья от экспертов
Исследование путей измерения абсолютного значения силы тяжести в морских условиях
Объект и цель научной работы. Исследование путей измерения абсолютного значения силы тяжести в морских условиях. Материалы и методы. Использован метод проведения экспериментальных исследований. Основные результаты. Исследованы возможности измерения абсолютного значения силы тяжести в морских условиях. Предложена концепция и создан макет морского интегрированного гравиметрического комплекса. Рассмотрены его конструкция и принцип работы. Приведены результаты испытаний макета на стенде имитации морского волнения. Заключение. Показана принципиальная возможность измерения абсолютного значения силы тяжести на слабо качающемся основании. Потенциальная точность морской съемки с использованием интегрированного комплекса может составлять около 0,1 мГал, что в перспективе позволит существенно повысить качество геодезической информации для труднодоступных районов Земли.
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек
Содержание
- Способ измерения абсолютной силы
- Математический маятник
- Физический маятник
- Баллистический метод
- Абсолютная и относительная сила
- главная
- измерения
- метрологическая экспертиза
- форум
- полезная информация
- Измерения. Выбор средств измерений
- 1. Основные положения
- 2. Измерение геометрических величин (измерение длины)
- 3. Измерение физических величин
- 4. Измерение давления
- 5. Измерение массы
- 6. Измерение температуры
- 7. Измерение твёрдости
- 8. Измерение силы
- 9. Измерение электрических величин — напряжения,
- силы тока, сопротивления и мощности
- 10. Измерение. Методы неразрушающего контроля
- Измерение силы
Способ измерения абсолютной силы
Среди динамических методов наиболее важными являются:
- измерение периода колебаний маятника
- измерение периода колебаний маятника под действием силы тяжести и силы, ей противодействующей
- измерение времени свободного падения тел
- измерение частоты колебаний струны, которая натянута подвешенной на ней массой.
Измерения силы тяжести бывают абсолютными и относительными.
При абсолютных измерениях определяют полную величину силы тяжести. При относительных – определяют не полное значение, а приращение в данном пункте относительно некоторого другого, исходного, поле в котором обычно известно.
Динамические методы могут быть как абсолютными, так и относительными. Статические – только относительными. Приборы, предназначенные для относительных определений силы тяжести, называют гравиметрами.
В настоящее время статические гравиметры являются основными приборами для относительных определений силы тяжести.
Математический маятник
Среди динамических методов измерения силы тяжести долгое время главенствовал маятниковый метод, доведенный до высокой степени совершенства.
Маятником называется любое твердое тело, способное совершать колебания около горизонтальной оси.
В теории колебаний важную роль играет модель математического маятника. Это идеальная модель, то есть модель, которую можно реализовать лишь в некотором приближении.
Математический маятник представляет собой материальную точку, с массой m, подвешенную на нерастяжимой и невесомой нити длиной l (рис18.1).
Дифференциальное уравнение движения имеет вид:
если задать начальные условия 

Интеграл в этом выражении относится к классу эллиптических первого рода и не приводится к элементарным функциям. Обычно чтобы получить решение в явном виде, подынтегральную функцию разлагают в ряд (по φ), а затем почленно интегрируют. В нашем случае такая процедура приводит к выражению
Решение получается сложным, потому, что уравнение (18.1) является нелинейным. Однако при малых начальных отклонениях угла φ можно положить 
Для него период колебаний равен
Как следует из этой формулы, при малых амплитудах период колебаний не зависит от амплитуды. Это свойство маятника называется изохронностью.
Поскольку математический маятник является идеальной моделью, ее, как правило, невозможно реализовать с необходимой степенью точности. Поэтому на практике при определениях силы тяжести используют физический маятник.
Физический маятник
Под физическим маятником понимают любое тяжелое твердое тело, свободно вращающееся вокруг горизонтальной оси.
Обозначим ось вращения как ось x (рис. 18.2).
Уравнение движения имеет вид:
здесь Ix– момент инерции, Mx – сумма моментов сил, ω – угловая скорость вращения.
Пусть центр тяжести маятника находится в точке C на расстоянии a от оси вращения O. Тогда сумма моментов действующих сил равна:
где M – масса тела. Тогда уравнение движения примет вид:
Если ввести новую переменную 


Если эту величину отложить на рисунке, вдоль линии, соединяющей точку O и центр тяжести C, получим точку O’, которая называется центром качания, а длина l отрезка OO’ называется приведенной длиной физического маятника. Особенность положения центра качания в том, что физический маятник, подвешенный к нему будет качаться с тем же периодом.
Маятниковые приборы позволяют выполнять как абсолютные, так и относительные определения силы тяжести. При абсолютных определениях измеряют период колебания и приведенную длину маятника. При относительных определениях силы тяжести достаточно измерить только период колебания маятника в двух пунктах.
Действительно, пусть

Маятниковые позволяют определить период колебаний с точностью 
Баллистический метод
В настоящее время измерения малых интервалов и времени падения тел достиг очень высокой точности, поэтому появилась возможность высокоточных абсолютных измерений силы тяжести способом падающего груза, или баллистическим способом.
В вертикальной вакуумной камере высотой примерно 50 см в качестве падающего груза используется стеклянная призма (рис 18.3).
Путь падения призмы измеряют с помощью лазерного интерферометра, а время падения – с помощью атомных часов. Пучок когерентного света от лазера полупрозрачным стеклом разделяется на два пучка. Пучки света проходят разные пути, а затем сводятся вместе. В результате будет наблюдаться интерференционная картина в виде чередования темных и светлы полос (интерференционных полос), ширина и число которых зависят от спектрального состава источника света и разности оптических путей световых пучков.
Число полос N связано с разностью хода лучей Δ и длиной волны света λ соотношением
время и путь свободно падающего тела связаны соотношением
Однако на практике пользуются более сложной формулой
Это связано с тем, что в начале пути призма может получить небольшое дополнительное ускорение. Чтобы избавиться в выражении (18.12) от априорно неизвестной начальной скорости v0 , измерения проводят дважды. Тогда из системы двух уравнений получим:
Точность абсолютных измерений баллистическим методом на сегодняшний день чрезвычайно высока – порядка одного микрогала (0.001 мГал) при времени одного измерения около 10 с. Для повышения точности выполняются многократные измерения, которые потом статически обрабатываются.
Источник
Абсолютная и относительная сила
Абсолютная сила – предельное, максимальное усилие, которое спортсмен может развить в динамическом или статическом режиме. Примером проявления абсолютной силы в динамическом режиме является поднимание штанги или приседание со штангой предельного веса. В статическом режиме абсолютная сила может быть проявлена, например, когда максимальное усилие прилагается к неподвижному объекту («выжимание» неподвижно закрепленной штанги).
Относительная сила — величина силы, приходящаяся на 1 кг веса спортсмена. Этот показатель применяется в основном для того, чтобы объективно сравнить силовую подготовленность различных спортсменов.
Между этими двумя понятиями имеются определенные соотношения, которые выражаются формулой:
Относительная сила = (Абсолютная сила)/(Собственный вес)
Из этой формулы следуют два вывода:
1) с увеличением веса показатели относительной силы у людей примерно равного уровня подготовленности будут различаться, и проигрывать в этом случае будет атлет с большим весом;
2) относительно сильнее спортсмен будет тогда, когда станет развивать абсолютную силу одновременно стремясь удержать свой вес стабильным.
В видах спорта, где приходится иметь дело с перемещением снарядов предельного веса или другими отягощениями, результат особенно или в большей мере зависит от показателей абсолютной силы. Высокие же показатели относительной силы имеют определяющее значение в видах спорта, включающих перемещение спортсменом своего тела в пространстве без дополнительных внешних отягощений, а также в тех видах спорта, где нужно ограничивать свой вес в рамках установленных весовых категорий.
Результаты исследований позволяют утверждать, что уровень абсолютной силы человека в большей степени обусловлен факторами среды (тренировка, самостоятельные занятия и др.). В то же время показатели относительной силы в большей мере испытывают на себе влияние генотипа (В. И. Лях, 1997; цит. по: Ж. К. Холодов, В. С. Кузнецов, 2003).
Источник
главная
измерения
метрологическая экспертиза
форум
полезная информация

Измерения. Выбор средств измерений
1. Основные положения
2. Измерение геометрических величин (измерение длины)
3. Измерение физических величин
4. Измерение давления
5. Измерение массы
6. Измерение температуры
7. Измерение твёрдости
8. Измерение силы
9. Измерение электрических величин — напряжения,
силы тока, сопротивления и мощности
10. Измерение. Методы неразрушающего контроля
Измерение силы
Силой называется всякое воздействие на данное тело, сообщающее ему ускорение или вызывающее его деформацию. Сила векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел.
Сила характеризуется числовым значением, направлением в пространстве и точкой приложения.
За единицу силы в СИ принят ньютон (Н). Ньютон — это сила, которая придает массе 1 кг в направлении действия этой силы ускорение 1 м/с 2 .
В технических измерениях допускаются единицы силы:
1 кгс (килограмм-сила) = 9,81 Н;
1 т c (тонна-сила) = 9,81 х 103 Н.
Измерение силы осуществляют посредством динамометров, силоизмерительных машин и прессов, а также непосредственным нагружением при помощи грузов и гирь.
Динамометры — приборы, измеряющие силу упругости.
Динамометры изготовляют трёх типов:
По способу регистрации измеряемых усилий динамометры подразделяют на:
— указывающие — применяют главным образом для измерений статических усилий, возникающих в конструкциях, установленных на стендах, при приложении к ним внешних сил и для измерения силы тяги при плавном передвижении изделия;
— считающие и пишущие динамометры, регистрирующие переменные усилия, применяют чаще всего при определении силы тяги паровозов и тракторов, так как вследствие сильной тряски и неизбежных рывков при ускорении их движения, а также неравномерности загрузок изделия создаются переменные усилия.
Наибольшее распространение имеют динамометры общего назначения пружинные, указывающие.
Основные параметры и размеры динамометров общего назначения, пружинных со шкальным отсчётным устройством, предназначенных для измерений статических растягивающих усилий, устанавливает ГОСТ 13837.
Выбор пружинных динамометров общего назначения в обыкновенном исполнении, применяемых для измерений статических растягивающих усилий, должен осуществляться согласно настоящего документа.
Основные технические параметры пружинных динамометров общего назначения в обыкновенном исполнении, применяемых для измерений статических растягивающих усилий приведены в таблице 12.1.
Пределы измерений и погрешность динамометра должны определяться одним из двух способов:
— по таблицам приложения 2 ОСТ 1 00380.
Для измерения силы тяги двигателей летательных аппаратов при стендовых испытаниях следует применять силоизмерительные системы. Структурные схемы и принцип действия силоизмерительных систем приведены в рекомендуемом приложении 3 ОСТ 1 00380.
Рабочие средства измерений, применяемые в силоизмерительных системах, приведены в справочном приложении 4 ОСТ 1 00380.
Предел допускаемой погрешности измерений системы не должен превышать допускаемого значения по ОСТ 1 01021 и ОСТ1 02512.
Пример — Необходимо определить верхний предел измерений и основную приведенную погрешность динамометра для измерений силы (160± 10) кгс.
наибольший предельный размер параметра
160 кгс+ 10 кгс= 170 кгс;
наименьший предельный размер параметра
160 кгс-10 кгс= 150 кгс;
170 кгс-150 кгс =20 кгс.
основную допустимую абсолютную погрешность измерений (по формуле (7.1)):

нижний предел рабочей части шкалы (по формуле (7.2)):
верхний предел рабочей части шкалы (по формуле (7.3)):
Вди > 170 кгс + 6,6 кгс = 176,6 кгс.
Выбираем по таблице 12.1 динамометр общего назначения с верхним пределом Вди= 2,0 Н (204 кгс). Нормирующее значение для определения основной приведенной погрешности динамометра равно конечному значению его шкалы.
Определяем предел допускаемой основной приведённой погрешности динамометра (по формуле (7.10)):
Находим меньшее ближайшее значение погрешности 

Способ с использованием таблиц.
В боковике таблицы приложения 2 ОСТ 1 00380 находим строку с диапазоном измерений от 20 до 200 кгс, в котором измеряемая величина может принимать одно из значений.
На этой же строке во второй графе находим значение верхнего предела измерений динамометра. Этим значением является 200 кгс. На этой же строке находим меньшее ближайшее значение допуска по отношению к заданному. Этим значением является 12 кгс.
В оглавлении таблицы, по значению допуска 12 кгс, находим соответствующее ему значение погрешности 
Вывод — для измерения силы (160 ± 10) кгс выбираем динамометр с верхним пределом 2,0 Н (204 кгс), класса точности 2.
Таблица 12.1 – Основные технические параметры пружинных динамометров общего назначения в обыкновенном исполнении, применяемых для измерений статических растягивающих усилий
Источник
Магнитное поле. Силы
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: сила Ампера, сила Лоренца.
В отличие от электрического поля, которое действует на любой заряд, магнитное поле действует только на движущиеся заряженные частицы. При этом оказывается, что сила зависит не только от величины, но и от направления скорости заряда.
Сила Лоренца
Сила, с которой магнитное поле действует на заряженную частицу, называется силой Лоренца. Опыт показывает, что вектор силы Лоренца находится следующим образом.
1. Абсолютная величина силы Лоренца равна:
(1)
Здесь — абсолютная величина заряда,
— скорость заряда,
— индукция магнитного поля,
— угол между векторами
и
.
2. Сила Лоренца перпендикулярна обоим векторам и
. Иными словами, вектор
перпендикулярен плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля.
Остаётся выяснить, в какое полупространство относительно данной плоскости направлена сила Лоренца.
3. Взаимное расположение векторов ,
и
для положительного заряда
показано на рис. 1.
Рис. 1. Сила Лоренца
Направление силы Лоренца определяется в данном случае по одному из двух альтернативных правил.
Правило часовой стрелки. Сила Лоренца направлена туда, глядя откуда кратчайший поворот вектора скорости частицы v к вектору магнитной индукции B виден против часовой стрелки.
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление скорости частицы, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Лоренца.
Для отрицательного заряда направление силы Лоренца меняется на противоположное.
Всё вышеперечисленное является обобщением опытных фактов. Формула (1) позволяет связать размерность индукции магнитного поля с размерностями других физических величин:
Сила Ампера
Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.
Происхождение силы Ампера легко понять. Ведь ток в металле является направленным движением электронов, а на каждый электрон действует сила Лоренца. Все эти силы Лоренца, действующие на свободные электроны, имеют одинаковое направление и одинаковую величину; они складываются друг с другом и дают результирующую силу Ампера.
Направление силы Ампера определяется по тем же двум правилам, сформулированным выше.
Правило часовой стрелки . Сила Ампера направлена туда, глядя откуда кратчайший поворот тока к полю виден против часовой стрелки .
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление тока, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Ампера .
Взаимное расположение тока, поля и силы Ампера указано на рис. 2.
Рис. 2. Сила Ампера
На этом рисунке проводник имеет длину , а угол между направлениями тока и поля равен
. Мы сейчас выведем выражение для абсолютной величины силы Ампера.
На каждый свободный электрон действует сила Лоренца:
где — скорость направленного движения свободных электронов в проводнике.
Пусть — число свободных электронов в данном проводнике,
— их концентрация (число в единице объёма). Тогда:
где — объём проводника,
— площадь его поперечного сечения. Получаем:
Мы не случайно выделили скобками четыре сомножителя. Ведь это есть не что иное, как сила тока: (вспомните выражение силы тока через скорость направленного движения свободных зарядов!). В результате приходим к окончательной формуле для силы Ампера:
(2)
Хорошую возможность поупражняться в нахождении направлений магнитного поля и силы Ампера даёт взаимодействие параллельных токов. Оказывается, два параллельных провода отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают (рис. 3).
Рис. 3. Взаимодействие параллельных токов
Обязательно убедитесь в этом самостоятельно! Делаем так. Сначала берём произвольную точку на первом проводе и определяем направление магнитного поля, создаваемого в этой точке вторым проводом (правило вам известно — см. предыдущий листок>). Ну а затем находим направление силы Ампера, действующей на первый провод со стороны магнитного поля второго провода.
Рамка с током в магнитном поле
В листках по термодинамике мы говорили о важности циклически работающих машин: они снабжают нас энергией. Понимание законов термодинамики позволило сконструировать тепловые двигатели, которые исправно служат нам и по сей день.
Понимание же законов электромагнетизма дало возможность создать циклическую машину другого типа — электродвигатель.
Мы рассмотрим один из элементов электродвигателя — рамку с током в магнитном поле. Разобравшись в её поведении, мы сможем уловить основную идею функционирования электродвигателя.
Пусть прямоугольная рамка может вращаться вокруг горизонтальной оси (рис. 4, слева). Рамка находится в вертикальном однородном магнитном поле
. Ток течёт по рамке в направлении
; это направление показано соответствующими стрелками.
Рис. 4. Рамка с током в магнитном поле
Вектор называется вектором нормали; он перпендикулярен плоскости рамки и направлен туда, глядя откуда ток кажется циркулирующим против часовой стрелки. (Иными словами, вектор
сонаправлен с вектором индукции магнитного поля, которое создаётся током в рамке.) Поворот рамки измеряется углом
между векторами
и
.
Теперь определим направления сил Ампера, которые действуют на рамку со стороны магнитного поля. Эти силы расставлены на рисунке; вот вам ещё одно упражнение на правило часовой стрелки (левой руки) — обязательно проверьте правильность указанных направлений!
Силы и
, приложенные к сторонам
и
, действуют вдоль оси вращения. Они лишь растягивают рамку и не вызывают её вращение.
Куда более интересны силы и
, приложеные соответственно к сторонам
и
. Они лежат в горизонтальной плоскости и перпендикулярны оси вращения. Эти силы вращают рамку в направлении по часовой стрелке, если смотреть справа (рис. 4, правая часть). Вычислим момент этой пары сил относительно оси
вращения рамки.
Пусть длина стороны равна
. Тогда
Пусть длина стороны равна
. Плечо
силы
, как видно из рис. 4 (справа) равно:
Таким же будет плечо силы . Отсюда получаем момент сил, вращающий рамку:
Теперь заметим, что — площадь рамки. Окончательно имеем:
(3)
В этой формуле площадь служит единственной геометрической характеристикой рамки.Это наводит на мысль, что только площадь рамки и существенна в выражении для вращающего момента. И действительно, можно доказать (разбивая рамку на бесконечно узкие полоски, неотличимые от прямоугольников), что формула (3) справедлива для рамки любой формы с площадью .
Как видно из формулы (3), максимальный вращающий момент равен:
Эта максимальная величина момента достигается при , то есть когда плоскость рамки параллельна магнитному полю.
Вращающий момент становится равным нулю при и
. Оба этих положения по-своему интересны.
При плоскость рамки перпендикулярна полю, а векторы
и
направлены в разные стороны. Данное положение является положением неустойчивого равновенсия: стоит хоть немного шевельнуть рамку, как силы Ампера начнут её вращать в том же направлении, поворачивая вектор
к вектору
(убедитесь!).
При плоскость рамки также перпендикулярна полю, а векторы
и
сонаправлены. Это — положение устойчивого равновенсия: при отклонении рамки возникает вращающий момент, стремящийся вернуть рамку назад (убедитесь!). Начнутся колебания рамки, постепенно затухающие из-за трения. В конце концов рамка остановится в положении
; в этом положении вектор индукции магнитного поля рамки сонаправлен с вектором
индукции внешнего магнитного поля (вот почему при намагничивании вещества элементарные токи ориентируются так, что их поля направлены в сторону внешнего магнитного поля). Полезное сопоставление: рамка занимает такое положение, что её положительная нормаль ориентируется в том же направлении, что и северный конец стрелки компаса, помещённой в это магнитное поле.
Таким образом, поведение рамки в магнитном поле становится ясным: если отклонить рамку от положения устойчивого равновесия и отпустить, то рамка будет совершать колебания. С точки зрения совершения механической работы это не очень хорошо: если намотать нить на ось вращения и подвесить к нити груз, то груз будет то подниматься, то опускаться.
Но вот если исхитриться и заставить ток менять направление в нужные моменты, то вместо колебаний рамки начнётся её непрерывное вращение и, соответственно, непрерывный подъём подвешенного груза. Тогда-то и получится полноценный электродвигатель; идея с переменой направления тока реализуется с помощью коллектора и щёток.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Магнитное поле. Силы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Содержание:
- Определение и формула силы
- Второй закон Ньютона
- Единицы измерения силы
- Примеры решения задач
Определение и формула силы
Определение
Силой называют векторную величину, которая характеризует взаимодействия тел. Ее модуль определяет «степень»
(интенсивность) воздействия. Направление силы совпадает с направлением ускорения, которое приобретает тело при взаимодействии с другими телами.
Силы способны изменять скорости тел и вызывать их деформации. Примером деформированного тела служит сжатая (растянутая) пружина.
Две силы считают равными по модулю и противоположными по направлению, если они приложены к одному телу, но ускорение такого тела равно нулю.
Второй закон Ньютона
Равнодействующая всех сил приложенных к телу (векторная сумма всех сил)
($bar{F}$) равна производной от импульса тела по времени:
$$bar{F}=sum_{i=1}^{n} bar{F}_{i}=frac{d bar{p}}{d t}(1)$$
где $bar{p}=m bar{v}$ — импульс тела, m–масса рассматриваемого тела,
$bar{v}$ — скорость. Надо отметить, что уравнение (1) строго применимо только относительно
материальной точки. Если рассматривается протяженное тело, то под скоростью понимают скорость движения центра масс тела.
Если масса материальной точки (m)не изменяется во времени, то формула, определяющая результирующую силу, приложенную к ней
(второй закон Ньютона) можно представить в виде:
$$bar{F}=m frac{d bar{v}}{d t}=m bar{a}(2)$$
где $bar{a}$ – ускорение, которое материальная точка приобретает в результате
воздействия на нее силы. Выражение (2) показывает то, что если
$bar{F}$=0, то тело (материальная точка) движется равномерно и прямолинейно или покоится.
Если сила, приложенная к телу, является постоянной (по модулю и направлению), то формулу для нее можно представить в виде:
$$F=frac{Delta p}{Delta t}=frac{mleft(v_{2}-v_{1}right)}{t_{2}-t_{1}}$$
Единицы измерения силы
Основной единицей измерения момента силы в системе СИ является: [F]=Н=(кг•м)/с2
В СГС: [F]=дин
1Н=105 дин
Примеры решения задач
Пример
Задание. Уравнения $x=alpha t^{3}, y=beta t$ ($alpha$ и
$beta$ – постоянные коэффициенты) задают движение материальной точки массы m=const.
Как изменяется по модулю сила, которая действует на точку?
Решение. В качестве основы для решения задачи используем второй закон Ньютона в виде:
$bar{F} = mbar{a} (1.1)$
Зная законы изменения координат точки в зависимости от времени определим уравнения изменения составляющих ускорения.
Для этого найдем производные по времени от соответствующих координат:
$$
begin{array}{c}
a_{x}=frac{d^{2} x}{d t^{2}}=6 alpha t(1.2) \
a_{y}=frac{d^{2} y}{d t^{2}}=0(1.3)
end{array}
$$
Так как модуль ускорения равен:
$$a=sqrt{a_{x}^{2}+a_{y}^{2}}(1.4)$$
то, учитывая выражения (1.2) и (1.3), получаем:
$a = 6 alpha t (1.5)$
Так как ay=0, то получаем, что сила, которая действует на нашу точку, направлена по оси X, так как направление ускорение
и силы совпадают, а мы получили:
$$bar{a}=6 alpha t cdot bar{i}(1.6)$$
где $bar{i}$ – единичный вектор, направленный по оси X.
Исходя из второго закона Ньютона, имеем:
$$F=m cdot 6 alpha t, bar{F}=m 6 alpha t cdot bar{i}$$
Ответ. Так как $F=m cdot 6 alpha t$, то с течением времени сила увеличивается по модулю.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
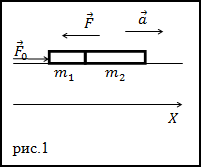
Задание. Два параллелепипеда лежат на горизонтальной поверхности. Они соприкасаются. Данные тела могут
скользить по поверхности опоры без трения. Масса одного тела равна m1, второго — m2. Первое тело толкнули с силой F0.
Какова сила давления тел друг на друга (F)?
Решение. Сделаем рисунок.
Рассмотрим, какие силы приложены к первому телув момент толчка, запишем для него второй закон Ньютона:
$$bar{F}_{0}+bar{F}+m_{1} bar{g}+bar{N}=m_{1} bar{a}(2.1)$$
где $m_{1} bar{g}$ – сила тяжести,
$bar{N}$ – реакция опоры,
$bar{a}$ – ускорение тела.
В проекции на ось Xуравнение (2.1) примет вид:
$$F_{0}-F=m_{1} a rightarrow F=F_{0}-m_{1} a(2.2)$$
Рассмотрим силы, приложенные к двум параллелепипедам как системе:
$$bar{F}_{0}+left(m_{1}+m_{2}right) bar{g}+overline{N^{prime}}=left(m_{1}+m_{2}right) bar{a}(2.3)$$
В проекции на ось X уравнение (2.3) примет вид:
$$F_{0}=left(m_{1}+m_{2}right) a(2.4)$$
Из уравнения (2.4) выразим ускорение:
$$a=frac{F_{0}}{m_{1}+m_{2}}$$
Подставим правую часть выражения (2.5) в (2.2) вместо ускорения:
$$F=F_{0}-m_{1} cdot frac{F_{0}}{m_{1}+m_{2}}$$
Ответ. $F=F_{0}-m_{1} cdot frac{F_{0}}{m_{1}+m_{2}}$
Читать дальше: Формула сопротивления.