Абсолютная и относительная частота
Абсолютная частота
Абсолютная частота определяет как часто определенное событие происходит в ходе эксперимента. Это всегда натуральное число между нулем и общим числом попыток.
i
Подсказка
Абсолютная частота относится только к количеству частоты определенного события.
Относительная частота
Относительная частота описывает насколько велика пропорция абсолютной частоты в общем количестве экспериментов. Она вычисляется следующим образом:
$text{Относительная частота} n_i$ $=frac{text{Абсолютная частота} f_i}{text{Количество попыток} N}$
Пример
Монету подбрасывают 10 раз. 6 раз выпадает орел и 4 раза решка. Определите абсолютную и относительную частоту.
Aбсолютная частота:
$f_{10}(орел)=6$
$f_{10}(решка)=4$
Относительная частота:
$N=10$
$n_{10}(орел)=frac{6}{10}=frac{3}{5}$
$n_{10}(решка)=frac{4}{10}=frac{2}{5}$
Абсолютная частота — всего одна статистическая мера используется в области изучение, — это количество раз, когда данные повторяются в наборе из них, значение, которое наблюдается в случайный эксперимент для каждой характеристики, время, в течение которого фазы или явления, которые наблюдая.
Его использование очень распространено в Описательная статистика, поскольку с помощью этой меры можно узнать, как наблюдения одной и той же характеристики распределены в выборке.
Следовательно, его расчет очень прост, так как он требует только подсчета того, сколько раз наблюдается характеристика или сколько раз она появляется в группе данных.
Его представление можно выразить через следующие номенклатуры: Fя, Иксяили же пя, где буквы f, x, n соответствуют частоте, а буква i обозначает i-ю итерацию проводимого эксперимента.
В этой статье вы найдете:
Расчет абсолютной частоты
Существует очень простой способ проверить точность ваших вычислений, то есть всех абсолютных частот выборочной совокупности, и это получить сумму всех из них.
Это означает, что сумма каждой из абсолютных частот выборки точно соответствует общему количеству данных того же самого, эти данные представлены как N.
В этом случае формула для расчета абсолютной частоты:
я = п
Ʃ fя = f1+ f2+ f3 +… + Fп = N
я = п
Полезность абсолютной частоты
Абсолютная частота позволяет:
- Графически изобразить частота появления каждого из выборочных данных с помощью частотных гистограмм, гистограмм, круговых диаграмм и других элементов, специально разработанных для каждого исследования.
- Узнайте больше о характеристиках выборки, совокупности и вселенной.
- Создай таблица частот как для количественных, так и для качественных переменных, которые можно расположить по порядку.
- Создавайте частотные таблицы с дискретными переменными, те, которые упорядочены от наивысшего к наименьшему, и таблицы частоты с непрерывными переменными, которые позволяют упорядочить их от низшего к высшему и сгруппировать в классы или интервалы.
- Рассчитать Накопленная абсолютная частота и Относительная частота, все важно заполнить таблицу частот, расчет других измерений статистика и разработка соответствующей графики
Примеры абсолютной частоты
Чтобы проиллюстрировать абсолютную частоту, будут рассмотрены две формы, рассматривая значения в дискретных переменных и непрерывных переменных.
Пример абсолютной частоты для дискретных переменных
Компания хочет развлечь детей своих 20 сотрудников (таким образом, N = 20) и сделать им подарок, после консультации были получены следующие данные:
2, 1, 0, 2, 4, 3, 4, 3, 2, 0, 1, 3, 2, 1, 1, 3, 0, 2, 2, 0
Табулирование данных дает следующую таблицу:
| Количество детей | Fя |
| 0 | 4 |
| 1 | 4 |
| 2 | 6 |
| 3 | 4 |
| 4 | 2 |
| Общее | 20 |
Затем можно проверить, что все данные были подсчитаны, поскольку сумма всех абсолютных частот полностью совпадает с размером выборки: Всего = 20 равно N = 20.
Таким же образом можно определить частоту количества детей каждого работника: 4 работника не имеют детей, 4 имеют только 1 ребенка, 6 рабочих имеют 2 детей, 4 имеют 3 детей и, наконец, 2 из них имеют 4 дети.
Пример абсолютной частоты для непрерывных переменных
Та же компания из предыдущего примера также должна знать рост каждого из своих сотрудников (N по-прежнему = 20), в этом случае данные будут десятичными числами, учитывая эту характеристику, удобнее работать с интервалами данных, так как иначе работа табулирование.
После выполнения соответствующих измерений были получены следующие 20 измерений:
1.67, 1.72, 1.90, 1.76, 1.72, 1.96, 1.78, 1.68, 1.87, 1.84, 1.92, 1.72, 1.71, 1.88, 1.77, 1.66, 1.73, 1.82, 1.90, 1.79
Табулирование данных дает следующую таблицу:
| Рост сотрудника | фи |
| [1.60 – 1.70) | 3 |
| [1.70 – 1.80) | 9 |
| [1.80 – 1.90) | 4 |
| [1.90 – 2.00) | 4 |
| Общее | 20 |
Символ «[» указывает, что номер, следующий за ним, включен в категорию, а символ «)» указывает, что номер, предшествующий ему, не включен в категорию.
Тогда можно проверить, что все данные, поскольку сумма всех абсолютных частот полностью совпадает с размером выборки: Total = 20 равно N = 20.
Таким же образом можно определить частоту роста рабочих: 3 сотрудника имеют рост от 1,60 до 1,70, Рост 9 сотрудников от 1,70 до 1,80, рост 4 сотрудников от 1,80 до 1,90 и, наконец, 4 сотрудника ростом от 1,90 до 2.00.
Графическое представление абсолютной частоты
Есть разные способы построить абсолютную частоту, некоторые из них:
- Диаграммы секторов: Этот график состоит из круга, разделенного на секторы, пропорциональные относительной частоте, которую он представляет.
- Гистограмма абсолютной частоты: представляет каждый Переменная в виде столбиков, его основание пропорционально соответствующей абсолютной частоте.
- Диаграммы многоугольника или прямоугольника: выполняется путем рисования линий, соединяющих самые высокие точки столбцов гистограммы абсолютной частоты.
Содержание
- — Что такое абсолютная и относительная частота?
- — Как вы рассчитываете общую частоту?
- — Какая сумма всех частот?
- — В чем разница между частотой и относительной частотой?
- — Что является абсолютным в статистике?
- — Как найти недостающую частоту в статистике?
- — Где вы строите кумулятивную частоту?
- — Какая общая частота?
- — Какая частота занятий?
- — Как узнать частоту занятий?
Абсолютная частота — это количество раз, когда определенное значение появляется в статистическом исследовании. Обозначается он через fi. Сумма абсолютных частот равна общему количеству данных, которое обозначается буквой N. Эта сумма обычно обозначается греческой буквой Σ (заглавная сигма), которая представляет собой «сумму».
Что такое абсолютная и относительная частота?
Абсолютная частота может быть отправной точкой для более детального статистического анализа. Относительная частота, например, получается из абсолютной частоты. … В отличие от абсолютной частоты, относительная частота обычно выражается в процентах или дробях, а не целым числом.
Как вы рассчитываете общую частоту?
Как вы это делаете:
- Подсчитайте общее количество предметов. На этой диаграмме их всего 40.
- Разделите количество (частоту) на общее число. Например, 1/40 =. 025 или 3/40 =. 075.
Какая сумма всех частот?
Сумма всех частот для всех классов равна равно количеству элементов в данных и это суммирование называется кумулятивной частотой, которая определяет количество записей этих статистических данных.
В чем разница между частотой и относительной частотой?
Частота — это количество раз, когда значение данных встречается. … Относительная частота — это отношение (доля или пропорция) количества раз, когда значение данных встречается в наборе всех результатов, к общему количеству результатов.
Что является абсолютным в статистике?
Абсолютное значение число — это его расстояние от нуля на числовой прямой. Например, -7 отстоит от нуля на 7 единиц, поэтому его абсолютное значение будет 7. Таким образом, абсолютное значение числа относится к величине числа безотносительно к его знаку. …
Как найти недостающую частоту в статистике?
, где L = младший класс, содержащий медиану, N = общее количество студентов, f = частота класса, содержащего медиану, cf = совокупная частота перед классом медианы, h = интервал класса, чтобы вычислить значение x.
…
| Метки | Частота (f) | Накопленная частота (см) |
|---|---|---|
| 50 – 60 | 10 | 65 + х + у + 10 = 75 + х + у |
Где вы строите кумулятивную частоту?
Диаграмма совокупной частоты строится путем нанесения совокупной частоты на границу верхнего класса соответствующей группы. Границы высшего класса для этой таблицы: 35, 40, 45, 50 и 55. Суммарная частота составляет нанесен на вертикальную ось а длина отложена по горизонтальной оси.
Какая общая частота?
Общая частота составляет значение, полученное сложением всех частот в таблице распределения частот. Относительная частота — это значение, полученное путем деления абсолютной частоты на общую частоту. Относительная кумулятивная частота — это значение, полученное как кумулятивная частота от общей частоты.
Какая частота занятий?
Частота занятий относится к количеству наблюдений в каждом классе; n представляет собой общее количество наблюдений во всем наборе данных. В примере с супермаркетом общее количество наблюдений равно 200. Относительная частота может быть выражена как доля (дробь) от общего числа или как процент от общего числа.
Как узнать частоту занятий?
Найдена относительная частота класса. разделив частоту на количество значений в выборке данных — это дает долю, попадающую в этот класс. Накопленная относительная частота находится путем деления относительной частоты на число в выборке.
Интересные материалы:
Можно ли добавлять эфирные масла в увлажнитель?
Можно ли добиться абсолютного нуля?
Можно ли еще играть в Diablo 2?
Можно ли есть размороженный замороженный картофель?
Можно ли ездить на велосипеде со сломанной спицей?
Можно ли играть в Hearthstone офлайн?
Можно ли использовать кондиционер без шампуня?
Можно ли использовать мой компьютер в течение 12 часов?
Можно ли использовать Pine Sol на ламинатных полах?
Можно ли использовать просроченный цвет волос?
What Is Absolute Frequency?
Absolute frequency is a statistical term describing the number of times a particular piece of data or a particular value appears during a trial or set of trials. Essentially, absolute frequency is a simple count of the number of times a value is observed. Absolute frequency is usually expressed as a whole number and is considered a very basic level of statistical analysis.
Understanding Absolute Frequency
Absolute frequency is often a component of basic data collection. For example, if you ask 10 friends if blue is their favorite color and three say yes and seven say no, you have enough information to determine absolute frequency: the absolute frequency of «yes» is equal to three and that of «no» is equal to seven. The number of values tracked often increases with sample size or trial scope. For example, if you ask 100 people if their favorite color is blue, the absolute frequency will likely increase. However, there is no additional complexity in the tracking of how many times a given value occurs.
Absolute frequency is used in some data visualizations. For example, the absolute frequency of survey responses will often be displayed on a graph to provide an easily digested view of the majority of responses for a particular question.
Absolute frequency can be used to show the most commonly occurring data piece in a trial or study, but it isn’t usually used as a primary statistical measurement.
Key Takeaways
- Absolute frequency is a simple count of how many times a particular response or value occurs over the course of the study.
- While absolute frequency is a very basic form of statistical analysis, it can be used as an input for more advanced statistical analysis, such as relative frequency.
- Absolute frequency is often displayed as a graph to give a visual representation of where the majority of occurrences cluster.
- «Absolute frequency» is sometimes called «raw count,» and sometimes called simply «frequency.»
Absolute Frequency vs. Relative Frequency
Absolute frequency can be the starting point for a more nuanced statistical analysis. Relative frequency, for example, is derived from absolute frequency. When the absolute frequency of values is tracked over the entire trial, the absolute frequency for a particular value can then be divided by the total number of values for that variable throughout the trial to get the relative frequency. The relative frequency is what we most often reference, whether it is the winning percentage of our favorite sports team or the percentage of fund managers that beat the market. Unlike absolute frequency, relative frequency is usually expressed as a percentage or fraction rather than a whole number.
Sometimes, when relative frequencies are very small, they are given in terms of «per thousand,» «per million,» etc., as in total number of crimes in a city per thousand people. Such adjustments are called «per capita.»
Example of Absolute Frequency
Imagine an accounting conference that wants to collect data on drinking habits in the profession. The conference organizer asks a room of 50 accountants how many glasses of wine they have had over the past week. After each of the 50 accountants gives their answer, it is put into a table displaying the absolute frequencies.
| Number of Alcoholic Drinks Per Week | |
|---|---|
| Number of Drinks per Week | Responses |
| 0 | 11 |
| 1 | 0 |
| 2 | 2 |
| 3 | 4 |
| 4 | 8 |
| 5 | 13 |
| 6+ | 12 |
There are a few observations you can make from the table displaying absolute frequency: more accountants drink some amount of alcohol than no alcohol. However, the most valuable observations that can be made from this data set involve more analysis. For example, 50% of all the accountants at the conference have five or more drinks per week.
However, as a statistical study, this survey leaves much to be desired. For one, there is no demographic information beyond the profession of the respondents. The gender of the respondents is not revealed. This is important, given there are different health guidelines for alcohol consumption by sex. We also don’t know the strength, or the alcohol by volume (ABV), of a particular drink being reported. Like absolute frequency, our example survey is just the beginning of a real analysis of alcohol consumption within the accounting profession.
Абсолютная частота — это количество раз, когда каждый элемент статистического обзора встречается. Это число показывает, сколько раз на переменную отвечали или наблюдали ее.
Идея частоты относится к повторению чего-либо, и в статистике они информируют о появлении или достижении исследуемых переменных.
В статистических исследованиях после сбора данных полезно организовать их в таблицы для облегчения чтения и интерпретации. Эти таблицы называются частотными таблицами. Эти таблицы записывают простую абсолютную частоту и совокупную абсолютную частоту в дополнение к другим значениям.
Простая абсолютная частота
Простая абсолютная частота или абсолютная частота — это запись количества повторений исследуемой переменной. Поскольку это счетчик, он представлен натуральными числами, что означает, что абсолютная частота является дискретной величиной.
Пример
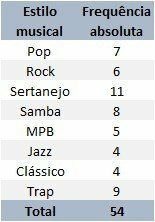
Был проведен опрос учеников 3-го курса старших классов, в ходе которого их спросили об их музыкальных предпочтениях. В опросе приняли участие 54 студента.
Результат был организован и представлен в следующей таблице частот:
Какова абсолютная частота переменной самбы?
разрешение
Переменные — это музыкальные стили, а абсолютные частоты — это количество ответов для каждого из них.
Таблица посещаемости показывает, что на Самбу ответили восемь студентов. Таким образом, абсолютная частота переменной Samba равна 8.
Накопленная абсолютная частота
Накопленная абсолютная частота или накопленная частота — это сумма простых абсолютных частот каждой переменной. В накопленной абсолютной частоте числовые значения складываются, накапливая, от одной переменной к другой, до последней изученной переменной.
Пример
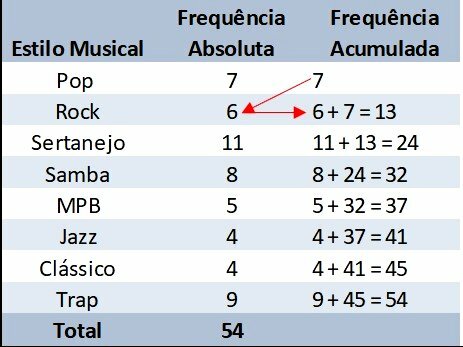
Заполняя таблицу в предыдущем примере, мы имеем:
В накопленной частоте к каждой строке добавляем абсолютную частоту с предыдущей накопленной. Таким образом, мы накапливаем значения для каждой строки таблицы.
Последняя строка столбца накопленной частоты уже представляет общее количество респондентов.
Упражнения с абсолютной частотой
Упражнение 1
В следующей таблице частот показано количество пользователей транспортных средств, работающих на бензине, спирте, гибком топливе и дизельном топливе, которые заправились на заправочной станции за последний час. Определяет абсолютную частоту пользователей гибких транспортных средств.
| Бензин | 23 |
|---|---|
| алкоголь | 16 |
| сгибать | |
| дизель | 8 |
| ВСЕГО | 61 |
См. Ответ
Правильный ответ: за последний час заправлено 14 машин Flex.
Общее количество клиентов, заполнившихся за последний час, представляет собой сумму абсолютных частот транспортных средств для каждого вида топлива.
23 + 16 + гибкий + 8 = 61
Решая уравнение для переменной flex, мы имеем:
flex = 61 — 23 — 16 — 8
flex = 14
Таким образом, за последний час было залито 14 машин Flex.
Упражнение 2.
В ходе опроса была собрана информация о намерениях избирателей в отношении шести кандидатов, которые будут баллотироваться на следующих выборах управляющего большим кондоминиумом.
| Кандидаты | Абсолютная частота |
|---|---|
| В | 98 |
| B | 67 |
| Ç | 143 |
| D | 178 |
| И | 86 |
| F | 76 |
Постройте столбец с кумулятивной абсолютной частотой и ответьте, какое общее количество избирателей ответило на опрос.
См. Ответ
Мы будем использовать ту же таблицу, что и вопрос, в качестве основы.
Чтобы построить сводную таблицу частот, мы должны повторить первое значение, 98. После этого мы добавляем абсолютное значение следующей строки, пока таблица не будет заполнена.
| Кандидаты | Абсолютная частота | Накопленная частота |
|---|---|---|
| В | 98 | 98 |
| B | 67 | 165 |
| Ç | 143 | 308 |
| D | 178 | 486 |
| И | 86 | 572 |
| F | 76 | 648 |
Общее количество проголосовавших указано в последней строке — 648 человек.
Упражнение 3.
(EEAR 2009) Если абсолютные частоты с 1-го по 6-й классы распределения равны соответственно 5, 13, 20, 30, 24 и 8, то совокупная частота 4-го класса этого распределения равна
а) 68.
б) 82.
в) 28%.
г) 20%.
См. Ответ
Правильный ответ: а) 68.
Организуя данные в частотную таблицу, мы получим:
| Абсолютная частота | Накопленная частота | |
|---|---|---|
| 1-й класс | 5 | 5 |
| 2 класс | 13 | 18 |
| 3 класс | 20 | 38 |
| 4 класс | 30 | 68 |
Следовательно, в 4 классе совокупная частота составляет 68.
Вам может быть интересно:
- Относительная частота
- Среднее, модное и медианное
- медиана
- Среднее арифметическое
- Средневзвешенное арифметическое значение
- Статистика
- Среднее геометрическое
- Дисперсионные меры
- Дисперсия и стандартное отклонение
Практические упражнения на:
- Упражнения на среднее арифметическое
- Статистика — упражнения
- Средние, модные и средние упражнения