Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как найти координаты точки
Поддержать сайт
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».
Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).
Запомните!
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,663 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,987 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Задачи с векторами только на первый взгляд кажутся сложными, особенно если задача связана с трехмерным пространством. Но не стоит пугаться ведь если разобраться по-лучше в данной тематике задачи решаются в два счета. Так например в данной статье мы разберем тематику определения координат вектора, исходными данными для которого известны координаты начальной и конечной точки.
Для того чтобы определить координаты некоторого вектора MN⃗vec{MN}, зная координаты начала и конца, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Задача 1
Рассмотрим первый вариант задачи. Вектор задан в двухмерном пространстве {x,y}. Тогда у каждой точки вектора существует две координаты, соответственно относящиеся к оси ОХ и ОУ. Формула для определения координаты вектора в таком случае принимает вид:
MN⃗=Mx−Nx;My−Ny.vec{MN}={M_x{-N}_x;M_y{-N}_y}.
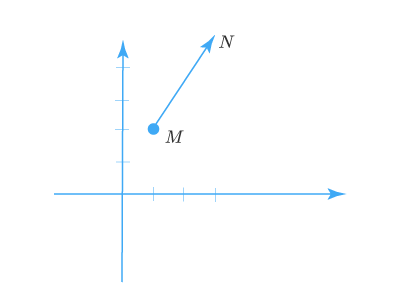
Рассмотрим на примере: На некоторой плоскости заданы точки M и N, координаты которых равны соответственно (1,2) и (3,5). Необходимо найти координаты вектора MN⃗vec{MN}
Решение
Возьмем некоторую плоскость ОХУОХУ и отметим точки ММ и NN. Затем соединим исходные точки и рассчитаем координаты полученного вектора. MN⃗={3−1;5−2}=2;3.vec{MN}=left{3-1;5-2right}={2;3}.
Вот так вот мы получили простое решение искомой задачи. Вариация таких задач может сочетать в себе нахождение не только координат вектора, но и отдельных координат исходных точек вектора.
Но у меня задача может быть не только одно- или двухмерное, но также трехмерное или как мы будем называть их n-мерное. Формула тогда в таком случае немного изменит вид, но смысл не меняется.
Задача 2
Сформулируем формулу для определения координат вектора расположенного в n-мерном пространстве.
Такое пространство подразумевает координаты точек в виде M(M1;M2;M3;..;Mn)M(M_1;M_2{;M}_3;..{;M}_n) и формула примет вид:
MN⃗=Mx−Nx;My−Ny;..;Mn−Nn.vec{MN}={M_x{-N}_x;M_y{-N}_y{;..;M}_n{-N}_n}.
Рассмотрим задачу на примере 5-мерного пространства. Необходимо найти координаты точки N вектора
MN⃗={3,8,4,1,7}vec{MN}={3,8,4,1,7}, если известны координаты точки M(1,9,6,7,4).M(1,9,6,7,4).
Решение
Не стоит пугаться при виде слов 5-мерное пространство, т.к. рисовать данную систему координат не обязательно. Стоит лишь правильно понимать и применять формулу которую мы рассмотрели выше. Перепишем ее еще раз для нашего случая.
MN⃗={M1−N1;M2−N2;M3−N3;M4−N4;M5−N5}.vec{MN}= {M_1{-N}_1;M_2{-N}_2{;M_3{-N}_3{;M}_4{-N}_4;M}_5{-N}_5}.
Тогда рассмотрим систему:
{1−N1=39−N2=86−N3=47−N4=14−N5=7begin{cases}1-N_1=3 \
9-N_2=8 \
6-N_3=4\
7-N_4=1\
4-N_5=7end{cases}
и решив данную систему, получим
{N1=−2N2=1N3=2N4=6N5=−3begin{cases}N_1=-2\
N_2=1\
N_3=2\
N_4=6\
N_5=-3\ end{cases}
Тогда получим ответ на задачу N(−2,1,2,6,−3).N(-2,1,2,6,-3).
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Координатная плоскость
Указать положение точки на плоскости можно с помощью координат. Для этого проведем на плоскости две перпендикулярные координатные прямые так, чтобы их начала отсчета совпадали.
Эти прямые называют осями координат, точку их пересечения О — начало отсчета.
Горизонтальная ось — ось абсцисс, обозначают буквой 
, поэтому еще называют ось , пишут: 
.
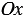
Вертикальная ось — ось ординат, обозначают буквой 
, поэтому еще называют ось , пишут: 
.
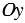
Оси и вместе образуют прямоугольную систему координат на плоскости. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
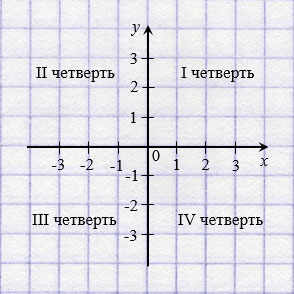
Координатные оси разбивают плоскость на четыре части, которые называют координатными четвертями и нумеруют так, как показано на рисунке ниже.
Отметим на координатной плоскости точку А. Проведем через нее прямую АВ, перпендикулярную оси абсцисс (АВ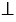 
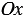
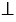
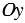
), и прямую АС, перпендикулярную оси ординат (АС ).
Точка В на оси имеет координату 5, а точка С на оси — координату 
3 . Число 5 называют абсциссой точки А, число 3 — ординатой точки А. Числа 5 и 3 однозначно определяют положение точки А на координатной плоскости, поэтому их называют координатами точки А и записывают: А(5; 3).
Обратите внимание, записывая координаты точки, абсциссу всегда ставят на первое место, а ординату — на второе. Если числа 5 и 3 поменять местами, то получим координаты другой точки — точки К(3; 5) (смотри рисунок выше).
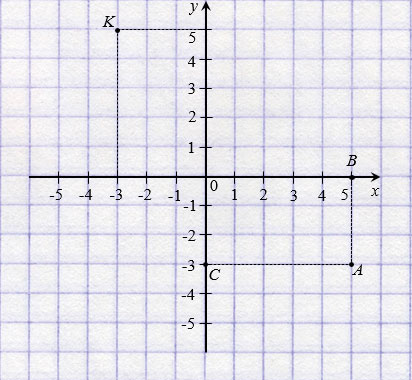
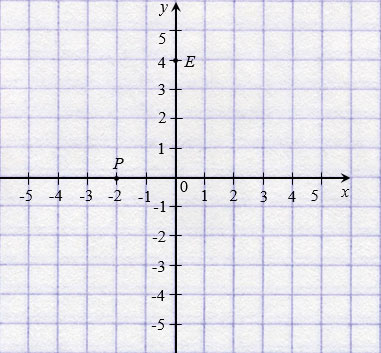
У начала координат абсцисса и ордината равны нулю, записывают так: О(0; 0). Если точка лежит на оси абсцисс, то ее ордината равна нулю, а если на оси ординат, то нулю равна ее абсцисса. На рисунке ниже: Р(2; 0); Е(0; 4).
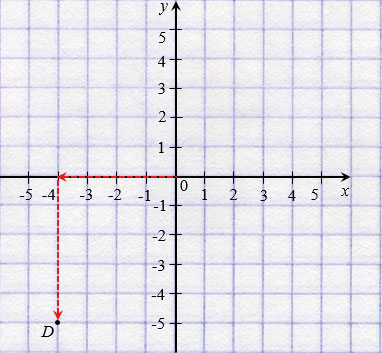
Чтобы попасть в точку D с координатами (4; 5), нужно сначала пройти по оси от начала отсчета влево на 4 единицы, а потом — на 5 единиц вниз.
Две точки с противоположными абсциссами и ординатами симметричны относительно начала координат.
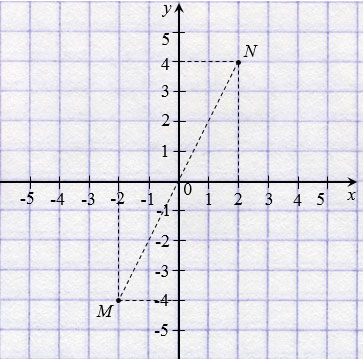
На рисунке ниже точки N(2; 4) и М(2; 4) симметричны относительно начала координат.
Две точки, имеющие равные ординаты и противоположные абсциссы, симметричны относительно оси ординат.
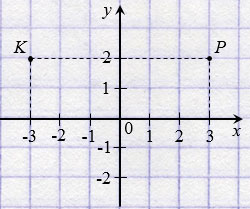
На рисунке ниже точки Р(3; 2) и К(3; 2) симметричны относительно оси ординат.
Две точки, имеющие равные абсциссы и противоположные ординаты, симметричны относительно оси абсцисс.
На рисунке ниже точки Р(3; 2) и Е(3; 2) симметричны относительно оси абсцисс.
Советуем посмотреть:
Перпендикулярные прямые
Осевая и центральная симметрии
Параллельные прямые
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1312,
Мерзляк, Полонский, Якир, Учебник
Номер 1318,
Мерзляк, Полонский, Якир, Учебник
Номер 1319,
Мерзляк, Полонский, Якир, Учебник
Номер 1328,
Мерзляк, Полонский, Якир, Учебник
Задание 1391,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1401,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1442,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1534,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1535,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1573,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 750,
Мерзляк, Полонский, Якир, Учебник
Номер 777,
Мерзляк, Полонский, Якир, Учебник
Номер 827,
Мерзляк, Полонский, Якир, Учебник
Номер 836,
Мерзляк, Полонский, Якир, Учебник
Номер 870,
Мерзляк, Полонский, Якир, Учебник
Номер 874,
Мерзляк, Полонский, Якир, Учебник
Номер 942,
Мерзляк, Полонский, Якир, Учебник
Номер 996,
Мерзляк, Полонский, Якир, Учебник
Номер 1137,
Мерзляк, Полонский, Якир, Учебник
Номер 1213,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 308,
Мерзляк, Полонский, Якир, Учебник
Номер 310,
Мерзляк, Полонский, Якир, Учебник
Номер 330,
Мерзляк, Полонский, Якир, Учебник
Номер 332,
Мерзляк, Полонский, Якир, Учебник
Номер 342,
Мерзляк, Полонский, Якир, Учебник
Номер 10,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
Номер 352,
Мерзляк, Полонский, Якир, Учебник
Номер 359,
Мерзляк, Полонский, Якир, Учебник
Номер 362,
Мерзляк, Полонский, Якир, Учебник
Актуальные цены на услуги геодезистов в Москве и Московской области в 2022 году.
Прямая геодезическая задача состоит в том, что по известным координатам начального пункта А(хА,уА), линии АВ, дирекционному углу этой линии αАВ и ее горизонтальному проложению sАВ — вычисляют координаты конечной точки В(хВ, уВ). Прямая геодезическая задача решается разными способами, один из них это онлайн решение, которым может воспользоваться любой кому лень разбираться с формулами.
Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.
Дано: Точка А( XA, YA ), SAB и αAB.
Найти: точку В( XB, YB ).
Непосредственно имеем:
ΔX = XB – XA ;
ΔY = YB – YA .
Разности ΔX и ΔY точек последующей и предыдущей называются приращениями. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:
ΔX = SAB · cos αAB ;
ΔY = SAB · sin αAB .
Так как в этих формулах SAB всегда число положительное, то знаки приращений ΔX и ΔY зависят от знаков cos αAB и sin αAB. Для различных значений углов знаки ΔX и ΔY представлены в таблице ниже.
Таблица знаков приращений координат ΔX и ΔY
| Приращения | Четверть окружности в которую направлена линия | |||
| I (СВ) | II (ЮВ) | III (ЮЗ) | IV (СЗ) | |
| ΔX | + | – | – | + |
| ΔY | + | + | – | – |
При помощи румба, приращения вычисляют по формулам:
ΔX = SAB · cos rAB ;
ΔY = SAB · sin rAB .
Знаки приращениям дают в зависимости от названия румба.
Вычислив приращения, находим искомые координаты другой точки:
XB = XA + ΔX ;
YB = YA + ΔY .
Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения. Прямая геодезическая задача чаще всего используется при вычислении координат в теодолитном ходе.