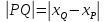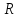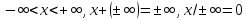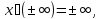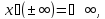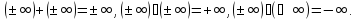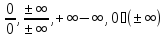Как найди длину промежутка

1. Длина интервала на числовой прямой

Пусть
точки
иимеют координатына числовой оси. Тогда длина интервала
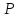
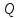
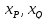
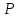
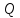
(отрезка) с концамиивычисляется по формуле

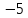
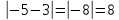
Пример. Расстояние от точкидо точкиравно.

1. Расширенная область действительных чисел

Присоединим
к

два элемента —и,
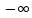
полагая, что для всех

Для
всех положительных
будем считать, что

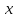
а
для отрицательных
—

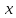
Полагаем
также

Таким
образом, неопределенными остаются
операции:

Вещественные
числа вместе с
образуютрасширенную числовую прямую.
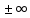
Можно убедиться, что основные
арифметические правила (ассоциативность,
коммутативность, дистрибутивность)
остаются верными и для расширенной
системы чисел, при условии определенности
всех входящих операций.

19

Соседние файлы в папке LEKTsII

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Найти длину промежутка значит найти расстояние от точки с координатой (-3) до точки с координатой (1). Это расстояние равно сумме длин отрезков от (0) до (-3) и от (1) до (0).

Расстояние от (-3) до (0) равно d₁=3, расстояние от (1) до (0) равно d₂=1 , сумма этих длин равна d=d₁+d₂=3+1=4 .

Из этих соображений вывели правило, чтобы найти расстояние между двумя точками, надо найти модуль разности между координатами этих точек:

Длина отрезка — это то же самое, что и расстояние между двумя точками.

Можно рассмотреть несколько случаев, когда эта длина неизвестна

пример 1

есть на прямой три точки, которые образуют три отрезка

Чтобы найти отрезок побольше, нужно два меньших сложить.

Чтобы найти меньший отрезок, нужно от большого отнять другой меньший

АС=АВ-СВ или СВ=АВ-АС

пример 2

найдем длину отрезка на координатной прямой.

отрезок лежит между точками А(-5) и В(9), тогда его длина 9-(-5)=14

пример 3

найдем длину отрезка на координатной плоскости.

здесь тоже все просто — по координатам находим длину условных катетов прямоугольного треугольника а дальше по формуле Пифагора находим длину.

Числовые промежутки

Числовые промежутки или просто промежутки — это числовые множества, которые можно изобразить на координатной прямой. К числовым промежуткам относятся лучи, отрезки, интервалы и полуинтервалы.

Виды числовых промежутков

Название	Изображение	Неравенство	Обозначение
Открытый луч		x > a	(a; +∞)
	x 2. Открытые лучи обозначаются с помощью круглых скобок — (2; +∞), данная запись читается так: открытый числовой луч от двух до плюс бесконечности .

Множество, которому соответствует неравенство x числовой луч от двух до плюс бесконечности и числовой луч от минус бесконечности до двух . Квадратная скобка в обозначении показывает, что точка 2 принадлежит числовому промежутку.

Отрезок

Отрезок — это множество точек прямой, лежащих между двумя граничными точками, принадлежащими данному множеству. Такие множества задаются двойными нестрогими неравенствами.

Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный отрезок, можно задать двойным неравенством -2 ⩽ x ⩽ 3 или обозначить [-2; 3], такая запись читается так: отрезок от минус двух до трёх .

Интервал и полуинтервал

Интервал — это множество точек прямой, лежащих между двумя граничными точками, не принадлежащими данному множеству. Такие множества задаются двойными строгими неравенствами.

Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный интервал, можно задать двойным неравенством -2 интервал от минус двух до трёх .

Полуинтервал — это множество точек прямой, лежащих между двумя граничными точками, одна из которых принадлежит множеству, а другая не принадлежит. Такие множества задаются двойными неравенствами:

Обозначаются данные полуинтервалы так: (-2; 3] и [-2; 3). Читается это так: полуинтервал от минус двух до трёх, включая 3 , и полуинтервал от минус двух до трёх, включая минус два .

Источник

∑ Некоторые алгебраические понятия — определения и работа с ними

Числовые промежутки. Контекст. Определение

Равенство (уравнение) имеет одну точку на числовой прямой (хотя это точка зависит от проделанных преобразований и выбранного корня). Само решение уравнения будет числовым множеством (иногда состоящим из одного числа). Однако, всё это на числовой прямой (визуализации множества вещественных чисел) будет отображаться лишь точечно, но существуют также более обобщённые типы отношений между двумя числами — неравенства. В них числовая прямая разделяется некоторым числом и от неё отсекается определённая часть — значения выражения или числовой промежуток.

Тему числовых промежутков логично обсуждать вместе с неравенствами, но это отнюдь не означает, что она связана лишь с ними. Числовые промежутки (интервалы, отрезки, лучи) являются множеством значений переменной, удовлетворяющих некоему неравенству. То есть, по сути, это множество всех точек на числовой прямой, ограниченной какими-то рамками. Поэтому наиболее тесно связана тема числовых промежутков с понятием переменной. Там, где есть переменная, или произвольная точка x на числовой прямой, и её применяют, используют, есть и числовые промежутки, интервалы — значения x. Часто значение может быть любым, но это тоже числовой промежуток, охватывающий всю числовую прямую.

Введём понятие числового промежутка. Среди числовых множеств, то есть множеств, объектами которых являются числа, выделяют так называемые числовые промежутки. Их ценность в том, что очень легко вообразить множество, соответствующее указанному числовому промежутку, и наоборот. Поэтому с их помощью удобно записывать множество решений неравенства. Тогда как множеством решения уравнения будет не числовой промежуток, а просто несколько чисел на числовой прямой, с неравенствами, иначе говоря, любыми ограничениями значения переменной появляются числовые промежутки.

— это множество всех точек числовой прямой, ограниченное данным числом или числами (точками на числовой прямой).

Числовой промежуток любого вида (множество значений x, заключённых между некоторыми числами) всегда можно представить тремя видами математических обозначений: специальными обозначениями промежутков, цепочками неравенств (одним неравенством или двойным неравенством) или геометрически на числовой прямой. По сути, все эти обозначения имеют один смысл. Они дают ограничение(-я) для значений какого-то математического объекта, переменной величины (некоторой переменной, любого выражения с переменной, функции и т.д.).

Из вышесказанного можно понять, что так как можно по-разному ограничить область числовой прямой (есть разные типы неравенств), то и типы числовых промежутков бывают разные.

Виды числовых промежутков

Каждый тип числового промежутка имеет собственное название, особое обозначение. Для обозначения числовых промежутков используют круглую и квадратную скобку. Круглая скобка означает, что конечная, определяющая границу, точка на числовой прямой (конец) у этой скобки не входит во множество точек данного промежутка. Квадратная скобка означает, что конец входит в промежуток. С бесконечностью (с этой стороны промежуток не ограничен) используют круглую скобку. Иногда вместо круглых скобок можно писать квадратные, повёрнутые в обратную сторону: (a;b) ⇔]a;b[

Вид промежутка (название)	Геометрическое изображение (на числовой прямой)	Обозначение	Запись с помощью неравенств (для краткости всегда цепочками)
Интервал (открытый)		(a;b)	a x x ≤ b
Полуинтервал (полусегмент)		[a;b)	a ≤ x x ≤ b
Луч		[a;+∞)	x ≥ a
Луч		(-∞;b]	x ≤ b
Открытый луч		(a;+∞)	x > a
Открытый луч		(-∞;b)	x x ∈ ℝ (обычно говорят о множестве вещественных чисел, для представления комплексных чисел используют уже комплексную плоскость, а не прямую)
Равенство		[a;a] или x=a	x = a (частный случай нестрогого неравенства: a ≤ x ≤ a — интервал длины 1, где оба конца совпадают — отрезок, состоящий из одной точки)
Пустое множество		∅	Пустое множество тоже является промежутком — у переменной x нет значений (пустое множество). Обозначение: x∈∅⇔x∈ .

С названиями промежутков может возникнуть путаница: есть огромное количество вариантов. Поэтому лучше всегда точно их указывать. В англоязычной литературе используется только термин интервал («interval») — открытый, замкнутый, полуоткрытый (полузамкнутый). Вариаций много.

С помощью промежутков в математике обозначается очень большое количество вещей: есть промежутки изоляции при решении уравнений, промежутки интегрирования, промежутки сходимости рядов. Промежутками принято всегда обозначать при при исследовании функции её область значений и область определения. Промежутки очень важны, например, есть теорема Больцано — Коши (можно узнать больше в «Википедии»).

Системы и совокупности неравенств

Система неравенств

Итак, переменную x или значение некоторого выражения можно сравнить с какой-то постоянной величиной — это неравенство, но можно сравнивать это выражение с несколькими величинами — двойное неравенство, цепочка неравенств и т. д. Именно это было показано выше — как интервал и отрезок. И то, и то является системой неравенств.

Итак, если ставится задача найти множество общих решений двух или больше неравенств, то можно говорить о (также как с уравнениями — хотя можно сказать, что уравнения — это частный случай).

Тогда очевидно, что значение переменной, использованной в неравенствах, при котором каждое из них обращается в верное, называется .

Все неравенства, входящие в систему объединяют фигурной скобкой — «<«. Иногда их записывают в виде двойного неравенства (как показано выше) или даже цепочкой неравенств. Пример типичной записи: f &ApplyFunction; x ≤ 30 g &ApplyFunction; x ≥ 5 .

Решение систем линейных неравенств с одной переменной в общем случае сводится к вот этим 4 видам: x > a x > b (1) x > a x b (2) x a x > b (3) x a x b (4) . Здесь предполагается, что b > a.

Любую систему можно решать графически с использованием числовой прямой. Там, где решения составляющих систему неравенств пересекаются и будет решение самой системы.

Представим для каждого случая графическое решение.

(1) x>b (2) a (3) x (4) x∈∅

Итак, что же получается? В случае (1) решением является промежуток (a;+∞). В случае (2) решение — промежуток (a;b). Случай (3) — это пример открытого луча (-∞;a). В случае (4) же решения отдельных неравенств не пересекаются — система не имеет решений.

Далее, системы неравенств можно классифицировать как равносильные, если они имеют общее множество решений. Отсюда (как можно видеть выше) следует, что более сложные системы можно упрощать (например, используя геометрическое решение).

Фигурную скобку можно условно, грубо говоря, назвать эквивалентом союза «И» для неравенств

Совокупность неравенств

Однако, бывают и другие случаи. Так кроме пересечения множеств решений бывает их объединение: если ставится задача найти множество всех таких значений переменной, каждое из которых является решением хотя бы одного из данных неравенств, то говорят, что надо .

Итак, все неравенства в совокупности объединяют скобкой совокупности «[«. Если значение переменной удовлетворяет хотя бы одному неравенству из совокупности, то оно принадлежит множеству решений всей совокупности. Также и с уравнениями (опять же их можно назвать частным случаем).

Если фигурная скобка — и, то скобка совокупности — это, условно, говоря простым языком, эквивалент союза «ИЛИ» для неравенств (хотя это, конечно, будет логическое или, включающее случай, удовлетворяющий обоим условиям).

Итак, — это значение переменной, при котором хотя бы одно неравенство, обращается в верное.

Множество решений, как совокупности, так и системы неравенств, можно определить через две основные бинарные операции для работы с множествами — пересечение и объединение. Множество решений системы неравенств — это пересечение множеств решений неравенств, её составляющих. Множество решений совокупности неравенств — это объединение множеств решений неравенств, её составляющих. Это тоже можно проиллюстрировать. Допустим у нас есть система и совокупность из двух неравенств. Множество решений первого обозначим A, а множество решений второго обозначим B. Прекрасной иллюстрацией будет диаграмма Эйлера-Венна.

A ∪ B — решение системы неравенств A ∩ B — решение совокупности неравенств fedor1113
К остальным темам

Источник

Таблица числовых промежутков: виды, обозначения, изображения

Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.

Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств. В заключение будет рассмотрена таблица промежутков.

Виды числовых промежутков

Каждый числовой промежуток характеризуется:

• названием;
• наличием обычного или двойного неравенства;
• обозначением;
• геометрическим изображением на координатой прямой.

Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.

Произведем описание числовых промежутков с выше указанными сторонами:

• Открытый числовой луч. Название связано с тем, что его опускают, оставляя открытым.

Этот промежуток имеет соответствующие неравенства x a или x > a , где a является некоторым действительным числом. То есть на такое луче имеются все действительные числа, которые меньше a — ( x a ) или больше a — ( x > a ) .

Множество чисел, которые будут удовлетворять неравенству вида x a обозначается виде промежутка ( − ∞ , a ) , а для x > a , как ( a , + ∞ ) .

Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x a включает в себя точки, которые расположены левее, а для x > a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при помощи штриховки. Рассмотрим рисунк, приведенный ниже.

Из вышеприведенного рисунка видно, что числовые промежутки соответствуют части прямой, то есть лучам с началом в a . Иначе говоря, называется лучами без начала. Поэтому он и получил название открытый числовой луч.

Рассмотрим несколько примеров.

При заданном строгом неравенстве x > − 3 задается открытый луч. Эту запись можно представить в виде координат ( − 3 , ∞ ) . То есть это все точки, лежащие правее, чем — 3 .

Если имеем неравенство вида x 2 , 3 , то запись ( − ∞ , 2 , 3 ) является аналогичной при задании открытого числового луча.

• Числовой луч. Геометрический смысл в том, что начало не отбрасывается, иначе говоря, луч оставляет за собой свою полноценность.

Его задание идет с помощью нестрогих неравенств вида x ≤ a или x ≥ a . Для такого вида приняты специальные обозначения вида ( − ∞ , a ] и [ a , + ∞ ) , причем наличие квадратной скобки имеет значение того, что точка включена в решение или в множество. Рассмотрим рисунок, приведеный ниже.

Для наглядного примера зададим числовой луч.

Неравенство вида x ≥ 5 соответствует записи [ 5 , + ∞ ) , тогда получаем луч такого вида:

• Интервал. Задавание при помощи интервалов записывается при помощи двойных неравенств a x b , где а и b являются некоторыми действительными числами, где a меньше b , а x является переменной. На таком интервале имеется множество точек и чисел, которые больше a , но меньше b . Обозначение такого интервала принято записывать в виде ( a , b ) . Наличие круглых скобок говорит о том, что число a и b не включены в это множество. Координатная прямая при изображении получает 2 выколотые точки.

Рассмотрим рисунок, приведенный ниже.

Пример интервала − 1 x 3 , 5 говорит о том, что его можно записать в виде интервала ( − 1 , 3 , 5 ) . Изобразим на координатной прямой и рассмотрим.

• Числовой отрезок. Данный промежуток отличается тем, что он включает в себя граничные точки, тогда имеет запись вида a ≤ x ≤ b . Такое нестрогое неравенство говорит о том, что при записи в виде числового отрезка применяют квадратные скобки [ a , b ] , значит, что точки включаются во множество и изображаются закрашенными.

Рассмотрев отрезок, получим , что его задание возможно при помощи двойного неравенства 2 ≤ x ≤ 3 , которое изображаем в виде 2 , 3 . На координатной прямой данный точки будут включены в решение и закрашены.

• Полуинтервалы. Это промежуточные интервалы с включением приграничных точек. Они записываются при помощи двойных неравенств вида a x ≤ b или a ≤ b c , где ( a , b ] и [ a , b ) . Изобразим на координатной прямой.

Если имеется полуинтервал ( 1 , 3 ] , тогда его обозначение можно в виде двойного неравенства 1 x ≤ 3 , при чем на координатной прямой изобразится с точками 1 и 3 , где 1 будет исключена, то есть выколота на прямой.

Таблица числовых промежутков

Промежутки могут быть изображены в виде:

• открытого числового луча;
• числового луча;
• интервала;
• числового отрезка;
• полуинтервала.

Чтобы упростить процесс вычисления, необходимо пользоваться специальной таблицей, где имеются обозначения всех видов числовых промежутков прямой.

Источник

Длина отрезка

Отрезок — это геометрическая фигура, которая имеет начало и конец, значит отрезки можно измерять.

Измерить отрезок — значит найти его длину (расстояние между его концами).

Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.

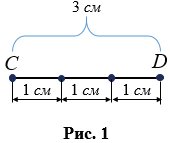
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.

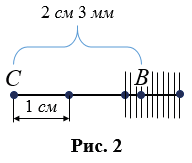
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).

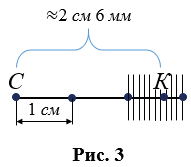
Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:

• Если нужны более точные измерения, то процесс деления продолжается, т.е. миллиметр также можно разделить на 10 равных частей и т.д. Такая точность в повседневной жизни не нужна, поэтому пользуются приближенными значениями, но имеет важную роль при проведении каких-либо исследований для совершения научных открытий.

За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.

Длина отрезка — это всегда какое-то положительное число.

Свойства длин отрезков:

1. Равные отрезки имеют равные длины.
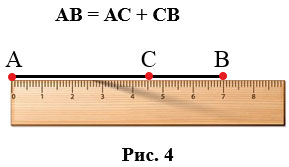
2. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков. Так на Рис.4 точка С делит отрезок АВ на два отрезка АС и СВ. Приложим линейку и видим, что АС = 4,5 см, СВ = 2,5 см, АВ = 7 см, т.е. АС + СВ = АВ.

1. Если длина одного отрезка MN в n раз больше длины другого отрезка PQ, то записываютMN = nPQ. На Рис.5 даны два отрезка MN и PQ, приложим к ним линейку и видим, что MN = 8 см, PQ = 2 см, т.е. MN больше PQ в 4 раза, тогда можно записать, что MN = 4PQ.

Поделись с друзьями в социальных сетях:

Источник

Узнай длину каждого отрезка. Какой из них длиннее и на сколько сантиметров? Решить задачу разными способами.

Ответ или решение 1

Нам дан рисунок на котором изображены два отрезка http://bit.ly/2BiFMZ3 красный и зеленый. Нужно найти длины отрезков и на сколько один отрезок длиннее второго разными способами.

Чтобы решить задачу будем действовать по следующему алгоритму действий

• на рисунке помимо отрезков изображена еще и линейка, с помощью нее мы можем ответить на вопрос какая длина красного отрезка;
• вторым шагом мы можем с помощью линейка найти на сколько длина красного отрезка больше длинны зеленого;
• третьим шагом зная длину красного отрезка и на сколько зеленый отрезок меньше красного мы можем найти длину зеленого отрезка;
• второй способ решения задачи измерить длину двух отрезков, а затем найти на сколько один отрезок длиннее второго.

Узнаем длины отрезков и на сколько один отрезок длиннее второго

Первый способ решения задачи.

Смотрим на рисунок и определяем длину красного отрезка. Она равна 10 см.

Длину зеленого отрезка вычислить сложнее, так как его начало не совпадает с началом числового луча.

Зато мы можем сна рисунке увидеть на сколько красный отрезок длиннее зеленого.

Смотрим на рисунок и видим, что эта разница в длинах равна 3 см.

Теперь мы можем легко найти длину зеленого отрезка. Для этого из длины красного отрезка вычтем разницу в длинах красного и зеленого отрезков и получим длину зеленого отрезка.

10 см — 3 см = 7 см длина зеленого отрезка.

Второй способ решения задачи.

Длинна красного отрезка видна с рисунка и равна 10 см, берем линейку и меряем длину зеленого отрезка — он равен 7 см.

Разница в длине: 10 см — 7 см = 3 см.

Ответ: красный отрезок 10 см, зеленый отрезок 7 см, разница в длине 3 см.

Источник

Как узнать на сколько сантиметров один отрезок длиннее другого, разными способами

Ответ или решение 2

Рассмотрим варианты определения разности длины отрезков.

Первый способ

Предположим, что у нас имеют два отрезка, каждый из которых имеет свою длину. Наша задача определить определить на сколько сантиметров один из отрезков больше другого.

определяемся с отрезками и первым способом решения:

• первый отрезок имеет длину X см и он больше второго отрезка;
• второй отрезок имеет длину Y cм и он меньше первого отрезка;
• нужно определить на сколько см первый отрезок больше второго.

В результате решением будет: X-Y= Z, где Z это величина в сантиметрах на которую первый отрезок больше другого. И характерность этого способа в том, что мы узнавали насколько именно сантиметров первый отрезок длиннее второго.

Второй способ

Второй способ также подразумевает наличие двух отрезков разной длинны. Но во втором способе нашей задачей будет определение длины отрезка, который нужно добавить до величины второго отрезка, чтобы достичь длины первого отрезка

В этом способе решение будет выглядеть как: Y+Z=X

Разница способов заключается в подходе, который зависит от условия задачи. Если нужно определить, на сколько один отрезок больше другого, мы пользуемся первым способом. Если нужно определить, какой длинны отрезок нужно добавить до второго отрезка, чтобы получить первым, тогда мы используем второй способ.

Оба способа одинаково хороши и отличаются лишь акцентом в задаче, который изначально ставиться для задания пути желаемого решения. В обеих случаях используется одинаковый логический подход, одна общая формула.

Способ 1. Необходимо измерить длину каждого отрезка, а затем вычислить их разность математическим способом.

Способ 2. Нужно совместить начала отрезков (при этом они должны располагаться на одной прямой) и измерить расстояние от конца одного отрезка до другого.

Источник

Урок 3 Бесплатно Отрезок. Длина отрезка

Начнем знакомство с одним из разделов математики, который называется геометрия.

Слово геометрия древнегреческого происхождения, оно означает «землемерие» («гео» — земля, «метрео» — измерять).

Геометрия — древняя наука, возникла в результате практической деятельности человека: строительства зданий и дорог, установления земельных наделов и определения их размеров.

Становление данной науки происходило тысячелетиями.

В настоящее время геометрия — наука, занимающаяся изучением геометрических фигур, их свойствами, размерами и преобразованиями.

Сегодня обратим внимание на основные, базовые геометрические фигуры, такие как точка и отрезок.

Узнаем, что называют ломаной линией, какие геометрические фигуры называют многоугольниками, рассмотрим их основные элементы и характеристики.

Научимся сравнивать, находить длины отрезков.

Познакомимся с различными единицами измерения отрезков.

Рассмотрим свойства измерения длин отрезков.

Отрезок

Геометрическая фигура- это математическая модель, в которой рассматривается только форма и размер, не обращая внимания на иные свойства и состояния (цвет, из какого материала изготовлены, в каком состоянии находятся).

Как здания складываются из кирпичиков, так и сложные геометрические фигуры состоят из базовых фигур.

Одной такой элементарной фигурой является точка.

Точка — это неделимая фигура, не имеет частей и размеров (высоты, радиуса, длины и т.д.), направления и других характеристик.

В реальности моделью, которая дает представление о точке может стать, например, след, оставленный острием карандаша, или отверстие на бумаге от швейной иглы.

Слово «точка» с латинского языка означает мгновенное касание, укол.

Точку принято рассматривать как некоторое место в пространстве или на плоскости.

Принято обозначать точки заглавными латинскими буквами (А, В, С и т.д.).

Две точки на плоскости можно соединить бесконечным множеством линий.

Самой короткой линией, соединяющей две точки на плоскости, будет прямая, проведенная по линейке через эти две точки.

Кратчайшая линия между двумя точками называется отрезком.

Любые две точки можно соединить только одним отрезком.

Отрезок — это часть прямой линии, ограниченной двумя точками.

Точки, ограничивающие отрезок, называются концами отрезка.

Отрезок обозначают указанием имен его концов.

Через точки А и В с помощью линейки провели прямую.

А и В — концы отрезка.

Так как отрезок обозначают именами точек, получим отрезок АВ или ВА.

Пишут и говорят так: «Отрезок АВ» или «Отрезок ВА».

В названии отрезка не важно в каком порядке указываются его концы.

Отрезок АВ и ВА — это один и тот же отрезок.

Отрезок можно построить с помощью линейки.

Для этого необходимо к отмеченным на плоскости точкам приложить линейку и провести прямую от одного конца отрезка до другого.

Чтобы с помощью линейки начертить отрезок, который длиннее чем сама линейка, нужно поступить следующим образом:

Между точками А и В отметить точку С.

Затем передвинем линейку так, чтобы левый конец линейки оказался около точки С, по правому концу линейки отложим точку D.

Последовательно соединив концы отрезков, получится отрезок AD, который длиннее, чем линейка.

У меня есть дополнительная информация к этой части урока!

Давайте разберемся, как могут располагаться точки по отношению к отрезку:

1. Точка лежит на отрезке.

Говорят: «Точка G принадлежит отрезку ».

Записывают это так: G ∈ AB

2. Точка не лежит на отрезке.

Говорят: «Точка не принадлежит отрезку ».

Записывают это так: R ∉ AB

Пройти тест и получить оценку можно после входа или регистрации

Длина отрезка

Каждый отрезок имеет определенную длину, значение которой является числом.

Длина в геометрии — это величина, которая характеризует протяженность.

Длина отрезка — это расстояние между концами отрезка.

Так как каждый отрезок имеет длину, отрезки можно измерять и сравнивать.

Существует несколько способов сравнения отрезков.

1. Приблизительный способ сравнения.

Данный способ сравнения применяют только в том случае, когда длины отрезков явно отличаются.

Пример: Даны два отрезка АВ и ЕР

Очевидно, что отрезок АВ длиннее отрезка ЕР, значит, АВ > ЕР

2. Совмещение отрезков — более точный способ сравнения отрезков.

Метод заключается в следующем: совмещаются два отрезка друг с другом так, чтобы совпали их концы с одной стороны.

По расположению других концов относительно друг друга можно оценить какой из отрезков длиннее, а какой короче.

Если при наложении отрезков друг на друга длины отрезков совпадут, то отрезки равны (отрезки в этом случае будут равными фигурами).

Если при наложении отрезков друг на друга один из отрезков будет составлять часть второго, то первый отрезок является короче второго (т.е. длина первого меньше длины второго).

Пример: Даны два отрезка АВ и ОЕ

Сравним данные отрезки методом совмещения отрезков.

Совместим левый конец А отрезка АВ и левый конец О отрезка ОЕ.

Можно заметить, что отрезок ОЕ составляет часть отрезка АВ.

Значит, отрезок ОЕ короче отрезка АВ.

Данный метод удобен, если есть возможность перемещать отрезки, совмещать один с другим.

3. Сравнение отрезков с помощью измерителя.

Если нет возможности перемещать сравниваемые отрезки, то можно использовать промежуточный измеритель.

В математике для этих целей используют специальный чертежный инструмент, который называется циркулем.

Чтобы сравнить отрезки с помощью циркуля, необходимо совместить концы отрезка с ножками циркуля.

Не меняя раствор циркуля, приложить его ко второму отрезку и сравнить.

1. Если ножки циркуля совпадают с концами сравниваемого отрезка, то отрезки считаются равными.
2. Если отрезок выходит за пределы расставленных ножек циркуля, то он больше исходного отрезка.
3. Если же отрезок находится между концами измерителя, то сравниваемый отрезок меньше исходного.

Если нет возможности сравнить отрезки наложением и нет циркуля под рукой, то в качестве измерителя можно использовать нитку.

В таком случае нужно нитку приложить к исходному отрезку, на нитке по отрезку сделать замер, затем нитку приложить ко второму отрезку, оценить расположение замера на нитке по отношению к исследуемому отрезку, сделать вывод.

Пусть даны три отрезка СD, АЕ, BG

Сравним эти отрезки с помощью циркуля.

Соединим ножки циркуля с концами С и D отрезка СD.

Приложим циркуль с заданным раствором к отрезку АЕ.

Концы измерителя совпали с точками отрезка АЕ, значит, отрезки CD и AE равны: (CD = AE).

Приложим циркуль с заданным раствором к отрезку BG.

Отрезок выходит за концы измерителя, т.е. является частью отрезка BG, следовательно, отрезок BG длиннее отрезка СD: (BG > СD).

Все рассмотренные способы сравнения длины отрезков проводят без определения значения длины сравниваемых отрезков.

4. Существует еще один способ сравнения длины отрезков путем измерения их длинны.

Для этого необходимо сначала измерить длину каждого отрезка, далее сравнить полученные значения их длины и сделать вывод.

Большим будет являться тот отрезок, длина которого больше.

Соответственно, если длины измеряемых отрезков равны, то и отрезки равны.

У меня есть дополнительная информация к этой части урока!

Ломаная линия

Если последовательно соединить отрезки так, чтобы конец одного отрезка являлся началом следующего (при этом соседние отрезки не лежат на одной прямой), то образуется геометрическая фигура, которая называется ломаной линией.

Отрезки, из которых состоит ломаная линия, называют звеньями.

Концы отрезков называют вершинами ломаной.

Самые крайние вершины ломаной называют концами ломаной

Обозначение ломаной линии составляют из названий вершин этой ломаной, называя их по порядку.

Длиной ломаной называется сумма длин всех ее звеньев.

На рисунке изображена ломаная линия АBCDE.

Вершины ломаной АBCDE: А, B, C, D, Е.

Звенья ломаной АBCDE: AB, BC, CD, DE.

A и E — концы ломаной.

Найдем длину ломаной АВСDE:

АВСDE = AB+ BC+ CD+ DE = 2 см + 3 см + 4 см + 5 см = 14 см

Ломаная, концы которой совмещаются, называется замкнутой.

Многоугольником называется фигура, ограниченная замкнутой ломаной линией, звенья которой не пересекаются.

Отрезки (звенья) ломаной линии называют сторонами многоугольника.

Общие точки двух отрезков (сторон) многоугольника называют его вершинами.

Каждая пара сторон многоугольника, сходящиеся в одной точке, образуют углы многоугольника.

Количество сторон и количество углов в многоугольнике совпадают.

Вершины, стороны и углы многоугольника обозначаются аналогично ломаной линии.

Многоугольник принято обозначать и называть по его вершинам, начиная с любой вершины и называя их последовательно, в любом порядке.

На рисунке изображен многоугольник АBCDEF.

Вершины многоугольника АBCDEF: А, B, C, D, Е, F.

Стороны многоугольника АBCDEF: AB, BC, CD, DE, EF, FA.

Любые многоугольники можно сравнить: два многоугольника называются равными, если они совпадают при наложении.

Зная длину каждой стороны многоугольника, можно найти периметр этого многоугольника.

Периметр многоугольника — это сумма длин всех сторон.

Периметр многоугольника принято обозначать заглавной латинской буквой Р

Найдем периметр многоугольника АBCDEF (изображенного на рисунке):

Р_АВСDEF = AB+ BC+ CD+ DE+ EF+ FA = 2 см + 3 см + 2 см + 2 см + 3 см + 2 см = 14 см.

Существует огромное множество различных видов многоугольников.

Обычно многоугольники различают по числу сторон и углов.

Например: пятиугольник имеет 5 углов и 5 сторон, шестиугольник — 6 углов и 6 сторон.

Многоугольник с наименьшим числом вершин, сторон и углов называют треугольником.

Треугольник — плоская геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.

Треугольник часто обозначают символом «Δ» и тремя заглавными латинскими буквами, которые обозначают его вершины.

На рисунке изображен треугольник АBC (Δ АBC).

А, В, С — вершины треугольника АBC.

Отрезки AB, BC, АC— стороны треугольника АBC.

Периметр треугольника- это сумма длин трех его сторон.

Найдем периметр треугольника АBC (изображенного на рисунке):

Р_АВС = AB+ BC+ АС = 4 см + 6 см + 3 см = 13 см.

Пройти тест и получить оценку можно после входа или регистрации

Источник