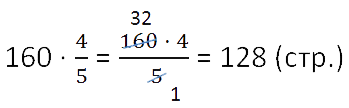Как легко найти дробь от числа

Одна из простой, но интересной темы – это как найти дробь от целого (от числа).

Как найти часть от целого? У нас есть какое-то значение и нам нужно найти долю или дробь от этого значения.

К примеру, пицца весит 540 г. Сколько весит кусок пиццы, если ее разделили на 6 одинаковых кусков?

Пиццу разрезали на 6 одинаковых кусков, значит, один кусок – это 1/6 от всей пиццы.

Начертим схему: чертим отрезок, разделим его на 6 равных частей. Удобнее начертить отрезок длиной 6 или 12 см (см. статью здесь).

Если пиццу разрезали, то и весь вес надо разделить: 540:6=90 (г)

Если нужно узнать вес двух кусков, т.е. 2/6

то эти 90 взять 2 раза: 90х2= 180 (г)

В итоге, 540 : 6 х 2, или, зная правила работы с дробями — 540 х 2/6.

Видим, что для того, чтобы найти 2/6 от целой пиццы нужно просто умножить общий вес на значение этой части — 2/6.

Как-то странно. Не правда ли? И, тем не менее: чтобы найти часть, мы умножаем, а не делим. Потому что если вспомнить, что дробь, вернее, горизонтальная черта дроби — это деление. Итак:

Решение:

7/8 от 24 — 24:8х7=21

3/5 от 60 – 60:5х3=45

3/4 от 12 – 12:4х3=9

7/8 от 64 – 64:8х7=56

Нахождение дроби от числа

Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, ^a/_b) на данное число n.

Дробь от числа = n ⋅

a/b

n ⋅ a/b

Пример 1

Решение

5/12

⋅ 24 =

5 ⋅ 24/12

120/12

= 10

Пример 2

Решение

4/9

⋅ 7 =

4 ⋅ 7/9

28/9

1/9

Таким образом, результат нахождения дроби числа не всегда бывает целым числом.

Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.

Нахождение числа по значению дроби

Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:

Пример:

Один ряд кинозала вмещает 20 кресел, что составляет

2/5

от всей вместимости зала. Определите, сколько всего посадочных мест в зале.

Решение

Общее количество кресел равняется:

20 :

2/5

= 20 ⋅

5/2

20 ⋅ 5/2

= 50

Источник

Download Article

Finding the fraction of a number is the same as multiplying the number and the fraction. This simple method can be used for any kind of number (percent, fraction, mixed number, decimal), but is easiest with whole numbers. To solve the problem, you will need to know basic multiplication and division.

1
Write out the problem. If the problem you are working with is a word problem, first you need to write out all of the numbers involved in the calculation. If you were given the numbers written out already, you can skip this step.
- For example: What is one-third of seven?
- When you see “of” written between two numbers in a word problem, think of it as meaning multiply. Thus, one-third of seven actually means one-third multiplied by seven.
- Writing out the problem gives you (¹/₃) x 7.
2
Multiply the whole number by the numerator. When working with whole numbers, you will only multiply the number by the numerator (the top number) of the fraction. The denominator remains the same throughout the multiplication process.^[1]
- For example: (¹/₃) x 7 = ⁷/₃.
Advertisement
3
Divide by the denominator. Divide the product by the denominator (the bottom number) of the fraction. At this stage, the fraction might be an improper fraction, meaning that the numerator is larger than the denominator, or it will just need to be reduced.^[2]
- For example: After multiplying, the fraction is ⁷/₃. Three doesn’t divide evenly into seven so you will have a remainder. Three goes into seven twice with one leftover; therefore, the final answer is the mixed number 2¹/₃.

1
Simplify the improper fraction. An improper fraction is one where the numerator is a larger number than the denominator. Always simplify an improper fraction before writing the final answer. To simplify, divide the numerator by the denominator and write the remainder as a fraction.^[3]
- For example: ¹⁰/₃
- Divide: 10/3 = 9 remainder 1
- Write the remainder as a fraction: ¹/₃
2
Write the mixed number. A mixed number contains both a whole number and a fraction. It is the simplest form of an improper fraction. To write the mixed number, simply write the whole number and the fraction that was created by the remainder.^[4]
- For example: ¹⁰/₃, 3 goes into 10 3 times with a remainder of 1. The mixed number is 3¹/₃.
3
Reduce a fraction to its simplest form. Once you have multiplied through, you need to reduce the fraction. You can divide by a smaller number until the fraction is completely reduced.^[5]
- For example: Simplify the fraction ⁴/₈. Divide both numbers by four to simplify. The simplest form of ⁴/₈ is ¹/₂.

Add New Question

Question

Jack has $48, he spends $18. What fraction of his money is left?

There is 30 left. 30 is 30/48 of 48. 30/48 = 5/8.
Question

If Susan works 10 hours a day, and her boss allows her to use (1/8) of the 10 hours for lunch. How long is her lunch break?

Find the answer with this equation: 10 x 1/8 = 10/8 = 1¼ = 1 hour and 15 minutes.
Question

What fraction represents 3 x 3/2?

Multiply the whole number by the numerator, and keep the denominator.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To find a fraction of a whole number, multiply the whole number by the numerator of the fraction. Divide the product by the denominator of the fraction, then reduce the answer to a mixed number in its simplest form. If you want to learn how to reduce the fraction into its simplest form, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 151,049 times.

Did this article help you?

Источник

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Нахождение дроби от числа

Поддержать сайт

Дроби используют в математике, чтобы кратко обозначить часть
рассматриваемой величины.

Но если есть часть, то обязательно есть и целое (то, отчего
была взята эта часть).

Зная целое, можно найти его часть, указанную соответствующей дробью.

Запомните!

Чтобы найти дробь (часть) от числа, нужно это число
умножить на данную дробь.

Пример. Рассмотрим задачу.

В книге 160 страниц. Юра прочитал
книги. Сколько страниц
прочитал Юра?

Прежде всего найдём в задаче целое. Это — вся книга и в ней всего
160 страниц.

Посмотрим на дробь (часть) от целого:

.
Знаменатель равен 5, значит, целое разделили
на 5 частей и мы можем найти сколько страниц составляет

часть.

160 : 5 = 32 (стр.) — составляет часть страниц.
Числитель дроби равен 4, значит взято 4 части.
32 · 4 = 128 (стр.) — составляют книги.

Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.

Ответ: Юра прочитал 128 страниц.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Скачать материал

Сейчас обучается 50 человек из 27 регионов

Сейчас обучается 27 человек из 13 регионов

Сейчас обучается 75 человек из 34 регионов

Описание презентации по отдельным слайдам:

1 слайд

«Как находить дробь от числа и число по его дроби, соблюдая правила дорожного движения».
Тема урока:
1
Сергиенко В.А. Дробь от числа.
2 слайд

Чтобы найти

дробь от числа,
нужно умножить число
на эту дробь.
Чтобы найти

Число по данному
значению его дроби,
надо это значение
разделить на дробь.

правила
3 слайд

Прочитай задачи и определи:

к какому виду они относятся.
разминка
4 слайд

В дачном поселке 30 домов.
от всех домов -двухэтажные.
Сколько двухэтажных домов?
5 слайд

В конюшне стоят лошади.
0,2 всех лошадей — вороные.
Сколько лошадей в конюшне,
если вороных в ней 14?

14:0,2=140:2=70 (лошадей)-в конюшне.

Ответ: 70 лошадей.
6 слайд

В 6 классе 25 учащихся. Девочки составляют 0,8 всех учащихся.
Сколько в классе мальчиков?
7 слайд

От трубы отрезали 6 метров,
что составляет длины всей
трубы.
Найдите длину трубы.
8 слайд

Сведения госавтоинспекции
За 9 месяцев по Московской области произошло 10862 ДТП.
Погибло – 2126 человек,
из них – 58 детей.
Ранено 13510 человек,
из них – 968 детей.
10 слайд

РЕШЕНИЕ ЗАДАЧ

НАХОЖДЕНИЕ
ДРОБИ ОТ ЧИСЛА
И ЧИСЛА ПО ЕГО ДРОБИ.
11 слайд

Задача №1.
Из 120 опрошенных школьников не выполняют

правила дорожного движения учащихся и

не всегда соблюдают всех учащихся.

Сколько детей выполняют ПДД, если они
составляют остальную часть?

СОСТАВИТЬ КРАТКУЮ ЗАПИСЬ
12 слайд

КРАТКАЯ ЗАПИСЬ
Задача №1

Ответ:
54 ученика выполняют ПДД.
1 способ
2 способ
Решите задачу №1 двумя способами
13 слайд

задача № 2.
Из 120 опрошенных школьников не выполняют

правила дорожного движения учащихся и

не всегда соблюдают оставшихся

учащихся.

Сколько детей выполняют ПДД, если они
составляют остальную часть?
14 слайд

Задача №1.
Из 120 опрошенных школьников не выполняют

правила дорожного движения учащихся и

не всегда соблюдают

Сколько детей выполняют ПДД, если они
составляют остальную часть?

всех учащихся.
оставшихся учащихся.
Задача № 2.
СОСТАВИТЬ КРАТКУЮ ЗАПИСЬ
15 слайд

КРАТКАЯ ЗАПИСЬ
Задача №1

Задача №2
Ответ:
54 ученика выполняют ПДД.
Ответ:
63 ученика выполняют ПДД.
РЕШЕНИЕ
16 слайд

Домашнее задание:
Решить задачу №2
другим способом
17 слайд

Нарушения, которые чаще всего допускают дети:
Переход улицы перед близко движущимся транспортом – 27%.
Переход улицы на красный сигнал светофора – 27%.
Невнимательность при переходе улицы – 17%.
Неожиданный выход из-за транспортных средств — 9%
Игры на проезжей части-20%
18 слайд

РЕШЕНИЕ ЗАДАЧ

НАХОЖДЕНИЕ
ДРОБИ ОТ ЧИСЛА
И ЧИСЛА ПО ЕГО ДРОБИ.
19 слайд

Задача №1.
Из 120 опрошенных школьников не выполняют

правила дорожного движения учащихся и

не всегда соблюдают всех учащихся.

Сколько детей выполняют ПДД, если они
составляют остальную часть?

Ответ:
54 ученика выполняют ПДД.
Составить к задаче №1 обратную задачу
20 слайд

Задача №1.
Из опрошенных школьников не выполняют

правила дорожного движения учащихся и

не всегда соблюдают всех учащихся.

Сколько детей выполняют ПДД, если они
составляют остальную часть?

Ответ:
54 ученика выполняют ПДД.

54 ученика выполняют ПДД.
Сколько детей было опрошено?
Обратная задача
СОСТАВИТЬ КРАТКУЮ ЗАПИСЬ
21 слайд

КРАТКАЯ ЗАПИСЬ
Задача №1

Обратная задача
Ответ:
54 ученика выполняют ПДД.
Ответ:
120 учеников опрошено.
РЕШИТЬ
ДВУМЯ
СПОСОБАМИ
22 слайд

Придумайте задачу заданного типа, используя данные:

и решите ее любым способом.

задание
23 слайд

Задача№1

Ответ:16
Задача №2

Ответ:28
Задача №3

Ответ:400
Бонус
24 слайд

1.Главная автомагистраль.
2.Штрихи на дороге, обозначающие пешеходный переход.
3.Дорога для пешеходов.
4.Край дороги.
5.Пересечение двух улиц.
6.Сотрудник милиции, работающий на дороге.
7.Место ожидания транспорта.
8.Наказание за нарушение ПДД.
1.Шоссе.

2.Зебра.
3.Тротуар.

4.Обочина.
5.Перекресток.

6.Регулировщик.
7.Остановка.
8.Штраф.
ВИКТОРИНА
25 слайд

Спасибо за урок!
26 слайд

Решение задачи №1
(1 способ)
Ответ: 54 человека выполняют ПДД.
27 слайд

Решение задачи №1
(2 способ)
Ответ: 54 человека выполняют ПДД.
28 слайд

Решение задачи №2

Ответ:63 человека выполняют ПДД.

Краткое описание документа:

Саша Чернов сел делать домашнее задание и сидел за столом 2 часа. 20 минут из них он ковырял в носу и думал о мороженом. 10 минут искал в ящике стола ластик, чтобы стереть с учебника истории неприличную картинку, на рисование которой затратил перед этим 40 минут. Остальное время Саша спрягал немецкие глаголы. Сколько глаголов проспрягал Саша, если на каждый глагол у него ушло по 25 минут

Как находить дробь от числа и число по его дроби, соблюдая правила дорожного движения».В дачном поселке 30 домов. от всех домов -двухэтажные.

l Сколько двухэтажных домов? В 6 классе 25 учащихся. Девочки составляют 0,8 всех учащихся.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 265 336 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

08.03.2015
938
2

Задачи на смекалку. 6 класс.

Учебник: «Математика (в 2 частях)», Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Тема: 7. Наименьшее общее кратное

08.03.2015
4781
31

08.03.2015
1595
4

Рейтинг:
4 из 5

08.03.2015
17785
174

08.03.2015
773
2

08.03.2015
6784
0

Источник

Похожие статьи

Нахождение дроби от числа

Нахождение числа по значению дроби

References

About This Article

Did this article help you?

Нахождение дроби от числа

Ваши комментарии

Описание презентации по отдельным слайдам:

Краткое описание документа:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

Не пропустите также: