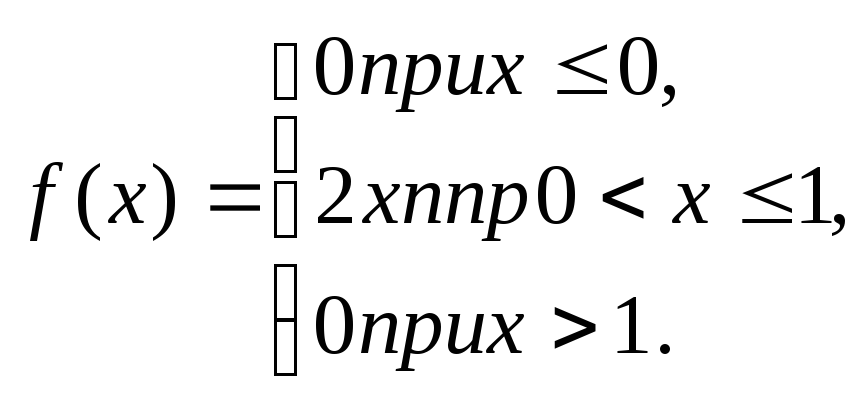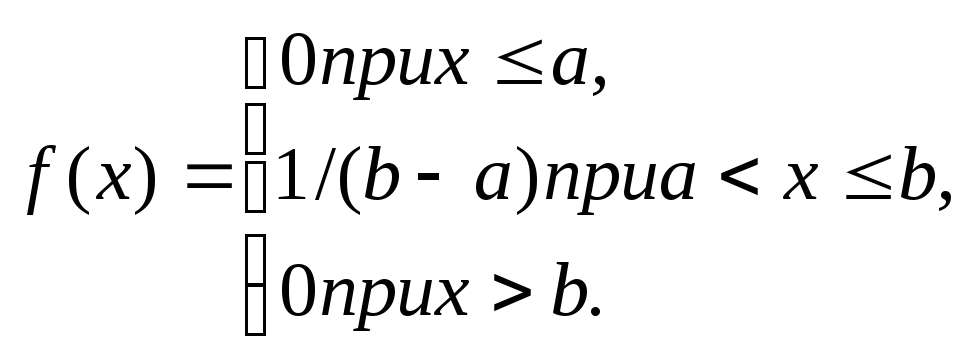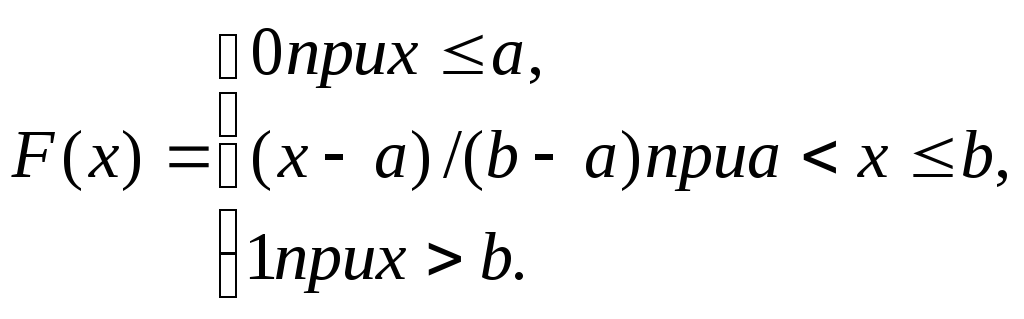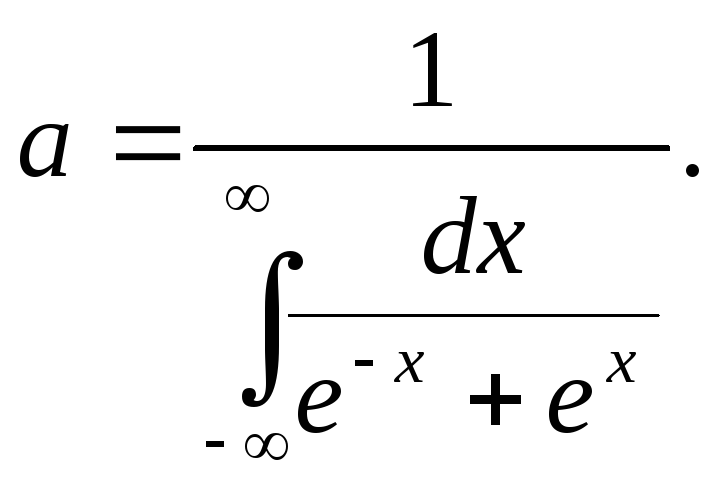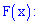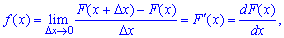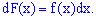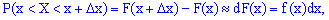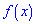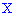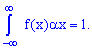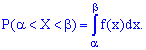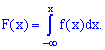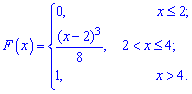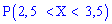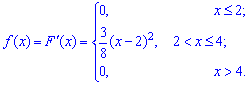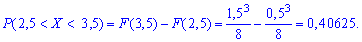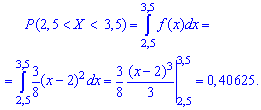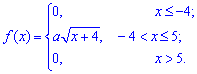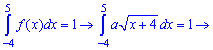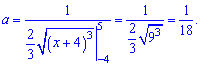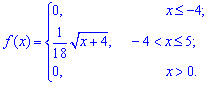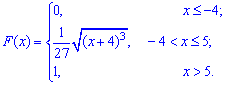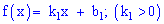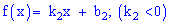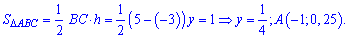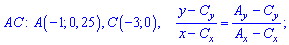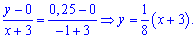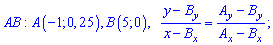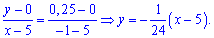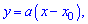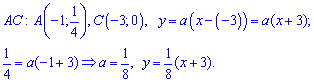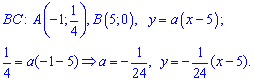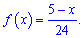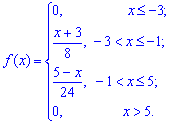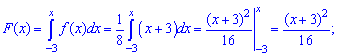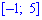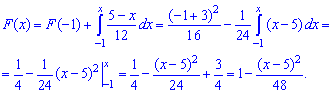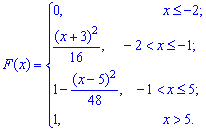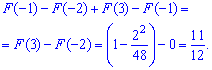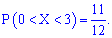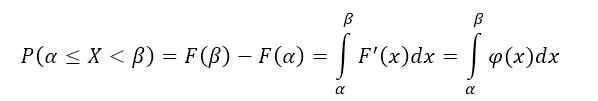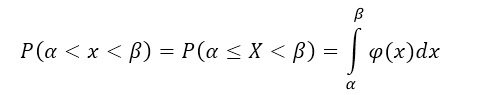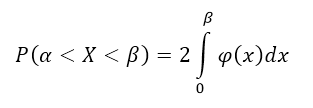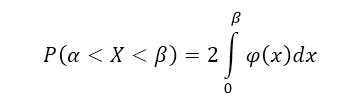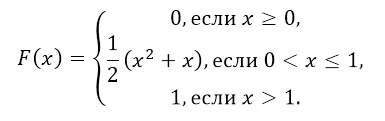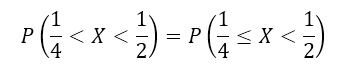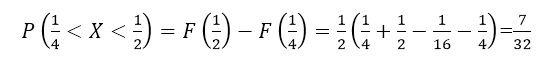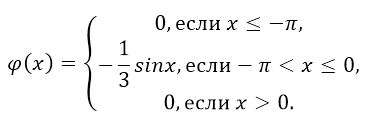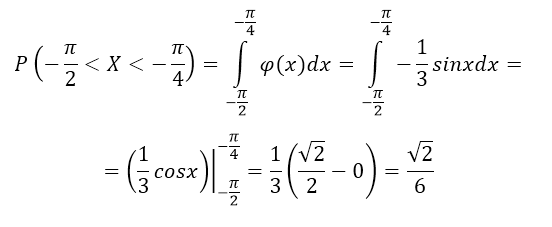Зная плотность
распределения, можно вычислить вероятность
того, что непрерывная случайная величина
примет значение, принадлежащее заданному
интервалу. Вычисление основано на
следующей теореме.
Теорема. Вероятность
того, что непрерывная случайная величина
X
примет значение, принадлежащее интервалу
(а,
b),
равна определенному интегралу от
плотности распределения, взятому в
пределах от а до b:
Р(а<Х<b)
=
Доказательство.
Используем соотношение (**) (см. гл. X,
§ 2)
Р(а
Х<b)
= F(b)
— F(a).
По формуле Ньютона
— Лейбница,
F(b)
— F(a)=.
Таким образом,
Р(а
Х<b)
=
Так как Р(а
Х<b)
= Р(а<Х<b),то
окончательно получим
Р(а<Х<b)
=
(*)
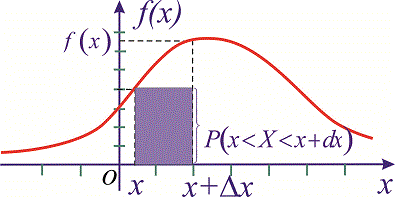
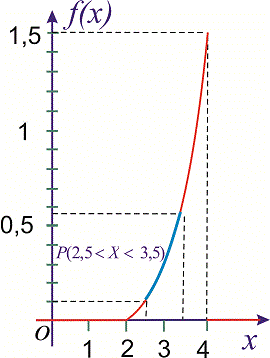
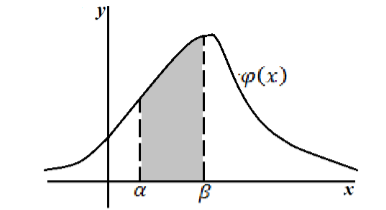
Геометрически
полученный результат можно истолковать
так: вероятность того, что непрерывная
случайная величина примет значение,
принадлежащее интервалу (а,b),
равна площади
криволинейной трапеции, ограниченной
осью Ох,
кривой
распределения f
(х)
и прямыми х
=а и х=b.
Замечание. В
частности, если f
(х)
— четная
функция и концы интервала симметричны
относительно начала координат, то
Р(-а<Х<a)
= Р(|Х|<a)
=2
Пример.
Задана плотность вероятности случайной
величины X
Найти вероятность
того, что в результате испытания X
примет
значение, принадлежащее интервалу (0,5;
1).
Решение. Искомая
вероятность
Р (0,5
< X
< 1)=
§ 3. Нахождение функции распределения по известной плотности распределения
Зная плотность
распределения f(х),
можно найти функцию распределения F
(х)
по формуле
F(x)
=
Действительно, мы
обозначили через F
(х)
вероятность
того, что случайная величина примет
значение, меньшее х,
т. е.
F(x)
= P(X<x).
Очевидно, неравенство
X
< х
можно записать
в виде двойного неравенства —<X
< х,
следовательно,
F(х)=Р(—<X
< х)
(*)
Полагая в формуле
(*) (см. § 2) а=—,b
= х, имеем
Р(—<X
< х)
=
Наконец, заменив
Р (—<
X
< х) на F
(х),
в силу (*), окончательно получим
F(x)
=
Таким образом,
зная плотность распределения, можно
найти функцию распределения. Разумеется,
по известной функции распределения
может
быть найдена
плотность распределения, а именно:
f(x)=Г’(x).
Пример.
Найти функцию распределения по данной
плотности распределения:
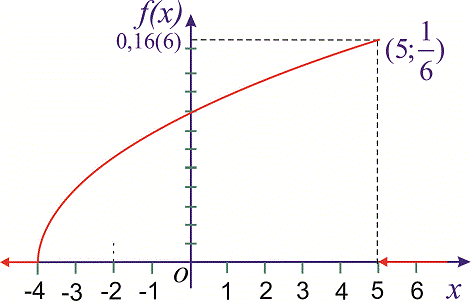
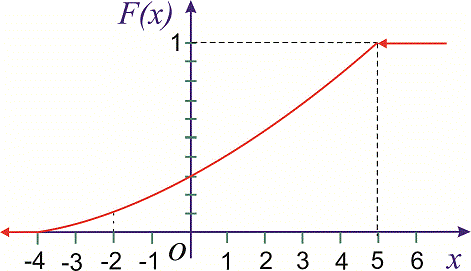
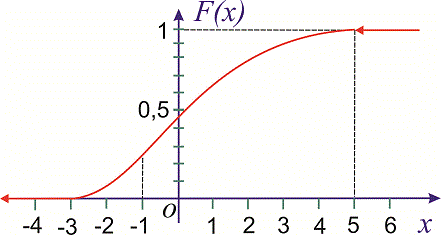
Построить график
найденной функции.
Решение. Воспользуемся
формулой F(x)=
Если x
a,
то f(x)
=0, следовательно, F(x)=0.
Если a<x
b,то
f(x)=1/(b
— а),
следовательно,
.
Если х
> b,
то
F(x)=
Итак, искомая
функция распределения
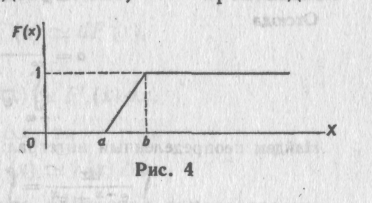
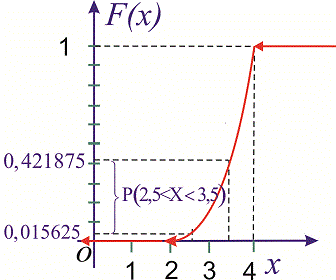
График этой функции
изображен на рис. 4.
§ 4. Свойства плотности распределения
Свойство 1. Плотность
распределения—неотрицательная
функция:
f(x)
0.
Доказательство.
Функция распределения — неубывающая
функция, следовательно, ее производная
F‘(х)=f(х)—функция
неотрицательная.
Геометрически
это свойство означает, что точки,
принадлежащие графику плотности
распределения, расположены либо над
осью Ох, либо
на этой оси.
График плотности
распределения называют кривой
распределения.
Свойство 2.
Несобственный
интеграл от плотности распределения в
пределах от —
до
равен единице:
Доказательство.
Несобственный интеграл
выражает
вероятность события, состоящегов
том, что
случайная величина примет значение,
принадлежащее интервалу (—,
).
Очевидно, такое событие достоверно,
следовательно, вероятность его равна
единице.
Геометрически это
означает, что вся площадь криволинейной
трапеции, ограниченной осью Ох
и кривом
распределения, равна единице.
В частности, если
все возможные значения случайной
величины принадлежат интервалу (а,
b),
то
Пример. Плотность
распределения случайной величины X
задана:
f
(x)=
Найти постоянный
параметр а.
Решение. Плотность
распределения должна удовлетворять
условию
,
поэтому потребуем, чтобы выполнялось
равенство
Отсюда
Найдем неопределенный
интеграл:
Вычислим несобственный
интеграл:
Таким образом,
искомый параметр
a=.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для непрерывных случайных величин наряду с законом распределения вероятностей рассматривают плотность вероятностей, которую обозначают так 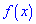
Плотностью вероятностей случайной величины 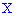
откуда дифференциал
Поскольку прирост определяют зависимости
куплена плотности вероятностей на прирост случайной величины 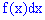
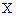
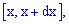
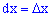
Геометрически на графике плотности вероятностей 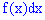
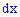
Свойства плотности вероятностей
1. Плотность вероятностей принимает положительные значения 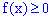
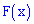
2. Условие нормирования случайной величины
3.Вероятность попадания случайной величины в промежуток 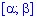
4. Функция распределения вероятностей непрерывной случайной величины определяется через плотность распределения вероятностей интегрированием
—————————————
Рассмотрим задачи для закрепления материала на практике.
Пример 1. Закон распределения случайной величины 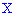
Найти плотность распределения вероятностей 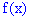
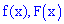
Решение. Вычисляем функцию плотности вероятностей
Графики функций 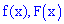
Вероятность события 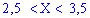
Согласно приведенной выше формулы получим
На этом задача решена.
———————————————
Пример 2. По заданной функцией плотности распределения вероятностей
установить параметры 
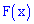
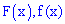
Решение. Значение постоянной 
При найденном значении 
Функция распределения вероятностей определяется интегрированием:
Записываем общий вид функции 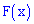
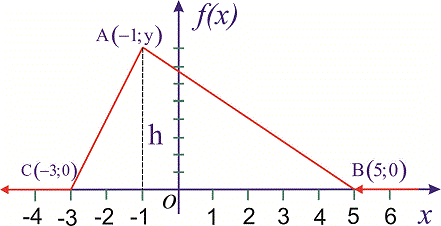
Графики функций распределения вероятностей и ее плотности показаны на рисунках ниже
—————————————
Пример 3. Случайная величина 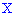
Записать выражения для плотности вероятностей и функции распределения вероятностей, построить график 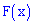
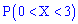
Решение. На промежутках 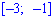
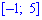
для первого и второго участки соответственно. Для нахождения неизвестных констант 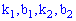
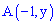
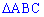
При известных координатах всех вершин находим уравнение прямых
Есть другой способ нахождения уравнения прямых, предусматривающий отыскания по одной константе на уравнение. Если известна точка пересечения прямой с осью ординат 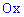
где 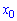
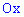

Со временем второй метод для Вас станет проще и практичнее в использовании. Плотность вероятностей примет значение
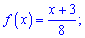
а ее функция примет вид
Функцию распределения вероятностей 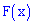
а) на промежутке 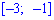
2) на промежутке
Следовательно, функция распределения вероятностей такая
Ее график приведен ниже
Вычисляем вероятность события 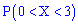
или
Следовательно, вероятность равна
————————-
Хорошо проанализируйте приведенные примеры — это поможет научиться быстро находить плотность распределения вероятностей и выполнять построение графика. Будьте внимательны при интегрировании и выбирайте удобную для вычислений методику.
Плотность распределения вероятностей непрерывной случайной величины
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).
Плотностью распределения вероятностей непрерывной случайной величины
называют функцию
– первую производную от функции распределения
:
Из этого определения следует, что
функция распределения является первообразной для плотности распределения.
Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.
Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.
Вероятность того, что непрерывная
случайная величина
примет
значение, принадлежащее интервалу
равна
определенному интегралу от плотности распределения, взятому в пределах от
до
:
Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу
, равна площади криволинейной трапеции, ограниченной
осью
, кривой распределения
и прямыми
и
.
В частности, если
– четная
функция и концы интервала симметричны относительно начала координат, то:
Зная плотность распределения
можно найти
функцию распределения
по формуле:
Свойства плотности распределения
Свойство 1.
Плотность
распределения – неотрицательная функция:
Свойство 2.
Несобственный
интеграл от плотности распределения в пределах от
до
равен единице:
Смежные темы решебника:
- Дискретная случайная величина
- Непрерывная случайная величина
- Интегральная функция распределения вероятностей
Примеры решения задач
Пример 1
Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:
1)
определить коэффициент A;
2) найти
функцию распределения F(x);
3)
схематично построить графики F(x) и f(x);
4) найти
математическое ожидание и дисперсию X;
5) найти
вероятность того, что X примет значение из
интервала (α,β):
α=1; β=1.7
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1)
Постоянный параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Получаем:
2)
Функцию распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем
отметить, что:
Остается
найти выражение для
, когда
принадлежит
интервалу
.
Получаем:
3) Построим графики
и
:
График плотности распределения
График функции распределения
4)
Математическое ожидание находим по формуле:
Для
нашего примера:
Дисперсию
можно найти по формуле:
5)
Вероятность того, что случайная величина примет значение из интервала
:
Пример 2
Плотность
распределения вероятности непрерывной случайной величины равна
, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).
Решение
Нормировочный множитель
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Плотность
вероятности:
Математическое
ожидание находим по формуле:
Для
нашего примера:
Дисперсию
можно найти по формуле:
Пример 3
Непрерывная
случайная величина
имеет плотность распределения:
Найти
величину a, вероятность P(X<0) и математическое
ожидание X.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Постоянный
параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Плотность
вероятности имеет вид:
Вероятность:
Математическое
ожидание находим по формуле:
Для
нашего примера:
Задачи контрольных и самостоятельных работ
Задача 1
Плотность
распределения непрерывной случайной величины X имеет вид:
Найти:
а)
параметр a;
б)
функцию распределения F(x);
в)
вероятность попадания случайной величины X в интервал (6.5; 11);
г)
математическое ожидание M(X) и дисперсию D(X);
Построить
график функций f(x) и F(x).
Задача 2
Задана
функция распределения непрерывной случайной величины:
Найти и
построить график функции плотности распределения вероятностей.
Задача 3
Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).
Задача 4
Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).
α=1,β=2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 5
Непрерывная
случайная величина
задана плотностью распределения вероятностей.
Требуется
найти:
— функцию
распределения вероятностей;
—
математическое ожидание;
—
дисперсию;
— среднее
квадратическое отклонение;
— вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;
—
построить графики функции распределения и плотности распределения вероятностей.
Задача 6
Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).
Задача 7
Случайная
величина X~N(a,σ)
a=25;
σ=4; α=13; β=30; δ=0.1.
Требуется:
—
составить функцию плотности распределения и построить ее график;
— найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);
— найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.
Задача 8
Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:
Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 9
Случайная
величина X задана функцией распределения вероятностей F(x).
Требуется:
1. Найти
функцию плотности распределения f(x).
2. Найти M(X).
3. Найти
вероятность P(α<X<β)
4.
Построить графики f(x) и F(x).
α=2, β=4.5
Задача 10
Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).
M(X)=-1; D(X)=8
Задача 11
Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:
а) найти
параметр C;
б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);
в)
построить графики функций F(x) и f(x);
г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);
д)
вычислить вероятность попадания в интервал P(a≤x≤b)
е)
определить, квантилем какого порядка является точка xp;
ж)
вычислить квантиль порядка p
a=π/4; b=π/3; xp=π/2; p=0.75
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Пусть нам задана функция плотности распределения непрерывной случайной величины. Тогда с её помощью мы можем найти вероятность того, что случайная величина попадет в интервал $(alpha ,beta )$.
Для начала вспомним несколько свойств функции распределения вероятности $F(x)$, которые понадобятся нам в дальнейшем.
Свойство 1: Для любых $X$ выполняется равенство:
Сформулируем и докажем следующую теорему:
Вероятность того, что непрерывная случайная величина $X$ примет значение из интервала $(alpha ,beta )$ равна значению определенного интеграла от $alpha $ до $beta $ плотности распределения $varphi (x)$.
Доказательство.
Используя свойство 1, имеем:
[Pleft(alpha le XИспользуя формулу Ньютона-Лейбница, получим:
Рисунок 1.
Так как случайная величина $X$ непрерывна, то и функция распределения $F(x)$ также непрерывна. Следовательно, по свойству 2, получим:
Рисунок 2.
ч. т. д.
Геометрически данную теорему можно интерпретировать следующим образом: Вероятность попадания случайной непрерывной величины $X$ в интервал $(alpha ,beta )$ равна площади криволинейной трапеции, ограниченной кривыми $y=varphi left(xright), x=alpha ,$ $x=beta $ и $y=0$ (рис. 1).
Рисунок 3. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал $(alpha ,beta )$.
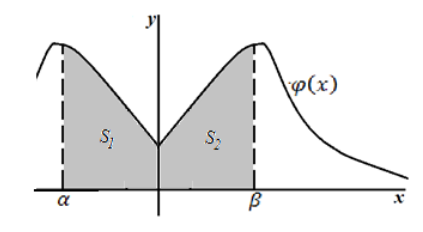
Следствие 1: Если плотность распределения $varphi (x)$ — четная функция, а значения $alpha и beta $ равны по абсолютной величине (по модулю), причем $alpha ne beta $, то вероятность попадания непрерывной случайной величины в интервал $(alpha ,beta )$ можно найти по формуле:
Рисунок 4.
«Вероятность попадания непрерывной величины в заданный интервал » 👇
Этот факт может быть легко показан геометрически:
Рисунок 5.
Очевидно, что $S_1=S_2$.
Используя геометрический смысл плотности распределения, и получаем, что
Рисунок 6.
Примеры задач на нахождение вероятности попадания непрерывной случайной величины в заданный интервал
Пример 1
Функция распределения имеет вид:
Рисунок 7.
Найти вероятности попадания случайной величины в интервал $(frac{1}{4},frac{1}{2})$.
Решение: Очевидно, что функция $F(x)$ непрерывна на сей области определения (в том числе непрерывна справа на всем интервале $(frac{1}{4},frac{1}{2})$). Значит по свойству 2, получим
Рисунок 8.
Теперь, пользуясь свойством 1, получим:
Рисунок 9.
Ответ: $frac{7}{32}$.
Пример 2
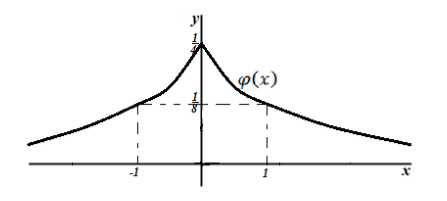
Плотность распределения задана в виде:
Рисунок 10.
Найти вероятности попадания случайной величины в интервал $(-frac{pi }{2},-frac{pi }{4})$.
Решение: Используя теорему 1, получим:
Рисунок 11.
Ответ: $frac{sqrt{2}}{6}$.
Пример 3
Функция плотности распределения имеет вид:
[varphi left(xright)=frac{1}{4x^2+4}]
Построить график плотности распределения и найти вероятность попадания случайной величины в интервал $left(-2,2right).$
Решение: Построим график функции $varphi left(xright)$:
Рисунок 12.
Функция $varphi left(xright)$ четна, концы интервала $left(-2,2right)$ симметричны относительно начала координат, следовательно, по следствию 1, получаем:
[Pleft(-2Ответ: $frac{1}{2}arctg2.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Как найти вероятность из графиков плотности вероятности
Перевод
Ссылка на автора
Прежде чем идти дальше, давайте посмотрим правде в глаза.
Если вы достаточно давно работаете в области наук о данных, есть вероятность, что вы, возможно, построили графики плотности вероятности (аналогичные приведенным ниже), чтобы понять общее распределение ваших данных.
Ну … Во-первых, что за график плотности? Отличное и ясное объяснение Уилл Кёрсен это:
график плотности является сглаженной, непрерывной версией гистограммы, оцененной по данным.
Наиболее распространенная форма оценки известна как оценка плотности ядра (KDE).
В этом методе непрерывная кривая (ядро) рисуется в каждой отдельной точке данных, и все эти кривые затем складываются, чтобы сделать единую плавную оценку плотности.
Ядро, наиболее часто используемоеGaussian(который создает гауссову кривую колокола в каждой точке данных)
график плотности вероятностипросто означает график плотности функции плотности вероятности (ось Y) против точек данных переменной (ось X).
Как правило, графики плотности вероятности используются дляпонимать распределение данныхдля непрерывной переменной, и мы хотимзнать вероятность (или вероятность) получения диапазона значенийчто непрерывная переменная может принять.
Но вот в чем дело.
Показывая графики плотности вероятности, мы можем понять только распределение данных.визуальноне зная точную вероятность для определенного диапазона значений.
Другими словами, трудно оценить количественно вероятность под кривой, просто посмотрев на график.
Однако получение точной вероятности под кривойчрезвычайно важно(Я расскажу вам почему в следующем разделе), особенно когда вы представляете заинтересованным сторонам бизнеса.
В этой статье я покажу вам полный код, который я использовал для вычисления вероятности, и объясню вам шаг за шагом, как вы можете это сделать.
К концу этой статьи, я надеюсь, вы лучше поймете распределение данных, рассчитав фактическую вероятность в пределах диапазона значений, и впоследствии сможете убедить заинтересованные стороны в ваших взглядах.
Вы можете получить набор данных и блокнот Jupyter от моего GitHub,
Давайте начнем!
Почему графики плотности вероятности недостаточно убедительны?
Оглядываясь на график плотности выше, вы, возможно, пришли к выводу, что рейсы авиакомпании Alaska Airlines выполняются раньше, чем United Airlines.
Представьте, что теперь ваш босс задает этот вопрос и оспаривает ваше утверждение,«Как раньше сравниваются рейсы авиакомпании Alaska Airlines с United Airlines и насколько высоки шансы на это? У вас есть какие-либо числовые доказательства того, что ваш вывод верен?
Вы ошеломлены. Потому что вывод приходит из вашего наблюдения за общим распределением данных.
Что еще хуже, теперь у вас нет никаких числовых доказательств — точной вероятности — в поддержку вашего заявления.
Вы не очень хорошо подготовлены, и ваш авторитет в качестве ученого по данным мгновенно развалится, если вы не сможете доказать свою точку зрения.
Вот тут и возникает важность вычисления вероятности по графикам плотности вероятности.
К сожалению, очень трудно рассчитать вероятность, если вы используете Seaborn для построения графиков плотности, используяdistplot,
Потратив некоторое трудное время на выяснение того, как рассчитать вероятность, я решил использоватьKernelDensityотsklearn,
Этот метод работает как шарм, и я очень рад поделиться этим с вами! 👇🏻
Вот как найти вероятность из графиков плотности вероятности
Мы будем использовать данные о чаевых, которые включают некоторые факторы, которые могут повлиять на количество чаевых, которые дают клиенты в ресторане. Вы можете получить данные Вот,
Поскольку наша цель здесь — найти вероятность по графикам плотности, чтобы упростить ее, мы сосредоточимся на ответе на один вопрос —Клиенты дают больше советов во время обеда / ужина?
Поскольку данные уже достаточно очищены, мы можем начать строить графики плотности и напрямую вычислять соответствующие значения вероятности.
Для следующих шагов, пожалуйста, обратитесь к блокнот для полной реализации кода с использованием функций.
1. Составьте графики плотности вероятности
Поскольку Seaborn не предоставляет каких-либо функциональных возможностей для вычисления вероятности из KDE, таким образом, код выполняет эти 3 шага (как показано ниже) для построения графиков плотности вероятности и вывода объектов KDE для последующего расчета вероятности.
- График нормализованных гистограмм
- Выполнить оценку плотности ядра (KDE)
- Плотность вероятности заговора
Теперь, когда у нас есть график плотности вероятности количества советов на обед и ужин, время для сравнения
Просто взглянув на диапазон от 1 до 3 долларов советов, данных клиентами, мы можем заключить, чтоклиенты обычно дают чаевые 1-3 доллара в обеденное время по сравнению с обедом
Опять же, для того, чтобы получить числовые доказательства (или вероятностные значения), подкрепляющие наше утверждение, давайте посчитаем вероятность того, что клиенты дадут чаевые в размере 1–3 доллара США во время обеда и ужина для сравнения.
2. Рассчитать вероятность
Как только мы сделали графики плотности вероятности с помощью функцииplot_prob_densityу нас будут выходные объекты KDE из этой функции в качестве входных данных для вычисления вероятности с использованием следующей функции —get_probability,
И вот оно!
Сумма вероятности под нормализованной кривой плотности всегда равна 1. Поскольку вероятность — это область под кривой, мы можем затем указать диапазон значений (в данном случае чаевые от 1 до 3 долларов США) для расчета вероятности в этом диапазоне.
Следовательно, вероятность — это просто умножение значений плотности вероятности (ось Y) и количества подсказок (ось X).
Умножение выполняется для каждой точки оценки, и эти умноженные значения затем суммируются для вычисления окончательной вероятности.
Рассчитанные вероятности подтверждают нашу первоначальную претензию — клиенты обычно дают чаевые в размере 1–3 долл. Во время обеда по сравнению с обедомс вероятностью 63% более 49%.
Последние мысли
Спасибо за чтение.
Я надеюсь, что эта статья дает вамлучшее понимание графиков плотности вероятностии самое главное, показывает, какрассчитать фактическую вероятность в диапазоне значенийпод кривой плотности вероятности.
Расчет вероятности довольно прост, но не тривиален. Это играет решающую роль длядать заинтересованным сторонам лучшее понимание ваших графиков плотности вероятности, чтобы придумать действенные идеи, основанные на численных доказательствахвместо субъективного и неоднозначного наблюдения.
Как всегда, если у вас есть какие-либо вопросы или комментарии, не стесняйтесь оставлять свои отзывы ниже, или вы всегда можете связаться со мной по LinkedIn, До тех пор, до встречи в следующем посте! 😄
об авторе
Адмонд ли известен как один из самых востребованныхученые-данные и консультантыпомогая основателям стартапов и различным компаниям решать их проблемы, используя данные с большим опытом вконсалтинг по науке о данных и знание отрасли,
Вы можете связаться с ним на LinkedIn, средний, щебет, а также facebook или забронировать встречу с ним здесь если вы ищете консалтинга для вашей компании.