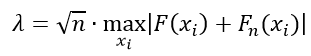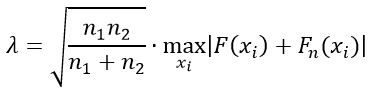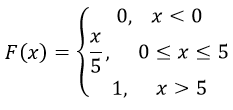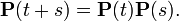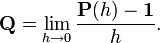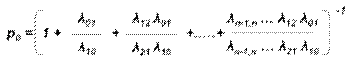Критерий Колмогорова для простой
гипотезы является наиболее простым
критерием проверки гипотезы о виде
закона распределения. Он связывает
эмпирическую функцию распределения
с функцией распределения
непрерывной случайной величиныX.
Пусть
— конкретная выборка из распределения
с неизвестной непрерывной функцией
распределенияи
— эмпирическая функция распределения.
Выдвигается простая гипотеза:
(альтернативная
:
,
).
Сущность критерия Колмогорова состоит
в том, что вводят в рассмотрение функцию
(7)
называемой статистикой Колмогорова,
представляющей собой максимальное
отклонение эмпирической функции
распределения
от гипотетической (т. е. соответствующей
теоретической) функции распределения.
Колмогоров доказал, что при
закон распределения случайной величины
независимо от вида распределения с. в.X стремится кзакону распределения Колмогорова:
где К(х) — функция распределения
Колмогорова, для которой составлена
таблица, ее можно использовать для
расчетов уже прип ≥ 20:
-
α
0,1
0,05
0,02
0,01
0,001
1,224
1.358
1,520
1,627
1,950
Найдем
такое, что
Рассмотрим уравнение
С помощью функции Колмогорова найдем
значение (корень)
этого уравнения.
Тогда по теореме Колмогорова,
откуда
Если
,
то гипотезунет оснований опровергнуть; в противном
случае — ее опровергают.
Пример 3. Монету бросали 4040 раз
(Бюффон). Получиливыпадений герба и
выпадений решётки. Проверить, используя
а) критерий Колмогорова;
б) критерий Пирсона, согласуются ли эти
данные с гипотезой
о симметричности монеты (
0.05).
Случайная величина X
принимает два значения:(решётка);
(герб).
Гипотеза
:
.
а) По таблице распределения Колмогорова
находим корень уравнения
при
.
Следует
.
Тогда
Для нахождения по выборке
строим функции
и
и вычисляем величину.
|
|
решётка
|
герб
|
|
|
0,5 |
0,5 |
|
xi |
решётка x1 = -1 |
герб
x2 = |
|
ni |
1992 |
2048 |
|
pi |
|
|
Максимальное отклонение
от
равно 0,007, т.е.= 0,007. Поскольку
,
то нет оснований отвергать, гипотезу;
опытные данные согласуются с гипотезойо симметричности монеты.
б) Вычисляем статистику χ2
По таблице
распределения
находим критическую точку
Так как,
то опытные данные согласуются с гипотезой
о симметричности монеты.
7. Критерий однородности Смирнова
Для проверки гипотез вида (2) (см. 20.2) об
однородности двух или более выборок
применяют критерий однородности:
(8)
Здесь, мы ограничимся частным случаем
этой критерии для двух выборок (т.е.).
В качестве критической статистики
применяется критерий однородности
Смирнова, которая имеет вид:
(9)
где
число
элементов выборок;количество
элементов соответственно первой и
второй выборок, попавших вй
интервал.
При условии справедливости гипотезывеличина
будет распределена приблизительно по
законус
степенью свободы. Гипотеза
опровергается,
еслиили
ипринимается при всех остальных
значениях критерия.
Рассмотрим следующую производственную
задачу.
Пример
4. Ниже в таблице
приведены условные
данные о заработной
плате работников двух видов предприятий:
текстильной и машиностроительной
отраслей, полученные в результате
социологического опроса. Объёмы двух
выборок выразятся как
.
-
№
п
/пИнтервал
зарплатыв
у.е.Количество
элементов выборки, попавших в данный
интервалТекстиль
Машиностроение
1
130-150
4
1
5
3
2
150-170
4
1
5
3
3
170-200
15
8
23
7
4
200-250
51
43
94
8
5
250-300
22
34
56
-12
6
300-350
3
7
10
-4
7
350-400
1
3
4
-2
8
400-450
0
3
3
-3
Решение. Проверим
гипотезу (при уровне
значимости
)
о том, что распределения вероятностей
по заработной плате в анализируемых
отраслях не отличаются друг от друга.
Далее вычисления величины
по формуле критерии Смирнова (9) с учётом
данных в таблице даёт
(10)
Задание.Самостоятельно проверьте
это равенство.
Из таблицы значений
-распределения (см. приложение) определяем
критическую точку:.
Следовательно, гипотезу о совпадении
вероятностных распределений заработной
платы в двух отраслях необходимо
отвергнуть, т.к..
При этом, вероятность допускаемой
ошибки равна 0,05.
Критерий однородности
Смирнова относится к непараметрическим
критериям (в отличие
от критерия Пирсона), так как используемая
в нём критическая статистика никак не
зависит от наших предположений
относительно распределения закона
случайной величины.
Соседние файлы в папке Теория вероятностей от исмоилова
- #
- #
- #
- #
- #
- #
- #
- #
- #
06.02.20162.36 Mб71~WRL0002.tmp
- #
06.02.20161.87 Mб67~WRL0005.tmp
- #
06.02.20161.01 Mб66~WRL0205.tmp
Уравнения Колмогорова.
Предельные вероятности состояний
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в
происходят под воздействием простейших потоков событий с интенсивностями
; так, переход системы из состояния
в
будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния
в
— под воздействием потока «окончаний ремонтов» первого узла и т.п.
Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния:
.
Вероятностью i-го состояния называется вероятность того, что в момент
система будет находиться в состоянии
. Очевидно, что для любого момента
сумма вероятностей всех состояний равна единице:
(8)
Рассмотрим систему в момент и, задав малый промежуток
, найдем вероятность
того, что система в момент
будет находиться в состоянии
. Это достигается разными способами.
1. Система в момент с вероятностью
находилась в состоянии
, а за время
не вышла из него.
Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной
. А вероятность того, что система не выйдет из состояния
, равна
. Вероятность того, что система будет находиться в состоянии
по первому способу (т.е. того, что находилась в состоянии
и не выйдет из него за время
), равна по теореме умножения вероятностей:
2. Система в момент с вероятностями
(или
) находилась в состоянии
или
и за время
перешла в состояние
.
Потоком интенсивностью (или
— с- рис. 1) система перейдет в состояние
с вероятностью, приближенно равной
(или
). Вероятность того, что система будет находиться в состоянии
по этому способу, равна
(или
).
Применяя теорему сложения вероятностей, получим
откуда
Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную
(обозначим ее для простоты
):
Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.
Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:
(9)
Сформулируем правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии
, т.е. при начальных условиях
.
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы в предельном стационарном режиме, т.е. при
, которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии. Например, если предельная вероятность состояния
, т.е.
, то это означает, что в среднем половину времени система находится в состоянии
.
Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:
(10)
Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом, согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при
Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или
(11)
(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).
Решив систему (11), получим , т.е. в предельном, стационарном режиме система
в среднем 40% времени будет находиться в состоянии
(оба узла исправны), 20% — в состоянии
(первый узел ремонтируется, второй работает), 27% — в состоянии
(второй узел ремонтируется, первый работает) и 13% времени — в состоянии
(оба узла ремонтируются)
Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).
Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел —
. В то же время первый узел находится в ремонте в среднем долю времени, равную
, а второй узел —
. Поэтому средний чистый доход
в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен
ден. ед.
Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь
и система линейных алгебраических уравнений (10), описывающая стационарный режим системы
, вместе с нормировочным условием (8) примет вид:
Решив систему, получим .
Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход
в единицу времени:
ден.ед.
Так как больше
(примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.
Процесс гибели и размножения
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения. Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.
Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния
возможны переходы только либо в состояние
, либо в состояние
.
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или
.
По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния
(12)
для состояния имеем
, которое с учетом (12) приводится к виду
(13)
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:
(14)
к которой добавляется нормировочное условие
(15)
При анализе численности популяций считают, что состояние соответствует численности популяции, равной
, и переход системы из состояния
в состояние
происходит при рождении одного члена популяции, а переход в состояние
— при гибели одного члена популяции.
Решая систему (14), (15), можно получить
(16)
(17)
Легко заметить, что в формулах (17) для коэффициенты при
есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния
, а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния
.
Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.
Решение. По формуле (16) найдем
по (17)
т.е. в установившемся, стационарном режиме в среднем 70,6% времени система будет находиться в состоянии , 17,6% — в состоянии
и 11,8% — в состоянии
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Критерий Колмогорова применяется для проверки гипотезы распределения непрерывных функций СВ.
Объем выборки n≥50.
Критерий Колмогорова находится по формуле:
Если проведено две выборки, то формула критерия Колмогорова примет вид:
Fn(xi) — значения эмпирической функции распределения;
F(xi) — значения теоретической функции распределения.
При λ<λкр ⇒ различия между значения эмпирической функции и теоретической функции распределения не значительные ⇒ принимаем гипотезу.
Критерий Колмогорова часто применяют для проверки полученных значений в ходе эксперимента и подчиняются ли они нормальному закону распределения случайной величины.
Пример
Приведена таблица результатов исследования n=100
| Количество предметов | 1 | 2 | 3 | 4 | 5 |
| Частота | 18 | 16 | 26 | 22 | 18 |
На уровне значимости α=0,2 с помощью критерия Колмогорова определите подчиняются ли данные выборки на интервале [0,5] при n=100 равномерному закону распределения случайной величины.
Решение
Запишем функцию равномерного закона распределения случайной величины
| xi | F(xi)=0,2xi | xni | Fn(xi) | |F(xi)– Fn(xi)| |
| 1 | 0,2 | 18 | 0,18 | 0,02 |
| 2 | 0,4 | 16 | 0,34 | 0,06 |
| 3 | 0,6 | 26 | 0,6 | 0 |
| 4 | 0,8 | 22 | 0,82 | 0,02 |
| 5 | 1 | 18 | 1 | 0 |
| max=0,06 |
Отсюда λ=0,6 и по таблице критических значений критерий Колмогорова при α=0,2 λкр=0,65.
λ<λкр ⇒ принимаем гипотезу.
9832
Уравнения Колмогорова.
Предельные вероятности состояний
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.
Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .
Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:
Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.
1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.
Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:
2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .
Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).
Применяя теорему сложения вероятностей, получим
Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):
Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.
Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:
Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .
Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:
Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при
Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или
(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).
Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)
Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).
Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен
Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:
Решив систему, получим .
Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:
Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.
Процесс гибели и размножения
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.
Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .
По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния
для состояния имеем , которое с учетом (12) приводится к виду
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:
к которой добавляется нормировочное условие
При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние — при гибели одного члена популяции.
Решая систему (14), (15), можно получить
Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .
Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.
Уравнение Колмогорова — Чепмена
Уравнение Колмогорова — Чепмена для однопараметрического семейства непрерывных линейных операторов P(t) 
Чаще всего этот термин используется в теории однородных марковскихслучайных процессов, где P(t) 
Для неоднородных процессов рассматриваются двухпараметрические семейства операторов 

Для систем с дискретным временем параметры t,h,s принимаютнатуральные значения.
Прямое и обратное уравнения Колмогорова
Формально дифференцируя уравнение Колмогорова—Чепмена по sпри s = 0 получаем прямое уравнение Колмогорова:
Формально дифференцируя уравнение Колмогорова — Чепмена по tпри t = 0 получаем обратное уравнение Колмогорова
Необходимо подчеркнуть, что для бесконечномерных пространств оператор Q уже не обязательно непрерывен, и может быть определен не всюду, например, быть дифференциальным оператором в пространстве распределений.
Примеры
Рассмотрим однородные марковские случайные процессы в R n для которых оператор переходных вероятностей P(t) задаётся переходной плотностью p(t,x,y): вероятность перехода из области U в область Wза время t есть 
При 


Тогда оператор 


а обратное уравнение Колмогорова
Пусть оператор 
(это означает, что q(x,y) есть линейная комбинация первых и вторых производных δ(x − y) с непрерывными коэффициентами). Матрицаaij симметрична. Пусть она положительно определена в каждой точке (диффузия). Прямое уравнение Колмогорова имеет вид
Это уравнение называется уравнением Фоккера — Планка. Вектор bjв физической литературе называется вектором сноса, а матрица aij —тензором диффузии Обратное уравнение Колмогорова в этом случае
Модели СМО, описываемые типа «гибель и размножение», их характеристики
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов – так называемый процесс гибели и размножения.
Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис.1:
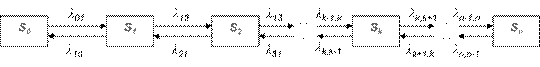
Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния Sk возможны переходы только в состояние Sk-1, либо в состояние Sk+1.* (При анализе численности популяций считают, что состояние Sk соответствует численности популяции равной k, и переход системы из состояния Sk в состояние Sk+1 происходит при рождении одного члена популяции, а переход в состояние Sk-1 – при гибели одного члена популяции. )
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями λk,k+1 или λk+1,k.
По графу, представленному на рис. 1, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений получим:
для состояния S0
для состояния S1 – (λ12 + λ10 ) p1 = λ01 p0 + λ21 p2, которое с учетом (1) приводится к виду
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:
к которой добавляется нормировочное условие
Решая систему (3), (4), можно получить:
Подставляя p1, p2. pn в нормировочное условие, получим:
Легко заметить, что в формулах (5) для p1, p2,…, pn коэффициенты при p0 есть слагаемые, стоящие после единицы в формуле (6). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния Sk (k=1, 2, …, n), а знаменатели – произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния Sk
Ошибка
404
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
источники:
http://lektsii.org/17-9177.html
http://infourok.ru/statya-na-temu-chastnye-resheniya-uravneniya-kolmogorova-chepmena-i-ih-svyaz-s-uravneniyami-matematicheskoj-fiziki-5547634.html
Большинство старшеклассников сейчас занимаются по учебнику Колмогорова, который рассчитан сразу на два года обучения (десятый и одиннадцатый). Это очень удобно, так как в одном месте собраны все нужные материалы и задания. Такая книга имеет готовые домашние задания того же автора (издательство «Просвещение» 2015 год).
Что же такое ГДЗ Колмогорова по алгебре за 10-11 класс и как ими пользоваться
Данное пособие включает в себя правильные ответы ко всем упражнениям, включая не только задачи, но вопросы на повторение и задания повышенной сложности. Решения подробно расписаны, что позволяет по пунктам разобрать тот или иной номер.
Благодаря такому сборнику школьник сможет готовиться к предстоящим контрольным, проверочным, тестам, пробникам и даже экзаменам. Стоит только правильно использовать онлайн-помощник:
- Сначала самостоятельно выполните заданное на дом упражнение (важно тоже расписывать каждое свое действие, чтобы потом можно было легко обнаружить ошибку);
- Только после этого стоит открыть решебник и сверить результаты с ключами из сборника;
- В самом конце исправьте недочеты и проанализируйте свое решение (это нужно для того, чтобы понять, какие есть пробелы в знаниях и в будущем больше не допускать подобных просчетов).
Учебно-методический комплекс работает в онлайн-режиме без перебоев круглосуточно и доступно с любого устройства (телефон, планшет, ноутбук, компьютер и т. д.). Главное – иметь выход в интернет. Найти интересующее также не составит никакого труда, так как платформа имеет интуитивно понятную навигацию: стоит просто кликнуть на нужное и перед вами откроется страница с решениями.
Какие темы содержит в себе решебник по алгебре для 10-11 классов (авторы: А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын)
Все содержание идентично главной книге. Оно отвечает требованиям школьной программы и ФГОС (федерального государственного образовательного стандарта):
- Тригонометрические функции;
- Производная и ее применения;
- Первообразная и интеграл;
- Показательная и логарифмическая f.
Таким пособием могут пользоваться даже учителя, чтобы составлять карточки для индивидуальной, парной и групповой работы на уроке или просто разрабатывать план интересного и занимательного занятия.
Родители могут применять ГДЗ по алгебре при проверке уровня знаний своего ребенка. Особенно это удобно в тех случаях, когда после тяжелого трудового дня вообще никакие цифры в голове не складываются или же, если мамы и папы немного подзабыли некоторые правила и формулы. В сборнике есть не только решения, но и нужные графики и рисунки, помогающие сверить все пункты задания.