Электростатическая индукция – это явление разделения электрических зарядов и их распределение по поверхности проводника во внешнем электрическом поле.
Простое объяснение
Электростатическая индукция означает перераспределение носителей заряда в объекте, вызванное близлежащими электрическими зарядами. Это означает, что если поместить заряженный объект рядом с нейтральным проводником, то на одном конце проводника образуется положительный электрический заряд, а на другом — отрицательный. Благодаря этому влиянию измеряемый электрический потенциал также одинаков в каждой точке проводника.
Обычная незаряженная среда имеет равное количество положительных и отрицательных электрических зарядов в каждой точке среды. Они расположены близко друг к другу, поэтому преобладает нейтральный электрический заряд. Положительные электрические заряды — имеют ядра атомов. Они неподвижны в структуре вещества и поэтому не могут двигаться. Отрицательные электрические заряды — это электроны, связанные с атомными ядрами. В электропроводящих объектах некоторые из этих электронов могут свободно перемещаться в материале.
Если заряженный объект приблизить к нейтральному проводнику, это приведет к разделению электрических зарядов в проводнике. Это обусловлено действующей силой заряженного объекта, описываемой законом Кулона. То, как электрический заряд распределяется в проводнике, зависит от того, заряжен ли внешний объект положительно или отрицательно.
Если вы поднесете к проводнику положительно заряженный предмет, он притянет к себе отрицательно заряженные электроны проводника. Это приводит к появлению отрицательного электрического заряда в проводнике с той стороны, с которой вы приближаетесь к положительно заряженному объекту. Аналогично этому на противоположной от него стороне возникает скопление положительного электрического заряда. Эти зоны электрического заряда называются индуцированными электрическими зарядами. С другой стороны, если объект, к которому вы приближаетесь, заряжен отрицательно, то происходит обратный процесс.
Обратите внимание, что проводник по-прежнему не заряжен, поскольку число носителей электрического заряда остается прежним. Это всего лишь перераспределение электрического заряда. Процесс является обратимым. Если вы снова удалите внешний объект, электроны вернутся к своему первоначальному распределению.
Физика и формулы, описывающие явление
Самый простой способ показать, что происходит во время электростатический индукции, — это использовать проводящую сферу. Даже если абсолютное число смещённых электронов кажется большим, сдвиг относительно невелик по отношению к общему количеству носителей электрического заряда. Это легче представить, посмотрев на распределение электрического заряда на поверхности сферы.
Если вы проводите эксперимент с электростатической индукцией, вы должны ограничить напряженность электрического поля значениями ниже Emax =105 В/м. Это предотвращает «фальсификацию результата» нежелательными разрядами. Такие разряды возникают в воздухе при значениях Eкрит =107 В/м — 109 В/м. Это напряженность электрического пробоя, которая описывает напряженность электрического поля, выше которой происходит пробой напряжения в изоляторе (диэлектрике). Обычно они имеют форму дуги или искры.
С помощью этого вы можете оценить поверхностную плотность электрического заряда σ на поверхности вашей сферы:
σ = 2 * Emax * ε0 * εr ≈ 1, 789 * 10-6 Кл/м²
Величины ε0 и εr обозначают соответственно абсолютную диэлектрическую проницаемость вакуума и относительную диэлектрическую проницаемость рассматриваемой среды.
Таким образом, на каждом квадратном сантиметре поверхности вашей сферы вы найдете избыточный электрический заряд в 1,8 * 10-10 Кл что соответствует 1,1 * 109 электронов. Количество электронов можно определить по заряду электрона, который равен e=1,602 * 10-19 Кл.
Конечно, теперь вам нужно знать, сколько атомов занимает примерно один квадратный сантиметр, чтобы вы могли определить соотношение. Если ваша сфера сделана из меди, то у вас есть около 8 * 1014 атомов в одном квадратном сантиметре. Каждый из этих атомов дает электрон проводимости. Теперь разделите количество дополнительных атомов в этом квадратном сантиметре на количество существующих.
1,1 * 109 / 8 * 1014 = 1,4 * 10-6 = 1 / 723 000 .
Итак, вы теперь знаете, что на почти 700 000 свободно движущихся электронов приходится еще один из-за электростатической индукции.
Электрические проводники
Как известно из закона Кулона, одноименные электрические заряды отталкиваются друг от друга, а разноименные притягиваются. Благодаря этим знаниям, если вы поместите проводящий материал в электрическое поле или в непосредственной близости от заряженного объекта, вы измените плотность его электрического заряда. Неважно, положительно или отрицательно заряжен объект, потому что он будет отталкивать одноименные носители электрического заряда материала и притягивать разноимённые, как уже говорилось выше. Это создает в материале области с различной плотностью электрического заряда. Общая плотность электрического заряда проводника остается неизменной.
Вывод: электростатическая индукция не изменяет общий электрический заряд проводника .
Такое перераспределение электрического заряда наблюдается только на граничных поверхностях, т.е. на поверхности проводника. Поскольку носители электрического заряда могут свободно перемещаться внутри, электрическое поле в проводнике отсутствует.
Электростатическая индукция и поляризация
В отличие от проводников, носители электрического заряда в изоляторе (диэлектрике) не могут свободно перемещаться. В случае электростатической индукции это приводит к поляризации, то есть к образованию электрических полей на поверхности и внутри диэлектрика. Поляризация на стороне, обращенной в сторону от электрического поля, соответствует внешнему полю, а на стороне, обращенной к нему, имеет противоположный электрический заряд.
Такая форма поляризации называется поляризацией смещения (деформационной поляризацией). В этом процессе положительные атомные ядра смещаются в одном направлении, а отрицательная электронная оболочка — в другом.
В этом процессе электронная оболочка не деформируется. При переменном электрическом поле, можно наблюдать, что электронная оболочка раскачивается взад и вперед, как шарик на ниточке.
Применение
Эффект электростатический индукции используется во многих процессах. Механические эффекты смещения носителей электрического заряда используются, например, в электроскопе. Он используется для измерения электрического напряжения без электрического тока.
В ускорителях частиц, через так называемые пеллетроны, электростатическая индукция используется для достижения высоких напряжений до 32 миллионов вольт.
Список использованной литературы
- Электризация через влияние. // Элементарный учебник физики / Под ред. Г.С. Ландсберга. — 13-е изд. — М.: ФИЗМАТЛИТ, 2003. — Т. 2. Электричество и магнетизм. — С. 24—27.
- Фадеева А. А., Засов А. В., Киселев Д. Ф. Физика 8. – М.: Просвещение.

21
б) потенциал в плоскости диска: ϕ(ρ, 0) = (q/R) arcsin(q/R), ϕ(ρ, 0) = V для ρ ≤ R.
Поверхностная плотность заряда на диске может быть вычислена с учетом граничного условия E2n − E1n = 4πσ, а т.к. E2n = −E1n, то E2n = −2πσ. В результате
|
1 ∂ϕ |
q |
|||||||
|
σ(ρ) = − |
|z=0 |
= |
Z0∞ sin(kR)J0(kρ)dk. |
(75) |
||||
|
2π ∂z |
2πR |
Интеграл в (75) является известным разрывным интегралом [4], тождественно равным нулю при ρ > R, а при ρ < R значение интеграла
|
равно: |
q |
1 |
||||
|
σ(ρ) = |
√ |
. |
||||
|
2πR |
||||||
|
R2 − ρ2 |
Комментарий:интегрируемая особенность в σ при ρ → R связана с предположением о бесконечно малой толщине диска.
Задание на дом: решить задачи 2.13–2.15 на стр 33.
1.6 Метод изображений.
Данный метод используется в тех задачах, в которых требуется определить поле одного или нескольких точечных зарядов при условии заданности поля на некоторых поверхностях. Суть метода изображений состоит в подборе эффективной системы точечных зарядов, которые обеспечивают требуемые граничные условия. Эти заряды называются «зарядами-изображениями». Заряды — изображения, как правило, находятся вне объема пространства, где определяется поле, поскольку потенциал создаваемого ими поля должен удовлетворять уравнению Лапласа в этом объеме.
В качестве простейшего примера можно рассмотреть точечный заряд вблизи бесконечной проводящей проволоки, имеющей нулевой потенциал (см. решение примера 1.4.1 ). В этом случае заряд q в точке ~a есть заряд-изображение.
Пример 1.6.1 Найти поле, создаваемое зарядом q, расположенным на расстоянии l от центра заземленной металлической сферы радиуса R. Определить распределение индуцированного заряда на поверхности сферы и полный индуцированный заряд.

22
Условие заземленности сферы означает равенство нулю ее потенциала. Допустим, что можно ввести один фиктивный заряд qx для удовлетворения условия ϕ(R, θ, ϕ) = 0. Из симметрии системы ясно, что он может быть расположен на оси 0z. Однако величина и местоположение данного заряда на оси 0z заранее не известны. Обозначим радиус-вектор заряда qx через
|
~ ~ |
|||||||||||||||||||||||||
|
lxk, k — единичный вектор по оси z. Тогда поле в произвольной точке |
|||||||||||||||||||||||||
|
пространства определяется выражением (см. рис 10): |
|||||||||||||||||||||||||
|
ϕ(~r ) = |
q |
+ |
qx |
. |
|||||||||||||||||||||
|
r1 |
r2 |
||||||||||||||||||||||||
|
= ~r − ~kl и ~r2 = ~r − ~klx или ~r1 = q |
, r2 = |
||||||||||||||||||||||||
|
По определению: ~r1 |
r2 − 2l~kr~ + l2 |
||||||||||||||||||||||||
|
r |
r2 − 2~kr~lx + lx2 |
. На поверхности сферы должно выполняться: |
|||||||||||||||||||||||
|
√ |
q |
qx |
(76) |
||||||||||||||||||||||
|
ϕ(R, θ, ϕ) = |
+ |
= 0. |
|||||||||||||||||||||||
|
q |
|||||||||||||||||||||||||
|
R2 − 2Rl cos θ + l2 |
R2 − 2Rlx cos θ + lx2 |
||||||||||||||||||||||||
|
Приводя последнее выражение к общему знаменателю, получим: |
|||||||||||||||||||||||||
|
qx2(R2 − 2Rl cos θ + l2) = q2(R2 − 2Rlx cos θ + lx2). |
|||||||||||||||||||||||||
|
Так как (76) имеет место при любых значениях угла θ, имеем: |
|||||||||||||||||||||||||
|
q2(R2 |
+ l2) = q2(R2 + l2); |
2q2Rl = 2q2Rlx. |
(77) |
||||||||||||||||||||||
|
x |
x |
x |
|||||||||||||||||||||||
|
Решая данную систему относительно qX и lx, получаем: |
|||||||||||||||||||||||||
|
qx = −q |
R |
R2 |
(78) |
||||||||||||||||||||||
|
; |
lx = |
. |
|||||||||||||||||||||||
|
l |
l |
||||||||||||||||||||||||
|
В результате поле в произвольной точке пространства есть: |
|||||||||||||||||||||||||
|
ϕql(r, θ, ϕ) = |
q |
qx |
. |
(79) |
|||||||||||||||||||||
|
√r2 − 2rl cos θ + l2 − qr2 − 2rlx cos θ + lx2 |
Для определения плотности индуцированного заряда воспользуемся граничным условием:
|
E2n = |
− |
∂ϕ |
! r=R = 4πσ. |
||||||||
|
∂r |
| |
||||||||||
|
Подставляя (79) |
в (80), получим: |
||||||||||
|
σ = |
1 ∂ϕql |
= |
1 |
q(l2 − R2) |
. |
||||||
|
− |
4π ∂r |
|r=R |
−4πR (R2 − 2Rl cos θ + l)3/2 |
||||||||
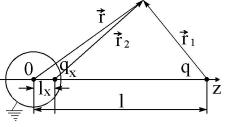
Рис. 10:
23
Полный индуцированный заряд может быть найден интегрированием по поверхности сферы.
|
π |
2π |
R |
||||
|
q. = I |
σdS = Z0 |
Z0 |
σR2 sin θ dθdϕ = −q |
, |
(82) |
|
|
l |
т.е. полный индуцированный заряд на поверхности сферы равен величине заряда-изображения.
Комментарий: если точечный заряд q находится внутри сферы, нужно лишь изменить знак на противоположный в выражении (81) для σ, поскольку внешняя нормаль к проводнику направлена теперь к центру сферы.
Угловое распределение поверхностного заряда аналогично найденному, но полный наведенный заряд равен −q.
Пример 1.6.2. Точечный заряд q расположен на расстоянии l от центра заряженной до величины Q сферы радиуса R. Найти потенциал электростатического поля вне сферы [5].
Для нахождения решения воспользуемся принципом суперпозиции и решением предыдущей задачи. Представим, что проводящая сфера заземлена. Тогда q0 = −qR/l — полный заряд на сфере, на основании (82). Разомкнем заземляющий провод и внесем на сферу заряд Q − q0. Полный заряд на сфере при этом станет равным Q. Очевидно, однако, что внесенный дополнительный заряд Q − q равномерно распределится по поверхности сферы, поскольку электростатическое поле заряда q уже уравновешено зарядом q0. Таким образом, вне сферы потенциал дополнительного заряда Q − q0 равен точечному потенциалу той же величины, расположенному в центре сферы. На основании принципа суперпозиции с учетом (79)
|
ϕ(r, θ, ϕ) = ϕql(r) + |
Q l + R q |
, |
(83) |
|
|
l r |
||||
где ϕql определяется выражением (79).
Пример 1.6.3. Точечный заряд расположен на расстоянии l от центра сферического проводника радиуса R с заданным потенциалом V . Найти поле вне проводника [5].
Очевидно, что V имеет вид (83) с той лишь разницей, что Q−q0 заменяется на V R. Действительно, как видно из (83) и (79), ϕql = 0, а член (Q −q0)/R =
|
24 |
|||||||
|
V R/R = V . Таким образом, |
|||||||
|
V R |
|||||||
|
ϕ(r, θ, ϕ) = ϕql(r) + |
. |
||||||
|
r |
|||||||
|
Пример |
1.6.4. |
Проводящая |
сфера |
радиуса R |
помещена в |
||
|
~ |
. Найти поле в |
||||||
|
однородное электрическое поле напряженностью E0 |
|||||||
|
любой точке пространства [5]. |
|||||||
|
Под действием внешнего поля заряды |
|||||||
|
проводника |
перераспределяются |
по |
|||||
|
поверхности. Очевидно, что на поверхности |
|||||||
|
проводника поле имеет только нормальную |
|||||||
|
составляющую, |
т.е. |
наличие |
проводника |
||||
|
делает поле |
неоднородным. Для |
определения |
Рис. 11: |
||||
|
поля воспользуемся |
искусственным приемом |
||||||
|
~ |
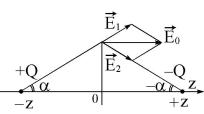
с помощью двух точечных зарядов (см. рис. 11) [5]. Можно |
||||||
|
описания E0 |
считать, что однородное поле создано зарядами ±Q, расположенными в бесконечно удаленных точках. Действительно, если R конечно, но велико,
|
имеем: |
2Q |
|
|
E ‘ 2 |
Q |
cos α ‘ |
|
. |
||
|
z2 |
z2 |
В пределе z → ∞, Q → ∞ при условии Q/z2 = const данное приближение становится точным.
Поместим проводящую сферу в начало координат. Поле будет определяться по принципу суперпозиции полями реальных зарядов ±Q, находящихся на расстоянии ±z, и полем зарядов изображений, равных
±Q R/z и расположенных в точках z = ±R2/z (см. пример 1.6.2 ). Полный потенциал равен: ϕ = ϕQ,−|z| + ϕ−Q,|z|, где ϕq,l определено выражением (79).
|
При условии |z| → ∞, разлагая ϕ в ряд, найдем: |
|||||||||||||||||||||||||||||||
|
ϕ = |
Q |
1 |
− |
r |
cos θ |
Q |
1 + |
r |
cos θ |
+ Q |
R |
1 + |
R2 |
cos θ |
|||||||||||||||||
|
|z| |
|z| |
r|z| |
|||||||||||||||||||||||||||||
|
|z| |
− |
|z| |
|z| |
− |
|||||||||||||||||||||||||||
|
R |
1 |
1 + |
2 |
cos θ = |
2Q |
||||||||||||||||||||||||||
|
− |
Q |
R |
(r |
− |
R3/r2) cos θ. |
||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||
|
|z| r |
z |
z |
|||||||||||||||||||||||||||||
|
Вычисляя предел данного выражения, получим: |
|||||||||||||||||||||||||||||||
|
θ |
r |
R3 |
cos θ = |
R3 |
|||||||||||||||||||||||||||
|
lim |
2 |
E0r cos θ(1 |
). |
||||||||||||||||||||||||||||
|
2 |
2 |
3 |
|||||||||||||||||||||||||||||
|
Q |
,z |
! |
− |
− r |
|||||||||||||||||||||||||||
|
→∞ →∞ −z |
− r |
Соседние файлы в папке Хасанов лекции
- #
- #
- #
- #
- #
- #
- #
- #
распространение электрического заряда из-за наличия других зарядов
Электростатическая индукция, также известная как «электростатическое влияние» или просто «влияние» в Европе и Латинской Америке — это перераспределение электрического заряда в объекте, вызванное влиянием соседних зарядов. В присутствии заряженного тела изолированный проводник развивает положительный заряд на одном конце и отрицательный — на другом. Индукция была открыта британским ученым Джоном Кантоном в 1753 году и шведским профессором Йоханом Карлом Вильке в 1762 году. Электростатические генераторы, такие как машина Вимшерста, генератор Ван де Граафа и электрофор используют этот принцип. Из-за индукции электростатический потенциал (напряжение ) постоянен в любой точке проводника. Электростатическая индукция также отвечает за притяжение легких непроводящих предметов, таких как воздушные шары, бумажные или пенополистирольные отходы, к статическим электрическим зарядам. Законы электростатической индукции применяются в динамических ситуациях до тех пор, пока справедливо квазистатическое приближение. Электростатическую индукцию не следует путать с Электромагнитная индукция.
Содержание
- 1 Пояснение
- 2 Заряд объекта индукцией
- 3 Электростатическое поле внутри проводящего объекта равно нулю
- 4 Находится индуцированный заряд на поверхности
- 5 Напряжение по всему проводящему объекту постоянно
- 6 Индукция в диэлектрических объектах
- 7 Примечания
- 8 Внешние ссылки
Объяснение


Нормальный незаряженный кусок Материя имеет равное количество положительных и отрицательных электрических зарядов в каждой своей части, расположенных близко друг к другу, поэтому ни одна из частей не имеет чистого электрического заряда. Положительные заряды — это атомы ‘ядра, которые связаны в структуре материи и не могут двигаться. Отрицательные заряды — это электроны атомов. В электропроводящих объектах, таких как металлы, некоторые электроны могут свободно перемещаться внутри объекта.
Когда заряженный объект приближается к незаряженному, электрически проводящему объекту, например, куску металла, сила соседнего заряда в соответствии с законом Кулона вызывает разделение этих внутренних сборов. Например, если рядом с объектом поднести положительный заряд (см. Изображение цилиндрического электрода возле электростатической машины), электроны в металле будут притягиваться к нему и перемещаться в сторону объекта, обращенного к нему. Когда электроны покидают область, они оставляют несбалансированный положительный заряд из-за ядер. Это приводит к образованию области отрицательного заряда на объекте, ближайшем к внешнему заряду, и области положительного заряда на стороне, удаленной от него. Они называются индуцированными зарядами. Если внешний заряд отрицательный, полярность заряженных областей будет обратной.
Поскольку этот процесс представляет собой просто перераспределение зарядов, которые уже были в объекте, он не меняет общий заряд объекта; у него по-прежнему нет нетто-заряда. Этот эффект индукции обратим; если соседний заряд удален, притяжение между положительным и отрицательным внутренними зарядами заставляет их снова смешиваться.
Зарядка объекта с помощью индукции


Однако эффект индукции также можно использовать для наложения чистого заряда на объект. Если, находясь близко к положительному заряду, вышеупомянутый объект на мгновение подключается через токопроводящий путь к электрическому заземлению, которое является большим резервуаром как положительных, так и отрицательных зарядов, некоторые отрицательных зарядов в земле будут течь в объект под действием близлежащего положительного заряда. Когда контакт с землей нарушается, объект остается с чистым отрицательным зарядом.
Этот метод можно продемонстрировать с помощью электроскопа с позолотой, который представляет собой прибор для обнаружения электрического заряда. Электроскоп сначала разряжается, а затем заряженный объект приближается к верхнему выводу прибора. Индукция вызывает разделение зарядов внутри металлического стержня электроскопа , так что верхний вывод получает общий заряд противоположной полярности по сравнению с полярностью объекта, а золотые листья получают заряд той же полярности.. Поскольку оба листа имеют одинаковый заряд, они отталкиваются друг от друга и расходятся. Электроскоп не получил чистого заряда: заряд внутри него просто перераспределился, поэтому, если заряженный объект отодвинуть от электроскопа, листья снова соберутся вместе.
Но если теперь кратковременно установить электрический контакт между клеммой электроскопа и землей, например, прикоснувшись к клемме пальцем, это заставит заряд течь от земли к клемме, притягиваясь зарядом на объект рядом с терминалом. Этот заряд нейтрализует заряд золотых листьев, поэтому листья снова собираются вместе. Электроскоп теперь содержит чистый заряд, противоположный по полярности заряженному объекту. Когда электрический контакт с землей нарушен, например при поднятии пальца дополнительный заряд, который только что попал в электроскоп, не может уйти, и инструмент сохраняет чистый заряд. Заряд удерживается в верхней части терминала электроскопа за счет притяжения индуцирующего заряда. Но когда индуцирующий заряд удаляется, заряд высвобождается и распространяется по клемме электроскопа к листам, так что золотые листы снова расходятся.
Знак заряда, оставшегося на электроскопе после заземления, всегда противоположен знаку внешнего индуцирующего заряда. Два правила индукции:
- Если объект не заземлен, соседний заряд вызовет одинаковые и противоположные заряды в объекте.
- Если какая-либо часть объекта на мгновение заземлена, в то время как индуцирующий заряд рядом, заряд, полярность противоположная индуцирующему, будет притягиваться от земли к объекту, и он останется с зарядом, противоположным индуцирующему заряду.
Электростатическое поле внутри проводящего объекта равно нулю
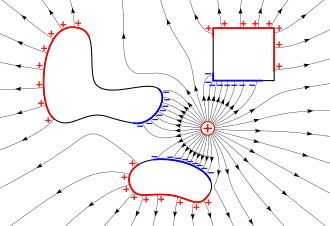
Остается вопрос, насколько велики индуцированные заряды. Движение зарядов вызывается силой, действующей на них электрическим полем внешнего заряженного объекта, по закону Кулона. Поскольку заряды в металлическом объекте продолжают разделяться, полученные положительная и отрицательная области создают собственное электрическое поле, которое противодействует полю внешнего заряда. Этот процесс продолжается до тех пор, пока очень быстро (в течение доли секунды) не будет достигнуто равновесие, при котором индуцированные заряды имеют точно правильный размер, чтобы нейтрализовать внешнее электрическое поле во внутренней части металлического объекта. Тогда оставшиеся подвижные заряды (электроны) внутри металла больше не ощущают силы, и результирующее движение зарядов прекращается.
Индуцированный заряд остается на поверхности
Поскольку подвижные заряды внутри металлический объект может свободно перемещаться в любом направлении, никогда не может быть статической концентрации заряда внутри металла; если бы он был, он притягивал бы заряд противоположной полярности, чтобы нейтрализовать его. Следовательно, при индукции подвижные заряды перемещаются под действием внешнего заряда, пока не достигают поверхности металла и собираются там, где они не могут двигаться границами.
Это устанавливает важный принцип электростатического заряда. заряды на проводящих объектах находятся на поверхности объекта. Внешние электрические поля индуцируют поверхностные заряды на металлических объектах, которые в точности нейтрализуют поле внутри.
Напряжение по всему проводящему объекту постоянно
электростатический потенциал или напряжение между двумя точками определяется как энергия (работа), необходимая для перемещения небольшого заряда через электрическое поле между двумя точками, деленная на размер заряда. Если существует электрическое поле, направленное из точки b { displaystyle mathbf {b}}









- ∇ V = E { displaystyle nabla V = mathbf {E} ,}
Так как внутри проводящего объекта не может быть электрического поля, которое могло бы воздействовать на заряды (E = 0) { displaystyle ( mathbf {E} = 0) ,}
- ∇ V = 0 { displaystyle nabla V = mathbf {0} , }
Другими словами, в электростатике электростатическая индукция обеспечивает постоянство потенциала (напряжения) во всем проводящем объекте.
Индукция в диэлектрических объектах

Подобный эффект индукции возникает в непроводящих (диэлектрических ) объектах и является причиной для притяжения небольших легких непроводящих предметов, таких как воздушные шары, обрывки бумаги или пенополистирол, к статическим электрическим зарядам (см. каталожный выше), а также статическое сцепление в одежде.
В непроводниках электроны связаны с атомами или молекулами и не могут свободно перемещаться вокруг объекта, как в проводниках; однако они могут немного двигаться внутри молекул. Если положительный заряд переносится около непроводящего объекта, электроны в каждой молекуле притягиваются к нему и перемещаются в сторону молекулы, обращенную к заряду, в то время как положительные ядра отталкиваются и слегка перемещаются в сторону противоположная сторона молекулы. Поскольку отрицательные заряды теперь ближе к внешнему заряду, чем положительные, их притяжение больше, чем отталкивание положительных зарядов, что приводит к небольшому чистому притяжению молекулы к заряду. Это называется поляризацией, а поляризованные молекулы называются диполями. Этот эффект микроскопический, но, поскольку молекул очень много, он создает достаточную силу для перемещения легкого объекта, такого как пенополистирол. Это принцип работы пробкового электроскопа.
Примечания
Внешние ссылки
- «Зарядка электростатической индукцией». Центр подготовки к экзаменам Regents. Городской школьный округ Освего. 1999. Архивировано с оригинального 28.08.2008. Проверено 25 июня 2008 г.
2017-03-24
В центре уединенного проволочного заряженного кольца радиуса $a$ потенциал равен $phi_{0}$. Это кольцо поднесли к заземленному шару радиуса $b$ так, что только центр О кольца оказался на поверхности шара. Найдите индуцированный на шаре заряд.
Решение:
Используя принцип суперпозиции, легко найти связь между значениями заряда на кольце или на сфере и потенциала в их центре.
$phi = k left ( frac{ Delta q_{1}}{R} + frac{ Delta q_{2}}{R} + cdots + frac{ Delta q_{N}}{R} right )$,
где $R$ — радиус, а $Delta q_{1}, cdots , Delta q_{N}$ — маленькие доли зарядов, на которые разбит весь заряд так, чтобы для каждого участка, занятого долей заряда, можно было бы использовать выражение потенциала точечного заряда
$Delta phi = k frac{ Delta q}{R}$.
Вынося $1/R$ за скобку, получаем $phi = kq/R$.
Отсюда заряд на кольце в задаче $q = phi_{0} R/k$.
В заземленном проводящем шаре заряд, как известно, расположен на поверхности, поле внутри равно нулю, а потенциал всюду одинаков и равен нулю, в том числе и в центре $O_{1}$.
По принципу суперпозиции суммируя вклады от распределенных по кольцу и на шаре и приравнивая сумму нулю, записываем для точки $O_{1}$
$k frac{q}{ sqrt{ a^{2} + b^{2}}} + k frac{Q}{b} = 0$,
откуда
$Q = — phi_{0} frac{ab}{4 pi epsilon_{0} sqrt{a^{2} + b^{2}}}$.
Содержание книги
Предыдующая страница
§10. Проводники и диэлектрики в электростатическом поле
10.4 Расчет поля в присутствии проводников. Метод изображений.
Мы уже подчеркивали, что основная проблема расчета полей в присутствии проводников заключается в появлении индуцированных зарядов, распределение которых заранее не известно. В связи с этим рассмотренные ранее методы, основанные на законе Кулона и принципе суперпозиции, в данном случае оказываются непригодными. Принципиально иной подход к решению данной задачи заключается в расчете распределения потенциала электростатического поля. Действительно, на поверхности проводника распределение заряда не известно, но ведь потенциал проводника постоянен!
Сам метод основан на решении уравнений [1] для потенциала поля. Сами эти уравнения довольно сложны и рассматриваются в курсе физики высшей школы, однако, их физический смысл основывается на законе Кулона и связи потенциала с напряженностью поля.
Однако в некоторых случаях можно рассчитать электрическое поле и распределение индуцированных на поверхности проводника зарядов, используя искусственный прием, который называется метод изображений.
Изложим кратко суть и дадим обоснование этого метода.
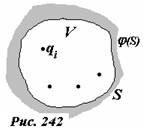
Пусть в некоторой области пространства V, ограниченной поверхностью S (в частном случае граница области может простираться до бесконечности), задано распределение зарядов qi (рис. 242).
Электрическое поле в выделенной области определяется однозначно, если
- — задано распределение зарядов внутри этой области;
- — задано распределение потенциала на границе области.
Заметим, что на границе области могут существовать заряды, однако даже при неизвестном их распределении, задание потенциала на границе однозначно определяет поле внутри области. Поэтому две различные задачи, но с одинаковыми распределениями зарядов внутри области и одинаковыми потенциалами на границе имеют внутри области одинаковые решения. Иногда при неизвестном распределении индуцированных зарядов на границе удается подобрать такое распределение зарядов вне рассматриваемой области, что для нового распределения выполненяются граничные условия исходной задачи. В этом случае дополнительные заряды называются зарядами-изображениями. Поиск изображений имеет смысл вести тогда, когда новая задача оказывается проще исходной и имеет простое решение.
Помимо задания распределения потенциала, в качестве граничных условий могут использоваться и некоторые другие, например, значение напряженности поля. Формулировке граничных условий, по этой причине уделяется серьезное внимание в курсе электродинамики.
Точечный заряд над плоской проводящей поверхностью.
Рассмотрим простейшую задачу, допускающую решение с помощью метода изображений.
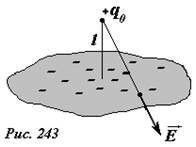
Пусть точечный заряд +q0 находится на расстоянии l от бесконечной металлической пластины (рис. 243).
Очередной раз мы пользуемся моделями – в данном случае под бесконечной, понимается пластина, размеры которой значительно больше расстояния до заряда. Кроме того, можно считать, что пластина заземлена, так как она «касается бесконечности».
Под действием электрического поля заряда +q0 электроны пластины придут в движения и начнут скапливаться под точечным зарядом, создавая отрицательный индуцированный заряд.
Если пластина реально заземлена, то эти заряды натекут из заземления. На большой незаземленной пластине возникнут положительные заряды на краях пластины, но так как эти края находятся далеко, то их полем в рассматриваемой области можно пренебречь.
Распределение поверхностной плотности индуцированных зарядов на пластине σ не известно, но известно, что ее потенциал постоянен и равен нулю.
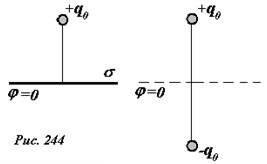
Легко придумать другую задачу, для которой будет выполнено такое же граничное условие. Действительно, рассмотрим поле, создаваемое двумя точечными зарядами q = +q0 и q’ = —q0 , находящимися на расстоянии 2l друг от друга (рис. 244). Во всех точках плоскости, перпендикулярной отрезку, соединяющими заряды и проходящей через ее середину, потенциал равен нулю, так как эти точки находятся на равном расстоянии от двух зарядов равных по величине и противоположных по направлению.
Сравним данную простую задачу (два точечных заряда) с исходной (точечный заряд и индуцированные им заряды σ на проводящей пластине): в полупространстве над пластиной распределения зарядов одинаковы (в обоих случаях – один точечный заряд), на граничной плоскости потенциалы равны; следовательно, в этом полупространстве электрические поля также одинаковы.
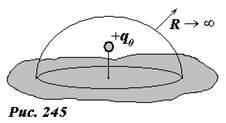
Строго говоря, мы должны рассматривать замкнутую область пространства, поэтому мысленно накроем заряд +q0 полусферой, опирающейся на плоскость, положим ее потенциал равным нулю и устремим ее радиус к бесконечности, и таким образом придем к рассматриваемому полупространству (рис. 245).
Таким образом, в верхнем полупространстве задачи эквивалентны – заряды и поле распределены одинаково. Следовательно, можно утверждать, что индуцированные на металлической пластине заряды σ создают в верхнем полупространстве такое же электрическое поле как заряд q’ = —q0, расположенный симметрично относительно верхней поверхности пластины. Следовательно, для расчета электрического поля следует зеркально симметрично под пластиной расположить заряд-изображение q’ = —q0. Подчеркнем, что реально никакого такого заряда не возникает, его роль – описать поле, создаваемое реальными индуцированными зарядами на поверхности пластины. Ввиду явной симметрии такое же поле возникает и в нижнем полупространстве (то есть поле заряда q’, расположенного в той же точке, что и исходный заряд +q0). Это поле индуцированных зарядов складывается с полем исходного заряда, поэтому и оказывается, что в нижнем полупространстве поле равно нулю, как и должно быть внутри проводника.
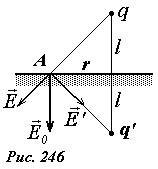
Напряженность суммарного поля у границы (~vec E_0) можно рассчитать по принципу суперпозиции как сумму полей, создаваемых исходным зарядом (~vec E)и его изображением (~vec E’) (рис. 246):
(~vec E_0 = vec E’ + vec E) .
Суммарный вектор направлен перпендикулярно границе и равен
(~E = 2 frac{q}{4 pi varepsilon_0 (l^2 + r^2)} cos alpha = frac{ql}{2 pi varepsilon_0 (l^2 + r^2)^{frac{3}{2}}}) ,
здесь r расстояние от основания перпендикуляра из заряда на плоскость пластины до рассматриваемой точки. Поверхностная плотность заряда у поверхности проводника связана с напряженностью поля соотношением (sigma = varepsilon_0 E) , поэтому распределение поверхностной плотности индуцированных зарядов на пластине осесимметрично и имеет вид
(~sigma = frac{ql}{2 pi (l^2 + r^2)^{frac{3}{2}}}) ,
Сила притяжения заряда к пластине определяется полем, создаваемым индуцированными зарядами, которое в свою очередь эквивалентно полю заряда изображения, поэтому равно силе взаимодействия двух точечных зарядов q и q’
(~F = -frac{q^2}{4 pi varepsilon_0 (2l)^2} = -frac{q^2}{16 pi varepsilon_0 l^2}) .
Энергия взаимодействия исходного и индуцированных зарядов равна только половине (!) энергии взаимодействия зарядов q и q’. Заметьте, что две задачи (заряд и пластина — два заряда) эквивалентны только в верхнем полупространстве. Реально поле существует только в верхней половине пространства. Так энергия взаимодействия есть энергия поля, то и энергия взаимодействия будет в два раза меньше. Поэтому
(~W = — frac{1}{2} frac{q^2}{4 pi varepsilon_0 (2l)} = -frac{q^2}{16 pi varepsilon_0 l}) .
Этот вывод можно пояснить следующим образом: при двух реальных точечных зарядах при перемещении одного из них второй остается неподвижным. Если же уносить заряд от проводящей границы, то его изображение также удаляется, поэтому совершаемая работа будет меньше.

Картина силовых линий также может быть рассчитана, как поле двух точечных зарядов (рис. 247). Обратите внимание, что во всех точках плоскости силовые линии перпендикулярны поверхности.
Продолжим развитие идей построения зарядов-изображений.
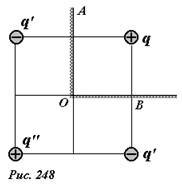
Пусть точечный заряд q находится на биссектрисе прямого двугранного угла AOB, образованного двумя бесконечными проводящими плоскостями (рис. 248). Попытаемся построить набор зарядов изображений так, чтобы удовлетворить граничным условиям — на гранях угла потенциал должен быть равен нулю. Прежде всего, зеркально отобразим исходный заряд в двух плоскостях — получим два изображения q’. Но эти три заряда не обеспечивают равенство нулю потенциала на гранях угла. Необходимо еще один раз отобразить изображения в другой грани — тем самым появляется еще один заряд-изображение q’’. Отметим, что этот заряд является одновременно изображением обоих зарядов q’. Однако его величина также равна q (а не 2q), так как единственное и основное правило построения — удовлетворение граничных условий. Легко проверить, что поле четырех зарядов имеет нулевой потенциал, как на плоскости OA, так и на плоскости OB. Таким образом, поле, образованное зарядом q и индуцированными на плоскостях зарядами эквивалентно полю четырех точечных зарядов, причем эта эквивалентность выполняется только в одной четверти угла, содержащей исходный заряд. В оставшихся четвертях поле отсутствует. Но картина силовых линий получается достаточно симпатичной, если построить поле четырех зарядов, подразумевая, что реально поле только в одной четверти, поэтому в остальных четвертях оно заштриховано (рис. 249).
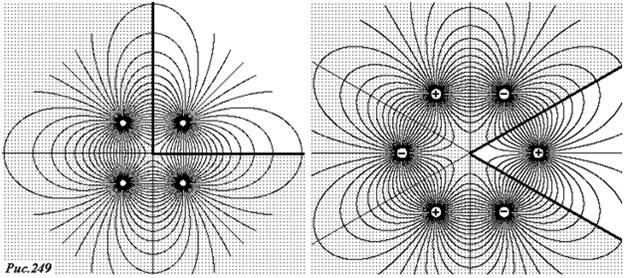
Совершенно аналогично можно построить поле заряда, помещенного на биссектрису двугранного угла, величина которого целое число раз укладывается в полном угле, например, в угле 60°. Шесть зарядов, знаки которых чередуются, расположенных в вершинах правильного шестиугольника, обеспечивают равенство нулю потенциала на гранях угла.
Изображение заряда в сфере.
Прежде, чем приступить к рассмотрению следующей группы задач, связанных с описанием взаимодействия точечного заряда и проводящей сферы, решим одну вспомогательную задачу.
Пусть электростатическое поле создается двумя точечными зарядами, находящимися на расстоянии l друг от друга. Величины и знаки зарядов различны и равны q1 и q2. Покажем, что поверхность нулевого потенциала этого поля представляет собой сферу.
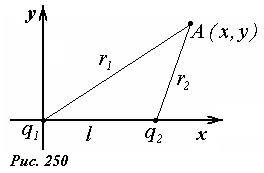
Выберем систему координат, так чтобы заряд q1 находился в начале координат, а заряд q2 на оси Ox (рис. 250). Так задача обладает осевой симметрией, то достаточно показать, что в плоскости xOy линия нулевого потенциала является окружностью. Запишем выражение для потенциала электростатического поля в произвольной точке A с координатами (x,y)
(~varphi = frac{q_1}{4 pi varepsilon_0 r_1} + frac{q_2}{4 pi varepsilon_0 r_2} = frac{1}{4 pi varepsilon_0} left (frac{q_1}{sqrt{x^2 + y^2}} + frac{q_2}{sqrt{(x — l)^2 + y^2}}right )) .
Полагая φ = 0, получим уравнение, определяющее линию нулевого потенциала. Обозначим (~frac{q_2}{q_1} = k) , и преобразуем это уравнение к виду:
(~left ( x + frac{l}{k^2 — 1} right )^2 + y^2 = frac{k^2 l^2}{(k^2 — 1)^2}) .
А это есть уравнение окружности радиуса (~R = frac{k l}{k^2 — 1}) с центром, лежащим на оси X в точке с координатой (~x_c = — frac{l}{k^2 — 1}). В пространстве, с учетом осевой симметрии (вращая вокруг оси X) эта линии образует сферу.
Итак, запомним – в поле создаваемом двумя точечными зарядами разными по знаку и величине, поверхность нулевого потенциала представляет собой сферу.
Рассмотрим теперь такую систему: точечный заряд q расположен на расстоянии l от центра металлической заземленной сферы радиуса R. Исследуем электрическое поле в этом случае.
На поверхности металлической заземленной сферы возникнут индуцированные заряды, распределение которых заранее не известно, однако потенциал сферы равен нулю. Мы показали, что поле двух точечных зарядов имеет в качестве поверхности нулевого потенциала сферу. Теперь мы можем использовать этот результат.
Для этого необходимо внутри сферы можно построить заряд изображение q’, такой, чтобы поле двух точечных зарядов имело нулевой потенциал на поверхности сферы. В этом случае вне сферы поле двух точечных зарядов q, q’ и поле, создаваемое зарядом q и зарядами, индуцированными на поверхности металлической сферы, будут одинаковыми. (Вне сферы распределения зарядов одинаковы, на границе — одинаковые граничные условия – поэтому поля вне сферы будут одинаковыми).
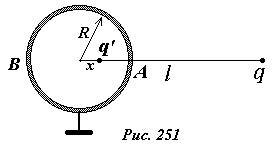
Для определения величины заряда-изображения q’ и его положения можно потребовать выполнения условия φ = 0 в двух точках сферы, например, A и B (рис. 251):
(~left{begin{matrix} frac{1}{4 pi varepsilon_0} frac{q}{l — R} + frac{1}{4 pi varepsilon_0} frac{q’}{R — x} = 0 \ frac{1}{4 pi varepsilon_0} frac{q}{l + R} + frac{1}{4 pi varepsilon_0} frac{q’}{R + x} = 0 end{matrix}right. ) .
Решив эту систему относительно неизвестных q’ и x, получим
(~left{begin{matrix} q’ = -q frac{R}{l} \ x = frac{R^2}{l} end{matrix}right. ) .
Таким образом, вне сферы поле эквивалентно полю двух точечных зарядов исходного q и найденного заряда изображения q’. Внутри сферы эти поля, конечно же, различаются — внутри реальной проводящей сферы поле отсутствует.
Для определения суммарного индуцированного заряда воспользуемся теоремой Гаусса. Окружим сферу замкнутой поверхностью. По теореме Гаусса, поток вектора напряженности электрического поля через эту поверхность равен суммарному заряду внутри поверхности, деленному на ε0. Так поле индуцированных зарядов эквивалентно полю заряда изображения, то и суммарный индуцированный заряд равен величине заряда-изображения (~q’ = -q frac{R}{l}) .
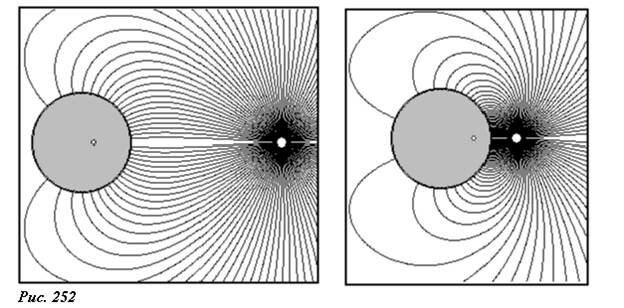
На рисунке 252 показаны силовые линии поля, при двух различных значениях расстояниях до точечного заряда. Обратите внимание, что при увеличении расстояния между зарядом и сферой искажения поля точечного заряда уменьшаются. Как всегда, у поверхности проводника силовые линии перпендикулярны границе, что соответствует условию равновесия индуцированных зарядов на поверхности проводника.
Еще раз подчеркнем — вне сферы поля эквивалентны, но это не значит, что индуцированные заряды концентрируются в одной точке — они распределены по поверхности сферы.
Силу взаимодействия между сферой и точечным зарядом можно найти как силу взаимодействия между двумя точечными зарядами q, q’ :
(~F = frac{q q’}{4 pi varepsilon_0 (l — x)^2} = -frac{q^2}{4 pi varepsilon_0} frac{Rl}{(l^2 — R^2)^2}) .
Заметим, что при l >> R сила взаимодействия становится равной
(~F = -frac{q^2}{4 pi varepsilon_0} frac{R}{l^3}) ,
то есть сила убывает обратно пропорционально кубу расстояния. Такая зависимость может быть качественно объяснена: величина заряда, индуцированного на сфере обратно пропорциональна расстоянию до исходного заряда, а сила взаимодействия между точечными зарядами обратно пропорциональна квадрату расстояния — следовательно, сила взаимодействия сферы и заряда обратно пропорциональна кубу расстояния.
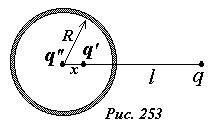
Рассмотрим, как изменится картина поля, если сфера не заземлена. Потенциал незаземленной сферы отличен от нуля, но по-прежнему постоянен, но величина его заранее не известна. Но для изолированной сферы суммарный индуцированный заряд равен нулю — в поле точечного заряда произойдет только перераспределение зарядов по поверхности сферы. Мы можем добиться выполнения граничных условий, поместив в центр шара еще один заряд-изображение q’’ = —q’ (рис. 253). Действительно, заряды q, q’ создают поле, потенциал которого на поверхности сферы равен нулю, а заряд, помещенный в центре сферы, на ее поверхности создает постоянный (но не равный нулю) потенциал, поэтому эквипотенциальность сферы не нарушится. Из теоремы Гаусса следует, что суммарный индуцированный заряд сферы равен сумме зарядов изображений, поэтому при выполнении условия q’’ = —q’, этот заряд окажется равным нулю.
Итак, вне сферы поле, создаваемое точечным зарядом q и индуцированными зарядами на поверхности, эквивалентно полю трех точечных зарядов q, q’, q’’.
Обратите внимание, число зарядов изображений определяется только необходимостью выполнения граничных условий.
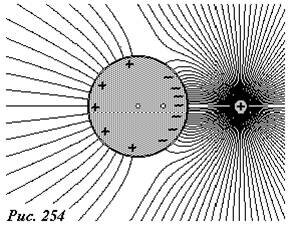
На рисунке 254 показана картина силовых линий электрического поля рассматриваемой системы зарядов. Обратите внимание, что имеются силовые линии, начинающиеся на положительных зарядах сферы. Незаземленная сфера гораздо меньше возмущает поле точечного заряда, чем заземленная. Действительно, на ней происходит только перераспределение зарядов.
Сила, действующая на заряд q, вычисляется как сумма сил, действующих со стороны двух изображений
(~F = frac{q q’}{4 pi varepsilon_0 (l — x)^2} + frac{q q»}{4 pi varepsilon_0 l^2}= -frac{q^2}{4 pi varepsilon_0} frac{R^3 (2l^2 — R^2)}{l^3 (l^2 — R^2)^2}) .
При l >> R сила взаимодействия
(~F = -frac{q^2}{2 pi varepsilon_0} frac{R^3}{l^5}) ,
убывает обратно пропорционально пятой степени расстояния, что также легко объяснимо: величина индуцированного дипольного момента пропорциональна величине внешнего поля (которое убывает обратно пропорционально квадрату расстояния), а величина поля диполя убывает обратно пропорционально кубу расстояния.
Заметим, что в данном случае можно вычислить потенциал сферы, не рассчитывая распределения зарядов на поверхности. По принципу суперпозиции, потенциал центра сферы равен сумме потенциалов заряда q и индуцированных зарядов на поверхности сферы. Все индуцированные заряды находятся на одном и том же расстоянии от центра и их сумма равна нулю, следовательно, равен нулю и потенциал, создаваемый ими в центре сферы. Поэтому потенциал в центре сферы, следовательно, и в любой ее точке, равен потенциалу поля точечного заряда (~varphi = frac{q}{4 pi varepsilon_0 l}) .
Суммарный заряд сферы остается равным нулю, но сфера приобретает индуцированный дипольный момент, который равен дипольному моменту двух зарядов-изображений
(~p = q’ x = q frac{R^3}{l^2}) .
Перепишем эту формулу в виде
(~p = q frac{R^3}{l^2} = frac{q}{4 pi varepsilon_0 l^2} varepsilon_0 (4 pi R^3) = 3V varepsilon_0 E_0) ,
где (~V = frac{4}{3} pi R^3) — объем сферы, (~E_0 = frac{q}{4 pi varepsilon_0 l^2}) — напряженность поля, создаваемого точечным зарядом в центре сферы. Таким образом, мы видим, что индуцированный дипольный момент сферы пропорционален напряженности внешнего поля. В общем случае связь между напряженностью внешнего поля и величиной индуцированного заряда записывают виде
(~p = alpha varepsilon_0 E) ,
где E — напряженность внешнего электрического поля, коэффициент пропорциональности α имеет размерность объема и называется поляризуемостью тела. Мы показали, что для проводящей сферы (аналогично шара), поляризуемость равна ее утроенному объему. В общем случае поляризуемость зависит от формы тела и его электрических свойств, однако по порядку величины она равна объему тела.
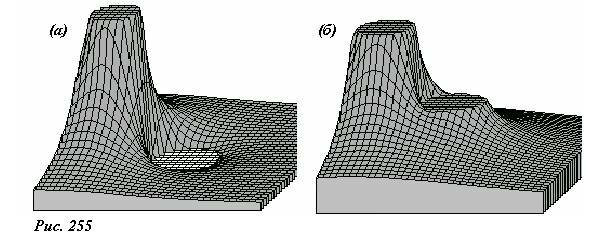
Достаточно интересно рассмотреть распределение потенциала в плоскости, проходящей через точечный заряд и центр сферы. Эти потенциальные функции для заземленной (а) и незаземленной (б) сфер изображены на рисунке 255. Функция, описывающая потенциал поля, вне сферы совпадает с потенциалом поля точечных зарядов (исходного и изображений), а внутри сферы равна нулю в случае (а) и постоянна в случае (б) – круглые горизонтальные площадки совпадает с сечением сферы. Резкое «возвышение» есть потенциал поля точечного заряда, который стремится к бесконечности, здесь, как и на других рисунках, он «обрезан».
Проводящий шар в однородном поле.
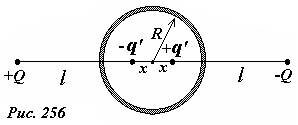
Посмотрим, какие изменения внесет проводящий шар, помещенный в однородное электрическое поле. Данная задача весьма популярна, известно несколько принципиально различных методов ее решения. Мы же воспользуемся уже полученными нами результатами. Поместим шар посредине между двумя одинаковыми по величине, но противоположными по знаку точечными зарядами +Q и —Q (рис. 256). Обозначим расстояния от зарядов до центра шара l.
Построим изображения каждого заряда в шаре — два заряда, величины которых равны (~q’ = Q frac{R}{l}) , и расположены на расстоянии (~x = frac{R^2}{l}) от центра шара. Теперь мысленно начнем уносить заряды Q на бесконечность (~l to infty) . При этом заряды-изображения будут приближаться к центру шара, образуя точечный диполь с дипольным моментом
(~p = 2q’ x = 2 frac{Q R^3}{l^2}) .
При увеличении расстояния между зарядами поле в области шара становится практически однородным с напряженностью
(~E = 2 frac{Q}{4 pi varepsilon_0 l^2}) .
Выразим индуцированный дипольный момент шара через напряженность поля
(~p = 4 pi varepsilon_0 R^3 E) .
как видите, этот дипольный момент не зависит от «придуманных» зарядов Q и расстояния l, поэтому и в однородном поле шар будет иметь такой же дипольный момент. Обратите внимание, что и в данном случае поляризуемость шара равна его утроенному объему.
Таким образом, поле индуцированных на поверхности шара зарядов эквивалентно полю точечного диполя, находящегося в центре шара. Картину силовых линий такого поля мы уже использовали ранее.
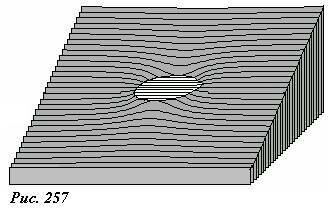
Неплохо также смотрится и распределение потенциала (рис. 257).
Заметим, что потенциал однородного поля изменяется по линейному закону, поэтому распределение потенциала в таком поле изображается наклонной плоскостью. При помещении в это поле проводящего шара на наклонной плоскости появляется горизонтальная площадка, постоянного потенциала на проводнике.
Задание для самостоятельной работы.
- Найдите распределение поверхностной плотности индуцированных зарядов на поверхности металлического шара, помещенного во внешнее электрическое поле.
Примечания
- ↑ Эти уравнения называются уравнениями С. Пуассона, или в частных случаях уравнениями П. Лапласа. С математической точки зрения они являются уравнениями в частных производных, поэтому их изучение далеко выходит за рамки наших возможностей.
Следующая страница





