График производной как найти наибольшее значение функции - Avtoru.top

Рассмотрим задания, в которых дан график производной функции и требуется найти, в какой точке данного отрезка эта функция принимает наибольшее значение.

№1

На рисунке изображён график производной функции f(x), определённой на интервале (-14;8). В какой точке отрезка [-11;-8] функция f(x) принимает наибольшее значение?

Решение:

Выделяем отрезок [-11;-8].

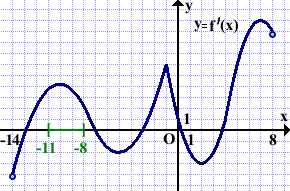
На этом отрезке производная f'(x) принимает положительные значения.

Следовательно, функция f(x) на этом отрезке возрастает, то есть бо́льшему значению аргумента соответствует бо́льшее значение функции:

x₁,x₂ ∈[-11;-8], x₂>x₁, ⇒ f(x₂)>f(x₁).

Поэтому наибольшее значение функция f(x) на отрезке принимает при наибольшем значении аргумента, то есть на правом конце отрезка, при x=-8.

Ответ: -8.

№2

На рисунке изображён график производной функции f(x), определённой на интервале (-7;9). В какой точке отрезка [4;8] функция f(x) принимает наибольшее значение?

Решение:

Выделяем отрезок [4;8].

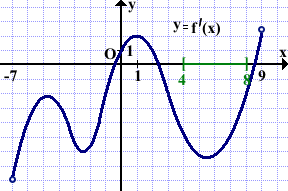
Так как этом отрезке производная f'(x)<o, то функция f(x) на [4;8] убывает, то есть бо́льшему значению аргумента соответствует меньшее значение функции:

x₁,x₂ ∈[4;8], x₂>x₁, ⇒ f(x₂)<f(x₁).

Поэтому наибольшее значение f(x) принимает в этом случае при наименьшем значении аргумента, то есть на левом конце отрезка, при x=4.

Ответ: 4.

№3

Функция y=f(x) определена на промежутке (-5;9). На рисунке изображён график её производной. Найти абсциссу точки, в которой функция y=f(x) принимает наибольшее значение.

Решение:

В точке с абсциссой x=6 производная меняет знак с плюса на минус.

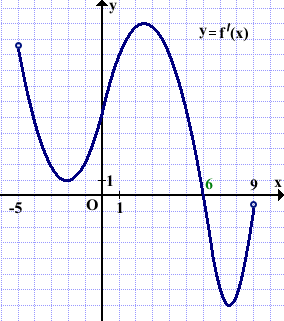
Следовательно, x=6 — точка максимума.

Производная f'(x) существует на всём интервале (-5;9), следовательно, функция f(x) непрерывна на (-5;9).

Если непрерывная функция f(x) имеет на заданном интервале (a;b) только одну точку экстремума x_o и это точка максимума, то на (a;b) функция принимает своё наибольшее значение в точке x_o.

Таким образом, функция f(x) на интервале (-5;9) принимает наибольшее значение в точке x=6.

Ответ: 6.

№4

Функция y=f(x) определена и непрерывна на отрезке [-1;9]. На рисунке изображён график её производной. Найти точку x_o, в которой функция принимает наибольшее значение, если f(-1)≥f(9).

Решение:

На промежутках (-1;3) и (8;9) производная f'(x)>0, поэтому на этих промежутках функция f(x) возрастает.

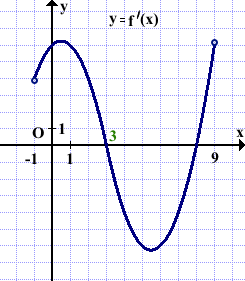
На промежутке (3;9) производная f'(x)<0, поэтому на (3;9) функция f(x) убывает.

Так как функция определена и непрерывна на отрезке [-1;9], то точки -1, 3, 8 и 9 можно включать в промежутки монотонности.

Следовательно, на отрезках [-1;3] и [8;9] функция f(x) возрастает, на отрезке [3;8] — убывает.

На промежутках возрастания наибольшее значение функция принимает на правом конце отрезка. На [-1;3] наибольшее значение f(x) принимает в точке x=3 (точке максимума), на [8;9] — в точке x=9.

Так как на [-1;3] f(x) возрастает, то f(3)>f(-1). По условию, f(-1)≥f(9), значит f(3)>f(9).

Таким образом, наибольшее значение функции f(x) принимает в точке x=3.

Ответ: 3.

Источник

Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).

Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.

Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.

Ответ: (11.)

Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.

Источник

Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.

Как найти наибольшее и наименьшее значения функции на отрезке?

Для этого мы следуем известному алгоритму:

1. Находим ОДЗ функции.

2. Находим производную функции

3. Приравниваем производную к нулю

4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:

Если на промежутке I производная функции $f^{prime}(x)>0$ , то функция y=f(x) возрастает на этом промежутке.

Если на промежутке I производная функции $f^{prime}(x)<0$ , то функция y=f(x) убывает на этом промежутке.

5. Находим точки максимума и минимума функции.

В точке максимума функции производная меняет знак с «+» на «-«.

В точке минимума функции производная меняет знак с «-» на «+».

6. Находим значение функции в концах отрезка,

затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции

Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.

Рассмотрим функцию . График этой функции выглядит так:

В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.

1. Рассмотрим функцию на отрезке

Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: f(0) , а наименьшее — в левом: f(-1) .

2. Рассмотрим функцию на отрезке

Очевидно, что наибольшее значение функция принимает в точке максимума f(0) , а наименьшее — в одном из концов отрезка, то есть надо найти значения f(-1) и f(1) и выбрать из них наименьшее.

3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть f(0) и f(2) .

Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть f(4/3) и f(-1) .

Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:

1. ОДЗ функции — множество действительных чисел.

2. $f^{prime}(x)=3x^2-4x$

3. , если x_1=0 или x_2=4/3

Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:

Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике

1. Задание B15 (№ 26695)

Найдите наибольшее значение функции на отрезке .

1. Функция определена при всех действительных значениях х

2. $y^{prime}= 15-3cosx$

cosx=5 Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.

y(0)=5

Ответ: 5.

2. Задание B15 (№ 26702)

Найдите наибольшее значение функции на отрезке [].

1. ОДЗ функции

2. $y^{prime}=3/{cos^2{x}}-3$

Производная равна нулю при , однако, в этих точках она не меняет знак:

$0<cos^2{x}<=1$ , следовательно, $3/{cos^2{x}}>=3$ , значит, $3/{cos^2{x}}-3>=0$ , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, при x=0 .

Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:

$y^{prime}=3/{cos^2{x}}-3={3-3cos^2{x}}/{cos^2{x}}={3sin^2{x}}/{cos^2{x}}=3tg^2{x}>=0$

у(0)=5

Ответ: 5.

3. Задание B15 (№ 26708)

Найдите наименьшее значение функции на отрезке [].

1. ОДЗ функции :

2. $y^{prime}=2/{cos^2{x}}-4$

3. $2/{cos^2{x}}-4=0$

$cos^2{x}=1/2$ ,

Расположим корни этого уравнения на тригонометрической окружности.

Промежутку принадлежат два числа: -{pi}/4 и {pi}/4

Расставим знаки. Для этого определим знак производной в точке х=0: $y^{prime}(0)=2/{cos^2(0)}-4=-2<0$ . При переходе через точки -{pi}/4 и {pi}/4 производная меняет знак.

Изобразим смену знаков производной функции на координатной прямой:

Очевидно, что точка является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции на отрезке , нужно сравнить значения функции в точке минимума и в левом конце отрезка, .

Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а таковым на является, следовательно подставим в уравнение функции

Ответ: -1

Вероятно, Ваш браузер не поддерживается. Попробуйте скачать

Firefox

И.В. Фельдман, репетитор по математике.

Источник

Определение

Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.

Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.

Пример 1

Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].

Решение

Сначала вычисляем производную исходной функции:

y′=3×2−12xy’=3x^2-12x

Затем приравниваем ее к нулевому значению и решаем уравнение:

3×2−12x=03x^2-12x=0

x(3x−12)=0x(3x-12)=0

x1=0x_1=0

x2=4x_2=4

Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.

Находим значение функции в точке x1x_1:

f(0)=9f(0)=9

Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:

f(−1)=−1−6+9=2f(-1)=-1-6+9=2

f(2)=8−24+9=−7f(2)=8-24+9=-7

Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.

Пример 2

Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.

Решение

Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:

y′=6xy’=6x

Приравниваем производную к нулю:

6x=06x=0

x=0x=0

Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.

Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.

Тест по теме “Наибольшие и наименьшие значения функции”

Не можешь разобраться в этой теме?

Обратись за помощью к экспертам

Гарантированные бесплатные доработки

Быстрое выполнение от 2 часов

Проверка работы на плагиат

Источник

Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.

Чтобы найти наибольшее или наименьшее значение функции необходимо:

Найти производную функции $f'(х)$
Найти стационарные точки, решив уравнение $f'(х)=0$
Проверить, какие стационарные точки входят в заданный отрезок.
Вычислить значение функции на концах отрезка и в стационарных точках из п.3
Выбрать из полученных результатов наибольшее или наименьшее значение.

Чтобы найти точки максимума или минимума необходимо:

Найти производную функции $f'(х)$
Найти стационарные точки, решив уравнение $f'(х)=0$
Разложить производную функции на множители.
Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.

Таблица производных некоторых элементарных функций:

Функция	Производная
$c$	$0$
$x$	$1$
$x^n, n∈N$	$nx^{n-1}, n∈N$
${1}/{x}$	$-{1}/{x^2}$
${1}/x{^n}, n∈N$	$-{n}/{x^{n+1}}, n∈N$
$√^n{x}, n∈N$	${1}/{n√^n{x^{n-1}}, n∈N$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	${1}/{cos^2x}$
$ctgx$	$-{1}/{sin^2x}$
$cos^2x$	$-sin2x$
$sin^2x$	$sin2x$
$e^x$	$e^x$
$a^x$	$a^xlna$
$lnx$	${1}/{x}$
$log_{a}x$	${1}/{xlna}$

Основные правила дифференцирования

1. Производная суммы и разности равна производной каждого слагаемого

$(f(x) ± g(x))′= f′(x)± g′(x)$

Пример:

Найти производную функции $f(x) = 3x^5 – cosx + {1}/{x}$

Производная суммы и разности равна производной каждого слагаемого

$f′(x)=(3x^5)′–(cosx)′+({1}/{x})’=15x^4+sinx-{1}/{x^2}$

2. Производная произведения.

$(f(x)∙g(x))′=f′(x)∙g(x)+f(x)∙g(x)′$

Пример:

Найти производную $f(x)=4x∙cosx$

$f′(x)=(4x)′∙cosx+4x∙(cosx)′=4∙cosx-4x∙sinx$

3. Производная частного

$({f(x)}/{g(x)})’={f^'(x)∙g(x)-f(x)∙g(x)’}/{g^2(x)}$

Пример:

Найти производную $f(x)={5x^5}/{e^x}$

$f'(x)={(5x^5)’∙e^x-5x^5∙(e^x)’}/{(e^x)^2}={25x^4∙e^x-5x^5∙e^x}/{(e^x)^2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))′=f′(g(x))∙g′(x)$

Пример:

$f(x)= cos(5x)$

$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$

Пример:

Найдите точку минимума функции $y=2x-ln⁡(x+11)+4$

Решение:

1. Найдем ОДЗ функции: $х+11>0; х>-11$

2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$

3. Найдем стационарные точки, приравняв производную к нулю

${2x+21}/{x+11}=0$

Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю

$2x+21=0; x≠-11$

$2х=-21$

$х=-10,5$

4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.

$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$

5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума.

Ответ: $-10,5$

Пример:

Найдите наибольшее значение функции $y=6x^5-90x^3-5$ на отрезке $[-5;1]$

Решение:

1. Найдем производную функции $y′=30x^4-270x^2$

2. Приравняем производную к нулю и найдем стационарные точки

$30x^4-270x^2=0$

Вынесем общий множитель $30x^2$ за скобки

$30x^2(x^2-9)=0$

$30x^2(х-3)(х+3)=0$

Приравняем каждый множитель к нулю

$x^2=0 ; х-3=0; х+3=0$

$х=0;х=3;х=-3$

3. Выберем стационарные точки, которые принадлежат заданному отрезку $[-5;1]$

Нам подходят стационарные точки $х=0$ и $х=-3$

4. Вычислим значение функции на концах отрезка и в стационарных точках из п.3

$y(-5)= 6∙(-5)^5-90∙(-5)^3-5=6∙(-3125)+90∙125-5= -18750+11250-5=-7505$

$y(-3)= 6∙(-3)^5-90∙(-3)^3-5=-1458+2430-5=967$

$y(0)= -5$

$y(1)= 6∙1^5-90∙1^3-5=6-90-5= -89$

Наибольшее значение равно $967$

Ответ: $967$

Источник

Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.

Тест по теме “Наибольшие и наименьшие значения функции”

Таблица производных некоторых элементарных функций:

Основные правила дифференцирования

Не пропустите также: