Работа с теодолитом – тема настоящей инструкции. Ниже поэтапно приведена методика измерения теодолитом, аккуратное выполнение пунктов которой обеспечит получение точных результатов. Настоящая инструкция предполагает, что пользователь обладает начальными знаниями о том, как работать с теодолитом, знаком с основными узлами и принципом работы прибора.
Установка теодолита в рабочее положение
Измерение горизонтальных углов теодолитом предполагает установку прибора в вершине определяемого угла. Для этого сначала ставят штатив так, чтобы центр площадки для установки штатива был примерно над точкой, а плоскость площадки – горизонтальна. Только после этого теодолит закрепляют на штативе, центрируют и горизонтируют прибор.
Центрирование теодолита — это проецирование оси вращения алидады и лимба по отвесной линии на вершину определяемого угла с точностью для механического отвеса ± 5 мм, ± 1-2 мм для оптического отвеса. Сначала проводится центрирование штатива с помощью механического отвеса с точностью 10-15 мм. При этом необходимо установить штатив горизонтально, чтобы регулировка подъемных винтов позволила произвести горизонтирование прибора. При установке прибора на штатив, производим окончательное центрирование теодолита, передвигаем оптический теодолит, ослабив становой винт.
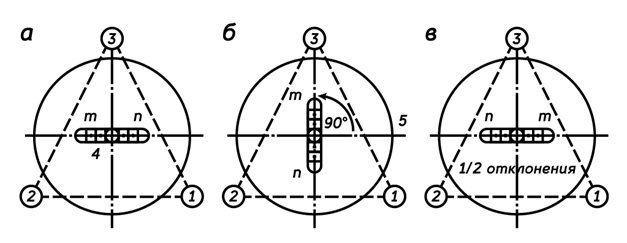
Горизонтирование теодолита – это последовательное горизонтирование плоскости лимба горизонтального угломерного круга (ГУК) и приведение вертикальной оси вращения в отвесное положение. Процесс горизонтирования контролируется по цилиндрическому уровню алидады ГУК и производится посредством подъёмных винтов теодолита. Поворачивая алидаду, направляют ось уровня по двум подъёмным винтам и перемещают пузырёк уровня в центр. Затем следует повернуть алидаду на 90° и, используя третий подъёмный винт, вновь перевести пузырёк в центр. Действия необходимо повторять до тех пор, пока пузырек не станет сходить с середины при всех позициях алидады горизонтального круга. Допустимое его отклонение не больше двух делений шкалы цилиндрического уровня.
Горизонтирование теодолита
Для получения достоверного результата работа с теодолитом требует соблюдения двух геометрических условий:
- ось вращения прибора находится в вертикальном положении;
- ось цилиндрического уровня — в горизонтальном положении.
Измерение горизонтального угла теодолитом
Визирование
Визирование – совмещение центра сетки нитей с точкой.
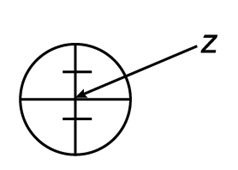
Сетка нитей – это стеклянная пластина с нанесёнными на нём линиями (характер их нанесения может быть разным). Пересечение средних линий называют центром сетки нитей Z.
Наведение центра нитей на точку
Для визирования теодолита на точку необходимо:
- Закрепить лимб.
- Открепить алидаду для того, чтобы по грубому визиру, расположенному наверху зрительной трубы, установить прибор примерно на искомую точку.
- Закрепить алидаду.
- Для наблюдения установить зрительную трубу так, чтобы сетка нитей имела резкое изображение. Эта операция называется установкой по глазу и производится вращением окулярного колена.
- Установить зрительную трубу так, чтобы точка визирования была видна наилучшим образом. Эта операция называется установкой по предмету и производится вращением кремальеры.
- Навести центр сетки нитей точно на точку визирования посредством наводящих винтов алидады и зрительной трубы. Если вертикальный круг оказывается с правой стороны от трубы, если смотреть со стороны окуляра, говорят «круг право» (КП). Если вертикальный круг оказался слева – «круг лево» (КЛ).
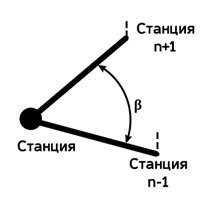
Измерение горизонтального угла β
Измерение горизонтального угла теодолитом предполагает установку прибора в вершине измеряемого горизонтального угла (т.н. станция), а рейки на станциях n+1 и n–1.
Перекрестие сетки нитей совмещают с самой нижней видимой точкой рейки так, чтобы вертикальная нить совпадала с осью рейки.
Затем выполняют следующую последовательность действий (первый полуприём):
- наводят центр сетки нитей на вершину заднего (правого) угла (n – 1) и снимают отсчёт по лимбу горизонтального круга — отсчёт а1;
- наводят на вершину переднего (левого) угла (n + 1) снимают отсчет а2;
- определяют значение угла при круге лево βкл=а1-а2.
Измерение горизонтального угла на станции n:
β – горизонтальный угол
До начала второго полуприёма (КП) разблокируют зрительную трубу и переводят через положение зенита. Затем разблокируют алидаду и поворачивают прибор на 180° , проводят измерения при КП. При втором полуприёме (КП) визирование и измерения производят аналогично, различия в значениях угла в двух полуприёмах (С) не должно превышать двойной точности прибора (t): С < 2t.
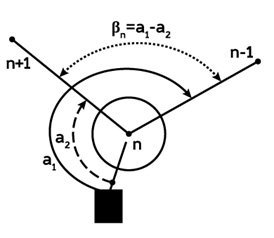
Измерение горизонтального угла β на станции n (КЛ):
n – станция
n–1 –- вершина заднего угла
n+1 – вершина переднего угла
а1 – отсчёт на вершину заднего угла
а2 – отсчёт на вершину переднего угла
Вычисление горизонтальных углов
При выполнении условия расхождения в значениях угла, полученных за два полуприёма, средний горизонтальный угол рассчитывают по формуле: βср = (βКЛ + βКП) /2.
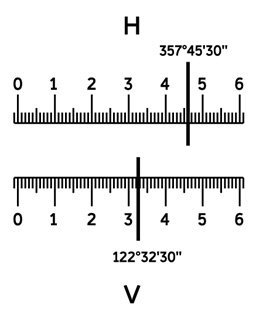
Лимб горизонтального угломерного круга оцифрован всегда от нуля до 360? через 1?, слева направо.
Отсчёт по горизонтальному кругу берут следующим образом:
- считывают по шкале алидады количество градусов отсчётного штриха (по рисунку – 125°);
- считывают минуты слева направо от нуля, учитывая, что цена деления на шкале ГУ – 5´ (по рисунку – 07´).
Отсчётный микроскоп теодолита RGK TO-15:
отсчёт по ГУК – «125°07´»
отсчёт по ВУК – «-0°35´»
Измерение вертикального угла теодолитом
Измеренный угол наклона может иметь как положительное, так и отрицательное значение, изменяясь от -90° до 90°.
Работа с теодолитом требует проводить горизонтирование алидады каждый раз при отсчёте. Горизонтальным считается положение, когда пузырёк цилиндрического уровня алидады или трубы расположен посередине ампулы. Однако, даже при нахождении пузырька в центре ампулы линия нулей отсчётного устройства может находиться под небольшим углом по отношению к линии горизонта, который называется место нуля вертикального круга (М0). Важной чертой измерения вертикальных углов является необходимость учёта места нуля вертикального круга. Для этого при создании съёмочного обоснования снимают отсчёты по вертикальному угломерному кругу (ВУК) при КЛ и КП, а при тахеометрической съёмке — на каждой станции перед началом работы определяют место нуля.
При измерении вертикальных углов теодолитом центр сетки нитей переводят на высоту инструмента, ранее отмеченную на рейке. Высоту инструмента определяют с помощью листа белой бумаги и рейки, приставляя её почти вплотную к окуляру. Пользователь при этом должен вести наблюдение в объектив. Лист передвигают по рейке, пока он не закроет ровно ½ поля зрения. Высоту инструмента на рейке удобно отмечать тонкой круглой резинкой.
Сначала снимают отсчёт, визируя при круге лево. Затем, переведя трубу через зенит, визируют и снимают отсчёт при круге права.
Существует несколько способов оцифровки лимба вертикального угломерного круга (ВУК). У теодолита RGK TO-15 (TO-05) оцифровка секторная, при которой ВУК разбит на 4 сектора по 90°, из которых два сектора имеют положительную оцифровку, а два других – отрицательную. Для взятия отсчёта:
- считывают количество градусов отсчётного штриха (по рисунку – «-0°»);
- считывают минуты – если вверху стоит «-0» – по отрицательной шкале от нуля до отсчётного штриха, если вверху стоит «+0» – по положительной шкале от нуля до отсчётного штриха (по рисунку – «-35?»).
Далее проводят вычисление вертикального угла. При этом отсчёты от 0° до 90° соответствуют измеряемому положительному вертикальному углу.
Вычисление вертикальных углов
После снятия отсчётов рассчитывают вертикальный угол через М0, либо по результатам двух отсчётов, полученных при визировании на цель в двух положениях зрительной трубы (КЛ и КП).
Расчётные формулы для секторной оцифровке лимба вертикального круга от нуля в обе стороны – по ходу и против хода часовой стрелки (RGK TO-05 и TO-15):
М0 = (КП + КЛ)/2; v = МО-КП; ν=КЛ−М0
При расчёте по этим формулам не обязательно добавлять 360°.
Измерение расстояний теодолитом
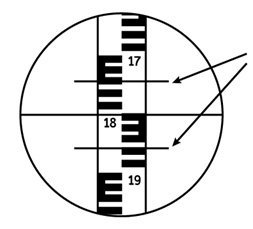
В этом разделе рассмотрим, как работать с теодолитом для измерения расстояний. В сетке нитей зрительной трубы теодолита имеются два дополнительных горизонтальных дальномерных штриха, расположенных по обе стороны от центра сетки нитей на равных расстояниях. Наличие этих штрихов позволяет производить измерение теодолитом расстояния D от прибора до рейки.
Для этого по рейке определяют величину дальномерного интервала n в сантиметрах, умножая полученное число на 100, затем полученное значение из сантиметров переводят в метры (дальномерный коэффициент зрительной трубы, как правило, равен 100) , т. е.
D = K*n =100*n
В случае, приведенном на рисунке:
- отчет по верхнему дальномерному штриху – 1747 мм;
- отчет по нижнему дальномерному штриху – 1856 мм.
Дальномерный интервал n равен разности отчетов по нижнему и верхнему дальномерным штрихам.
n = 1856-1747=109 мм = 10,9 см.
По формуле вычисляем расстояние: D = 100*10,9 см=1090 см = 10,9 м
Для измерения теодолитом расстояний при помощи нитяного дальномера относительная ошибка обычно составляет от 1/100 до 1/300.
Измерение теодолитом расстояния по дальномерным штрихам
Единицы мер в топографии и геодезии
Единицы мер в топографии и геодезии
Совокупность единиц физических величин, принятых в государстве для измерений называется системой мер.
При производстве геодезических измерений единицей угла служит градус, равный 1/360 части окружности или 1/90 части прямого угла (1º = 60΄, 1΄= 60΄΄). Пример: 11º 07´ 56´´.
Наряду с градусной системой мер в некоторых странах употребляется десятичная или децимальная система, в которой прямой угол делят на 100 частей, называемых градами. Град делится на 100 минут или сантиград, а минута – на 100 секунд. Пример: 46g 68s 98ss или 46,6898 g.
Значение угла может быть выражено в радианной мере. Радиан ρ – центральный угол, соответствующий длине дуге окружности, равной ее радиусу. Величина радиана – ρ = 57º 17΄ 44,8΄΄ или ρ° ≈ 57,3; ρ΄ ≈ 3438; ρ΄΄ ≈ 206 265, где ρ°, ρ΄, ρ΄΄ – число градусов, минут, секунд в радиане.
Единица длины – метр (м). За метр принята длина “архивного метра” платинового жезла, хранящегося в международном бюро мер и весов во Франции. Длина жезла была принята равной одной десятимиллионной части четверти Парижского меридиана. В 1889 г. была изготовлена 31 копия «архивного метра», две из которых были переданы в Россию. Для создания надежно воспроизводимого эталона метра в 1960 г. было решено выражать его через длину световых волн. В 1983 г. принято новое определение метра, согласно которому метр равен расстоянию, проходящему в вакууме плоской электромагнитной волной за 1/299 792 458 доли секунды. Кратные единицы метра –1 км = 1000 м; 1 дм = 0,1 м; 1 см = 0,01 м и 1мм = 0,001 м.
Единица площади – квадратный метр (м2). Кратные единицы – 1км2 = 1 000 000 м2 ; 1 см2 = 0,0001 м2 ; 10 000 м2 = 1 га; 1 км2 = 100 га.
Единица времени – секунда (s). Секунда равна 9 192 631 770 периодам излучения, соответствующего перехода между двумя сверхтонкими уровнями основного состояния атома Цезия-133. 1m(мин) = 60s; 1h (час) = 3600 s.
Единица температуры – градус по шкале Цельсия (°С).
Единицей массы служит килограмм (кг). Копия представляет платиново-иридиевую гирю – цилиндр диаметром и высотой 39 мм.
Единица силы – ньютон (Н). 1Н равен силе, сообщающей телу массой 1кг ускорение 1 м/сек2 в направлении действия силы.
Единицей измерения давления служит паскаль (Па). Паскаль равен давлению, вызываемому силой 1Н равномерно распределенной по нормальной к ней поверхности площадью 1м2. 1 Па = 9,87 × 10 –6 атм. или 7,60 × 10–3мм.рт.ст. Давление, равное 1013 г Па на уровне моря на широте 45° принято считать нормальным.
Вот еще по теме:
Топография
Предмет и задачи топографии и геодезии
Форма и размеры Земли
Методы проецирования земной поверхности
Cистемы координат, применяемые в топографии и геодезии
Понятие о плане и карте. Основные свойства и элементы топографических карт
Анализ топографических карт.Географическое описание местности
Геодезические опорные сети
Ориентирование направлений в топографии и геодезии
Понятие об электромагнитных измерениях расстояний
Определение сторон горизонта по небесным светилам и местным предметам
Понятие о спутниковых системах позиционирования
Плановая съемочная геодезическая сеть
Сколько 1 румб?
Румб обозначает также угол между двумя ближайшими целыми румбами. В этом смысле 8 румбов равны 90 градусов, а 1 румб равен 11 градусов.
Какие румбы бывают?
Четыре основных румба:
- North — Север
- East — Восток
- South — Юг
- West — Запад
Как определить румб на карте?
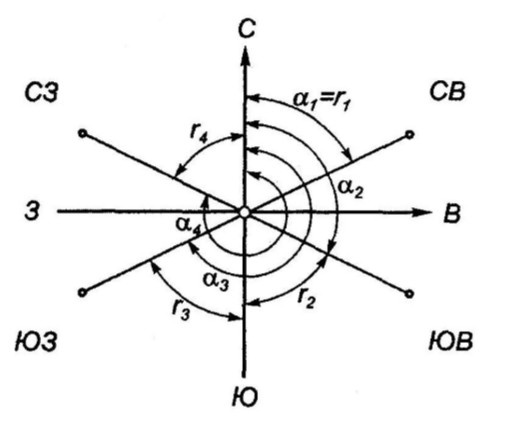
Румб отсчитывается от ближайшего конца меридиана – северного или южного, до заданной линии. Румбы принимают значения от 0° до 90° и обозначаются буквой r.
Что такое обратный румб?
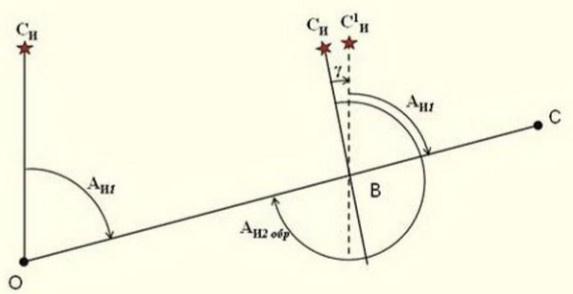
Дирекционный угол заданного направления α пр называется прямым, а противоположного – обратным α обр (рис. 6). Румб заданного направления r пр. называется прямым, а противоположного – обратным r обр. Прямой и обратный румбы равны по величине и отличаются только наименованием (рис.
Как перевести значение румба в градусы?
1 румб = 11.25 градуса; 1 градус = 0.08889 румба.
Как определить значение румба?
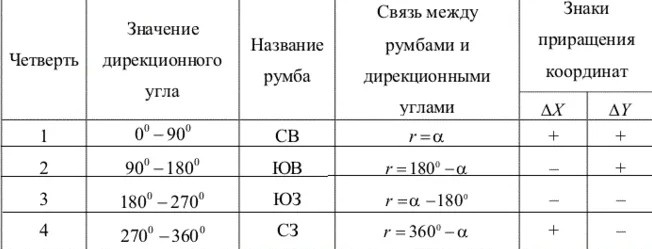
Направление (линия) может находиться в одной из четырех четвертей, и для однозначного её определения к градусной величине румба добавляется название четверти: СВ (северо-восток), ЮВ (юго-восток), ЮЗ (юго-запад) или СЗ (северо-запад). Румбы имеют значения от 0° до 90° и обозначаются буквой r.
Что такое 16 румбов?
В метеорологии принято разделять окружность горизонта на 16 румбов, т. е. через 22,5°. Главными называют направления на север (С, N), юг (Ю, S), восток (В, Е), запад (3, W).
Как определить направление румба?
Направление (линия) может находиться в одной из четырех четвертей, и для однозначного её определения к градусной величине румба добавляется название четверти: СВ (северо-восток), ЮВ (юго-восток), ЮЗ (юго-запад) или СЗ (северо-запад). Румбы имеют значения от 0° до 90° и обозначаются буквой r.
Как решить обратную геодезическую задачу?
Решение обратной геодезической задачи выполняется в следующем порядке:
- вычисляют приращения координат:
- из решения прямоугольного треугольника определяют румб линии: …
- по знакам приращений координат и по известному румбу линии определяют дирекционный угол линии …
- определяют горизонтальное проложение (длину линии)
В чем суть прямой и обратной геодезических задач?
Прямая геодезическая задача (прямая линейно-угловая засечка) заключается в том, что по известным координатам одной точки, вычисляют координаты другой точки, для чего необходимо знать горизонтальное проложение (длину) линии между этими точками и ориентирный (дирекционный) угол этой линии.
Как определить четверть в геодезии?
Направление (линия) может находиться в одной из четырех четвертей, и для однозначного её определения к градусной величине румба добавляется название четверти: СВ (северо-восток), ЮВ (юго-восток), ЮЗ (юго-запад) или СЗ (северо-запад). Румбы имеют значения от 0° до 90° и обозначаются буквой r.
Как найти румбы формула?
если дирекционный угол α равен 100°45′11″ тогда согласно таблицы румб вычисляется по формуле r=180°-α=180°-100°45′11″=79°14′49″, а название румба будет ЮВ; 3. если дирекционный угол α равен 210°17′42″ тогда согласно таблицы румб вычисляется по формуле r=α-180°=210°17′42″-180°=30°17′42″, а название румба будет ЮЗ; 4.
Что такое румбы горизонта?
РУМБ — (англ. rhumb) направление к точкам видимого горизонта относительно стран света или угол между двумя такими направлениями. В геодезии угол между меридианом и данным направлением, отсчитываемый от меридиана в обе стороны от 0 до 90 . ; в морской… … Большой Энциклопедический словарь
Как определить склонение магнитной стрелки?
Угол между истинным и магнитным меридианами данной точки называется склонением магнитной стрелки (δ). Если магнитный меридиан отклоняется от истинного к восток, то склонение δ называют восточным (со знаком плюс), а если к западу — западным (со знаком минус). Таким образом, имеем: Аи = Ам + (± δ).
Как обозначается румб?
r
Румбы имеют значения от 0° до 90° и обозначаются буквой r.
Как определить в какой четверти находится румб?
Направление (линия) может находиться в одной из четырех четвертей, и для однозначного её определения к градусной величине румба добавляется название четверти: СВ (северо-восток), ЮВ (юго-восток), ЮЗ (юго-запад) или СЗ (северо-запад). Румбы имеют значения от 0° до 90° и обозначаются буквой r.
Какие задачи ставятся перед Геодезией?
Геодезия решает научные и практические задачи.
- Научные задачи:
- — Определение формы и размеров Земли;
- — Изучение движений земной коры;
- — Определение внешнего гравитационного поля Земли;
- — Изучение внутреннего строения Земли;
- — Геодезическое изучение и картографирование небесных тел.
Исходными данными для выполнения работы являются :
измеренные, правые по ходу, горизонтальные углы (графа 2.табл. № 1,приложение 2);
горизонтальные проложения сторон (графа 2.табл. № 1, приложение 2) – эти данные для всех вариантов одинаковы.
Значения координат «х» и «у» первой вершины и дирекционного угла стороны 1-2 индивидуальны и, в зависимости от варианта, берутся по таблице № 1 приложения 1; заносятся в табл. № 1 в графы : 4, 12, 13, в строчки, отмеченные звездочками.
1.2 Вычисление координат вершин замкнутого теодолитного хода
Уравнивание измеренных углов
Измерения горизонтальных углов сопровождаются неизбежными ошибками (невязками).
Угловая невязка вычисляется по формуле:
|
fβ = Σ βизм – Σ β теор |
(1), |
Σ β изм = β1 + β 2+ … + βn — сумма измеренных горизонтальных углов,
Σ β теор — теоретическая сумма внутренних углов замкнутого
|
теодолитного хода, определяется по формуле: |
|
|
Σ β теор = 180˚ (n – 2) |
(2) |
|
n – количество измеренных углов. |
|
|
Полученную невязку сравнивают с допустимой : |
|
|
f β доп = ± 1,5´ √ n. |
(3) |
Если полученная невязка не превышает допустимую, то ее разбрасывают с обратным знаком на все измеренные углы, не дробя при этом менее чем на 0,1‘.
Вписывают полученные поправки (δ β ) над значениями углов (графа 2 таблицы 2). С учетом поправок и их знака вычисляют исправленные углы:
|
βиспр= βизм + δβ. |
( 4) |
||
|
Контролем правильного |
уравнивания |
измеренных |
|
|
горизонтальных |
углов служит равенство суммы исправленных |
||
|
горизонтальных |
углов теоретической сумме. |
5
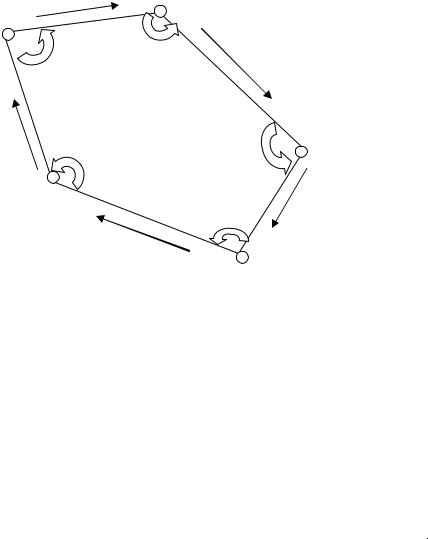
Пример: для построения плана был проложен замкнутый теодолитный ход в виде пятиугольника (рис. 1), в котором были измерены правые по ходу горизонтальные углы. Результаты измерений приведены в табл. 1.
Б
А
В
Д
Г
Рис. 1. Замкнутый теодолитный ход Точки А, Б, В, Г, Д – станции замкнутого теодолитного хода и
вершины горизонтальных правых по ходу углов. Стрелками показано направление хода.
Таблица 1. Результаты измерения и исправления горизонтальных углов
|
Номер вершины |
Горизонтальные углы, |
|
|
теодолитного хода |
измеренные |
исправленные |
|
А |
+ 0,3′ |
|
|
76° 11,3′ |
76° 11,6′ |
|
|
Б |
+ 0,4′ |
|
|
113° 49,1′ |
113° 49,5′ |
|
|
В |
+ 0,3′ |
|
|
101° 05,2′ |
101° 05,5′ |
|
|
Г |
+ 0,3′ |
|
|
98° 17,4′ |
98° 17,7′ |
|
|
Д |
+ 0,4′ |
|
|
150° 35,3′ |
150° 35,7′ |
|
|
Сумма углов |
539° 58.3′ |
540° |
Теоретическую сумму внутренних углов пятиугольника (которым является наш замкнутый теодолитный ход) вычисляем согласно формулы 2: 180°(5 – 2) = 540°.
Определяем угловую невязку: 539° 58.3′ — 540° = — 1,7′.
6
Вычисляем допустимую невязку: ± 1,5′ 5 = ± 3,35′
Т. к. полученная невязка меньше допустимой по абсолютной величине, распределяем ее на все измеренные углы с обратным знаком, т. е. с плюсом; причем к большим углам прибавим большие поправки.
Проверяем сумму исправленных углов, она равна 540°.
Вычисление дирекционных углов сторон теодолитного хода
Дирекционный угол (α ) – это угол, отсчитываемый от северного направления осевого меридиана до рассматриваемой стороны по ходу часовой стрелки. Он изменяется от 0˚ до 360˚.
Вычисление дирекционных углов сторон теодолитного хода выполняют по формуле:
|
αn = α n-1 + 180˚ — β прав.испр. |
(5), |
где α n-1 — дирекционный угол предыдущей стороны, α n— дирекционный угол последующей стороны,
β прав.испр. – правый исправленный угол между рассматриваемыми сторонами.
Вычисление дирекционных углов ведется в столбик, при этом следует помнить, что в одном градусе – 60 минут.
Контролем верного вычисления дирекционных углов служит равенство заданного дирекционного угла и вычисленного начальной стороны теодолитного хода.
Осевые меридианы
В
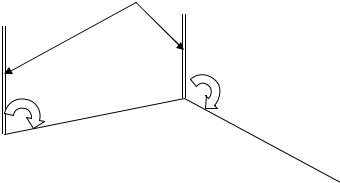
Рис. 2. Схема дирекционных углов сторон АБ и БВ
7
Пример: дирекционный угол стороны А-Б равен : 79° 58′.
Дирекционный угол стороны Б-В : 79° 58′ + 180° — 113° 49,5′ = 146° 08,5′ Дирекционный угол стороны В-Г: 146° 08,5′ + 180° — 101° 05,5′ = 225° 03′ Дирекционный угол стороны Г-Д: 225° 03′ + 180° — 98° 17,7′ = 306° 45,3′ Дирекционный угол стороны Д-А: 306° 45,3′ + 180° — 150° 35,7′ = 336° 9,6′ Дирекционный угол стороны А-Б: 336° 09,6′ + 180° — 76° 11,6′ = 439° 58′.
Если значения вычисленных дирекционных углов больше 360°, перед занесением результатов в таблицу, вычитаем 360°.
Например: дирекционный угол стороны А-Б: 439° 58′ — 360° = 79° 58′.
Определение румбов и знаков приращений координат
Румб – это острый угол, отсчитываемый от ближайшего окончания осевого меридиана до ориентируемой линии.
Вычисление румбов осуществляется в зависимости от того, в какой четверти геодезических прямоугольных координат находится ориентируемая линия.
Таблица 2. Значения румбов
|
Четверть |
Пределы |
Название |
Формула |
Знаки приращений |
|
|
изменения |
румба |
расчета румба |
координат |
||
|
дирекционных |
ΔX |
ΔY |
|||
|
углов |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0° — 90˚ |
С.В. |
r = α |
+ |
+ |
|
11 |
90˚ — 180˚ |
Ю.В. |
r= 180˚ -α |
— |
+ |
|
111 |
180˚ — 270˚ |
Ю.З. |
r= α — 180˚ |
— |
— |
|
1V |
270˚ — 360˚ |
С.З. |
r= 360˚ — α |
+ |
— |
Знаки приращений координат определяются также по положению рассматриваемой стороны, т.е. в зависимости от того, в какой четверти геодезических прямоугольных координат находится конкретная сторона теодолитного хода.
Пользуясь таблицей 2 или рисунком 3, определить значения румбов, их название относительно сторон света, знаки приращений координат; результаты занести в соответствующие графы таблицы 1 Приложения 2.
Например: Дирекционный угол стороны Б-В : 146° 08,5′, следовательно она находится во второй четверти.
|
Название румба |
Ю.В. |
|
|
Значение |
180˚ — 146° 08,5′ = 33° 51,5′. |
|
|
Знаки приращений координат: |
||
|
для |
X «минус» |
|
|
для |
Y «плюс». |
|
|
8 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Азимуты
Это направление, измеряемое в градусах по часовой стрелке от севера на азимутальной окружности. Азимутальный круг состоит из 360 градусов. Девяносто градусов соответствует востоку, 180 градусов — югу, 270 градусов — западу, а 360 градусов и 0 градусов — северу.
Слово «азимут» иногда используется как синоним азимута для обозначения направления (показания в градусах) от одного объекта к другому. Такое использование корректно только в первом (СВ) квадранте между 0° и 90°.
Азимуты также можно считывать с юга. Национальная геодезическая служба Национального управления океанических и атмосферных исследований (NOAA) (бывшая Береговая и геодезическая служба США) всегда использует юг в качестве нулевого направления. В пожарной службе дикой природы азимут всегда считывается с северной точки.
Направление ветра
Азимут часто используется для обозначения направления ветра. Традиционно направление ветра указывается как одна из восьми точек компаса (С, СВ, В, ЮВ, Ю, ЮЗ, З, СЗ). Однако графики направления ветра и скорости часто дают значение азимута, используя 0° и 360° для севера. Ветры называются по направлению, откуда они дуют. Например, западный ветер дует с запада (или 270°), а юго-восточный ветер дует с юго-востока (135°).
Обратный азимут и обратное визирование
Обратный азимут — это проекция азимута от начала координат до противоположной стороны азимутального круга. В азимутальном круге 360 градусов, поэтому противоположное направление будет 180 градусов (половина 360 градусов) от азимута.
Обратный азимут рассчитывается путем прибавления 180° к азимуту, если азимут меньше 180°, или вычитания 180° из азимута, если он больше 180°. Например, если азимут равен 320°, обратный азимут будет 320° — 180° = 140°. Если азимут равен 30°, обратный азимут будет равен 180° + 30° = 210°.
Обратное прицеливание — это метод прицеливания, в котором используется отсчет азимута, снятый в обратном направлении.
Компас – это инструмент, используемый для навигации и ориентации. Азимутальный компас градуирован/отмечен полным кругом в 360 градусов, который называется азимутальным кругом. Компоненты компаса включают магнитную стрелку, которая всегда указывает на магнитный север, градуированную окружность для откладывания углов от истинного севера и линию визирования для продолжения линии визирования при следовании курсу направления.
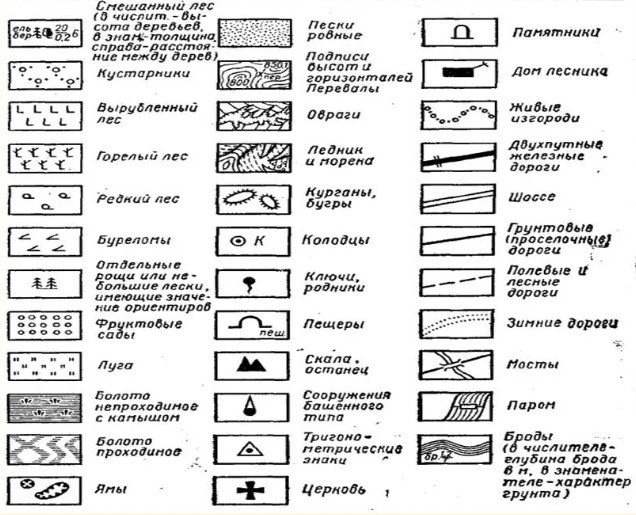
Условные знаки
Дирекционные углы и румбы
Дирекционные углы и румбы используются для ориентирования линий.
Дирекционным углом (α) линии называют угол, отсчитанный по ходу часовой стрелки от северного направления вертикальной линии километровой сетки (осевого меридиана зоны) до направления заданной линии. Пределы изменения дирекционного угла от 0º до 360º.
Это острый угол от ближайшего направления меридиана (северного или южного) до направления ориентирной линии. Пределы изменения румба от 0º до 90º.
Связь между дирекционными углами и румбами зависит от четверти, в которой находится заданное направление. Перевод дирекционных углов в румбы выполняется согласно таблице ниже.
Пример перевода дирекционных углов в румбы
- если дирекционный угол α равен 42°15′55″, тогда согласно таблице румб вычисляется по формуле r=α=42°15′55″, а название румба будет СВ;
- если дирекционный угол α равен 100°45′11″, тогда согласно таблице румб вычисляется по формуле r=180°-α=180°-100°45′11″=79°14′49″, а название румба будет ЮВ;
- если дирекционный угол α равен 210°17′42″, тогда согласно таблице румб вычисляется по формуле r=α-180°=210°17′42″-180°=30°17′42″, а название румба будет ЮЗ;
- если дирекционный угол α равен 335°28′32″, тогда согласно таблице румб вычисляется по формуле r=360°-α=360°-335°28′32″=24°31′28″, а название румба будет СЗ.