В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
- Примеры задач
Формула вычисления объема куба
1. Через длину ребра
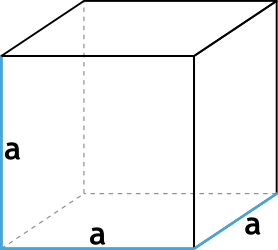
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a3
2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.
Следовательно, вычислить объем куба можно так:
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см3.
Задание 2
Известно, что объем куба равен 512 см3. Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
У куба 12 ребер – отрезков, которые являются сторонами квадратов (граней куба).
Также он имеет 8 вершин и 6 граней.
Онлайн-калькулятор объема куба
Формула объема куба
Для нахождения объема куба нужно перемножить его измерения – длину, ширину и высоту. Исходя из того, что куб состоит из квадратов, все его измерения одинаковы и численно равны длине ребра.
Формула для вычисления объема куба такова:
V=a3V=a^3
где aa — длина ребра куба.
Рассмотрим несколько примеров.
Найти объем куба, если периметр PP его грани aa равен 16 cм.16text{ cм.}
Решение
P=16P=16
Периметр PP грани куба связан с длиной его ребра aa по формуле:
P=a+a+a+a=4⋅aP=a+a+a+a=4cdot a
16=4⋅a16=4cdot a
a=164=4a=frac{16}{4}=4
Найдем объем нашего тела:
V=a3=43=64 см3V=a^3=4^3=64text{ см}^3
Ответ: 64 см3.64text{ см}^3.
Одна четвертая часть диагонали квадрата равна 3 см.3text{ см.} Найти объем куба, образованного данным четырехугольником.
Решение
Пусть dd — диагональ фигуры, тогда по условию:
d4=3frac{d}{4}=3
d=4⋅3=12d=4cdot 3=12
Найдем сторону этого квадрата. Обратимся за помощью к теореме Пифагора:
a2+a2=12a^2+a^2=12,
где aa — сторона квадрата.
2⋅a2=122cdot a^2=12
a=6a=sqrt{6}
Приходим к окончательным расчетам для объема:
V=a3=(6)3=66 см3V=a^3=(sqrt{6})^3=6sqrt{6}text{ см}^3
Ответ: 66 см3.6sqrt{6}text{ см}^3.
Чуть более сложный пример.
В куб вписан шар, площадь SS которого равна 64π64pi. Найти объем куба.
Решение
S=64πS=64pi
Первый шагом является нахождение радиуса RR данного шара. Формула его площади такова:
S=4⋅π⋅R2S=4cdotpicdot R^2
64π=4⋅π⋅R264pi=4cdotpicdot R^2
64=4⋅R264=4cdot R^2
644=R2frac{64}{4}=R^2
16=R216=R^2
R=4R=4
Для куба радиус вписанного шара является половиной его стороны aa:
a=2⋅R=2⋅4=8a=2cdot R=2cdot4=8
Объем вычисляется следующим образом:
V=a3=83=512 см3V=a^3=8^3=512text{ см}^3
Ответ: 512 см3.512text{ см}^3.
На Студворке вы можете оформить заказ контрольных работ для студентов по самым низким ценам!
Тест по теме «Объем куба»
Куб — это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Содержание:
- калькулятор объема куба
- формула объема куба через ребро
- формула объема куба через диагональ грани
- формула объема куба через периметр грани
- формула объема куба через диагональ куба
- формула объема куба через площадь полной поверхности
- примеры задач
Формула объёма куба через ребро
Формула объёма куба через диагональ грани
{V = Big( dfrac{d}{sqrt{2}} Big) ^3}
d — диагональ грани куба
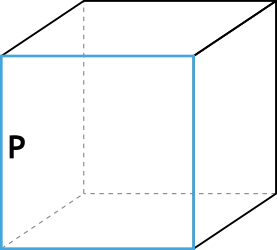
Формула объёма куба через периметр грани
{V= Big( dfrac{P}{4} Big) ^3}
P — периметр грани куба
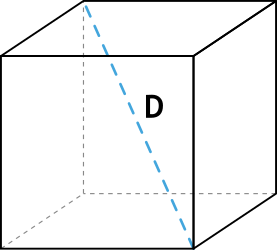
Формула объёма куба через диагональ куба
{V= dfrac{D^3}{3sqrt{3}}}
D — диагональ куба
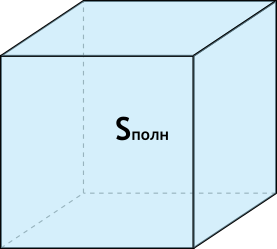
Формула объёма куба через площадь полной поверхности
{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}
Sполн — диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 : см^3
Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3
Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.
Как вычислить объем куба
Формула для вычисления объема куба: V=a^3=a*a*a — то есть сторона куба, возведенная в третью степень.
- Формула для вычисления объема куба: V=a^3=a*a*a.
- Объем куба равен произведению его ширины, длины и высоты. V = 4 * 4 * 4 = 4³ = 64 дм³; Площадь поверхности куба равна сумме площадей его граней.
- Формула для вычисления объема цилиндра: V=πr2h.
- Для вычисления объема куба необходимо найти значение стороны куба по формуле: d = a√3, где d — диагональ куба, а a — сторона куба.
- Для вычисления объема прямоугольного параллелепипеда используется формула: V = a * b * h.
- Объем тела определяется его формой и линейными размерами. Основное свойство объема — аддитивность.
- Формула для вычисления площади поверхности куба: S = 6 * H2. H2 = площадь одной грани куба, а у куба всего 6 граней.
- Используя значение площади основания параллелепипеда (S) и его высоты (h), можно вычислить его объем по формуле: V = a * b * h, где a и b — длина и ширина основания соответственно.
- Как рассчитать объем куба
- Как найти площадь и объем куба
- Какая формула объема
- Как найти объем куба Зная диаметр
- Как вычислить 1 кубический метр
- Чему равен объем
- Какая формула площадь куба
- Как найти объем через площадь
- Как вычислить объем прямоугольника
- Как искать объем
- Как определить объем бруска
- Как найти объем воды
- Как найти объем куба если ребро 4 см
- Как найти массу куба 5 класс
- Как найти объем куба со стороной 2 1 см
- В чем измеряется объем куба
- Чему равен объем куба с ребром 12 см
- Как рассчитать объем в трубе
- Как найти сторону куба из объема
- Как найти площадь куба если известен объем 5 класс
- Как найти площадь и периметр куба
Как рассчитать объем куба
Формула для вычисления объема куба: V=a^3=a*a*a — то есть сторона куба, возведенная в третью степень.
Как найти площадь и объем куба
Объём куба равен произведению его ширины, на длину и на высоту. У куба все ребра равны. V = 4 * 4 * 4 = 4³ = 64 дм³; Площадь поверхности куба равна сумме площадей его граней.
Какая формула объема
Объем рассчитывается по формуле V=πr2h. То есть умножаем число π (3,14159) на радиус в квадрате и на высоту h цилиндра. Пример: есть вертикальный цилиндрический резервуар диаметром 3 метра и высотой 5 метров. Рассчитываем объем: Радиус — 1,5 метра, в квадрате будет 2,25.
Как найти объем куба Зная диаметр
Для того, чтобы найти объём куба нам надо прежде всего найти значение стороны куба. Для этого существует формула: d = a√3, где d — диагональ куба, а a — сторона куба.
Как вычислить 1 кубический метр
При помощи формулы нахождения объема прямоугольного параллелепипеда, мы можем рассчитать ее объем: V = a * b * h, где V — это объем в метрах кубических, a — длина в метрах, b — ширина в метрах, h — высота в метрах.
Чему равен объем
Объём тела определяется его формой и линейными размерами. Основное свойство объёма — аддитивность, то есть объём любого тела равен сумме объёмов его (непересекающихся) частей.
|
Объём |
|
|---|---|
|
Размерность |
L3 |
|
Единицы измерения |
|
|
СИ |
м3 |
|
СГС |
см3 |
Какая формула площадь куба
Площадь поверхности куба можно вычислить через ребро куба по формуле: S = 6 * H2. H2 = площадь одной грани куба, а у куба всего 6 граней.
Как найти объем через площадь
V = a * b * h. В то же время произведение длины и ширины основания параллелепипеда есть не что иное как площадь его основания (S).
Как вычислить объем прямоугольника
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Как искать объем
Объем параллелепипеда равен произведению площади основания на высоту.V = a × b × h.
|
A |
длина параллелепипеда |
|---|---|
|
H |
высота параллелепипеда |
|
P (осн) |
периметр основания |
|
S (осн) |
площадь основания |
|
S (бок) |
площадь боковой поверхности |
Как определить объем бруска
Объем взятого прямоугольного бруска можно вычислить по формуле: V = L * S * h.
Как найти объем воды
V — обьем воды, S — скорость наполнения, t — время:
- Чтобы найти обьем воды V, перемножим скорость наполнения (л/ч) — d на время t. V = d * t.
- Для нахождения времени t, необходимо разделить обьем воды на скорость наполнения p.
- Чтобы вычислить скорость наполнения S, разделим обьем V на скорость наполнения t.
Как найти объем куба если ребро 4 см
У куба они равны также. Объем куба вычисляется как произведение значений всех трех его измерений: 4 * 4 * 4 = 4 ^ 3 = 64 м³. Как добавить хороший ответ?
Как найти массу куба 5 класс
2) Массу куба мы можем вычислить по формуле: m=pV, где p- плотность вещества, из которого состоит куб(p= 7900 кгм^3), а V- объём куба. Отсюда: m=7900*0,064=505,6 кг.
Как найти объем куба со стороной 2 1 см
V = a^3. Вычислим объем заданного куба, если нам известно, что его сторона равна 2,1 см. V = 2,1^3; V = 9,261 см ^3.
В чем измеряется объем куба
Куби́ческий метр (от куб и метр) (кубометр) (м3) — единица объёма, производная в Международной системе единиц (СИ), а также в системах единиц МКГСС и МТС. Одному кубическому метру равен объём куба с длиной ребра 1 метр.
Чему равен объем куба с ребром 12 см
V = a 3 = 12 3 = 12 * 12 * 12 = 144 * 12 = 1728 (см 3). Ответ: таким образом, объем искомого куба составляет 1728 см 3. Как добавить хороший ответ?
Как рассчитать объем в трубе
Объем жидкости в трубопроводе определяется по формуле V= π * d2 * L:4, в которой: π — число Пи; d — это внутренний диаметр трубы; L — суммарная длина трубопровода.
Как найти сторону куба из объема
V куба = а * а * а = а^3, где V куба — объем куба, а — длина ребра куба (все они у куба равны между собой). Исходя из приведенной формулы, чтобы определить ребро куба, необходимо извлечь корень третьей степени из его объема.
Как найти площадь куба если известен объем 5 класс
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть: S = 6a^2. 2) Используем формулу для объема куба: 125 = a^3; a = 5 см. 3) S = 6a^2 = 6 * 5 * 5 = 150 см^2.
Как найти площадь и периметр куба
Для того чтобы найти периметр, площадь и объём куба воспользуемся формулами: Периметр куба = 12 * a; Объем куба = a × a × a = a³; Площадь куба = 6 × a².
Оставить отзыв (1)
- В чем измеряется объем куба
- Как определить объем в м3
- Как посчитать объем куба формула
- Как правильно рассчитать объем
- Как рассчитать объем
- Как рассчитать объем куба
- Как рассчитать объем куба в литры
- По какой формуле найти объем куба
Загрузить PDF
Загрузить PDF
Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте). У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны. Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s3, где s — длина одного (любого) ребра куба.
-
1
Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если вы вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.
- Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.
-
2
Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза. Если s — длина ребра куба, то s * s *s = s3 и, таким образом, вы вычислите объем куба.
- Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть, другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и равна высоте, то этот процесс можно заменить возведением ребра куба в третью степень.
- В нашем примере объем куба равен 5 * 5 *5 = 53 = 125.
-
3
К ответу припишите единицы измерения объема (если вы этого не сделаете, ваша оценка может быть снижена). Так как объем — это количественная характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические единицы (кубические сантиметры, кубические метры и так далее).
- В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах (или в см3). Итак, объем куба равен 125 см3.
- Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих кубических единицах. Например, если ребро куба равно 5 м (а не 5 см), то его объем равен 125 м3.
Реклама
-
1
В некоторых задачах длина ребра куба не дана, но даны другие величины, с помощью которых можно найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем возведите длину ребра куба в третью степень и вычислите объем куба.
- Площадь поверхности куба равна 6s2, где s — длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так как у куба 6 равных граней).
- Рассмотрим пример. Площадь поверхности куба равна 50 см2. Найдите объем куба.
-
2
Разделите площадь поверхности куба на 6 (так как у куба 6 равных граней, вы получите площадь одной грани куба). В свою очередь площадь одной грани куба равна s2, где s — длина ребра куба.
- В нашем примере: 50/6 = 8,33 см2 (не забывайте, что площадь измеряется в квадратных единицах — см2, м2 и так далее).
-
3
Так как площадь одной грани куба равна s2, то извлеките квадратный корень из значения площади одной грани и получите длину ребра куба.
- В нашем примере, √8,33 = 2,89 см.
-
4
Возведите в куб полученное значение, чтобы найти объем куба (как описано в предыдущем разделе).
- В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см3. К ответу не забудьте приписать кубические единицы.
Реклама
-
1
Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом, если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив диагональ на √2.
- Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба равна 7/√2 = 4,96 см. Объем куба равен 4,963 = 122,36 см3.
- Запомните: d2 = 2s2, где d — диагональ грани куба, s — ребро куба. Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае ребер), то есть d2 = s2 + s2 = 2s2.
-
2
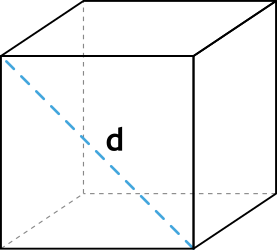
Разделите диагональ куба на √3, чтобы найти длину ребра куба. Таким образом, если в задаче дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3. Диагональ куба — отрезок, соединяющий две вершины, симметричные относительно центра куба, равный D2 = 3s2 (где D — диагональ куба, s — ребро куба).
- Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет — это ребро, а второй катет — это диагональ грани куба, равная 2s2), то есть D2 = s2 + 2s2 = 3s2.
- Рассмотрим пример. Диагональ куба равна 10 м. Найдем объем куба:
- D2 = 3s2
- 102 = 3s2
- 100 = 3s2
- 33,33 = s2
- 5,77 м = s
- Объем куба равен 5,773 = 192,45 м3
Реклама
Об этой статье
Эту страницу просматривали 605 392 раза.