Содержание:
- Определение и формула скорости
- Скорость в разных системах координат
- Частные случаи формул для вычисления скорости
- Единицы измерения скорости
- Примеры решения задач
Определение и формула скорости
Определение
Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора
$bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v.
Это векторная величина. Математически определение вектора мгновенной скорости записывается как:
$$bar{v}=frac{d bar{r}}{d t}=dot{bar{r}}(1)$$
Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения.
Модуль скорости можно определить как первую производную от длины пути (s) по времени:
$$v=frac{d s}{d t}=dot{s}(2)$$
Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.
Скорость в разных системах координат
Проекции скорости на оси декартовой системы координат запишутся как:
$$v_{x}=dot{x} ; v_{y}=dot{y} ; v_{z}=dot{z}(3)$$
Следовательно, вектор скоростив декартовых координатах можно представить:
$$bar{v}=dot{x} bar{i}+dot{y} bar{j}+dot{z} bar{k}(4)$$
где $bar{i}, bar{j}, bar{k}$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:
$$v=sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}}(5)$$
В цилиндрических координатах модуль скорости вычисляют при помощи формулы:
$$v=sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}}(6)$$
в сферической системе координат:
$$v=sqrt{(r)^{2}+(r dot{theta})^{2}+(r dot{varphi} sin theta)^{2}}(7)$$
Частные случаи формул для вычисления скорости
Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const).
При равномерном движении скорость можно вычислить, применяя формулу:
$$v=frac{s}{t}(8)$$
где s– длина пути, t – время, за которое материальная точка преодолела путь s.
При ускоренном движении скорость можно найти как:
$$bar{v}=int_{t_{1}}^{t_{2}} bar{a} d t(9)$$
где $bar{a}$ – ускорение точки,
$t_{1} leq t leq t_{2}$ – отрезок времени, в течение которого рассматривается скорость.
Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:
$$bar{v}=bar{v}_{0}+bar{a} t$$
где $bar{v}_0$ – начальная скорость движения,
$bar{a} = const$ .
Единицы измерения скорости
Основной единицей измерения скорости в системе СИ является: [v]=м/с2
В СГС: [v]=см/с2
Примеры решения задач
Пример
Задание. Движение материальной точки А задано уравнением:
$x=2 t^{2}-4 t^{3}$ . Точка начала свое движение при
t0=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.
Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для
этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:
$$v=frac{d x}{d t}=4 t-12 t^{2}(1.1)$$
Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент
времении сравним результат с нулем:
$$v(t=0,5)=4 cdot 0,5-12(0,5)^{2}=-1 lt 0$$
Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.
Ответ. Против оси X.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Скорость материальной точки является функцией от времени вида:
$$v=10left(1-frac{t}{5}right)$$
где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии
10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.
Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:
$$x=int_{0}^{t} v d t=int_{0}^{t} 10left(1-frac{t}{5}right) d t=10 t-frac{10 t^{2}}{2 cdot 5}=10 t-t^{2}(2.1)$$
Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:
$$x=10 cdot 10-(10)^{2}=0(m)$$
Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат
приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:
$$
begin{array}{c}
10 t-t^{2}=10(2.2) \
t_{1}=5+sqrt{15} approx 8,8(c) ; t_{2}=5-sqrt{15} approx 1,13(c)
end{array}
$$
Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:
$$10 t-t^{2}=-10(2.3)$$
При решении уравнения (2.3) нам подойдет корень равный:
$$t_{3}=5+6=11 (c)$$
Ответ. 1) $x=0 mathrm{~m}$ 2) $t_{1}=8,8 mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$
Читать дальше: Формула средней скорости.
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
- S — расстояние (путь), пройденное материальной точкой или телом (м);
- T — время за которое она преодолела путь (с).
Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
- неравномерную;
- среднюю;
- равномерно-переменную;
- поступательную;
- вращательную;
- ускоренную.
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
- V0 — начальная скорость;
- A — ускорение (имеет постоянное значение);
- t — время движения.
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r-1(t). То есть, с математической точки зрения, это первая производная.
Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t2/2 = (V2 — V20) /2*A.
Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V20 — 2* A * s)½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)½.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: {V} = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость
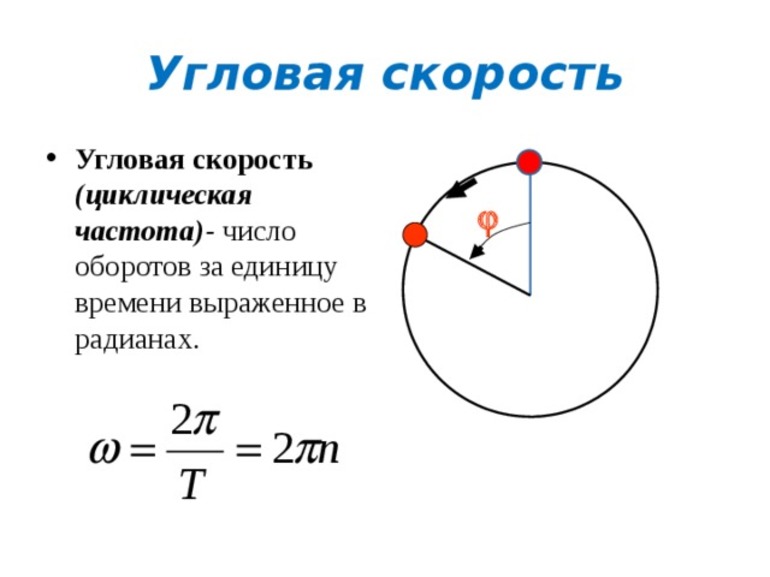
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора
В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
- Справочный портал «Калькулятор».
- Allcalc.
- Fxyz.
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
2.2.1 Как перевести из км/ч в м/с и т. д?
В задачах часто необходимо переводить из одних единиц измерения в другие:
1 км/ч = (1000 м)/(3600 с) = 5/18 м/с,
1 м/с = 18/5 км/ч,
1 км/с = 1000 м/с,
1 см/с = 0,01 м/с,
1 м/мин = 1/60 м/с.
Например, если то для того, чтобы перевести в м/с, нужно умножить на 5/18:
2.2.2 Как найти скорость тела, если известен закон движения?
Закон равномерного движения имеет вид:
Видим, что в этой формуле скорость стоит коэффициентом перед временем. Поэтому, если в условии задачи дан закон движения, необходимо посмотреть на коэффициент перед t — это и есть скорость.
Например, пусть закон движения имеет вид: В данном случае коэффициент перед t равен 5, следовательно,
2.2.3 Как определить скорость по графику координаты от времени?
Закон равномерного движения имеет вид:
Графиком этого закона является прямая линия. Так как — коэффициент перед t, то
является угловым коэффициентом прямой.
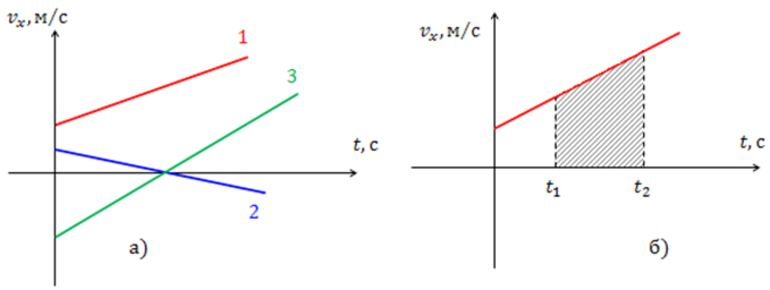
Для графика 1:
То, что график 1 «поднимается вверх», означает — тело едет в положительном направлении оси Ox.
Для графика 2:
То, что график 2 «опускается вниз», означает — тело едет в отрицательном направлении оси Ox.
Для определения и
выбираем такие точки на графике, в которых можно точно определить значения, как правило, это точки, находящиеся в вершинах клеток.
2.2.4 Как найти закон движения, если известны координаты тела в моменты времени и
?
Пусть в момент времени тело находилось в точке с координатой
а в момент времени
тело находилось в точке с координатой
Для времени имеем:
Для времени имеем:
Решая систему уравнений (2.19) и (2.20), получим
2.2.5 Как найти графически момент и координату встречи двух тел?
Пусть даны законы движения двух тел: и
Согласно пункту 2.5 графиками обоих законов являются прямые линии. Необходимо на одном графике построить оба закона.
Графики пересекаются в одной точке. Координаты этой точки и являются временем и местом встречи.
2.2.6 Как аналитически найти координату и время встречи двух тел?
Пусть даны законы движения двух тел: и
В момент встречи тела оказываются в одной координате, то есть
и необходимо решить уравнение:
Решение уравнения имеет вид:
Для нахождения координаты достаточно подставить вместо t найденное значение в любой из законов движения:
или
2.2.7 Как найти среднюю скорость, если тело половину пути проехало со скоростью а вторую половину пути
По определению (2.8):
В нашем случае, так как на каждой половине пути тело едет с постоянной скоростью, то
Получаем
В общем случае, если весь путь разбить на n равных участков, на каждом из которых тело едет с постоянной скоростью, то
Формула справедлива только если весь путь разбит на равные участки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.
2.2.8 Как найти среднюю скорость, если тело половину времени проехало со скоростью а вторую половину времени
По определению (2.8):
В нашем случае, так как каждую половину времени тело едет с постоянной скоростью, то
Получаем
В общем случае, если все время разбито на n равных промежутков, на каждом из которых тело едет с постоянной скоростью, то
Формула справедлива только если все время разбито на равные промежутки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.
2.2.9 Как найти скорость, с которой движется моторная лодка по течению реки?
Согласно формуле скорость тела относительно неподвижной системы отсчета
(в нашем случае земли), равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета
(в нашем случае — собственная скорость лодки).
При движении по течению вектора и
направлены в одну сторону, следовательно, получаем сложение двух векторов, направленных в одну сторону — используем формулу (1.15):
Таким образом, при движении любого тела по течению его скорость определяется формулой
2.2.10 Как найти скорость, с которой движется моторная лодка против течения реки?
Согласно формуле скорость тела относительно неподвижной системы отсчета
(в нашем случае земли) равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета
(в нашем случае — собственная скорость лодки).
Перепишем формулу в виде:
Вектора и
направлены в одну сторону, следовательно, получаем вычитание двух векторов, направленных в одну сторону — используем формулу
:
2.2.11 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена перпендикулярно течению реки?
Согласно формуле скорость тела относительно неподвижной системы отсчета
(в нашем случае земли), равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета
(в нашем случае — собственная скорость лодки).
В данном случае вектора и
направлены перпендикулярно, следовательно, получаем задачу о сложении взаимно перпендикулярных векторов — используем формулу
:
2.2.12 Как найти расстояние, на которое снесет лодку, если ее скорость направлена перпендикулярно скорости реки?
В результате сложения скоростей по формуле скорость тела относительно земли равна
и направлена по прямой OD. В результате, когда тело окажется на противоположном берегу, оно попадет в точке D, и его снесет на длину
Треугольник OAB подобен треугольнику OCD:
2.2.13 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена под углом φ к скорости течения реки?
Согласно формуле скорость тела относительно неподвижной системы отсчета
(в нашем случае земли), равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета
(в нашем случае — собственная скорость лодки).
В результате сложения скоростей по формуле скорость тела относительно земли равна
и направлена по прямой OB. Как видим, получили треугольник, в котором известен один из углов —
Тогда по теореме косинусов:
2.2.14 Как найти расстояние, на которое снесет лодку, если ее скорость направлена под углом к скорости течения реки?
В результате сложения скоростей по формуле скорость тела относительно земли равна
и направлена по прямой OB. В результате, когда тело окажется на противоположном берегу, оно попадет в точке В, и его снесет на длину
В задачах, когда движение происходит в плоскости, то есть и вдоль оси Ox, и вдоль оси Oy, необходимо введение системы координат для того, чтобы упростить рассмотрение задачи.
Проекция
Проекция
Формулы и
не просто результат математической операции нахождения проекции,
и
имеют физический смысл: со скоростью
тело плывет вдоль оси Ox, то есть по течению; со скоростью
тело переплывает реку. Например, время, за которое тело переплывет реку, можно найти просто поделив ширину реки на
Тогда
2.2.15 Под каким углом α нужно направить собственную скорость лодки, чтобы за минимальное время переплыть реку?
Согласно формуле скорость, с которой лодка переплывает реку, равна:
Очевидно, что время будет минимальным, если будет максимальным, то есть
2.2.16 С какой скоростью машина обгоняет вторую машину, если они движутся в одну сторону?
Пусть 1-ая машина движется вправо со скоростью а 2-ая машина также движется вправо со скоростью
Скорость обгона — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой
:
Так как и
направлены в одну сторону, то получили задачу о вычитании векторов, направленных в одну сторону — формула
:
Заметим, что при обгоне, естественно поэтому
2.2.17 За какое время проедут мимо друг друга два поезда, двигающиеся в одном направлении?
Пусть длина 1-го поезда а скорость 2-го поезда
Скорость обгона определяется формулой
Тогда
2.2.18 С какой скоростью машина едет навстречу вторую машину, если они движутся в противоположных направлениях?
Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется влево со скоростью
Скорость движения навстречу — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой
:
Перепишем эту формулу в виде:
Так как и
направлены в одну сторону, то получили задачу о вычитании векторов, направленных в одну сторону — формула
:
2.2.19 За какое время проедут мимо друг друга два поезда, двигающиеся в противоположных направлениях?
Пусть длина 1-го поезда а скорость 2-го поезда
Скорость обгона определяется формулой
Тогда
2.2.20 Как найти относительную скорость, если тела движутся по взаимно перпендикулярным направлениям?
Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется перпендикулярно первой со скоростью
Относительная скорость определяется формулой
:
Так как вектора и
перпендикулярны, то воспользуемся формулой
:
Одинаковое расстояние можно проехать за разное время.
Например, спортивная машина один километр может проехать быстрее, чем тяжело нагруженная грузовая машина. Одна и та же машина может ехать как быстрее, так и медленнее.
Обрати внимание!
Чтобы сравнить различные движения, необходимо знать скорость движения.
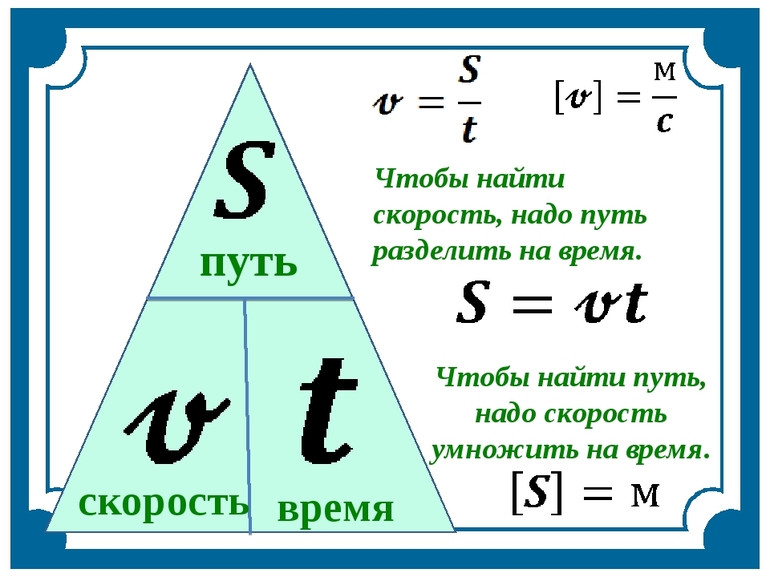
Скоростью движения называется величина, численно равная пути, проходимому телом в единицу времени.
Скорость вычисляется по формуле
v=st
, где
(s) — пройденный путь;
(t) — время.
Чем больше скорость, тем больший путь проходит тело за единицу времени. Если путь измеряется в метрах (м), а время движения в секундах (с), то скорость тела измеряется в (м/с).
Метр в секунду (м/с) — единица скорости в международной системе единиц.
Скорость можно выражать и в других единицах, например в км/с или в км/ч.
Различные примеры скорости:
1. скорость реактивного самолета — 3000 км/ч.
2. Скорость спринтера на дистанции — 37 км/ч.
3. Скорость звука в воздухе — 1224 км/ч.
4. Средняя скорость ходьбы — 6 км/ч.
5. Максимальная скорость гепарда — 114 км/ч.
6. Скорость улитки — 0,02 км/ч.