Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: 

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:
и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.
На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше 


Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.
Решение:
1) Цена деления нижней шкалы:
Цена деления средней шкалы:
Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10° 

- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
Электрическая постоянная (ранее также носила название диэлектрической постоянной) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона, при записи их в рационализованной форме, соответствующей Международной системе единиц (СИ) [1] .
Иногда, используя устаревшую терминологию, называют электрической (или диэлектрической) проницаемостью вакуума [2] . Измеряется в фарадах, делённых на метр.
Содержание
Определение [ править | править код ]
По определению в СИ электрическая постоянная ε 0 <displaystyle varepsilon _<0>> 


ε 0 = 1 μ 0 c 2 . <displaystyle varepsilon _<0>=<frac <1><mu _<0>c^<2>>>.>
Численное значение [ править | править код ]
В Международной системе единиц [ править | править код ]
До изменения СИ 2018—2019 годов [ править | править код ]
Поскольку в СИ для магнитной постоянной было справедливо точное равенство μ 0 = 4 π × 10 − 7 <displaystyle mu _<0>=4pi imes 10^<-7> > 
ε 0 = 1 4 π c 2 ⋅ 10 7 <displaystyle varepsilon _<0>=<frac <1><4pi c^<2>>>cdot 10^<7>> 
также являвшееся точным.
Учитывая, что скорости света в СИ приписано точное значение, по определению равное 299 792 458 м/с , из последнего соотношения следует численное значение ε 0 <displaystyle varepsilon _<0>> 
ε 0 = 1 4 π ⋅ 299792458 2 × 10 − 7 <displaystyle varepsilon _<0>=<frac <1><4pi cdot 299792458^<2> imes 10^<-7>>>> 
Или, выражая то же через основные единицы СИ,
ε ≈ 8,85418781762039 · 10 −12 м −3 ·кг −1 ·с 4 ·А 2 .
После изменений СИ 2018—2019 годов [ править | править код ]
С 2019 года вступили в силу изменения в СИ, включающие, в частности, переопределение ампера на основе фиксации численного значения элементарного заряда. Это привело к тому, что значение электрической постоянной стало экспериментально определяемой величиной, хотя численно её значение осталось прежним с высокой точностью. Значение электрической постоянной, рекомендованное CODATA [4] :
ε = 8,8541878128(13)· 10 −12 м −3 ·кг −1 ·с 4 ·А 2 , или Ф·м −1 .
В системе СГС [ править | править код ]
В системе СГС электрическая постоянная как коэффициент, связывающий напряжённость и индукцию электрического поля в вакууме, также может быть введена. При этом в различных вариантах системы СГС электрическая постоянная имеет разную размерность и значение. Конкретно, Гауссова система единиц и система СГСЭ построены так, что электрическая постоянная безразмерна и равна 1, а в системе СГСМ она равна ε = 1/c 2 ≈ 1,11265005605362 · 10 −21 с 2 ·см −2 .
Некоторые уравнения электродинамики в СИ [ править | править код ]
В материальных уравнениях, в вакууме, через электрическую постоянную связаны вектор электрической индукции D <displaystyle mathbf > 

D = ε 0 E . <displaystyle mathbf =varepsilon _<0> mathbf .>
Она также входит в запись закона Кулона (тоже в вакууме):
F 12 = 1 4 π ε 0 ⋅ q 1 q 2 r 12 2 r 12 r 12 . <displaystyle mathbf _<12>=<frac <1><4pi varepsilon _<0>>>cdot <frac <1>q_<2>><12>^<2>>> <frac <mathbf _<12>><12>>>.>
При использовании СИ произведение электрической постоянной на относительную диэлектрическую проницаемость называют абсолютной диэлектрической проницаемостью.
Комментировать
12 669 просмотров
Adblock
detector
 |
|||
| (Древне)греческий алфавит | |||
|---|---|---|---|
| Αα | Альфа | Νν | Ню |
| Ββ | Бета | Ξξ | Кси |
| Γγ | Гамма | Οο | Омикрон |
| Δδ | Дельта | Ππ | Пи |
| Εε | Эпсилон | Ρρ | Ро |
| Ζζ | Дзета | Σσς | Сигма |
| Ηη | Эта | Ττ | Тау |
| Θθ | Тета | Υυ | Ипсилон |
| Ιι | Йота | Φφ | Фи |
| Κκ | Каппа | Χχ | Хи |
| Λλ | Лямбда | Ψψ | Пси |
| Μμ | Мю | Ωω | Омега |
| История | |||
| Архаические локальные варианты[en] Ϝϝ · Ͷͷ · Ͱͱ · Ϻϻ · Ϙϙ · Ͳͳ |
|||
| Диакритики[en] · Лигатуры (ϛ, ϗ) | |||
| Цифры Ϛϛ (6) · Ϟϟ (90) · Ϡϡ (900) |
|||
| В других языках | |||
|
|||
| Похожие темы | |||
| Научные символы[en] | |||
|
|||
| Современный греческий алфавит |
|
||
| Буквы для других языков |
|
||
| Фонетические буквы | |||
| Буквы для арнаутского диалекта |
|||
| Альтернативные и устаревшие формы |
|||
| Диакритические знаки |
Что такое Wiki.sc Вики является главным информационным ресурсом в интернете. Она открыта для любого пользователя. Вики это библиотека, которая является общественной и многоязычной. Основа этой страницы находится в Википедии. Текст доступен по лицензии CC BY-SA 3.0 Unported License. Эпсилон зависит от вида материала, его значение ищут в таблице. Другие вопросы из категориине более чем на. находящемуся в воздухе заряда 2*10^-7 Кл его потенциал оказался равным 18 Кб. определите радиус шара Читайте такжеЭнергетическая характеристика электрического поля. 4.Чему равна работа сил электрического поля при перемещении заряда перпендикулярно силовым линиям поля? 5. Как связана работа с потенциалами начальной и конечной точек траектории? 6. Как называют поверхности равного потенциала? 7. Как называют разность потенциалов между двумя точками поля? 8. Как направлен вектор напряженности эл.поля относительно эквипотенциальной поверхности? 9. Как связаны напряжение и напряженность электростатического поля? 10. Чему равен потенциал поля точечного заряда (формула)? 3) увеличивается или уменьшается в зависимости от изменения объема 4) не изменяется Каково давление сжатия воздуха массой 12 кгв баллоне объемом 20 лпри 17оС? Каково давление азота плотностью 2,8 кг/м3, если его температура в сосуде равна 400 К? Какова молярная масса газа массой 0,017 г, находящегося в сосуде объемом 10 л под давлением 2.105Па и температурой 400К? Какое количество газа содержится в сосуде объемом 8,31 м3 под давлением 105Па и температуре 100К? Найдите среднюю кинетическую энергию поступательного движения молекул идеального газа при нормальных условиях. Какова среднеквадратичная скорость молекул массой 3.10-26 кг каждая, если они создают давление 105 Па и их концентрация равна 10 25м-3? Чему равна молярная газовая постоянная R, если плотность насыщенного водяного пара при 100оС и нормальном давлении равна 0,59 кг/м3? Какова температура газа по Цельсию, если по Кельвину она равна 273К? 2)Чему равна жесткость пружины, если скрепленное с ней тело массой 30 г совершает за 1 мин 300 колебаний? 2)чему равен импульс во время столкновения с землей 3)с какой высоты упал шар 4) чему равна полная механич энергия 2)Тело массой 6 кг движется со скоростью 2м/с.Чему равна кинетическая энергия тела? “> |
A dielectric medium showing orientation of charged particles creating polarization effects. Such a medium can have a lower ratio of electric flux to charge (more permittivity) than empty space
In electromagnetism, the absolute permittivity, often simply called permittivity and denoted by the Greek letter ε (epsilon), is a measure of the electric polarizability of a dielectric. A material with high permittivity polarizes more in response to an applied electric field than a material with low permittivity, thereby storing more energy in the material. In electrostatics, the permittivity plays an important role in determining the capacitance of a capacitor.
In the simplest case, the electric displacement field D resulting from an applied electric field E is
More generally, the permittivity is a thermodynamic function of state.[1] It can depend on the frequency, magnitude, and direction of the applied field. The SI unit for permittivity is farad per meter (F/m).
The permittivity is often represented by the relative permittivity εr which is the ratio of the absolute permittivity ε and the vacuum permittivity ε0
.
This dimensionless quantity is also often and ambiguously referred to as the permittivity. Another common term encountered for both absolute and relative permittivity is the dielectric constant which has been deprecated in physics and engineering[2] as well as in chemistry.[3]
By definition, a perfect vacuum has a relative permittivity of exactly 1 whereas at standard temperature and pressure, air has a relative permittivity of κair ≈ 1.0006.
Relative permittivity is directly related to electric susceptibility (χ) by
otherwise written as
The term «permittivity» was introduced in the 1880s by Oliver Heaviside to complement Thomson’s (1872) «permeability».[4] Formerly written as p, the designation with ε has been in common use since the 1950s.
Units[edit]
The standard SI unit for permittivity is farad per meter (F/m or F·m−1).[5]
Explanation[edit]
In electromagnetism, the electric displacement field D represents the distribution of electric charges in a given medium resulting from the presence of an electric field E. This distribution includes charge migration and electric dipole reorientation. Its relation to permittivity in the very simple case of linear, homogeneous, isotropic materials with «instantaneous» response to changes in electric field is:
where the permittivity ε is a scalar. If the medium is anisotropic, the permittivity is a second rank tensor.
In general, permittivity is not a constant, as it can vary with the position in the medium, the frequency of the field applied, humidity, temperature, and other parameters. In a nonlinear medium, the permittivity can depend on the strength of the electric field. Permittivity as a function of frequency can take on real or complex values.
In SI units, permittivity is measured in farads per meter (F/m or A2·s4·kg−1·m−3). The displacement field D is measured in units of coulombs per square meter (C/m2), while the electric field E is measured in volts per meter (V/m). D and E describe the interaction between charged objects. D is related to the charge densities associated with this interaction, while E is related to the forces and potential differences.
Vacuum permittivity[edit]
The vacuum permittivity ε0 (also called permittivity of free space or the electric constant) is the ratio D/E in free space. It also appears in the Coulomb force constant,
Its value is[6][7]
where
- c0 is the speed of light in free space,[a]
- µ0 is the vacuum permeability.
The constants c0 and μ0 were both defined in SI units to have exact numerical values until the 2019 redefinition of the SI base units. Therefore, until that date, ε0 could be also stated exactly as a fraction,
even if the result was irrational (because the fraction contained π).[9] In contrast, the ampere was a measured quantity before 2019, but since then the ampere is now exactly defined and it is μ0 that is an experimentally measured quantity (with consequent uncertainty) and therefore so is the new 2019 definition of ε0 (c0 remains exactly defined before and since 2019).
Relative permittivity[edit]
The linear permittivity of a homogeneous material is usually given relative to that of free space, as a relative permittivity εr (also called dielectric constant, although this term is deprecated and sometimes only refers to the static, zero-frequency relative permittivity). In an anisotropic material, the relative permittivity may be a tensor, causing birefringence. The actual permittivity is then calculated by multiplying the relative permittivity by ε0:
where χ (frequently written χe) is the electric susceptibility of the material.
The susceptibility is defined as the constant of proportionality (which may be a tensor) relating an electric field E to the induced dielectric polarization density P such that
where ε0 is the electric permittivity of free space.
The susceptibility of a medium is related to its relative permittivity εr by
So in the case of a vacuum,
The susceptibility is also related to the polarizability of individual particles in the medium by the Clausius-Mossotti relation.
The electric displacement D is related to the polarization density P by
The permittivity ε and permeability µ of a medium together determine the phase velocity v = c/n of electromagnetic radiation through that medium:
Practical applications[edit]
Determining capacitance[edit]
The capacitance of a capacitor is based on its design and architecture, meaning it will not change with charging and discharging. The formula for capacitance in a parallel plate capacitor is written as
where 



Gauss’s law[edit]
Permittivity is connected to electric flux (and by extension electric field) through Gauss’s law. Gauss’s law states that for a closed Gaussian surface, S,
where 



If the Gaussian surface uniformly encloses an insulated, symmetrical charge arrangement, the formula can be simplified to
where 
If all of the electric field lines cross the surface at 90°, the formula can be further simplified to
Because the surface area of a sphere is 

This formula applies to the electric field due to a point charge, outside of a conducting sphere or shell, outside of a uniformly charged insulating sphere, or between the plates of a spherical capacitor.
Dispersion and causality[edit]
In general, a material cannot polarize instantaneously in response to an applied field, and so the more general formulation as a function of time is
That is, the polarization is a convolution of the electric field at previous times with time-dependent susceptibility given by χ(Δt). The upper limit of this integral can be extended to infinity as well if one defines χ(Δt) = 0 for Δt < 0. An instantaneous response would correspond to a Dirac delta function susceptibility χ(Δt) = χδ(Δt).
It is convenient to take the Fourier transform with respect to time and write this relationship as a function of frequency. Because of the convolution theorem, the integral becomes a simple product,
This frequency dependence of the susceptibility leads to frequency dependence of the permittivity. The shape of the susceptibility with respect to frequency characterizes the dispersion properties of the material.
Moreover, the fact that the polarization can only depend on the electric field at previous times (i.e. effectively χ(Δt) = 0 for Δt < 0), a consequence of causality, imposes Kramers–Kronig constraints on the susceptibility χ(0).
Complex permittivity[edit]
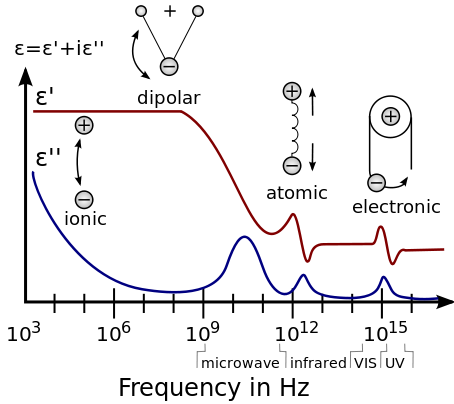
A dielectric permittivity spectrum over a wide range of frequencies. ε′ and ε″ denote the real and the imaginary part of the permittivity, respectively. Various processes are labeled on the image: ionic and dipolar relaxation, and atomic and electronic resonances at higher energies.[10]
As opposed to the response of a vacuum, the response of normal materials to external fields generally depends on the frequency of the field. This frequency dependence reflects the fact that a material’s polarization does not change instantaneously when an electric field is applied. The response must always be causal (arising after the applied field), which can be represented by a phase difference. For this reason, permittivity is often treated as a complex function of the (angular) frequency ω of the applied field:
(since complex numbers allow specification of magnitude and phase). The definition of permittivity therefore becomes
where
- D0 and E0 are the amplitudes of the displacement and electric fields, respectively,
- i is the imaginary unit, i2 = −1.
The response of a medium to static electric fields is described by the low-frequency limit of permittivity, also called the static permittivity εs (also εDC):
At the high-frequency limit (meaning optical frequencies), the complex permittivity is commonly referred to as ε∞ (or sometimes εopt[11]). At the plasma frequency and below, dielectrics behave as ideal metals, with electron gas behavior. The static permittivity is a good approximation for alternating fields of low frequencies, and as the frequency increases a measurable phase difference δ emerges between D and E. The frequency at which the phase shift becomes noticeable depends on temperature and the details of the medium. For moderate field strength (E0), D and E remain proportional, and
Since the response of materials to alternating fields is characterized by a complex permittivity, it is natural to separate its real and imaginary parts, which is done by convention in the following way:
where
- ε′ is the real part of the permittivity;
- ε″ is the imaginary part of the permittivity;
- δ is the loss angle.
The choice of sign for time-dependence, e−iωt, dictates the sign convention for the imaginary part of permittivity. The signs used here correspond to those commonly used in physics, whereas for the engineering convention one should reverse all imaginary quantities.
The complex permittivity is usually a complicated function of frequency ω, since it is a superimposed description of dispersion phenomena occurring at multiple frequencies. The dielectric function ε(ω) must have poles only for frequencies with positive imaginary parts, and therefore satisfies the Kramers–Kronig relations. However, in the narrow frequency ranges that are often studied in practice, the permittivity can be approximated as frequency-independent or by model functions.
At a given frequency, the imaginary part, ε″, leads to absorption loss if it is positive (in the above sign convention) and gain if it is negative. More generally, the imaginary parts of the eigenvalues of the anisotropic dielectric tensor should be considered.
In the case of solids, the complex dielectric function is intimately connected to band structure. The primary quantity that characterizes the electronic structure of any crystalline material is the probability of photon absorption, which is directly related to the imaginary part of the optical dielectric function ε(ω). The optical dielectric function is given by the fundamental expression:[12]
In this expression, Wc,v(E) represents the product of the Brillouin zone-averaged transition probability at the energy E with the joint density of states,[13][14] Jc,v(E); φ is a broadening function, representing the role of scattering in smearing out the energy levels.[15] In general, the broadening is intermediate between Lorentzian and Gaussian;[16][17] for an alloy it is somewhat closer to Gaussian because of strong scattering from statistical fluctuations in the local composition on a nanometer scale.
Tensorial permittivity[edit]
According to the Drude model of magnetized plasma, a more general expression which takes into account the interaction of the carriers with an alternating electric field at millimeter and microwave frequencies in an axially magnetized semiconductor requires the expression of the permittivity as a non-diagonal tensor.[18] (see also Electro-gyration).
If ε2 vanishes, then the tensor is diagonal but not proportional to the identity and the medium is said to be a uniaxial medium, which has similar properties to a uniaxial crystal.
Classification of materials[edit]
| εr″/εr′ | Current conduction | Field propagation |
|---|---|---|
| 0 | perfect dielectric lossless medium |
|
| ≪ 1 | low-conductivity material poor conductor |
low-loss medium good dielectric |
| ≈ 1 | lossy conducting material | lossy propagation medium |
| ≫ 1 | high-conductivity material good conductor |
high-loss medium poor dielectric |
| ∞ | perfect conductor |
Materials can be classified according to their complex-valued permittivity ε, upon comparison of its real ε′ and imaginary ε″ components (or, equivalently, conductivity, σ, when accounted for in the latter). A perfect conductor has infinite conductivity, σ = ∞, while a perfect dielectric is a material that has no conductivity at all, σ = 0; this latter case, of real-valued permittivity (or complex-valued permittivity with zero imaginary component) is also associated with the name lossless media.[19] Generally, when σ/ωε′ ≪ 1 we consider the material to be a low-loss dielectric (although not exactly lossless), whereas σ/ωε′ ≫ 1 is associated with a good conductor; such materials with non-negligible conductivity yield a large amount of loss that inhibit the propagation of electromagnetic waves, thus are also said to be lossy media. Those materials that do not fall under either limit are considered to be general media.
Lossy medium[edit]
In the case of a lossy medium, i.e. when the conduction current is not negligible, the total current density flowing is:
where
Note that this is using the electrical engineering convention of the Complex conjugate ambiguity; the physics/chemistry convention involves the complex conjugate of these equations.
The size of the displacement current is dependent on the frequency ω of the applied field E; there is no displacement current in a constant field.
In this formalism, the complex permittivity is defined as:[20][21]
In general, the absorption of electromagnetic energy by dielectrics is covered by a few different mechanisms that influence the shape of the permittivity as a function of frequency:
- First are the relaxation effects associated with permanent and induced molecular dipoles. At low frequencies the field changes slowly enough to allow dipoles to reach equilibrium before the field has measurably changed. For frequencies at which dipole orientations cannot follow the applied field because of the viscosity of the medium, absorption of the field’s energy leads to energy dissipation. The mechanism of dipoles relaxing is called dielectric relaxation and for ideal dipoles is described by classic Debye relaxation.
- Second are the resonance effects, which arise from the rotations or vibrations of atoms, ions, or electrons. These processes are observed in the neighborhood of their characteristic absorption frequencies.
The above effects often combine to cause non-linear effects within capacitors. For example, dielectric absorption refers to the inability of a capacitor that has been charged for a long time to completely discharge when briefly discharged. Although an ideal capacitor would remain at zero volts after being discharged, real capacitors will develop a small voltage, a phenomenon that is also called soakage or battery action. For some dielectrics, such as many polymer films, the resulting voltage may be less than 1–2% of the original voltage. However, it can be as much as 15–25% in the case of electrolytic capacitors or supercapacitors.
Quantum-mechanical interpretation[edit]
In terms of quantum mechanics, permittivity is explained by atomic and molecular interactions.
At low frequencies, molecules in polar dielectrics are polarized by an applied electric field, which induces periodic rotations. For example, at the microwave frequency, the microwave field causes the periodic rotation of water molecules, sufficient to break hydrogen bonds. The field does work against the bonds and the energy is absorbed by the material as heat. This is why microwave ovens work very well for materials containing water. There are two maxima of the imaginary component (the absorptive index) of water, one at the microwave frequency, and the other at far ultraviolet (UV) frequency. Both of these resonances are at higher frequencies than the operating frequency of microwave ovens.
At moderate frequencies, the energy is too high to cause rotation, yet too low to affect electrons directly, and is absorbed in the form of resonant molecular vibrations. In water, this is where the absorptive index starts to drop sharply, and the minimum of the imaginary permittivity is at the frequency of blue light (optical regime).
At high frequencies (such as UV and above), molecules cannot relax, and the energy is purely absorbed by atoms, exciting electron energy levels. Thus, these frequencies are classified as ionizing radiation.
While carrying out a complete ab initio (that is, first-principles) modelling is now computationally possible, it has not been widely applied yet. Thus, a phenomenological model is accepted as being an adequate method of capturing experimental behaviors. The Debye model and the Lorentz model use a first-order and second-order (respectively) lumped system parameter linear representation (such as an RC and an LRC resonant circuit).
Measurement[edit]
The relative permittivity of a material can be found by a variety of static electrical measurements. The complex permittivity is evaluated over a wide range of frequencies by using different variants of dielectric spectroscopy, covering nearly 21 orders of magnitude from 10−6 to 1015 hertz. Also, by using cryostats and ovens, the dielectric properties of a medium can be characterized over an array of temperatures. In order to study systems for such diverse excitation fields, a number of measurement setups are used, each adequate for a special frequency range.
Various microwave measurement techniques are outlined in Chen et al..[22] Typical errors for the Hakki-Coleman method employing a puck of material between conducting planes are about 0.3%.[23]
- Low-frequency time domain measurements (10−6 to 103 Hz)
- Low-frequency frequency domain measurements (10−5 to 106 Hz)
- Reflective coaxial methods (106 to 1010 Hz)
- Transmission coaxial method (108 to 1011 Hz)
- Quasi-optical methods (109 to 1010 Hz)
- Terahertz time-domain spectroscopy (1011 to 1013 Hz)
- Fourier-transform methods (1011 to 1015 Hz)
At infrared and optical frequencies, a common technique is ellipsometry. Dual polarisation interferometry is also used to measure the complex refractive index for very thin films at optical frequencies.
For the 3D measurement of dielectric tensors at optical frequency, Dielectric tensor tomography [1] can be used.
See also[edit]
- Acoustic attenuation
- Density functional theory
- Electric-field screening
- Green–Kubo relations
- Green’s function (many-body theory)
- Linear response function
- Rotational Brownian motion
- Electromagnetic permeability
Notes[edit]
- ^ Current practice of standards organizations such as NIST and BIPM is to use c0, rather than c, to denote the speed of light in vacuum according to ISO 31. In the original Recommendation of 1983, the symbol c was used for this purpose.[8]
References[edit]
- ^ Landau, L. D.; Lifshitz, E. M.; Pitaevskii, L. P. (2009). Electrodynamics of continuous media. Elsevier Butterworth-Heinemann. ISBN 978-0-7506-2634-7. OCLC 756385298.
- ^ IEEE Standards Board (1997). «IEEE Standard Definitions of Terms for Radio Wave Propagation». IEEE STD 211-1997: 6.
- ^ Braslavsky, S.E. (2007). «Glossary of terms used in photochemistry (IUPAC recommendations 2006)» (PDF). Pure and Applied Chemistry. 79 (3): 293–465. doi:10.1351/pac200779030293. S2CID 96601716.
- ^ Fleming, John Ambrose (1910). The Principles of Electric Wave Telegraphy. p. 340..
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16, p. 119
- ^ «2018 CODATA Value: vacuum electric permittivity». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «Latest (2018) values of the constants (NIST)». Physics.nist.gov. 2019-05-20. Retrieved 2022-02-05.
- ^ «Special Publication 330, Appendix 2″ (PDF). NIST: 45. Archived from the original (PDF) on 2016-06-03..
- ^ «Latest (2006) values of the constants (NIST)». Physics.nist.gov. 2017-07-01. Retrieved 2018-11-20.
- ^ «Dielectric Spectroscopy». Archived from the original on 2006-01-18. Retrieved 2018-11-20.
- ^
Hofmann, Philip (2015-05-26). Solid State Physics (2 ed.). Wiley-VCH. p. 194. ISBN 978-3527412822. - ^
Peter Y. Yu; Manuel Cardona (2001). Fundamentals of Semiconductors: Physics and Materials Properties. Berlin: Springer. p. 261. ISBN 978-3-540-25470-6. - ^
José García Solé, Jose Solé, Luisa Bausa (2001). An introduction to the optical spectroscopy of inorganic solids. Wiley. Appendix A1, pp, 263. ISBN 978-0-470-86885-0.{{cite book}}: CS1 maint: multiple names: authors list (link) - ^
John H. Moore; Nicholas D. Spencer (2001). Encyclopedia of chemical physics and physical chemistry. Taylor and Francis. p. 105. ISBN 978-0-7503-0798-7. - ^
Solé, José García; Bausá, Louisa E; Jaque, Daniel (2005-03-22). Solé and Bausa. p. 10. ISBN 978-3-540-25470-6. - ^
Hartmut Haug; Stephan W. Koch (1994). Quantum Theory of the Optical and Electronic Properties of Semiconductors. World Scientific. p. 196. ISBN 978-981-02-1864-5. - ^
Manijeh Razeghi (2006). Fundamentals of Solid State Engineering. Birkhauser. p. 383. ISBN 978-0-387-28152-0. - ^ Prati, E. (2003). «Propagation in Gyroelectromagnetic Guiding Systems». Journal of Electromagnetic Waves and Applications. 17 (8): 1177–1196. doi:10.1163/156939303322519810. S2CID 121509049.
- ^ Orfanidis, Sophocles J. «1: Maxwell’s Equations» (PDF). Electromagnetic Waves and Antennas. Rutgers University.
- ^ Seybold, John S. (2005). Introduction to RF Propagation. John Wiley & Sons. p. 22, eq. (2.6). ISBN 9780471743682.
- ^ Kaiser, Kenneth L. (2005). Electromagnetic Shielding. CRC Press. pp. 1–28, eqs. (1.80) and (1.81). ISBN 9780849363726.
- ^ Linfeng Chen; V. V. Varadan; C. K. Ong; Chye Poh Neo (2004). «Microwave theory and techniques for materials characterization». Microwave electronics. Wiley. p. 37. ISBN 978-0-470-84492-2.
- ^ Mailadil T. Sebastian (2008). Dielectric Materials for Wireless Communication. Elsevier. p. 19. ISBN 978-0-08-045330-9.
Further reading[edit]
- C. J. F. Bottcher, O. C. von Belle & Paul Bordewijk (1973) Theory of Electric Polarization: Dielectric Polarization, volume 1, (1978) volume 2, Elsevier ISBN 0-444-41579-3.
- Arthur R. von Hippel (1954) Dielectrics and Waves ISBN 0-89006-803-8
- Arthur von Hippel editor (1966) Dielectric Materials and Applications: papers by 22 contributors ISBN 0-89006-805-4.
External links[edit]
- Electromagnetism, a chapter from an online textbook
В этой статье мы расскажем о самых важных вещах, связанных с диэлектрической проницаемостью. Среди прочего, вы узнаете о важных ролях, которые она играет, и о её типичных значениях.
Простое объяснение
В повседневной жизни вы сталкиваетесь с различными веществами, такими как металлы, вода или кислород. Каждое из этих веществ по-разному реагирует на электрические поля.
Диэлектрическая проницаемость (диэлектрическая постоянная или абсолютная диэлектрическая проницаемость) ε описывает способность материала к поляризации электрическими полями и определяется следующим образом: ε = εr * ε0 .
Здесь εr — относительная проницаемость, а ε0 — электрическая постоянная (или диэлектрическая проницаемость вакуума).
Если понимать значение термина «проницаемость» буквально, то это мера того, насколько сильно материя «пропускает» электрическое поле. Поэтому проницаемость можно рассматривать как меру того, насколько материя может быть поляризована.
Диэлектрическая проницаемость вакуума
Особую роль играет диэлектрическая проницаемость вакуума (также называемая проницаемостью вакуума). В этом разделе мы расскажем вам о значении и единицах измерения проницаемости вакуума, о том, как она связана с другими константами, и о ее значении в контексте других важных законов.
Числовое значение и единица измерения
Диэлектрическая проницаемость вакуума ε0 имеет значение 8,85418781762039 * 10-12 или 8.85 * 10-12, что более практично для расчетов. Единицей измерения константы является [ Ф·м−1 ] или если выражать через основные единицы СИ [ м−3·кг−1·с4·А2 ].
Взаимосвязь с другими константами
Существует замечательная связь между электрической постоянно ε0, магнитной постоянно μ0 и скоростью света в вакууме с0. То есть верно следующее соотношение: c02 = 1 / ε0 * μ0 .
До 2019 года это уравнение точно определяло значение постоянной электрического поля. Однако в ходе пересмотра ситуация изменилась, и с 20 мая 2019 года как электрическая постоянная, так и магнитная постоянная имеют определенную погрешность измерения.
Это уравнение было первым указанием на то, что свет может быть электромагнитной волной.
Закон Кулона и электрический потенциал
Помимо связи со скоростью света, электрическая постоянная фигурирует в других важных законах электродинамики. К ним относятся, например:
- Закон Кулона:
- Электрический потенциал заряженной частицы : φ ( r ) = q / 4 * π * ε0 * r .
В частности, закон Кулона является основой электростатики, поэтому константа электрического поля также имеет большое значение.
Диэлектрическая проницаемость: общий случай
В этом разделе мы рассмотрим общий случай. Мы объясним физический смысл абсолютной диэлектрической проницаемости с помощью электроизоляционных материалов и объясним, что такое относительная диэлектрическая проницаемость.
Диэлектрическая проницаемость диэлектриков
В электроизолирующих материалах (диэлектриках) электрические заряды связаны с атомами или молекулами. Поэтому они могут лишь немного перемещаться внутри атомов или молекул. Электрическое поле может изменить распределение заряда в диэлектрике двумя важными способами: деформацией и вращением. Даже если отдельные электрические заряды могут двигаться незначительно, совокупность всех движений определяет поведение электроизоляционного материала.
Поляризация
В зависимости от того, состоит ли материал из полярных или неполярных молекул, реакция на внешнее электрическое поле различна. С неполярной молекулой происходит растягивание (деформация), при котором поле индуцирует дипольный момент в каждой молекуле материала. Все эти дипольные моменты направлены в ту же сторону, что и электрическое поле.
В полярной молекуле, с другой стороны, происходит вращение, так что и здесь все дипольные моменты направлены в сторону электрического поля. В целом внешнее электрическое поле вызывает образование в материале большого количества диполей, все из которых ориентированы в том же направлении, что и внешнее поле. Таким образом, материал поляризуется. Поляризация P описывает, сколько дипольных моментов приходится на единицу объема материала.
Таким образом, поляризация диэлектрика вызывается электрическим полем. Возникающие направленные дипольные моменты, в свою очередь, создают электрическое поле, противодействующее внешнему полю. Таким образом, это противоположное поле ослабляет внешнее поле. В целом, связь между поляризацией и внешним электрическим полем сложная. Для многих веществ, так называемых линейных диэлектриков, поляризация пропорциональна полю. Применяется следующее соотношение:
P = ε0 * χ * E , где
Здесь ε0 — электрическая постоянная, а χ — электрическая поляризуемость. Электрическое поле E в этом уравнении является полным полем. Поэтому причиной этого могут быть частично свободные заряды и частично сама поляризация.. Свободные заряды — это все те носители заряда, которые не являются результатом поляризации. Таким образом, это полное электрическое поле очень трудно рассчитать, поскольку мы обычно не имеем информации о распределении поляризационных зарядов.
Для справки: χ — коэффициент, зависящий от химического состава, концентрации, структуры (в том числе от агрегатного состояния) среды, температуры, механических напряжений и т. д. (от одних факторов более сильно, от других слабее, конечно же и в зависимости от диапазона изменений каждого), и называемый (электрической) поляризуемостью (а чаще, по крайней мере для того случая, когда он выражается скаляром — диэлектрической восприимчивостью) данной среды.
Википедия
Электрическая индукция
Чтобы иметь возможность рассчитать электрическое поле даже в присутствии диэлектрика, вводится электрическая индукция D. В линейной среде: D = ε0 * E + P = ε0 * E + ε0 * χe * E = ε0 * ( 1 + χe ) * E и поэтому D также пропорциональна E.
Если вы объедините константы вместе ε = ε0 * ( 1 + χe ), то получится: D = ε * E .
Постоянная ε и называется диэлектрической проницаемостью.
Относительная диэлектрическая проницаемость
Величина: εr = 1 + χe = ε / ε0 называется относительной проницаемостью (также относительной диэлектрической проницаемостью). С его помощью полное электрическое поле в присутствии диэлектрика определяется следующим образом: E = D / ε = D / εr * ε0 .
При постоянной электрической индукции относительная проницаемость, таким образом, определяет, насколько сильно ослабляется электрическое поле. Чем больше относительная проницаемость, тем больше ослабляется электрическое поле и, следовательно, уменьшается общая напряженность электрического поля.
Термин относительная проницаемость может привести к неправильному пониманию того, что относительная проницаемость для данного материала является константой. На самом деле, относительная проницаемость зависит от многих факторов. Среди них:
- температура материала;
- частота внешнего электрического поля;
- напряженность внешнего электрического поля.
Для некоторых материалов относительная проницаемость дополнительно зависит от направления. Следовательно, в случае таких материалов это не просто число, а часто тензор второго порядка.
Особенно наглядную иллюстрацию влияния диэлектриков с разной относительной проницаемостью можно получить, поместив диэлектрик между двумя пластинами конденсатора. Если измерить электрическое напряжение на конденсаторе до и после введения диэлектрика, то можно обнаружить, что напряжение на конденсаторе уменьшается ровно на величину εr относительной диэлектрической проницаемости. Это следует непосредственно из уравнения: E = U / d для величины электрического поля между пластинами конденсатора, расположенными на расстоянии d друг от друга. Это также иллюстрирует, почему εr называется относительной проницаемостью. Напряжение на конденсаторе уменьшается на коэффициент εr за счет введения диэлектрика, по сравнению со случаем, когда между пластинами только вакуум.
Относительные диэлектрические проницаемости отдельных материалов
Наконец, мы приводим таблицу с типичными значениями относительной диэлектрической проницаемости (относительной диэлектрической проницаемости) различных материалов. Следует отметить, что в таких таблицах обычно указывается относительная проницаемость, а не сама абсолютная диэлектрическая проницаемость. Поэтому, если вы ищете таблицу для определения абсолютной диэлектрической проницаемости определенного материала, вы должны помнить, что приведенное там значение не является непосредственно той проницаемостью, которую вы ищете. Однако для заданного значения относительной проницаемости можно вычислить соответствующую абсолютную диэлектрическую проницаемость без особых дополнительных усилий. То есть нужно применять следующую уже известную нам формулу: ε = εr * ε0 .
| Вещество | εr |
| Вакуум | ровно 1 |
| Гелий | 1,000065 |
| Медь | 5,6 |
| Воздух (сухой) | 1,00059 |
| Метанол | 32,6 |
| Бумага | 1 – 4 |
| Вода ( 20°C, 0 — 3 ГГц ) | 80 |
| Вода ( 0°C, 0 — 1 ГГц ) | 88 |
(если не указано иное: при 18°C и 50 Гц)
В предыдущем разделе мы упоминали, что относительная проницаемость зависит, помимо прочего, от температуры и частоты. Поэтому важно знать и температуру, и частоту, если вы хотите получить значение из таблицы. Например, относительная проницаемость воды при температуре 20°C и частоте 0 ГГц равна 80. Если температура 0°C, а частота та же, относительная проницаемость воды равна 88. Медь, с другой стороны, имеет относительную проницаемость 5,6. Это означает, что вода как среда уменьшит напряжение на конденсаторе в 80 раз, в то время как медь уменьшит его только в 5,6 раз.
Список использованной литературы
- Курс физики для ФМШ при НГУ, раздел «Электромагнитное поле», гл. 2: «Диэлектрики».
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. — М.: Мир, 1965.
- Сивухин Д. В. Общий курс физики. — М.. — Т. III. Электричество.
- Гольдштейн Л. Д., Зернов Н. В. Электромагнитные поля и волны. М.: Сов. радио, 1971. С. 11.
На чтение 9 мин Просмотров 2.1к. Опубликовано 11.09.2022 Обновлено 11.09.2022
Содержание
- Понятие ЭДС и единица измерения
- Где и как образуется электродвижущая сила
- Виды ЭДС
- Законы и формулы
- ЭДС аккумуляторной батареи
- ЭДС индукции
- Внутреннее сопротивление источника ЭДС
- Закон Ома для полной цепи
- Как найти мощность ЭДС
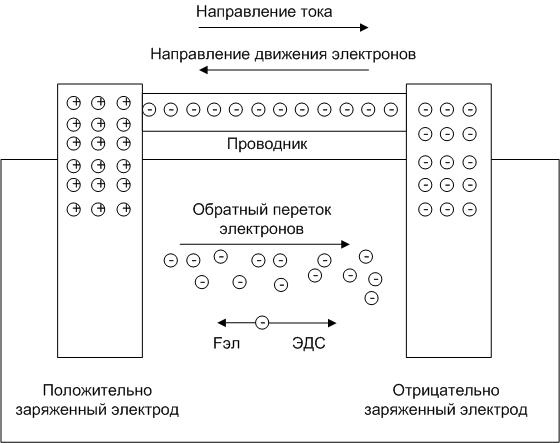
Чтобы в какой-либо среде (металле, растворе, ионизированном газе и т.п.) протекал электрический ток в течение продолжительного времени, недостаточно наличия свободных носителей заряда и электрического поля. Еще потребуется сила, которая будет разделять заряды в направлении, противоположном направлению электрического поля.
Понятие ЭДС и единица измерения
Если имеется заряженный предмет и соединить его с электрически нейтральным (или противоположно заряженным предметом), некоторое время в цепи будет существовать ток. Как только все свободные электроны перейдут от одного тела к другому, и заряды уравняются, ток прекратится.
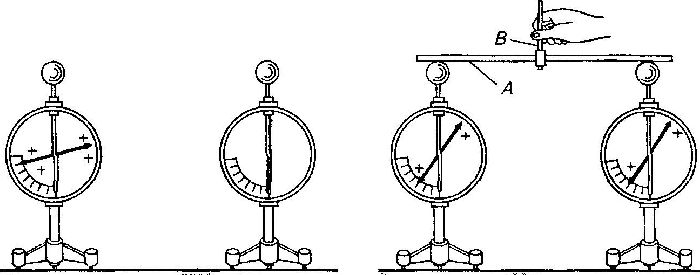
Это можно увидеть на примере школьного опыта с двумя электроскопами. Один из них заряжен (например, положительно), а другой заряда не имеет. Если их соединить металлическим стержнем, то заряды перейдут от одного прибора к другому. Количество зарядов уравновесится, потенциалы электроскопов станут равными, электрическое поле прекратит действие на электроны, и ток перестанет течь.
Чтобы ток продолжался, надо носители зарядов из второго электроскопа перенести обратно в первый. Для этого нужна сторонняя сила, действующая против направления электрического поля. Такая сила называется ЭДС. Расшифровка этого сокращения – электродвижущая сила.
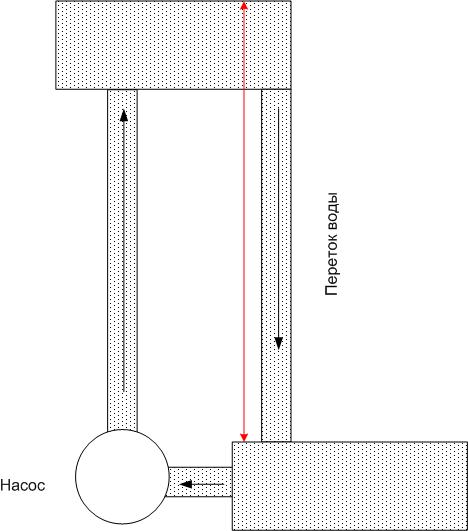
Можно провести аналогию с водой. Если есть два бассейна, один из которых находится выше другого, то вода может перетекать из верхнего водоема в нижний. Но как только запас воды закончится, переток прекратится. Чтобы он продолжался, надо воду из нижнего бассейна перекачивать обратно в верхний (например, с помощью насоса).
ЭДС обозначается греческой буквой ε (эпсилон), а иногда E. Измеряется ЭДС, как и напряжение, в вольтах (1 В). Понятие электродвижущей силы является не очень удачным – сила не измеряется в вольтах. Но этот термин укоренился и широко применяется.
Из-за сходства единиц измерения часто происходит путаница ЭДС и напряжения. Эти термины регулярно подменяются друг с другом. В некоторых случаях действительно принципиальной разницы нет, но в целом эти понятия различны.
В видео простыми словами объясняется чем отличаются ЭДС и напряжение
Где и как образуется электродвижущая сила
Электродвижущая сила образуется в источнике питания. Это необходимое условие существования разности потенциалов на выходных клеммах такого источника. Образовываться ЭДС может по-разному, в зависимости от устройства источника.
Виды ЭДС
Электродвижущая сила может быть различной природы (но всегда неэлектрической). В зависимости от типа источника питания ЭДС может быть:
- фотоэлектрического характера – возникает в полупроводниковых переходах при облучении видимым светом или ультрафиолетом (на этом эффекте основана работа солнечных батарей);
- электрохимической природы – всем известные гальванические элементы и аккумуляторы;
- термоэлектрической ЭДС – возникает при разности температур между холодным и горячим спаем металлов (термопары для генерации электроэнергии и измерения температуры);
- пьезоэлектрической природы (возникает при деформации некоторых материалов) – применяется в пьезозажигалках;
- ЭДС электромагнитного характера – генераторы электростанций, автомобилей и т.п.
В технике встречаются и некоторые другие виды ЭДС, но реже.
Законы и формулы
Электродвижущая сила совершает работу по переносу заряда, а движущийся заряд представляет собой электрический ток/ Этот ток равен I=qt, где q – заряд, перенесенный полем за время t. За это время поле совершает работу A=ε*q= ε*I*t.
Можно определить ЭДС, как отношение работы по переносу заряда к величине этого заряда:
ε=A/q=A/(I*t)
ЭДС аккумуляторной батареи
ЭДС аккумуляторной батареи определяется типом электрохимических реакций, протекающих внутри элемента. Для различных технологий батарей наибольшая электродвижущая сила составит:
- Свинцово-кислотные элементы – 2,17 вольта.
- Никель-кадмиевые батареи – 1,37 вольта.
- Никель-металлогидридные элементы – 1,37 вольта.
- Щелочные аккумуляторы – 1,45 вольта.
- Литий-ионные элементы – 4,2 вольта.
Электродвижущая сила химических источников тока не зависит от размеров и площади пластин. Чтобы повысить выходное напряжение, единичные аккумуляторы соединяют в батареи последовательно.
ЭДС индукции
Основной источник получения электроэнергии на Земле – генераторы постоянного и переменного тока. Их принцип действия основан на создании ЭДС индукции.
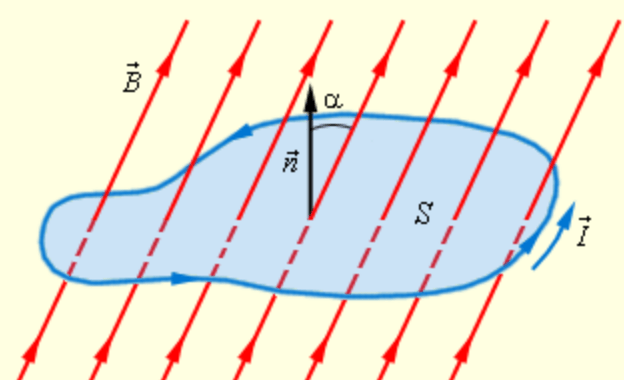
Если замкнутый контур находится в магнитном поле, и его пронизывает магнитный поток Ф, и этот поток изменяется во времени (по направлению или по величине), то в контуре возникает ЭДС. Ее величина равна:
ε=∆Ф/∆t, где Ф – магнитный поток, а t – время его изменения.
В свою очередь магнитный поток зависит от величины магнитной индукции и площади поверхности, охватываемой контуром. Следовательно, чтобы увеличить ЭДС, надо усиливать магнитное поле (повышением тока возбуждения), или увеличивать площадь витка (при разработке или изготовлении генератора), или заставить магнитный поток изменяться быстрее (например, увеличивая скорость вращения ротора генератора). Каждый путь имеет определенные технические ограничения, поэтому в генераторах делают большое количество витков, соединяя их последовательно. При этом электродвижущие силы всех контуров складываются.
Внутреннее сопротивление источника ЭДС
Пусть имеется источник тока — например, аккумулятор — с напряжением на разомкнутых клеммах (в отсутствие нагрузки) 12 вольт. Если его нагрузить на сопротивление в 5 Ом, напряжение на клеммах упадет (например, до 11,5 вольт). Если нагрузить аккумулятор на сопротивление 1 Ом, на его выходных терминалах напряжение снизится до 9,86 вольт.
Это явление легко объяснить, если ввести понятие внутреннего сопротивления источника питания. При разделении зарядов они движутся к соответствующим полюсам, но при этом взаимодействуют с кристаллической решеткой вещества, с ионами электролитов и отдают часть своей энергии. Движение носителей заряда замедляется, ток уменьшается, его ограничивает внутреннее сопротивление источника.
Это сопротивление включается последовательно с нагрузкой, и часть выходного напряжения падает на нем. Чем меньше сопротивление нагрузки, тем больше ток, тем больше потеря напряжения на внутреннем сопротивлении источника.
Внутреннее сопротивление определяется его конструкцией и типом ЭДС. Например, в аккумуляторе внутреннее сопротивление зависит от электрохимических реакций, протекающих в источнике тока.
Для анализа электрических цепей внутреннее сопротивление рисуется на схеме в виде резистора, подключенного внутри источника параллельно его выходным клеммам. На самом деле, конечно, никакого резистора там нет, но это удобно для рассмотрения процессов, протекающих в цепи.
Для наглядности рекомендуем видео-урок.
Закон Ома для полной цепи
Один из фундаментальных законов электротехники – закон Ома для участка цепи. Согласно ему, ток на участке цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Ток в полной цепи, в которую кроме нагрузки входит еще и источник, определяется величиной ЭДС, приложенной к внутреннему сопротивлению r и сопротивлению внешней нагрузки R, включенными последовательно. Общее значение сопротивления равно r+R. Следовательно, ток определяется соотношением I=ε/(R+r).
Как найти мощность ЭДС
Идеальный источник имеет нулевое внутреннее сопротивление. В нем напряжение под нагрузкой не уменьшается и всегда равно ЭДС. На практике таких источников не бывает.
Согласно закону Ома для полной цепи, формула ЭДС источника выглядит, как ε=I*R+I*r (в таком виде формулируется второй закон Кирхгофа). В этом выражении:
- I*R=Uвнеш – напряжение на внешней нагрузке;
- i*r=Uвнутр – падение напряжения на внутреннем сопротивлении источника.
Если источник идеален, то r=0 и вся ЭДС прикладывается к нагрузке. Чем выше r и выше ток, тем меньше напряжения достается потребителю, тем меньшая мощность выделяется на нем. Отсюда очевидно, что с ростом внутреннего сопротивления r, при равном токе, снижается напряжение на внешней нагрузке.
Внутреннее сопротивление источника можно рассчитать по результатам измерений напряжения на терминалах источника ЭДС по итогам двух замеров. Для этого надо воспользоваться законом Ома для полной цепи. Так, в рассмотренном примере, в первом случае падение напряжения на резисторе в 5 Ом составляет 11,5 вольт. Тогда можно найти ток в цепи по формуле:
I=U/R=11,5/5=2,3 А.
Выражение для ЭДС примет вид:
ε= 2,3*5+2,3*r=11,5+2,3*r.
Для второго замера на сопротивлении 1 Ом ток составит:
I=U/R=9,86/1=9,86 ампер
Следовательно,
ε= 9,86 *1+9,86 *r=9,86 +9,86 *r.
Левые части уравнений равны, тогда можно приравнять правые:
11,5+2,3*r=9,86 +9,86 *r
Путем несложных вычислений получается, что r=0,217 Ом. Если источник имеет меньшее внутреннее сопротивление, то при подключении той же нагрузки на ней будет большее напряжение. Напряжение на разомкнутых клеммах (на холостом ходу) в отсутствие ток будет примерно равно значению величины ЭДС. Таким образом, чем меньше внутреннее сопротивление, тем большее напряжение способен выдавать источник в нагрузку и тем больше мощность ЭДС.
Если же идеальный источник тока замкнуть накоротко, ток короткого замыкания будет бесконечным, так как R=r=0. На самом деле этого не происходит – в реальном источнике ток КЗ при R=0 ограничивается внутренним сопротивлением r.
Электродвижущая сила является одним из основополагающих понятий в физике. Ее суть и значение надо четко осознавать, в противном случае дальнейшее освоение электротехники будет затруднено.















 Ε , ε (название: э́псилон, греч. έψιλον ) — 5-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 5. Происходит от финикийской буквы
Ε , ε (название: э́псилон, греч. έψιλον ) — 5-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 5. Происходит от финикийской буквы  — хе. От буквы «эпсилон» произошли латинская E и кириллические Е, Ё, Є и Э. Название «эпсилон» (греч. Ε ψιλόν — «е простое») было введено для того, чтобы отличать эту букву от созвучного сочетания αι.
— хе. От буквы «эпсилон» произошли латинская E и кириллические Е, Ё, Є и Э. Название «эпсилон» (греч. Ε ψιλόν — «е простое») было введено для того, чтобы отличать эту букву от созвучного сочетания αι.