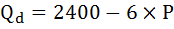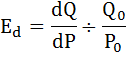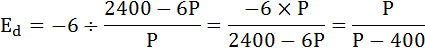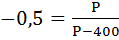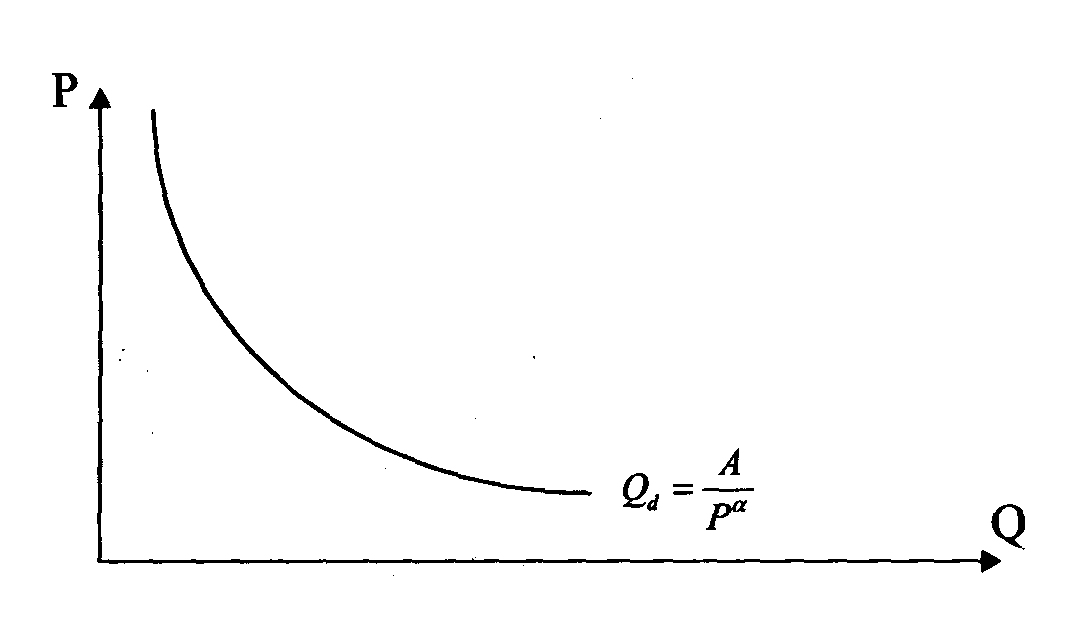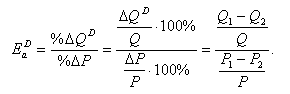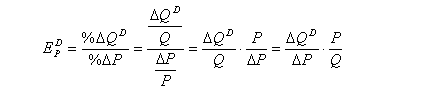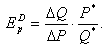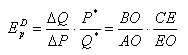Функция задана уравнением
а) Выведите формулу эластичности этого спроса.
б) При какой цене эластичность спроса по цене составит – 0,5?
в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?
Решение:
а) Так как в условии задачи нам дана непрерывная функция, для вывода формулы эластичности этого спроса воспользуемся коэффициентом точечной эластичности.
В точке (P0,Q0) точечная эластичность вычисляется как
Где
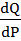
б)
Отсюда:
Р = 133,33
в) Чем больше P, тем больше эластичность по абсолютной величине. Поэтому на интервале цен от 200 до 300 она достигает максимума в точке Р=300.
Рассмотрим
линейную кривую спроса Q=a-bP. Наклон этой
кривой спроса есть константа(-b).
–b=
.Подставив
значение –b в формулу (3), получим
.
Для линейной кривой спроса наклон –
постоянная величина, он не зависит от
цены и величины спроса. Напротив, с
изменением цены отношение P/Q меняется
при движении вдоль кривой спроса
(рис.
7).
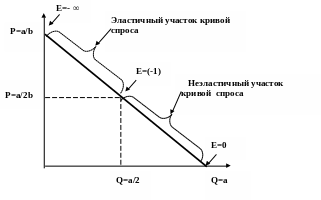
Следовательно,
для линейной кривой спроса эластичность
спроса по цене – переменная величина.
При
Р=0 эластичность спроса равна нулю. При
Q=0 коэффициент эластичности спроса
равен минус бесконечности. Если Q=a/2,
P=a/2b,
то эластичность спроса по цене E=
-1. Таким образом, точка единичной
эластичности спроса по цене находится
в середине линии спроса.
Спрос
является
-
неэластичным
при
; -
эластичным
при
.
Рис.
7
Пример
3.
Дана
функция спроса на товар Qd = 9 – 0,5Р.
Определить коэффициент эластичности
спроса по цене составит при цене 6 ден.
ед.
Решение:
По
формуле точечной эластичности
,
откуда
.
Ответ:
-0,5.
Пример
4.
Функция
спроса имеет следующий вид: Qd = 2100 – 3P.
При какой цене ценовая эластичность
спроса (ЕР)
составит (-0,75)?
Решение:
,
откуда
.
Получаем, что Р=300.
Ответ:
300.
1.4 Функция спроса с постоянной эластичностью
Рассмотрим
эластичность функции спроса: вида:
(Рис.8)
где
А и а — некоторые константы. Выведем
формулу эластичности для этой функции:

Таким
образом, мы выяснили, что значение
эластичности для подобной гиперболической
функции спроса не зависит от координаты
точки и при любом уровне цены равно -а.
Обратите внимание, что свойством
постоянной эластичности обладает не
всякая гиперболическая функция спроса,
а только удовлетворяющая указанному
выше общему уравнению.
Рис.
8
1.5. Эластичность и общий доход
Общий
доход (выручка) определяется как
произведение цены на проданное количество
товара. ТR=P∙Q.Выясним,
как общая выручка зависит от эластичности
спроса при линейной
функции спроса:
Q=a-bP.
Выручка — прямая функция от объема
продаж: TR=
F(Q).
Чтобы ее определить, надо выразить цену
товара через Q: Р=
(обратная функция спроса) и подставить
это выражение в ТR: ТR=P∙Q=(
)∙Q.
Графическое представление функции –
это парабола, ветви которой опущены
вниз. Вершина параболы (максимум выручки)
достигается при Q=a/2; P=a/2b,
то есть при единичной эластичности
спроса. При снижении цены товара (синяя
стрелка на графике) общая выручка
продавцов возрастает от нуля до максимума
на эластичном участке кривой спроса, а
затем она снижается от максимального
значения до нуля на неэластичном участке
кривой спроса.
При
снижении цены товара (красная стрелка
на графике) общая выручка продавцов
возрастает от нуля до максимума на
неэластичном участке кривой спроса, а
затем она снижается от максимального
значения до нуля на эластичном участке
кривой спроса.
Если
спрос на товар эластичен по цене, то
цена и общая выручки изменяются в
противоположных направлениях: P↓-
TR↑;
P↑- TR↓.
Если
спрос на товар неэластичен по цене, то
цена и общая выручка изменяются в одном
направлении:
P↓-
TR↓;
P↑- TR↑.
Рассчитаем
выручку для нелинейной функции спроса
вида
.
TR=
.
Таким образом, выручка постоянна и не
зависит от Р и Q
Рис.9
Пример
5.
По
исходным данным, приведенным в таблице,
определите общую выручку, коэффициент
эластичности спроса по цене, тип
эластичности спроса по цене для товаров
A, B, С.
|
Таблица |
||||||
|
Товар |
Товар |
Товар |
||||
|
Показатель |
В |
В |
В |
В |
В |
В |
|
Цена, |
4 |
3 |
10000 |
5000 |
500 |
250 |
|
Количество |
100 |
120 |
10 |
30 |
20 |
40 |
|
Выручка, |
||||||
|
Коэффициент |
||||||
|
Тип |
Решение:
Общую выручку можно найти по формуле
TR
= Q∙P,
где Q
– объем продаж, а Р
– цена товара. Для нахождения коэффициента
эластичности необходимо воспользоваться
формулой:
,
где ЕР
– коэффициент ценовой эластичности
спроса.
|
Товар |
Товар |
Товар |
||||
|
Выручка, |
400 |
360 |
100 000 |
150 000 |
10 000 |
10 000 |
|
Коэф. |
– 7/11 |
– 1,5 |
– 1 |
|||
|
Тип |
Неэластичный |
Эластичный |
Единичная |
Пример
6.
Цены
на товар снизились на 15%, а объем спроса
вырос с 200 ед. до 230 ед. Определите изменение
выручки и сделайте вывод об эластичности
спроса на товар.
Решение:
Общую выручку можно найти по формуле
TR
= Q∙P,
где Q
– количество, а Р – цена товара. до
изменения цены выручка составляла TR1
= 200∙Р, а после изменения цены выручка
стала равна TR2
= 230∙0,85Р = 195,5∙Р.
Поскольку,
при снижении цены выручка уменьшилась,
спрос является неэластичным.
Ответ:
неэластичный спрос.
Пример
7.
Цена
товара увеличилась на 1% при эластичности
спроса по цене, равной (-3). Как изменилась
выручка продавца?
Решение:
Общую выручку можно найти по формуле
TR
= Q∙P,
где Q
– количество, а Р – цена товара. Получаем,
что до изменения цены выручка составляла
TR1
= Q∙Р,
а после ее изменения выручка стала равна
TR2
= 0,97Q∙1,01Р
= 0,98Q∙Р.
Таким образом, выручка уменьшилась на
2%.
Ответ:
уменьшилась на 2%.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
5.5. Эластичность спроса по цене: углубление анализа
Анализируя поведение потребителя, мы обосновали закон спроса. Если цена на товар растёт, то, ceteris paribus (при прочих равных условиях), величина спроса на этот товар на рынке уменьшается, и наоборот. Но вот на сколько? Это зависит от чувствительности спроса к изменению цены, то есть от ценовой эластичности спроса. Знание эластичности спроса по цене имеет большое практическое значение. В правильной оценке эластичности спроса заинтересованы и фирмы, и правительство.
Напомним, что для измерения эластичности
используется коэффициент эластичности
спроса (ED), который
в самом общем виде представляет собой отношение процентного изменение величины
спроса к процентному изменению цены:
(1)
Коэффициент эластичности
показывает, на сколько процентов
изменится спрос, если цена изменится на 1 %. Поскольку цена и величина спроса
изменяются (по закону спроса) в противоположном друг другу направлении,
постольку коэффициент эластичности имеет знак «минус» , который, впрочем,
экономисты по молчаливому соглашению часто опускают. К примеру, | Еd | для электроэнергии равняется 0,13 – это значит, что если тариф на электроэнергию
повысится на 1 % , то спрос на неё понизится на 0,13 %. Если тариф повысится на 10 %, то спрос
понизится на 1,3 % и т.д.
Напомним также, что в зависимости от
степени чувствительности спроса к изменению цены можно выделить пять видов
эластичности:
1. Эластичный
спрос. Покупатели чувствительны к изменению цены. Спрос в
процентном отношении изменяется больше, чем цена, то есть для эластичного спроса | Еd
| >
1,0;
2. Неэластичный
спрос. Покупатели нечувствительны к изменению цены. Спрос в
процентном отношении изменяется меньше, чем цена, то есть для эластичного спроса | Еd
| <
1,0;
3. Единичная
эластичность спроса. Спрос в процентном отношении
изменяется так же как цена, то есть для
этого вида спроса | Еd | =
1,0;
4. Совершенно
эластичный спрос. Покупатели гиперчувствительны к
изменению цены. Например, при ничтожно малом повышении цены спрос стремится к
бесконечно малой величине. Для этого вида спроса| Еd | =
∞. На графике кривая спроса представляет собой прямую линию параллельную
абсциссе;
5. Совершенно
неэластичный спрос. Покупатели абсолютно нечувствительны к
изменению цены. При любом процентном изменении цены величина спроса остаётся
неизменной. Для этого вида спроса | Еd
| = 0.
На графике кривая спроса представляет собой прямую линию параллельную
ординате.
Существуют два способа точного
измерения эластичности. Ценовую эластичность спроса можно определить: (1) в
некотором диапазоне изменения цены – на отрезке (дуге) кривой спроса. Этот
способ измерения называется дуговой
эластичностью; (2) для определённого уровня цены, то есть в некоторой точке
кривой спроса. Этот способ называется точечной
эластичностью.
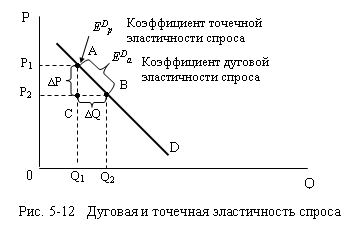
измеряется в ценовом диапазоне Р1
– Р2 на отрезке АВ
кривой спроса, а точечная – для уровня цены Р1 в точке А.
Выведем формулу для дуговой эластичности спроса.
Поскольку в приведенной выше формуле не ясно, какое
значение Q: Q1 или Q2, берётся
за базу, а это может сильно повлиять на результат измерения, экономисты
договорились брать среднее арифметическое значение. То есть, Q = (Q1 + Q2 /2. То же самое делается
по отношению к цене, выступающей в качестве базы: Р = (Р1 + Р2)/2. Тогда формула коэффициента
дуговой эластичности спроса по цене примет окончательный вид:
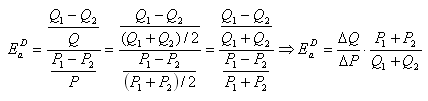
Дуговая эластичность спроса используется в случае
значительного изменения цены. Если же это изменение незначительно, то
целесообразно использовать точечную эластичность спроса. Коэффициент точечной
эластичности спроса легко выводится из формулы (2):
Посмотрим на рис. 5-12 и представим, что ∆P сжимается
так, что точка С приближается
вплотную к точке А. Тогда ∆Q также
сжимается и точка В стремится к точке
А как к своему пределу. Если мы
примем ∆P и, следовательно,
∆Q за
бесконечно малые величины, то получим измерение ценовой эластичности в точке А:
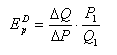
 Математическое приложение 5-2
Математическое приложение 5-2
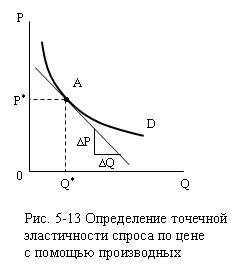
через производные. Предположим, требуется определить ЕDp в точке А кривой спроса на рис. 5-13:
Тогда
при бесконечно малом изменении Р
«скорость» изменения Q
будет dQ/dP и формула примет
вид:
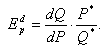
Коэффициент ценовой эластичности спроса
в точке можно определить по уравнению функции
спроса. Линейное уравнение имеет вид: QD = a – bP (например, QD = 10 – 2P). Коэффициент b показывает,
на сколько единиц изменяется величина спроса при изменении цены на 1 рубль (в
нашем примере b = — 2, что
означает, что каждый раз, когда цена изменяется на 1 рубль, величина спроса
изменяется в противоположном направлении на 2 единицы). То есть -b = -∆Q/∆Р = наклону
кривой спроса.
Тогда,
подставив b в уравнение (3) получим:
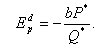
Пример.
Пусть функция спроса описывается
уравнением: QD
= 10 – 2P.
Определить ценовую эластичность спроса при Р* = 4.
Решение:
Подставим в уравнение (5) все данные, получим:
Измерение
точечной эластичности спроса геометрическим способом («правило РАРО»). Есть
простой способ измерения эластичности в любой точке кривой спроса с помощью
линейки. Этот способ известен как «правило РАРО» (PAPO rule).
Правило
РАРО гласит: чтобы
определить точечную эластичность нужно измерить расстояние от точки до
абсциссы, РА (point
– abscissa),
и
расстояние от точки до ординаты, РО (point – ordinate), а
затем отнести первое ко второму, то есть ЕD = РА/РО.
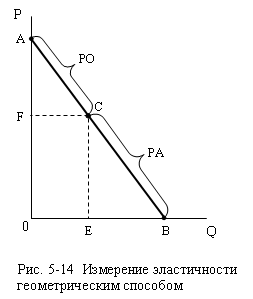
Выведем правило,
используя рис. 5-14. Определим эластичность в точке С.
Так как АОВ и СЕВ – подобные треугольники, то
и
Но (при пересечении сторон угла параллельными прямыми по
сторонам угла отсекаются пропорциональные отрезки).
И,
следовательно
СВ
– это расстояние от точки, в которой измеряется эластичность, до абсциссы (РА),
а СА – это расстояние от той же точки
до ординаты (РО).
На рис. 5-14 РА= 5,5
см., а РО = 4 см. Следовательно, ЕD=
5,5:4 = 1,375.
Правило РАРО универсально. Оно позволяет
определить эластичность спроса по цене, доходу, перекрёстную эластичность
спроса, эластичность предложения. Правило применимо и тогда, когда линии спроса
и предложения являются кривыми. В этом случае отрезки РА и РО находятся на
касательной, проведённой через интересующую нас точку на кривой спроса или
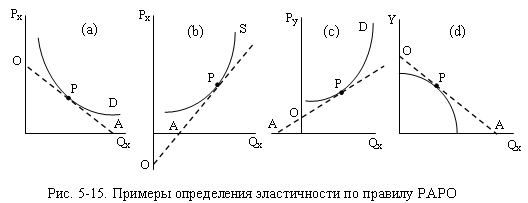
предложения (примеры приведены на рис. 5-15).
На рис. 5-15а спрос
в точке Р имеет единичную эластичность по цене (РА=РО). На рис. 5-15b ценовая
эластичность предложения в точке Р меньше единицы (PA<PO), то есть предложение
неэластично. На рис. 5-15с перекрёстная эластичность спроса на товар Х по цене
товара У больше единицы (PA>PO), то есть спрос эластичен. На
рис. 5-15d спрос на низший товар Х эластичен по доходу У (PA>PO).
Эластичность нельзя
отождествлять с наклоном кривой спроса (наклон линии представляет собой
отношение горизонтального изменения к вертикальному, то есть -∆Q/∆Р.
Рассмотрим рис. 5-16. В каждой точке кривой
спроса наклон одинаков. Поэтому в
формуле (5) — b является постоянной величиной. В то же время отношение P/Q при
движении по кривой спроса меняется. Поэтому эластичность в разных точках кривой
спроса будет разной. Применим «правило РАРО» для расчёта коэффициента
эластичности. В точке А эластичность
равна бесконечности (= АЕ/0). В точке В эластичность больше 1 ( = ВЕ/АВ).
В точке С, которая находится в середине кривой спроса эластичность равна единице (так как СЕ = СА, то СЕ/СА = 1). В точке D она меньше
единицы (= DE/DA). И
наконец, в Е эластичность равна 0 (= 0/AE).
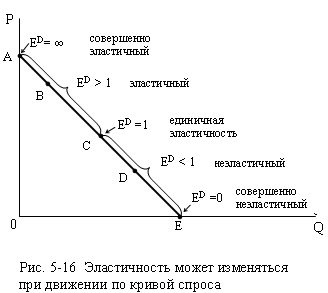
1) горизонтальная кривая спроса (эластичность в каждой точке равна бесконечности);
2) вертикальная кривая спроса (в каждой точке эластичность равна нулю);
3) кривая спроса, имеющая форму равносторонней гиперболы;
В последнем случае кривая описывается уравнением обратной пропорциональности:
,
где
с – есть некоторая постоянная величина.
Применительно к функции спроса уравнение
выглядит:
Тогда, учитывая, что с – это коэффициент при цене, который мы раньше обозначали как b, получим:
Следовательно, кривая спроса, имеющая форму
равносторонней гиперболы, имеет единичную эластичность (в любой её точке
эластичность спроса по цене равна –1).
Почему эластичность спроса по цене для
разных товаров различна? Основные факторы, определяющие эластичность:
1. Наличие
доступных товаров-субститутов. Чем больше таких товаров, тем больше эффект
замещения при изменении цены данного товара и тем эластичнее спрос.
2. Доля
расходов на товар в бюджете потребителя. Чем она больше, тем больше эффект
дохода и тем эластичнее спрос. Это зависимость помогает понять, почему при
высоких ценах (в верхней части кривой спроса) спрос эластичен, а при низких
ценах (нижняя часть кривой спроса) неэластичен. Более высокая цена
означает большую долю в расходах
потребителя при фиксированном бюджете.
3. Направление
эффекта дохода. В случае нормальных товаров эффект дохода усиливает эффект замещения
и спрос становится эластичнее. Для низших товаров эффект дохода ослабляет
действие эффекта замещения и спрос поэтому менее эластичен.
4. Время,
прошедшее после изменения цены. Чем продолжительнее этот период, тем больше
возможности у потребителя найти замещающие товары и тем эластичнее спрос.
повышение средней цены на зерно в России в 2003 году с 2,5 тыс. до 4,5 тыс.руб. за тонну улучшило положение сельхозпроизводителей, увеличив их доходы. В то же время повышение платы за проезд в муниципальном транспорте города Томска в 2003 г. с 3,5 до 4,5 рублей привело к тому, что выручка у Трамвайно-троллейбусного управления значительно упала.
Поскольку выручка определяется как произведение цены товара на количество проданного товара (ТR = P·Q), то результат зависит от того будет ли процентное изменение количества
больше или меньше процентного изменения цены, то есть от ценовой эластичности
спроса. Так, если цена повысится на 10 %, а физический объём продаж вследствие
этого сократится на 20 % (эластичность спроса по цене равна 2,0 – спрос эластичен), то выручка уменьшится.
Общее правило таково: при эластичном спросе доходы (расходы)
изменяются в направлении противоположном изменению цены. При неэластичном
спросе доходы (расходы) изменяются в том же направлении, что и цена. В случае единичной эластичности доход не
изменяется.
Все возможные случаи отражены в таблице 5-1.
|
Эластичность |
Цена |
Цена |
|
Эластичный спрос (>1) |
TR падает |
TR растёт |
|
Единичная эластичность (=1) |
TR не меняется |
TR не меняется |
|
Неэластичный спрос (<1) |
TR растёт |
TR падает |
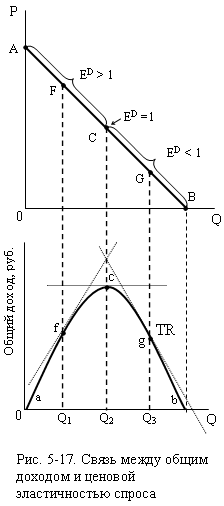
На рис.
5-17 показана связь между общим доходом (расходами) и ценовой эластичностью
спроса. Предположим, что цена товара всё время понижается, и мы движемся по
кривой спроса (на верхнем рисунке) вниз из точки А в точку В. На отрезке АС,
где спрос эластичен, снижение цены будет перекрываться ещё большим ростом (в
процентном отношении) величины спроса. Общий доход, следовательно, будет расти
(участок ас на нижнем рисунке). На
участке СА, где спрос неэластичен дальнейшее снижение цены вызывает уже меньший
рост (в процентном отношении) спроса, и доход падает (участок сb). В точке С, где
эластичный спрос переходит в неэластичный (эластичность равна единице) доход
перестаёт расти, достигая максимума при объёме Q2.
 Математическое приложение 5-3
Математическое приложение 5-3
Связь между ценовой эластичностью спроса и общим доходом можно определить с помощью методов предельного анализа.
Общий доход, TR = P∙Q. Следовательно,
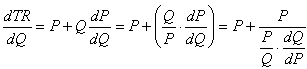
Так как ценовая эластичность спроса равна
(2)
то, подставив (2) в (1), получим:
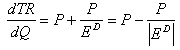
Таким образом, когда спрос эластичен, то есть │ED│ > 1, то
TR изменяется в том же направлении, что и Q, и в направлении противоположном Р (для нормальной, нисходящей кривой спроса).
Когда спрос имеет единичную эластичность, то есть │ED│ = 1, то
TR с изменением Q не меняется.
Когда спрос неэластичен, то есть │ED│ < 1, то
TR изменяется в направлении противоположном Q и в том же направлении что и Р (для нормальной кривой спроса).
Снова обратимся к рис. 5-17. Возьмём на кривой спроса точку F, в которой спрос эластичен. С понижением цены объём спроса будет расти. Изменение общего дохода, обусловленное бесконечно малым увеличением объёма продаж при уровне Q1, то есть dTR/dQ, показывается наклоном касательной к кривой общего дохода в точке f. Этот наклон положителен. Следовательно, общий доход будет увеличиваться.
При единичной эластичности спроса (точка С), наклон касательной к кривой общего дохода в точке с будет равен 0. Следовательно общий доход при объёме продаж Q2, не изменяется ни в сторону увеличения, ни в сторону уменьшения. Он достигает максимума.
Наконец, при неэластичном спросе, к примеру, в точке G, при снижении цены общий доход будет уменьшаться. Об этом говорит отрицательный наклон касательной к кривой общего дохода в точке g.
Содержание:
- Эластичность функции
- Определение и свойства эластичности функций
- Свойства эластичности функции
- Эластичность спроса относительно цены
- Эластичность предложения относительно цены
Эластичность функции
В экономических исследованиях приросты тех или иных показателей, характеризующих экономические процессы, чаще всего выражают в процентах к базовым значениям. Поэтому и изменение величин, которые связаны с ними функциональной зависимостью, также выражают в процентах. Для этого используют понятие эластичности функции, которое выражается через производную функции.
Определение и свойства эластичности функций
Пусть задана функция y = f (x). Если аргумент x получил приращение Δx и при этом функция y получила приращение Δy, то 

Определение. Предел отношения относительного приращения функции к относительному приращению аргумента при условии, что приращение аргумента стремится к нулю, если существует, называется эластичностью функции.
Обозначают эластичность функции y = f (x) относительно переменной x Ex(y). То есть,
Итак, если в точке x функция имеет производную, то эластичность определяется формулой 
Эластичность выражает приближенный процент приращения функции, который соответствует 1 % приращения аргумента.
Пример. Найти эластичность функции y = x2 – 4 x +7 и вычислить ее при x = 1, x = 2, x = 5.
Решение.
Итак, если x вырастет на 1 % с 1 до 1,01, то y снизится на 0,5 %. Если x вырастет на 1 % с 2 до 2,02, то значение переменной y практически не изменится. Если x вырастет на 1 % с 5 до 5,05, то y вырастет на 2,5 %.
Свойства эластичности функции
ТЕОРЕМА 1. Эластичность произведения двух функций равна сумме эластичности сомножителей:
Ex (U ⋅ V) = Ex (U) + Ex (V).
Доказательство. По определению эластичности
ТЕОРЕМА 2. Эластичность частного двух функций равна разности показателей эластичности делимого и делителя:
Доказательство. По определению эластичности
Эластичность спроса относительно цены
В анализе и прогнозах ценовой политики применяется понятие эластичности спроса и предложения.
Пусть p цена одного изделия, а Q — количество изделий, произведенных и проданных через некоторое время, что определяет спрос. Величина Q зависит от цены, т. е. Q является функцией от p: Q = f (p).
Пусть приращение цены Δp вызывает приращение ΔQ. тогда относительные приращения цены и спроса будут соответственно 
Отношение 
Эластичностью спроса относительно цены называется предел отношения относительного приращения спроса к относительному приращению цены при условии, что приращение цены стремится к нулю.
Эластичность спроса относительно цены приближенно определяет, как меняется спрос на данное изделие, если его цена возрастает на 1 %.
Так, например, если рост цены на 5 % вызывает падение спроса на 8 %, то эластичность будет
Если эластичность спроса η = –0,5, то 10 % роста стоимости товара вызывает падение спроса на (–0,5) 10% = –5%.
Определение. Если процент изменения спроса больше процента изменения цены (η < 1), то спрос называют эластичным, если процент изменения спроса меньше процента изменения цены (-1 < η < 0), то спрос называют не эластичным, а если процент изменения спроса равен проценту изменения цены (η = 1), то спрос называют нейтральным.
Пример. Установлено, что количество произведенных и проданных изделий Q по цене p определяется по формуле Q = 10000 – 500p (0 < p < 20). Определить, при какой цене спрос эластичный, нейтральный, не эластичный.
Решение. Эластичность спроса относительно цены
Спрос будет эластичным, если η < –1, 

Спрос нейтральный при цене p = 10 (руб.). Спрос будет не эластичный, когда -1 < η < 0.
Итак, спрос не эластичный при цене меньшей 10 руб. за изделие.
Пример 2. Установить связь между доходом предприятия и эластичностью спроса от цены.
Решение. Доход определяется как произведение стоимости каждого изделия на количество произведенных и проданных изделий Q : D (Q) = p⋅ Q.
Найдем маржинальный доход, учитывая, что Q есть функция от p.
Если η ≤ –1, то 1 + η < 0, а 
Если –1 < η < 0, то 1 + η > 0, а
То есть функция D (Q) дохода растет с ростом цены p, когда спрос не эластичный.
Эластичность предложения относительно цены
Понятие эластичности можно применять и к другим функциям экономического содержания.
Рассмотрим понятие эластичности предложения S в зависимости от цены товара p. Под предложением понимают количество некоторого товара, который предлагается на продажу за единицу времени. Как правило, предложение какого-либо товара является возрастающей функцией цены. Но бывают случаи, когда предложение повышается со снижением цены. Величина S является функцией от цены товара. То есть, S = S (p).
Пусть Δp — приращение цены, а ΔS — соответствующее приращение предложения. Тогда относительные приращения цены и предложения будут соответственно 

Эластичностью предложения относительно цены называется предел отношения относительного приращения предложения к относительному приращению цены при условии, что приращение цены стремится к нулю.
Эластичность предложения относительно цены приближенно определяет процент приращения предложения на 1 % приращения цены.
Пример 3. Функция предложения некоторого товара 
Решение.
Если p = 2, то
Следовательно, при цене p = 2 увеличение ее на 1 % вызовет увеличение предложения на 0,2 %.
Лекции:
- Разностные уравнения
- Случайная вероятность
- Эквивалентные бесконечно малые функции. Сравнение бесконечно больших функций
- Решение определённых интегралов
- Параллельные прямые
- Экстремум функции многих переменных
- Пределы в математике
- Дифференциал функции
- Объемы подобных фигур
- Алгебра логики