mat:geom:triangle-area
Содержание
Площадь треугольника

-
R — радиус описанной окружности
-
r — радиус вписанной окружности
-
p — полупериметр, $p = frac{a+b+c}{2}$
-
Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними.
-
Площадь треугольника равна произведению сторон, деленному на 4 радиуса описанной окружности.
-
Площадь треугольника по трем высотам легко выводится из формулы Герона
-
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.

$$ begin{align} mbox{По высоте: } ; & S = frac12 a cdot h_a \[10pt]
mbox{По произведению сторон: } ; & S = frac{abc}{4R} \[10pt]
mbox{По полупериметру: } ; & S = p cdot r \[10pt]
mbox{По двум сторонам: } ; & S = frac12 cdot a cdot b cdot sin{gamma} \[12pt]
mbox{Формула Герона: } ; & S = sqrt {p(p-a)(p-b)(p-c)} \[12pt]
mbox{По высотам: } ; & S = frac{1}{sqrt {(frac1{h_a}+frac1{h_b}+frac1{h_c})(-frac1{h_a}+frac1{h_b}+frac1{h_c})(frac1{h_a}-frac1{h_b}+frac1{h_c})(frac1{h_a}+frac1{h_b}-frac1{h_c})}} \[12pt]
mbox{По высотам и радиусу: } ; & S = frac{r}{sqrt3} (h_a+h_b+h_c) \[12pt]
mbox{По трем углам: } ; & S = 2R^2 sin{alpha} cdot sin{beta} cdot sin{gamma}
end{align} $$
$
$
Формула Герона
Интерактивная модель и калькулятор
Формула Герона для треугольника — это частный случай формулы Брахмагупты для четырехугольника, вписанного в окружность (одну из сторон положить равной 0):
$S={sqrt {(p-a)(p-b)(p-c)(p-d)}}$
где p — полупериметр четырехугольника
Треугольник является предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю.
Формула Пика
Площадь треугольника, нарисованного на клетчатой бумаге.
Если треугольник нарисован на клетчатой бумаге и все его вершины находятся в углах сетки, то площадь его можно вычислять по формуле Пика:
$$S = V+frac{G}{2}-1,$$
где $V$ — количество узлов сетки, находящихся внутри треугольника, $G$ — количество узлов сетки, находящихся на границе треугольника.

Подробнее — см. ниже Теорема Пика.

Целочисленные площади

Задача
Вычислить площадь Бермудского треугольника.
Бермудский Треугольник — широко известная аномальная зона. Расположен он в границах между Бермудскими островами, Майями во Флориде и Пуэрто-Рико.
Расстояние между вершинами треугольника в милях
| Norfolk | Bermuda | 850 |
| Bermuda | Santiago | 810 |
| Norfolk | Santiago | 894 |
В расчетах игнорировать кривизну поверхности Земли.
Задача
Может ли треугольник со сторонами больше километра иметь площадь, меньшую 1 мм²?
Теорема Пика. Нахождение площади решётчатого многоугольника
http://e-maxx.ru/algo/pick_grid_theorem
Многоугольник без самопересечений называется решётчатым, если все его вершины находятся в точках с целочисленными координатами (в декартовой системе координат).
Пусть дан некоторый решётчатый многоугольник, с ненулевой площадью.
Обозначим его площадь через $S$; количество точек с целочисленными координатами, лежащих строго внутри многоугольника — через $I$; количество точек с целочисленными координатами, лежащих на сторонах многоугольника — через $B$.
Тогда справедливо соотношение, называемое формулой Пика:
$$S = I -B/2 + 1$$
В частности, если известны значения $I$ и $B$ для некоторого многоугольника, то его площадь можно посчитать за $O(1)$, даже не зная координат его вершин.
Это соотношение открыл и доказал австрийский математик Георг Александр Пик (Georg Alexander Pick) в 1899 г.
Доказательство
Доказательство производится в несколько этапов: от самых простых фигур до произвольных многоугольников:
-
Единичный квадрат. В самом деле, для него S=1, B=4, I=0, и формула верна.
-
Произвольный невырожденный прямоугольник со сторонами, параллельными осям координат. Для доказательства формулы обозначим через $a$ и $b$ длины сторон прямоугольника. Тогда находим: $S=ab$, $I=(a-1)(b-1)$, $B=2(a+b)$. Непосредственной подстановкой убеждаемся, что формула Пика верна.
-
Прямоугольный треугольник с катетами, параллельными осям координат. Для доказательства заметим, что любой такой треугольник можно получить отсечением некоторого прямоугольника его диагональю. Обозначив через C число целочисленных точек, лежащих на диагонали, можно показать, что формула Пика выполняется для такого треугольника, независимо от значения C.
-
Произвольный треугольник. Заметим, что любой такой треугольник может быть превращён в прямоугольник приклеиванием к его сторонам прямоугольных треугольников с катетами, параллельными осям координат (при этом понадобится не более 3 таких треугольников). Отсюда можно получить корректность формулы Пика для любого треугольника.
-
Произвольный многоугольник. Для доказательства триангулируем его, т.е. разобьём на треугольники с вершинами в целочисленных точках. Для одного треугольника формулу Пика мы уже доказали. Дальше, можно доказать, что при добавлении к произвольному многоугольнику любого треугольника формула Пика сохраняет свою корректность. Отсюда по индукции следует, что она верна для любого многоугольника.
Задача
Обобщение на высшие размерности
К сожалению, эта столь простая и красивая формула Пика плохо обобщается на высшие размерности.
(подробнее по ссылке на источник)
Как можно найти I и B на практике?
$B = gcd(abs(x_0-x_1),abs(y_0-y_1)) — 1$, где $gcd$ — наибольший общий делитель, $(x_0;y_0), (x_1;y_1)$ — точки, соединённые стороной многоугольника.
тут интересно находить не площадь, а количество точек внутри, потому что другого алгоритма я не видел для подсчета этого количества.
Литература:
Учебники:
Площадь треугольника по высоте, проведенной к стороне — Геометрия 8 класс
Геометрия 9 класс Мерзляк, параграф 1 — формула Герона, по произведению сторон, через радиус вписанной и описанной окружности
· Последние изменения: 2020/02/21 17:21 —
kc
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
— полупериметр треугольника; a,b,c — стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a — основание треугольника; h — высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b — стороны треугольника; α — угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a— сторона треугольника; α и β — прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b — катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b — стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a — основание равнобедренного треугольника; α — угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a — сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h — высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r — радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r — радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c — стороны треугольника; r — радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p — полупериметр треугольника;a, b, c — стороны треугольника; r — радиус вписанной окружности треугольника.
Площадь треугольника. Онлайн-калькулятор
Онлайн-калькулятор для расчета площади треугольника поможет Вам найти площадь треугольника несколькими способами в зависимости от известных данных. Наш калькулятор не просто рассчитает площадь треугольника, но и покажет подробное решение, которое будет показано под калькулятором. Поэтому данный калькулятор удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений. С помощью данного калькулятора вы сможете найти площадь треугольника по следующим формулам: через основание и высоту, через две стороны и угол, по трем сторонам (формула Герона), через радиус вписанной окружности, через радиус описанной окружности.
Выберите способ расчета площади:
Основание треугольника:
a =
Рассчитать
Треугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).
Как найти площадь треугольника?
Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулой площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:
1) через основание и высоту
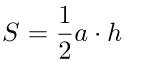
a – основание треугольника,
h – высота треугольника.
2) через две стороны и угол
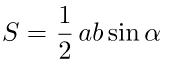
a, b – стороны треугольника,
α – угол между сторонами.
3) По трем сторонам. Формула Герона.
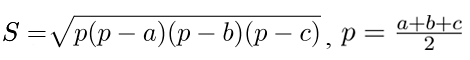
a, b, с – стороны треугольника,
p – полупериметр треугольника.
4) Через радиус вписанной окружности.
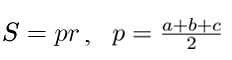
a, b, с – стороны треугольника,
p – полупериметр треугольника,
r – радиус вписанной окружности.
5) Через радиус описанной окружности.
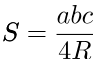
a, b, с – стороны треугольника,
R – радиус описанной окружности.
Вы всегда сможете проверить правильность расчета площади треугольника с помощью нашего калькулятора.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
33 395
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
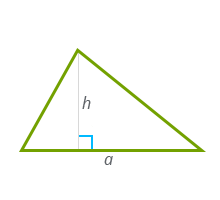
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
Делайте так:
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
( 32 оценки, среднее 4.44 из 5 )
Оцените статью
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯ
1. Составить равенства на основании равенства площадей.
2. Выразить две стороны через одну.
3. Подставить выражения в формулу Герона.
4. Приравнять к формуле площади треугольника по стороне и высоте.
5. Найти сторону.
6. Вычислить площадь по п. 4.
Все вопросы в агент.
Можно решить эту задачу вообще не используя формулу Герона.
Есть такая формула 1/r = 1/ha + 1/hb + 1/hc где r — радиус вписанной окружности, а ha, hb, hc — соответствующие высоты треугольника.
И использовать (после нахождения радиуса) формулу площади через радиус и полупериметр.










