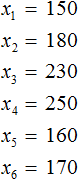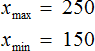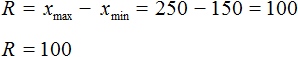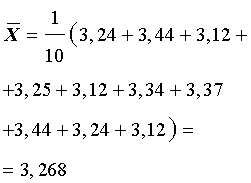Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
n = 6
Элементы выборки обозначаются с помощью переменных с индексами . Последний
элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.
Обозначим элементы нашей выборки через переменные
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?
Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.
Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
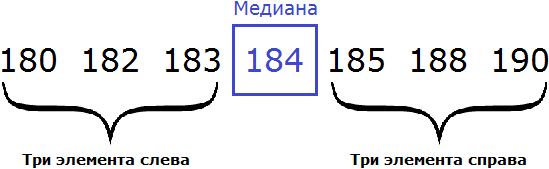
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
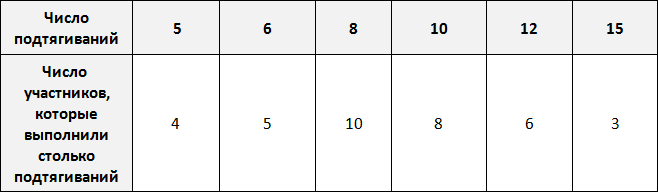
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:
Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:
Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:
Выполним деление в этих дробях:
Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:
Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:
(8.16 – формула Моды)
где хо – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1– частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:

где хо – нижняя граница медианного интервала;
NМе– порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число
семей |
Накоп-
ленные частоты |
в % к итогу |
| До 5000 | 600 | 600 | 6 |
| 5000-6000 | 700 | 1300
(600+700) |
13 |
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 )
(1300+1700) |
30 |
| 7000-8000
(хо) |
2500
(fМо) (fМе) |
5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 |
| 9000-10000 | 1500 | 9200 | 92 |
| Свыше 10000 | 800 | 10000 | 100 |
| Итого | 10000 | – | – |
Пример вычисления Моды. Найдем моду по формуле (8.16) см. обозначения в таблице, а h = 8000-7000=1000, т.е. получаем:
Пример вычисления Моды
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):
Пример вычисления Медианы
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Пример .СРЕДНИЙ, МЕДИАННЫЙ И МОДАЛЬНЫЙ УРОВЕНЬ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ ЦЕЛОМ ПО РОССИИ И ПО СУБЪЕКТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ЗА 2013 год см. по ссылке. Источник: оценка на основании данных выборочного обследования бюджетов домашних хозяйств и макроэкономического показателя денежных доходов населения
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если Мо<Ме<Х – имеет место правосторонняя асимметрия.
При Х<Ме<Мо следует сделать вывод о левосторонней асимметрии ряда.
Средние величины (арифметическая, гармоническая, геометрическая, квадратическая) см. по ссылке
Оценка статьи:
Загрузка…
Мода и медиана
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
Обратимся снова к нашему примеру со сборной по футболу:
Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке?
Все верно, это число ( displaystyle 181), так как два игрока имеют рост ( displaystyle 181) см; рост же остальных игроков не повторяется.
Тут все должно быть ясно и понятно, да и слово знакомое, правда?
Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») — отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.
Ключевое слово – СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.
Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания).
Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить.
Ну что, вернемся к нашей выборке футболистов?
Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»!
Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому).
Вот, что у меня получилось:
Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке.
Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное?
Все верно – игроков ( displaystyle 11), значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке.
Ищем число, которое оказалось посередине в нашем упорядоченном ряду:
Ну вот, чисел у нас ( displaystyle 11), значит, по краям остается по пять чисел, а рост ( displaystyle 183) см будет медианой в нашей выборке.
Не так уж и сложно, правда?
Частота и относительная частота
Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:
Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост ( 176)?
Все верно, один игрок. Таким образом, частота встречи игрока с ростом ( 176) в нашей выборке равна ( 1).
Сколько игроков имеет рост ( 178)? Да, опять же один игрок. Частота встречи игрока с ростом ( 178) в нашей выборке равна ( 1).
Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:
Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки).
То есть в нашем примере: ( 1+1+1+2+1+1+1+1+1+1=11)
Перейдем к следующей характеристике – относительная частота.
Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.
Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем ( left( n=11 right)) .
Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:
А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Оглавление страницы:
Статистика. Числовые характеристики ряда чисел
Средним арифметическим нескольких чисел называется число, равное отношению суммы этих чисел к их количеству.
Другими словами, среднее арифметическое – это дробь, в числителе которой стоит сумма чисел, а взнаменателе – их количество.
Пример:
- Вычислить среднее арифметическое данных чисел: 6, 10, 16, 20.
Среднее арифметрическое: ( 6 + 10 + 16 + 20 ) 4 = 52 4 = 13
Медиана ряда чисел – это число, стоящее посередине упорядоченного ряда чисел, если количество чисел в ряду нечётное.
Пример:
- Найти медиану ряда чисел: 12, 2, 11, 3, 7, 10, 3
Сперва упорядочим этот ряд (расположим числа в порядке возрастания, от меньшего к большему): 2, 3, 3, 7 , 10, 11, 12
Посередине данного упорядоченного ряда стоит число 7.
Медиана ряда чисел – это полусумма двух стоящих посередине упорядоченного ряда чисел, если количество чисел в ряду чётное.
Пример:
- Найти медиану ряда чисел: 8, 3, 10, 1, 16, 2, 3
Сперва упорядочим этот ряд (расположим числа в порядке возрастания, от меньшего к большему): 2, 3, 7 , 10 , 11, 12
Посередине данного упорядоченного ряда стоят два числа: 7 и 10.
Их полусумма равна: 7 + 10 2 = 17 2 = 8,5
Размах ряда чисел – это разность между наибольшим и наименьшим числом.
Пример:
- Найти размах ряда чисел: 8, 3, 10, 1, 16, 2, 3
Для удобства упорядочим этот ряд: 1, 2, 3, 3, 8, 10, 16
Наибольшее значение ряда: 16. Наименьшее значение ряда: 1.
Размах: 16 − 1 = 15
Мода ряда чисел – наиболее часто встречающееся число в этом ряду.
Ряд чисел может иметь более одной моды, а может вообще не иметь моды.
Примеры:
- Найти моду ряда: 1, 5, 6, 3 , 10, 32, 4, 3
Число, встречающееся в этом ряду чаще всех: 3.
Данный ряд имеет моду: 3.
- Найти моду ряда: 5, 2, 3, 4, 1, 0, 8
Каждое число в данном ряде встречается одинаковое количество раз (один раз).
Данный ряд не имеет моды.
- Найти моду ряда: 9 , 1 , 4 , 10 , 17 , 1 , 33 , 6 , 9 , 8 , 5 , 5
Числа 1, 5, 9 встречаются в этом ряде наибольшее количество раз (по два раза).
Данный ряд имеет три моды: 1, 5, 9.
Вероятности
Случайное событие – это событие, которое может произойти, а может не произойти.
Мы называем событие случайным, если нельзя утверждать, что это событие в данных обстоятельствах непременно произойдёт.
События обозначаются заглавными латинскими буквами.
Частота случайного события A в серии опытов – это отношение числа тех опытов, в которых событие A произошло, к общему числу проведенных опытов.
Примеры:
- Какова частота события «выпал орёл», если в серии опытов из 20 бросков монеты решка выпала 8 раз?
Если решка выпала 8 раз, то орёл выпал 20 − 8 = 12 раз.
Частота: 12 20 = 6 10 = 0,6
- Какова частота события «выпало чётное число очков» в серии опытов из восьми бросков кубика, если результаты представлены в виде числового ряда: 3, 2, 3, 5, 1, 1, 6, 4
Как мы видим, чётных чисел выпало три штуки.
Частота: 3 8 = 0,375
Каждое случайное событие делится на несколько элементарных исходов. Они делятся на благоприятные исходы и неблагоприятные исходы.
Например, для события «выпало четное число очков» при броске кубика:
- Благоприятные исходы:
«выпало два очка», «выпало четыре очка», «выпало шесть очков»
- Неблагоприятные исходы:
«выпало одно очко», «выпало три очка», «выпало пять очков»
Все возможные исходы = благоприятные исходы + неблагоприятные исходы.
Вероятность случайного события P ( A ) – это отношение благоприятных исходов m к общему числу исходов n. P ( A ) = m n
Вероятность случайного события лежит в пределах от 0 до 1. 0 ≤ P ( A ) ≤ 1
Сумма вероятностей всех элементарных исходов случайного эксперимента равна 1.
Примеры:
- Какова вероятность вытащить из шляпы, в которой лежат три синих шара, белого кролика?
Число благоприятных исходов: m = 0 , так как ни одного кролика нет.
Число всех возможных исходов: n = 3 , так как есть три объекта, которые можно достать из шляпы.
A=«достать кролика», посчитаем вероятность этого события. P ( A ) = m n = 0 3 = 0
- Какова вероятность вытащить из шляпы, в которой лежат три синих шара, синий шар?
Число благоприятных исходов: m = 3 , так как каждый из трех шариков синий, каждый подходит.
Число всех возможных исходов: n = 3 , так как есть три объекта, которые можно достать из шляпы.
A=«достать синий шар», посчитаем вероятность этого события. P ( A ) = m n = 3 3 = 1
- Какова вероятность вытащить из шляпы, в которой лежат три синих шара и девять красных шаров, синий шар?
Число благоприятных исходов: m = 3 , так как всего синих шаров в шляпе три.
Число всех возможных исходов: n = 3 + 9 = 12 , так как всего в шляпе 12 объектов, которые можно достать.
A=«достать синий шар», посчитаем вероятность этого события. P ( A ) = m n = 3 12 = 0,25
Событие A ¯ называется противоположным событию A, если событие A ¯ происходит тогда, когда событие A не происходит (то есть вместо события A происходит событие A ¯ ).
Примеры противоположных событий:
- A : «купить молоко», A ¯ : «не купить молоко»
- A : «прибор исправен», A ¯ : «прибор неисправен»
- A : «выпал орёл», A ¯ : «выпала решка»
- A : «на игральной кости выпало нечетное число», A ¯ : «на игральной кости выпало чётное число»
Вероятность противоположного события определяется по формуле: P ( A ¯ ) = 1 − P ( A )
Примеры:
- Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,28. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Пусть событие A: «ручка пишет плохо».
Противоположное событие: A ¯ : «ручка пишет хорошо»
P ( A ) = 0,28. Найдём вероятность противоположного события по формуле:
P ( A ¯ ) = 1 − P ( A ) = 1 − 0,28 = 0,72
- В среднем из 100 карманных фонариков, поступивших в продажу, 8 неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
Пусть событие A: «фонарик неисправен»
Противоположное событие A ¯ : «фонарик исправен»
P ( A ) = 8 100 = 0,08
P ( A ¯ ) = 1 − P ( A ) = 1 − 0,08 = 0,92
Ответ: 0,92
Теоремы о вероятностных событиях
Два события называются несовместными, если они не могут произойти одновременно, то есть если наступление одного из них исключает наступление другого. В противном случае события называются совместными.
Примеры несовместных событий:
- Выпадение 1, выпадение 5, выпадение 6 при бросании кости
За один бросок может выпасть либо 1, либо 5, либо 6. Одновременно два или три значения выпасть не могут, только одно.
- Выпадение орла, выпадение решки при броске монеты
За один бросок может выпасить либо орёл, либо решка, одновременно орёл и решка выпасть не могут.
Теорема сложения вероятностей несовместных событий:
Вероятность появления одного из двух (или более) несовместных событий равна сумме вероятностей этих событий.
P ( A + B ) = P ( A ) + P ( B )
Примеры:
- Паша на экзамене вытягивает билет. Все билеты относятся к одной из трех тем: «углы», «треугольники», «четырехугольники». Вероятность того, что Паше попадется билет по теме «треугольники» равна 0,22, вероятность того, что ему попадется билет по теме «четырехугольники» равна 0,31, вероятность того, что ему попадется билет по теме «углы» равна 0,47. Паша знает тему «углы» и тему «треугольники», но «четырехугольники» вызывают у него затруднения. Найдите вероятность того, что ему попадется билет по теме «треугольники» или по теме «углы».
Решение:
Событие A = «вытащить билет по теме углы» и событие B = «вытащить билет по теме треугольники» – несовместные.
Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:
P ( A + B ) = P ( A ) + P ( B )
P ( A + B ) = 0,47 + 0,22 = 0,69
Ответ: 0,69
- Макар играет в лотерею. Вероятность выиграть стиральную машину равна 0,001, вероятность выиграть денежный приз 0,013, вероятность выиграть сувенир 0,04. Найдите вероятность того, что лотерейный билет принесёт Макару какой-нибудь приз.
Решение:
Событие A = «выиграть машину», событие B = «выиграть денежный приз» и событие C = «выиграть сувенир» несовместные.
Вероятность появления одного из трех несовместных событий равна сумме вероятностей этих событий:
P ( A + B + C ) = P ( A ) + P ( B ) + P ( C )
P ( A + B + C ) = 0,001 + 0,013 + 0,04 = 0,054
Ответ: 0,054
Два события называются независимыми, если наступление одного из них не влияет на вероятность наступления другого. В противном случает события называются зависимыми.
Примеры независимых событий:
- Игральный кубик бросают два раза. Выпадение трех очков при первом броске и выпадение четырех очков при втором броске являются независимыми событиями.
При первом броске вероятность выпадания трех очков равна 1 6 , при втором броске вероятность выпадания четырех очков снова равна 1 6 . Не смотря на то, что кубик кидают два раза, у него по-прежнему остаётся шесть граней, при каждом новом броске может выпасть одно из шести чисел с той же самой вероятностью 1 6 , вне зависимости от того, что выпадало до этого.
- Монету бросают три раза. Выпадение орла при первом броске, выпадение орла при втором броске, выпадение орла при третье броске явлюятся независимыми событиями.
При первом броске вероятность выпадения орла равна 0,5, при втором броске вероятность выпадения орла равна 0,5, при третьем броске вероятность выпадения орла равна 0,5. Не смотря на то, что монету кидают несколько раз, при каждом новом броске может выпасть орёл или решка с той же самой вероятностью 0,5, вне зависимости от того, что выпадало до этого.
Примеры зависимых событий:
- В шляпе лежат три синих шара и два красных. Последовательно извлекются два шара. Извлечь в первый раз синий шар и извлечь во второй раз синий шар – два зависимых события.
Почему же они зависимые? Потому что первоначально вероятность вытащить синий шар равна 3 5 (всего шаров 5, синих 3). После того, как один синий шар вытащили, количество благоприятных исходов изменилась, общее количество шаров изменилось. При следующем вынимании шара из шляпы вероятность вытащить синий шар равна 2 4 = 1 2 (всего шаров 4, синих 2). Таким образом наступление первого события влияет на вероятность наступления второго.
Теорема умножения вероятностей независимых событий:
Вероятность появления двух (или более) независимых событий равна произведению вероятностей этих событий.
P ( A ⋅ B ) = P ( A ) ⋅ P ( B )
Примеры:
- В первой шляпе лежит один синий шар и один красный, во второй шляпе лежит 1 синий шар и 4 красных. Из каждой шляпы извлекли по одному шару. Найдите вероятность того, что оба шара красные.
Решение:
Событие A: «извлечь красный шар из первой шляпы».
Событие B: «извлечь красный шар из второй шляпы».
Оба этих события независимы друг от друга, так как при извлечении шпара из первой шляпы, вторая остаётся нетронутой. Найдём вероятности этих событий.
P ( A ) = 1 2 (всего шаров два, красных – один).
P ( B ) = 4 5 (всего шаров пять, красных четыре).
P ( A ⋅ B ) = P ( A ) ⋅ P ( B )
P ( A ⋅ B ) = 1 2 ⋅ 4 5 = 0,4
Ответ: 0,4
- Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся.
Решение:
Событие A: «попадание», событие B: «промах». По условию P ( A ) = 0,9. Найдём вероятность промаха, она равна
P ( B ) = 1 − P ( A ) = 1 − 0,9 = 0,1
Каждый из выстрелов – событие, не зависящее от предыдущих или последующих выстрелов, то есть все три события – независимые. Вероятность появления трех независимых событий равна произведению их вероятностей, то есть
P ( A ⋅ A ⋅ B ) = P ( A ) ⋅ P ( A ) ⋅ P ( B )
P ( A ⋅ A ⋅ B ) = 0,9 ⋅ 0,9 ⋅ 0,1 = 0,081
Ответ: 0,081
Симметричная монета в теории вероятности

Математическая монета, которая используется в теории вероятности, лишена многих качеств бычной моенты: цвета, размера, веса и достоинства. Она не сделана ни из какого материала и не может служить платёжным средством. Монета имеет две стороны, одна из которых орёл (О), а другая решка (Р). Монету бросают и она падает одной стороной вверх. Никаких других свойств у монеты нет. Рассмотрим различные опыты с монетой
Бросание одной монеты
Возможные исходы:
О
Р
Всего два исхода. Вероятность каждого исхода из двух возможных равна 1 2 = 0,5
Бросание двух монет (бросание одной монеты два раза подряд)
Возможные исходы:
О О
О Р
Р О
Р Р
Всего четыре исхода. Вероятность каждого исхода из четырех возможных равна 1 4 = 0,25
Бросание трех монет (бросание одной монеты три раза подряд)
Возможные исходы:
О О О
О О Р
О Р О
О Р Р
Р О О
Р О Р
Р Р О
Р Р Р
Всего восемь исходов. Вероятность каждого исхода из восьми возможных равна 1 8 = 0,125
Бросание четырех монет (бросание одной монеты четыре раза подряд)
Возможные исходы:
О О О О
О О О Р
О О Р О
О О Р Р
О Р О О
О Р О Р
О Р Р О
О Р Р Р
Р О О О
Р О О Р
Р О Р О
Р О Р Р
Р Р О О
Р Р О Р
Р Р Р О
Р Р Р Р
Всего шестнадцать исходов. Вероятность каждого исхода из шестнадцати возможных равна 1 16 = 0,0625
Примеры:
- Симметричную монету бросают три раза подряд. Какова вероятность, что решка выпадет ровно один раз?
Решение:
Всего восемь различных исходов (см. опыт с бросанием трех монет). Исходов, в которых решка выпала ровно один раз, три.
P = 3 8 = 0,375
Ответ: 0,375
- Cимметричную монету бросают четыре раза подряд. Найдите вероятность того, что орёл выпадет хотя бы два раза.
Решение:
В опыте с бросанием четырех монет всего шестнадцать различных исходов. Благоприятные исходы – те, в которых выпало два, три или четыре орла. Таких исходов всего одиннадцать.
P = 11 16 = 0,6875
Ответ: 0,6875
Симметричная игральная кость в теории вероятности
Математическая игральная кость, которая используется в теории вероятности, это правильная кость, у которой шансы на выпадение каждой грани равны. Подобно математической монете, математическая кость не имеет ни цвета, ни размера. Ни веса, ни иых материальных качеств. Рассмотрим различные опыты с игральной костью.
Бросание одной кости
Возможные исходы: 1, 2, 3, 4, 5, 6. Всего шесть исходов. Вероятность каждого исхода из шести возможных равна 1 6 .
Бросание двух костей (бросание одной кости два раза подряд)
Для того, чтобы перебрать все возможные варианты, составим таблицу:
Первое число в паре – количество очков, выпавших на первом кубике. Второе число в паре – количество очков, выпавших на втором кубике. Всего возможно тридцать шесть различных исходов.
Такую таблицу не составит труда нарисовать на экзамене, если попадётся задача на бросание двух кубиков. Сумма чисел в ячейке – сумма выпавших очков.
Примеры:
- Какова вероятность, что сумма очков при бросании двух кубиков, будет равна 7?
Решение:
Как видно из таблицы, всего 36 различных вариантов выпадания очков на двух кубиках. Благоприятных вариантов – когда сумма очков будет равна семи – всего 6.
P = 6 36 = 1 6
Ответ: 1 6
- Какова вероятность, что сумма очков при бросании двух кубиков, будет меньше десяти?
Решение:
Как видно из таблицы, всего 36 различных вариантов выпадания очков на двух кубиках. Благоприятные варианты – когда сумма очков будет равна 1, 2, 3, 4, 5, 6, 7, 8, или 9. Таких ячеек в таблице 30.
P = 30 36 = 5 6
Ответ: 5 6
Статистические исследования числовых рядов. Статистические характеристики числовых рядов
Очень часто из-за дороговизны или слишком большого числа наблюдений невозможно получить полной информации об объектах, событиях или наблюдениях. По этой причине информацию получают на основе анализа части всего множества объектов, событий или наблюдений, называемой рядом числовых данных, рядом выборочных данных или, просто, выборкой.
Выборка представляет собой конечный ряд чисел (выборочных данных), количество чисел в котором называют объемом выборки
Для обеспечения достоверности информации об объектах, событиях или наблюдениях, полученных на основе статистических исследований числовых рядов (анализа выборочных данных), отбор выборочных данных должен носить случайный характер и иметь достаточно большой объем, то есть выборка должны быть репрезентативной (представительной).
Статистические исследования числовых рядов (рядов чисел, рядов выборочных данных) удобно проводить в соответствии со следующей схемой, которую мы изложим на примере следующей выборки X :
| X = {3,24; 3,44; 3,12; 3,25; 3,12; 3,34; 3,37; 3,44; 3,24; 3,12} | (1) |
-
Определяем объем выборки (число чисел в числовом ряде).
В числовом ряде (1) десять чисел, поэтому объем выборки равен 10.
-
Вычисляем среднее арифметическое числового ряда X (среднее выборочное значение), которое обозначают
.
Для числового ряда (1)
-
Производим упорядочение числового ряда по возрастанию (ранжирование числовых данных). Полученный числовой ряд, который обозначим X1 , называют вариационным рядом.
Для числового ряда X вариационный ряд X1 имеет следующий вид:
X1 = {3,12; 3,12; 3,12; 3,24; 3,24; 3,25; 3,34; 3,37; 3,44; 3,44}
-
Вычисляем размах числового ряда X , то есть разность между наибольшим числом из числового ряда и наименьшим числом из числового ряда.
В числовом ряде X , как и в вариационном ряде X1 , число 3,44 является наибольшим числом, а число 3,12 является наименьшим числом. Поэтому размах числового ряда X равен
3,44 – 3,12 = 0,32
-
Вычисляем медиану числового ряда.
В случае, когда объем выборки (число членов числового ряда) – чётное число, медианой числового ряда является число, равное половине суммы двух чисел, стоящих в середине вариационного ряда.
Число членов ряда X равно чётному числу 10 , а в середине вариационного ряда X1 стоят числа 3,24 и 3,25 . Поэтому медиана числового ряда, которую обычно обозначают символом Me , равна
В случае, когда объем выборки (число членов числового ряда) –нечётное число, медианой числового ряда является число, стоящее в середине вариационного ряда.
Например, медианой числового ряда
{2; 3; 7; 9; 15}
является число 7 .
-
Составляем таблицу частот числового ряда.
Если взглянуть на числа (выборочные данные), составляющие вариационный ряд X1 , то можно заметить, некоторые числа повторяются, а другие встречаются лишь по одному разу. Это наблюдение приводит к следующему определению.
ОПРЕДЕЛЕНИЕ 1. Если выборочное данное встречается в вариационном ряде m раз, то число m называют частотой (абсолютной частотой) этого выборочного данного.
Воспользовавшись определением 1, сформируем для числового ряда X таблицу, содержащую две строки, которую называют таблицей частот (абсолютных частот) числового ряда. Для этого в первой строке таблицы запишем числа, составляющие вариационный ряд X1 , причем запишем числа в порядке возрастания и без повторений. Во второй строке таблицы запишем частоты (абсолютные частоты), соответствующие числам из первой строки таблицы.
ТАБЛИЦА ЧАСТОТ ЧИСЛОВОГО РЯДА
Числа, составляющие вариационный ряд (без повторений) 3,12 3,24 3,25 3,34 3,37 3,44 Частоты 3 2 1 1 1 2 Числа, составляющие вариационный ряд (без повторений) Частоты 3,12 3 3,24 2 3,25 1 3,34 1 3,37 1 3,44 2 ЗАМЕЧАНИЕ. Сумма частот, то есть сумма чисел, записанных во второй строке таблицы частот числового ряда, равна объему выборки (числу чисел в числовом ряде). В рассматриваемом случае это число 10 .
-
Составляем таблицу относительных частот (в процентах).
ОПРЕДЕЛЕНИЕ 2. Относительной частотой (в процентах) выборочного данного называют число процентов, которое составляет частота этого выборочного данного от всего объема выборки (количества членов числового ряда).
Для того, чтобы сформировать таблицу относительных частот числового ряда, заменим частоты, записанные во второй строке таблицы частот числового ряда, на соответствующие им относительные частоты. В результате получим следующую таблицу.
ТАБЛИЦА ОТНОСИТЕЛЬНЫХ ЧАСТОТ (В ПРОЦЕНТАХ)
Числа, составляющие вариационный ряд (без повторений) 3,12 3,24 3,25 3,34 3,37 3,44 Относительные частоты (%) 30% 20% 10% 10% 10% 20% Числа, составляющие вариационный ряд (без повторений) Относительные частоты (%) 3,12 30% 3,24 20% 3,25 10% 3,34 10% 3,37 10% 3,44 20% -
Находим моду числового ряда.
ОПРЕДЕЛЕНИЕ 3. Модой числового ряда называют выборочное данное с наибольшей частотой.
Из таблицы частот числового ряда видно, что модой числового ряда X является число 3,12 , поскольку его частота 3 является наибольшей. Очевидно, что и относительная частота этого выборочного данного является самой большой (30%) .
ЗАМЕЧАНИЕ. Объем выборки, среднее выборочное значение, размах, медиана и мода числового ряда являются одними из статистических характеристик числовых рядов.