Частота катушки как найти

Как ни странно, в катушках индуктивности нас в первую очередь интересует индуктивность. Измерить индуктивность не сложно. Готовые RLC-метры стоят недорого. Если RLC-метра нет, но есть осциллограф, индуктивность можно определить с его помощью. Также нормальный антенный анализатор без труда измеряет как индуктивность, так и емкость. Но у катушек индуктивности есть еще по крайней мере два важных свойства — частота собственного резонанса и добротность. Давайте разберемся, почему эти свойства важны и как их измерить.

Суть проблемы

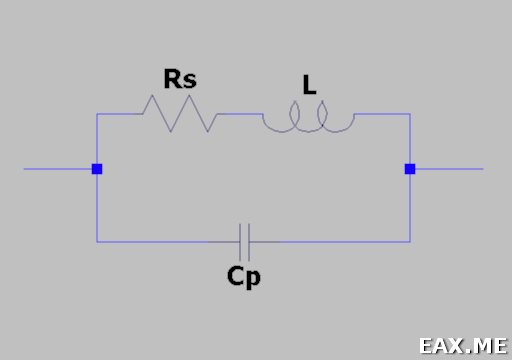
Катушки индуктивности, существующие в реальном мире, можно описать при помощи следующей модели:

Здесь L — это индуктивность катушки. Катушка мотается неким проводником, а реальный проводник имеет отличные от нуля потери. Резистор Rs (он же ESR, equivalent series resistance) как раз отображает эти потери. Конденсатор Cp — это паразитная емкость между витками катушки.

Можно заметить, что индуктивность L и конденсатор Cp образуют параллельный колебательный контур. У этого контура есть резонансная частота. Она и называется частотой собственного резонанса катушки (self-resonant frequency). Ниже этой частоты катушка ведет себя, как катушка. Однако выше она начинает вести себя больше как конденсатор. Определив частоту собственного резонанса, мы поймем, на каких частотах может быть использована катушка.

Rs имеет сложную природу, и работать с ним напрямую неудобно. Поэтому вместо того, чтобы говорить об Rs, говорят о добротности (quality factor или Q). Добротность — это безразмерная величина, характеризующая скорость затухания колебаний в колебательной системе. Чем больше Q, тем меньше затухания.

Для катушек индуктивности добротность определяется, как отношение реактивного сопротивления к Rs:

Реактивное сопротивление является функцией от частоты. Rs на самом деле тоже зависит от частоты. В мире любительского радио обычно говорят о Q на рабочих частотах катушки. Предполагается, что на этом интервале частот добротность меняется незначительно.

Стоит упомянуть, что различают холостую добротность (unloaded Q) и нагруженную добротность (loaded Q). В рамках этой статьи под добротностью понимается исключительно холостая добротность. Нагруженная добротность возникает, когда катушку помещают в конкретную электрическую цепь.

Испытуемый

Попробуем определить частоту собственного резонанса и добротность такой катушки:

Катушка намотана проводом МГТФ площадью сечения 0.35 кв.мм на трубе ПВХ с внешним диаметром 25 мм. Для принудительного шага я мотал два параллельных провода. Затем один провод постепенно отматывался, а второй фиксировался лаком. Длина намотки составила 30 мм, индуктивность — 2 мкГн.

Такой способ намотки был использован с целью получить не самую позорную добротность. За годы экспериментов радиолюбители выработали хорошие практики, позволяющие максимизировать добротность. Основные рекомендации:

• Толстый проводник предпочтительнее тонкого;
• Любой диэлектрик в качестве каркаса катушки или изолятора проводника уменьшает добротность;
• Charles Michaels, W7XC (SK) рекомендует в катушках с воздушным диэлектриком использовать отношение длины катушки к ее диаметру (L/D) не более 2:1. Здесь речь идет о намотке виток к витку;
• Если же катушка мотается на каркасе, рекомендуется L/D = 1:1;
• Tom Rauch, W8JI рекомендует использовать расстояние между витками, равное толщине проводника и L/D от 1 до 4;

Кое-какие подробности можно найти в 9-ой главе книги ON4UN’s Low Band DXing, 5th Edition, в разделе 3.7.2 Making or Buying High-Q Loading Coils. Отмечу, что просто следовать этим советам недостаточно. Если ваша задача — получить как можно большую добротность, нужно брать конкретные доступные материалы, мотать катушки и измерять.

На самом деле, мной было намотано пять катушек пятью разными способами. Приведенная выше имела максимальную добротность.

Ищем собственный резонанс

Для определения частоты собственного резонанса было решено воспользоваться анализатором спектра. С тем же успехом подойдет осциллограф с генератором сигналов, или RTL-SDR с генератором шума. Но анализатор спектра удобнее.

Для подключения катушки между следящим генератором и входом анализатора было использовано такое приспособление:

Экраны BNC-разъемов соединены между собой, а жилы идут к «банановым» коннекторам. К этим коннекторам и подключается катушка.

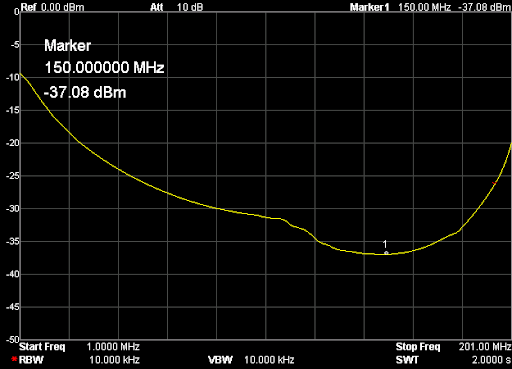
В итоге получаем такую АЧХ:

Перед нами частоты от 1 до 201 МГц, цена деления по горизонтали — 20 МГц. Собственный резонанс, если верить графику, пришелся где-то на 150 МГц. Ниже аттенюация сигнала увеличивается с ростом частоты. Так и должна работать катушка. Выше аттенюация уменьшается с ростом частоты. Это поведение конденсатора.

Какие выводы отсюда можно сделать? Катушку можно использовать на частотах где-то до 37 МГц. На частотах, приближающихся к частоте собственного резонанса, использовать катушки нельзя. Причина заключается в том, что добротность падает по мере приближения к частоте собственного резонанса. На частоте собственного резонанса добротность равна нулю. Рекомендуется использовать катушки на частотах в 4+ раза ниже частоты собственного резонанса.

Определяем добротность

Для определения добротности воспользуемся подходом из статьи Fixture for Measuring Inductor Q with your Antenna Analyzer [PDF], которую написал Phil Salas, AD5X. По инструкции из статьи было изготовлено такое устройство:

Идея довольно простая. Антенный анализатор подключается к BNC разъему, а катушка подключается к «банановым» коннекторам. В первом положении тумблера антенный анализатор измеряет эквивалент нагрузки 50 Ом. Для эквивалента нагрузки было использовано 20 соединенных параллельно резисторов 1 кОм ± 1%. Во втором положении измеряется последовательный колебательный контур, образованный этим же резистором 50 Ом, измеряемой катушкой и КПЕ.

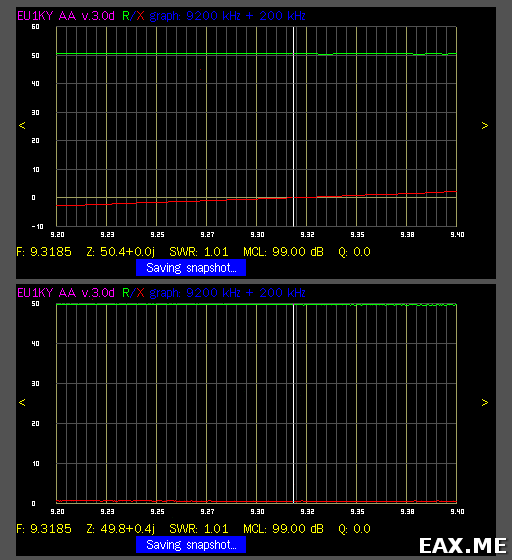
На резонансной частоте последовательный LC-контур представляет собой КЗ, и мы увидим чисто активное сопротивление около 50 Ом:

В данном случае (первый график) резонанс попал на 9.3185 МГц. Антенный анализатор видит 50.4 Ом. Переключаем тумблер в другое положение. Видим сопротивление резистора без контура. Оно составило 49.8 Ом (второй график). Есть также небольшая реактивность в 0.4j. Ею мы пренебрежем, поскольку это всего лишь:

… 6.8 нГн, почти в 300 раз меньше измеряемых 2 мкГн.

Смотрите, что получается. С контуром было 50.4 Ом, а без контура — 49.8 Ом. Разница в 0.6 Ом включает в себя Rs катушки, а также потери на конденсаторе. Но конденсаторы обладают существенно большей добротностью (> 1000), чем катушки. Поэтому разница в 0.6 Ом приходится преимущественно на Rs катушки.

Теперь у нас есть все необходимое для вычисления добротности:

Добротность порядка 200 — это неплохой результат. Обычные покупные катушки для сквозного монтажа имеют добротность в пределах 100. Не удивительно, что бывалые радиолюбители предпочитают мотать катушки самостоятельно. Случайная самодельная катушка из медной проволоки будет иметь добротность уже порядка 100-150. Согласно Low Band DXing, после некоторой практики можно легко делать катушки с добротностью ~400. В качестве потолка в различных источниках приводится Q от 800 до 1000.

Домашнее задание: Смотайте катушку с индуктивностью побольше, порядка 70 мкГн. Для такой катушки вам понадобится каркас около 70 мм и 30 витков эмалированной проволоки диаметром 0.9 мм. Каким вышел Rs? Куда попала частота собственного резонанса? Сравните с приведенными выше результатами.

Внимательный читатель может поинтересоваться, а почему номинал резистора был выбран именно 50 Ом? Это сделано лишь по той причине, что ошибка измерения антенного анализатора при таком сопротивлении минимальна. В теории, с тем же успехом можно использовать любое другое сопротивление, лишь бы оно было чисто активным.

Заключение

Допустим, мы спаяли генератор или фильтр, и он работает не так, как ожидалось. Причина может заключаться к собственном резонансе катушек. Слишком большие потери в согласующем устройстве? Причина может быть в низкой добротности компонентов. Теперь мы имеем больше шансов правильно диагностировать такие проблемы, или еще лучше — вообще избегать их.

Дополнение: Измеряем параметры кварцевых резонаторов

Метки: Электроника.

О расчете собственного резонанса однослойной катушки индуктивности

На заре развития радиотехники было обнаружено, что катушка не идеальная индуктивность. На определенной частоте она входит в режим резонанса даже при отсутствии внешней емкости, а выше этой частоты импеданс катушки носит уже емкостный характер. Для объяснения этого явления предположили, что кроме индуктивности реальная катушка обладает еще собственной емкостью (предположительно между соседними витками) и реальную катушку стали представлять в виде модели из сосредоточенных RLC элементов, в которой L —  индуктивность, C — собственная емкость, названная паразитной, а с помощью активного R учитываются различные потери в катушке. Такая модель катушки имеет одну резонансную частоту, которую назвали частотой собственного резонанса. Долгое время эта модель всех устраивала и стала классической моделью реальной катушки во всех учебниках.

Ведь катушки в подавляющем большинстве практических применений работают на частотах намного ниже частоты собственного резонанса и задачей конструктора является, по сути, обеспечение этого условия. При этом большинство инженеров с этой целью пытались уменьшить эту самую «межвитковую» паразитную емкость. В случае же, если катушка работает на частотах близких к собственному резонансу, как например в спиральных резонаторах или катушках Теслы, RLC-модель дает неверные результаты, но для таких случаев были разработаны альтернативные алгоритмы расчета и все остались довольны не особо задумываясь о причинах таких не стыковок.

В нашу цифровую эпоху появились программы, которые дали возможность моделировать поведение любых высокочастотных устройств с высокой степени точности — так называемые электромагнитные симуляторы. Это мощные пакеты типа CST Studio, ANSYS HFSS и многие другие. Давайте проведем исследование однослойной спиральной катушки в программе HFSS. В первой модели мы поместим катушку над идеальной проводящей поверхностью и запитаем от точечного источника с внутренним сопротивлением 50 МОм. Второй конец катушки заземлен. Расчет будем вести в режиме HFSS Design, использующий метод конечных элементов. Отметим, что популярный ANSYS Maxwell 3D для подобного расчета непригоден.Вторую катушку рассчитаем методом HFSS Design-IE, использующий метод моментов. В отличии от популярных у радиолюбителей симуляторов на основе ядра NEC, например MMANA, здесь сегментация идет не на отрезки провода, а по его поверхности на элементарные треугольные площадки. При такой сегментации для успешного расчета требуется не менее 8-16 Гб оперативной памяти компьютера. Запитаем катушку через короткие выводы от такого же источника. Поскольку катушка не заземлена, в этой модели первый резонанс — полуволновой.В результате исследования мы получили графики импеданса на зажимах источника относительно частоты. Из графиков видно, что у катушки не один, а множество резонансов. Из этого следует вывод, что наша катушка — это совсем не одиночный LC-контур с собственной индуктивностью и паразитной емкостью в виде сосредоточенных элементов, как принято считать, а длинная линия с распределенными параметрами. Такая линия состоит из одного провода, но это не должно никого смущать. То, что в даже одиночном проводе наблюдаются волновые резонансные явления, хорошо иллюстрирует пример полуволнового вибратора Герца. Ведь волновые явления как в длинных линиях, так и в вибраторе отображают тот факт, что электромагнитное взаимодействие распространяется с конечной скоростью. На то чтобы электромагнитное взаимодействие «добралось» от одного конца провода до другого затрачивается определенное время, и когда это время сравнимо с периодом колебаний рабочей частоты возникают явления резонанса. И катушка в этом плане недалеко ушла от вибратора, поскольку несмотря на малые ее габариты, длина провода, которым она намотана, может иметь величину сравнимую с длиной волны. Частоту собственного резонанса вибратора мы можем довольно легко определить зная его длину, учтя коэффициент укорочения. В катушке, кроме того, необходимо учесть связь между витками.

В учебниках по электродинамике [1] можно найти описание работы спиральных волноводов с поверхностными электромагнитными (ЭМ) волнами, распространяющимися вдоль провода спирали. Такие волноводы применяются как замедляющие структуры в спиральных антеннах и лампах бегущей волны. Длина одного витка и шаг намотки у них сравним с длиной волны. В частности, у спиральной антенны длина витка L равна длине волны, а шаг намотки p равен четверти длины волны.Фазовая скорость волны вдоль оси спирального волновода значительно ниже скорости света, на чем и основано его применение как замедляющей структуры.

[1]

где:

• v_ax — скорость волны вдоль оси спирали;
• с — скорость света;

Относительная фазовая скорость волны вдоль оси такого волновода зависит только от геометрии спирали и не зависит от частоты, поскольку влияние витков друг на друга минимально и ЭМ-волна распространяется вдоль провода такой спирали, так же как и у вибратора. Отметим, что фазовая скорость ЭМ волны относительно провода спирали в таком волноводе близка к скорости света.

В нашей же катушке, и длина отдельного витка, и даже длина всей намотки, и тем более шаг намотки намного меньше длины волны. В этом случае, кроме основной моды в таком спиральном волноводе существуют высшие моды колебаний, распространяющиеся непосредственно вдоль ее оси. Другими словами, ЭМ волна распространяется не только вдоль длины провода, но часть ее «перепрыгивает от витка к витку». Относительная фазовая скорость вдоль оси катушки определяется следующим приближенным выражением:

[2]

где:

• λ₀ — длина волны рабочей частоты в свободном пространстве;
• D, p — диаметр и шаг намотки;
• c — скорость света;

Как видно из формулы, скорость зависит от диаметра катушки, шага намотки и длины волны. По сути, катушка — тот же спиральный волновод с медленными волнами, но работающий в другом режиме колебаний. Во избежании различных спекуляций отметим то обстоятельство, что благодаря наличию высших мод, волна «добирается» до другого конца катушки быстрее чем непосредственно вдоль провода. Поэтому фазовая скорость волны относительно провода выше скорости света, причем в разы. Это не противоречит теории относительности. Достаточно упомянуть, что в полых волноводах фазовая скорость волны тоже выше скорости света. Для понимания этого кажущегося парадокса следует различать фазовую и групповую скорости электромагнитной волны. Для чего отсылаю к учебникам…

Катушка с одним заземленным концом резонирует на частотах nλ₀/4, где n – целое число, λ₀ — длина волны рабочей частоты и f_srf = v_ax/λ₀. Поэтому увеличение частоты собственного резонанса сводится к увеличению значения v_ax. Из-за наличия высших мод ЭМ-волны, частота первого резонанса катушки всегда выше частоты, рассчитанной исходя из длины провода. По этой же причине высшие по частоте резонансы не кратны первому и друг другу. При изменении шага намотки v_ax имеет максимум при шаге спирали примерно равном радиусу намотки (радиус a = D / 2). Однако катушки с большим шагом намотки (p ≈ a) не представляют практического интереса, поскольку имеют малую индуктивность. При увеличении шага намотки частота собственного резонанса катушки растет (при p < a), но рост этот идет за счет снижения величины индуктивности. При фиксированной индуктивности, если увеличивать шаг намотки, нам приходится добавлять витки и выигрыша мы практически не получаем.

У коротких катушек на каркасах большого диаметра последующие резонансы отстоят от первого далеко выше по частоте, что можно видеть по результатам HFSS моделирования:

На частотах много ниже частоты первого резонанса пространственные задержки намного меньше периода колебаний, ЭМ-поле вокруг катушки представляет собой поле соленоида и скорость распространения волны вдоль ее оси можно не учитывать. В таком случае RLC-модель из сосредоточенных элементов будет вполне рабочей и достаточно точно отображает поведение катушки. Стоит только помнить, что паразитная собственная емкость — это вовсе не статическая емкость между витками. В таком режиме работают катушки из всех наших трех моделей в КВ диапазоне и ниже. Однако уже на частоте первого резонанса начинают проявляться волновые эффекты, связанные с ограниченной скоростью передачи электромагнитных взаимодействий и катушку следует рассматривать только как спиральный волновод. В этом случае RLC модель не только не годится для расчетов, но и приводит к неверному пониманию самого механизма возникновения резонансных явлений в катушке. В этой связи хочется отметить наличие в Сети ложной идеи о том, что в катушке одновременно происходят как волновой резонанс, так и LC-резонанс на сосредоточенных индуктивности и пресловутой «межвитковой емкости». Такое утверждение равносильно тому, что в катушке имеются два механизма распространения электромагнитных взаимодействий. Один происходит, как обычно, со скоростью света и определяет волновой резонанс. Второй осуществляется мгновенно с бесконечной скоростью в виртуальных сосредоточенных элементах катушки. Ведь фазовый сдвиг между током и напряжением в реактивных элементах — это совсем не то пространственное запаздывание, о котором идет речь. На самом деле катушка, как набор идеальных сосредоточенных RLC элементов, и катушка, как цепь с распределенными параметрами  — это две разные математические модели одной и той же реальной катушки. Первая модель не учитывает ограниченную скорость передачи взаимодействий, основана на предположении, что плотность тока во всех витках всегда одинакова, что не имеет место при собственном резонансе спирали. Поэтому эта модель ограничена и применима только на низких частотах. Вторая модель — более полная, учитывает то, что не учла первая и применима на любой частоте. В этом нет ничего необычного. Любая цепь, физические размеры которой сравнимы с длиной волны, не может рассматриваться как цепь из сосредоточенных элементов, в которой не учитывается ограниченная скорость передачи электромагнитных взаимодействий. Именно по этой причине О.Хевисайд и предложил в 1885 г. свою теорию длинных линий, а заодно кстати и само абстрактное математическое понятие «индуктивность». Как положительную реактивность.

Особо хотелось бы отметить следующий момент. На низких частотах, где, как мы выяснили, RLC модель справедлива, можно считать, что как индуктивность так и собственная емкость катушки не зависят от частоты, а определяются только геометрией намотки. Это общеизвестный факт, который зафиксирован например в формуле Нагаока. Однако реально параметры спиральной длинной линии зависят от частоты. Не только v_ax, но и погонная емкость и погонная индуктивность и, как следствие — величины собственной индуктивности и собственной емкости катушки в целом. Только на низких частотах эта зависимость пренебрежимо мала, а вот уже на частотах близких к первому резонансу значения индуктивности и собственной емкости катушки начинают заметно «плыть» по частоте. В итоге, мы сталкиваемся с ситуацией, что эти значения, измеренные или рассчитанные на низкой частоте, не пригодны для расчета частоты собственного резонанса катушки как LC резонанса по формуле Томсона. Расчет даст неверный результат! Неверный, Карл! Таким образом, мы приходим к выводу, что расчеты, основанные на понятии о LC-резонансе в катушке, полностью теряют смысл, что еще раз доказывает несостоятельность RLC-модели катушки не только для объяснения физических явлений при собственном резонансе, но и для расчетов в этой частотной области. Поэтому приходится прибегать к более сложному численному методу из работы [5], включающему в себя функции Бесселя и прочий суровый матан, что и делает Coil64.

Как видно из HFSS-моделей, у катушки как первый резонанс так и все последующие связаны исключительно с волновыми явлениями в катушке. Возможны практические случаи, когда катушка работает в диапазоне частот, в который попадает не только ее первый резонанс, но и более высокие. Очень хорошо такой случай описан в статье И.Гончаренко об анодном дросселе коротковолнового передатчика [2]. На этом примере хорошо видно, что для правильного понимания механизма резонансных явлений в катушке необходимо пользоваться теорией длинных линий.

Кроме фазовой скорости волны в катушке на частоту собственного резонанса оказывает влияние так называемый торцевой эффект, подобный хорошо известному аналогичному понятию из теории антенн, от которого зависит коэффициент укорочения вибратора. Этот эффект проявляется от того, что ЭМ-поле вокруг катушки занимает пространство большее, чем сама катушка. Наличие торцевого эффекта понижает резонансную частоту и этот эффект более выражен у коротких катушек с большим диаметром, что еще раз подтверждает родственную связь резонансных явлений в катушке и в вибраторе. Учитывая фазовую скорость вдоль оси катушки и явление торцевого эффекта мы можем оценочно определить частоту собственного резонанса катушки по следующей весьма приближенной формуле от G3RBJ:

[3]

где:

• f_srf — частота собственного резонанса [МГц]
• ĺ_w — длина провода катушки с учетом торцевого эффекта [м]
• l_w — реальная длина провода катушки [м]
• D, p, l — диаметр, шаг и длина намотки, соответственно [м]
• 0,25 — коэффициент, определяющий четвертьволновый резонанс (для полуволнового — 0,5)

Если конструктору необходимо создать катушку, имеющую минимальные габариты и максимальную частоту собственного резонанса при заданной индуктивности, то наиболее оптимальна будет намотка с расстоянием между витками, равном диаметру провода,  при отношении l/D ≈ 1..1,5. Хотелось бы обратить внимание конструкторов, что здесь идет речь о вычислении собственной резонансной частоты «голой катушки в вакууме», т.е. одной проволочной спирали без учета влияния каркаса, сердечника, экрана, изоляции провода и т.п. Все эти, трудно поддаваемые учету факторы, приводят к уменьшению этой частоты. Причем влияние оказывает все — любой проводник, печатная плата, корпус конструкции. В наших HFSS-моделях влияющие факторы — это выводы спирали и, особенно, сплошная земля в 1-ой и 3-ей моделях. Даже если вы соберетесь измерить частоту собственного резонанса экспериментально, это будет непростой задачей, так как щупы измерительного оборудования также оказывают влияние, даже если катушка где то висит в воздухе!

Необходимо отметить, что строгого аналитического решения уравнений Максвелла для цилиндрической проволочной спирали не существует, поэтому в теории спиральный волновод представляют в виде эквивалентной модели из тонкостенного сплошного цилиндра с анизотропной проводимостью. Однако численные методы решения уравнений Максвелла (чем в принципе и занимается HFSS) приводят нас к вполне однозначным результатам. В итоге, следует иметь ввиду, что вышеприведенная простая аналитическая формула [3] является весьма приблизительной и не может быть применима к любой катушке с произвольной геометрией намотки. Поэтому в Coil64 расчет частоты собственного резонанса основан не на аналитическом, а на численном методе из работы [5], который проверен практическими измерениями. При этом не учитывается влияние экрана, каркаса и других факторов. Расчет имеет точность около 10% при 0,04 < l/D < 40. Для некоторых катушек, например для очень длинных соленоидов с большим числом витков, этот метод может давать неверный результат. На практике же следует придерживаться следующего простого условия: если длина провода, которым намотана катушка, меньше четверти длины волны на наивысшей рабочей частоте, то катушка будет работать ниже своего первого резонанса.

Ссылки по теме:

1. Техническая электродинамика, Семенов Н.А., Изд. «Связь» Москва, 1973, стр.318-323.
2. Моделирование анодного дросселя как распределенной структуры — И.Гончаренко (DL2KQ) 2007-2012
3. Паразитные резонансы в катушке П-контура — И.Гончаренко (DL2KQ)
4. Высокочастотные катушки, спиральные резонаторы и увеличение напряжения из-за когерентных пространственных мод 2001г. (Оригинал статьи здесь)
5. THE SELF-RESONANCE AND SELF-CAPACITANCE OF SOLENOID COILS — applicable theory, models and calculation methods. By David W Knight (G3YNH)
6. The self-resonance and self-capacitance of solenoid coils by David W Knight — основная статья с массой полезных ссылок по теме, в том числе на экспериментальные исследования с наглядными фото (G3YNH)
7. SELF-RESONANCE IN COILS and the self-capacitance myth. By Alane Payne (G3RBJ)
8. О собственной емкости катушки.
9. Измерение частоты собственного резонанса катушки индуктивности — А. Алексеев (R2AUK)
10. Как создать модель и рассчитать параметры однослойной катушки индуктивности в электромагнитном симуляторе ANSYS HFSS;

Ну, в общем, chip-chip прав — на частоте резонанса у параллельного контура (или катушки с большой конструктивной ёмкостью) повышается сопротивление. Получается, что на частотах далёких от резонансной, уровень переменного напряжения на резисторе будет больше, чем на резонансной. Можно и свип-генератором пользоваться, но я обычно ручками, ручками…

Включать осциллограф параллельно катушке (а не резистору) я бы не рекомендовал — щуп обычно имеет ёмкость, которая может повлиять на показания. Хотя, если это очень многовитковая катушка и её конструктивная ёмкость большая (более 1 нФ), то лишние 50-100 пФ не очень повлияют… Ну, можно, конечно, делитель у щупа включить.