Абсолютная погрешность как найти метрология

2.1. Погрешности измерений, их классификация

Истинное значение
физической величины
– значение физической величины, которое
идеальным образом отражало бы в
количественном и качественном отношениях
соответствующее свойство объекта.

Результат любого
измерения отличается от истинного
значения физической величины на некоторое
значение, зависящее от точности средств
и методов измерения, квалификации
оператора, условий, в которых проводилось
измерение, и т. д. Отклонение результата
измерения от истинного значения
физической величины называется
погрешностью
измерения.

Поскольку определить
истинное значение физической величины
в принципе невозможно, так как это
потребовало бы применения идеально
точного средства измерений, то на
практике вместо понятия истинного
значения физической величины применяют
понятие действительного
значения измеряемой величины,
которое настолько точно приближается
к истинному значению, что может быть
использовано вместо него. Это может
быть, например, результат измерения
физической величины образцовым средством
измерения.

Абсолютная
погрешность измерения
(Δ) – это разность между результатом
измерения х
и действительным (истинным) значением
физической величины х_и:

Δ
= х –
х_и.
(2.1)

Относительная
погрешность измерения
(δ) – это отношение абсолютной погрешности
к действительному (истинному) значению
измеряемой величины (часто выраженное
в процентах):

δ
= (Δ / х_и)·100 %
(2.2)

Приведенная
погрешность (γ)
– это выраженное в процентах отношение
абсолютной погрешности к нормирующему
значению Х_N
– условно принятому значению физической
величины, постоянному во всем диапазоне
измерений:

γ =
(Δ /Х_N)·100 %
(2.3)

Для приборов с
нулевой отметкой на краю шкалы нормирующее
значение Х_N
равно конечному значению диапазона
измерений. Для приборов с двухсторонней
шкалой, т. е. с отметками шкалы,
расположенными по обе стороны от нуля
значение Х_N
равно арифметической сумме модулей
конечных значений диапазона измерения.

Погрешность
измерения (результирующая
погрешность)
является суммой двух составляющих:
систематической
и случайной
погрешностей.

Систематическая
погрешность
– это составляющая погрешности измерения,
остающаяся постоянной или закономерно
изменяющаяся при повторных измерениях
одной и той же величины. Причинами
появления систематической погрешности
могут являться неисправности средств
измерений, несовершенство метода
измерений, неправильная установка
измерительных приборов, отступление
от нормальных условий их работы,
особенности самого оператора.
Систематические погрешности в принципе
могут быть выявлены и устранены. Для
этого требуется проведение тщательного
анализа возможных источников погрешностей
в каждом конкретном случае.

Систематические
погрешности подразделяются на:

• методические;

• инструментальные;

• субъективные.

Методические
погрешности
происходят от несовершенства метода
измерения, использования упрощающих
предположений и допущений при выводе
применяемых формул, влияния измерительного
прибора на объект измерения. Например,
измерение температуры с помощью термопары
может содержать методическую погрешность,
вызванную нарушением температурного
режима объекта измерения вследствие
внесения термопары.

Инструментальные
погрешности
зависят от погрешностей применяемых
средств измерения. Неточность градуировки,
конструктивные несовершенства, изменения
характеристик прибора в процессе
эксплуатации и т. д. являются причинами
основных погрешностей инструмента
измерения.

Субъективные
погрешности
вызываются неправильными отсчетами
показаний прибора человеком (оператором).
Например, погрешность от параллакса,
вызванная неправильным направлением
взгляда при наблюдении за показаниями
стрелочного прибора. Использование
цифровых приборов и автоматических
методов измерения позволяет исключить
такого рода погрешности.

Во многих случаях
систематическую погрешность в целом
можно представить как сумму двух
составляющих: аддитивной
(∆_а)
и
мультипликативной
(∆_м).

Если реальная
характеристика средства измерения
смещена относительно номинальной так,
что при всех значениях преобразуемой
величины Х
выходная величина Y
оказывается больше (или меньше) на одну
и ту же величину Δ, то такая погрешность
называется аддитивной
погрешностью нуля (рис.
2.1).

Мультипликативная
погрешность
– это погрешность чувствительности
средства измерения.

Такой подход
позволяет легко скомпенсировать влияние
систематической погрешности на результат
измерения путем введения раздельных
поправочных коэффициентов для каждой
из этих двух составляющих.

Рис.
2.1. К пояснению понятий аддитивной

и
мультипликативной погрешностей

Случайная
погрешность (∆_с)
– это составляющая погрешности измерения,
изменяющаяся случайным образом при
повторных измерениях одной и той же
величины. Наличие случайных погрешностей
выявляется при проведении ряда измерений
постоянной физической величины, когда
оказывается, что результаты измерений
не совпадают друг с другом. Часто
случайные погрешности возникают из-за
одновременного действия многих
независимых причин, каждая из которых
в отдельности слабо влияет на результат
измерения.

Во многих случаях
влияние случайных погрешностей можно
уменьшить путем выполнения многократных
измерений с последующей статистической
обработкой полученных результатов.

В некоторых случаях
оказывается, что результат одного
измерения резко отличается от результатов
других измерений, выполненных при тех
же контролируемых условиях. В этом
случае говорят о грубой погрешности
(промахе измерения). Причиной могут
послужить ошибка оператора, возникновение
сильной кратковременной помехи, толчок,
нарушение электрического контакта и
т. д. Такой результат, содержащий
грубую
погрешность
необходимо выявить, исключить и не
учитывать при дальнейшей статистической
обработке результатов измерений.

Причины
возникновения погрешностей измерений

Имеется ряд
слагаемых погрешностей, которые являются
доминирующими в общей погрешности
измерений. К ним относятся:

1. Погрешности,
   зависящие от средств измерений.
   Нормируемую допустимую погрешность
   средства измерения следует рассматривать
   как погрешность измерения при одном
   из возможных вариантов использования
   этого средства
   измерения.

2. Погрешности,
   зависящие от установочных мер.
   Установочные меры могут быть универсальными
   (концевые меры) и специальными
   (изготовленными по виду измеряемой
   детали). Погрешность измерения будет
   меньшее, если установочная мера будет
   максимально подобна измеряемой детали
   о конструкции, массе, материалу, его
   физическим свойствам, способу базирования
   и т. д. Погрешности от концевых мер длины
   возникают из-за погрешности изготовления
   или погрешности аттестации, а также
   из-за погрешности их притирки.

3. Погрешности,
   зависящие от измерительного усилия.
   При оценке влияния измерительного
   усилия на погрешность измерения
   необходимо выделить упругие деформации
   установочного узла и деформации в зоне
   контакта измерительного наконечника
   с деталью.

4. Погрешности,
   происходящие от температурных деформаций.
   Погрешности возникают из-за разности
   температур объекта измерения и
   измерительного средства. Существует
   два основных источника, обуславливающих
   погрешность от температурных деформаций:
   отклонение температуры воздуха от
   20 °С и кратковременные колебания
   температуры воздуха в процессе измерения.

5. Погрешности,
   зависящие от оператора
   (субъективные погрешности). Возможны
   четыре вида субъективных погрешностей:

• погрешность
  отсчитывания
  (особенно важна, когда обеспечивается
  погрешность измерения, не превышающая
  цену деления);

• погрешность
  присутствия
  (проявляется в виде влияния теплоизлучения
  оператора на температуру окружающей
  среды, а тем самым и на измерительное
  средство);

• погрешность
  действия
  (вносится оператором при настройке
  прибора);

• профессиональные
  погрешности
  (связаны с квалификацией оператора, с
  отношением его к процессу измерения).

1. Погрешности при
   отклонениях от правильной геометрической
   формы.

2. Дополнительные
   погрешности при измерении внутренних
   размеров.

При характеристике
погрешностей средств измерений часто
пользуются

понятием
предела допускаемой погрешности средств
измерений.

Предел допускаемой
погрешности средства измерений
– это наибольшая, без учета знака,
погрешность средства измерений, при
котором оно может быть признано и
допущено к применению. Определение
применимо к основной и дополнительной
погрешности средств измерений.

Учет всех нормируемых
метрологических характеристик средств
измерений является сложной и трудоемкой
процедурой. На практике такая точность
не нужна. Поэтому для средств измерений,
используемых в повседневной практике,
принято деление на классы
точности,
которые дают их обобщенную метрологическую
характеристику.

Требования к
метрологическим характеристикам
устанавливаются в стандартах на средства
измерений конкретного типа.

Классы точности
присваиваются средствам измерений с
учетом результатов государственных
приемочных испытаний.

Класс точности
средства измерений
– обобщенная характеристика средства
измерений, определяемая пределами
допускаемых основных и дополнительных
погрешностей. Класс точности может
выражаться одним числом или дробью
(если аддитивная и мультипликативная
погрешности сопоставимы – например,
0,2/0,05 – адд./мульт.).

Обозначения классов
точности наносятся на циферблаты, щитки
и корпуса средств измерений, приводятся
в нормативно-технических документах.
Классы точности могут обозначаться
буквами (например, М, С и т. д.) или
римскими цифрами (I,
II,
III
и т. д.). Обозначение классов точности
по ГОСТу 8.401-80 может сопровождаться
дополнительными условными знаками:

• 0,5;
  1,6; 2,5 и т. д. – для приборов, приведенная
  погрешность которых составляет 0,5; 1,6;
  2,5 % от нормирующего значения X_N.
  При этом X_N
  принимается равным большему из модулей
  пределов измерений, если нулевое
  значение входного (выходного) сигнала
  находится на краю или вне диапазона
  измерений;

• 0,1,
  0,4, 1,0 и т. д. – для приборов, у которых
  относительная
  погрешность
  составляет 0,1; 0,4; 1,0 % непосредственно
  от полученного значения измеряемой
  величины x;

• 0,02/0,01 – для
  приборов, у которых измеряемая величина
  не может отличаться от значения x,
  показанного указателем, больше, чем на
  [С+d(|X_N/x|-1)]%,
  где C
  и d
  – числитель и знаменатель соответственно
  в обозначении класса точности; X_N
  – больший
  (по модулю) из пределов измерений
  прибора.

Примеры обозначения
классов точности приведены на рис. 2.2.

Рис.
2.2. Лицевые панели приборов:

а
– вольтметра
класса точности 0,5; б
– амперметра
класса точности 1,5;

в
– амперметра
класса точности 0,02/0,01;

г
– мегомметра класса точности 2,5 с
неравномерной шкалой

Метрологическая
надежность средств измерения

В процессе
эксплуатации любого средства измерения
может возникнуть неисправность или
поломка, называемые отказом.

Метрологическая
надежность
средств
измерения
– это свойство средств измерений
сохранять установленные значения
метрологических характеристик в течение
определенного времени при нормальных
режимах и рабочих условиях эксплуатации.
Она характеризуется интенсивностью
отказов, вероятностью безотказной
работы и наработкой на отказ.

Интенсивность
отказов
определяется выражением:

,
(2.1)

где
L
– число отказов; N
– число однотипных элементов; ∆t
– промежуток времени.

Для средств
измерения, состоящего из
n
типов элементов, интенсивность
отказов
рассчитывается как

(2.2)

где
m_i
–
количество элементов i-го
типа.

Вероятность
безотказной работы:

(2.3)

Наработка на
отказ:

(2.4)

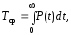
Для внезапного
отказа, интенсивность отказов которого
не зависит от времени работы средства
измерения:

(2.5)

Межповерочный
интервал, в
течение которого обеспечивается заданная
вероятность безотказной работы,
определяется по формуле:

,
(2.6)

где
P_мо
– вероятность метрологического отказа
за время между поверками; P(t)
– вероятность безотказной работы.

В процессе
эксплуатации может производиться
корректировка межповерочного интервала.

Поверка средств
измерения

В основе обеспечения
единообразия средств измерений лежит
система передачи размера единицы
измеряемой величины. Технической формой
надзора за единообразием средств
измерений является государственная
(ведомственная) поверка средств измерений,
устанавливающая их метрологическую
исправность.

Поверка
– определение метрологическим органом
погрешностей средства измерений и
установление его пригодности к применению.

Пригодным к
применению в течение определенного
межповерочного
интервала
времени признают те СИ, поверка которых
подтверждает их соответствие
метрологическим и техническим требованиям
к данному СИ.

Средства измерений
подвергают первичной, периодической,
внеочередной, инспекционной и экспертной
поверкам.

Первичной поверке
подвергаются
СИ при выпуске из производства или
ремонта, а также СИ, поступающие по
импорту.

Периодической
поверке подлежат
СИ, находящиеся в эксплуатации или на
хранении через определенные межповерочные
интервалы, установленные с расчетом
обеспечения пригодности к применению
СИ на период между поверками.

Инспекционную
поверку производят
для выявления пригодности к применению
СИ при осуществлении госнадзора и
ведомственного метрологического
контроля за состоянием и применением
СИ.

Экспертную
поверку выполняют
при возникновении спорных вопросов по
метрологическим характеристикам (MX),
исправности СИ и пригодности их к
применению.

Достоверная
передача размера единиц во всех звеньях
метрологической цепи от эталонов или
от исходного образцового средства
измерений к рабочим средствам измерений
производится в определенном порядке,
приведенном в поверочных схемах.

Поверочная схема
– это утвержденный в установленном
порядке документ, регламентирующий
средства, методы и точность передачи
размера единицы физической величины
от государственного эталона или исходного
образцового средства измерений рабочим
средствам.

Различают
государственные, ведомственные и
локальные поверочные схемы органов
государственной или ведомственных
метрологических служб.

Государственная
поверочная схема
распространяется на все средства
измерений данной ФВ, имеющиеся в стране.
Устанавливая многоступенчатый порядок
передачи размера единицы ФВ от
государственного эталона, требования
к средствам и методам поверки,
государственная поверочная схема
представляет собой структуру
метрологического обеспечения определённого
вида измерений в стране. Эти схемы
разрабатываются главными центрами
эталонов и оформляются одним ГОСТом
ГСИ.

Локальные
поверочные схемы
распространяются на средства измерений,
подлежащие поверке в данном метрологическом
подразделении на предприятии, имеющем
право поверки средств измерений, и
оформляются в виде стандарта предприятия.
Ведомственные и локальные поверочные
схемы не должны противоречить
государственным и должны учитывать их
требования применительно к специфике
конкретного предприятия.

Ведомственная
поверочная схема
разрабатывается органом ведомственной
метрологической службы, согласовывается
с главным центром эталонов – разработчиком
государственной поверочной схемы
средств измерений данной ФВ и
распространяется только на средства
измерений, подлежащие внутриведомственной
поверке.

Поверочная схема
устанавливает передачу размера единиц
одной или нескольких взаимосвязанных
величин. Она должна включать не менее
двух ступеней передачи размера. Поверочную
схему для СИ одной и той же величины,
существенно отличающихся по диапазонам
измерений, условиям применения и методам
поверки, а также для СИ нескольких ФВ
допускается подразделять на части. На
чертежах поверочной схемы должны быть
указаны:

• наименования СИ
  и методов поверки;

• номинальные
  значения ФВ или их диапазоны;

• допускаемые
  значения погрешностей СИ;

• допускаемые
  значения погрешностей методов поверки.
  Правила расчета параметров поверочных
  схем и оформления чертежей поверочных
  схем приведены в ГОСТ 8.061-80 «ГСИ.
  Поверочные схемы. Содержание и построение»
  и в рекомендациях МИ 83-76 «Методика
  определения параметров поверочных
  схем».

Калибровка
средств измерения

Калибровка
средства измерений
– это
совокупность операций, выполняемых
калибровочной лабораторией с целью
определения и подтверждения действительных
значений метрологических характеристик
и (или) пригодности средства измерений
к применению в сферах, не подлежащих
государственному метрологическому
контролю и надзору в соответствии с
установленными требованиями.

Результаты
калибровки средств измерений удостоверяются
калибровочным
знаком,
наносимым на средства измерений, или
сертификатом
о калибровке,
а также записью
в эксплуатационных документах.

Поверку (обязательная
госповерка) может выполнять, как правило,
орган государственной метрологической
службы, а калибровку –
любая
аккредитованная и неаккредитованная
организация.

Поверка обязательна
для средств измерений, применяемых в
сферах, подлежащих государственному
метрологическому контролю (ГМК),
калибровка же –
процедура
добровольная, поскольку относится к
средствам измерений, не подлежащим ГМК.
Предприятие вправе самостоятельно
решать вопрос о выборе форм и режимов
контроля состояния средств измерений,
за исключением тех областей применения
средств измерений, за которыми государства
всего мира устанавливают свой контроль
– это
здравоохранение, безопасность труда,
экология и др.

Освободившись от
государственного контроля, предприятия
попадают под не менее жёсткий контроль
рынка. Это означает, что свобода выбора
предприятия по «метрологическому
поведению» является относительной, все
равно необходимо соблюдать метрологические
правила.

В развитых странах
устанавливает и контролирует исполнение
этих правил негосударственная организация,
именуемая «национальной калибровочной
службой». Эта служба берёт на себя
функции регулирования и разрешения
вопросов, связанных со средствами
измерений, не подпадающими под контроль
государственных метрологических служб.

Желание иметь
конкурентоспособную продукцию побуждает
предприятия иметь измерительные
средства, дающие достоверные результаты.

Внедрение системы
сертификации продукции дополнительно
стимулирует поддержание измерительных
средств на соответствующем уровне. Это
согласуется с требованиями систем
качества, регламентируемыми стандартами
ИСО серии 9000.

Построение
Российской системы калибровки (РСК)
основывается на следующих принципах:

• добровольность
  вступления;

• обязательность
  получения размеров единиц от
  государственных эталонов;

• профессионализм
  и компетентность персонала;

• самоокупаемость
  и самофинансирование.

Основное звено
РСК –
калибровочная
лаборатория. Она представляет собой
самостоятельное предприятие или
подразделение в составе метрологической
службы предприятия, которое может
осуществлять калибровку средств
измерений для собственных нужд или для
сторонних организаций. Если калибровка
проводится для сторонних организаций,
то калибровочная лаборатория должна
быть аккредитована органом РСК.
Аккредитацию осуществляют государственные
научные метрологические центры или
органы Государственной метрологической
службы в соответствии со своей компетенцией
и требованиями, установленными в ГОСТе
51000.2-95 «Общие требования к аккредитующему
органу».

Порядок аккредитации
метрологической службы утвержден
постановлением Госстандарта РФ от 28
декабря 1995 г. № 95 «Порядок аккредитации
метрологических служб юридических лиц
на право проведения калибровочных
работ».

Методы поверки
(калибровки) средств измерения

Допускается
применение четырех методов
поверки
(калибровки) средств измерений:

• непосредственное
  сличение с эталоном;

• сличение с помощью
  компаратора;

• прямые измерения
  величины;

• косвенные измерения
  величины.

Метод
непосредственного сличения
поверяемого (калибруемого) средства
измерения с эталоном соответствующего
разряда широко применяется для различных
средств измерений в таких областях, как
электрические и магнитные измерения,
для определения напряжения, частоты и
силы тока. В основе метода лежит проведение
одновременных измерений одной и той же
физической величины поверяемым
(калибруемым) и эталонным приборами.
При этом определяют погрешность как
разницу показаний поверяемого и
эталонного средств измерений, принимая
показания эталона за действительное
значение величины. Достоинства этого
метода в его простоте, наглядности,
возможности применения автоматической
поверки (калибровки), отсутствии
потребности в сложном оборудовании.

Метод сличения
с помощью компаратора
основан на использовании прибора
сравнения, с помощью которого сличаются
поверяемое (калибруемое) и эталонное
средства измерения. Потребность в
компараторе возникает при невозможности
сравнения показаний приборов, измеряющих
одну и ту же величину, например, двух
вольтметров, один из которых пригоден
для постоянного тока, а другой –
переменного.
В подобных ситуациях в схему поверки
(калибровки) вводится промежуточное
звено –
компаратор.
Для приведенного примера потребуется
потенциометр, который и будет компаратором.
На практике компаратором может служить
любое средство измерения, если оно
одинаково реагирует на сигналы как
поверяемого (калибруемого), так и
эталонного измерительного прибора.
Достоинством данного метода специалисты
считают последовательное во времени
сравнение двух величин.

Метод прямых
измерений
применяется, когда имеется возможность
сличить испытуемый прибор с эталонным
в определенных пределах измерений. В
целом этот метод аналогичен методу
непосредственного сличения, но методом
прямых измерений производится сличение
на всех числовых отметках каждого
диапазона (и поддиапазонов, если они
имеются в приборе). Метод прямых измерений
применяют, например, для поверки или
калибровки вольтметров постоянного
электрического тока.

Метод косвенных
измерений
используется, когда действительные
значения измеряемых величин невозможно
определить прямыми измерениями либо
когда косвенные измерения оказываются
более точными, чем прямые. Этим методом
определяют вначале не искомую
характеристику, а другие, связанные с
ней определенной зависимостью. Искомая
характеристика определяется расчетным
путем. Например, при поверке (калибровке)
вольтметра постоянного тока эталонным
амперметром устанавливают силу тока,
одновременно измеряя сопротивление.
Расчетное значение напряжения сравнивают
с показателями калибруемого (поверяемого)
вольтметра. Метод косвенных измерений
обычно применяют в установках
автоматизированной поверки (калибровки).

Погрешности измерений, представление результатов эксперимента

1. Шкала измерительного прибора
2. Цена деления
3. Виды измерений
4. Погрешность измерений, абсолютная и относительная погрешность
5. Абсолютная погрешность серии измерений
6. Представление результатов эксперимента
7. Задачи

п.1. Шкала измерительного прибора

Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.

Примеры шкал различных приборов:

п.2. Цена деления

Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.

Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.

Пример определения цены деления:

Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*}

п.3. Виды измерений

Вид измерений

Определение

Пример

Прямое измерение

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Косвенное измерение

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.

Составляющие погрешности измерений

Причины

Инструментальная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Погрешность метода

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Погрешность оператора

Определяется субъективным фактором, ошибками экспериментатора.

Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$

Если величина (a_0) — это истинное значение, а (triangle a) — погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).

Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$

Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$

Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.

Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

• определение длины с помощью линейки или мерной ленты;
• определение объема с помощью мензурки.

Пример получения результатов прямых измерений с помощью линейки:

Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$

Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

№ опыта	1	2	3	Сумма
Масса, г	99,8	101,2	100,3	301,3
Абсолютное отклонение, г	0,6	0,8	0,1	1,5

Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}

п.6. Представление результатов эксперимента

Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то

• абсолютная погрешность их суммы равна сумме абсолютных погрешностей

$$ triangle (a+b)=triangle a+triangle b $$

• абсолютная погрешность их разности также равна сумме абсолютных погрешностей

$$ triangle (a-b)=triangle a+triangle b $$

Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:

• относительная погрешность их произведения равна сумме относительных погрешностей

$$ delta_{acdot b}=delta_a+delta_b $$

• относительная погрешность их частного также равна сумме относительных погрешностей

$$ delta_{a/b}=delta_a+delta_b $$

Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:

• относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности

$$ delta_{a^2}=2delta_a $$

• относительная погрешность куба (a^3) равна утроенной относительной погрешности

$$ delta_{a^3}=3delta_a $$

• относительная погрешность произвольной натуральной степени (a^n) равна

$$ delta_{a^n}=ndelta_a $$

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

№ мензурки	a, мл	b, мл	n	(triangle=frac{b-a}{n+1}), мл
1	20	40	4	(frac{40-20}{4+1}=4)
2	100	200	4	(frac{200-100}{4+1}=20)
3	15	30	4	(frac{30-15}{4+1}=3)
4	200	400	4	(frac{400-200}{4+1}=40)

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

№ мензурки	Объем (V_0), мл	Абсолютная погрешность (triangle V=frac{triangle}{2}), мл	Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%})
1	68	2	3,0%
2	280	10	3,6%
3	27	1,5	5,6%
4	480	20	4,2%

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?

Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})