15п 4 на окружности
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Как обозначать числа с пи на числовой окружности?
Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.
Обозначаем числа (2π), (π), (frac ), (-frac ), (frac )
Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.
Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.
Отметим точку (frac ) . (frac ) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.
Обозначим на окружности точки (-) (frac ) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.
Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.
Теперь рассмотрим пример посложнее. Отметим на окружности число (frac ) . Для этого дробь (frac ) переведем в смешанный вид (frac ) (=1) (frac ) , т.е. (frac ) (=π+) (frac ) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.
Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac ) .
Обозначаем числа (frac ), (frac ), (frac )
Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac ) , (frac ) и (frac ) .
(frac ) – это половина от (frac ) (то есть, (frac ) (=) (frac ) (:2)) , поэтому расстояние (frac ) – это половина четверти окружности.
(frac ) – это треть от (π) (иначе говоря, (frac ) (=π:3)), поэтому расстояние (frac ) – это треть от полукруга.
(frac ) – это половина (frac ) (ведь (frac ) (=) (frac ) (:2)) поэтому расстояние (frac ) – это половина от расстояния (frac ) .
Вот так они расположены друг относительно друга:
Замечание: Расположение точек со значением (0), (frac ) ,(π), (frac ) , (frac ) , (frac ) , (frac ) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.
Разные расстояние на окружности наглядно:
Обозначаем числа (frac ), (-frac ), (frac )
Обозначим на окружности точку (frac ) , для этого выполним следующие преобразования: (frac ) (=) (frac ) (=) (frac ) (+) (frac ) (=π+) (frac ) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac ) .
Отметим на окружности точку (-) (frac ) . Преобразовываем: (-) (frac ) (=-) (frac ) (-) (frac ) (=-π-) (frac ) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac ) .
Нанесем точку (frac ) , для этого преобразуем (frac ) (=) (frac ) (=) (frac ) (-) (frac ) (=2π-) (frac ) . Значит, чтобы поставить точку со значением (frac ) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac ) .
Обозначаем числа (10π), (-3π), (frac ) ,(frac ), (-frac ), (-frac )
Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.
Из этого примера можно сделать вывод:
Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.
То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».
Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).
Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).
Кстати, там же будут находиться все нечетные (π).
Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).
Сейчас обозначим число (frac ) . Как обычно, преобразовываем: (frac ) (=) (frac ) (+) (frac ) (=3π+) (frac ) (=2π+π+) (frac ) . Два пи – отбрасываем, и получается что, для обозначения числа (frac ) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac ) (т.е. половину окружности и еще четверть).
Отметим (frac ) . Вновь преобразования: (frac ) (=) (frac ) (=) (frac ) (+) (frac ) (=5π+) (frac ) (=4π+π+) (frac ) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac ) – и мы найдем место точки (frac ) .
Нанесем на окружность число (-) (frac ) .
(-) (frac ) (= -) (frac ) (-) (frac ) (=-10π-) (frac ) . Значит, место (-) (frac ) совпадает с местом числа (-) (frac ) .
Обозначим (-) (frac ) .
(-) (frac ) (=-) (frac ) (+) (frac ) (=-5π+) (frac ) (=-4π-π+) (frac ) . Для обозначение (-) (frac ) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac ) .
Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
Базовым объектом изучения в тригонометрии является угол.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
 |
Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным . |
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |  |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
 |
Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac =frac =frac .) Тогда радианная мера угла: $$ angle AOB=frac =frac =frac $$ |
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (pi) | (frac ) | (2pi) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
 |
Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например: |
| Отметим на числовой окружности точки, соответствующие (frac , frac , frac , frac , pi), а также (-frac , -frac , -frac , -frac , -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности. |
 |
| Отметим на числовой окружности точки, соответствующие (frac , frac , frac ), и (-frac ). Все четыре точки совпадают, т.к. begin Mleft(frac right)=Mleft(frac +2pi kright)\ frac -2pi=-frac \ frac +2pi=frac \ frac +4pi=frac end |
 |
п.5. Интервалы и отрезки на числовой окружности
Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
| Числовой промежуток | Соответствующая дуга числовой окружности |
| Отрезок | |
$$ -frac lt t lt frac $$  а также, с учетом периода $$ -frac +2pi klt tltfrac +2pi k $$ |
 |
| Интервал | |
$$ -frac leq t leq frac $$  а также, с учетом периода $$ -frac +2pi kleq tleqfrac +2pi k $$ |
 |
| Полуинтервал | |
$$ -frac leq t ltfrac $$  а также, с учетом периода $$ -frac +2pi kleq tltfrac +2pi k $$ |
 |
п.6. Примеры
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?
Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^ =frac .\ EC=60^ =frac .\ AE=EC+CD=90^ +30^ =120^ =frac .\ ED=EC+CD=60^ +90^ =150^ =frac . end
Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; frac ; frac ; frac ).
| Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac =-90^ , frac =135^ \ frac =210^ , frac =315^ end |  |
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; 5pi; frac ; frac ).
| Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac =frac cdotpi=-6pi+frac rightarrow frac =90^ \ 5pi=4pi+pirightarrow pi=180^ \ frac =frac pi=3pi-frac rightarrow pi-frac =frac \ frac =frac pi=7pi-frac rightarrow pi-frac =frac end |
 |
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
 |
Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac =1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac approx frac =4,71, 2piapprox 6,28 end |
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb )), запишите количество полученных базовых точек.
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
Как обозначать числа с пи на числовой окружности?
Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.
Обозначаем числа (2π), (π), (frac<π><2>), (-frac<π><2>), (frac<3π><2>)
Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.
Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.
Отметим точку (frac<π><2>) . (frac<π><2>) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.
Обозначим на окружности точки (-) (frac<π><2>) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.
Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.
Теперь рассмотрим пример посложнее. Отметим на окружности число (frac<3π><2>) . Для этого дробь (frac<3><2>) переведем в смешанный вид (frac<3><2>) (=1) (frac<1><2>) , т.е. (frac<3π><2>) (=π+) (frac<π><2>) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.
Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac<3π><2>) .
Обозначаем числа (frac<π><4>), (frac<π><3>), (frac<π><6>)
Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac<π><4>) , (frac<π><3>) и (frac<π><6>) .
(frac<π><4>) – это половина от (frac<π><2>) (то есть, (frac<π><4>) (=) (frac<π><2>) (:2)) , поэтому расстояние (frac<π><4>) – это половина четверти окружности.
(frac<π><4>) – это треть от (π) (иначе говоря, (frac<π><3>) (=π:3)), поэтому расстояние (frac<π><3>) – это треть от полукруга.
(frac<π><6>) – это половина (frac<π><3>) (ведь (frac<π><6>) (=) (frac<π><3>) (:2)) поэтому расстояние (frac<π><6>) – это половина от расстояния (frac<π><3>) .
Вот так они расположены друг относительно друга:
Замечание: Расположение точек со значением (0), (frac<π><2>) ,(π), (frac<3π><2>) , (frac<π><4>) , (frac<π><3>) , (frac<π><6>) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.
Разные расстояние на окружности наглядно:
Обозначаем числа (frac<7π><6>), (-frac<4π><3>), (frac<7π><4>)
Обозначим на окружности точку (frac<7π><6>) , для этого выполним следующие преобразования: (frac<7π><6>) (=) (frac<6π + π><6>) (=) (frac<6π><6>) (+) (frac<π><6>) (=π+) (frac<π><6>) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac<π><6>) .
Отметим на окружности точку (-) (frac<4π><3>) . Преобразовываем: (-) (frac<4π><3>) (=-) (frac<3π><3>) (-) (frac<π><3>) (=-π-) (frac<π><3>) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac<π><3>) .
Нанесем точку (frac<7π><4>) , для этого преобразуем (frac<7π><4>) (=) (frac<8π-π><4>) (=) (frac<8π><4>) (-) (frac<π><4>) (=2π-) (frac<π><4>) . Значит, чтобы поставить точку со значением (frac<7π><4>) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac<π><4>) .
Обозначаем числа (10π), (-3π), (frac<7π><2>) ,(frac<16π><3>), (-frac<21π><2>), (-frac<29π><6>)
Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.
Из этого примера можно сделать вывод:
Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.
То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».
Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).
Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).
Кстати, там же будут находиться все нечетные (π).
Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).
Сейчас обозначим число (frac<7π><2>) . Как обычно, преобразовываем: (frac<7π><2>) (=) (frac<6π><2>) (+) (frac<π><2>) (=3π+) (frac<π><2>) (=2π+π+) (frac<π><2>) . Два пи – отбрасываем, и получается что, для обозначения числа (frac<7π><2>) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac<π><2>) (т.е. половину окружности и еще четверть).
Отметим (frac<16π><3>) . Вновь преобразования: (frac<16π><3>) (=) (frac<15π + π><3>) (=) (frac<15π><3>) (+) (frac<π><3>) (=5π+) (frac<π><3>) (=4π+π+) (frac<π><3>) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac<π><3>) – и мы найдем место точки (frac<16π><3>) .
Нанесем на окружность число (-) (frac<21π><2>) .
(-) (frac<21π><2>) (= -) (frac<20π><2>) (-) (frac<π><2>) (=-10π-) (frac<π><2>) . Значит, место (-) (frac<21π><2>) совпадает с местом числа (-) (frac<π><2>) .
Обозначим (-) (frac<29π><6>) .
(-) (frac<29π><6>) (=-) (frac<30π><6>) (+) (frac<π><6>) (=-5π+) (frac<π><6>) (=-4π-π+) (frac<π><6>) . Для обозначение (-) (frac<29π><6>) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac<π><6>) .
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
http://cos-cos.ru/ege/zadacha209/237/
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
0 голосов
268 просмотров
СРОЧНО! Выразите в градусной мере угол 15пи/4
- срочно
- выразите
- 10 — 11 классы
- алгебра
Алгебра
valeriyamarkova_zn
13 Май, 18
|
268 просмотров
Дан 1 ответ
0 голосов
Правильный ответ
675 градусов это правильно
ALDR5_zn
13 Май, 18
Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать! Если вы, конечно, собираетесь находить точки на числовой окружности.
Обозначаем числа (2π), (π), (frac{π}{2}), (-frac{π}{2}), (frac{3π}{2})
Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.

Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.

Отметим точку (frac{π}{2}). (frac{π}{2}) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.

Обозначим на окружности точки (-)(frac{π}{2}). Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.

Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.

Теперь рассмотрим пример посложнее. Отметим на окружности число (frac{3π}{2}). Для этого дробь (frac{3}{2}) переведем в смешанный вид (frac{3}{2})(=1)(frac{1}{2}), т.е. (frac{3π}{2})(=π+)(frac{π}{2}). Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

Задание 1. Отметьте на числовой окружности точки (-2π),(-)(frac{3π}{2}).
Обозначаем числа (frac{π}{4}), (frac{π}{3}), (frac{π}{6})
Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac{π}{4}), (frac{π}{3}) и (frac{π}{6}).
(frac{π}{4}) – это половина от (frac{π}{2}) (то есть, (frac{π}{4}) (=)(frac{π}{2})(:2)) , поэтому расстояние (frac{π}{4}) – это половина четверти окружности.

(frac{π}{4}) – это треть от (π) (иначе говоря,(frac{π}{3})(=π:3)), поэтому расстояние (frac{π}{3}) – это треть от полукруга.

(frac{π}{6}) – это половина (frac{π}{3}) (ведь (frac{π}{6})(=)(frac{π}{3})(:2)) поэтому расстояние (frac{π}{6}) – это половина от расстояния (frac{π}{3}).

Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением (0), (frac{π}{2}),(π), (frac{3π}{2}), (frac{π}{4}), (frac{π}{3}), (frac{π}{6}) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.
Разные расстояние на окружности наглядно:
Обозначаем числа (frac{7π}{6}), (-frac{4π}{3}), (frac{7π}{4})
Обозначим на окружности точку (frac{7π}{6}), для этого выполним следующие преобразования: (frac{7π}{6})(=)(frac{6π + π}{6})(=)(frac{6π}{6})(+)(frac{π}{6})(=π+)(frac{π}{6}). Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac{π}{6}).

Отметим на окружности точку (-)(frac{4π}{3}). Преобразовываем: (-)(frac{4π}{3})(=-)(frac{3π}{3})(-)(frac{π}{3})(=-π-)(frac{π}{3}). Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac{π}{3}).

Нанесем точку (frac{7π}{4}), для этого преобразуем (frac{7π}{4})(=)(frac{8π-π}{4})(=)(frac{8π}{4})(-)(frac{π}{4})(=2π-)(frac{π}{4}). Значит, чтобы поставить точку со значением (frac{7π}{4}), надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac{π}{4}).

Задание 2. Отметьте на числовой окружности точки (-)(frac{π}{6}),(-)(frac{π}{4}),(-)(frac{π}{3}),(frac{5π}{4}),(-)(frac{7π}{6}),(frac{11π}{6}), (frac{2π}{3}),(-)(frac{3π}{4}).
Обозначаем числа (10π), (-3π), (frac{7π}{2}) ,(frac{16π}{3}), (-frac{21π}{2}), (-frac{29π}{6})
Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.

Из этого примера можно сделать вывод:
Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.
То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».
Еще один вывод:
Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).
Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).

Кстати, там же будут находиться все нечетные (π).
Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).
Сейчас обозначим число (frac{7π}{2}). Как обычно, преобразовываем: (frac{7π}{2})(=)(frac{6π}{2})(+)(frac{π}{2})(=3π+)(frac{π}{2})(=2π+π+)(frac{π}{2}). Два пи – отбрасываем, и получается что, для обозначения числа (frac{7π}{2}) нужно от нуля в положительную сторону пройти расстояние равное (π+)(frac{π}{2}) (т.е. половину окружности и еще четверть).

Отметим (frac{16π}{3}). Вновь преобразования: (frac{16π}{3})(=)(frac{15π + π}{3})(=)(frac{15π}{3})(+)(frac{π}{3})(=5π+)(frac{π}{3})(=4π+π+)(frac{π}{3}). Ясно, что от нуля надо пройти расстояние равное (π+)(frac{π}{3}) – и мы найдем место точки (frac{16π}{3}).

Нанесем на окружность число (-)(frac{21π}{2}).
(-)(frac{21π}{2})(= -)(frac{20π}{2})(-)(frac{π}{2})(=-10π-)(frac{π}{2}). Значит, место (-)(frac{21π}{2}) совпадает с местом числа (-)(frac{π}{2}).

Обозначим (-)(frac{29π}{6}).
(-)(frac{29π}{6})(=-)(frac{30π}{6})(+)(frac{π}{6})(=-5π+)(frac{π}{6})(=-4π-π+)(frac{π}{6}). Для обозначение (-)(frac{29π}{6}), на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac{π}{6}).

Задание 3. Отметьте на числовой окружности точки (-8π),(-7π), (frac{11π}{4}),(-)(frac{7π}{3}),(frac{17π}{6}),(-)(frac{20π}{3}),(-)(frac{11π}{2}).
Скачать статью
Построение тригонометрической окружности
А теперь сделай вот что: возьми-ка в руки циркуль и нарисуй любую (самую любую, но лучше достаточно немаленькую) окружность.
Получилось?
Ну да ладно, задачка не самая сложная. Так, ты не потерял ту точку, в которой у тебя был центр (куда ты прикладывал острую ножку циркуля)? Я вот у себя потерял, растяпа! Ну ладно, найду!
А что пока делать тебе?
А вот что: проведи через эту точку две линии, которые пересекаются «прямым крестиком», то есть под прямым углом. И пусть их точка пересечения – это центр (который ты не потерял!) окружности.
Нарисовал? У меня получилось что-то вроде вот этого.
Правда я чуть-чуть поторопился и сразу «обозвал» эти прямые ( displaystyle x) и ( displaystyle y) и точку пересечения через ( displaystyle O).
А что такое в таком случае ( displaystyle R)?
Это радиус нашей окружности.
Как называлась наша тема? Единичная окружность.
Тогда будем считать ( но не будем так рисовать!), что ( displaystyle R=1 ).
А рисовать мы так не будем, потому что на такой крошечной картинке ты ничего не разберешь! Ты же понимаешь, что когда инженеры проектируют самолеты, скажем, они не рисуют его в натуральную величину?
Так и мы не будем рисовать единичную окружность в самом деле единичной. Это нам нужно исключительно для удобства.
Теперь отмечаем: ( displaystyle OR=1). Что же мы с тобой на самом деле сделали? А вот что:
Мы поместили нашу окружность в систему координат ( displaystyle mathbf{X0Y}), сделав центр окружности началом координат!
Это позволит изучать свойства такой окружности уже не с геометрической, а с математической точки зрения. Этот подход был придуман хитрым математиком и философом Рене Декартом еще в 17 веке!
Перегнать фигуру в цифры, каково, а?
Но допустим, мы поместили нашу окружность в координаты. В скольких точках она пересекается с осями системы координат?
В четырех. Вот они:
Эти точки ( displaystyle left( A; B; C; D right)) имеют координаты:
( displaystyle Aleft( 1,0 right)); ( displaystyle Bleft( 0,1 right)); ( displaystyle Cleft( -1;0 right)); ( displaystyle Dleft( 0;-1 right)).
Теперь вспомни, как называются области, на которые этот «координатный крестик» делит всю плоскость?
Они называются координатные четверти.
Тогда посмотри на рисунок. Наша окружность тоже оказалась разрезанной на 4 равные дольки. Давай пронумеруем каждую из этих долек против часовой стрелки:
Ты уже можешь догадаться, как называются эти самые дольки:
1 четверть, 2 четверть, 3 четверть, 4 четверть
(Прямо как четверти в школе!)
Углы на тригонометрической окружности
Теперь давай сделаем еще вот что. Снова посмотрим на предыдущую картинку.
Чему на ней равен ( displaystyle angle AOB)?
Он равен ( displaystyle 90{}^circ ).
Также, как и ( displaystyle angle BOC), как и угол ( displaystyle angle COD), и угол ( displaystyle angle DOA).
( displaystyle angle text{AOB}=angle text{BOC}=angle text{COD}=angle text{DOA}=90{}^circ )
Тогда чему равна их сумма?
Она равна ( displaystyle 360{}^circ ).
Вместе же эти 4 угла составляют всю окружность целиком!
Градусная мера окружности равна ( displaystyle 360{}^circ )!
( displaystyle angle Atext{OC}=angle text{AOB}+angle text{BOC}=180{}^circ )
Что еще можно вытянуть? А вот что:
( displaystyle angle Atext{OD}=angle text{AOB}+angle text{BOC}+angle text{COD}=270{}^circ )
Отметим эти значения также на нашей окружности:
Однако, ты нередко можешь увидеть и вот такую картинку:
где вместо привычных нам градусов появляются некие буковки «пи» ( displaystyle pi ) с цифрами.
В чем же тут дело, кто прав и кто виноват?
Ну так вот, кто прав, кто виноват, решать, увы, не нам. Но чтобы «воз не был поныне там», нам нужно уделить этому моменту пару минут времени.
В самом деле, есть два способа измерять углы:
- Через градусы
- Через радианы
Как измерять углы через градусы мы все знаем. Это нам привычно. Однако в некоторых случаях их измеряют по-другому (как в градуснике есть несколько шкал: цельсий, кельвин, фаренгейт и т. д.), а именно: через радианы.
Для того, чтобы перейти от одной формы записи к другой, используется вот такое основное соотношение:
( displaystyle 180{}^circ =pi ~рад.)
И все, больше знать ничего не надо!
По пропорции ты легко получишь, что для того, чтобы пересчитать угол из градусов в радианы, нужно применить вот такую незамысловатую формулу:
( displaystyle P~рад.=frac{alpha {}^circ cdot pi }{180})
И наоборот: от радиан к градусам:
( displaystyle alpha {}^circ =frac{P~рад.cdot 180}{pi })
Ты должен уметь ориентироваться и в той, и в другой форме записи.
Потренируйся на следующих примерах:
- Перевести угол в ( displaystyle 30) градусов в радианы;
- Перевести угол ( displaystyle frac{pi }{4}) радиан в градусы;
- Перевести угол в ( displaystyle 60) градусов в радианы;
- Перевести угол в ( displaystyle frac{pi }{2}) радиан в градусы;
- Перевести угол в ( displaystyle 120) градусов в радианы;
- Перевести угол в ( displaystyle frac{3pi }{4}) радиан в градусы;
- Перевести угол в ( displaystyle 150) градусов в радианы.
Я сделаю только первые два, а остальные реши сам!
- ( P~рад.=frac{30cdot pi }{180}=frac{pi }{6}), тогда угол в ( displaystyle 30) градусов равен углу в ( displaystyle frac{pi }{6}) радиан;
- ( alpha {}^circ =frac{frac{pi }{4}cdot 180}{pi }=frac{45pi }{pi }=45{}^circ ), тогда угол в ( displaystyle frac{pi }{4}) радиан равен углу в ( displaystyle 45) градусов.
Все очень просто, не так ли? Остальные значения ты можешь найти в следующей таблице:
| ( displaystyle 0{}^circ ) | ( displaystyle 30{}^circ ) | ( displaystyle 45{}^circ ) | ( displaystyle 60{}^circ ) | ( displaystyle 90{}^circ ) | ( displaystyle 120{}^circ ) | ( displaystyle 135{}^circ ) | ( displaystyle 150{}^circ ) | ( displaystyle 180{}^circ ) |
| ( displaystyle 0) | ( displaystyle frac{pi }{6}) | ( displaystyle frac{pi }{4}) | ( displaystyle frac{pi }{3}) | ( displaystyle frac{pi }{2}) | ( displaystyle frac{2pi }{3}) | ( displaystyle frac{3pi }{4}) | ( displaystyle frac{5pi }{6}) | ( displaystyle pi ) |
| ( displaystyle 210{}^circ ) | ( displaystyle 225{}^circ ) | ( displaystyle 240{}^circ ) | ( displaystyle 270{}^circ ) | ( displaystyle 300{}^circ ) | ( displaystyle 315{}^circ ) | ( displaystyle 330{}^circ ) | ( displaystyle 360{}^circ ) |
| ( displaystyle frac{7pi }{6}) | ( displaystyle frac{5pi }{4}) | ( displaystyle frac{4pi }{3}) | ( displaystyle frac{3pi }{2}) | ( displaystyle frac{5pi }{3}) | ( displaystyle frac{7pi }{4}) | ( displaystyle frac{11pi }{6}) | ( displaystyle 2pi ) |
Так что впредь не удивляйся, когда ты увидишь вместо привычных градусов углы в радианах. Теперь ты знаешь, что это такое, и с чем его едят!
Синус, косинус, тангенс и котангенс на тригонометрической окружности
Но мы с тобой и так слишком увлеклись. Ты давно уже, наверное, заждался обещанных синусов и косинусов на тригонометрической окружности. Не смею более отвлекаться!
Давай сделаем вот что: совместим два знакомых нам объекта: тригонометрическую окружность (пока в том виде, в котором она у нас есть) и прямоугольный треугольник.
Что нам нужно, чтобы наш треугольник «целиком влез» в окружность?
Его гипотенуза должна быть не более единицы. Пусть же она у нас в точности будет равна единице.
Совместим мы их вот так:
Я нарисовал прямоугольный треугольник с центром в начале координат и гипотенузой равной ( 1). Это так потому, что окружность-то у меня единичная!
Тогда по определению синуса и косинуса:
- ( sin alpha =frac{AB}{OB}=frac{AB}{1}=AB)
- ( cos alpha =frac{OA}{OB}=frac{OA}{1}=OA)
А что же такое отрезки ( OA) и ( OB)? Чему равны их длины?
Смотри, сейчас будет самое главное: мы взяли угол ( alpha ) и провели луч, соединяющий этот угол с точкой на окружности.
Обозначим эту точку через ( B). Пусть ( B) имеет координаты ( Bleft( x,y right)).
Тогда длина отрезка ( OA) равна ( x), а длина отрезка ( AB)–равна ( y).
Но мы с тобой помним, что ( sin alpha =AB), ( cos alpha =OA), тогда:
- ( y=sin alpha )
- ( x=cos alpha )
Ух ты! Это надо еще раз обдумать, что же мы такое получили.
Давай проговорим еще раз: мы выбрали некоторый угол ( alpha ) и хотим найти его синус и косинус.
Что мы делаем?
- Проводим единичную окружность с центром, совпадающим с вершиной угла;
- Ищем точку пересечения нашего угла с окружностью;
- Её «иксовая» координата – это косинус нашего угла;
- Её «игрековая» координата – это синус нашего угла.
Вот и все! Теперь синус и косинус искать стало намного проще! Допустим, мы хотим найти синус, косинус ( 30) градусов.
Отмечаем ( 30) градусов на окружности и «достраиваем» этот угол до треугольника (как показано на рисунке выше).
Как найти ( x) и ( y)?
Да очень просто: в прямоугольном треугольнике катет, лежащий против угла в ( 30) градусов равен половине гипотенузы (это известный факт из геометрии 7 класса).
Так как гипотенуза равна ( 1), то противолежащий ей катет равен ( 0,5), откуда:
( sin 30{}^circ =0,5)
Что касается косинуса: для этого нам потребуется заметить, что выполняется тривиальное утверждение (основное тригонометрическое тождество):
( si{{n}^{2}}alpha +co{{s}^{2}}alpha =1)
Как ты думаешь, откуда оно берется? Да это же пресловутая теорема Пифагора!
Наши катеты в треугольничке равны ( x) и ( y), которые в свою очередь совпадают с ( cos alpha ) и ( sin alpha ). Гипотенуза в треугольнике равна ( 1).
Тогда:
( {{x}^{2}}+{{y}^{2}}=1) или, что то же самое,
( si{{n}^{2}}alpha +co{{s}^{2}}alpha =1)
Эта формула позволит по известному синусу вычислить неизвестный косинус и наоборот.
В частности, если:
( si{{n}^{2}}30{}^circ +co{{s}^{2}}30{}^circ =1) и ( sin 30{}^circ =0,5), то
( frac{1}{4}+co{{s}^{2}}30{}^circ =1)
( displaystyle co{{s}^{2}}30{}^circ =frac{3}{4})
( displaystyle cos 30{}^circ =pm sqrt{frac{3}{4}}=pm frac{sqrt{3}}{2})
Определение знака синуса, косинуса, тангенса и котангенса
Вообще, этот вопрос заслуживает особого внимания, но здесь все просто: у угла ( displaystyle 30) градусов и синус и косинус положительны (смотри рисунок), тогда берем знак «плюс».
( displaystyle cos 30{}^circ =frac{sqrt{3}}{2})
Теперь попробуй на основе вышеизложенного найти синус и косинус углов: ( displaystyle 60{}^circ ) и ( displaystyle 45{}^circ )
Можно схитрить: в частности для угла в ( displaystyle 60{}^circ ) градусов. Так как если один угол прямоугольного треугольника равен ( displaystyle 60{}^circ ) градусам, то второй – ( displaystyle 30{}^circ ) градусам. Теперь вступают в силу знакомые тебе формулы:
( displaystyle sin 30{}^circ =cos 60{}^circ )
( displaystyle sin 60{}^circ =cos 30{}^circ )
Тогда так как ( displaystyle sin 30{}^circ =0,5), то и ( displaystyle cos 60{}^circ =0,5). Так как ( displaystyle cos 30{}^circ =frac{sqrt{3}}{2}), то и ( displaystyle sin 60{}^circ =frac{sqrt{3}}{2}).
C ( displaystyle 45) градусами все еще проще: так если один из углов прямоугольного треугольника равен ( displaystyle 45) градусам, то и другой тоже равен ( displaystyle 45) градусам, а значит такой треугольник равнобедренный.
Значит, его катеты равны. А значит равны его синус и косинус.
Тогда:
( displaystyle si{{n}^{2}}45{}^circ +co{{s}^{2}}45{}^circ =2si{{n}^{2}}45{}^circ =1)
( displaystyle si{{n}^{2}}45{}^circ =co{{s}^{2}}45{}^circ =1/2)
Откуда: ( displaystyle sin 45{}^circ =cos 45{}^circ =sqrt{1/2}=frac{sqrt{2}}{2})
Теперь найди сам по новому определению (через икс и игрек!) синус и косинус углов в ( displaystyle 0) градусов и ( displaystyle 90) градусов. Здесь уже никакие треугольники нарисовать не получится! Уж слишком они будут плоские!
У тебя должно было получиться:
( displaystyle sin 0{}^circ =0), ( displaystyle cos 0{}^circ =1), ( displaystyle sin 90{}^circ =1), ( displaystyle cos 90{}^circ =0).
Тангенс и котангенс ты можешь отыскать самостоятельно по формулам:
( displaystyle text{t}g alpha =frac{sin alpha }{cos alpha }), ( displaystyle ctg alpha =frac{cos alpha }{sin alpha })
Обрати внимание, что на ноль делить нельзя!!
Теперь все полученные числа можно свести в таблицу:
Здесь приведены значения синуса, косинуса, тангенса и котангенса углов I четверти.
Для удобства углы приведены как в градусах, так и в радианах (но ты-то теперь знаешь связь между ними!). Обрати внимание на 2 прочерка в таблице: а именно у котангенса нуля и тангенса ( displaystyle 90) градусов. Это неспроста!
В частности:
( displaystyle ctg 0=frac{cos 0}{sin 0}=frac{1}{0}=?????)
Поэтому мы с тобой будем считать, что тангенс ( displaystyle 90) градусов и котангенс нуля просто-напросто не определены!
Теперь давай обобщим понятие синус и косинус на совсем произвольный угол. Я рассмотрю здесь два случая:
- Угол лежит в пределах от ( displaystyle 0) до ( displaystyle 360) градусов;
- Угол больше ( displaystyle 360) градусов.
Честно говоря, я скривил немного душой, говоря про «совсем все» углы. Они бывают также и отрицательными! Но этот случай мы с тобой рассмотрим чуть позже. Вначале остановимся на первом случае.
Если угол лежит в 1 четверти – то тут все понятно, мы этот случай уже рассмотрели и даже таблицы нарисовали.
Теперь же пусть наш угол больше ( displaystyle 90) градусов и не больше чем ( displaystyle 360).
Это значит, что он расположен либо во 2, либо в 3 или же в 4 четверти.
Как мы поступаем? Да точно так же!
Давай рассмотрим вместо вот такого случая…
…вот такой:
То есть рассмотрим угол ( displaystyle alpha ), лежащий во второй четверти. Что мы можем сказать про него?
У точки ( displaystyle {{M}_{1}}), которая является точкой пересечения луча и окружности по-прежнему имеет 2 координаты (ничего сверхъестественного, правда?). Это координаты ( displaystyle {{x}_{1}}) и ( displaystyle {{y}_{1}}).
Причем первая координата отрицательная, а вторая – положительная! Это значит, что у углов второй четверти косинус отрицателен, а синус – положителен!
Удивительно, правда? До этого мы еще ни разу не сталкивались с отрицательным косинусом.
Да и в принципе этого не могло быть, когда мы рассматривали тригонометрические функции как отношения сторон треугольника.
Кстати, подумай, у каких углов косинус равен ( displaystyle -1)? А у каких ( displaystyle -1) равен синус?
Аналогично можно рассмотреть углы во всех остальных четвертях. Я лишь напомню, что угол отсчитывается против часовой стрелки! (так, как это показано на последнем рисунке!).
Конечно, можно и отсчитывать в другую сторону, но вот подход к таким углам будет уже несколько другой.
Исходя из приведенных выше рассуждений, можно расставить знаки у синуса, косинуса, тангенса (как синус деленный на косинус) и котангенса (как косинус деленный на синус) для всех четырех четвертей.
Но еще раз повторюсь, нет смысла запоминать этот рисунок. Все, что тебе нужно знать:
Синус – это игрек. Косинус – это икс. Тангенс – это синус деленный на косинус. Котангенс – это косинус деленный на синус.
Углы больше 360 градусов
А как быть с углами, большими чем ( displaystyle 360) градусов?
Возьму я, скажем, угол в ( displaystyle 30) градусов (( displaystyle frac{pi }{6}) радиан) и пойду от него против часовой стрелки…
На рисунке я нарисовал спираль, но ты-то понимаешь, что на самом деле у нас нет никакой спирали: у нас есть только окружность.
Так куда же мы попадем, если стартуем от определенного угла и пройдем полностью весь круг (( displaystyle 360) градусов или ( displaystyle 2pi ) радиан)?
Куда мы придем? А придем мы в тот же самый угол!
Это же, конечно, справедливо и для любого другого угла:
Взяв произвольный угол ( displaystyle alpha ) и пройдя полностью всю окружность, мы вернемся в тот же самый угол ( displaystyle alpha ).
Что же нам это даст? А вот что: если ( displaystyle sin alpha =y,~cos alpha =x), то
( displaystyle sin left( alpha +2pi k right)=y), ( displaystyle cos left( alpha +2pi k right)=x), откуда окончательно получим:
( displaystyle sin left( alpha +2pi k right)=sinalpha )
( displaystyle cos left( alpha +2pi k right)=cosalpha )
Для любого целого ( displaystyle k). Это значит, что синус и косинус являются периодическими функциями с периодом ( displaystyle 2pi ).
Таким образом, нет никакой проблемы в том, чтобы найти знак теперь уже произвольного угла: нам достаточно отбросить все «целые круги», которые умещаются в нашем угле и выяснить, в какой четверти лежит оставшийся угол.
Например, найти знак:
- ( displaystyle text{sin}1000{}^circ ),
- ( displaystyle text{cos} 605{}^circ ),
- ( displaystyle text{cos}frac{16pi }{7}),
- ( displaystyle text{sin}frac{19pi }{4}).
Проверяем:
Отрицательные углы
Отрицательные углы в тригонометрии откладываются на тригонометрическом круге вниз от начала, по направлению движения часовой стрелки:
Давай вспомним, как мы до этого откладывали углы на тригонометрической окружности.
Мы шли от положительного направления оси ( displaystyle Ox) против часовой стрелки:
Тогда на нашем рисунке построен угол, равный ( displaystyle 180+45=225{}^circ ). Аналогичным образом мы строили все углы.
Однако ничего нам не запрещает идти от положительного направления оси ( displaystyle Ox) по часовой стрелке.
Мы будем тоже получать различные углы, но они будут уже отрицательными:
А следующей картинке изображено два угла, равные по абсолютной величине (если не знаешь, что это такое, читай здесь про «Модуль числа»), но противоположные по знаку:
В целом правило можно сформулировать вот так:
- Идем против часовой стрелки – получаем положительные углы
- Идем по часовой стрелке – получаем отрицательные углы
Схематично правило изображено вот на этом рисунке:
Ты мог бы задать мне вполне резонный вопрос: ну углы нам нужны для того, чтобы измерять у них значения синуса, косинуса, тангенса и котангенса.
Так есть ли разница, когда у нас угол положительный, а когда – отрицательный? Я отвечу тебе: как правило есть.
Однако ты всегда можешь свести вычисление тригонометрической функции от отрицательного угла к вычислению функции в угле положительном.
Посмотри на следующую картинку:
Я построил два угла, они равны по абсолютному значению, но имеют противоположный знак. Отметим для каждого из углов его синус и косинус на осях.
Что мы с тобой видим? А вот что:
Синусы у углов ( displaystyle alpha ) и ( displaystyle -alpha ) противоположны по знаку!
Тогда если ( displaystyle text{sin} text{ }!!alpha!!text{ }=text{y}),
то ( displaystyle sin left( -text{ }!!alpha!!text{ } right)=-text{y})
( displaystyle sin left( -text{ }!!alpha!!text{ } right)=-text{sin} text{ }!!alpha!!text{ }).
Косинусы у углов ( displaystyle alpha ) и ( displaystyle -alpha ) совпадают!
Тогда если ( displaystyle text{cos} text{ }!!alpha!!text{ }=text{x}),
то и ( displaystyle cos left( -text{ }!!alpha!!text{ } right)=text{x})
( displaystyle cos left( -text{ }!!alpha!!text{ } right)=text{cos} text{ }!!alpha!!text{ })
Так как ( displaystyle text{tg}left( -text{ }!!alpha!!text{ } right)=frac{text{sin}left( -text{ }!!alpha!!text{ } right)}{text{cos}left( -text{ }!!alpha!!text{ } right)}=frac{-text{sin}left( text{ }!!alpha!!text{ } right)}{text{cos}left( text{ }!!alpha!!text{ } right)}), то:
( displaystyle text{tg}left( -text{ }!!alpha!!text{ } right)=-text{tg }!!alpha!!text{ })
Так как ( displaystyle text{ctg}left( -text{ }!!alpha!!text{ } right)=frac{text{cos}left( -text{ }!!alpha!!text{ } right)}{text{sin}left( -text{ }!!alpha!!text{ } right)}=frac{text{cos}left( text{ }!!alpha!!text{ } right)}{-text{sin}left( text{ }!!alpha!!text{ } right)}), то:
( displaystyle text{ctg}left( -text{ }!!alpha!!text{ } right)=-text{ctg} text{ }!!alpha!!text{ })
Таким образом, мы всегда можем избавиться от отрицательного знака внутри любой тригонометрической функции: либо просто уничтожив его, как у косинуса, либо поставив его перед функцией, как у синуса, тангенса и котангенса.
Кстати, вспомни-ка, как называется функция ( displaystyle f(x)), у которой для любого допустимого ( displaystyle x) выполняется:( displaystyle f(-x)=-f(x))?
Такая функция называется нечетной.
А если же для любого допустимого ( displaystyle x) выполняется: ( displaystyle f(-x)=f(x))? То в таком случае функция называется четной.
Таким образом, мы с тобой только что показали, что:
Синус, тангенс и котангенс – нечетные функции, а косинус – четная.
Таким образом, как ты понимаешь, нет никакой разницы, ищем ли мы синус от положительного угла или отрицательного: справиться с минусом очень просто. Так что нам не нужны таблицы отдельно для отрицательных углов.
С другой стороны, согласись, было бы очень удобно зная только тригонометрические функции углов первой четверти, уметь вычислять аналогичные функции и для остальных четвертей.
Можно ли это сделать? Конечно, можно!
У тебя есть по крайней мере 2 пути: первый – строить треугольник и применять теорему Пифагора (так мы с тобой и отыскали значения тригонометрических функций для основных углов первой четверти)
Второй – запомнив значения функций для углов в первой четверти и некое несложное правило, уметь вычислять тригонометрические функции для всех остальных четвертей.
Второй способ избавит тебя от долгой возни с треугольниками и с Пифагором, поэтому мне он видится более перспективным:
Итак, данный способ (или правило) называется формулами приведения.
Формулы приведения
Грубо говоря, эти формулы помогут тебе не запоминать вот такую таблицу (она между прочим содержит 98 чисел!):
…если ты помнишь вот эту (всего на 20 чисел):
То есть ты сможешь не забивать себе голову совершенно ненужными 78 числами! Пусть, например, нам нужно вычислить ( displaystyle text{sin} 855{}^circ ). Ясно, что в маленькой таблице такого нет. Что же нам делать? А вот что:
Во-первых, нам понадобятся следующие знания:
Синус и косинус имеют период ( displaystyle 2pi ) (( displaystyle 360) градусов)
То есть
( displaystyle sinleft( 2pi k+x right)=sin x)
( displaystyle cosleft( 2pi k+x right)=cos x)
Тангенс (котангенс) имеют период ( displaystyle pi ) (( displaystyle 180) градусов)
( displaystyle tgleft( pi k+x right)=tg x)
( displaystyle ctgleft( pi k+x right)=ctg x)
( displaystyle k) – любое целое число
Синус и тангенс – функции нечетные, а косинус – четная:
( displaystyle sinleft( -x right)=-sin x)
( displaystyle tgleft( -x right)=-tgleft( x right))
( displaystyle cosleft( -x right)=cosleft( x right))
Первое утверждение мы уже доказали с тобой, а справедливость второго установили совсем недавно.
Непосредственно правило приведения выглядит вот так:
Если мы вычисляем значение тригонометрической функции от отрицательного угла – делаем его положительным при помощи группы формул о четности.
Например:
( displaystyle sinleft( -855{}^circ right)=-sin855{}^circ),
( displaystyle cosleft( -855{}^circ right)=cos855{}^circ).
Отбрасываем для синуса и косинуса его периоды: ( displaystyle 2pi k) (по ( displaystyle 360) градусов), а для тангенса – ( displaystyle pi k) (( displaystyle 180) градусов).
Например:
( displaystyle sin 855{}^circ =sinleft( 2cdot 360{}^circ +135{}^circ right)=sin 135{}^circ )( displaystyle tg 225{}^circ =tgleft( 180{}^circ +45{}^circ right)=tg 45{}^circ )
Если оставшийся «уголок» меньше ( displaystyle 90) градусов, то задача решена: ищем его в «малой таблице».
Иначе ищем, в какой четверти лежит наш угол ( displaystyle alpha ): это будет 2, 3 или 4 четверть. Смотрим, какой знак имеет искомая функция в четверти. Запомнили этот знак!!!
Представляем угол ( displaystyle alpha )в одной из следующих форм:
- ( displaystyle alpha =90+beta ) (если во второй четверти)
- ( displaystyle alpha =180-beta ) (если во второй четверти)
- ( displaystyle alpha =180+beta ) (если в третьей четверти)
- ( displaystyle alpha =270-beta ) (если в третьей четверти)
- ( displaystyle alpha =270+beta ) (если в четвертой четверти)
- ( displaystyle alpha =360-beta ) (если в четвертой четверти)
…так, чтобы оставшийся угол ( displaystyle beta ) был больше нуля и меньше ( displaystyle 90) градусов.
Например:
( displaystyle 135{}^circ =180{}^circ -45{}^circ )
( displaystyle 135{}^circ =90{}^circ +45{}^circ )
( displaystyle 315{}^circ =270{}^circ+45{}^circ )
( displaystyle 240{}^circ =180{}^circ +60{}^circ )
( displaystyle 240{}^circ =270{}^circ -30{}^circ )…
В принципе не важно, в какой из двух альтернативных форм для каждой четверти ты представишь угол. На конечном результате это не скажется.
Теперь смотрим, что у нас получилось: если ты выбрал запись через ( displaystyle 180) или ( displaystyle 360) градусов плюс минус что-либо, то знак функции меняться не будет: ты просто убираешь ( displaystyle 180) или ( displaystyle 360) и записываешь синус, косинус или тангенс оставшегося угла.
Если же ты выбрал запись через ( displaystyle 90) или ( displaystyle 270) градусов, то синус меняем на косинус, косинус на синус, тангенс на котангенс, котангенс – на тангенс.
Ставим перед получившимся выражением знак, который мы запомнили.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
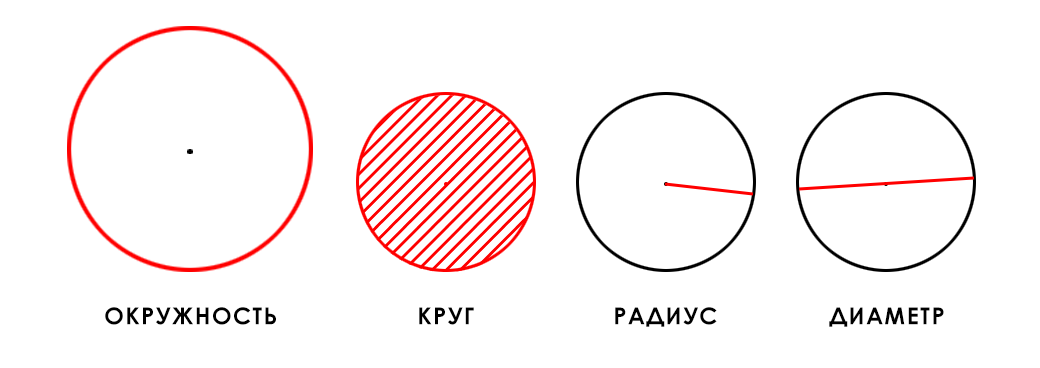
Что такое окружность?
Окружность – это замкнутая плоская кривая, ограничивающая круг.
Или, другими словами, окружность представляет собой множество точек, удаленных на одно и тоже расстояние от центра круга на длину радиуса этого круга. А длина окружности – это длина этой кривой, которую образует это множество точек и которая ограничивает собой круг. Это хорошо видно на иллюстрации выше.
Как найти длину окружности?
Чтобы вычислить длину окружности, нужно знать радиус, диаметр или площадь круга. Причём достаточно только чего-то одного из этих элементов.
По диаметру
Диаметр — это такой отрезок, который соединяет две точки на окружности и проходит через центр круга. Чтобы найти длину окружности через диаметр, просто умножаем диаметр окружности на число Пи и получаем длину окружности.
Формула будет такой:
L = π × d
Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.
Например, нам нужно посчитать периметр канализационной трубы диаметром 100 мм. Окружность этой трубы можно найти весьма несложными расчётами:
L = 3,14 × 100 = 314 мм.
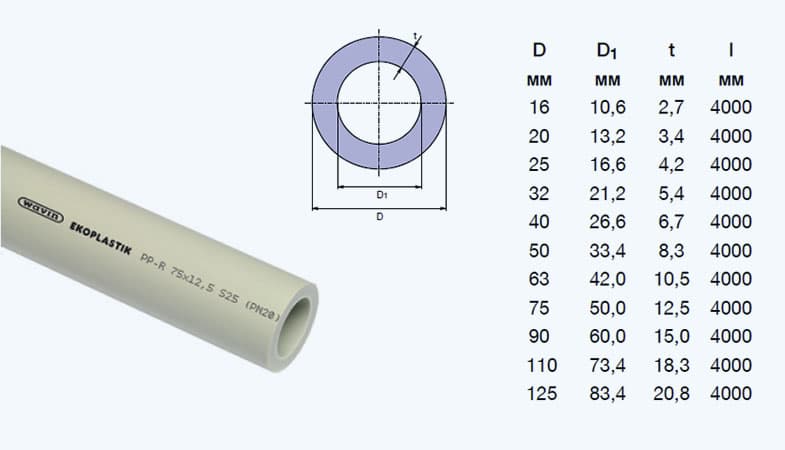
Кстати, у труб есть 2 окружности и 2 диметра: внутренние и внешние. Это хорошо показано на рисунке ниже.
Всегда обращайте внимание, какой именно диаметр известен и какую длину окружности вам требуется вычислить. Часто внутренний диаметр обозначается малой d или D1, а наружный просто – D или DN.
Зная радиус
Радиус окружности — это отрезок, который соединяет центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление длины окружности будет похоже на предыдущий случай: умножаем радиус на два и на число пи и получаем длину окружности.
Формула расчёта выглядит следующим образом:
L = 2π × R
Где L – длина окружности, π – константа (приблизительно 3,14), а r – это радиус.
К примеру, нужно посчитать длину внутренней окружности трубы, с внутренним радиусом 26 мм. В этом случае периметр получается следующим образом:
L = 2 × 3,14 × 26 = 163,28 мм.
Также обратите внимание, что в число Пи взято с точностью до двух знаков после запятой, и всегда расчёт через Пи идёт с округлением и является приблизительным.
Через площадь круга
И, пожалуй, самым редким случаем калькуляции периметра круга будет тот, когда нам известна только площадь этого круга. В этом случае, чтобы рассчитать длину окружности, можно воспользоваться следующей формулой:
L = (4Sπ)1/2
Где L – длина окружности, S – площадь круга, а π – константа, равная 3,14.
То есть длина окружности равна квадратному корню произведения площади круга, числу пи, умноженному на четыре. На всякий случай, корень и степень ½ – это одно и то же.
Возьмём пример, к нам прилетели инопланетяне и оставили круги на полях.
Площадь одного из этих кругов составила аж 1146,5 квадратных метра. Чтобы рассчитать длину окружности, нужно сделать следующее:
- Умножить 4 на 3,14, и полученное произведение умножить на площадь круга 1146,5. Получаем 14400,04.
- И теперь находим квадратный корень из этого числа и получаем примерно 120 метров. Это и есть длина окружности.
Как и в прошлых случаях из-за наличия числа Пи, которое является иррациональным, ответ будет считаться с округлением.
❓Вопросы и ответы
И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.
Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?
Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:
- Площадь круга
- Длина окружности
- Диаметр
- Радиус
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?
Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.
Что такое внутренняя и внешняя окружность? Чем они отличаются?
Внутренняя и внешняя окружность (а также диаметр) чаще всего используются для расчёта параметров труб, у которых есть стенки ненулевой ширины. Поэтому окружность внутри трубы всегда меньше окружности снаружи. Для окружности снаружи используется обозначение L или LN, а диаметра – D или DN. А для периметра и диаметра круга внутри добавляется нижний индекс «единица»: L1 и D1, или используются буквы в нижнем регистре (малые): l и d.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии