Загрузить PDF
Загрузить PDF
Расстояние (обозначим как d) – это длина прямой между двумя точками. Расстояние можно найти между двумя неподвижными точками, а можно найти расстояние, пройденное движущимся телом. В большинстве случаев расстояние может быть вычислено по следующим формулам: d = s × t, где d — расстояние, s – скорость, t – время; d = √((x2 — x1)2 + (y2 — y1)2, где (x1, y1) и (x2, y2) – координаты двух точек.
-
1
Чтобы вычислить расстояние, пройденное движущимся телом, вам необходимо знать скорость тела и время в пути, чтобы подставить их в формулу d = s × t.
- Пример. Автомобиль едет со скоростью 120 км/ч в течение 30 минут. Необходимо вычислить пройденное расстояние.
-
2
Перемножьте скорость и время и вы найдете пройденное расстояние.
- Обратите внимание на единицы измерения величин. Если они различны, вам необходимо конвертировать одну из них так, чтобы она соответствовала другой единице. В нашем примере скорость измеряется в километрах в час, а время – в минутах. Поэтому необходимо конвертировать минуты в часы; для этого значение времени в минутах необходимо разделить на 60 и вы получите значение времени в часах: 30/60 = 0,5 часов.
- В нашем примере: 120 км/ч х 0,5 ч = 60 км. Обратите внимание, что единица измерения «час» сокращается и остается единица измерения «км» (то есть расстояние).
-
3
Описанную формулу можно использовать для вычисления входящих в нее величин. Для этого обособьте нужную величину на одной стороне формулы и подставьте в нее значения двух других величин. Например, для вычисления скорости используйте формулу s = d/t, а для вычисления времени – t = d/s.
- Пример. Автомобиль проехал 60 км за 50 минут. В этом случае его скорость равна s = d/t = 60/50 = 1,2 км/мин.
- Обратите внимание, что результат измеряется в км/мин. Чтобы конвертировать эту единицу измерения в км/ч, умножьте результат на 60 и получите 72 км/ч.
-
4
Данная формула вычисляет среднюю скорость, то есть предполагается, что в течение всего времени в пути тело имеет постоянную (неизменную) скорость. Это годится в случае абстрактных задач и моделирования движения тел. В реальной жизни скорость тела может меняться, то есть тело может ускоряться, замедляться, останавливаться или двигаться в обратном направлении.
- В предыдущем примере мы нашли, что автомобиль, проехавший 60 км за 50 минут, ехал со скоростью 72 км/ч. Это справедливо только при условии, что с течением времени скорость автомобиля не менялась. Например, если в течение 25 минут (0,42 часов) автомобиль ехал со скорость 80 км/ч, а в течение еще 25 минут (0,42 часов) – со скоростью 64 км/час, он тоже проедет 60 км за 50 минут (80 х 0,42 + 64 х 0,42 = 60).
- Для решения задач, включающих меняющуюся скорость тела, лучше использовать производные, а не формулу для вычисления скорости по расстоянию и времени.
Реклама
-
1
Найдите две точки пространственных координат. Если вам даны две неподвижные точки, то, чтобы вычислить расстояние между этими точками, необходимо знать их координаты; в одномерном пространстве (на числовой прямой) вам понадобятся координаты x1 и x2, в двумерном пространстве – координаты (x1,y1) и (x2,y2), в трехмерном пространстве – координаты (x1,y1,z1) и (x2,y2,z2).
-
2
Вычислите расстояние в одномерном пространстве (точки лежат на одной горизонтальной прямой) по формуле: d = |x2 — x1|, то есть вы вычитаете «х» координаты, а затем находите модуль полученного значения.
- Обратите внимание, что в формулу включены скобки модуля (абсолютного значения). Модуль числа – это неотрицательное значение этого числа (то есть модуль отрицательного числа равен этому числу со знаком плюс).
- Пример. Машина находится между двумя городами. До города, который находится перед ней, 5 км, а до города за ней – 1 км. Вычислите расстояние между городами. Если взять машину за точку отсчета (за 0), то координата первого города x1 = 5, а второго x2 = -1. Расстояние между городами:
- d = |x2 — x1|
- = |-1 — 5|
- = |-6| = 6 км.
-
3
Вычислите расстояние в двумерном пространстве по формуле: d = √((x2 — x1)2 + (y2 — y1)2). То есть вы вычитаете «х» координаты, вычитаете «у» координаты, возводите полученные значения в квадрат, складываете квадраты, а затем из полученного значения извлекаете квадратный корень.
- Формула для вычисления расстояния в двумерном пространстве основана на теореме Пифагора, которая гласит, что гипотенуза прямоугольного треугольника равна квадратному корню из суммы квадратов обоих катетов.
- Пример. Найдите расстояние между двумя точками с координатами (3, -10) и (11, 7) (центр окружности и точка на окружности, соответственно).
- d = √((x2 — x1)2 + (y2 — y1)2)
- d = √((11 — 3)2 + (7 — -10)2)
- d = √(64 + 289)
- d = √(353) = 18,79
-
4
Вычислите расстояние в трехмерном пространстве по формуле: d = √((x2 — x1)2 + (y2 — y1)2 + (z2 — z1)2). Эта формула является видоизмененной формулой для вычисления расстояния в двумерном пространстве с добавлением третьей координаты «z».
- Пример. Космонавт находится в открытом космосе недалеко от двух астероидов. Первый из них расположен в 8 километрах перед космонавтом, в 2 км справа от него и в 5 км ниже него; второй астероид находится в 3 км позади космонавта, в 3 км слева от него, и в 4 км выше него. Таким образом, координаты астероидов (8,2,-5) и (-3,-3,4). Расстояние между астероидами вычисляется следующим образом:
- d = √((-3 —
2 + (-3 — 2)2 + (4 — -5)2)
- d = √((-11)2 + (-5)2 + (9)2)
- d = √(121 + 25 + 81)
- d = √(227) = 15,07 км
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 61 245 раз.
Была ли эта статья полезной?
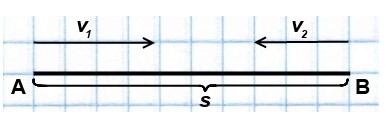
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n
где v1, v2, v3, vn – значения скоростей объекта на отдельных участках пути S,
n – количество этих участков,
vср – средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
vср=(S1+S2+…+Sn)/t,
где vср – средняя скорость объекта на всем протяжении пути,
S1, S2, Sn – отдельные неравномерные участки всего пути,
t – общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
vср=S/(t1+t2+…+tn),
где S – общее пройденное расстояние,
t1, t2, tn – время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn,
где S1/t1, S2/t2, Sn/tn – формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
На чтение 10 мин. Просмотров 6.7k.
Вычислить скорость, время и расстояние часто бывает необходимо в повседневной жизни, когда мы рассчитываем время на дорогу. Все эти величины (время, расстояние и скорость) связаны между собой математической формулой и зная две из них всегда можно найти третью. Мы с вами рассмотрим, что понимается под этими величинами, как их найти, решим несколько задач.
Скорость, время и расстояние — это ключевые параметры при решении задач на движение. Эти задачи есть и в ЕГЭ и в ОГЭ по математике. Сегодня мы подробнее остановимся на этих величинах.
Расстояние
Расстояние — это физическая величина, означающая длину между двумя объектами. Расстояние обозначается буквой S и измеряется в единицах длины: метрах. Метр — это международно-принятая единица измерения длины. Однако встречаются и другие единицы длины — километр, сантиметр, миллиметр. В этом случае целесообразно перевести единицы длины в международную систему единиц (СИ).
Например: расстояние от Земли до Солнца равно 149 597 870 700 метров.
Расстояние связано со скоростью и временем:
S=v cdot t
Вот тут таблица длин и их перевода в международную систему единиц — то есть в метры.
| Единицы длины | СИ |
| 1 сантиметр | 0,01 м |
| 1 километр | 1000 м |
| 1 дециметр | 0,1 м |
| 1 миллиметр | 0,001 м |
| 1 микрометр | 1·10-6 м |
| 1 миля | 1609,34 м |
| 1 фут | 0,3048 м |
| 1 ярд | 0,9144 м |
| 1 дюйм | 0,0254 м |
| 1 морская миля | 1852 м |
Время
Время — это физическая величина, которая обозначает непрерывное и необратимое (возможно) движение от прошлого к будущему через настоящее. Это фундаментальная физическая величина, единица измерения времени — секунда. Однако, в задачах могут использоваться и другие единицы времени — часы, минуты, дни.
Время можно найти по формуле:
t=frac{S}{v}
Ученые о времени
По словам греческого философа Парменида (ок. 450 г. до н.э.), время и движение были иллюзиями. Его ученик Зенон Элейский разработал два знаменитых парадокса: «Ахиллес и черепаха» и «Парадокс летящей стрелы», чтобы доказать его утверждения. Платон, живший на пару поколений позже, считал, что время создано вместе со вселенной и существует независимо. Он рассматривал время как пустой контейнер, который можно заполнить движущимися вещами и событиями. Его ученик Аристотель считал, что время не существует независимо от событий, но время есть изменение и движение.
Аристотель пришел к выводу, что время не состоит из последовательных неделимых моментов «сейчас», как пытался сказать Зенон с помощью своего парадокса стрелы. Согласно Аристотелю, не существует серии моментов «сейчас», потому что такие моменты не могли бы исчезнуть в течение их собственной длительности или в следующий момент «сейчас». Исааку Ньютону (1642–1726) время понадобилось в качестве переменной в его уравнениях, и он начал думать о времени с научной точки зрения. Ньютон поддерживал идею Платона о независимости времени. Он разделил время на абсолютное (математическое) время и относительное (обычное) время.
Абсолютное время, или продолжительность, является реальным и математическим, и оно течет неуклонно, независимо от чего-либо внешнего. Относительное время кажущееся и является внешней мерой длительности, которая может быть обнаружена органами чувств с помощью движения, которое может быть точным или неточным.
Готфрид Лейбниц (1646–1716) был согласен с Аристотелем и думал, что без событий и перемен не было бы времени. Физик- теоретик Ли Смолин писал в 2010 году, что исследования квантовой гравитации подтверждают, что четырехмерное пространство-время имеет смысл только в том случае, если время реально, фундаментально и даже является единственным аспектом реальности, который мы непосредственно ощущаем.
Скорость
Скорость обозначается буквой — это физическая величина, которая обозначает какое расстояние проходит объект в единицу времени. Единица измерения скорости — м/с. Однако, встречаются также и км/ч и см/с (эти измерения не входят в международную систему единиц измерения). Скорость показывает как быстро изменяется расстояние во времени.
Например, выражение 9 м/с означает, что тело за 1 секунду проходит 9 метров. То есть за 1 секунду 9 метров, за 2 секунду еще 9 метров, итого за 2 секунду — 18 метров. В курсе школьной математики мы считаем, что скорость равномерная во времени. То есть тело за равные промежутки времени проходит равные расстояния. То есть 9 м/с означает 9 метров в любую из секунд движения тела. Однако, в реальности движение бывает равномерное и неравномерное. Мы не рассматриваем неравномерное движение в курсе математики (1-6 класс), однако в курсе алгебры элементы кинематики с неравномерным движением рассматриваются.
Еще примеры: скорость 100 км/ч — это прохождение расстояния в 100 километров за 1 час.
Формула скорости
Скорость можно найти через расстояние и время по формуле:
v=frac{S}{t}
Средняя скорость
Если движение тела можно разбить на несколько участков и в пределах каждого участка скорость тела не меняется, то целесообразно говорить о средней скорости.
Формула средней скорости:
v=frac{S_{весь ; путь}}{t_{всё ; время}}=frac{S_1+S_2+…+ S_n}{t_1+t_2+…+ t_n}
То есть средняя скорость это отношение всего пути, ко всему времени.
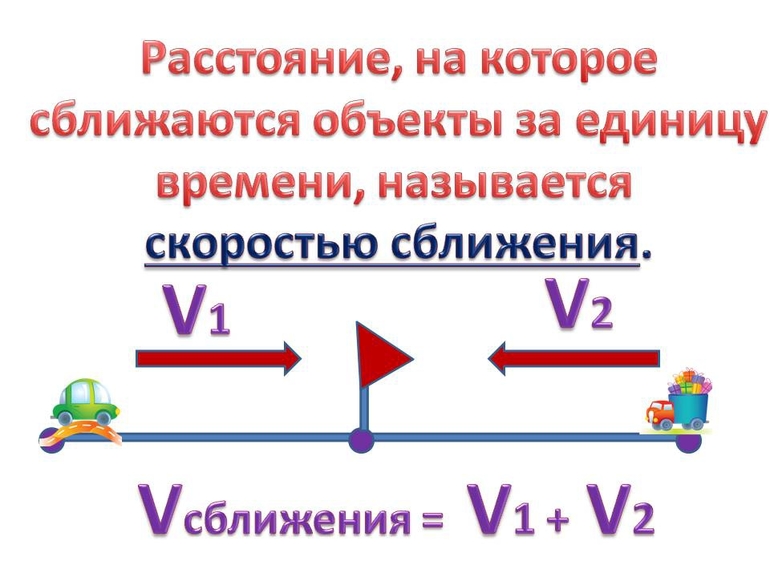
Скорости сближения и удаления
Понятие скорости ученики изучают еще в 4 классе, а далее это понятие расширяется и уточняется. Вводятся такие понятия как скорость сближения и скорость удаления. Не все педагоги используют эти понятия в своей работе, поскольку эти понятия можно использовать только при решении небольшого класса задач на движение и они ограничивают решение задач и другими условиями (например, если тела удаляются или сближаются не по одной прямой, а по перпендикулярным прямым). И все же, давайте мы уточним, о чем вообще идет речь.
Скорость удаления
Если два тела удаляются друг от друга, двигаясь по одной прямой, то в таких случаях говорят о скорости удаления. То есть скорость удаления характеризует расстояние, которое увеличивается по мере удаления двух тел в единицу времени.
Допустим есть два пешехода, которые удаляются друг от друга, первый пешеход удаляется со скоростью 3 км/ч, а второй пешеход со скоростью 4 км/ч. Тогда скорость удаления будет:
3+4=7 км/ч.
Действительно, расстояние, пройденное первым пешеходом за один час будет 3 километра, а расстояние, пройденное вторым пешеходом за то же время будет 4 километра. Тогда при удалении пешеходов друг от друга расстояние между ними увеличивается на 7 километров в каждый час или наши пешеходы удаляются со скоростью 7 км/ч. Мы должны сложить скорости объектов.
Формула скорости удаления:
v_{удаления}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Напомним, что это понятие можно использовать только если тела двигаются в разных направлениях, располагаемых на одной прямой.
Скорость сближения двух тел
Аналогично, рассмотрим ситуацию, если два пешехода двигаются навстречу друг к другу. Один пешеход за один час проходит расстояние 2 км, а второй пешеход за то же время проходит 5 км.
Значит, расстояние между ними будем уменьшаться со скоростью 5+2 = 7 км/ч.
Формула скорости сближения:
v_{сближения}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Если один пешеход догоняет другого. То скорость сближения при движении в одном направлении можно определить, если вычесть из большей скорости меньшую.
То есть, если у нас второго пешехода (=3км/ч) догоняет первый пешеход (
=5 км/ч), то скорость их сближения будет 2 км/ч:
Формула скорости сближения при движении вдогонку:
v_{сближения}=v_1-v_2
где
— скорость одного тела,
— скорость другого тела. При этом
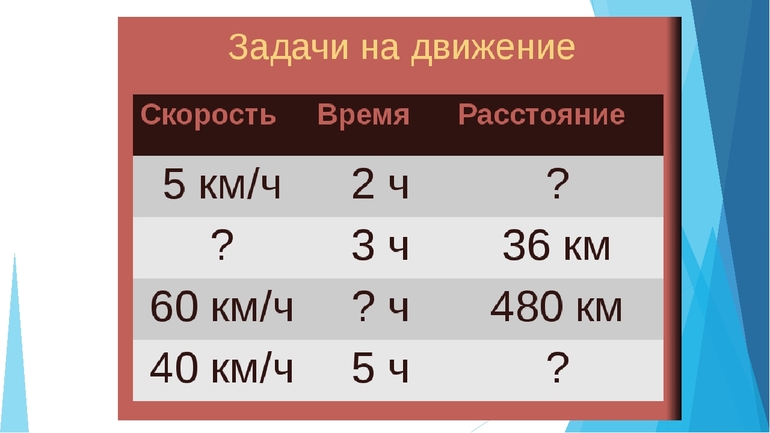
Таблица «скорость, время, расстояние» при решении задач на движение
При решении задач на движение очень удобно пользоваться такой таблицей, в которой три столбца с данными по скорости, времени движения тел и расстоянию, которое они проходят. Эта таблица, кстати помогает легко запомнить формулы скорости, времени и расстояния, если представить что первый столбец — это первый множитель, второй столбец — второй множитель, а третий столбец — произведение.
| Скорость, v, м/с | Время, t, с | Расстояние, S, м |
Простой пример, найти скорость велосипедиста, если за 5 часов он прошел 45 километров.
Составляем таблицу и записываем в нее данные:
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км |
| ? | 5 | 45 |
Теперь видно, что неизвестна скорость в первом столбце, значит, неизвестен первый множитель. Чтобы определить неизвестный множитель надо произведение разделить на известный множитель: = 45/5 = 9 км/ч.
Важно! В задачах все единицы измерения должны быть приведены либо к международной системе единиц (метр, секунда, м/с) либо к одним единицам измерения (то есть если в задаче есть и м/с и км/ч можно привести всё либо к м/с (тогда и время в секундах и расстояние в метрах), либо к км/ч (тогда и время в часах будет и расстояние в километрах))
Рассмотрим теперь некоторые примеры решения задач
Примеры задач на движение
Задача 1
Школьник идет домой со скоростью 2 км/ч. Расстояние от школы до дома 1 км. За какое время школьник дойдет до дома?
Решение:
Найдем время по формуле: displaystyle t=frac{S}{v}=frac{1}{2}ч.
Школьник дойдет до дома за полчаса.
Ответ: 0,5 ч.
Задача 2
Автомобилист и велосипедист выехали в город из деревни одновременно. Скорость автомобилиста 50 км/ч. Расстояние до города 100 км. Какова скорость велосипедиста, если известно, что он прибыл в город на 8 часов позже автомобилиста?
Решение: Составим таблицу
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км | |
| Автомобилист | 50 | 100/50 | 100 |
| Велосипедист | x | 100/x | 100 |
Пусть скорость велосипедиста x. В таблице мы сразу смогли написать соотношения для времени движения. По условию задачи дано, что велосипедист прибыл в город на 8 часов позже автомобилиста. Запишем это:
displaystyle frac{100}{x}-frac{100}{50}=8
Мы отнимаем от времени, которое потратил велосипедист (он же потратил больше времени) время, которое потратил автомобилист и получаем 8 часов.
Решим полученное уравнение.
displaystyle frac{100}{x}-2=8
displaystyle frac{100}{x}=10
x=10
Ответ: 10 км/ч
Задача 3
Стрела пролетает 180 метров за 0,05 минуты. Найдите ее скорость.
Решение: прежде чем решать задачу, переведем все единицы в одну систему единиц. Минуты переведем в секунды.
В одной минуте 60 секунд. Значит, чтобы узнать сколько секунд в 0,05 минутах, умножим 0,05 на 60, получим:
0,05 cdot 60=3 c.
Тогда displaystyle v= frac{180}{3}=60 м/с.
Ответ: 60 м/с
Задача 4
Турист прошел лесной участок длиной 10 км со скоростью 5 км/ч, а затем шел по полю 20 км, со скоростью 4 км/ч. Какова средняя скорость туриста?
Решение:
Определим весь путь который прошел турист:
displaystyle S_{весь ; путь}=S_1+S_2=10+20=30 км.
Для прохождения лесного участка турист потратил: displaystyle t_1= frac{S_1}{v_1}=frac{10}{5}=2ч, а на второй участок времени ушло: displaystyle t_2= frac{S_2}{v_2}=frac{20}{4}=5ч
Все время: displaystyle t_{всё ; время}=t_1+t_2=2+5=7ч
Тогда найдем среднюю скорость:
displaystyle v_{ср}= frac{S_{весь ; путь}}{t_{всё ; время}}=frac{30}{7}=4 frac{2}{7} км/ч.
Ответ: displaystyle v_{ср}=4 frac{2}{7}
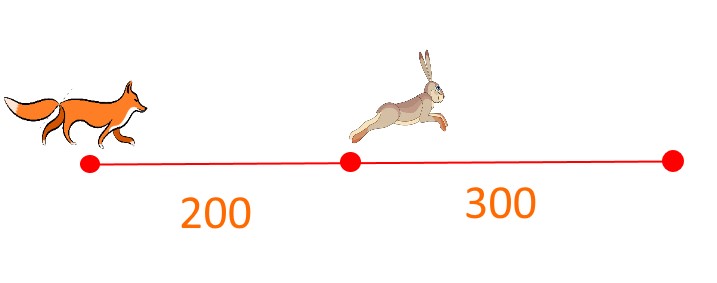
Задача 5
Лиса гонится за зайцем. Скорость лисы 20 м/с, а скорость зайца 15 м/с. Догонит ли лиса зайца, если заяц находится на расстоянии 300 метров от безопасного места, а лиса находится на расстоянии 200 метров от зайца?
Решение:
Заяц добежит до норы за displaystyle t= frac{300}{15}=20 секунд.
Лиса же за 20 секунд пробежит расстояние displaystyle S= 20 cdot 20=400 метров.
Лиса не догонит зайца.
Действительно, скорость сближения лисы и зайца:
displaystyle v=v_{лисы}-v_{зайца}=20-15=5 м/с
То есть, чтобы преодолеть расстояние 200 метров, которое изначально существует между лисой и зайцем, лисе понадобиться displaystyle t=frac{200}{5}=40 с
Заяц же уже 20 секунд будет в безопасном месте.
Ответ: лиса зайца не догонит.
Понятие о времени
Существует характеристика, с которой приходится сталкиваться каждый день вне зависимости от возраста, социального статуса, различных способностей и умений. С её помощью определяют будущее, прошедшее и настоящее. По сути, это маркер, определяющий событие. Называют его временем. Рассматривая движение, всегда учитывают эту характеристику, как и её прогрессию.
Время является частью пространственной координаты. Но если относительно других осей можно перемещаться в различных направлениях, относительно него движение определяется только вперёд или назад. Неотъемлемой частью, связанной со временем, является пространство, благодаря которому и возможно понять суть параметра.
Исследованием характеристики занимались философы и учёные в различные периоды существования человечества. Видеть и слышать время невозможно, в отличие от осязаемого пространства, которое возможно наблюдать сразу и везде. Причём в нём можно перемещаться.
Дискуссии, как правильно воспринимать время, не утихают до сих пор. Платон считал, что оно есть не что иное, как движение. Аристотель предполагал, что время — количественное измерение перемещения. Оно было добавлено к классической геометрии Евклида, действующей на ограниченное число измерений. В итоге стало рассматриваться четырёхмерное пространство.
Сегодня так и нет ответов на следующие вопросы о времени:
- из-за чего происходит его течение;
- почему оно определяется только в одном направлении;
- является ли параметр одномерным, как многие учёные считают;
- можно ли обнаружить кванты характеристики.
В классической физике для определения временного изменения используется специальная координата пространство-время. Принято будущие события обозначать знаком плюс, а прошедшие минусом. Единица измерения времени связана с вращением планеты вокруг своей оси и Солнца. Этот выбор был сделан условно и привязан к удобству жизнедеятельности человечества.
В Международной системе единиц принято за секунду принимать интервал, равный 9 192 631 770 периодам излучения атома цезия-133 в покое при нуле градусов по Кельвину. Обозначают параметр латинской буквой t. Таким образом, время — физическая величина, связанная с перемещением какого-либо тела относительно выбранной системы координат.
Расстояние и скорость
Положение каждой физической точки можно описать с помощью координатных осей. Другими словами, системой, которая по отношению к исследуемому телу остаётся неизменной. Изменение положения относительно другого объекта можно представить пройденным расстоянием. Фактически это путь, для которого известно начало и конец. С физической точки зрения, расстояние — величина, являющаяся размерностью длины, и выражающаяся в её единицах.
В математике мера пройденного пути тесно связана с метрическим пространством, то есть положением, где существует пара (x, d), определённая в декартовом произведении. Соответственно, если координату принять за x, y, можно сказать следующее:
- начало пути и его конец обозначают точками с координатами d (x, y) и p (x, y);
- пройденное расстояние можно определить, отняв из конечных координат начальные;
- изменение положения будет нулевым, когда d = p.
В физике расстояние измеряют единицами длины. В соответствии с СИ за размерность берут метр. Расстояние — мера пройденного пути, то есть длина. Если необходимо просто определить изменение положения без учёта, когда и как оно произошло, используют координатные оси. Но при нахождении пройденного пути за время в формуле для расстояния должна учитываться ещё одна величина — скорость.
Обозначают эту характеристику символом V. Характеризует она быстроту перемещения в выбранной системе отсчёта. По определению скорость равняется производной радиус-вектора точки по времени. Иными словами, это значение, задающееся положением в пространстве относительно неизменной координаты, за которую чаще всего принимается начало.
Одно и то же расстояние можно преодолеть за разное время. Например, чтобы пройти 7 километров человеку понадобится затратить порядка одного часа, на автомобиле же этот путь можно преодолеть за 10 минут, а то и меньше. Вот как раз эти отличия и зависят от скорости движения.
Но на самом деле не всё так однозначно. Скорость необязательно должна быть одинаковой на всём пути. На определённых промежутках она может увеличиваться или уменьшаться, поэтому в математике под её значением понимают среднюю величину. Считается, что тело движется равномерно при прохождении установленного расстояния.
Общая формула
Скорость, время, расстояние — это 3 фундаментальных величины, связанные друг с другом. Исследуя одну характеристику, обязательно нужно учитывать две других. Фактически скорость — это физическая величина, определяющая, какую длину преодолеет физическое тело за единицу времени. Например, значение 120 км/ч показывает, что объект сможет преодолеть 120 километров за один час. В математическом виде связь между тремя характеристиками может быть записана в виде следующей формулы:
S = V * t, где:
- S — пройденное объектом расстояние;
- V — средняя скорость тела;
- t — время, затраченное на преодоление пути.
Зная это равенство и любых 2 параметра, можно выполнить расчёт третьего, так для времени она будет иметь вид t = S / V, а скорости V = S / t. Проверить правильность формулы для скорости времени и расстояния можно путём анализа размерности. Если в выражение подставить единицы измерения, то после сокращения должна получиться величина, соответствующая определяемой. S = V * t = (м / с) * с = м (метр). Что и требовалось получить. Аналогично можно проверить и 2 оставшиеся формулы: t = s / v = м / (м/с) = м * с / м = с (секунда) и V = S / t = м / с (метр на секунду).
Действительно, пусть имеется физическое тело, находящееся в каком-то месте. Через некоторое время, неважно по каким причинам, оно переместилось в другую точку, при этом не выходя за пределы установленного пространства. Если тело представить в декартовой плоскости, причём за начало принять координату (0, 0), через время объект изменит своё положение, определяющееся значением (x1, y2). В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.
Значит, чтобы тело достигло второй координаты, ему необходимо затратить время. При этом пройденный путь будет находиться в прямой зависимости от него. Расстояние и время должны связываться третьей величиной, которой как раз и является скорость. То есть параметр, определяющий, за сколько тело сможет преодолеть определённую длину.
Как видно, выражение, связывающее 3 величины, довольно простое. Но оно не учитывает, что скорость может быть непостоянной, поэтому если объект проходит свой путь неравномерно, в выражение подставляют среднее значение. Находится оно как сумма всех отдельных скоростей на неравномерных участках: Vср = ΔS / Δt.
Решение задач
Чтобы уметь решать простые задания в средних классах по математике, связанных с движением, нужно знать всего одну формулу. При этом необходимо пристальное внимание уделять размерности. Все вычисления осуществляются в СИ. Вот некоторые из типовых заданий, используемые при обучении школьников в четвёртом классе средней школы:
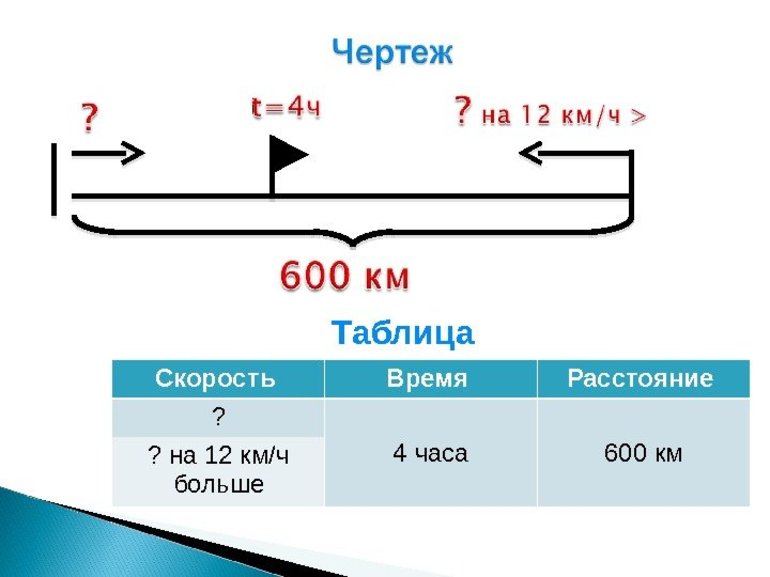
- Из населённого пункта А в точку Б выехала колонна грузовиков. Навстречу им отправился легковой автомобиль. Скорость грузоперевозчиков составляет 80 км/ч, а пассажирской машины 60 км/ч. Встретились они в точке C через полтора часа. Определить расстояние между А и Б. Решение этой задачи будет состоять из нескольких шагов. На первом можно найти путь, который проехала колона: 80 * 1,2 = 96 км. На втором вычислить пройденное расстояние второй: 60 * 1,2 = 72 км. Отсюда общий путь будет равен сумме: АС + СБ = 72 + 96 = 168 км.
- Корабль, скорость которого в стоячих водах равна 30 км/ч, идёт по течению, а после возвращается. Скорость реки равняется трём километрам в час, промежуточная остановка занимает 5 часов. Путь от начала до возврата корабль проходит за 30 часов. Найти, сколько километров составляет весь рейс. Чтобы решить задачу, удобно составить таблицу. В столбцах нужно записать расстояние, скорость и время, а в строках расчётные данные для таких событий, как стоянка, ход по и против течения. Учитывая условие, рабочая формула примет вид: (S / 28) + (S / 22) + 5 = 30. Выражение можно упростить. В итоге должно получиться: 25 * S / 308 = 25 → S = 308. Так как путь корабля состоял из двух одинаковых расстояний, искомое расстояние будет: P = 2 * S = 308 * 2 = 616 км.
- Железнодорожный состав проезжает мост за 45 секунд. Длина переправы составляет 450 метров. При этом стрелочник, смотря прямо, видит проходящий поезд всего 15 секунд. Найти длину состава и скорость его движения. Если принять, что поезд движется со скоростью V, то его длина будет равняться D = 15 * V. Так как состав за 45 секунд проходит расстояние 45 * V = 450 + 15 * V, из равенства легко определить скорость: V = 45 * V – 15 * V = 450 → V = 450 / 3 0 = 15 м / с. Следовательно, длина состава: D = 15 * 15 = 225 м.
Все задачи на движение можно разделить на несколько типов: перемещение навстречу, движение вдогонку, нахождение параметров относительно неподвижного объекта. Но, несмотря на их виды, все они решаются по одинаковому алгоритму, поэтому для удобства можно сделать памятку, указав в ней формулы и размерность величин.
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
v=S/t, где
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
- vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
N=F*v*cos α , где N — механическая мощность,
F — сила,
v — скорость,
cos α — косинус угла между векторами силы и скорости.
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.









 2 + (-3 — 2)2 + (4 — -5)2)
2 + (-3 — 2)2 + (4 — -5)2)